Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T14:36:08.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Survival Probabilities Based on Pareto Claim Distributions: Comment

Published online by Cambridge University Press:  29 August 2014

Marc J. Goovaerts  and
Nelson de Pril
Marc J. Goovaerts
Affiliation:
Instituut voor Actuariële Wetenschappen, K. U. Leuven
Nelson de Pril
Affiliation:
Instituut voor Actuariële Wetenschappen, K. U. Leuven
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper Seal (1980) calculated numerically survival probabilities based on Pareto claim distributions.

The Pareto density may be written as

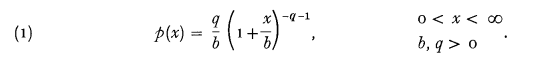
Generalizing, the Pareto distribution may be regarded as a special case of the so-called beta-prime distribution (Keeping, 1962, p. 83) with density function

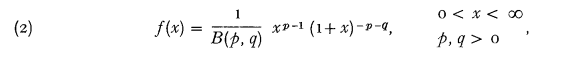
where B(p, q) = 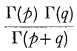is the beta function.

In his paper Seal (1980, Appendix 1) arrived at a contradiction concerning this beta-prime distribution. He found on one side that all derivatives of the characteristic function exist at the origin and on the other side that only the moments of order n < q exist. In this note we will show that this contradiction is due to the use of an incorrect expression for the characteristic function of the beta-prime distribution, which was taken over from Johnson and Kotz (1970, Ch. 26) and Oberhettinger (1973, Table A).

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 11 , Issue 2 , December 1980 , pp. 154 - 157
Copyright
Copyright © International Actuarial Association 1980

References

REFERENCES

Johnson, N. L. and Kotz, S. (1970). Distributions in Statistics: Continuous Univariate Distributions, 2, Wiley, New York.Google Scholar
Keeping, E. S. (1962). Introduction to Statistical Inference, Von Nostrand, Princeton, New Jersey.Google Scholar
Magnus, W., Oberhettinger, F., and Soni, R. P., (1966). Formulas and Theorems for the Special Functions of the Mathematical Physics, Springer, Berlin.CrossRefGoogle Scholar
Oberhettinger, F. (1973). Fourier Transforms of Distributions and Their Inverses, Academic Press, New York.Google Scholar
Seal, H. L. (1980). Survival Probabilities Based on Pareto Claim Distributions, Astin Bulletin, 11, 61–71.CrossRefGoogle Scholar
Slater, L. J. (1960). Confluent Hypergeometric Functions, Cambridge University Press, Cambridge.Google Scholar