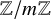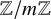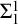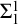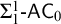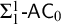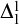240 results in 03BXX
DECIDABLE FRAGMENTS OF THE QUANTIFIED ARGUMENT CALCULUS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 September 2023, pp. 736-761
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALGEBRAIC SEMANTICS FOR RELATIVE TRUTH, AWARENESS, AND POSSIBILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 154-177
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
WEAK WELL ORDERS AND FRAÏSSÉ’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 September 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROOF SYSTEMS FOR TWO-WAY MODAL MU-CALCULUS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 September 2023, pp. 1-50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERLEAVING LOGIC AND COUNTING
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 July 2023, pp. 503-587
- Print publication:
- December 2023
-
- Article
- Export citation
EXTENDED FRAMES AND SEPARATIONS OF LOGICAL PRINCIPLES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 July 2023, pp. 311-353
- Print publication:
- September 2023
-
- Article
- Export citation
Decidability of the class of all the rings
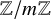 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONNEXIVE IMPLICATIONS IN SUBSTRUCTURAL LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 878-909
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
TESTING DEFINITIONAL EQUIVALENCE OF THEORIES VIA AUTOMORPHISM GROUPS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1097-1118
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
SUBJECT-MATTER AND INTENSIONAL OPERATORS III: STATE-SENSITIVE SUBJECT-MATTER AND TOPIC SUFFICIENCY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 1070-1096
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
RELEVANT CONSEQUENCE RELATIONS: AN INVITATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 June 2023, pp. 762-792
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IS CANTOR’S THEOREM A DIALETHEIA? VARIATIONS ON A PARACONSISTENT APPROACH TO CANTOR’S THEOREM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 860-877
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
AN EGOCENTRIC LOGIC OF KNOWING HOW TO TELL THEM APART
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIG IN REVERSE MATHEMATICS: THE UNCOUNTABILITY OF THE REALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1607-1640
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE AXIOMATIZABILITY OF TRANSITIVE MODAL LOGICS OF FINITE DEPTH AND WIDTH WITH RESPECT TO PROPER-SUCCESSOR-EQUIVALENCE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 951-964
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
THE STRENGTH OF AN AXIOM OF FINITE CHOICE FOR BRANCHES IN TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1367-1386
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNPRINCIPLED
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 435-474
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FIRST-ORDER FRIENDLINESS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1055-1069
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-CONTRACTIVE LOGICS, PARADOXES, AND MULTIPLICATIVE QUANTIFIERS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 996-1017
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HYBRID PARTIAL TYPE THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1-43
-
- Article
- Export citation