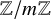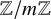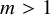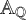1 Introduction
In his classical 1968 paper on the first-order theory of finite fields, Ax asked if the first-order theory of the class of all the rings
![]() $\mathbb {Z}/m\mathbb {Z}$
, for all
$\mathbb {Z}/m\mathbb {Z}$
, for all
![]() $m>1$
, is decidable [Reference Ax1, Problem 5, p. 270]. In that paper, Ax proved that the existential theory of this class is decidable. He proved this via his result that the theory of the class of all the rings
$m>1$
, is decidable [Reference Ax1, Problem 5, p. 270]. In that paper, Ax proved that the existential theory of this class is decidable. He proved this via his result that the theory of the class of all the rings
![]() $\mathbb {Z}/p^n\mathbb {Z}$
(p and n varying) is decidable. This used Chebotarev’s density theorem.
$\mathbb {Z}/p^n\mathbb {Z}$
(p and n varying) is decidable. This used Chebotarev’s density theorem.
In this paper, we give a positive solution to Ax’s problem using our work on the model theory of adeles in [Reference Derakhshan and Macintyre6]. We use our coding of the Boolean algebra of subsets of the index set
![]() $\{\mathrm {Primes}\}\cup \{\infty \}$
in terms of idempotents in
$\{\mathrm {Primes}\}\cup \{\infty \}$
in terms of idempotents in
![]() $\mathbb {A}_{\mathbb {Q}}$
together with definability in the language of rings of the set of idempotents in
$\mathbb {A}_{\mathbb {Q}}$
together with definability in the language of rings of the set of idempotents in
![]() $\mathbb {A}_{\mathbb {Q}}$
with finite support to reduce Ax’s problem to the decidability of
$\mathbb {A}_{\mathbb {Q}}$
with finite support to reduce Ax’s problem to the decidability of
![]() $\mathbb {A}_{\mathbb {Q}}$
proved first by Weispfenning [Reference Weispfenning8] and later us [Reference Derakhshan and Macintyre6].
$\mathbb {A}_{\mathbb {Q}}$
proved first by Weispfenning [Reference Weispfenning8] and later us [Reference Derakhshan and Macintyre6].
2 Definability in adele rings
In this section, we state some results and concepts from [Reference Derakhshan and Macintyre6],[Reference Derakhshan and Macintyre5] on adele rings that we shall use. We only need the case
![]() $K=\mathbb {Q}$
and state the required results in this case. We denote the language of rings by
$K=\mathbb {Q}$
and state the required results in this case. We denote the language of rings by
![]() $\mathcal {L}_{rings}=\{+,-,\cdot ,0,1\}$
.
$\mathcal {L}_{rings}=\{+,-,\cdot ,0,1\}$
.
![]() $\mathbb {Q}_p$
denotes the field of p-adic numbers,
$\mathbb {Q}_p$
denotes the field of p-adic numbers,
![]() $v_p(x)$
the p-adic valuation on
$v_p(x)$
the p-adic valuation on
![]() $\mathbb {Q}_p$
and
$\mathbb {Q}_p$
and
![]() $\mathbb {Z}_p:=\{x\in \mathbb {Q}_p: v_p(x)\geq 0\}$
the valuation ring.
$\mathbb {Z}_p:=\{x\in \mathbb {Q}_p: v_p(x)\geq 0\}$
the valuation ring.
2.1 Adeles
![]() $\mathbb {A}_{\mathbb {Q}}$
denotes the ring of adeles of
$\mathbb {A}_{\mathbb {Q}}$
denotes the ring of adeles of
![]() $\mathbb {Q}$
and is defined as the restricted direct product of all the completions of
$\mathbb {Q}$
and is defined as the restricted direct product of all the completions of
![]() $\mathbb {Q}$
over the index set
$\mathbb {Q}$
over the index set
![]() $V_{\mathbb {Q}}=\{\infty ,2,3, \ldots \}$
, the set of all primes p together with
$V_{\mathbb {Q}}=\{\infty ,2,3, \ldots \}$
, the set of all primes p together with
![]() $\infty $
. It is the subring of the direct product of the real field
$\infty $
. It is the subring of the direct product of the real field
![]() $\mathbb {R}$
and all the p-adic fields
$\mathbb {R}$
and all the p-adic fields
![]() $\mathbb {Q}_p$
for all primes p consisting of all the elements f such that
$\mathbb {Q}_p$
for all primes p consisting of all the elements f such that
![]() $f(p)$
is in
$f(p)$
is in
![]() $\mathbb {Z}_p$
for all but finitely many p.
$\mathbb {Z}_p$
for all but finitely many p.
See Cassels and Frohlich [Reference Cassels and Fröhlich3], and especially Cassels’ article [Reference Cassels2], for properties of adele rings.
We shall construe adeles as functions on
![]() $V_{\mathbb {Q}}$
taking values in the stalks
$V_{\mathbb {Q}}$
taking values in the stalks
![]() $\mathbb {Q}_p$
, where
$\mathbb {Q}_p$
, where
![]() $p\in V_{\mathbb {Q}}$
.
$p\in V_{\mathbb {Q}}$
.
To
![]() $\infty $
corresponds the real field
$\infty $
corresponds the real field
![]() $\mathbb {R}$
and to finite p correspond
$\mathbb {R}$
and to finite p correspond
![]() $\mathbb {Q}_p$
. One sets
$\mathbb {Q}_p$
. One sets
![]() $\mathbb {Q}_{\infty }=\mathbb {R}$
.
$\mathbb {Q}_{\infty }=\mathbb {R}$
.
2.2 Uniform definition of valuation
Each of the stalks
![]() $\mathbb {Q}_p$
, where
$\mathbb {Q}_p$
, where
![]() $p\leq \infty $
, is a locally compact field of characteristic
$p\leq \infty $
, is a locally compact field of characteristic
![]() $0$
, with a canonical choice of metric, and thus a canonical choice of unit ball (which is a subring in the case of
$0$
, with a canonical choice of metric, and thus a canonical choice of unit ball (which is a subring in the case of
![]() $p<\infty $
).
$p<\infty $
).
The following theorem shows that the unit ball
![]() $\mathbb {Z}_p$
is uniformly
$\mathbb {Z}_p$
is uniformly
![]() $\mathcal {L}_{rings}$
-definable without parameters in
$\mathcal {L}_{rings}$
-definable without parameters in
![]() $\mathbb {Q}_p$
for all
$\mathbb {Q}_p$
for all
![]() $p<\infty $
. Note that the unit ball in
$p<\infty $
. Note that the unit ball in
![]() $\mathbb {R}$
is also
$\mathbb {R}$
is also
![]() $\mathcal {L}_{rings}$
-definable.
$\mathcal {L}_{rings}$
-definable.
Theorem 2.1 [Reference Cluckers, Derakhshan, Leenknegt and Macintyre4, Theorem 2].
There is an
![]() $\mathcal {L}_{rings}$
-formula
$\mathcal {L}_{rings}$
-formula
![]() $\Phi _{val}(x)$
without parameters that uniformly defines the valuation ring of all Henselian valued fields with finite or pseudo-finite residue field.
$\Phi _{val}(x)$
without parameters that uniformly defines the valuation ring of all Henselian valued fields with finite or pseudo-finite residue field.
2.3 The Boolean algebra
We denote the language of Boolean algebras by
![]() $\{\wedge ,\vee ,\neg ,0,1\}$
. The set
$\{\wedge ,\vee ,\neg ,0,1\}$
. The set
![]() $\mathbb {B}_{\mathbb {Q}}=\{e\in \mathbb {A}_{\mathbb {Q}}: a^2=a\}$
of idempotents in
$\mathbb {B}_{\mathbb {Q}}=\{e\in \mathbb {A}_{\mathbb {Q}}: a^2=a\}$
of idempotents in
![]() $\mathbb {A}_{\mathbb {Q}}$
forms a Boolean algebra with Boolean operations
$\mathbb {A}_{\mathbb {Q}}$
forms a Boolean algebra with Boolean operations
![]() $\mathbb {B}_{\mathbb {Q}}$
carries a partial order defined by
$\mathbb {B}_{\mathbb {Q}}$
carries a partial order defined by
![]() $e\leq f$
if and only if
$e\leq f$
if and only if
![]() $e=ef$
(product in the ring).
$e=ef$
(product in the ring).
An idempotent e is called minimal if it is nonzero and minimal with respect to this order. Let
![]() $\mathrm {atom}(x)$
be an
$\mathrm {atom}(x)$
be an
![]() $\mathcal {L}_{rings}$
-formula expressing that x is a minimal idempotent (i.e., an atom).
$\mathcal {L}_{rings}$
-formula expressing that x is a minimal idempotent (i.e., an atom).
There is a bijective correspondence between subsets of
![]() $V_{\mathbb {Q}}$
and idempotents e in
$V_{\mathbb {Q}}$
and idempotents e in
![]() $\Bbb A_{\mathbb {Q}}$
given by
$\Bbb A_{\mathbb {Q}}$
given by
![]() $X \longmapsto e_X$
, where for
$X \longmapsto e_X$
, where for
![]() $X\subseteq V_{\mathbb {Q}}$
,
$X\subseteq V_{\mathbb {Q}}$
,
 $$ \begin{align*}e_X(p)=\begin{cases} 1 & \text{if }p\in X,\\ 0 & \text{if }p\notin X. \end{cases}\end{align*} $$
$$ \begin{align*}e_X(p)=\begin{cases} 1 & \text{if }p\in X,\\ 0 & \text{if }p\notin X. \end{cases}\end{align*} $$
Conversely, if
![]() $e\in \Bbb A_{\mathbb {Q}}$
is idempotent, let
$e\in \Bbb A_{\mathbb {Q}}$
is idempotent, let
![]() $X=\{p\in V_{\mathbb {Q}}: e(p)=1\}$
. Then
$X=\{p\in V_{\mathbb {Q}}: e(p)=1\}$
. Then
![]() $e=e_{X}$
.
$e=e_{X}$
.
2.4 Idempotents with finite support
The support of an adele
![]() $a\in \mathbb {A}_{\mathbb {Q}}$
is defined by
$a\in \mathbb {A}_{\mathbb {Q}}$
is defined by
We denote by
![]() $\mathcal {F}in_{\mathbb {Q}}$
the set of all idempotents e in
$\mathcal {F}in_{\mathbb {Q}}$
the set of all idempotents e in
![]() $\mathbb {A}_{\mathbb {Q}}$
with finite support, that is,
$\mathbb {A}_{\mathbb {Q}}$
with finite support, that is,
![]() $\mathrm {supp}(e)$
is a finite set.
$\mathrm {supp}(e)$
is a finite set.
A basic result in the model theory of adeles [Reference Derakhshan and Macintyre6] is the following.
Theorem 2.2 [Reference Derakhshan and Macintyre6].
![]() $\mathcal {F}in_{\mathbb {Q}}$
is an
$\mathcal {F}in_{\mathbb {Q}}$
is an
![]() $\mathcal {L}_{rings}$
-definable subset of
$\mathcal {L}_{rings}$
-definable subset of
![]() $\mathbb {A}_{\mathbb {Q}}$
.
$\mathbb {A}_{\mathbb {Q}}$
.
2.5 Boolean values
If
![]() $e\in \mathbb {A}_{\mathbb {Q}}$
is a minimal idempotent, then the ring
$e\in \mathbb {A}_{\mathbb {Q}}$
is a minimal idempotent, then the ring
![]() $\Bbb A_{\mathbb {Q}}/(1-e)\Bbb A_{\mathbb {Q}}$
is naturally isomorphic to
$\Bbb A_{\mathbb {Q}}/(1-e)\Bbb A_{\mathbb {Q}}$
is naturally isomorphic to
![]() $e\Bbb A_{\mathbb {Q}}$
by the map
$e\Bbb A_{\mathbb {Q}}$
by the map
and if e corresponds to the prime
![]() $p\in \{\mathrm {Primes}\}\cup \{\infty \}$
, then
$p\in \{\mathrm {Primes}\}\cup \{\infty \}$
, then
via the map
For an
![]() $\mathcal {L}_{\mathrm {{rings}}}$
-formula
$\mathcal {L}_{\mathrm {{rings}}}$
-formula
![]() $\Phi (x_1,\dots ,x_n)$
and
$\Phi (x_1,\dots ,x_n)$
and
![]() $a_1,\dots ,a_n\in \Bbb A_{\mathbb {Q}}$
, the (ring-theoretic) Boolean value
$a_1,\dots ,a_n\in \Bbb A_{\mathbb {Q}}$
, the (ring-theoretic) Boolean value
![]() $[[\Phi (a_1,\dots ,a_n)]]$
is defined to be the supremum of all the minimal idempotents e in
$[[\Phi (a_1,\dots ,a_n)]]$
is defined to be the supremum of all the minimal idempotents e in
![]() $\Bbb B_{\mathbb {Q}}$
such that
$\Bbb B_{\mathbb {Q}}$
such that
This supremum exists since
![]() $\mathbb {B}_{\mathbb {Q}}$
is a complete Boolean algebra.
$\mathbb {B}_{\mathbb {Q}}$
is a complete Boolean algebra.
For any given
![]() $\mathcal {L}_{rings}$
-formula
$\mathcal {L}_{rings}$
-formula
![]() $\Phi (x_1,\dots ,x_n)$
, there is another
$\Phi (x_1,\dots ,x_n)$
, there is another
![]() $\mathcal {L}_{rings}$
-formula
$\mathcal {L}_{rings}$
-formula
![]() $\Phi ^*(y,x_1,\dots ,x_n)$
, that can be effectively constructed from
$\Phi ^*(y,x_1,\dots ,x_n)$
, that can be effectively constructed from
![]() $\Phi (x_1,\dots ,x_n)$
, such that for any
$\Phi (x_1,\dots ,x_n)$
, such that for any
![]() $a_1,\dots ,a_n\in \mathbb {A}_{\mathbb {Q}}$
we have
$a_1,\dots ,a_n\in \mathbb {A}_{\mathbb {Q}}$
we have
This follows by induction on the complexity of
![]() $\Phi (x_1,\dots ,x_n)$
from the quantifier-free case which is straightforward.
$\Phi (x_1,\dots ,x_n)$
from the quantifier-free case which is straightforward.
The function from
![]() $\mathbb {A}_{\mathbb {Q}}^n$
into
$\mathbb {A}_{\mathbb {Q}}^n$
into
![]() $\mathbb {B}_{\mathbb {Q}}$
defined by
$\mathbb {B}_{\mathbb {Q}}$
defined by
is
![]() $\mathcal {L}_{\mathrm {{rings}}}$
-definable for any
$\mathcal {L}_{\mathrm {{rings}}}$
-definable for any
![]() $\Phi (x_1,\dots ,x_n)$
.
$\Phi (x_1,\dots ,x_n)$
.
Indeed, the set
where
is definable since by
![]() $(*)$
,
$(*)$
,
![]() $W_{x_1,\dots ,x_n}$
equals
$W_{x_1,\dots ,x_n}$
equals
and thus Z is defined by the formula
(which is expressible as an
![]() $\mathcal {L}_{rings}$
-formula since the ordering on
$\mathcal {L}_{rings}$
-formula since the ordering on
![]() $\mathbb {B}_{\mathbb {Q}}$
is
$\mathbb {B}_{\mathbb {Q}}$
is
![]() $\mathcal {L}_{rings}$
-definable).
$\mathcal {L}_{rings}$
-definable).
Let
![]() $\Psi _{\mathbb {R}}$
denote a sentence that holds in
$\Psi _{\mathbb {R}}$
denote a sentence that holds in
![]() $\mathbb {R}$
but does not hold in any
$\mathbb {R}$
but does not hold in any
![]() $\mathbb {Q}_p$
for
$\mathbb {Q}_p$
for
![]() $p<\infty $
, for example
$p<\infty $
, for example
We call a minimal idempotent e real if
![]() $e\mathbb {A}_{\mathbb {Q}}\models \Psi _{\mathbb {R}}$
.
$e\mathbb {A}_{\mathbb {Q}}\models \Psi _{\mathbb {R}}$
.
We denote by
![]() $e_{\mathbb {R}}$
the supremum of all the real minimal idempotents (note that there is only one real minimal idempotent in
$e_{\mathbb {R}}$
the supremum of all the real minimal idempotents (note that there is only one real minimal idempotent in
![]() $\mathbb {B}_{\mathbb {Q}}$
).
$\mathbb {B}_{\mathbb {Q}}$
).
![]() $e_{\mathbb {R}}$
is supported only on the set
$e_{\mathbb {R}}$
is supported only on the set
![]() $\{\infty \}$
.
$\{\infty \}$
.
We put
![]() $e_{fin}:=1-e_{\mathbb {R}}$
. This idempotent is supported on the set of all primes except infinity.
$e_{fin}:=1-e_{\mathbb {R}}$
. This idempotent is supported on the set of all primes except infinity.
We define
![]() $[[\Phi (a_1,\cdots ,a_n)]]^{real}$
to be the supremum of all the minimal idempotents e such that
$[[\Phi (a_1,\cdots ,a_n)]]^{real}$
to be the supremum of all the minimal idempotents e such that
Let
![]() $\Psi _{fin}$
denote an
$\Psi _{fin}$
denote an
![]() $\mathcal {L}_{rings}$
-sentence that holds in
$\mathcal {L}_{rings}$
-sentence that holds in
![]() $\mathbb {Q}_p$
for all
$\mathbb {Q}_p$
for all
![]() $p<\infty $
and does not hold in
$p<\infty $
and does not hold in
![]() $\mathbb {R}$
. For example, we can take
$\mathbb {R}$
. For example, we can take
![]() $\Psi _{fin}$
to be the negation of the
$\Psi _{fin}$
to be the negation of the
![]() $\Psi _{\mathbb {R}}$
given above, namely
$\Psi _{\mathbb {R}}$
given above, namely
which is true in any p-adic field
![]() $\mathbb {Q}_p$
by taking x to be p.
$\mathbb {Q}_p$
by taking x to be p.
We define
![]() $[[\Phi (a_1,\cdots ,a_n)]]^{fin}$
to be the supremum of all the minimal idempotents e such that
$[[\Phi (a_1,\cdots ,a_n)]]^{fin}$
to be the supremum of all the minimal idempotents e such that
An argument similar to that above on the definability of the Boolean value
![]() $[[\Phi (x_1,\dots ,x_n)]]$
shows that the functions given by
$[[\Phi (x_1,\dots ,x_n)]]$
shows that the functions given by
from
![]() $\mathbb {A}_{\mathbb {Q}}^n$
into
$\mathbb {A}_{\mathbb {Q}}^n$
into
![]() $\mathbb {B}_{\mathbb {Q}}$
are
$\mathbb {B}_{\mathbb {Q}}$
are
![]() $\mathcal {L}_{\mathrm {{rings}}}$
-definable for any
$\mathcal {L}_{\mathrm {{rings}}}$
-definable for any
![]() $\Phi (x_1,\dots ,x_n)$
.
$\Phi (x_1,\dots ,x_n)$
.
We remark that the definability of
![]() $\mathcal {F}in_{\mathbb {Q}}$
in Theorem 2.2 together with the definability of the Boolean values
$\mathcal {F}in_{\mathbb {Q}}$
in Theorem 2.2 together with the definability of the Boolean values
![]() $[[\Phi (x_1,\dots ,x_n)]]$
imply the definability of the sets of the form
$[[\Phi (x_1,\dots ,x_n)]]$
imply the definability of the sets of the form
which occur as ‘basic’ sets in the quantifier elimination theorem for adele rings in [Reference Derakhshan and Macintyre6].
3 Ax’s problem
Theorem 3.1. The class of all
![]() $\mathbb {Z}/m\mathbb {Z}$
is uniformly interpretable in
$\mathbb {Z}/m\mathbb {Z}$
is uniformly interpretable in
![]() $\mathbb {A}_{\mathbb {Q}}$
.
$\mathbb {A}_{\mathbb {Q}}$
.
Proof. Our proof consists of two parts.
Part 1. By uniform definability of the
![]() $\mathbb {Z}_p$
in
$\mathbb {Z}_p$
in
![]() $\mathbb {Q}_p$
for
$\mathbb {Q}_p$
for
![]() $p<\infty $
using the formula
$p<\infty $
using the formula
![]() $\Phi _{\mathrm {val}}(x)$
, the set of elements of
$\Phi _{\mathrm {val}}(x)$
, the set of elements of
![]() $\mathbb {A}_{\mathbb {Q}}$
whose
$\mathbb {A}_{\mathbb {Q}}$
whose
![]() $\mathbb {Q}_p$
-component lies in
$\mathbb {Q}_p$
-component lies in
![]() $\mathbb {Z}_p$
for each
$\mathbb {Z}_p$
for each
![]() $p<\infty $
is definable since it equals
$p<\infty $
is definable since it equals
(and is isomorphic to
![]() $\mathbb {R} \times \widehat {\mathbb {Z}}$
).
$\mathbb {R} \times \widehat {\mathbb {Z}}$
).
Consider a positive integer m. Suppose m factors as a nontrivial product of coprime prime powers
![]() $q_j^{r_j}$
.
$q_j^{r_j}$
.
Consider the element g which takes value
![]() $1$
at all minimal idempotents (including that corresponding to the infinite place
$1$
at all minimal idempotents (including that corresponding to the infinite place
![]() $\infty $
) except those corresponding to the
$\infty $
) except those corresponding to the
![]() $q_j$
, and takes value
$q_j$
, and takes value
![]() $q_j^{r_j}$
at
$q_j^{r_j}$
at
![]() $q_j$
. Then
$q_j$
. Then
![]() $g-1$
is an element of finite support (and the stated conditions on g can be expressed by
$g-1$
is an element of finite support (and the stated conditions on g can be expressed by
![]() $\mathcal {L}_{rings}$
-formulas).
$\mathcal {L}_{rings}$
-formulas).
The quotient
![]() $(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
is naturally isomorphic to the product over the finitely many j of the quotients
$(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
is naturally isomorphic to the product over the finitely many j of the quotients
![]() $\mathbb {Z}_{q_j} / q_{j}^{r_j}\mathbb {Z}_{q_j}$
, and this is isomorphic to the product of the finitely many
$\mathbb {Z}_{q_j} / q_{j}^{r_j}\mathbb {Z}_{q_j}$
, and this is isomorphic to the product of the finitely many
![]() $\mathbb {Z}/q_{j}^{r_j}\mathbb {Z}$
, which is obviously isomorphic to
$\mathbb {Z}/q_{j}^{r_j}\mathbb {Z}$
, which is obviously isomorphic to
![]() $\mathbb {Z}/m\mathbb {Z}$
. Note that the set of all g satisfying the conditions above is
$\mathbb {Z}/m\mathbb {Z}$
. Note that the set of all g satisfying the conditions above is
![]() $\mathcal {L}_{rings}$
-definable in
$\mathcal {L}_{rings}$
-definable in
![]() $\mathbb {A}_{\mathbb {Q}}$
.
$\mathbb {A}_{\mathbb {Q}}$
.
Part 2. Suppose
![]() $g-1$
is an element of finite support. In addition, suppose that g takes values in
$g-1$
is an element of finite support. In addition, suppose that g takes values in
![]() $\mathbb {Z}_p$
for all
$\mathbb {Z}_p$
for all
![]() $p<\infty $
and at some prime
$p<\infty $
and at some prime
![]() $p<\infty $
, g takes as value a p-adic nonunit. These conditions can be stated as
$p<\infty $
, g takes as value a p-adic nonunit. These conditions can be stated as
and
where
![]() $0$
denotes the zero element of the Boolean algebra
$0$
denotes the zero element of the Boolean algebra
![]() $\mathbb {B}_{\mathbb {Q}}$
and
$\mathbb {B}_{\mathbb {Q}}$
and
![]() $1$
denotes the top element of the Boolean algebra
$1$
denotes the top element of the Boolean algebra
![]() $\mathbb {B}_{\mathbb {Q}}$
(namely, the adele with
$\mathbb {B}_{\mathbb {Q}}$
(namely, the adele with
![]() $1$
at every coordinate). These conditions can be expressed by
$1$
at every coordinate). These conditions can be expressed by
![]() $\mathcal {L}_{rings}$
-formulas (using Theorem 2.2).
$\mathcal {L}_{rings}$
-formulas (using Theorem 2.2).
Then g takes value
![]() $1$
at all but finitely many elements of
$1$
at all but finitely many elements of
![]() $V_{\mathbb {Q}}$
. Assume that g takes value
$V_{\mathbb {Q}}$
. Assume that g takes value
![]() $1$
at the infinite prime, and note that this is a definable condition on g since the set
$1$
at the infinite prime, and note that this is a definable condition on g since the set
is
![]() $\mathcal {L}_{rings}$
-definable in
$\mathcal {L}_{rings}$
-definable in
![]() $\mathbb {A}_{\mathbb {Q}}$
(since
$\mathbb {A}_{\mathbb {Q}}$
(since
![]() $h(\infty )=1$
is equivalent to
$h(\infty )=1$
is equivalent to
![]() $e_{\mathbb {R}}h=e_{\mathbb {R}}$
).
$e_{\mathbb {R}}h=e_{\mathbb {R}}$
).
Now, consider
![]() $(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
. It is clear that this quotient is a product over finitely many primes
$(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
. It is clear that this quotient is a product over finitely many primes
![]() $q_j$
of quotients of
$q_j$
of quotients of
![]() $\mathbb {Z}_{q_j}$
by the ideal generated by an element of
$\mathbb {Z}_{q_j}$
by the ideal generated by an element of
![]() $\mathbb {Z}_{q_j}$
. When that element is a unit the quotient is the trivial ring and can be discarded. For at least one prime, the element is not a unit and then generates the same ideal as some power of the prime
$\mathbb {Z}_{q_j}$
. When that element is a unit the quotient is the trivial ring and can be discarded. For at least one prime, the element is not a unit and then generates the same ideal as some power of the prime
![]() $q_j$
. Then as in Part 1,
$q_j$
. Then as in Part 1,
![]() $(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
is isomorphic to
$(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
is isomorphic to
![]() $\mathbb {Z}/m\mathbb {Z}$
for some
$\mathbb {Z}/m\mathbb {Z}$
for some
![]() $m>1$
.
$m>1$
.
The assumptions imposed on g are all
![]() $\mathcal {L}_{rings}$
-definable in
$\mathcal {L}_{rings}$
-definable in
![]() $\mathbb {A}_{\mathbb {Q}}$
because of the
$\mathbb {A}_{\mathbb {Q}}$
because of the
![]() $\mathcal {L}_{rings}$
-definability of
$\mathcal {L}_{rings}$
-definability of
![]() $\mathcal {F}in_{\mathbb {Q}}$
and of the Boolean values in
$\mathcal {F}in_{\mathbb {Q}}$
and of the Boolean values in
![]() $\mathbb {A}_{\mathbb {Q}}$
, and the uniform
$\mathbb {A}_{\mathbb {Q}}$
, and the uniform
![]() $\mathcal {L}_{rings}$
-definability of
$\mathcal {L}_{rings}$
-definability of
![]() $\mathbb {Z}_p$
in
$\mathbb {Z}_p$
in
![]() $\mathbb {Q}_p$
(Theorems 2.1 and 2.2).
$\mathbb {Q}_p$
(Theorems 2.1 and 2.2).
This argument gives the intended interpretation of the class of all
![]() $\mathbb {Z}/m\mathbb {Z}$
(for all
$\mathbb {Z}/m\mathbb {Z}$
(for all
![]() $m>1$
) in
$m>1$
) in
![]() $\mathbb {A}_{\mathbb {Q}}$
.
$\mathbb {A}_{\mathbb {Q}}$
.
Corollary 3.1. The class of all
![]() $\mathbb {Z}/m\mathbb {Z}$
(
$\mathbb {Z}/m\mathbb {Z}$
(
![]() $m>1$
) is decidable.
$m>1$
) is decidable.
Proof. Let
![]() $\mathfrak {X}$
denote the set of all g in
$\mathfrak {X}$
denote the set of all g in
![]() $\mathbb {A}_{\mathbb {Q}}$
such that
$\mathbb {A}_{\mathbb {Q}}$
such that
![]() $g-1$
has finite support, g takes value
$g-1$
has finite support, g takes value
![]() $1$
at the infinite prime, g takes values in
$1$
at the infinite prime, g takes values in
![]() $\mathbb {Z}_p$
for all
$\mathbb {Z}_p$
for all
![]() $p<\infty $
, and g takes as value a p-adic nonunit at some
$p<\infty $
, and g takes as value a p-adic nonunit at some
![]() $p<\infty $
. By Part 2 of the proof of Theorem 3.1,
$p<\infty $
. By Part 2 of the proof of Theorem 3.1,
![]() $\mathfrak {X}$
is an
$\mathfrak {X}$
is an
![]() $\mathcal {L}_{rings}$
-definable subset of
$\mathcal {L}_{rings}$
-definable subset of
![]() $\mathbb {A}_{\mathbb {Q}}$
.
$\mathbb {A}_{\mathbb {Q}}$
.
By Parts 1 and 2 of the proof of Theorem 3.1, any ring from the class
![]() $\{\mathbb {Z}/m\mathbb {Z}: m>1\}$
is isomorphic to a ring from the class
$\{\mathbb {Z}/m\mathbb {Z}: m>1\}$
is isomorphic to a ring from the class
and conversely any
![]() $(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
, where
$(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
, where
![]() $g\in \mathfrak {X}$
, is isomorphic to
$g\in \mathfrak {X}$
, is isomorphic to
![]() $\mathbb {Z}/m\mathbb {Z}$
for some
$\mathbb {Z}/m\mathbb {Z}$
for some
![]() $m>1$
.
$m>1$
.
Thus, deciding whether an
![]() $\mathcal {L}_{rings}$
-sentence
$\mathcal {L}_{rings}$
-sentence
![]() $\Psi $
holds in
$\Psi $
holds in
![]() $\mathbb {Z}/m\mathbb {Z}$
for all m is equivalent to deciding whether
$\mathbb {Z}/m\mathbb {Z}$
for all m is equivalent to deciding whether
![]() $\Psi $
holds in
$\Psi $
holds in
![]() $(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
for all
$(\mathbb {R} \times \hat {\mathbb {Z}})/(g)$
for all
![]() $g\in \mathfrak {X}$
. Since
$g\in \mathfrak {X}$
. Since
![]() $\mathbb {R} \times \hat {\mathbb {Z}}$
and
$\mathbb {R} \times \hat {\mathbb {Z}}$
and
![]() $\mathfrak {X}$
are definable in
$\mathfrak {X}$
are definable in
![]() $\mathbb {A}_{\mathbb {Q}}$
, this decision procedure can be carried out because of the decidability of
$\mathbb {A}_{\mathbb {Q}}$
, this decision procedure can be carried out because of the decidability of
![]() $\mathbb {A}_{\mathbb {Q}}$
.
$\mathbb {A}_{\mathbb {Q}}$
.
For a proof of the decidability of
![]() $\mathbb {A}_{\mathbb {Q}}$
, see [Reference Derakhshan and Macintyre6, Section 7.1] or [Reference Weispfenning8].
$\mathbb {A}_{\mathbb {Q}}$
, see [Reference Derakhshan and Macintyre6, Section 7.1] or [Reference Weispfenning8].
We would like to end with some remarks on the connection between our work and that of Ax [Reference Ax1] and Feferman–Vaught [Reference Feferman and Vaught7] and the role (and need) for the model theory and definability in adele rings from [Reference Derakhshan and Macintyre6].
One might have thought that an easier solution to Ax’s problem could be given without adeles using Ax’s decidability results for the
![]() $\mathbb {Z}/p^{n} \mathbb {Z}$
for p and n varying [Reference Ax1] combined with the Feferman–Vaught technology for products [Reference Feferman and Vaught7]. But, as we describe below, this would require redoing variants of proofs that are analogous to our proof of decidability of adeles in [Reference Derakhshan and Macintyre6], going back into details of Feferman–Vaught and making ad hoc adjustments and giving interpretations similar to those given in this paper but in a not very meaningful context. There would be a subtle flaw if one would just try to combine the results in [Reference Ax1] and [Reference Feferman and Vaught7] because of the following points.
$\mathbb {Z}/p^{n} \mathbb {Z}$
for p and n varying [Reference Ax1] combined with the Feferman–Vaught technology for products [Reference Feferman and Vaught7]. But, as we describe below, this would require redoing variants of proofs that are analogous to our proof of decidability of adeles in [Reference Derakhshan and Macintyre6], going back into details of Feferman–Vaught and making ad hoc adjustments and giving interpretations similar to those given in this paper but in a not very meaningful context. There would be a subtle flaw if one would just try to combine the results in [Reference Ax1] and [Reference Feferman and Vaught7] because of the following points.
Feferman–Vaught [Reference Feferman and Vaught7] work with products of families of L-structures
![]() $(\mathfrak {A}_i)_{i\in I}$
, for varying index sets I and some fixed first-order language L. There is the associated Boolean algebra
$(\mathfrak {A}_i)_{i\in I}$
, for varying index sets I and some fixed first-order language L. There is the associated Boolean algebra
![]() $Powerset(I)$
consisting of subsets of I in an extension
$Powerset(I)$
consisting of subsets of I in an extension
![]() $\mathfrak {S}$
of the language of Boolean algebras (e.g., with a predicate for the ideal of finite subsets of I). One then equips the products
$\mathfrak {S}$
of the language of Boolean algebras (e.g., with a predicate for the ideal of finite subsets of I). One then equips the products
![]() $\prod _{i\in I} \mathfrak {A}_i$
with relations defined using
$\prod _{i\in I} \mathfrak {A}_i$
with relations defined using
![]() $\mathfrak {S}$
and Boolean values of L-formulas in the Boolean algebra
$\mathfrak {S}$
and Boolean values of L-formulas in the Boolean algebra
![]() $Powerset(I)$
, thus obtaining the generalized product
$Powerset(I)$
, thus obtaining the generalized product
![]() $\mathcal {P}(\mathfrak {A},\mathfrak {S})$
. A general procedure attaches to definitions in the generalized products
$\mathcal {P}(\mathfrak {A},\mathfrak {S})$
. A general procedure attaches to definitions in the generalized products
![]() $\mathcal {P}(\mathfrak {A},\mathfrak {S})$
definitions in the Boolean structure
$\mathcal {P}(\mathfrak {A},\mathfrak {S})$
definitions in the Boolean structure
![]() $\mathfrak {S}$
, by the intermediary of the Boolean values of L-formulas.
$\mathfrak {S}$
, by the intermediary of the Boolean values of L-formulas.
The relevant Feferman–Vaught theorem for decidability of a class consisting of products from a decidable class of structures is the following.
Theorem 3.2 [Reference Feferman and Vaught7, Theorem 5.6].
Let
![]() $\mathcal {K}$
be a class of L-structures. Let
$\mathcal {K}$
be a class of L-structures. Let
![]() $\mathcal {P}_{\mathcal {K},\mathcal {S}}$
be the class of all structures
$\mathcal {P}_{\mathcal {K},\mathcal {S}}$
be the class of all structures
![]() $\mathcal {P}(\mathfrak {A},\mathfrak {S})$
which are generalized products of an indexed family
$\mathcal {P}(\mathfrak {A},\mathfrak {S})$
which are generalized products of an indexed family
![]() $\mathfrak {A}=(\mathfrak {A_i})_{i\in I}$
, where
$\mathfrak {A}=(\mathfrak {A_i})_{i\in I}$
, where
![]() $\mathfrak {S}$
is an expansion of
$\mathfrak {S}$
is an expansion of
![]() $Powerset(I)$
and belongs to a fixed class
$Powerset(I)$
and belongs to a fixed class
![]() $\mathcal {S}$
of Boolean expansions of the sets
$\mathcal {S}$
of Boolean expansions of the sets
![]() $Powerset(I)$
where I is a nonempty set, and for each
$Powerset(I)$
where I is a nonempty set, and for each
![]() $i\in I$
,
$i\in I$
,
![]() $\mathfrak {A_i}\in \mathcal {K}$
. Suppose the theory of
$\mathfrak {A_i}\in \mathcal {K}$
. Suppose the theory of
![]() $\mathcal {K}$
is decidable and the theory of
$\mathcal {K}$
is decidable and the theory of
![]() $\mathcal {S}$
is decidable. Then the theory of
$\mathcal {S}$
is decidable. Then the theory of
![]() $\mathcal {P}_{\mathcal {K},\mathcal {S}}$
is decidable.
$\mathcal {P}_{\mathcal {K},\mathcal {S}}$
is decidable.
For Ax’s problem, what does one take for the class
![]() ${\mathcal K}$
and the enriched Boolean structure? It is no good simply to take
${\mathcal K}$
and the enriched Boolean structure? It is no good simply to take
![]() ${\mathcal K}$
as the set of all
${\mathcal K}$
as the set of all
![]() $\mathbb {Z}/p^n \mathbb {Z}$
for p and n varying and the Boolean structure to be atomic Boolean algebras with a predicate for the ideal of finite sets. Among the products one would get are rings which are products of factors which are not simply a
$\mathbb {Z}/p^n \mathbb {Z}$
for p and n varying and the Boolean structure to be atomic Boolean algebras with a predicate for the ideal of finite sets. Among the products one would get are rings which are products of factors which are not simply a
![]() $\mathbb {Z}/p^n \mathbb {Z}$
but can be nontrivial powers of such rings, and so one does interpret more than the
$\mathbb {Z}/p^n \mathbb {Z}$
but can be nontrivial powers of such rings, and so one does interpret more than the
![]() $\mathbb {Z}/m\mathbb {Z}$
. We do get a decidability result, but for a class bigger than the class of all
$\mathbb {Z}/m\mathbb {Z}$
. We do get a decidability result, but for a class bigger than the class of all
![]() $\mathbb {Z}/m\mathbb {Z}$
, for
$\mathbb {Z}/m\mathbb {Z}$
, for
![]() $m>1$
. A similar problem arises if we try to work with generalized products of the
$m>1$
. A similar problem arises if we try to work with generalized products of the
![]() $\mathbb {Q}_p$
or
$\mathbb {Q}_p$
or
![]() $\mathbb {Z}_p$
instead of the
$\mathbb {Z}_p$
instead of the
![]() $\mathbb {Z}/p^n\mathbb {Z}$
.
$\mathbb {Z}/p^n\mathbb {Z}$
.
There are devices for doing better in the ring formalism, by considering axioms excluding that distinct minimal idempotents have distinct finite characteristics for the residue fields of the stalks at these idempotents. But this is an infinite set of axioms, and the naive decidability does not immediately combine with it to give the decidability one wants.
In this paper, we get a short and intelligible solution to Ax’s problem via decidability and definability in
![]() $\mathbb {A}_{\mathbb {Q}}$
, but we have to work quite hard to get such a solution without using adeles and definability results from [Reference Derakhshan and Macintyre6]. We remark that [Reference Derakhshan and Macintyre6] uses Feferman–Vaught [Reference Feferman and Vaught7] and Ax [Reference Ax1].
$\mathbb {A}_{\mathbb {Q}}$
, but we have to work quite hard to get such a solution without using adeles and definability results from [Reference Derakhshan and Macintyre6]. We remark that [Reference Derakhshan and Macintyre6] uses Feferman–Vaught [Reference Feferman and Vaught7] and Ax [Reference Ax1].
We believe that the interpretations given in the proofs of Theorem 3.1 and Corollary 3.1 between
![]() $\mathbb {A}_{\mathbb {Q}}$
and the finite rings
$\mathbb {A}_{\mathbb {Q}}$
and the finite rings
![]() $\mathbb {Z}/m\mathbb {Z}$
should be of an independent interest.
$\mathbb {Z}/m\mathbb {Z}$
should be of an independent interest.
Acknowledgement
Angus Macintyre was supported by a Leverhulme Emeritus Fellowship.
Competing interest
The authors have no competing interest to declare.