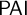1 Introduction
This paper is the third in a sequence concerned with producing semantic frameworks including components that are adequate to the task of representing subject-matter or topic of intensional sentences. The work outlined in [Reference Ferguson13, Reference Ferguson14] aimed to address perceived limitations in standard topic-sensitive frameworks on the market, e.g., legacy systems of analytic implication studied by Parry [Reference Parry24], Angell [Reference Angell, Norman and Sylvan1], Deutsch [Reference Deutsch8] or more recent work on topic-sensitive intentional modals (TSIMs) studied by Berto and collaborators including Hawke and Özgün (in, e.g., [Reference Berto5]).
The first piece [Reference Ferguson13] took issue with the tendency of standard frameworks to treat the assignment of topics to intensional sentences in the same way as the assignment of topics to extensional sentences, i.e., by the coarse fusion of the topics of subformulae. The work investigated scenarios in which such an approach seemed implausible and identified a number of conditions characteristic of the topic-theoretic peculiarities of different types of intensional conditionals. These considerations drove the development of a flexible semantics and proof theory for a system of conditional agnostic analytic implication (
![]() $\mathsf {CA}/\mathsf {PAI}$
) in which the subject-matter of intensional formulae is determined on the basis of more nuanced and fine-grained considerations than fusion alone.
$\mathsf {CA}/\mathsf {PAI}$
) in which the subject-matter of intensional formulae is determined on the basis of more nuanced and fine-grained considerations than fusion alone.
Its sequel [Reference Ferguson14] was concerned with decoupling this framework from the Parry-style setting in order to apply the techniques and tools developed for
![]() $\mathsf {CA}/\mathsf {PAI}$
to the setting of TSIMs.Footnote
1
The work applied these tools to introduce more granular and expressive variants of Berto’s systems
$\mathsf {CA}/\mathsf {PAI}$
to the setting of TSIMs.Footnote
1
The work applied these tools to introduce more granular and expressive variants of Berto’s systems
![]() $\mathsf {KRI}$
(the logic of knowability relative to information) and
$\mathsf {KRI}$
(the logic of knowability relative to information) and
![]() $\mathsf {PHB}$
(the logic of plain hyperintensional belief). Notably, the novel emendations resolved several long-standing limitations of the frameworks. For example, by introducing adequate machinery for evaluating nested operators, the variant
$\mathsf {PHB}$
(the logic of plain hyperintensional belief). Notably, the novel emendations resolved several long-standing limitations of the frameworks. For example, by introducing adequate machinery for evaluating nested operators, the variant
![]() $\mathsf {KRI}$
of [Reference Ferguson14] improved on stock
$\mathsf {KRI}$
of [Reference Ferguson14] improved on stock
![]() $\mathsf {KRI}$
by satisfying Fagin and Halpern’s requirement of [Reference Fagin and Halpern11] that any “viable logic of knowledge” must capture an agent’s meta-reasoning.
$\mathsf {KRI}$
by satisfying Fagin and Halpern’s requirement of [Reference Fagin and Halpern11] that any “viable logic of knowledge” must capture an agent’s meta-reasoning.
Despite the advances of the framework introduced in [Reference Ferguson12] and implemented across [Reference Ferguson13, Reference Ferguson14] in freeing the standard topic-theoretic frameworks from several counterintuitive assumptions, there remain several limitations to the applicability of the underlying framework left to resolve.
Before identifying any one target in detail, it will help us to review some relevant notions to set the stage. Especially relevant are two conditions described as principles of Negation Transparency and Junctive Transparency. Where t is a function assigning sentences topics and
![]() $\oplus $
is a fusion operator that simply merges two topics into one, these can be described as:
$\oplus $
is a fusion operator that simply merges two topics into one, these can be described as:
-
• Negation Transparency:
 ${t}(\neg \varphi )={t}(\varphi )$
.
${t}(\neg \varphi )={t}(\varphi )$
. -
• Junctive Transparency:
 ${t}(\varphi \wedge \psi )={t}(\varphi \vee \psi )={t}(\varphi )\oplus {t}(\psi )$
.
${t}(\varphi \wedge \psi )={t}(\varphi \vee \psi )={t}(\varphi )\oplus {t}(\psi )$
.
This is to say that the topic of a formula
![]() $\varphi $
is the same as the topic of its negation
$\varphi $
is the same as the topic of its negation
![]() $\neg \varphi $
while the topics of conjunctions and disjunctions are merely the fusions of the topics of their immediate subformulae.
$\neg \varphi $
while the topics of conjunctions and disjunctions are merely the fusions of the topics of their immediate subformulae.
Topic transparency is more-or-less unobjectionable in extensional cases. It is not implausible that extensional connectives are topic-theoretically inert and make no more contribution to the topic of a whole than punctuation marks. Indeed, in many sequent calculi, extensional conjunctions and disjunctions are interchangable with commas in a multiset.
In contrast to the topic-theoretic inertness of extensional connectives, many intensional operators—conditionals or modals—appear to play a transformative role in determining the topics of complexes in which they appear, i.e., distinct types of intensional conditionals can have distinct topic-theoretic features. Some conditionals appear to be topic-theoretically additive, nontrivially contributing to a complex’s subject-matter beyond that of its subformulae. For other conditionals, the topic of a complex may omit some elements of the topics of its antecedent and consequent. The potential topic-theoretic features of conditionals are as varied as intensional conditionals themselves.
The standard accounts of topic on offer entirely fail to acknowledge this diversity, effectively treating all operators as interchangeable. For an intensional conditional
![]() $\rightarrow $
, this is reflected in a condition of Intensional Transparency—the coarse identification of
$\rightarrow $
, this is reflected in a condition of Intensional Transparency—the coarse identification of
![]() $t(\varphi \rightarrow \psi )$
and
$t(\varphi \rightarrow \psi )$
and
![]() $t(\varphi )\oplus t(\psi )$
. We can briefly consider several of the consequences of Intensional Transparency that reveal distinct types of conditionals whose topic-theoretic features cannot be modeled on the standard approaches.
$t(\varphi )\oplus t(\psi )$
. We can briefly consider several of the consequences of Intensional Transparency that reveal distinct types of conditionals whose topic-theoretic features cannot be modeled on the standard approaches.
One consequence is a constraint requiring that intensional conditionals are topic-theoretically non-ampliative in the sense that a conditional
![]() $\varphi \rightarrow \psi $
may include no subject-matter not already present in those of
$\varphi \rightarrow \psi $
may include no subject-matter not already present in those of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. Formally:
$\psi $
. Formally:
-
• Non-Ampliativity:
 $t(\varphi \rightarrow \psi )\leq t(\varphi )\oplus t(\psi )$
.
$t(\varphi \rightarrow \psi )\leq t(\varphi )\oplus t(\psi )$
.
Reference [Reference Ferguson13] cites the intuitionistic conditional as a connective whose topic-theoretic properties are incompatible with this constraint. Following Brouwer–Heyting–Kolmogorov readings, it is natural to expect that a conditional
![]() $\varphi \rightarrow \psi $
is (in part) about a particular construction f transforming proofs of its antecedent into proofs of its consequent. Although this f is not counted among the topics of
$\varphi \rightarrow \psi $
is (in part) about a particular construction f transforming proofs of its antecedent into proofs of its consequent. Although this f is not counted among the topics of
![]() $\varphi $
or
$\varphi $
or
![]() $\psi $
, it is reasonable to expect that f is a constituent of the overall conditional’s subject-matter. Consequently, a framework in which Non-Ampliativity holds is incapable of faithfully capturing the topic-theoretic properties of the intuitionistic conditional.Footnote
2
$\psi $
, it is reasonable to expect that f is a constituent of the overall conditional’s subject-matter. Consequently, a framework in which Non-Ampliativity holds is incapable of faithfully capturing the topic-theoretic properties of the intuitionistic conditional.Footnote
2
Complementing this constraint is a further consequence dictating that the subject-matter of an intensional conditional must preserve the subject-matters of its subformulae in toto, that is, imposing an expectation of non-explicativity. Formally:
-
• Non-Explicativity:
 $t(\varphi )\oplus t(\psi )\leq t(\varphi \rightarrow \psi )$
.
$t(\varphi )\oplus t(\psi )\leq t(\varphi \rightarrow \psi )$
.
For intensional conditionals that shift contexts, such topic-theoretic preservation is doubtful.
Reference [Reference Ferguson13] identifies counterfactuals as a species of conditional whose context-shifting leads to violations of Non-Explicativity. The incongruity between Non-Explicativity and counterfactual conditionals can be made clear by an example. Consider a sentence in which a necessary property is falsely attributed to an individual identified through a definite description, e.g.,
-
I: “The inventor of bifocals is a tiger.”
Although false, on many theories—such as Hawke’s issue-based theory of [Reference Hawke18]—Benjamin Franklin constitutes part of the subject-matter of [I]. A counterfactual conditional
![]() $\varphi $
in which [I] appears as antecedent, however, shifts contexts from the actual world to states in which [I] is true. In virtue of the impossibility of Franklin’s being a tiger, Franklin will be excluded from the subject-matter in any context relevant to
$\varphi $
in which [I] appears as antecedent, however, shifts contexts from the actual world to states in which [I] is true. In virtue of the impossibility of Franklin’s being a tiger, Franklin will be excluded from the subject-matter in any context relevant to
![]() $\varphi $
’s evaluation and, plausibly, from the subject-matter of
$\varphi $
’s evaluation and, plausibly, from the subject-matter of
![]() $\varphi $
itself. But such phenomena cannot be captured in the presence of Non-Explicativity.
$\varphi $
itself. But such phenomena cannot be captured in the presence of Non-Explicativity.
The system introduced in [Reference Ferguson13] of conditional agnostic analytic implication (
![]() $\mathsf {CA}/\mathsf {PAI}$
) provided a concrete implementation of this intuition by a modification of Parry’s
$\mathsf {CA}/\mathsf {PAI}$
) provided a concrete implementation of this intuition by a modification of Parry’s
![]() $\mathsf {PAI}$
. The work served as a proof-of-concept witnessing that the framework was sufficiently general to accommodate a wide range of semantic conditions regulating the subject-matters of conditionals while remaining robust enough to continue to accommodate the standard theories’ assumptions.
$\mathsf {PAI}$
. The work served as a proof-of-concept witnessing that the framework was sufficiently general to accommodate a wide range of semantic conditions regulating the subject-matters of conditionals while remaining robust enough to continue to accommodate the standard theories’ assumptions.
The formal framework at the heart of
![]() $\mathsf {CA}/\mathsf {PAI}$
succeeds in dismantling many artificial barriers to the development of nuanced theories about intensional subject-matter.
$\mathsf {CA}/\mathsf {PAI}$
succeeds in dismantling many artificial barriers to the development of nuanced theories about intensional subject-matter.
![]() $\mathsf {CA}/\mathsf {PAI}$
supports reasoning about topic-theoretic contexts in which the conditions of Non-Explicativity and Non-Ampliativity—among others—are unsuitable. But for all the modularity and granularity made available by this more general framework, barriers remain hindering the expression of several exceedingly natural topic-theoretic intuitions.
$\mathsf {CA}/\mathsf {PAI}$
supports reasoning about topic-theoretic contexts in which the conditions of Non-Explicativity and Non-Ampliativity—among others—are unsuitable. But for all the modularity and granularity made available by this more general framework, barriers remain hindering the expression of several exceedingly natural topic-theoretic intuitions.
2 Topic sufficiency and intensional conditionals
Most importantly, the refined framework inherits one problematic feature from its predecessors, namely, its commitment to a constraint that the topic of an intensional conditional must be a function of the subject-matters of its antecedent and consequent.
In short, this tacit assumption stipulates that the topics of a conditional’s antecedent and consequent suffice to determine the topic of the complex. Following this characterization, we formally introduce the constraint as Topic Sufficiency:
-
• Topic Sufficiency: For an intensional conditional
 $\rightarrow $
, if
$\rightarrow $
, if
 $t(\varphi )=t(\xi )$
and
$t(\varphi )=t(\xi )$
and
 $t(\psi )=t(\zeta )$
, then
$t(\psi )=t(\zeta )$
, then
 $t(\varphi \rightarrow \psi )=t(\xi \rightarrow \zeta )$
.
$t(\varphi \rightarrow \psi )=t(\xi \rightarrow \zeta )$
.
The condition is remarkably entrenched, reflected in virtually all topic-theoretic frameworks in which conditionals are assigned topics.Footnote 3
There exists phenomenological evidence against this principle; however, this evidence motivates an examination of the thesis of Topic Sufficiency and discussion of generalizing semantic frameworks capable of more faithfully representing a broader range of cases. In this section, we will consider some informal examples, allowing the illustrations to direct the selection of criteria on the adequacy of formal accounts of topic.
2.1 State-sensitive subject-matter
Let us make a brief phenomenological observation concerning the following conditional:
-
II: “If Dr. Xi had continued her research into autonomous vehicles, self-driving cars would have already reached a wide user-base.”
Although the fictional Dr. Xi and her research appear to make up part of the subject-matter of [II],Footnote 4 an utterer of the above sentence seems to form an intention towards a still more complex subject-matter. The objects that the utterer speaks about are not limited to the constituents and roles mentioned in [II]. Rather, to consider [II] involves fixing and considering situations over which the conditional will be evaluated. If one takes seriously that to assert [II] is to speak about these situations, the situations themselves must constitute part of the conditional’s overall subject-matter. In other words, in some intensional contexts, subject-matter appears to be state-sensitive.
The requirement of a state-sensitive account of subject-matters is reinforced by the way in which the relevant counterfactual situations are determined; [II] is apparently about a restricted class of situations—e.g., those in which the antecedent is supposed to be true. But in general, the truth conditions of a sentence cannot be inferred or recovered from its subject-matter, in which case some non-topic-theoretic contribution must be made by the proposition to the overall subject-matter.
In short, if [II] is about a collection of counterfactual scenarios whose extent is not uniquely determined by the subject-matters of its antecedent and consequent, then [II] will act as a counterexample to Topic Sufficiency.
2.2 Counterexamples to topic sufficiency
In this section, we undertake a closer examination of the thesis of Topic Sufficiency reflected in the framework of [Reference Ferguson13, Reference Ferguson14]. This discussion will help identify the requirements of a semantic framework capable of more faithfully representing state-sensitive subject-matter. We begin by surveying several scenarios in which our intuitions likely conflict with Topic Sufficiency.
For the first illustration, consider the following scenario: A team of coworkers is aware that a colleague, John, will likely soon resign in favor of a position at a different organization. Several of the team members hold a meeting to prepare for this contingency. A member of the team begins the discussion by asking:
-
Q1: “What steps should we take if John resigns from his position?”
Now, consider two potential responses to [Q1] that participants might offer:
-
R1: “Should John resign, we will have to find a replacement.”
-
R2: “Should John not resign, we will have to find a replacement.”
According to Negation Transparency, the subject-matters of the antecedents of [R1] and [R2] are identical. The subject-matters of the responses’ consequents, too, are trivially identical. Thus, Topic Sufficiency amounts to a requirement that the subject-matters of [R1] and [R2] must coincide.
Consider, however, the responses to [R1] and [R2] that one would expect from the questioner. Clearly, the act of asking [Q1] fixes the scope of the discussion, limiting the range of acceptable topics to contingencies in which John resigns. Now, insofar as [R1] describes a recommendation that is responsive to or conditioned on these very contingencies, [R1] remains within the boundaries of the discussion. In other words, the questioner would likely believe [R1] to be on-topic. In contrast, the response [R2] fails to align with the contingencies at the heart of the discussion. One would therefore anticipate that the questioner would reject [R2] as off-topic. Simply put, [R1] is on-topic and [R2] is off-topic.
The prediction that the subject-matters of [R1] and [R2] are identical requires that [R1] is on-topic precisely when [R2] is on-topic; a single topic cannot be both on-topic and off-topic with respect to a single context. But we have just considered a context in which the responses’ degrees of topicality are distinct. The condition of Topic Sufficiency therefore conflicts with very plausible assumptions concerning the topics of intensional conditionals.
I should acknowledge that—as a referee has pointed out—this is not the uniquely plausible explanation for a participant in a conversation initiated by [Q1] having different reactions to responses [R1] and [R2]. On another interpretation—an interpretation described clearly by Leahy in [Reference Leahy21]—initiating a conversation with [Q1] serves to set the common ground of the discourse so that conversants tacitly agree to treat “John has resigned from his position” as true during the conversation. The utterance of a conditional, carrying with it the presupposition that its antecedent is true, acts to enter its antecedent into the common ground. Although the antecedent of [R1]—that John has resigned—is consistent with the common ground, the common ground cannot be consistently updated with the presupposition of [R2]. Consequently, to utter [R2] conflicts with conversational norms in a way not incurred by an utterance of [R1].
We need not adjudicate whether topic-theoretic or pragmatic explanations of this phenomenon are more correct. Indeed, it is not clear that the two are necessarily incompatible. But it is fair to note that the type of explanation laid out in [Reference Leahy21] rests heavily on a conditional’s antecedent when pinning down its presuppositions while a similar topic-theoretic phenomenon can be replicated without somehow privileging the antecedent, as we will now see.
Many accounts presume that the states a conditional is about are fixed—e.g., hypothesized—in virtue of their satisfying or making true the antecedent of the conditional. For example, this presumption is a hallmark of the theory described by Kratzer in [Reference Kratzer, Stechow and Wunderlich20] in which the role of the antecedent (the “if-clause”) is that of a restrictor, i.e., the antecedent serves to restrict the set of worlds or states against which the consequent is to be evaluated. But as we’ve noted, determining the extent of the situations a conditional is about requires access to the antecedent’s truth conditions. The subject-matter of a sentence, however, is in general insufficient to pin down its truth conditions. For example, on standard accounts,
![]() $\varphi \vee \neg \varphi $
and
$\varphi \vee \neg \varphi $
and
![]() $\varphi \wedge \neg \varphi $
are predicted to have the same topic but have markedly different truth conditions. Consequently, possessing the topics of the conditional’s subformulae is insufficient to decisively fix the selection of states.
$\varphi \wedge \neg \varphi $
are predicted to have the same topic but have markedly different truth conditions. Consequently, possessing the topics of the conditional’s subformulae is insufficient to decisively fix the selection of states.
Although in the foregoing examples the role of the antecedent plays an outsized role in determining the topics that are germane to a discussion, an adequate framework should acknowledge the possibility of the consequent playing a role.Footnote 5 Ed Mares’ discussion of counterfactual conditionals in [Reference Mares22, pp. 144–146] recalls some remarks due to Gabbay’s [Reference Gabbay16] that illustrate a consequent’s role in the determination of situations against which a conditional is evaluated and—following our reasoning—that a conditional is about. One of Gabbay’s examples centers on the following two conditionals:
-
III: “If I were the Pope, I would have allowed the use of the pill in India.”
-
IV: “If I were the Pope, I would have dressed more humbly.”
Gabbay detects an unmistakable influence of the consequents over constraining the acceptable states for the evaluation of [III] and [IV], noting “clearly, in the first statement, we must assume that India remains overpopulated and poor in resources, while in the second example nothing of the sort is required” [Reference Gabbay16, p. 98].
We can produce a more direct illustration of how topic may be influenced by the proposition expressed by a consequent. Consider a query:
-
Q2: “Why might Rebecca have left the party early?”
along with two potential responses to [Q2]:
-
R3: “If Rebecca were scheduled for an early shift at work, she would have left early.”
-
R4: “If Rebecca were scheduled for an early shift at work, she would not have left early.”
Conventionally, the asking of [Q2] signals the initiation of collective abductive activity, serving as invitation to a collaborative investigation after explanations for a target proposition, i.e., that Rebecca has departed. Intensional conditionals including this target as consequent are a prototypical class of candidate explanations; upon their introduction, the explanatory value and plausibility of the link between antecedent and the target proposition can be evaluated.
[R3] seems to express such a link between a potential explanation (the possibility of an early shift) and the target proposition made salient by [Q2]. Prima facie, its introduction to the discussion successfully poses the type of response necessary for the discussion to proceed. In contrast, [R4] describes no explanatory path to the target proposition. Informally, one is led to say that the utterer of [R4] has veered off topic. While the case remains analogous to the [Q1] case, the scenario of [Q2] illustrates that the consequent can contribute more to the topic of an intensional conditional than is predicted by Topic Sufficiency.
Collectively, these observations identify a collection of desiderata for topic-theoretic frameworks in which Topic Sufficiency is not assumed by default.
2.3 Compositionality and contents
The foregoing examples reinforce one insight—and uncover another—concerning compositionality. Together, these observations lead to the fundamental assumptions guiding the formal proposal to follow. We can review them in order.
First is that they provide a new perspective from which to recapitulate a particular lesson implicit in Parry’s work as regards compositionality. One of Parry’s insights is that truth conditions—or propositions in the sense of sets of worlds—are not “internally” compositional in the sense that truth conditions for complex sentences are not always determined by the truth conditions of their subsentences. Sentences including operators like Parry’s analytic implication
![]() $\rightarrow $
, Fine’s subject-matter inclusion
$\rightarrow $
, Fine’s subject-matter inclusion
![]() $\preccurlyeq $
, or Berto’s topic-sensitive intentional modals can only be evaluated after one has determined the topics of their parts. When a language is expanded to include such notions, truth conditions are no longer functions of further truth conditions and are compositional only for appeal to an external semantic category.
$\preccurlyeq $
, or Berto’s topic-sensitive intentional modals can only be evaluated after one has determined the topics of their parts. When a language is expanded to include such notions, truth conditions are no longer functions of further truth conditions and are compositional only for appeal to an external semantic category.
We draw an analogous conclusion here. Our considerations suggest that topic itself is not “internally” compositional, i.e., the topic of a complex is not in general a function of the topics of its parts. Rather, cases exist in which truth conditions of subformulae play a hand in determining a sentence’s topic. Thus, the task of assigning topic must in some cases reach beyond the internal resources of a class of topics to an external semantic category of truth conditions.
These two lessons require a refinement rather than a rejection of compositionality. As we have considered matters, the categories of proposition and topic joined by their mutual sufficiency. This harmonious relationship is reflected in a sort of reciprocal compositionality between the two.
The possibility of interdependence between propositions and topic suggests that we consider a class of semantic items that is internally compositional. This interdependence would be respected by the internal compositionality of the class of contents—pairs including both a topic and a proposition. This is in harmony with the account of topic offered by Berto in [Reference Berto5] as a development of the intuitions underlying Yablo’s [Reference Yablo29]. Compare the implicit “two-component” model (2C-semantics) that falls out of considerations of interdependence with the model described by Berto and Hawke in [Reference Berto5], in which a meaning P is treated as a pair of truth conditions
![]() $C_{P}$
and topic
$C_{P}$
and topic
![]() $T_{P}$
.
$T_{P}$
.
The core features of two-component approaches follow closely to our needs—the possibility of interdependence and irreducibility—are described succinctly by Berto and Hawke:
A 2C-semantics can allow all kinds of important connections between truth conditions and topics. But according to 2C, facts about either cannot be reduced to facts about the other in the sense described above. [Reference Berto5, p. 27]
In what follows, this notion of content will play an important role in our formal models and it will become clear that the logic to be introduced is authentically two-component in the sense described by Berto and Hawke.
3 State-sensitive analytic implication
As in [Reference Ferguson13], we return to the setting of Parry’s
![]() $\mathsf {PAI}$
in order to demonstrate the robustness of the framework to be proposed, e.g., an intuitive axiomatization may substantiate the framework’s constancy and coherence while introducing a range of natural extensions may underscore its versatility and breadth. Not only does Parry’s logic have historical merit as the progenitor of topic-sensitive techniques in logic, but the elegance of the
$\mathsf {PAI}$
in order to demonstrate the robustness of the framework to be proposed, e.g., an intuitive axiomatization may substantiate the framework’s constancy and coherence while introducing a range of natural extensions may underscore its versatility and breadth. Not only does Parry’s logic have historical merit as the progenitor of topic-sensitive techniques in logic, but the elegance of the
![]() $\mathsf {PAI}$
model theory developed by Fine in [Reference Fine15] and the perspicuity and accessibility of its axiomatization make it an attractive setting.
$\mathsf {PAI}$
model theory developed by Fine in [Reference Fine15] and the perspicuity and accessibility of its axiomatization make it an attractive setting.
Most importantly, the parallels between its topic-theoretic machinery and that of alternative frameworks guarantees the portability of insights won in the setting of analytic implication. This portability ensures that the results of the present investigation can immediately transfer to the topic-theoretic framework of topic-sensitive intentional modals developed by Berto and his collaborators. What we show here, e.g., for the strict conditional of Parry applies equally well not only for the variably-strict conditionals but—with appropriate adjustments—to a whole host of topic-sensitive intensional operators. As seen in [Reference Ferguson14], a wide range of applications can be quickly drawn from modifications to Parry’s system; their implementation in
![]() $\mathsf {PAI}$
can be viewed simply as a sort of stress test or proof of concept.
$\mathsf {PAI}$
can be viewed simply as a sort of stress test or proof of concept.
3.1 Conditional agnostic analytic implication
Now, let us take our first steps towards a positive formalization of the core intuition. In this section, we review the framework of [Reference Ferguson13]. This work modified Parry’s
![]() $\mathsf {PAI}$
to yield the logic of
$\mathsf {PAI}$
to yield the logic of
![]() $\mathsf {CA}/\mathsf {PAI}$
offering not only the flexibility to drop conditions like Non-Ampliativity and Non-Explicativity, but the modularity to impose semantic constraints corresponding to a wide range of topic-theoretic assumptions as needed.
$\mathsf {CA}/\mathsf {PAI}$
offering not only the flexibility to drop conditions like Non-Ampliativity and Non-Explicativity, but the modularity to impose semantic constraints corresponding to a wide range of topic-theoretic assumptions as needed.
Although investigations into systems related to
![]() $\mathsf {PAI}$
were carried out by Dunn in [Reference Dunn10] and Urquhart in [Reference Urquhart28], the first model theory for
$\mathsf {PAI}$
were carried out by Dunn in [Reference Dunn10] and Urquhart in [Reference Urquhart28], the first model theory for
![]() $\mathsf {PAI}$
was described by Kit Fine in [Reference Fine15].Footnote
6
Fine’s semantics for Parry’s system equips each world w of an
$\mathsf {PAI}$
was described by Kit Fine in [Reference Fine15].Footnote
6
Fine’s semantics for Parry’s system equips each world w of an
![]() $\mathsf {S4}$
Kripke model with join semilattices of topics
$\mathsf {S4}$
Kripke model with join semilattices of topics
![]() $\langle \mathcal {T},\oplus \rangle $
and forms the background for the following definitions.
$\langle \mathcal {T},\oplus \rangle $
and forms the background for the following definitions.
Let
![]() $\mathcal {L}$
be a propositional language including negation (
$\mathcal {L}$
be a propositional language including negation (
![]() $\neg $
), conjunction (
$\neg $
), conjunction (
![]() $\wedge $
), disjunction (
$\wedge $
), disjunction (
![]() $\vee $
), and an intensional conditional
$\vee $
), and an intensional conditional
![]() $\rightarrow $
. We informally refer as well to the material conditional
$\rightarrow $
. We informally refer as well to the material conditional
![]() defined from
defined from
![]() $\neg $
and
$\neg $
and
![]() $\vee $
in the standard way.
$\vee $
in the standard way.
Definition 1. A
![]() $\mathsf {CA}/\mathsf {PAI}$
Fine model is a tuple
$\mathsf {CA}/\mathsf {PAI}$
Fine model is a tuple
![]() $\langle W,R,\mathcal {T},\oplus ,\multimap ,v,{t},h\rangle $
such that:
$\langle W,R,\mathcal {T},\oplus ,\multimap ,v,{t},h\rangle $
such that:
-
• R is a reflexive and transitive binary relation on W.
-
• For each
 $w\in W$
,
$w\in W$
,
 $\langle \mathcal {T}_{w},\oplus _{w}\rangle $
is a join semilattice.
$\langle \mathcal {T}_{w},\oplus _{w}\rangle $
is a join semilattice. -
• v is a valuation from atomic formulae to W
-
• For each
 $w\in W$
,
$w\in W$
,
 ${t}_{w}$
is a function mapping atomic formulae to
${t}_{w}$
is a function mapping atomic formulae to
 $\mathcal {T}_{w}$
.
$\mathcal {T}_{w}$
. -
• For each
 $w\in W$
,
$w\in W$
,
 $\multimap _{w}$
is a binary function from
$\multimap _{w}$
is a binary function from
 $\mathcal {T}_{w}\times \mathcal {T}_{w}\rightarrow \mathcal {T}_{w}$
.
$\mathcal {T}_{w}\times \mathcal {T}_{w}\rightarrow \mathcal {T}_{w}$
. -
• For all
 $w,w'$
such that
$w,w'$
such that
 $wRw'$
,
$wRw'$
,
 $h_{w,w'}:\mathcal {T}_{w}\rightarrow \mathcal {T}_{w'}$
is a homomorphism such that:
$h_{w,w'}:\mathcal {T}_{w}\rightarrow \mathcal {T}_{w'}$
is a homomorphism such that:-
– for atoms p,
 $h_{w,w'}(t_{w}(p))=t_{w'}(p)$
,
$h_{w,w'}(t_{w}(p))=t_{w'}(p)$
, -
–
 $h_{w,w'}(a\oplus _{w}b)=h_{w,w'}(a)\oplus _{w'}h_{w,w'}(b)$
,
$h_{w,w'}(a\oplus _{w}b)=h_{w,w'}(a)\oplus _{w'}h_{w,w'}(b)$
, -
–
 $h_{w,w'}(a\multimap _{w}b)=h_{w,w'}(a)\multimap _{w'}h_{w,w'}(b)$
.
$h_{w,w'}(a\multimap _{w}b)=h_{w,w'}(a)\multimap _{w'}h_{w,w'}(b)$
.
-
A couple of remarks are in order. First, as a join semilattice, each
![]() $\langle \mathcal {T}_{w},\oplus _{w}\rangle $
defines a partial order
$\langle \mathcal {T}_{w},\oplus _{w}\rangle $
defines a partial order
![]() $\leq _{w}$
so that
$\leq _{w}$
so that
![]() $a\leq _{w}b$
if
$a\leq _{w}b$
if
![]() $a\oplus _{w}b=b$
which will also be preserved by a homomorphism
$a\oplus _{w}b=b$
which will also be preserved by a homomorphism
![]() $h_{w,w'}$
. Moreover, the introduction of homomorphisms
$h_{w,w'}$
. Moreover, the introduction of homomorphisms
![]() $h_{w,w'}$
acts as a generalization of Fine’s stipulation that topic inclusion between atoms be preserved across accessible worlds. In other words, the requirement that
$h_{w,w'}$
acts as a generalization of Fine’s stipulation that topic inclusion between atoms be preserved across accessible worlds. In other words, the requirement that
![]() $h_{w,w'}(t_{w}(p))=t_{w'}(p)$
ensures that if
$h_{w,w'}(t_{w}(p))=t_{w'}(p)$
ensures that if
![]() $wRw'$
then for atoms p and q,
$wRw'$
then for atoms p and q,
![]() ${t}_{w}(p)\leq _{w}{t}_{w}(q)$
implies
${t}_{w}(p)\leq _{w}{t}_{w}(q)$
implies
![]() ${t}_{w'}(p)\leq _{w'}{t}_{w'}(q)$
, whence topic inclusion between sentences will persist across accessible worlds. Finally, note that the assumption that R is reflexive and transitive is made only to preserve continuity with the system
${t}_{w'}(p)\leq _{w'}{t}_{w'}(q)$
, whence topic inclusion between sentences will persist across accessible worlds. Finally, note that the assumption that R is reflexive and transitive is made only to preserve continuity with the system
![]() $\mathsf {PAI}$
; not only could Definition 1 be modified to include analytic strict implications for weaker systems of modal logic, but one could follow, e.g., Sylvan’s work in [Reference Sylvan27] to produce conditional-agnostic versions of relevant containment logics.
$\mathsf {PAI}$
; not only could Definition 1 be modified to include analytic strict implications for weaker systems of modal logic, but one could follow, e.g., Sylvan’s work in [Reference Sylvan27] to produce conditional-agnostic versions of relevant containment logics.
The novel element of Definition 1 is the introduction of a binary function
![]() $\multimap $
. The features of our
$\multimap $
. The features of our
![]() $\multimap $
function will become clear through its role in definitions.
$\multimap $
function will become clear through its role in definitions.
Definition 2. The topic assignment function
![]() ${t}_{w}$
is extended through the language:
${t}_{w}$
is extended through the language:
-
•
 ${t}_{w}(\neg \varphi )={t}_{w}(\varphi )$
.
${t}_{w}(\neg \varphi )={t}_{w}(\varphi )$
. -
•
 ${t}_{w}(\varphi \star \psi )={t}_{w}(\varphi )\oplus _{w}{t}_{w}(\psi )$
for
${t}_{w}(\varphi \star \psi )={t}_{w}(\varphi )\oplus _{w}{t}_{w}(\psi )$
for
 $\star $
extensional.
$\star $
extensional. -
•
 ${t}_{w}(\varphi \rightarrow \psi )={t}_{w}(\varphi )\multimap _{w}{t}_{w}(\psi )$
.
${t}_{w}(\varphi \rightarrow \psi )={t}_{w}(\varphi )\multimap _{w}{t}_{w}(\psi )$
.
Truth at a world is defined:
Definition 3. Truth conditions are defined recursively:
-
•
 $w\Vdash p$
if
$w\Vdash p$
if
 $w\in v(p)$
.
$w\in v(p)$
. -
•
 $w\Vdash \neg \varphi $
if
$w\Vdash \neg \varphi $
if
 $w\nVdash \varphi $
.
$w\nVdash \varphi $
. -
•
 $w\Vdash \varphi \wedge \psi $
if
$w\Vdash \varphi \wedge \psi $
if
 $w\Vdash \varphi $
and
$w\Vdash \varphi $
and
 $w\Vdash \psi $
.
$w\Vdash \psi $
. -
•
 $w\Vdash \varphi \rightarrow \psi $
if
$w\Vdash \varphi \rightarrow \psi $
if
 $\begin {cases} \mbox {for all }w'\mbox { such that }wRw'\mbox {, if }w'\Vdash \varphi \mbox { then }w'\Vdash \psi ,\\ {t}_{w}(\psi )\leq _{w}{t}_{w}(\varphi ). \end {cases}$
$\begin {cases} \mbox {for all }w'\mbox { such that }wRw'\mbox {, if }w'\Vdash \varphi \mbox { then }w'\Vdash \psi ,\\ {t}_{w}(\psi )\leq _{w}{t}_{w}(\varphi ). \end {cases}$
Given truth conditions for negation and conjunction, those for disjunction (
![]() $\vee $
) and material implication (
$\vee $
) and material implication (
![]() ) can be inferred from the above.
) can be inferred from the above.
The truth conditions for analytic implication are “double-barrelled” (as pejoratively described by Sylvan in [Reference Routley, Plumwood, Meyer and Brady26]) by dividing into parallel truth-theoretic and topic-theoretic components, framing analytic implication as an early case of a “two-component” approach to semantic content in the sense of [Reference Berto, Hawke and Hornischer7]. We will return to this double-barrelled representation in Section 4.2, where it will play an important role. Having reviewed the features of
![]() $\mathsf {CA}/\mathsf {PAI}$
models acting as a point of departure for our investigation, we introduce the structure of the state-sensitive model theory.
$\mathsf {CA}/\mathsf {PAI}$
models acting as a point of departure for our investigation, we introduce the structure of the state-sensitive model theory.
3.2 Models for state-sensitive analytic implication
We have considered reasons to reject Topic Sufficiency in the previous section, discussing natural language examples of conditionals whose subject-matter is not determined functionally by the subject-matters of their parts. The intuition common to these cases rests in an observation that often an intensional conditional
![]() $\varphi \rightarrow \psi $
is about classes of states (or situations) whose extent cannot be inferred by the topics of
$\varphi \rightarrow \psi $
is about classes of states (or situations) whose extent cannot be inferred by the topics of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
alone, i.e.,
$\psi $
alone, i.e.,
![]() $t(\varphi \rightarrow \psi )$
is not determined merely by
$t(\varphi \rightarrow \psi )$
is not determined merely by
![]() $t(\varphi )$
and
$t(\varphi )$
and
![]() $t(\psi )$
. Recast as a formal critique of the
$t(\psi )$
. Recast as a formal critique of the
![]() $\multimap _{w}$
function of Definition 1, this intuition diagnoses a defect the failure to admit sets of situations or worlds as additional arguments.
$\multimap _{w}$
function of Definition 1, this intuition diagnoses a defect the failure to admit sets of situations or worlds as additional arguments.
To accommodate such arguments, we need not add new argument places to the function
![]() $\multimap _{w}$
. Rather, we preserve the arity of
$\multimap _{w}$
. Rather, we preserve the arity of
![]() $\multimap _{w}$
by modifying its domain so that its arguments are pairs of contents rather than topics.
$\multimap _{w}$
by modifying its domain so that its arguments are pairs of contents rather than topics.
This is reflected in an even more refined model—a state-sensitive model—upon minimal modifications to Definition 1. Let
![]() $w{\uparrow }$
denote the R-cone of w. Let
$w{\uparrow }$
denote the R-cone of w. Let
![]() denote the set
denote the set
![]() $\lbrace w'\in w{\uparrow }\mid w'\Vdash \varphi \rbrace $
, i.e., the collection of worlds accessible from w at which
$\lbrace w'\in w{\uparrow }\mid w'\Vdash \varphi \rbrace $
, i.e., the collection of worlds accessible from w at which
![]() $\varphi $
is true. Then:
$\varphi $
is true. Then:
Definition 4. An
![]() $\mathsf {S}/\mathsf {PAI}$
Fine model is a tuple
$\mathsf {S}/\mathsf {PAI}$
Fine model is a tuple
![]() $\langle W,R,\mathcal {T},\mathcal {C},\oplus ,\multimap ,v,{t}\rangle $
revising Definition 1 by the clauses:
$\langle W,R,\mathcal {T},\mathcal {C},\oplus ,\multimap ,v,{t}\rangle $
revising Definition 1 by the clauses:
-
• For each
 $w\in W$
,
$w\in W$
,
 $\mathcal {C}_{w}$
is a set of contents defined recursively below.
$\mathcal {C}_{w}$
is a set of contents defined recursively below. -
• For any
 $\langle a,X\rangle \in \mathcal {C}_{w}$
,
$\langle a,X\rangle \in \mathcal {C}_{w}$
,
 $h_{w,w'}(\langle a,X\rangle )=\langle h_{w,w'}(a),X\cap (w{\uparrow })\rangle $
.
$h_{w,w'}(\langle a,X\rangle )=\langle h_{w,w'}(a),X\cap (w{\uparrow })\rangle $
. -
• For each
 $w\in W$
,
$w\in W$
,
 $\multimap _{w}$
is a binary function from
$\multimap _{w}$
is a binary function from
 $\mathcal {C}_{w}\times \mathcal {C}_{w}\rightarrow \mathcal {T}_{w}$
.
$\mathcal {C}_{w}\times \mathcal {C}_{w}\rightarrow \mathcal {T}_{w}$
. -
• Whenever
 $wRw'$
,
$wRw'$
,
 $h_{w,w'}(c\multimap _{w}d)=h_{w,w'}(c)\multimap _{w'}h_{w,w'}(d)$
.
$h_{w,w'}(c\multimap _{w}d)=h_{w,w'}(c)\multimap _{w'}h_{w,w'}(d)$
.
Note that the functions
![]() $h_{w,w'}$
are now polymorphic, taking both topics from
$h_{w,w'}$
are now polymorphic, taking both topics from
![]() $\mathcal {T}_{w}$
and contents from
$\mathcal {T}_{w}$
and contents from
![]() $\mathcal {C}_{w}$
as arguments. Having made this remark, it is an appropriate time to be more explicit in how such contents are being represented in our models. We construct each set
$\mathcal {C}_{w}$
as arguments. Having made this remark, it is an appropriate time to be more explicit in how such contents are being represented in our models. We construct each set
![]() $\mathcal {C}_{w}$
by means of an intermediary—a function
$\mathcal {C}_{w}$
by means of an intermediary—a function
![]() $c_{w}$
assigning contents to sentences:
$c_{w}$
assigning contents to sentences:
Definition 5. We define a function
![]() $c_{w}$
. Where
$c_{w}$
. Where
![]() $\pi _{0}$
and
$\pi _{0}$
and
![]() $\pi _{1}$
are projection functions onto first and second coordinates, respectively, let
$\pi _{1}$
are projection functions onto first and second coordinates, respectively, let
![]() $c^{0}_{w}=\pi _{0}\circ c_{w}$
and
$c^{0}_{w}=\pi _{0}\circ c_{w}$
and
![]() $c^{1}_{w}=\pi _{1}\circ c_{w}$
. Then:
$c^{1}_{w}=\pi _{1}\circ c_{w}$
. Then:
-
•
 $c_{w}(p)=\langle t_{w}(p),v(p)\cap w{\uparrow }\rangle $
.
$c_{w}(p)=\langle t_{w}(p),v(p)\cap w{\uparrow }\rangle $
. -
•
 $c_{w}(\neg \varphi )=\langle c^{0}_{w}(\varphi ),w{\uparrow }\smallsetminus c^{1}_{w}(\varphi )\rangle $
.
$c_{w}(\neg \varphi )=\langle c^{0}_{w}(\varphi ),w{\uparrow }\smallsetminus c^{1}_{w}(\varphi )\rangle $
. -
•
 $c_{w}(\varphi \wedge \psi )=\langle c^{0}_{w}(\varphi )\oplus _{w}c^{0}_{w}(\psi ),c^{1}_{w}(\varphi )\cap c^{1}_{w}(\psi )\rangle $
.
$c_{w}(\varphi \wedge \psi )=\langle c^{0}_{w}(\varphi )\oplus _{w}c^{0}_{w}(\psi ),c^{1}_{w}(\varphi )\cap c^{1}_{w}(\psi )\rangle $
. -
•
 $c_{w}(\varphi \vee \psi )=\langle c^{0}_{w}(\varphi )\oplus _{w}c^{0}_{w}(\psi ),c^{1}_{w}(\varphi )\cup c^{1}_{w}(\psi )\rangle $
.
$c_{w}(\varphi \vee \psi )=\langle c^{0}_{w}(\varphi )\oplus _{w}c^{0}_{w}(\psi ),c^{1}_{w}(\varphi )\cup c^{1}_{w}(\psi )\rangle $
. -
•
 .
.
![]() $c_{w}$
assigns an element
$c_{w}$
assigns an element
![]() $c_{w}(\varphi )$
to each sentence in
$c_{w}(\varphi )$
to each sentence in
![]() $\mathcal {L}$
, which induces a succinct definition for each
$\mathcal {L}$
, which induces a succinct definition for each
![]() $\mathcal {C}_{w}$
:
$\mathcal {C}_{w}$
:
Definition 6. The set of contents
![]() $\mathcal {C}_{w}$
at a world w is the set
$\mathcal {C}_{w}$
at a world w is the set
![]() $c_{w}[\mathcal {L}]$
—the image of the language under
$c_{w}[\mathcal {L}]$
—the image of the language under
![]() $c_{w}$
$c_{w}$
One can note that an extension of each
![]() $t_{w}$
over the language follows by setting
$t_{w}$
over the language follows by setting
![]() $t_{w}(\varphi )=c^{0}_{w}(\varphi )$
. This allows us to retain the stock
$t_{w}(\varphi )=c^{0}_{w}(\varphi )$
. This allows us to retain the stock
![]() $\mathsf {CA}/\mathsf {PAI}$
truth conditions from Definition 3 and aids in the illumination of an important feature of the content assigned to a conditional
$\mathsf {CA}/\mathsf {PAI}$
truth conditions from Definition 3 and aids in the illumination of an important feature of the content assigned to a conditional
![]() $\varphi \rightarrow \psi $
.
$\varphi \rightarrow \psi $
.
We had used the notation
![]() for purposes of economy in Definition 5, which could be fully expressed in the following terms:
for purposes of economy in Definition 5, which could be fully expressed in the following terms:
![]() .
.
The interdependence of topic and proposition is clearly recognizable between this presentation and the assignment of
![]() $t_{w}(\varphi \rightarrow \psi )$
in Definition 5. The influence of truth conditions over topic is reflected in the sensitivity of the value
$t_{w}(\varphi \rightarrow \psi )$
in Definition 5. The influence of truth conditions over topic is reflected in the sensitivity of the value
![]() $c^{0}_{w}(\varphi \rightarrow \psi )$
to
$c^{0}_{w}(\varphi \rightarrow \psi )$
to
![]() $c^{1}_{w}(\varphi )$
and
$c^{1}_{w}(\varphi )$
and
![]() $c^{1}_{w}(\psi )$
while the converse case is seen for the topic-theoretic clause
$c^{1}_{w}(\psi )$
while the converse case is seen for the topic-theoretic clause
![]() $c^{0}_{w'}(\psi )\leq _{w'}c^{0}_{w'}(\varphi )$
that shapes the proposition
$c^{0}_{w'}(\psi )\leq _{w'}c^{0}_{w'}(\varphi )$
that shapes the proposition
![]() $c^{1}_{w}(\varphi \rightarrow \psi )$
.
$c^{1}_{w}(\varphi \rightarrow \psi )$
.
This interdependence also brings corresponding risks of interdefinition, e.g., hidden circularity in apparently recursive definitions. For this reason it is fitting to show that the models described above are in fact well-defined.
Observation 1.
![]() $\mathsf {S}/\mathsf {PAI}$
models are well-defined.
$\mathsf {S}/\mathsf {PAI}$
models are well-defined.
Proof. The content of any formula requires only that contents have been assigned to simpler formulae, e.g.,
![]() $\varphi \rightarrow \psi $
requires that the contents
$\varphi \rightarrow \psi $
requires that the contents
![]() $c_{w}(\varphi )$
and
$c_{w}(\varphi )$
and
![]() $c_{w}(\psi )$
have been determined only up to the complexity of
$c_{w}(\psi )$
have been determined only up to the complexity of
![]() $\varphi $
. Thus, all the machinery is determined iteratively from the functions
$\varphi $
. Thus, all the machinery is determined iteratively from the functions
![]() $t_{w}$
and v in tandem with the determination of
$t_{w}$
and v in tandem with the determination of
![]() $\Vdash $
.
$\Vdash $
.
We now turn our attention to matters of topic preservation.
Lemma 1. If
![]() $wRw'$
then
$wRw'$
then
![]() $h_{w,w'}(t_{w}(\varphi ))=t_{w'}(\varphi )$
and
$h_{w,w'}(t_{w}(\varphi ))=t_{w'}(\varphi )$
and
![]() $h_{w,w'}(c_{w}(\varphi ))=c_{w'}(\varphi )$
.
$h_{w,w'}(c_{w}(\varphi ))=c_{w'}(\varphi )$
.
Proof. The basis steps are established by definition, so suppose that the property holds of subformulae of
![]() $\varphi $
. In case
$\varphi $
. In case
![]() $\varphi $
is a conjunction, we have
$\varphi $
is a conjunction, we have
 $$ \begin{align*} \begin{array}{lcc} h_{w,w'}(c_{w}(\psi\wedge\xi)) & = &h_{w,w'}(\langle t_{w}(\psi)\oplus_{w} t_{w}(\xi),c^{1}_{w}(\psi)\cap c^{1}_{w}(\xi))\rangle\\ & = &\langle h_{w,w'}(t_{w}(\psi))\oplus_{w'} h_{w,w'}(t_{w}(\xi)), (c^{1}_{w}(\psi)\cap c^{1}_{w}(\xi))\cap w'{\uparrow}\rangle\\ & = &\langle t_{w'}(\psi)\oplus_{w'} t_{w'}(\xi), (c^{1}_{w}(\psi)\cap w'{\uparrow})\cap(c^{1}_{w}(\xi)\cap w'{\uparrow})\rangle\\ & = &\langle t_{w'}(\psi)\oplus_{w'} t_{w'}(\xi), c^{1}_{w'}(\psi)\cap c^{1}_{w'}(\xi))\rangle\\ & = &c_{w'}(\psi\wedge\xi). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lcc} h_{w,w'}(c_{w}(\psi\wedge\xi)) & = &h_{w,w'}(\langle t_{w}(\psi)\oplus_{w} t_{w}(\xi),c^{1}_{w}(\psi)\cap c^{1}_{w}(\xi))\rangle\\ & = &\langle h_{w,w'}(t_{w}(\psi))\oplus_{w'} h_{w,w'}(t_{w}(\xi)), (c^{1}_{w}(\psi)\cap c^{1}_{w}(\xi))\cap w'{\uparrow}\rangle\\ & = &\langle t_{w'}(\psi)\oplus_{w'} t_{w'}(\xi), (c^{1}_{w}(\psi)\cap w'{\uparrow})\cap(c^{1}_{w}(\xi)\cap w'{\uparrow})\rangle\\ & = &\langle t_{w'}(\psi)\oplus_{w'} t_{w'}(\xi), c^{1}_{w'}(\psi)\cap c^{1}_{w'}(\xi))\rangle\\ & = &c_{w'}(\psi\wedge\xi). \end{array} \end{align*} $$
This gives us identity of
![]() $h_{w,w'}(t_{w}(\varphi ))$
and
$h_{w,w'}(t_{w}(\varphi ))$
and
![]() $t_{w'}(\varphi )$
for free. Simple modifications yield arguments to establish the cases of disjunction or material conditional.
$t_{w'}(\varphi )$
for free. Simple modifications yield arguments to establish the cases of disjunction or material conditional.
The proof of a conditional
![]() $\psi \rightarrow \xi $
is slightly more interesting. Note briefly that
$\psi \rightarrow \xi $
is slightly more interesting. Note briefly that
when
![]() $wRw'$
. Then:
$wRw'$
. Then:

Again, as
![]() $t_{w}(\psi \rightarrow \xi )=c^{0}_{w}(\psi \rightarrow \xi )$
, the case of
$t_{w}(\psi \rightarrow \xi )=c^{0}_{w}(\psi \rightarrow \xi )$
, the case of
![]() $t_{w}$
follows trivially from the case of
$t_{w}$
follows trivially from the case of
![]() $c_{w}$
.
$c_{w}$
.
Lemma 1 straightforwardly leads to the persistence of topic inclusion for all formulae.
Lemma 2. If
![]() $t_{w}(\varphi )\leq _{w} t_{w}(\psi )$
and
$t_{w}(\varphi )\leq _{w} t_{w}(\psi )$
and
![]() $wRw'$
then
$wRw'$
then
![]() $t_{w'}(\varphi )\leq _{w'} t_{w'}(\psi )$
.
$t_{w'}(\varphi )\leq _{w'} t_{w'}(\psi )$
.
Proof. Expand the identity
![]() $t_{w}(\varphi )\leq _{w} t_{w}(\psi )$
to
$t_{w}(\varphi )\leq _{w} t_{w}(\psi )$
to
![]() $t_{w}(\varphi )\oplus _{w}t_{w}(\psi )=t_{w}(\psi )$
and apply
$t_{w}(\varphi )\oplus _{w}t_{w}(\psi )=t_{w}(\psi )$
and apply
![]() $h_{w,w'}$
to yield
$h_{w,w'}$
to yield
![]() $h_{w,w'}(t_{w}(\varphi )\oplus _{w}t_{w}(\psi ))=h_{w,w'}(t_{w}(\psi ))$
. As
$h_{w,w'}(t_{w}(\varphi )\oplus _{w}t_{w}(\psi ))=h_{w,w'}(t_{w}(\psi ))$
. As
![]() $h_{w,w'}$
preserves structure, we infer
$h_{w,w'}$
preserves structure, we infer
![]() $h_{w,w'}(t_{w}(\varphi ))\oplus _{w'}h_{w,w'}(t_{w}(\psi ))=h_{w,w'}(t_{w}(\psi ))$
, which by appeal to Lemma 1 yields
$h_{w,w'}(t_{w}(\varphi ))\oplus _{w'}h_{w,w'}(t_{w}(\psi ))=h_{w,w'}(t_{w}(\psi ))$
, which by appeal to Lemma 1 yields
![]() $t_{w'}(\varphi )\oplus _{w'}t_{w'}(\psi )=t_{w'}(\psi )$
. Of course, this is just to say that
$t_{w'}(\varphi )\oplus _{w'}t_{w'}(\psi )=t_{w'}(\psi )$
. Of course, this is just to say that
![]() $t_{w'}(\varphi )\leq _{w'}t_{w'}(\psi )$
as needed.
$t_{w'}(\varphi )\leq _{w'}t_{w'}(\psi )$
as needed.
Now, we offer a definition for validity in
![]() $\mathsf {S}/\mathsf {PAI}$
in a standard fashion:
$\mathsf {S}/\mathsf {PAI}$
in a standard fashion:
Definition 7.
![]() $\Gamma \vDash _{\mathsf {S}/\mathsf {PAI}}\varphi $
if for all points w in all
$\Gamma \vDash _{\mathsf {S}/\mathsf {PAI}}\varphi $
if for all points w in all
![]() $\mathsf {S}/\mathsf {PAI}$
models, if
$\mathsf {S}/\mathsf {PAI}$
models, if
![]() $w\Vdash \gamma $
for each
$w\Vdash \gamma $
for each
![]() $\gamma \in \Gamma $
, also
$\gamma \in \Gamma $
, also
![]() $w\Vdash \varphi $
.
$w\Vdash \varphi $
.
Having defined validity, we can now proceed to examine some logical features of
![]() $\mathsf {S}/\mathsf {PAI}$
. As a consequence of Lemma 2, we get the following easily:
$\mathsf {S}/\mathsf {PAI}$
. As a consequence of Lemma 2, we get the following easily:
Lemma 3. In an
![]() $\mathsf {S}/\mathsf {PAI}$
model, if
$\mathsf {S}/\mathsf {PAI}$
model, if
![]() $wRw'$
, then if
$wRw'$
, then if
![]() $w\Vdash \varphi \rightarrow \psi $
then
$w\Vdash \varphi \rightarrow \psi $
then
![]() $w'\Vdash \varphi \rightarrow \psi $
.
$w'\Vdash \varphi \rightarrow \psi $
.
In order to produce a maximally modular and minimally dogmatic tool, no properties beyond its functionality are imposed on each
![]() $\multimap _{w}$
. As it turns out, functionality alone is enough to secure a number of intuitively correct validities:
$\multimap _{w}$
. As it turns out, functionality alone is enough to secure a number of intuitively correct validities:
Proposition 1. The following are valid in state-sensitive
![]() $\mathsf {S}/\mathsf {PAI}$
models:
$\mathsf {S}/\mathsf {PAI}$
models:
-
•
 $((\varphi \wedge \psi )\rightarrow \xi )\rightarrow ((\psi \wedge \varphi )\rightarrow \xi )$
.
$((\varphi \wedge \psi )\rightarrow \xi )\rightarrow ((\psi \wedge \varphi )\rightarrow \xi )$
. -
•
 $(\varphi \rightarrow (\psi \vee \xi ))\rightarrow (\varphi \rightarrow (\xi \vee \psi ))$
.
$(\varphi \rightarrow (\psi \vee \xi ))\rightarrow (\varphi \rightarrow (\xi \vee \psi ))$
.
In other words, applying commutation—or distribution or DeMorgan’s laws—to the antecedent or consequent of an intensional conditional remains topic-preserving in this setting. In contrast, there are some surprising cases in which entailments valid in
![]() $\mathsf {CA}/\mathsf {PAI}$
turn out invalid in the weaker
$\mathsf {CA}/\mathsf {PAI}$
turn out invalid in the weaker
![]() $\mathsf {S}/\mathsf {PAI}$
. Consider the axiom
$\mathsf {S}/\mathsf {PAI}$
. Consider the axiom
![]() $[R]$
:
$[R]$
:
Despite some intuitive appeal—which we will soon review—the framework is not adequate to ensure its validity.
Proposition 2. The axiom
![]() $[R]$
is not valid in state-sensitive
$[R]$
is not valid in state-sensitive
![]() $\mathsf {S}/\mathsf {PAI}$
models.
$\mathsf {S}/\mathsf {PAI}$
models.
Proof. Consider a simple countermodel with two worlds, w and
![]() $w'$
with
$w'$
with
![]() $wRw'$
, both of which make p and q true, while r is true only at
$wRw'$
, both of which make p and q true, while r is true only at
![]() $w'$
. Also, let
$w'$
. Also, let
![]() $\mathcal {T}_{w}$
include distinct elements a and b with
$\mathcal {T}_{w}$
include distinct elements a and b with
![]() $a\leq _{w} b$
, taking special note that
$a\leq _{w} b$
, taking special note that
![]() $t_{w}(p\vee q)=t_{w}(p\wedge q)$
. Finally, assume of
$t_{w}(p\vee q)=t_{w}(p\wedge q)$
. Finally, assume of
![]() $\multimap _{w}$
merely that for contents
$\multimap _{w}$
merely that for contents
![]() $d,e\in \mathcal {C}_{w}$
,
$d,e\in \mathcal {C}_{w}$
,
![]() $\pi _{0}(d\multimap _{w}e)=a$
if
$\pi _{0}(d\multimap _{w}e)=a$
if
![]() $\pi _{0}(d)=\lbrace w,w'\rbrace $
and
$\pi _{0}(d)=\lbrace w,w'\rbrace $
and
![]() $\pi _{0}(d\multimap _{w}e)=b$
if
$\pi _{0}(d\multimap _{w}e)=b$
if
![]() $\pi _{0}(d)=\lbrace w'\rbrace $
. Then because
$\pi _{0}(d)=\lbrace w'\rbrace $
. Then because
![]() and
and
![]() ,
,
Thus,
![]() $w\nVdash ((p\vee q)\rightarrow r)\rightarrow ((p\wedge q)\rightarrow r)$
as the requisite subject-matter inclusion condition is not satisfied.
$w\nVdash ((p\vee q)\rightarrow r)\rightarrow ((p\wedge q)\rightarrow r)$
as the requisite subject-matter inclusion condition is not satisfied.
The state-sensitive
![]() $\mathsf {S}/\mathsf {PAI}$
models can be shown to allow the same modularity and degree of semantic control as the
$\mathsf {S}/\mathsf {PAI}$
models can be shown to allow the same modularity and degree of semantic control as the
![]() $\mathsf {CA}/\mathsf {PAI}$
models of Definition 1. This can receive a tentative illustration through describing a semantic condition on
$\mathsf {CA}/\mathsf {PAI}$
models of Definition 1. This can receive a tentative illustration through describing a semantic condition on
![]() $\multimap _{w}$
that guarantees the validity of
$\multimap _{w}$
that guarantees the validity of
![]() $((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
. It is desirable that such semantic conditions are elegant and admit natural interpretations. To this end, we pause to reconsider the proof of Proposition 2 (an activity serving as a preparatory exercise in anticipation of investigating extensions of
$((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
. It is desirable that such semantic conditions are elegant and admit natural interpretations. To this end, we pause to reconsider the proof of Proposition 2 (an activity serving as a preparatory exercise in anticipation of investigating extensions of
![]() $\mathsf {S}/\mathsf {PAI}$
in the sequel).
$\mathsf {S}/\mathsf {PAI}$
in the sequel).
The countermodel of Proposition 2 was constructed to interdict the content-inclusion requirement that
![]() $c_{w}(p\wedge q)\multimap _{w}c_{w}(r)\leq _{w}c_{w}(p\vee q)\multimap _{w}c_{w}(r)$
, thereby falsifying the target formula. Intuitively, such a move appears to conflict with our earlier discussion of this section. To make the potential conflict more clear, note that
$c_{w}(p\wedge q)\multimap _{w}c_{w}(r)\leq _{w}c_{w}(p\vee q)\multimap _{w}c_{w}(r)$
, thereby falsifying the target formula. Intuitively, such a move appears to conflict with our earlier discussion of this section. To make the potential conflict more clear, note that
![]() guarantees that the states that
guarantees that the states that
![]() $(p\wedge q)\rightarrow r$
is about are included among the states that
$(p\wedge q)\rightarrow r$
is about are included among the states that
![]() $(p\vee q)\rightarrow r$
is about, i.e.,
$(p\vee q)\rightarrow r$
is about, i.e.,
![]() $(p\vee q)\rightarrow r$
is about at least as much as
$(p\vee q)\rightarrow r$
is about at least as much as
![]() $(p\wedge q)\rightarrow r$
(and possibly more). Moreover, the subject-matters of the sentences’ antecedents and consequents, respectively, are identical to one another. Consequently, every constituent determining the subject-matter of
$(p\wedge q)\rightarrow r$
(and possibly more). Moreover, the subject-matters of the sentences’ antecedents and consequents, respectively, are identical to one another. Consequently, every constituent determining the subject-matter of
![]() $(p\wedge q)\rightarrow r$
is included in a constituent of the subject-matter of
$(p\wedge q)\rightarrow r$
is included in a constituent of the subject-matter of
![]() $(p\wedge q)\rightarrow r$
. In a very real sense, the topic of
$(p\wedge q)\rightarrow r$
. In a very real sense, the topic of
![]() $(p\vee q)\rightarrow r$
ought to include the topic of
$(p\vee q)\rightarrow r$
ought to include the topic of
![]() $(p\wedge q)\rightarrow r$
.
$(p\wedge q)\rightarrow r$
.
It might be seen as counterintuitive that this inclusion would not be respected by semantic conditions governing the situation-theoretic subject-matters of the complexes. The foregoing reflections on the determination of the subject-matter of intensional conditionals in practice directly translate to a semantic condition that enforces the validity of
![]() $[R]$
:
$[R]$
:
Definition 8. An
![]() $\mathsf {S}/\mathsf {PAI}$
model is propositionally monotonic if for all w and contents
$\mathsf {S}/\mathsf {PAI}$
model is propositionally monotonic if for all w and contents
![]() $d,e,f\in \mathcal {C}_{w}$
,
$d,e,f\in \mathcal {C}_{w}$
,
This property of propositional monotonicity is at least strong enough to ensure the validity of
![]() $[R]$
:
$[R]$
:
Observation 2. The axiom
![]() $[R]$
is valid in propositionally monotonic models.
$[R]$
is valid in propositionally monotonic models.
Proof. To prove that the satisfaction of the condition entails validity of the sentence, assume that the condition holds. First, we cover the alethic component by observing that for arbitrary w, whenever
![]() $w\Vdash (\varphi \vee \psi )\rightarrow \xi $
, it follows that
$w\Vdash (\varphi \vee \psi )\rightarrow \xi $
, it follows that
![]() $w\Vdash (\varphi \wedge \psi )\rightarrow \xi $
. Assume that
$w\Vdash (\varphi \wedge \psi )\rightarrow \xi $
. Assume that
![]() $w\Vdash (\varphi \vee \psi )\rightarrow \xi $
. Then at any
$w\Vdash (\varphi \vee \psi )\rightarrow \xi $
. Then at any
![]() $w'$
such that
$w'$
such that
![]() $wRw'$
, should
$wRw'$
, should
![]() $w'\Vdash \varphi \wedge \psi $
, also
$w'\Vdash \varphi \wedge \psi $
, also
![]() $w'\Vdash \varphi \vee \psi $
, which, by hypothesis, entails that
$w'\Vdash \varphi \vee \psi $
, which, by hypothesis, entails that
![]() $w'\Vdash \xi $
. Also, because
$w'\Vdash \xi $
. Also, because
![]() $t_{w}(\varphi \vee \psi )=t_{w}(\varphi \wedge \psi )$
, whenever
$t_{w}(\varphi \vee \psi )=t_{w}(\varphi \wedge \psi )$
, whenever
![]() $t_{w}(\xi )\leq _{w} t_{w}(\varphi \vee \psi )$
, it follows that
$t_{w}(\xi )\leq _{w} t_{w}(\varphi \vee \psi )$
, it follows that
![]() $t(\xi )_{w}\leq _{w} t_{w}(\varphi \wedge \psi )$
. Thus
$t(\xi )_{w}\leq _{w} t_{w}(\varphi \wedge \psi )$
. Thus
![]() $w\Vdash (\varphi \wedge \psi )\rightarrow \xi $
. To establish content inclusion, note that because
$w\Vdash (\varphi \wedge \psi )\rightarrow \xi $
. To establish content inclusion, note that because
![]() $t_{w}(\varphi \vee \psi )=t_{w}(\varphi \wedge \psi )$
and
$t_{w}(\varphi \vee \psi )=t_{w}(\varphi \wedge \psi )$
and
![]() , the condition guarantees that
, the condition guarantees that
![]() $c_{w}(\varphi \wedge \psi )\multimap _{w}c_{w}(\xi )\leq _{w} c_{w}(\varphi \vee \psi )\multimap _{w}c_{w}(\xi )$
, i.e.,
$c_{w}(\varphi \wedge \psi )\multimap _{w}c_{w}(\xi )\leq _{w} c_{w}(\varphi \vee \psi )\multimap _{w}c_{w}(\xi )$
, i.e.,
![]() $t_{w}((\varphi \wedge \psi )\rightarrow \xi )\leq _{w} t_{w}((\varphi \vee \psi )\rightarrow \xi )$
. Between these two observations, we conclude that for every w,
$t_{w}((\varphi \wedge \psi )\rightarrow \xi )\leq _{w} t_{w}((\varphi \vee \psi )\rightarrow \xi )$
. Between these two observations, we conclude that for every w,
![]() $w\Vdash ((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
.
$w\Vdash ((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
.
We have not yet introduced sufficient machinery to go further and investigate whether the condition is characteristic for the extension of
![]() $\mathsf {S}/\mathsf {PAI}$
including
$\mathsf {S}/\mathsf {PAI}$
including
![]() $((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
. We will return to this question in Section 4.4.
$((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
. We will return to this question in Section 4.4.
3.3 Axioms for state sensitive analytic implication
Having introduced its model theory, we now turn to a modification of Parry’s axioms for
![]() $\mathsf {PAI}$
to introduce a Hilbert-style calculus for
$\mathsf {PAI}$
to introduce a Hilbert-style calculus for
![]() $\mathsf {S}/\mathsf {PAI}$
.
$\mathsf {S}/\mathsf {PAI}$
.
Our formulation borrows the following idiom from the presentation of
![]() $\mathsf {CA}/\mathsf {PAI}$
in [Reference Ferguson13]: Interpreting axioms of the form
$\mathsf {CA}/\mathsf {PAI}$
in [Reference Ferguson13]: Interpreting axioms of the form
![]() $\varphi \rightarrow \psi $
in which
$\varphi \rightarrow \psi $
in which
![]() $\varphi $
or
$\varphi $
or
![]() $\psi $
have
$\psi $
have
![]() $\rightarrow $
as the primary connective encapsulate principles concerning the topics of conditionals, the adoption of any such axiom restricts the generality of the framework. In such cases, we follow a pattern of replacing the main
$\rightarrow $
as the primary connective encapsulate principles concerning the topics of conditionals, the adoption of any such axiom restricts the generality of the framework. In such cases, we follow a pattern of replacing the main
![]() $\rightarrow $
operator of an axiom
$\rightarrow $
operator of an axiom
![]() $[An]$
by a material
$[An]$
by a material
![]() to yield an axiom labeled as
to yield an axiom labeled as
![]() $[An^{\dagger }]$
. In all cases, we preserve as much of
$[An^{\dagger }]$
. In all cases, we preserve as much of
![]() $\mathsf {PAI}$
and
$\mathsf {PAI}$
and
![]() $\mathsf {CA}/\mathsf {PAI}$
as possible without running afoul of our guiding principles.
$\mathsf {CA}/\mathsf {PAI}$
as possible without running afoul of our guiding principles.
Two notational comments must precede the introduction of the Hilbert calculus. First, we inherit Parry’s notation so that when
![]() $f(\varphi )$
is a formula in which
$f(\varphi )$
is a formula in which
![]() $\varphi $
appears,
$\varphi $
appears,
![]() $f(\psi )$
is a formula resulting from the replacement of one or more instances of
$f(\psi )$
is a formula resulting from the replacement of one or more instances of
![]() $\varphi $
with
$\varphi $
with
![]() $\psi $
in
$\psi $
in
![]() $f(\varphi )$
. Second, we use the notation
$f(\varphi )$
. Second, we use the notation
![]() $\mathbf {t}_{\varphi }$
as shorthand for the formula
$\mathbf {t}_{\varphi }$
as shorthand for the formula
![]() .Footnote
7
With these notational issues covered, we are equipped to describe an axiomatization of
.Footnote
7
With these notational issues covered, we are equipped to describe an axiomatization of
![]() $\mathsf {S}/\mathsf {PAI}$
:
$\mathsf {S}/\mathsf {PAI}$
:
Definition 9. The logic of state-sensitive analytic implication
![]() $\mathsf {S}/\mathsf {PAI}$
is determined by the following axioms:
$\mathsf {S}/\mathsf {PAI}$
is determined by the following axioms:

and rules:

Consequence can be defined in a familiar way:
Definition 10.
![]() $\Gamma \vdash _{\mathsf {S}/\mathsf {PAI}}\varphi $
if there is a Hilbert-style proof from assumptions
$\Gamma \vdash _{\mathsf {S}/\mathsf {PAI}}\varphi $
if there is a Hilbert-style proof from assumptions
![]() $\Gamma $
terminating with the formula
$\Gamma $
terminating with the formula
![]() $\varphi $
.
$\varphi $
.
Let us conclude with further proof-theoretic observations. It was shown in [Reference Ferguson13] that the simple
![]() $\mathsf {PAI}$
theorems described by Dunn as “normal form theorems” in [Reference Dunn10] continue to hold in
$\mathsf {PAI}$
theorems described by Dunn as “normal form theorems” in [Reference Dunn10] continue to hold in
![]() $\mathsf {CA}/\mathsf {PAI}$
. Happily, these “normal form theorems” remain provable in
$\mathsf {CA}/\mathsf {PAI}$
. Happily, these “normal form theorems” remain provable in
![]() $\mathsf {S}/\mathsf {PAI}$
as well. We single out several useful theorems for their utility in what follows:
$\mathsf {S}/\mathsf {PAI}$
as well. We single out several useful theorems for their utility in what follows:
Lemma 4. The following are provable:
 $$ \begin{align*} \begin{aligned} [T9] &\quad \varphi\vee\varphi\leftrightarrow\varphi, & & [T16] & \neg(\varphi\wedge\psi)\leftrightarrow(\neg\varphi\vee\neg\psi), \\ [ID] &\quad \varphi\rightarrow\varphi, & &[S2] & (\varphi\vee\neg\varphi\vee\psi)\rightarrow(\varphi\vee\neg\varphi). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} [T9] &\quad \varphi\vee\varphi\leftrightarrow\varphi, & & [T16] & \neg(\varphi\wedge\psi)\leftrightarrow(\neg\varphi\vee\neg\psi), \\ [ID] &\quad \varphi\rightarrow\varphi, & &[S2] & (\varphi\vee\neg\varphi\vee\psi)\rightarrow(\varphi\vee\neg\varphi). \end{aligned} \end{align*} $$
4 Metatheoretical features of
 $\mathsf {S}/\mathsf {PAI}$
$\mathsf {S}/\mathsf {PAI}$
The foregoing section laid out a number of definitions whose utility critically depends on our establishing certain metatheoretical results. This section includes the metatheoretical investigations necessary to justify our definitions concerning
![]() $\mathsf {S}/\mathsf {PAI}$
.
$\mathsf {S}/\mathsf {PAI}$
.
4.1 Soundness of the axioms
Soundness requires establishing that the axioms of Definition 9 are valid, that is, true at every point in any
![]() $\mathsf {S}/\mathsf {PAI}$
model and that the rules preserve truth. In this section, we will consider the axioms in order, prioritizing proofs of the less obvious cases.
$\mathsf {S}/\mathsf {PAI}$
model and that the rules preserve truth. In this section, we will consider the axioms in order, prioritizing proofs of the less obvious cases.
Observation 3. Axioms
![]() $[A1]$
–
$[A1]$
–
![]() $[A5]$
are valid.
$[A5]$
are valid.
Proof. Each of axioms
![]() $[A1]$
–
$[A1]$
–
![]() $[A5]$
is of the form
$[A5]$
is of the form
![]() $\varphi \rightarrow \varphi '$
where both
$\varphi \rightarrow \varphi '$
where both
![]() $t_{w}(\varphi )=t_{w}(\varphi ')$
and
$t_{w}(\varphi )=t_{w}(\varphi ')$
and
![]() . These facts suffice to ensure that
. These facts suffice to ensure that
![]() $w\Vdash \varphi \rightarrow \varphi '$
holds.
$w\Vdash \varphi \rightarrow \varphi '$
holds.
Observation 4. Axiom
![]() $[A6]$
and axioms
$[A6]$
and axioms
![]() $[A7^{\dagger }]$
–
$[A7^{\dagger }]$
–
![]() $[A11^{\dagger }]$
are valid.
$[A11^{\dagger }]$
are valid.
Proof. Because
![]() $t_{w}(\varphi )\leq _{w} t_{w}(\varphi )\oplus _{w} t_{w}(\psi \wedge \neg \psi )=t_{w}(\varphi \vee (\psi \wedge \neg \psi ))$
, an appropriate topic inclusion relationship is guaranteed to hold for
$t_{w}(\varphi )\leq _{w} t_{w}(\varphi )\oplus _{w} t_{w}(\psi \wedge \neg \psi )=t_{w}(\varphi \vee (\psi \wedge \neg \psi ))$
, an appropriate topic inclusion relationship is guaranteed to hold for
![]() $[A6]$
at any point w. Further, consistency dictates that for any w at which
$[A6]$
at any point w. Further, consistency dictates that for any w at which
![]() $\varphi \vee (\psi \wedge \neg \psi )$
is true, the formula
$\varphi \vee (\psi \wedge \neg \psi )$
is true, the formula
![]() $\varphi $
is the only satisfiable disjunct, whence
$\varphi $
is the only satisfiable disjunct, whence
![]() $w\Vdash \varphi $
. These observations jointly ensure the validity of
$w\Vdash \varphi $
. These observations jointly ensure the validity of
![]() $[A6]$
. The validity of the axioms
$[A6]$
. The validity of the axioms
![]() $[A7^{\dagger }]$
–
$[A7^{\dagger }]$
–
![]() $[A11^{\dagger }]$
can be easily established along similar lines.
$[A11^{\dagger }]$
can be easily established along similar lines.
To prove validity of axiom
![]() $[A12^{\dagger }]$
, we provide an introductory lemma.
$[A12^{\dagger }]$
, we provide an introductory lemma.
Lemma 5. Say that formulae
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are w-indiscernible if
$\psi $
are w-indiscernible if
![]() $c_{w}(\varphi )=c_{w}(\psi )$
. Then for w-indiscernible
$c_{w}(\varphi )=c_{w}(\psi )$
. Then for w-indiscernible
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
,
$\psi $
,
![]() $f(\varphi )$
and
$f(\varphi )$
and
![]() $f(\psi )$
will also be w-indiscernible.
$f(\psi )$
will also be w-indiscernible.
Proof. We prove this by induction on complexity of the depth in which
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are nested in
$\psi $
are nested in
![]() $f(\varphi )$
and
$f(\varphi )$
and
![]() $f(\psi )$
, respectively. For basis step, note that when the depth is zero,
$f(\psi )$
, respectively. For basis step, note that when the depth is zero,
![]() $f(\varphi )=\varphi $
, in which case
$f(\varphi )=\varphi $
, in which case
![]() $f(\psi )=\psi $
and w-indiscernibility follows trivially. As induction hypothesis, assume w-indiscernibility of
$f(\psi )=\psi $
and w-indiscernibility follows trivially. As induction hypothesis, assume w-indiscernibility of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
and let
$\psi $
and let
![]() $\psi $
be an immediate subformula of
$\psi $
be an immediate subformula of
![]() $f(\psi )$
in each of the following cases:
$f(\psi )$
in each of the following cases:
![]() $\bullet $
When
$\bullet $
When
![]() $f(\psi )=\neg \psi $
, Negation Transparency entails
$f(\psi )=\neg \psi $
, Negation Transparency entails
![]() $t_{w}(\neg \varphi )=t_{w}(\neg \psi )$
and because
$t_{w}(\neg \varphi )=t_{w}(\neg \psi )$
and because
![]() , it also follows that
, it also follows that
![]() . So
. So
![]() $c_{w}(f(\varphi ))=c_{w}(f(\psi ))$
.
$c_{w}(f(\varphi ))=c_{w}(f(\psi ))$
.
![]() $\bullet $
For conjunction, suppose without loss of generality that
$\bullet $
For conjunction, suppose without loss of generality that
![]() $f(\psi )=\psi \wedge \xi $
. The definition of
$f(\psi )=\psi \wedge \xi $
. The definition of
![]() $\oplus _{w}$
ensures that
$\oplus _{w}$
ensures that
![]() $t_{w}(\varphi \wedge \xi )=t_{w}(\psi \wedge \xi )$
and set-theoretic operations ensure that
$t_{w}(\varphi \wedge \xi )=t_{w}(\psi \wedge \xi )$
and set-theoretic operations ensure that
![]() , whence
, whence
![]() $c_{w}(f(\varphi ))=c_{w}(f(\psi ))$
. The argument holds mutatis mutandis for disjunction and the material conditional.
$c_{w}(f(\varphi ))=c_{w}(f(\psi ))$
. The argument holds mutatis mutandis for disjunction and the material conditional.
![]() $\bullet $
For the case in which
$\bullet $
For the case in which
![]() $f(\psi )=\psi \rightarrow \xi $
, the functionality of
$f(\psi )=\psi \rightarrow \xi $
, the functionality of
![]() $\multimap _{w}$
and w-indiscernibility of
$\multimap _{w}$
and w-indiscernibility of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
jointly ensure that
$\psi $
jointly ensure that
![]() $c_{w}(\varphi )\multimap _{w}c_{w}(\xi )=c_{w}(\psi )\multimap _{w}c_{w}(\xi )$
, whence
$c_{w}(\varphi )\multimap _{w}c_{w}(\xi )=c_{w}(\psi )\multimap _{w}c_{w}(\xi )$
, whence
![]() $c^{0}_{w}(\varphi \rightarrow \xi )=c^{0}_{w}(\psi \rightarrow \xi )$
. Likewise, the truth-theoretic and topic-theoretic identity between the antecedents establishes that
$c^{0}_{w}(\varphi \rightarrow \xi )=c^{0}_{w}(\psi \rightarrow \xi )$
. Likewise, the truth-theoretic and topic-theoretic identity between the antecedents establishes that
![]() , which ensures that
, which ensures that
![]() $c^{1}_{w}(\varphi \rightarrow \xi )=c^{1}_{w}(\psi \rightarrow \xi )$
. Together,
$c^{1}_{w}(\varphi \rightarrow \xi )=c^{1}_{w}(\psi \rightarrow \xi )$
. Together,
![]() $c_{w}(\varphi \rightarrow \xi )=c_{w}(\psi \rightarrow \xi )$
as well. The case in which
$c_{w}(\varphi \rightarrow \xi )=c_{w}(\psi \rightarrow \xi )$
as well. The case in which
![]() $f(\psi )=\xi \rightarrow \psi $
follows along similar lines.
$f(\psi )=\xi \rightarrow \psi $
follows along similar lines.
Induction easily establishes the property that w-indiscernibility of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
entails w-indiscernibility of any
$\psi $
entails w-indiscernibility of any
![]() $f(\varphi )$
and
$f(\varphi )$
and
![]() $f(\psi )$
irrespective of the depth in which
$f(\psi )$
irrespective of the depth in which
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are nested.
$\psi $
are nested.
Observation 5. Axiom
![]() $[A12^{\dagger }]$
is valid.
$[A12^{\dagger }]$
is valid.
Proof. To prove validity, assume that
![]() $w\Vdash (\varphi \leftrightarrow \psi )\wedge f(\varphi )$
. That
$w\Vdash (\varphi \leftrightarrow \psi )\wedge f(\varphi )$
. That
![]() $w\Vdash \varphi \leftrightarrow \psi $
guarantees that
$w\Vdash \varphi \leftrightarrow \psi $
guarantees that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are w-indiscernible. By Lemma 5, we infer w-indiscernibility of
$\psi $
are w-indiscernible. By Lemma 5, we infer w-indiscernibility of
![]() $f(\varphi )$
and
$f(\varphi )$
and
![]() $f(\psi )$
, whence
$f(\psi )$
, whence
![]() . Thus, because
. Thus, because
![]() $w\Vdash f(\varphi )$
, it follows that
$w\Vdash f(\varphi )$
, it follows that
![]() $w\Vdash f(\psi )$
.
$w\Vdash f(\psi )$
.
Observation 6. Axiom
![]() $[A14^{\dagger }]$
is valid.
$[A14^{\dagger }]$
is valid.
Proof. If
![]() $\neg \varphi \rightarrow \varphi $
holds at w,
$\neg \varphi \rightarrow \varphi $
holds at w,
![]() $\varphi $
must hold at every point in
$\varphi $
must hold at every point in
![]() $w{\uparrow }$
. In case
$w{\uparrow }$
. In case
![]() $\varphi \rightarrow \psi $
holds at w as well,
$\varphi \rightarrow \psi $
holds at w as well,
![]() $\psi $
must also hold at every point in
$\psi $
must also hold at every point in
![]() $w{\uparrow }$
, whence it holds vacuously that for every
$w{\uparrow }$
, whence it holds vacuously that for every
![]() $w'\in w{\uparrow }$
at which
$w'\in w{\uparrow }$
at which
![]() $\neg \psi $
is true,
$\neg \psi $
is true,
![]() $\psi $
is true. By Negation Transparency,
$\psi $
is true. By Negation Transparency,
![]() $t_{w}(\neg \psi )=t_{w}(\psi )$
, ensuring that the axiom is valid.
$t_{w}(\neg \psi )=t_{w}(\psi )$
, ensuring that the axiom is valid.
Observation 7. Axiom
![]() $[D2]$
is valid.
$[D2]$
is valid.
Proof. Suppose
![]() $w\Vdash \varphi \rightarrow \psi $
. Then by Lemma 2,
$w\Vdash \varphi \rightarrow \psi $
. Then by Lemma 2,
![]() $\varphi \rightarrow \psi $
will continue to hold at all
$\varphi \rightarrow \psi $
will continue to hold at all
![]() $w'\in w{\uparrow }$
, whence it vacuously holds that all accessible points making true
$w'\in w{\uparrow }$
, whence it vacuously holds that all accessible points making true
![]() $\neg (\varphi \rightarrow \psi )$
also make true
$\neg (\varphi \rightarrow \psi )$
also make true
![]() $\varphi \rightarrow \psi $
. By Negation Transparency,
$\varphi \rightarrow \psi $
. By Negation Transparency,
![]() $t_{w}(\neg (\varphi \rightarrow \psi ))=t_{w}(\varphi \rightarrow \psi )$
. As the truth-theoretic and topic-theoretic conditions are met, it follows that
$t_{w}(\neg (\varphi \rightarrow \psi ))=t_{w}(\varphi \rightarrow \psi )$
. As the truth-theoretic and topic-theoretic conditions are met, it follows that
![]() $w\Vdash \neg (\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \psi )$
.
$w\Vdash \neg (\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \psi )$
.
Observation 8. Axioms
![]() $[S1]$
and
$[S1]$
and
![]() $[S3]$
are valid.
$[S3]$
are valid.
Proof. As
![]() $\mathbf {t}_{\varphi }$
—and thus
$\mathbf {t}_{\varphi }$
—and thus
![]() $\mathbf {t}_{\varphi }\vee \xi $
—is true at every point, every point w trivially satisfies the truth-theoretic conditions for both
$\mathbf {t}_{\varphi }\vee \xi $
—is true at every point, every point w trivially satisfies the truth-theoretic conditions for both
![]() $[S1]$
and
$[S1]$
and
![]() $[S3]$
. It is easily confirmed that both
$[S3]$
. It is easily confirmed that both
![]() $t_{w}(\mathbf {t}_{\varphi })\leq _{w}t_{w}(\varphi )$
and
$t_{w}(\mathbf {t}_{\varphi })\leq _{w}t_{w}(\varphi )$
and
![]() $t_{w}(\mathbf {t}_{\varphi }\vee \xi )\leq _{w}t_{w}(\mathbf {t}_{\varphi }\vee \psi \vee \xi )$
hold at any w, whence the axioms’ respective topic-theoretic conditions are also met.
$t_{w}(\mathbf {t}_{\varphi }\vee \xi )\leq _{w}t_{w}(\mathbf {t}_{\varphi }\vee \psi \vee \xi )$
hold at any w, whence the axioms’ respective topic-theoretic conditions are also met.
We will skip rules, although showing them to be validity preserving is straightforward. These considerations together provide the necessary components for a standard proof of soundness:
Theorem 1. If
![]() $\Gamma \vdash _{\mathsf {S}/\mathsf {PAI}}\varphi $
then
$\Gamma \vdash _{\mathsf {S}/\mathsf {PAI}}\varphi $
then
![]() $\Gamma \vDash _{\mathsf {S}/\mathsf {PAI}}\varphi $
.
$\Gamma \vDash _{\mathsf {S}/\mathsf {PAI}}\varphi $
.
4.2 Some important facts
Having established soundness, we now turn to the more difficult task of proving completeness. This preliminary section will lay the necessary groundwork to prepare for a completeness proof through the technique of canonical models.
The ultimate target of this section is a demonstration of a syntactic representation of Sylvan’s “double-barrelled” analysis of analytic implication as a joint condition including distinct truth-theoretic and topic-theoretic components. To adequately describe this representation, we briefly revisit our modest notational device
![]() $\mathbf {t}_{\varphi }$
, which will now be actively conscripted. Interpreted as a tautology with an identifiable topic, the presence of
$\mathbf {t}_{\varphi }$
, which will now be actively conscripted. Interpreted as a tautology with an identifiable topic, the presence of
![]() $\mathbf {t}_{\varphi }$
aids in the encoding of a number of important properties within the language itself. For example:
$\mathbf {t}_{\varphi }$
aids in the encoding of a number of important properties within the language itself. For example:
![]() $\bullet \ \mathbf {t}_{\varphi }$
can be leveraged as a mark of topic-theoretic equivalence by interpreting the formula
$\bullet \ \mathbf {t}_{\varphi }$
can be leveraged as a mark of topic-theoretic equivalence by interpreting the formula
![]() $\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
as a syntactic proxy for the identity of the subject-matters of formulae
$\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
as a syntactic proxy for the identity of the subject-matters of formulae
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. Because the truth-theoretic conditions for
$\psi $
. Because the truth-theoretic conditions for
![]() $\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
are trivially satisfied in virtue of the tautological character of each
$\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
are trivially satisfied in virtue of the tautological character of each
![]() $\mathbf {t}_{\xi }$
, the truth of
$\mathbf {t}_{\xi }$
, the truth of
![]() $\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
stands or falls precisely with the identity of the topics of
$\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
stands or falls precisely with the identity of the topics of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
.
$\psi $
.
![]() $\bullet \ \mathbf {t}_{\varphi }$
is critical in adequately representing
$\bullet \ \mathbf {t}_{\varphi }$
is critical in adequately representing
![]() $\mathsf {S4}$
necessity by interpreting the sentence
$\mathsf {S4}$
necessity by interpreting the sentence
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi $
as a proxy for the necessity of
$\mathbf {t}_{\varphi }\rightarrow \varphi $
as a proxy for the necessity of
![]() $\varphi $
. Insofar as the topics of
$\varphi $
. Insofar as the topics of
![]() $\varphi $
and
$\varphi $
and
![]() $\mathbf {t}_{\varphi }$
are identical, the topic-theoretic conditions on the truth of
$\mathbf {t}_{\varphi }$
are identical, the topic-theoretic conditions on the truth of
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi $
are trivially satisfied. As
$\mathbf {t}_{\varphi }\rightarrow \varphi $
are trivially satisfied. As
![]() $\mathbf {t}_{\varphi }$
is a tautology, the satisfaction of the formula’s truth-theoretic conditions requires that
$\mathbf {t}_{\varphi }$
is a tautology, the satisfaction of the formula’s truth-theoretic conditions requires that
![]() $\varphi $
is true at every accessible world.
$\varphi $
is true at every accessible world.
Returning to the syntactic surrogate of the double-barrelled analysis, the adequacy of the double-barrelled analysis will appear through the following equivalence:

We set off to establish the fidelity of this representation by observing some important facts and lemmas. We do this in stages determined by individual components of the double-barrelled analysis. The goal for the first stage is to establish that an analytic implication
![]() $\varphi \rightarrow \psi $
encodes appropriate topic-theoretic conditions, namely, that the topic of
$\varphi \rightarrow \psi $
encodes appropriate topic-theoretic conditions, namely, that the topic of
![]() $\varphi $
includes the topic of
$\varphi $
includes the topic of
![]() $\psi $
. The topic-theoretic condition itself receives a representation in the formula
$\psi $
. The topic-theoretic condition itself receives a representation in the formula
![]() $\mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
, whence the task requires showing that provability of
$\mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
, whence the task requires showing that provability of
![]() $\varphi \rightarrow \psi $
entails provability of
$\varphi \rightarrow \psi $
entails provability of
![]() $\mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
.
$\mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
.
Lemma 6. If
![]() $\Gamma \vdash \varphi \rightarrow \psi $
then
$\Gamma \vdash \varphi \rightarrow \psi $
then
![]() $\Gamma \vdash \mathbf {t}_{\varphi \rightarrow \psi }\rightarrow (\varphi \rightarrow \psi )$
.
$\Gamma \vdash \mathbf {t}_{\varphi \rightarrow \psi }\rightarrow (\varphi \rightarrow \psi )$
.
Proof. Suppose that
![]() $\Gamma \vdash \varphi \rightarrow \psi $
. By
$\Gamma \vdash \varphi \rightarrow \psi $
. By
![]() $[D2]$
and
$[D2]$
and
![]() $[MP]$
,
$[MP]$
,
![]() $\Gamma \vdash \neg (\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \psi )$
. By Lemma 4, also
$\Gamma \vdash \neg (\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \psi )$
. By Lemma 4, also
![]() $\Gamma \vdash (\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \psi )$
. So by
$\Gamma \vdash (\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \psi )$
. So by
![]() $[A10^{\dagger }]$
and
$[A10^{\dagger }]$
and
![]() $[T9]$
, conclude that
$[T9]$
, conclude that
![]() $\Gamma \vdash (\neg (\varphi \rightarrow \psi )\vee (\varphi \rightarrow \psi ))\rightarrow (\varphi \rightarrow \psi )$
, i.e.,
$\Gamma \vdash (\neg (\varphi \rightarrow \psi )\vee (\varphi \rightarrow \psi ))\rightarrow (\varphi \rightarrow \psi )$
, i.e.,
![]() $\Gamma \vdash \mathbf {t}_{\varphi \rightarrow \psi }\rightarrow (\varphi \rightarrow \psi )$
.
$\Gamma \vdash \mathbf {t}_{\varphi \rightarrow \psi }\rightarrow (\varphi \rightarrow \psi )$
.
Lemma 7.
![]() $\vdash (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\leftrightarrow \mathbf {t}_{\varphi \wedge \psi }$
.
$\vdash (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\leftrightarrow \mathbf {t}_{\varphi \wedge \psi }$
.
Proof. For left-to-right, note that by some permutations and definitions, we can establish that
![]() $\vdash (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\leftrightarrow [[(\varphi \wedge \psi )]\vee [(\neg \varphi \wedge \psi )\vee (\varphi \wedge \neg \psi )\vee (\neg \varphi \wedge \neg \psi )]]$
. First, by Lemma 4,
$\vdash (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\leftrightarrow [[(\varphi \wedge \psi )]\vee [(\neg \varphi \wedge \psi )\vee (\varphi \wedge \neg \psi )\vee (\neg \varphi \wedge \neg \psi )]]$
. First, by Lemma 4,
![]() $\vdash (\varphi \wedge \psi )\rightarrow (\varphi \wedge \psi )$
. Second, straightforward appeals to
$\vdash (\varphi \wedge \psi )\rightarrow (\varphi \wedge \psi )$
. Second, straightforward appeals to
![]() $[A10^{\dagger }]$
,
$[A10^{\dagger }]$
,
![]() $[T9]$
, and
$[T9]$
, and
![]() $[T16]$
show that
$[T16]$
show that
![]() $\vdash [(\neg \varphi \wedge \psi )\vee (\varphi \wedge \neg \psi )\vee (\neg \varphi \wedge \neg \psi )]\rightarrow \neg (\varphi \wedge \psi )$
. Thus,
$\vdash [(\neg \varphi \wedge \psi )\vee (\varphi \wedge \neg \psi )\vee (\neg \varphi \wedge \neg \psi )]\rightarrow \neg (\varphi \wedge \psi )$
. Thus,
![]() $\vdash [[(\varphi \wedge \psi )]\vee [(\neg \varphi \wedge \psi )\vee (\varphi \wedge \neg \psi )\vee (\neg \varphi \wedge \neg \psi )]]\rightarrow [\neg (\varphi \wedge \psi )\vee (\varphi \wedge \psi )]$
. Recognizing the consequent of this formula as
$\vdash [[(\varphi \wedge \psi )]\vee [(\neg \varphi \wedge \psi )\vee (\varphi \wedge \neg \psi )\vee (\neg \varphi \wedge \neg \psi )]]\rightarrow [\neg (\varphi \wedge \psi )\vee (\varphi \wedge \psi )]$
. Recognizing the consequent of this formula as
![]() $\mathbf {t}_{\varphi \wedge \psi }$
, appeal to
$\mathbf {t}_{\varphi \wedge \psi }$
, appeal to
![]() $[A7^{\dagger }]$
establishes that
$[A7^{\dagger }]$
establishes that
![]() $\vdash (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\rightarrow \mathbf {t}_{\varphi \wedge \psi }$
.
$\vdash (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\rightarrow \mathbf {t}_{\varphi \wedge \psi }$
.
For right-to-left, it is straightforward to show that
![]() $\vdash \mathbf {t}_{\varphi \wedge \psi }\rightarrow [(\varphi \vee \neg \varphi \vee \neg \psi )\wedge (\psi \vee \neg \psi \vee \neg \varphi )]$
. By Lemma 4, both
$\vdash \mathbf {t}_{\varphi \wedge \psi }\rightarrow [(\varphi \vee \neg \varphi \vee \neg \psi )\wedge (\psi \vee \neg \psi \vee \neg \varphi )]$
. By Lemma 4, both
![]() $\vdash (\varphi \vee \neg \varphi \vee \neg \psi )\rightarrow \mathbf {t}_{\varphi }$
and
$\vdash (\varphi \vee \neg \varphi \vee \neg \psi )\rightarrow \mathbf {t}_{\varphi }$
and
![]() $\vdash (\psi \vee \neg \psi \vee \neg \varphi )\rightarrow \mathbf {t}_{\psi }$
, whence appeals to
$\vdash (\psi \vee \neg \psi \vee \neg \varphi )\rightarrow \mathbf {t}_{\psi }$
, whence appeals to
![]() $[A7^{\dagger }]$
and
$[A7^{\dagger }]$
and
![]() $[A9^{\dagger }]$
establish that
$[A9^{\dagger }]$
establish that
![]() $\vdash \mathbf {t}_{\varphi \wedge \psi }\rightarrow (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })$
.
$\vdash \mathbf {t}_{\varphi \wedge \psi }\rightarrow (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })$
.
Lemma 8. If
![]() $\Gamma \vdash \varphi \rightarrow \psi $
then
$\Gamma \vdash \varphi \rightarrow \psi $
then
![]() $\Gamma \vdash \varphi \leftrightarrow (\varphi \wedge \psi )$
.
$\Gamma \vdash \varphi \leftrightarrow (\varphi \wedge \psi )$
.
Proof. Applying
![]() $[A9^{\dagger }]$
to the identity
$[A9^{\dagger }]$
to the identity
![]() $(\varphi \wedge \psi )\rightarrow (\varphi \wedge \psi )$
yields
$(\varphi \wedge \psi )\rightarrow (\varphi \wedge \psi )$
yields
![]() $(\varphi \wedge \psi )\rightarrow \varphi $
. For the other direction, an application of
$(\varphi \wedge \psi )\rightarrow \varphi $
. For the other direction, an application of
![]() $[A9^{\dagger }]$
secures
$[A9^{\dagger }]$
secures
![]() , so by
, so by
![]() $[ADJ]$
and hypothetical syllogism, we easily infer
$[ADJ]$
and hypothetical syllogism, we easily infer
![]() $\varphi \rightarrow (\varphi \wedge \psi )$
.
$\varphi \rightarrow (\varphi \wedge \psi )$
.
Lemma 9. If
![]() $\Gamma \vdash \varphi \rightarrow \psi $
then
$\Gamma \vdash \varphi \rightarrow \psi $
then
![]() $\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
.
$\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
.
Proof. Suppose that
![]() $\Gamma \vdash \varphi \rightarrow \psi $
. Then by Lemma 8, we have
$\Gamma \vdash \varphi \rightarrow \psi $
. Then by Lemma 8, we have
![]() $\Gamma \vdash \varphi \leftrightarrow (\varphi \wedge \psi )$
and by Lemma 4 we have
$\Gamma \vdash \varphi \leftrightarrow (\varphi \wedge \psi )$
and by Lemma 4 we have
![]() . By
. By
![]() $[ADJ]$
, we can conjoin these and use an instance of
$[ADJ]$
, we can conjoin these and use an instance of
![]() $[A12^{\dagger }]$
to yield
$[A12^{\dagger }]$
to yield
![]() . By definitions, instances of distribution, and applications of
. By definitions, instances of distribution, and applications of
![]() $[A7^{\dagger }]$
, we can infer that
$[A7^{\dagger }]$
, we can infer that
![]() ; by
; by
![]() $[A8^{\dagger }]$
,
$[A8^{\dagger }]$
,
![]() . But
. But
![]() $(\psi \vee \neg \psi \vee \neg \varphi )\rightarrow (\psi \vee \neg \psi )$
is a theorem by Lemma 4, and by applying
$(\psi \vee \neg \psi \vee \neg \varphi )\rightarrow (\psi \vee \neg \psi )$
is a theorem by Lemma 4, and by applying
![]() $[A7^{\dagger }]$
, we infer that
$[A7^{\dagger }]$
, we infer that
![]() , i.e.,
, i.e.,
![]() $\mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
.
$\mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
.
The second stage of the double-barrelled analysis—that analytic implication
![]() $\rightarrow $
exhibits the properties of an
$\rightarrow $
exhibits the properties of an
![]() $\mathsf {S4}$
strict conditional—can now be approached. Because a strict conditional is emulated by a formula of the form,
$\mathsf {S4}$
strict conditional—can now be approached. Because a strict conditional is emulated by a formula of the form,
![]() , the task is then to show that
, the task is then to show that
![]() $\varphi \rightarrow \psi $
entails
$\varphi \rightarrow \psi $
entails
![]() . We require a lemma:
. We require a lemma:
Lemma 10.
![]() .
.
Proof. By definitions and applications of distribution, we infer theoremhood of
![]() and, by
and, by
![]() $[A8^{\dagger }]$
,
$[A8^{\dagger }]$
,
![]() . By Lemma 4, we infer that
. By Lemma 4, we infer that
![]() $(\varphi \vee \neg \varphi \vee \psi )\rightarrow (\varphi \vee \neg \varphi )$
, and by
$(\varphi \vee \neg \varphi \vee \psi )\rightarrow (\varphi \vee \neg \varphi )$
, and by
![]() $[A7^{\dagger }]$
,
$[A7^{\dagger }]$
,
![]() , i.e.,
, i.e.,
![]() .
.
Lemma 11. If
![]() $\Gamma \vdash \varphi \rightarrow \psi $
then
$\Gamma \vdash \varphi \rightarrow \psi $
then
![]() .
.
Proof. By Lemma 4 and hypothesis,
![]() $[ADJ]$
yields
$[ADJ]$
yields
![]() $\Gamma \vdash (\varphi \rightarrow \psi )\wedge (\neg \varphi \rightarrow \neg \varphi )$
; by an instance of
$\Gamma \vdash (\varphi \rightarrow \psi )\wedge (\neg \varphi \rightarrow \neg \varphi )$
; by an instance of
![]() $[A10^{\dagger }]$
, we thereby may infer that
$[A10^{\dagger }]$
, we thereby may infer that
![]() $\Gamma \vdash (\varphi \vee \neg \varphi )\rightarrow (\neg \varphi \vee \psi )$
, i.e.,
$\Gamma \vdash (\varphi \vee \neg \varphi )\rightarrow (\neg \varphi \vee \psi )$
, i.e.,
![]() . By an appropriate instance of
. By an appropriate instance of
![]() $[A9^{\dagger }]$
, we appeal to Lemma 10 to infer that
$[A9^{\dagger }]$
, we appeal to Lemma 10 to infer that
![]() .
.
Jointly, Lemmas 9 and 11 amount to the left-to-right direction of our desired equivalence. Our third stage involves establishing the right-to-left direction.
Lemma 12. If
![]() then
then
![]() $\Gamma \vdash \varphi \rightarrow \psi $
.
$\Gamma \vdash \varphi \rightarrow \psi $
.
Proof. By Lemma 4, the hypothesis, and
![]() $[ADJ]$
,
$[ADJ]$
,
![]() $\Gamma \vdash (\varphi \rightarrow \varphi )\wedge (\varphi \rightarrow (\neg \varphi \vee \psi ))$
. By appeal to appropriate instances of
$\Gamma \vdash (\varphi \rightarrow \varphi )\wedge (\varphi \rightarrow (\neg \varphi \vee \psi ))$
. By appeal to appropriate instances of
![]() $[A2]$
and
$[A2]$
and
![]() $[A9^{\dagger }]$
, we infer that
$[A9^{\dagger }]$
, we infer that
![]() $\Gamma \vdash \varphi \rightarrow (\varphi \wedge (\neg \varphi \vee \psi ))$
and, by
$\Gamma \vdash \varphi \rightarrow (\varphi \wedge (\neg \varphi \vee \psi ))$
and, by
![]() $[A5]$
,
$[A5]$
,
![]() $\Gamma \vdash \varphi \rightarrow ((\varphi \wedge \neg \varphi )\vee (\varphi \wedge \psi ))$
. By an instance of
$\Gamma \vdash \varphi \rightarrow ((\varphi \wedge \neg \varphi )\vee (\varphi \wedge \psi ))$
. By an instance of
![]() $[A6]$
, we continue to infer that
$[A6]$
, we continue to infer that
![]() $\Gamma \vdash \varphi \rightarrow (\varphi \wedge \psi )$
and by theoremhood of
$\Gamma \vdash \varphi \rightarrow (\varphi \wedge \psi )$
and by theoremhood of
![]() $(\varphi \wedge \psi )\rightarrow \psi $
,
$(\varphi \wedge \psi )\rightarrow \psi $
,
![]() $[ADJ]$
and
$[ADJ]$
and
![]() $[A7^{\dagger }]$
give us
$[A7^{\dagger }]$
give us
![]() $\Gamma \vdash \varphi \rightarrow \psi $
.
$\Gamma \vdash \varphi \rightarrow \psi $
.
Lemma 13. If
![]() $\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
then
$\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
then
![]() .
.
Proof. Suppose that
![]() $\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
, i.e.,
$\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
, i.e.,
![]() $\Gamma \vdash (\varphi \vee \neg \varphi )\rightarrow (\psi \vee \neg \psi )$
. Then by Lemma 4,
$\Gamma \vdash (\varphi \vee \neg \varphi )\rightarrow (\psi \vee \neg \psi )$
. Then by Lemma 4,
![]() $(\varphi \vee \neg \varphi )\rightarrow (\varphi \vee \neg \varphi )$
is a theorem, and an appeal to
$(\varphi \vee \neg \varphi )\rightarrow (\varphi \vee \neg \varphi )$
is a theorem, and an appeal to
![]() $[A10^{\dagger }]$
ensures that
$[A10^{\dagger }]$
ensures that
![]() $\Gamma \vdash (\varphi \vee \neg \varphi )\rightarrow (\varphi \vee \neg \varphi \vee \psi \vee \neg \psi )$
.
$\Gamma \vdash (\varphi \vee \neg \varphi )\rightarrow (\varphi \vee \neg \varphi \vee \psi \vee \neg \psi )$
.
Now, by Lemma 4,
![]() $(\varphi \vee \neg \varphi \vee \psi \vee \neg \psi )\rightarrow (\varphi \vee \neg \varphi \vee \psi )$
and
$(\varphi \vee \neg \varphi \vee \psi \vee \neg \psi )\rightarrow (\varphi \vee \neg \varphi \vee \psi )$
and
![]() $(\varphi \vee \psi \vee \neg \psi )\rightarrow (\varphi \vee \neg \varphi \vee \psi \vee \neg \psi )$
are also theorems. Between
$(\varphi \vee \psi \vee \neg \psi )\rightarrow (\varphi \vee \neg \varphi \vee \psi \vee \neg \psi )$
are also theorems. Between
![]() $[A2]$
and
$[A2]$
and
![]() $[A9^{\dagger }]$
, then, we can infer that
$[A9^{\dagger }]$
, then, we can infer that
![]() $(\varphi \vee \neg \varphi )\rightarrow ((\varphi \vee \neg \varphi \vee \psi )\wedge (\varphi \vee \neg \varphi \vee \psi \vee \neg \psi ))$
. But because, as we saw in earlier lemmas, distributions and definitions ensure theoremhood of
$(\varphi \vee \neg \varphi )\rightarrow ((\varphi \vee \neg \varphi \vee \psi )\wedge (\varphi \vee \neg \varphi \vee \psi \vee \neg \psi ))$
. But because, as we saw in earlier lemmas, distributions and definitions ensure theoremhood of
![]() ,
,
![]() $[A9^{\dagger }]$
ensures that
$[A9^{\dagger }]$
ensures that
![]() , i.e.,
, i.e.,
![]() .
.
We now show the right-to-left direction, whereby the joint provability of topic inclusion and strict conditional behavior suffice to prove the corresponding conditional
![]() $\varphi \rightarrow \psi $
:
$\varphi \rightarrow \psi $
:
Lemma 14. If
![]() $\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
and
$\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
and
![]() then
then
![]() $\Gamma \vdash \varphi \rightarrow \psi $
.
$\Gamma \vdash \varphi \rightarrow \psi $
.
Proof. Suppose that
![]() $\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
. Then by Lemma 13,
$\Gamma \vdash \mathbf {t}_{\varphi }\rightarrow \mathbf {t}_{\psi }$
. Then by Lemma 13,
![]() . By Lemma 4,
. By Lemma 4,
![]() $\varphi \rightarrow \mathbf {t}_{\varphi }$
, whence
$\varphi \rightarrow \mathbf {t}_{\varphi }$
, whence
![]() $[A7^{\dagger }]$
guarantees that
$[A7^{\dagger }]$
guarantees that
![]() . Applying
. Applying
![]() $[A7^{\dagger }]$
again to the hypothesis that
$[A7^{\dagger }]$
again to the hypothesis that
![]() in turn yields that
in turn yields that
![]() . But by Lemma 12, this entails that
. But by Lemma 12, this entails that
![]() $\Gamma \vdash \varphi \rightarrow \psi $
.
$\Gamma \vdash \varphi \rightarrow \psi $
.
With Lemmas 9, 11, and 14 established, we conclude this section with a justification of the proposed syntactic characterization of the double-barrelled analysis:
Theorem 2.
![]() $\Gamma \vdash \varphi \rightarrow \psi $
iff
$\Gamma \vdash \varphi \rightarrow \psi $
iff

With Theorem 2 in hand, we are able to proceed to proving completeness.
4.3 Completeness of the axioms
We prove completeness through the method of canonical models. Before defining the canonical model itself, we introduce some definitions. A satisfactory account of the canonical model’s accessibility relation will make use of the following definition:
Definition 11. For a theory
![]() $\Gamma $
, the set
$\Gamma $
, the set
![]() $\Gamma ^{\Box }=\lbrace \varphi \mid \mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma \rbrace $
.
$\Gamma ^{\Box }=\lbrace \varphi \mid \mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma \rbrace $
.
We anticipate the definition of the canonical model by introducing the notation:
Definition 12. For maximally consistent prime theories
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Xi $
,
$\Xi $
,
![]() $\Gamma R^{\star }\Xi $
if
$\Gamma R^{\star }\Xi $
if
![]() $\Gamma ^{\Box }\subseteq \Xi $
. We give expedient syntactic interpretations to familiar notions:
$\Gamma ^{\Box }\subseteq \Xi $
. We give expedient syntactic interpretations to familiar notions:
-
•
 $\Gamma {\uparrow }^{\star }=\lbrace \Xi \mid \Gamma R^{\star }\Xi \rbrace $
.
$\Gamma {\uparrow }^{\star }=\lbrace \Xi \mid \Gamma R^{\star }\Xi \rbrace $
. -
•
 .
.
Although the decorations
![]() $\_^{\star }$
indicate that the above notions are defined syntactically and prevent confusion with earlier semantic definitions, eventually, it will become clear that the syntactic abuses of notation are justified.
$\_^{\star }$
indicate that the above notions are defined syntactically and prevent confusion with earlier semantic definitions, eventually, it will become clear that the syntactic abuses of notation are justified.
The importance of the relationship between a set
![]() $\Gamma ^{\Box }$
and other maximally consistent prime theories is immeasurable and it is worth pausing to get a better understanding of the properties of any such
$\Gamma ^{\Box }$
and other maximally consistent prime theories is immeasurable and it is worth pausing to get a better understanding of the properties of any such
![]() $\Gamma ^{\Box }$
. Thus, we make a detour and prove some important closure properties holding of
$\Gamma ^{\Box }$
. Thus, we make a detour and prove some important closure properties holding of
![]() $\Gamma ^{\Box }$
. The initial lemma shows that any such set
$\Gamma ^{\Box }$
. The initial lemma shows that any such set
![]() $\Gamma ^{\Box }$
at least includes all instances of axioms:
$\Gamma ^{\Box }$
at least includes all instances of axioms:
Lemma 15 (Closure Under Axioms)
For all axioms
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi \in \Gamma ^{\Box }$
.
$\varphi \in \Gamma ^{\Box }$
.
Proof. Let
![]() $\varphi $
be an instance of an axiom. By Lemma 4,
$\varphi $
be an instance of an axiom. By Lemma 4,
![]() $\varphi \rightarrow \varphi \in \Gamma $
and by rule
$\varphi \rightarrow \varphi \in \Gamma $
and by rule
![]() $[MOD] \ \neg \varphi \rightarrow \varphi \in \Gamma $
. Between
$[MOD] \ \neg \varphi \rightarrow \varphi \in \Gamma $
. Between
![]() $[A10^{\dagger }]$
and
$[A10^{\dagger }]$
and
![]() $[T9]$
, we can infer that
$[T9]$
, we can infer that
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
, whence
$\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
, whence
![]() $\varphi \in \Gamma ^{\Box }$
.
$\varphi \in \Gamma ^{\Box }$
.
Having established that each
![]() $\Gamma ^{\Box }$
is populated, it now merits investigating its closure under the four rules of our calculus. First is adjunction (
$\Gamma ^{\Box }$
is populated, it now merits investigating its closure under the four rules of our calculus. First is adjunction (
![]() $[ADJ]$
):
$[ADJ]$
):
Lemma 16 (Closure Under
 $[ADJ\mbox {]}$
)
$[ADJ\mbox {]}$
)
If
![]() $\varphi \in \Gamma ^{\Box }$
and
$\varphi \in \Gamma ^{\Box }$
and
![]() $\varphi \in \Gamma ^{\Box }$
then
$\varphi \in \Gamma ^{\Box }$
then
![]() $\varphi \wedge \psi \in \Gamma ^{\Box }$
.
$\varphi \wedge \psi \in \Gamma ^{\Box }$
.
Proof. By hypothesis,
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi $
and
$\mathbf {t}_{\varphi }\rightarrow \varphi $
and
![]() $\mathbf {t}_{\psi }\rightarrow \psi $
. Through the use of
$\mathbf {t}_{\psi }\rightarrow \psi $
. Through the use of
![]() $[A9^{\dagger }]$
, we can infer that
$[A9^{\dagger }]$
, we can infer that
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $(\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\rightarrow \varphi \wedge \psi $
and by Lemma 7, ultimately infer that
$(\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\psi })\rightarrow \varphi \wedge \psi $
and by Lemma 7, ultimately infer that
![]() $\mathbf {t}_{\varphi \wedge \psi }\rightarrow \varphi \wedge \psi \in \Gamma $
, whence
$\mathbf {t}_{\varphi \wedge \psi }\rightarrow \varphi \wedge \psi \in \Gamma $
, whence
![]() $\varphi \wedge \psi \in \Gamma ^{\Box }$
.
$\varphi \wedge \psi \in \Gamma ^{\Box }$
.
Closure can be established for modus ponens with respect to
![]() (
(
![]() $[MP1]$
):
$[MP1]$
):
Lemma 17 (Closure Under
 $[MP1\mbox {]}$
)
$[MP1\mbox {]}$
)
If
![]() and
and
![]() $\varphi \in \Gamma ^{\Box }$
then
$\varphi \in \Gamma ^{\Box }$
then
![]() $\psi \in \Gamma ^{\Box }$
.
$\psi \in \Gamma ^{\Box }$
.
Proof. Suppose that
and
![]() $\varphi \in \Gamma ^{\Box }$
. Then
$\varphi \in \Gamma ^{\Box }$
. Then
and
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
. By an appeal to
$\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
. By an appeal to
![]() $[A9^{\dagger }]$
, we can infer that
$[A9^{\dagger }]$
, we can infer that
![]() $\Gamma $
includes
$\Gamma $
includes
. By appeal to Lemma 7, we infer the inclusion of
and—with a bit of permutation—an appeal to
![]() $[A6]$
will get
$[A6]$
will get
. Putting these together, we get
Of course,
![]() is provable, whence by an appeal to an appropriate instance of
is provable, whence by an appeal to an appropriate instance of
![]() $[A14^{\dagger }]$
, we are able to conclude that
$[A14^{\dagger }]$
, we are able to conclude that
![]() $\neg \psi \rightarrow \psi \in \Gamma $
. Because
$\neg \psi \rightarrow \psi \in \Gamma $
. Because
![]() $\psi \rightarrow \psi \in \Gamma $
, it nearly immediately follows that
$\psi \rightarrow \psi \in \Gamma $
, it nearly immediately follows that
![]() $\mathbf {t}_{\psi }\rightarrow \psi $
, i.e., that
$\mathbf {t}_{\psi }\rightarrow \psi $
, i.e., that
![]() $\psi \in \Gamma ^{\Box }$
.
$\psi \in \Gamma ^{\Box }$
.
Closure under
![]() $[MP1]$
very quickly establishes closure under modus ponens with respect to
$[MP1]$
very quickly establishes closure under modus ponens with respect to
![]() $\rightarrow $
(
$\rightarrow $
(
![]() $[MP2]$
):
$[MP2]$
):
Lemma 18 (Closure Under
 $[MP2\mbox {]}$
)
$[MP2\mbox {]}$
)
If
![]() $\varphi \rightarrow \psi \in \Gamma ^{\Box }$
and
$\varphi \rightarrow \psi \in \Gamma ^{\Box }$
and
![]() $\varphi \in \Gamma ^{\Box }$
then
$\varphi \in \Gamma ^{\Box }$
then
![]() $\psi \in \Gamma ^{\Box }$
.
$\psi \in \Gamma ^{\Box }$
.
Proof. By appeal to Lemma 15, we infer that
![]() $\Gamma ^{\Box }$
includes an appropriate copy of
$\Gamma ^{\Box }$
includes an appropriate copy of
![]() $[A11^{\dagger }]$
from which an appeal to Lemma 17 establishes that
$[A11^{\dagger }]$
from which an appeal to Lemma 17 establishes that
![]() . That
. That
![]() $\psi \in \Gamma ^{\Box }$
then follows from a second appeal to Lemma 17.
$\psi \in \Gamma ^{\Box }$
then follows from a second appeal to Lemma 17.
Finally, we establish closure of
![]() $\Gamma ^{\Box }$
under the last of our rules:
$\Gamma ^{\Box }$
under the last of our rules:
Lemma 19 (Closure Under
 $[MOD\mbox {]}$
)
$[MOD\mbox {]}$
)
![]() $\neg \varphi \rightarrow \varphi \in \Gamma ^{\Box }$
for any axiom
$\neg \varphi \rightarrow \varphi \in \Gamma ^{\Box }$
for any axiom
![]() $\varphi $
.
$\varphi $
.
Proof. An application of
![]() $[MOD]$
entails that
$[MOD]$
entails that
![]() $\neg \varphi \rightarrow \varphi \in \Gamma $
. An appeal to our earlier Lemma 6 ensures that
$\neg \varphi \rightarrow \varphi \in \Gamma $
. An appeal to our earlier Lemma 6 ensures that
![]() $\Gamma $
also includes
$\Gamma $
also includes
![]() $\mathbf {t}_{\neg \varphi \rightarrow \varphi }\rightarrow (\neg \varphi \rightarrow \varphi )$
, i.e., that
$\mathbf {t}_{\neg \varphi \rightarrow \varphi }\rightarrow (\neg \varphi \rightarrow \varphi )$
, i.e., that
![]() $\neg \varphi \rightarrow \varphi \in \Gamma ^{\Box }$
.
$\neg \varphi \rightarrow \varphi \in \Gamma ^{\Box }$
.
The merits of the foregoing Lemmas 15–19 can be recognized through the utility of the following type of closure they establish, namely, the closure of
![]() $\Gamma ^{\Box }$
under theoremhood:
$\Gamma ^{\Box }$
under theoremhood:
Lemma 20. For
![]() $\varphi $
a theorem of
$\varphi $
a theorem of
![]() $\mathsf {S}/\mathsf {PAI}$
,
$\mathsf {S}/\mathsf {PAI}$
,
![]() $\varphi \in \Gamma ^{\Box }$
.
$\varphi \in \Gamma ^{\Box }$
.
Proof. This follows from induction on complexity of proofs. If
![]() $\varphi $
is an axiom, then the property follows from Lemma 15. Otherwise, the theoremhood follows from the application of one of the four rules. But Lemmas 16–19 show that
$\varphi $
is an axiom, then the property follows from Lemma 15. Otherwise, the theoremhood follows from the application of one of the four rules. But Lemmas 16–19 show that
![]() $\Gamma ^{\Box }$
is closed under each of these rules.
$\Gamma ^{\Box }$
is closed under each of these rules.
The foregoing lemmas permit us to infer a critical lemma and corollary that illuminate the workings of elements of
![]() $\Gamma ^{\Box }$
as regards the theories in the family
$\Gamma ^{\Box }$
as regards the theories in the family
![]() $\Gamma {\uparrow }^{\star }$
:
$\Gamma {\uparrow }^{\star }$
:
Lemma 21.
![]() $\Gamma ^{\Box }\vdash \varphi $
iff for all
$\Gamma ^{\Box }\vdash \varphi $
iff for all
![]() $\Xi \in \Gamma {\uparrow }^{\star }$
,
$\Xi \in \Gamma {\uparrow }^{\star }$
,
![]() $\varphi \in \Xi $
.
$\varphi \in \Xi $
.
Proof. Left-to-right holds by definition. Suppose that
![]() $\varphi $
is a member of every theory
$\varphi $
is a member of every theory
![]() $\Xi \in \Gamma {\uparrow }^{\star }$
. Then
$\Xi \in \Gamma {\uparrow }^{\star }$
. Then
![]() $\Gamma ^{\Box }\vdash \varphi $
(for otherwise, simple reasoning would show the existence of an extension in which
$\Gamma ^{\Box }\vdash \varphi $
(for otherwise, simple reasoning would show the existence of an extension in which
![]() $\neg \varphi $
holds). By the compactness of
$\neg \varphi $
holds). By the compactness of
![]() $\mathsf {S}/\mathsf {PAI}$
, there exists a sequence of formulae
$\mathsf {S}/\mathsf {PAI}$
, there exists a sequence of formulae
![]() $\xi _{0},...,\xi _{n-1}\in \Gamma ^{\Box }$
such that
$\xi _{0},...,\xi _{n-1}\in \Gamma ^{\Box }$
such that
![]() $\bigwedge _{i<n}\xi _{i}\vdash \varphi $
. Importantly, by Lemma 16,
$\bigwedge _{i<n}\xi _{i}\vdash \varphi $
. Importantly, by Lemma 16,
![]() $\bigwedge _{i<n}\xi _{i}\in \Gamma ^{\Box }$
. By the classical deduction theorem,
$\bigwedge _{i<n}\xi _{i}\in \Gamma ^{\Box }$
. By the classical deduction theorem,
![]() is an
is an
![]() $\mathsf {S}/\mathsf {PAI}$
theorem, whence by Lemma 20,
$\mathsf {S}/\mathsf {PAI}$
theorem, whence by Lemma 20,
![]() . As
. As
![]() $\bigwedge _{i<n}\xi _{i}\in \Gamma ^{\Box }$
, Lemma 17 can be applied to establish that
$\bigwedge _{i<n}\xi _{i}\in \Gamma ^{\Box }$
, Lemma 17 can be applied to establish that
![]() $\varphi \in \Gamma ^{\Box }$
, whence
$\varphi \in \Gamma ^{\Box }$
, whence
![]() $\Gamma ^{\Box }\vdash \varphi $
.
$\Gamma ^{\Box }\vdash \varphi $
.
Corollary 1.
![]() iff for all
iff for all
![]() $\Xi \in \Gamma {\uparrow }^{\star }$
,
$\Xi \in \Gamma {\uparrow }^{\star }$
,
![]() $\varphi \in \Xi $
only if
$\varphi \in \Xi $
only if
![]() $\psi \in \Xi $
.
$\psi \in \Xi $
.
The importance of Corollary 1 lies in the image it depicts in which the syntactic behavior of the inclusion of
![]() mimics the semantics of a strict conditional. Having thoroughly examined the device of
mimics the semantics of a strict conditional. Having thoroughly examined the device of
![]() $\Gamma ^{\Box }$
, we now aim to provide a satisfactory account of the canonical model’s concept semilattices. This task requires the introduction of some preliminary definitions:
$\Gamma ^{\Box }$
, we now aim to provide a satisfactory account of the canonical model’s concept semilattices. This task requires the introduction of some preliminary definitions:
Definition 13. For a theory
![]() $\Gamma $
,
$\Gamma $
,
![]() $\sim _{\Gamma }$
is an equivalence relation such that
$\sim _{\Gamma }$
is an equivalence relation such that
![]() $\varphi \mathrel {\sim _{\Gamma }}\psi $
if
$\varphi \mathrel {\sim _{\Gamma }}\psi $
if
![]() $\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }\in \Gamma $
and
$\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }\in \Gamma $
and
![]() is the equivalence class of formulae induced by
is the equivalence class of formulae induced by
![]() $\sim _{\Gamma }$
.
$\sim _{\Gamma }$
.
Definition 14. For a maximally consistent prime theory
![]() $\Gamma $
,
$\Gamma $
,
![]() .
.
It should be clear that the value of these definitions for
![]() and
and
![]() rests on their serviceability as syntactic proxies for topics and contents of
rests on their serviceability as syntactic proxies for topics and contents of
![]() $\varphi $
, respectively. This observation motivates the next definition:
$\varphi $
, respectively. This observation motivates the next definition:
Definition 15. The functions
![]() $\oplus _{\Gamma }$
and
$\oplus _{\Gamma }$
and
![]() $\multimap _{\Gamma }$
are defined so that:
$\multimap _{\Gamma }$
are defined so that:
-
•
 ,
, -
•
 .
.
With these functions defined we have introduced all of the definitions necessary to describe canonical models.
Definition 16. The
![]() $\mathsf {S}/\mathsf {PAI}$
canonical model is
$\mathsf {S}/\mathsf {PAI}$
canonical model is
![]() $\mathfrak {M}=\langle W,R,\mathcal {T},\mathcal {C},\oplus ,\multimap ,v,{t},h\rangle $
where:
$\mathfrak {M}=\langle W,R,\mathcal {T},\mathcal {C},\oplus ,\multimap ,v,{t},h\rangle $
where:
-
•
 $W=\lbrace \Delta \mid \Delta \mbox { a maximally consistent prime theory}\rbrace $
,
$W=\lbrace \Delta \mid \Delta \mbox { a maximally consistent prime theory}\rbrace $
, -
•
 $R=\lbrace \langle \Gamma ,\Xi \rangle \mid \Gamma ^{\Box }\subseteq \Xi \rbrace $
,
$R=\lbrace \langle \Gamma ,\Xi \rangle \mid \Gamma ^{\Box }\subseteq \Xi \rbrace $
, -
•
 $\Gamma \in v(p)$
iff
$\Gamma \in v(p)$
iff
 $p\in \Gamma $
,
$p\in \Gamma $
, -
• For all
 $\Gamma \in W$
:
$\Gamma \in W$
: 
Definition 16 induces an ancillary definition associating any maximally consistent prime theory with a particular canonical model:
Definition 17. For
![]() $\Gamma $
a maximally consistent prime
$\Gamma $
a maximally consistent prime
![]() $\mathsf {S}/\mathsf {PAI}$
theory, its canonical model
$\mathsf {S}/\mathsf {PAI}$
theory, its canonical model
![]() $\mathfrak {M}_{\Gamma }$
is the submodel of
$\mathfrak {M}_{\Gamma }$
is the submodel of
![]() $\mathfrak {M}$
where
$\mathfrak {M}$
where
![]() $W_{\Gamma }=\lbrace \Delta \mid \Gamma R\Delta \rbrace $
.
$W_{\Gamma }=\lbrace \Delta \mid \Gamma R\Delta \rbrace $
.
Having offered the definition, we must now establish its utility by showing that the objects so defined are models appropriate to our requirements.
First, we show that topic assignments persist along R as required. This is made easier by the following observation:
Lemma 22.
![]() iff
iff
![]() $\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Gamma $
.
$\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Gamma $
.
Proof. Because
![]() $a\leq _{\Gamma }b$
is shorthand for
$a\leq _{\Gamma }b$
is shorthand for
![]() $b=a\oplus _{\Gamma } b$
, the requirement is to prove that
$b=a\oplus _{\Gamma } b$
, the requirement is to prove that
![]() $\Gamma \vdash \mathbf {t}_{\psi \wedge \varphi }\leftrightarrow \mathbf {t}_{\psi }$
iff
$\Gamma \vdash \mathbf {t}_{\psi \wedge \varphi }\leftrightarrow \mathbf {t}_{\psi }$
iff
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
. But because
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
. But because
![]() $\vdash \mathbf {t}_{\psi \wedge \varphi }\rightarrow \mathbf {t}_{\psi }$
can be easily established, the requirement is simply to show that
$\vdash \mathbf {t}_{\psi \wedge \varphi }\rightarrow \mathbf {t}_{\psi }$
can be easily established, the requirement is simply to show that
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\psi \wedge \varphi }$
iff
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\psi \wedge \varphi }$
iff
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
.
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
.
For left-to-right, suppose that
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\psi \wedge \varphi }$
. Then appeal to Lemma 7 and
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\psi \wedge \varphi }$
. Then appeal to Lemma 7 and
![]() $[A8^{\dagger }]$
assures us that
$[A8^{\dagger }]$
assures us that
![]() $\mathbf {t}_{\psi \wedge \varphi }\rightarrow \mathbf {t}_{\varphi }$
; by
$\mathbf {t}_{\psi \wedge \varphi }\rightarrow \mathbf {t}_{\varphi }$
; by
![]() $[A7^{\dagger }]$
, then
$[A7^{\dagger }]$
, then
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
.
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
.
For right-to-left, suppose that
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
. By, e.g., Lemma 4 and
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }$
. By, e.g., Lemma 4 and
![]() $[A9^{\dagger }]$
,
$[A9^{\dagger }]$
,
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow (\mathbf {t}_{\psi }\wedge \mathbf {t}_{\varphi })$
; but Lemma 7 again establishes equivalence between the consequent and
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow (\mathbf {t}_{\psi }\wedge \mathbf {t}_{\varphi })$
; but Lemma 7 again establishes equivalence between the consequent and
![]() $\mathbf {t}_{\psi \wedge \varphi }$
itself, whence
$\mathbf {t}_{\psi \wedge \varphi }$
itself, whence
![]() $\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\psi \wedge \varphi }$
.
$\Gamma \vdash \mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\psi \wedge \varphi }$
.
Observation 9. If
![]() $\Gamma R\Delta $
and
$\Gamma R\Delta $
and
![]() $t_{\Gamma }(\varphi )\leq _{\Gamma }t_{\Gamma }(\psi )$
then
$t_{\Gamma }(\varphi )\leq _{\Gamma }t_{\Gamma }(\psi )$
then
![]() $t_{\Delta }(\varphi )\leq _{\Delta }t_{\Delta }(\psi )$
.
$t_{\Delta }(\varphi )\leq _{\Delta }t_{\Delta }(\psi )$
.
Proof. The hypothesis that
![]() $t_{\Gamma }(\varphi )\leq _{\Gamma }t_{\Gamma }(\psi )$
means that
$t_{\Gamma }(\varphi )\leq _{\Gamma }t_{\Gamma }(\psi )$
means that
![]() $\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Gamma $
. By Lemma 6,
$\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Gamma $
. By Lemma 6,
![]() $\Gamma \vdash \mathbf {t}_{\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }}\rightarrow (\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi })$
, whence
$\Gamma \vdash \mathbf {t}_{\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }}\rightarrow (\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi })$
, whence
![]() $\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Gamma ^{\Box }$
. The hypothesis that
$\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Gamma ^{\Box }$
. The hypothesis that
![]() $\Gamma R\Delta $
means that
$\Gamma R\Delta $
means that
![]() $\Gamma ^{\Box }\subseteq \Delta $
, whence
$\Gamma ^{\Box }\subseteq \Delta $
, whence
![]() $\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Delta $
and
$\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\varphi }\in \Delta $
and
![]() $t_{\Delta }(\varphi )\leq _{\Delta }t_{\Delta }(\psi )$
.
$t_{\Delta }(\varphi )\leq _{\Delta }t_{\Delta }(\psi )$
.
We show that R has the necessary properties so that
![]() $\langle W,R\rangle $
is an
$\langle W,R\rangle $
is an
![]() $\mathsf {S4}$
Kripke frame:
$\mathsf {S4}$
Kripke frame:
Observation 10. R is reflexive and transitive.
Proof. For reflexivity, note that for any
![]() $\varphi \in \Gamma ^{\Box }$
,
$\varphi \in \Gamma ^{\Box }$
,
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
. But as a tautology,
$\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
. But as a tautology,
![]() $\mathbf {t}_{\varphi }\in \Gamma $
and by
$\mathbf {t}_{\varphi }\in \Gamma $
and by
![]() $[MP]$
,
$[MP]$
,
![]() $\varphi \in \Gamma $
. Thus,
$\varphi \in \Gamma $
. Thus,
![]() $\Gamma ^{\Box }\subseteq \Gamma $
, i.e.,
$\Gamma ^{\Box }\subseteq \Gamma $
, i.e.,
![]() $\Gamma R\Gamma $
. For transitivity, suppose that
$\Gamma R\Gamma $
. For transitivity, suppose that
![]() $\Gamma R\Xi R\Theta $
. We show
$\Gamma R\Xi R\Theta $
. We show
![]() $\Gamma R\Theta $
. Pick a
$\Gamma R\Theta $
. Pick a
![]() $\varphi \in \Gamma ^{\Box }$
. Then
$\varphi \in \Gamma ^{\Box }$
. Then
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
. By Lemma 6, also
$\mathbf {t}_{\varphi }\rightarrow \varphi \in \Gamma $
. By Lemma 6, also
![]() $\mathbf {t}_{\mathbf {t}_{\varphi }\rightarrow \varphi }\rightarrow (\mathbf {t}_{\varphi }\rightarrow \varphi )\in \Gamma $
. Thus,
$\mathbf {t}_{\mathbf {t}_{\varphi }\rightarrow \varphi }\rightarrow (\mathbf {t}_{\varphi }\rightarrow \varphi )\in \Gamma $
. Thus,
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi $
is an element of
$\mathbf {t}_{\varphi }\rightarrow \varphi $
is an element of
![]() $\Gamma ^{\Box }$
, and thus an element of
$\Gamma ^{\Box }$
, and thus an element of
![]() $\Xi $
. But if
$\Xi $
. But if
![]() $\mathbf {t}_{\varphi }\rightarrow \varphi \in \Xi $
,
$\mathbf {t}_{\varphi }\rightarrow \varphi \in \Xi $
,
![]() $\varphi \in \Xi ^{\Box }$
, whence
$\varphi \in \Xi ^{\Box }$
, whence
![]() $\varphi \in \Theta $
.
$\varphi \in \Theta $
.
We furthermore need to demonstrate that our definitions for
![]() $\oplus $
and
$\oplus $
and
![]() $\multimap $
are well-defined, that is, that these are in fact functions.
$\multimap $
are well-defined, that is, that these are in fact functions.
Lemma 23. Each
![]() $\oplus _{\Gamma }$
is a well-defined and total function.
$\oplus _{\Gamma }$
is a well-defined and total function.
Proof. As
![]() $\mathcal {T}_{\Gamma }$
is defined in terms of the language, Definition 16 assigns a value to
$\mathcal {T}_{\Gamma }$
is defined in terms of the language, Definition 16 assigns a value to
![]() $\oplus _{\Gamma }$
for all pairs of arguments. It remains to show that such values are unique. That
$\oplus _{\Gamma }$
for all pairs of arguments. It remains to show that such values are unique. That
![]() $\oplus _{\Gamma }$
is a function means that if
$\oplus _{\Gamma }$
is a function means that if
![]() $\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }\in \Gamma $
then
$\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }\in \Gamma $
then
![]() $\mathbf {t}_{\varphi \wedge \xi }\leftrightarrow \mathbf {t}_{\psi \wedge \xi }\in \Gamma $
. Assume that the former condition holds; then by selecting instances of
$\mathbf {t}_{\varphi \wedge \xi }\leftrightarrow \mathbf {t}_{\psi \wedge \xi }\in \Gamma $
. Assume that the former condition holds; then by selecting instances of
![]() $[A9^{\dagger }]$
and the theorem
$[A9^{\dagger }]$
and the theorem
![]() $\mathbf {t}_{\xi }\rightarrow \mathbf {t}_{\xi }$
, we may straightforwardly infer that
$\mathbf {t}_{\xi }\rightarrow \mathbf {t}_{\xi }$
, we may straightforwardly infer that
![]() $(\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\xi })\leftrightarrow (\mathbf {t}_{\psi }\wedge \mathbf {t}_{\xi })\in \Gamma $
. By Lemma 7, we have as theorems
$(\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\xi })\leftrightarrow (\mathbf {t}_{\psi }\wedge \mathbf {t}_{\xi })\in \Gamma $
. By Lemma 7, we have as theorems
![]() $\mathbf {t}_{\varphi \wedge \xi }\leftrightarrow (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\xi })$
and
$\mathbf {t}_{\varphi \wedge \xi }\leftrightarrow (\mathbf {t}_{\varphi }\wedge \mathbf {t}_{\xi })$
and
![]() $\mathbf {t}_{\psi \wedge \xi }\leftrightarrow (\mathbf {t}_{\psi }\wedge \mathbf {t}_{\xi })$
. Thus, by several applications of rules to appropriate instances of
$\mathbf {t}_{\psi \wedge \xi }\leftrightarrow (\mathbf {t}_{\psi }\wedge \mathbf {t}_{\xi })$
. Thus, by several applications of rules to appropriate instances of
![]() $[A7^{\dagger }]$
, we can infer that
$[A7^{\dagger }]$
, we can infer that
![]() $\mathbf {t}_{\varphi \wedge \xi }\leftrightarrow \mathbf {t}_{\psi \wedge \xi }\in \Gamma $
. So in case
$\mathbf {t}_{\varphi \wedge \xi }\leftrightarrow \mathbf {t}_{\psi \wedge \xi }\in \Gamma $
. So in case
![]() and
and
![]() , we are guaranteed that
, we are guaranteed that
![]() .
.
We turn next to the task of showing
![]() $\multimap _{\Gamma }$
to be well-defined, starting with a lemma:
$\multimap _{\Gamma }$
to be well-defined, starting with a lemma:
Lemma 24.
![]() $c_{\Gamma }(\varphi )=c_{\Gamma }(\psi )$
iff
$c_{\Gamma }(\varphi )=c_{\Gamma }(\psi )$
iff
![]() $\varphi \leftrightarrow \psi \in \Gamma $
.
$\varphi \leftrightarrow \psi \in \Gamma $
.
Proof.
![]() $\bullet $
For right-to-left, suppose that
$\bullet $
For right-to-left, suppose that
![]() $\varphi \leftrightarrow \psi $
. Then note two things: First, by Lemma 9,
$\varphi \leftrightarrow \psi $
. Then note two things: First, by Lemma 9,
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
, whence
$\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
, whence
![]() . Second, by Lemma 6,
. Second, by Lemma 6,
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $\mathbf {t}_{\varphi \rightarrow \psi }\rightarrow (\varphi \rightarrow \psi )$
and
$\mathbf {t}_{\varphi \rightarrow \psi }\rightarrow (\varphi \rightarrow \psi )$
and
![]() $\mathbf {t}_{\psi \rightarrow \varphi }\rightarrow (\psi \rightarrow \varphi )$
, whence
$\mathbf {t}_{\psi \rightarrow \varphi }\rightarrow (\psi \rightarrow \varphi )$
, whence
![]() $\Gamma ^{\Box }$
includes
$\Gamma ^{\Box }$
includes
![]() $\varphi \leftrightarrow \psi $
. Thus, for any
$\varphi \leftrightarrow \psi $
. Thus, for any
![]() $\Xi $
such that
$\Xi $
such that
![]() $\Gamma R\Xi $
,
$\Gamma R\Xi $
,
![]() $\varphi \in \Xi $
iff
$\varphi \in \Xi $
iff
![]() $\psi \in \Xi $
, i.e.,
$\psi \in \Xi $
, i.e.,
![]() . Together, this establishes that
. Together, this establishes that
![]() , i.e.,
, i.e.,
![]() $c_{\Gamma }(\varphi )=c_{\Gamma }(\psi )$
.
$c_{\Gamma }(\varphi )=c_{\Gamma }(\psi )$
.
![]() $\bullet $
For left-to-right, suppose that
$\bullet $
For left-to-right, suppose that
![]() $c_{\Gamma }(\varphi )=c_{\Gamma }(\psi )$
. As
$c_{\Gamma }(\varphi )=c_{\Gamma }(\psi )$
. As
![]() ,
,
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
by definition. Likewise, because
$\mathbf {t}_{\varphi }\leftrightarrow \mathbf {t}_{\psi }$
by definition. Likewise, because
![]() , Lemma 21 ensures that
, Lemma 21 ensures that
![]() and
and
![]() are elements of
are elements of
![]() $\Gamma $
. These facts are sufficient for an appeal to Lemma 14 to establish that
$\Gamma $
. These facts are sufficient for an appeal to Lemma 14 to establish that
![]() $\Gamma \vdash \varphi \leftrightarrow \psi $
.
$\Gamma \vdash \varphi \leftrightarrow \psi $
.
Lemma 25. Each
![]() $\multimap _{\Gamma }$
is a well-defined and total function.
$\multimap _{\Gamma }$
is a well-defined and total function.
Proof. By Definition 16, some value for
![]() $\multimap _{\Gamma }$
is defined for all pairs of arguments from
$\multimap _{\Gamma }$
is defined for all pairs of arguments from
![]() $\mathcal {C}_{\Gamma }$
. To show that this value is unique, assume that
$\mathcal {C}_{\Gamma }$
. To show that this value is unique, assume that
![]() $c_{\Gamma }(\varphi )=c_{\Gamma }(\varphi ')$
and
$c_{\Gamma }(\varphi )=c_{\Gamma }(\varphi ')$
and
![]() $c_{\Gamma }(\psi )=c_{\Gamma }(\psi ')$
. By Lemma 24,
$c_{\Gamma }(\psi )=c_{\Gamma }(\psi ')$
. By Lemma 24,
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $\varphi \leftrightarrow \varphi '$
and
$\varphi \leftrightarrow \varphi '$
and
![]() $\psi \leftrightarrow \psi '$
. By Lemma 4 we also know that
$\psi \leftrightarrow \psi '$
. By Lemma 4 we also know that
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $\mathbf {t}_{\varphi \rightarrow \psi }\rightarrow \mathbf {t}_{\varphi \rightarrow \psi }$
, providing the grounds to use modus ponens on instance of
$\mathbf {t}_{\varphi \rightarrow \psi }\rightarrow \mathbf {t}_{\varphi \rightarrow \psi }$
, providing the grounds to use modus ponens on instance of
![]() $[A12^{\dagger }]$
:
$[A12^{\dagger }]$
:
to ensure that
![]() $\mathbf {t}_{\varphi \rightarrow \psi }\rightarrow \mathbf {t}_{\varphi '\rightarrow \psi }\in \Gamma $
. A similar procedure establishes that
$\mathbf {t}_{\varphi \rightarrow \psi }\rightarrow \mathbf {t}_{\varphi '\rightarrow \psi }\in \Gamma $
. A similar procedure establishes that
![]() $\mathbf {t}_{\varphi '\rightarrow \psi }\rightarrow \mathbf {t}_{\varphi '\rightarrow \psi '}\in \Gamma $
. By small modifications to this process, one eventually can infer that
$\mathbf {t}_{\varphi '\rightarrow \psi }\rightarrow \mathbf {t}_{\varphi '\rightarrow \psi '}\in \Gamma $
. By small modifications to this process, one eventually can infer that
![]() $\Gamma $
includes
$\Gamma $
includes
![]() $\mathbf {t}_{\varphi \rightarrow \psi }\leftrightarrow \mathbf {t}_{\varphi '\rightarrow \psi '}$
, i.e., that
$\mathbf {t}_{\varphi \rightarrow \psi }\leftrightarrow \mathbf {t}_{\varphi '\rightarrow \psi '}$
, i.e., that
![]() . Consequently,
. Consequently,
![]() $c_{\Gamma }(\varphi )\multimap _{\Gamma } c_{\Gamma }(\psi )=c_{\Gamma }(\varphi ')\multimap _{\Gamma } c_{\Gamma }(\psi ')$
.
$c_{\Gamma }(\varphi )\multimap _{\Gamma } c_{\Gamma }(\psi )=c_{\Gamma }(\varphi ')\multimap _{\Gamma } c_{\Gamma }(\psi ')$
.
The final step is to establish that the functions
![]() $h_{\Gamma ,\Xi }$
exhibit the properties required by Definition 4:
$h_{\Gamma ,\Xi }$
exhibit the properties required by Definition 4:
Lemma 26. If
![]() $\Gamma R\Xi $
the function
$\Gamma R\Xi $
the function
![]() $h_{\Gamma ,\Xi }$
enjoys the following properties:
$h_{\Gamma ,\Xi }$
enjoys the following properties:
-
•
 $h_{\Gamma ,\Xi }(t_{\Gamma }(p))=t_{\Xi }(p)$
and
$h_{\Gamma ,\Xi }(t_{\Gamma }(p))=t_{\Xi }(p)$
and
 $h_{\Gamma ,\Xi }(c_{\Gamma }(p))=c_{\Xi }(p)$
for atoms p.
$h_{\Gamma ,\Xi }(c_{\Gamma }(p))=c_{\Xi }(p)$
for atoms p. -
•
 .
. -
•
 .
.
Proof. The definition of
![]() $h_{\Gamma ,\Xi }$
establishes the initial atomic cases. For induction, we first examine the case of
$h_{\Gamma ,\Xi }$
establishes the initial atomic cases. For induction, we first examine the case of
![]() $\oplus _{\Gamma }$
:
$\oplus _{\Gamma }$
:

We examine the case of
![]() $\multimap _{\Gamma }$
:
$\multimap _{\Gamma }$
:

Collectively, the foregoing lemmas tender an assurance that the relation R, concept semi-lattices, and other model-theoretic components suffice to satisfy Definition 4. We may thereby conclude that
![]() $\mathfrak {M}$
(and each
$\mathfrak {M}$
(and each
![]() $\mathfrak {M}_{\Gamma }$
) is in fact an
$\mathfrak {M}_{\Gamma }$
) is in fact an
![]() $\mathsf {S}/\mathsf {PAI}$
model.
$\mathsf {S}/\mathsf {PAI}$
model.
Lemma 27.
![]() $\varphi \in \Gamma $
iff
$\varphi \in \Gamma $
iff
![]() $\Gamma \Vdash \varphi $
.
$\Gamma \Vdash \varphi $
.
Proof. In the atomic case, this is handled by the valuation function v. Thus, as induction hypothesis, suppose that the result has been established for all formulae of lesser complexity than
![]() $\varphi $
.
$\varphi $
.
![]() $\bullet $
In case
$\bullet $
In case
![]() $\varphi =\neg \psi $
,
$\varphi =\neg \psi $
,
![]() $\neg \psi \in \Gamma $
holds if (by maximality of
$\neg \psi \in \Gamma $
holds if (by maximality of
![]() $\Gamma $
) and only if (by consistency of
$\Gamma $
) and only if (by consistency of
![]() $\Gamma $
)
$\Gamma $
)
![]() $\psi \notin \Gamma $
. But by induction hypothesis, this is equivalent to
$\psi \notin \Gamma $
. But by induction hypothesis, this is equivalent to
![]() $\Gamma \nVdash \psi $
, i.e.,
$\Gamma \nVdash \psi $
, i.e.,
![]() $\Gamma \Vdash \neg \psi $
.
$\Gamma \Vdash \neg \psi $
.
![]() $\bullet $
In case
$\bullet $
In case
![]() $\varphi = \psi \wedge \xi $
,
$\varphi = \psi \wedge \xi $
,
![]() $\psi \wedge \xi \in \Gamma $
if (by
$\psi \wedge \xi \in \Gamma $
if (by
![]() $[ADJ]$
) and only if (by theoremhood of
$[ADJ]$
) and only if (by theoremhood of
![]() $(\psi \wedge \xi )\rightarrow \psi $
and
$(\psi \wedge \xi )\rightarrow \psi $
and
![]() $(\psi \wedge \xi )\rightarrow \xi $
) both
$(\psi \wedge \xi )\rightarrow \xi $
) both
![]() $\psi \in \Gamma $
and
$\psi \in \Gamma $
and
![]() $\xi \in \Gamma $
. By induction hypothesis, this is equivalent to the conjunction of
$\xi \in \Gamma $
. By induction hypothesis, this is equivalent to the conjunction of
![]() $\Gamma \Vdash \psi $
and
$\Gamma \Vdash \psi $
and
![]() $\Gamma \Vdash \xi $
, a condition which is equivalent to
$\Gamma \Vdash \xi $
, a condition which is equivalent to
![]() $\Gamma \Vdash \psi \wedge \xi $
.
$\Gamma \Vdash \psi \wedge \xi $
.
![]() $\bullet $
Finally, consider the case in which
$\bullet $
Finally, consider the case in which
![]() $\varphi =\psi \rightarrow \xi $
. By Theorem 2,
$\varphi =\psi \rightarrow \xi $
. By Theorem 2,
![]() $\psi \rightarrow \xi \in \Gamma $
holds precisely when
$\psi \rightarrow \xi \in \Gamma $
holds precisely when
![]() and
and
![]() $\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\xi }\in \Gamma $
.
$\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\xi }\in \Gamma $
.
-
•
 holds exactly when
holds exactly when
 . By Corollary 1, this is equivalent to the case when at every
. By Corollary 1, this is equivalent to the case when at every
 $\Xi $
such that
$\Xi $
such that
 $\Gamma R\Xi $
, if
$\Gamma R\Xi $
, if
 $\psi \in \Xi $
then
$\psi \in \Xi $
then
 $\xi \in \Xi $
. By induction hypothesis, this is equivalent to saying that at all accessible
$\xi \in \Xi $
. By induction hypothesis, this is equivalent to saying that at all accessible
 $\Xi $
, if
$\Xi $
, if
 $\Xi \Vdash \psi $
then
$\Xi \Vdash \psi $
then
 $\Xi \Vdash \xi $
$\Xi \Vdash \xi $
-
•
 $\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\xi }\in \Gamma $
holds if and only if
$\mathbf {t}_{\psi }\rightarrow \mathbf {t}_{\xi }\in \Gamma $
holds if and only if
 $\psi \wedge \xi \mathrel {\sim }_{\Gamma }\psi $
, i.e., if
$\psi \wedge \xi \mathrel {\sim }_{\Gamma }\psi $
, i.e., if
 . But by construction, this is equivalent to
. But by construction, this is equivalent to
 ${t}_{\Gamma }(\xi )\leq _{\Gamma }{t}_{\Gamma }(\psi )$
by Lemma 22.
${t}_{\Gamma }(\xi )\leq _{\Gamma }{t}_{\Gamma }(\psi )$
by Lemma 22.
Jointly, the two above semantic conditions are equivalent to
![]() $\Gamma \Vdash \psi \rightarrow \xi $
.
$\Gamma \Vdash \psi \rightarrow \xi $
.
Lemma 27, of course, immediately captures completeness of the axioms.
Theorem 3. If
![]() $\Gamma \vDash _{\mathsf {S}/\mathsf {PAI}}\varphi $
then
$\Gamma \vDash _{\mathsf {S}/\mathsf {PAI}}\varphi $
then
![]() $\Gamma \vdash _{\mathsf {S}/\mathsf {PAI}}\varphi $
.
$\Gamma \vdash _{\mathsf {S}/\mathsf {PAI}}\varphi $
.
4.4 The restrictor axiom, revisited
To conclude, we return to make good on a promissory note issued in Section 3.2, in which we had considered an axiom en passant:
This axiom
![]() $[R]$
might be thought of as a restrictor axiom as it encapsulates an intuition that restrictions in the states that a conditional is about should be tracked by corresponding restrictions in the conditional’s overall subject-matter. This principle seems extremely natural—if not necessitated—if one takes states to make up a part of a conditional’s topic.
$[R]$
might be thought of as a restrictor axiom as it encapsulates an intuition that restrictions in the states that a conditional is about should be tracked by corresponding restrictions in the conditional’s overall subject-matter. This principle seems extremely natural—if not necessitated—if one takes states to make up a part of a conditional’s topic.
To illustrate, suppose that
![]() $(\varphi \wedge \psi )\rightarrow \xi $
is evaluated over the states at which
$(\varphi \wedge \psi )\rightarrow \xi $
is evaluated over the states at which
![]() $\varphi \wedge \psi $
is true while
$\varphi \wedge \psi $
is true while
![]() $(\varphi \vee \psi )\rightarrow \xi $
is evaluated over the states at which
$(\varphi \vee \psi )\rightarrow \xi $
is evaluated over the states at which
![]() $\varphi \vee \psi $
is true. Intuitively, the states that
$\varphi \vee \psi $
is true. Intuitively, the states that
![]() $(\varphi \wedge \psi )\rightarrow \xi $
is about are a subset of the states that
$(\varphi \wedge \psi )\rightarrow \xi $
is about are a subset of the states that
![]() $(\varphi \vee \psi )\rightarrow \xi $
is about. One might expect to see this reflected as a principle of topic inclusion. In response, we can define a system
$(\varphi \vee \psi )\rightarrow \xi $
is about. One might expect to see this reflected as a principle of topic inclusion. In response, we can define a system
![]() $\mathsf {resS}/\mathsf {PAI}$
—restrictor monotone
$\mathsf {resS}/\mathsf {PAI}$
—restrictor monotone
![]() $\mathsf {S}/\mathsf {PAI}$
—as follows:
$\mathsf {S}/\mathsf {PAI}$
—as follows:
Definition 18.
![]() $\mathsf {resS}/\mathsf {PAI}=\mathsf {S}/\mathsf {PAI}\oplus ((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
.
$\mathsf {resS}/\mathsf {PAI}=\mathsf {S}/\mathsf {PAI}\oplus ((\varphi \vee \psi )\rightarrow \xi )\rightarrow ((\varphi \wedge \psi )\rightarrow \xi )$
.
Recall from Section 3.2 the description of a particular feature of propositional monotonicity—that for all
![]() $d,e,f\in \mathcal {C}_{w}$
,
$d,e,f\in \mathcal {C}_{w}$
,
in case
![]() $\pi _{0}(d)=\pi _{0}(e)$
and
$\pi _{0}(d)=\pi _{0}(e)$
and
![]() $\pi _{1}(d)\subseteq \pi _{1}(e)$
—whose imposition sufficed to determine models for which this
$\pi _{1}(d)\subseteq \pi _{1}(e)$
—whose imposition sufficed to determine models for which this
![]() $\mathsf {resS}/\mathsf {PAI}$
is sound. We had ended prematurely, having not yet defined the necessary tools for a completeness proof.
$\mathsf {resS}/\mathsf {PAI}$
is sound. We had ended prematurely, having not yet defined the necessary tools for a completeness proof.
Serendipitously—and somewhat surprisingly—it turns out that this property does serve to characterize a model theory for
![]() $\mathsf {resS}/\mathsf {PAI}$
:
$\mathsf {resS}/\mathsf {PAI}$
:
Observation 11.
![]() $\mathsf {resS}/\mathsf {PAI}$
is characterized by propositional monotonicity.
$\mathsf {resS}/\mathsf {PAI}$
is characterized by propositional monotonicity.
Proof. Soundness follows from Observation 2, leaving only completeness. Fix contents
![]() and make two assumptions: A first, topic-theoretic assumption that
and make two assumptions: A first, topic-theoretic assumption that
![]() and a second, propositional assumption that
and a second, propositional assumption that
![]() . Now, take note of two facts. From the first assumption on topic, we note that
. Now, take note of two facts. From the first assumption on topic, we note that
![]() is identical to both
is identical to both
![]() and
and
![]() . From the assumption, basic set theory ensures that
. From the assumption, basic set theory ensures that
![]() and
and
![]() .
.
Jointly, these entail that
(on the one hand) and that
(on the other). These identities ensure two further equivalences:

Now, in virtue of the restrictor axiom
![]() $[R]$
, by Lemmas 9 and 22,
$[R]$
, by Lemmas 9 and 22,
. Putting this all together, we get the following picture:
But, given the arbitrary choice of elements from
![]() $\mathcal {C}_{\Gamma }$
, this is just the condition of propositional monotonicity.
$\mathcal {C}_{\Gamma }$
, this is just the condition of propositional monotonicity.
Clearly, there remains an abundance of axiomatic extensions that could be investigated. Insofar as each serves as an axiomatic representation of a distinct topic-theoretic condition, this setting invites the articulation and modeling of a remarkable range of detailed theories of intensional subject-matter as extensions of
![]() $\mathsf {S}/\mathsf {PAI}$
.
$\mathsf {S}/\mathsf {PAI}$
.
5 Concluding remarks
As we conclude, we might pause to summarize what we have accomplished. We began by considering several settings displaying plausible topic-theoretic features for which standard topic-theoretic frameworks appear inadequate. Reflecting on features common to these scenarios led us to identify among the standard frameworks potential causes for these inadequacies and permitted us to rough out the types of constraints that might replace them. As this sketch took form, we continued to sharpen the image by providing a concrete implementation in which the topic-theoretic machinery of Parry’s
![]() $\mathsf {PAI}$
was remolded until our intuitions could be accommodated. We concluded by demonstrating the modularity and versatility of the new framework by examining several of its extensions and their corresponding semantic assumptions.
$\mathsf {PAI}$
was remolded until our intuitions could be accommodated. We concluded by demonstrating the modularity and versatility of the new framework by examining several of its extensions and their corresponding semantic assumptions.
It is worth underscoring that the above systems have played the role of a vehicle through which a more fundamental contribution could be conveyed, a laboratory in which to formally assess the contribution on its philosophical merits and its mathematical tractability. Behind this particular implementation is a more general framework whose underlying topic-theoretic representation is subtle enough to account for situations in which Topic Sufficiency breaks down. (And given some reflection on the examples we have reviewed, I suspect that such situations are more common than not.) This continues the earlier work of [Reference Ferguson13], further refining the core Parry intuitions to produce a model of topic suitable for a wider range of settings.
Acknowledgments
I appreciate the extremely helpful remarks of two reviewers for this journal and the feedback of the audience at Logica 2022.
Funding
This paper was written with the support of the MetaMuSo project (Czech Science Foundation project GA22-01137S).