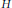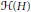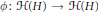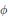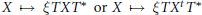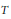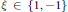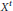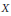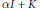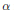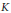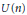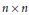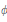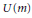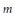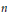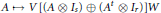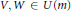Let 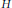H$H$ be a complex Hilbert space, and 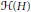\mathcal{H}\left( H \right)$\mathcal{H}\left( H \right)$ be the real linear space of bounded selfadjoint operators on 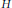H$H$. We study linear maps 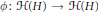\phi :\,\mathcal{H}(H)\,\to \,\mathcal{H}(H)$\phi :\,\mathcal{H}(H)\,\to \,\mathcal{H}(H)$ leaving invariant various properties such as invertibility, positive definiteness, numerical range, etc. The maps 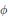\phi$\phi$ are not assumed a priori continuous. It is shown that under an appropriate surjective or injective assumption 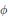\phi$\phi$ has the form 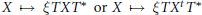X\mapsto \xi TX{{T}^{*}}orX\mapsto \xi T{{X}^{t}}{{T}^{*}}$X\mapsto \xi TX{{T}^{*}}orX\mapsto \xi T{{X}^{t}}{{T}^{*}}$, for a suitable invertible or unitary 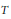T$T$ and 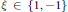\xi \,\in \,\{1,\,-1\}$\xi \,\in \,\{1,\,-1\}$, where 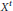{{X}^{t}}${{X}^{t}}$ stands for the transpose of 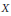X$X$ relative to some orthonormal basis. Examples are given to show that the surjective or injective assumption cannot be relaxed. The results are extended to complex linear maps on the algebra of bounded linear operators on 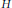H$H$. Similar results are proved for the (real) linear space of (selfadjoint) operators of the form 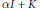\alpha I\,+\,K$\alpha I\,+\,K$, where 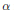\alpha$\alpha$ is a scalar and 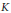K$K$ is compact.

Let U(n)$U(n)$ be the group of n\,\times \,n$n\,\times \,n$ unitary matrices. We show that if \phi $\phi$ is a linear transformation sending U(n)$U(n)$ into U(m)$U(m)$, then m$m$ is a multiple of n$n$, and \phi $\phi$ has the form

A\,\mapsto \,V[(A\,\otimes \,{{I}_{s}})\,\otimes \,({{A}^{t}}\,\otimes \,{{I}_{r}})]W $$A\,\mapsto \,V[(A\,\otimes \,{{I}_{s}})\,\otimes \,({{A}^{t}}\,\otimes \,{{I}_{r}})]W$$

for some V,\,W\,\in \,U(m)$V,\,W\,\in \,U(m)$. From this result, one easily deduces the characterization of linear operators that map U(n)$U(n)$ into itself obtained by Marcus. Further generalization of the main theorem is also discussed.