Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T02:19:48.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Maps Transforming the Unitary Group

Published online by Cambridge University Press:  20 November 2018

Wai-Shun Cheung  and
Chi-Kwong Li
Wai-Shun Cheung
Affiliation:
Centro de Estruturas Lineares e Combinatórias, Universidade de Lisboa, av. Prof. Gama Pinto, 2, 1649-003 Lisboa, Portugal
Chi-Kwong Li
Affiliation:
Department of Mathematics, College of William and Mary, Williamsburg, Virginia 23187, U.S.A., email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

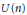Let $U(n)$ be the group of 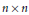$n\,\times \,n$ unitary matrices. We show that if 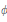$\phi $ is a linear transformation sending 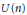$U(n)$ into 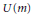$U(m)$, then 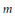$m$ is a multiple of 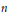$n$, and 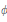$\phi $ has the form

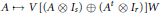$$A\,\mapsto \,V[(A\,\otimes \,{{I}_{s}})\,\otimes \,({{A}^{t}}\,\otimes \,{{I}_{r}})]W$$

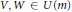for some $V,\,W\,\in \,U(m)$. From this result, one easily deduces the characterization of linear operators that map 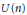$U(n)$ into itself obtained by Marcus. Further generalization of the main theorem is also discussed.

Keywords

15A04linear mapunitary groupgeneral linear group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 1 , 01 March 2003 , pp. 54 - 58
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Auerbach, H., Sur les groupes bornés de substitutions linéaires. C. R. Acad. Sci. Paris 195 (1932), 1367–1369.Google Scholar
[2] Christensen, E., On invertibility preserving linear mappings, simultaneous triangularization and Property L. Linear Algebra Appl. 301(1999), 153–170.Google Scholar
[3] Deutsch, E. and Schneider, H., Bounded groups and norm-hermitian matrices. Linear Algebra Appl. 9 (1974), 9–27.Google Scholar
[4] Guterman, A., Li, C. K. and Šemrl, P., Some general techniques on linear preserver problems. Linear Algebra Appl. 315 (2000), 61–81.Google Scholar
[5] Marcus, M., All linear operators leaving the unitary group invariant. Duke Math. J. 26 (1959), 155–163.Google Scholar
[6] Marcus, M. and Purves, R., Linear transformations on algebras of matrices II: The invariance of the elementary symmetric functions. Canad. J. Math. 11 (1959), 383–396.Google Scholar