Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T01:37:17.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Maps on Selfadjoint Operators Preserving Invertibility, Positive Definiteness, Numerical Range

Published online by Cambridge University Press:  20 November 2018

Chi-Kwong Li ,
Leiba Rodman  and
Peter Šemrl
Chi-Kwong Li
Affiliation:
Department of Mathematics, College of William and Mary, P.O. Box 8795, Williamsburg, Virginia 23187-8795, U.S.A., e-mail: [email protected]
Leiba Rodman
Affiliation:
Department of Mathematics, College of William and Mary, P.O. Box 8795, Williamsburg, Virginia 23187-8795, U.S.A., e-mail: [email protected]
Peter Šemrl
Affiliation:
Department of Mathematics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

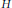Let $H$ be a complex Hilbert space, and 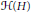$\mathcal{H}\left( H \right)$ be the real linear space of bounded selfadjoint operators on 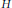$H$. We study linear maps 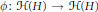$\phi :\,\mathcal{H}(H)\,\to \,\mathcal{H}(H)$ leaving invariant various properties such as invertibility, positive definiteness, numerical range, etc. The maps 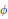$\phi$ are not assumed a priori continuous. It is shown that under an appropriate surjective or injective assumption 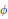$\phi$ has the form 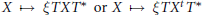$X\mapsto \xi TX{{T}^{*}}orX\mapsto \xi T{{X}^{t}}{{T}^{*}}$, for a suitable invertible or unitary 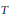$T$ and 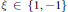$\xi \,\in \,\{1,\,-1\}$, where 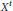${{X}^{t}}$ stands for the transpose of 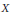$X$ relative to some orthonormal basis. Examples are given to show that the surjective or injective assumption cannot be relaxed. The results are extended to complex linear maps on the algebra of bounded linear operators on 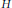$H$. Similar results are proved for the (real) linear space of (selfadjoint) operators of the form 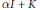$\alpha I\,+\,K$, where 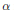$\alpha$ is a scalar and 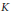$K$ is compact.

Keywords

47B1547B49linear mapselfadjoint operatorinvertiblepositive definitenumerical range
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 216 - 228
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Aupetit, B., Une généralisation du théorème de Gleason-Kahane- Żelazko pour les algèbres de Banach. Pacific J. Math. 85 (1979), 11–17.Google Scholar
[2] Aupetit, B., Trace and spectrum preserving mappings in Jordan-Banach algebras. Monatsh.Math. 125 (1998), 179–187.Google Scholar
[3] Aupetit, B., Sur les transformations qui conservent le spectre. Banach Algebras ‘97, de Gruyter, Berlin, 1998, 55–78.Google Scholar
[4] Aupetit, B., Spectrum-preserving linear mappings between Banach algebras or Jordan-Banach algebras. J. LondonMath. Soc. 62 (2000), 917–924.Google Scholar
[5] Aupetit, B. and du Toit Mouton, H., Spectrum preserving linear mappings in Banach algebras. Studia Math. 109 (1994), 91–100.Google Scholar
[6] Baruch, E. M. and Loewy, R., Linear preservers on spaces of Hermitian or real symmetric matrices. Linear Algebra Appl. 183 (1993), 89–102.Google Scholar
[7] Brešar, M. and Šemrl, P., Mappings which preserve idempotents, local automorphisms, and local derivations. Canad. J. Math. 45 (1993), 483–496.Google Scholar
[8] Brešar, M. and Šemrl, P., Linear maps preserving the spectral radius. J. Funct. Anal. 142 (1996), 360–368.Google Scholar
[9] Brešar, M. and Šemrl, P., Invertibility preserving maps preserve idempotents. Michigan Math. J. 45 (1998), 483–488.Google Scholar
[10] Brešar, M. and Šemrl, P., Spectral characterization of idempotents and invertibility preserving linear maps. Exposition. Math. 17 (1999), 185–192.Google Scholar
[11] Coburn, L. A. and Lebow, A., Components of invertible elements in quotient algebras of operators. Trans. Amer.Math. Soc. 130 (1968), 359–365.Google Scholar
[12] Conway, J. B., A course in operator theory. Amer.Math. Soc., Providence, Rhode Island, 2000.Google Scholar
[13] Fong, C. K., Norm estimates related to self-commutators. Linear Algebra Appl. 74 (1986), 151–156.Google Scholar
[14] Gohberg, I. C., On linear operators depending analytically on a parameter. Dokl. Akad. Nauk SSSR 78 (1951), 629–632.Google Scholar
[15] Halmos, P. R., Commutators of operators. Amer. J. Math. 74 (1952), 237–240.Google Scholar
[16] Jafarian, A. A. and Sourour, A. R., Spectrum-preserving linear maps. J. Funct. Anal. 66 (1986), 255–261.Google Scholar
[17] Kaplansky, I., Algebraic and analytic aspects of operator algebras. Amer.Math. Soc., Providence, Rhode Island, 1970.Google Scholar
[18] Loewy, R. and Pierce, S., Linear preservers of balanced nonsingular inertia classes. Linear Algebra Appl. 223/224 (1995), 483–449.Google Scholar
[19] Marcus, M. and Moyls, B. N., Linear transformations on algebras of matrices. Canad. J. Math. 11 (1958), 61–66.Google Scholar
[20] Martindale, W. S. 3rd, Jordan homomorphisms of the symmetric elements of a ring with involution. J. Algebra 5 (1967), 232–249.Google Scholar
[21] Newburgh, J. D., The variation of spectra. Duke Math. J. 18 (1951), 165–176.Google Scholar
[22] Omladič, M., On operators preserving the numerical range. Linear Algebra Appl. 134 (1990), 31–51.Google Scholar
[23] Pearcy, C. and Topping, D., Sum of small number of idempotents. Michigan Math. J. 14 (1967), 453–465.Google Scholar
[24] Pellegrini, V. J., Numerical range preserving operators on a Banach algebra. Studia Math. 54 (1975), 143–147.Google Scholar
[25] Pierce, S. et. al., A Survey of Linear Preserver Problems. Linear and Multilinear Algebra (1–2) 33(1992).Google Scholar
[26] Schneider, H., Positive operators and an inertia theorem. Numer.Math. 7 (1965), 11–17.Google Scholar
[27] Sourour, A., Invertibility preserving linear maps on L(X). Trans. Amer.Math. Soc. 348 (1996), 13–30.Google Scholar