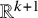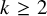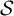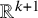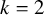1 Introduction
Let
![]() $\mathcal {S}$
be an abstract simplicial k-complex with vertex set
$\mathcal {S}$
be an abstract simplicial k-complex with vertex set
![]() $V(\mathcal {S})$
and edge set
$V(\mathcal {S})$
and edge set
![]() $E(\mathcal {S})$
. The lower bound theorem concerns the quantity
$E(\mathcal {S})$
. The lower bound theorem concerns the quantity
![]() $g_2(\mathcal {S})$
defined by
$g_2(\mathcal {S})$
defined by
 $$ \begin{align} g_2(\mathcal{S}) = |E(\mathcal{S})| -(k+1)|V(\mathcal{S})| + \binom{k+2}2. \end{align} $$
$$ \begin{align} g_2(\mathcal{S}) = |E(\mathcal{S})| -(k+1)|V(\mathcal{S})| + \binom{k+2}2. \end{align} $$
Barnette [Reference Barnette3] showed that
![]() $g_2(\mathcal {S}) \geq 0$
if
$g_2(\mathcal {S}) \geq 0$
if
![]() $\mathcal {S}$
is the boundary complex of a
$\mathcal {S}$
is the boundary complex of a
![]() $(k+1)$
-dimensional convex polytope. This was later generalised to simplicial spheres (Stanley [Reference Stanley18]) and pseudomanifolds (Kalai [Reference Kalai10], Tay [Reference Tay20]).
$(k+1)$
-dimensional convex polytope. This was later generalised to simplicial spheres (Stanley [Reference Stanley18]) and pseudomanifolds (Kalai [Reference Kalai10], Tay [Reference Tay20]).
Readers familiar with the rigidity theory of bar-joint frameworks will note that the right-hand side of (1.1) arises naturally in that theory and indeed is nonnegative if the 1-skeleton of
![]() $\mathcal {S}$
is a generically rigid graph in
$\mathcal {S}$
is a generically rigid graph in
![]() $\mathbb R^{k+1}$
. This was proved by Asimov and Roth [Reference Asimow and Roth2]. This connection between rigidity theory and polytopal combinatorics, noted by Kalai [Reference Kalai10] and Gromov [Reference Gromov8], has been fundamental to much of the work on lower bound theorems for various classes of simplicial complexes.
$\mathbb R^{k+1}$
. This was proved by Asimov and Roth [Reference Asimow and Roth2]. This connection between rigidity theory and polytopal combinatorics, noted by Kalai [Reference Kalai10] and Gromov [Reference Gromov8], has been fundamental to much of the work on lower bound theorems for various classes of simplicial complexes.
Around the same time as [Reference Kalai10], Fogelsanger proved that the 1-skeleton of a minimal homology k-cycle is generically rigid in
![]() $\mathbb R^{k+1}$
for
$\mathbb R^{k+1}$
for
![]() $k\geq 2$
[Reference Fogelsanger7]. It is not difficult to see that a k-pseudomanifold is a minimal homology k-cycle; see Section 3 for definitions. Thus, Fogelsanger’s result provides a generalisation and independent proof of the lower bound theorem for pseudomanifolds. Fogelsanger’s proof technique is different to the previous proofs of the lower bound theorem: it is a direct proof based on a rigidity lemma of Whiteley for vertex splitting [Reference Whiteley23], and an ingenious decomposition result (more on this below).
$k\geq 2$
[Reference Fogelsanger7]. It is not difficult to see that a k-pseudomanifold is a minimal homology k-cycle; see Section 3 for definitions. Thus, Fogelsanger’s result provides a generalisation and independent proof of the lower bound theorem for pseudomanifolds. Fogelsanger’s proof technique is different to the previous proofs of the lower bound theorem: it is a direct proof based on a rigidity lemma of Whiteley for vertex splitting [Reference Whiteley23], and an ingenious decomposition result (more on this below).
In the present paper we consider
![]() $\mathbb {Z}_2$
-symmetric simplicial complexes (i.e., simplicial complexes
$\mathbb {Z}_2$
-symmetric simplicial complexes (i.e., simplicial complexes
![]() $\mathcal {S}$
with a free automorphism of order two). Such complexes were referred to as centrally symmetric simplicial complexes in [Reference Klee, Nevo, Novik and Zheng11]. The term
$\mathcal {S}$
with a free automorphism of order two). Such complexes were referred to as centrally symmetric simplicial complexes in [Reference Klee, Nevo, Novik and Zheng11]. The term
![]() $\mathbb {Z}_2$
-symmetric is more suitable for our purposes since we will consider realisations of k-dimensional complexes in
$\mathbb {Z}_2$
-symmetric is more suitable for our purposes since we will consider realisations of k-dimensional complexes in
![]() ${\mathbb R}^{k+1}$
which have an arbitrary symmetry of order two, not just a point inversion through the origin.
${\mathbb R}^{k+1}$
which have an arbitrary symmetry of order two, not just a point inversion through the origin.
Note that if P is a centrally symmetric simplicial polytope in
![]() $\mathbb R^{k+1}$
, that is,
$\mathbb R^{k+1}$
, that is,
![]() $-P = P$
, then the boundary complex of P is a
$-P = P$
, then the boundary complex of P is a
![]() $\mathbb {Z}_2$
-symmetric simplicial complex of dimension k. Stanley [Reference Stanley19] showed, in particular, that if
$\mathbb {Z}_2$
-symmetric simplicial complex of dimension k. Stanley [Reference Stanley19] showed, in particular, that if
![]() $\mathcal {S}$
is the boundary complex of such a polytope, then
$\mathcal {S}$
is the boundary complex of such a polytope, then
 $$ \begin{align} g_2(\mathcal{S}) \geq \binom{k+1}2 - (k+1). \end{align} $$
$$ \begin{align} g_2(\mathcal{S}) \geq \binom{k+1}2 - (k+1). \end{align} $$
Later, Sanyal, Werner and Ziegler [Reference Sanyal, Werner and Ziegler13] used a rigidity-based approach to obtain further properties of the f-vector of centrally symmetric polytopes. In particular, their results imply that (1.2) follows from an earlier rigidity result of Whiteley [Reference Whiteley22] that the 1-skeleton of every convex
![]() $(k+1)$
-polytope is infinitesimally rigid in
$(k+1)$
-polytope is infinitesimally rigid in
![]() $\mathbb R^{k+1}$
. More recently, Klee, Nevo, Novik and Zheng [Reference Klee, Nevo, Novik and Zheng11] used techniques from rigidity theory to characterise the cases for which equality can hold in Stanley’s Theorem. While centrally symmetric simplicial polytopes have been the topic of much research since Stanley’s paper, the extension of this theory from simplicial polytopes to more general families of simplicial complexes is less developed than in the non-symmetric case. One significant result in that direction is the recent proof by Novik and Zheng of the
$\mathbb R^{k+1}$
. More recently, Klee, Nevo, Novik and Zheng [Reference Klee, Nevo, Novik and Zheng11] used techniques from rigidity theory to characterise the cases for which equality can hold in Stanley’s Theorem. While centrally symmetric simplicial polytopes have been the topic of much research since Stanley’s paper, the extension of this theory from simplicial polytopes to more general families of simplicial complexes is less developed than in the non-symmetric case. One significant result in that direction is the recent proof by Novik and Zheng of the
![]() $\mathbb Z_2$
-symmetric upper bound conjecture for simplicial spheres [Reference Novik and Zheng12]. In this paper, we address the lower bound conjecture for a larger class of
$\mathbb Z_2$
-symmetric upper bound conjecture for simplicial spheres [Reference Novik and Zheng12]. In this paper, we address the lower bound conjecture for a larger class of
![]() $\mathbb Z_2$
-symmetric simplicial complexes – namely, the circuits of the simplicial matroid. Precise definitions will be given in Section 3, but for now, it suffices to note that a simplicial k-circuit is a minimal homology k-cycle over
$\mathbb Z_2$
-symmetric simplicial complexes – namely, the circuits of the simplicial matroid. Precise definitions will be given in Section 3, but for now, it suffices to note that a simplicial k-circuit is a minimal homology k-cycle over
![]() $\mathbb Z_2$
in Fogelsanger’s terminology.
$\mathbb Z_2$
in Fogelsanger’s terminology.
Our approach is to extend Fogelsanger’s rigidity theorem and proof techniques to the
![]() $\mathbb {Z}_2$
-symmetric setting. The extension is not straightforward and, in particular, makes use of a new notion of a framework with partial symmetry which we have not seen in the rigidity literature. Our extension of Fogelsanger’s decomposition technique is powerful enough to show that the graph of any
$\mathbb {Z}_2$
-symmetric setting. The extension is not straightforward and, in particular, makes use of a new notion of a framework with partial symmetry which we have not seen in the rigidity literature. Our extension of Fogelsanger’s decomposition technique is powerful enough to show that the graph of any
![]() $\mathbb {Z}_2$
-symmetric simplicial k-circuit can be realised as an infinitesimally rigid framework having a specified point group symmetry of order two in
$\mathbb {Z}_2$
-symmetric simplicial k-circuit can be realised as an infinitesimally rigid framework having a specified point group symmetry of order two in
![]() $\mathbb {R}^{k+1}$
, unless
$\mathbb {R}^{k+1}$
, unless
![]() $k=2$
and the point group is the half-turn rotation group in
$k=2$
and the point group is the half-turn rotation group in
![]() $\mathbb {R}^3$
.
$\mathbb {R}^3$
.
We shall see that when
![]() $k=2$
and the point group is the half-turn rotation group in
$k=2$
and the point group is the half-turn rotation group in
![]() $\mathbb {R}^3$
, every symmetric realisation of a
$\mathbb {R}^3$
, every symmetric realisation of a
![]() $\mathbb {Z}_2$
-symmetric planar graph is infinitesimally flexible. The smallest such example is the famous Bricard octahedron [Reference Bricard4], given in Figure 1. The Bricard octahedron was the source of inspiration for Connelly’s flexible polytope [Reference Connelly5]. More generally, the rigidity of symmetric and non-convex realisations of 1-skeletons of polytopes has been one of the central topics in rigidity theory; see, for example, [Reference Servatius17, Reference Schlenker14]. We believe that our rigidity theorem will have a substantial impact in rigidity theory because it gives the first extension of rigidity results on symmetric convex polytopes to a more general family including non-convex symmetric realisations of polytopes and a larger family of simplicial complexes that includes pseudomanifolds.
$\mathbb {Z}_2$
-symmetric planar graph is infinitesimally flexible. The smallest such example is the famous Bricard octahedron [Reference Bricard4], given in Figure 1. The Bricard octahedron was the source of inspiration for Connelly’s flexible polytope [Reference Connelly5]. More generally, the rigidity of symmetric and non-convex realisations of 1-skeletons of polytopes has been one of the central topics in rigidity theory; see, for example, [Reference Servatius17, Reference Schlenker14]. We believe that our rigidity theorem will have a substantial impact in rigidity theory because it gives the first extension of rigidity results on symmetric convex polytopes to a more general family including non-convex symmetric realisations of polytopes and a larger family of simplicial complexes that includes pseudomanifolds.

Figure 1 The Bricard octahedron.
The paper is organised as follows. We first give preliminary facts on the infinitesimal rigidity of frameworks under a point group symmetry in Section 2. In Section 3, we review Fogelsanger’s decomposition technique for simplicial circuits using an approach from [Reference Cruickshank, Jackson and Tanigawa6]. We then provide an extension of Fogelsanger’s rigidity theorem to realisations of simplicial k-circuits in which several pairs of vertices are constrained to lie symmetrically in
![]() ${\mathbb R}^{k+1}$
. In Section 5, we extend Fogelsanger’s decomposition result to
${\mathbb R}^{k+1}$
. In Section 5, we extend Fogelsanger’s decomposition result to
![]() $\mathbb Z_2$
-symmetric simplicial k-circuits and use this to prove our main theorem on the rigidity of
$\mathbb Z_2$
-symmetric simplicial k-circuits and use this to prove our main theorem on the rigidity of
![]() $\mathbb {Z}_2$
-symmetric simplicial circuits. The application to the lower bound theorem is given in Section 6. We close the paper by giving some final remarks and open problems in Section 7.
$\mathbb {Z}_2$
-symmetric simplicial circuits. The application to the lower bound theorem is given in Section 6. We close the paper by giving some final remarks and open problems in Section 7.
2 Preliminaries on rigidity and symmetry
In this section, we introduce some basic results on the infinitesimal rigidity of frameworks and their extensions to the symmetric case.
Throughout the paper, we use the following basic conventions and notation. All graphs considered will be finite, undirected and simple (i.e., without loops or multiple edges). For
![]() $X\subseteq V(G)$
, let
$X\subseteq V(G)$
, let
![]() $E_G[X]=\{uv\in E(G): u, v\in X\}$
. The subgraph of G induced by X is given by
$E_G[X]=\{uv\in E(G): u, v\in X\}$
. The subgraph of G induced by X is given by
![]() $G[X]=(X, E_G[X])$
. For
$G[X]=(X, E_G[X])$
. For
![]() $v\in V(G)$
,
$v\in V(G)$
,
![]() $N_G(v)$
denotes the set of vertices adjacent to v in G.
$N_G(v)$
denotes the set of vertices adjacent to v in G.
2.1 Infinitesimal rigidity
A graph drawn in Euclidean space with straight line edges is called a (bar-joint) framework and denoted by a pair
![]() $(G,p)$
of the graph G and the point configuration
$(G,p)$
of the graph G and the point configuration
![]() $p: V(G)\rightarrow \mathbb {R}^d$
. We will also refer to
$p: V(G)\rightarrow \mathbb {R}^d$
. We will also refer to
![]() $(G,p)$
as a realisation of G in
$(G,p)$
as a realisation of G in
![]() ${\mathbb R}^d$
.
${\mathbb R}^d$
.
An infinitesimal motion of a framework
![]() $(G,p)$
is a map
$(G,p)$
is a map
![]() $\dot {p}: V(G)\rightarrow \mathbb {R}^d$
satisfying
$\dot {p}: V(G)\rightarrow \mathbb {R}^d$
satisfying
For a skew-symmetric matrix S and
![]() $t\in \mathbb {R}^d$
, it is not difficult to check that
$t\in \mathbb {R}^d$
, it is not difficult to check that
![]() $\dot {p}$
defined by
$\dot {p}$
defined by
![]() $\dot {p}(v)=Sp(v)+t\ (v\in V(G))$
is an infinitesimal motion of
$\dot {p}(v)=Sp(v)+t\ (v\in V(G))$
is an infinitesimal motion of
![]() $(G,p)$
. Such an infinitesimal motion is called trivial. The framework
$(G,p)$
. Such an infinitesimal motion is called trivial. The framework
![]() $(G,p)$
is infinitesimally rigid if every infinitesimal motion of
$(G,p)$
is infinitesimally rigid if every infinitesimal motion of
![]() $(G,p)$
is trivial. We say that the graph G is rigid in
$(G,p)$
is trivial. We say that the graph G is rigid in
![]() $\mathbb {R}^d$
if G has an infinitesimally rigid realisation in
$\mathbb {R}^d$
if G has an infinitesimally rigid realisation in
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
Since (2.1) is a system of linear equations in
![]() $\dot {p}$
, we can represent it by a matrix of size
$\dot {p}$
, we can represent it by a matrix of size
![]() $|E(G)|\times d|V(G)|$
. This matrix is called the rigidity matrix
$|E(G)|\times d|V(G)|$
. This matrix is called the rigidity matrix
![]() $R(G,p)$
of
$R(G,p)$
of
![]() $(G,p)$
. The rows of
$(G,p)$
. The rows of
![]() $R(G,p)$
are indexed by edges of G. In addition, for each vertex
$R(G,p)$
are indexed by edges of G. In addition, for each vertex
![]() $v \in V(G)$
, we have a corresponding set of d columns. For an edge
$v \in V(G)$
, we have a corresponding set of d columns. For an edge
![]() $uv \in E(G)$
, the corresponding row of
$uv \in E(G)$
, the corresponding row of
![]() $R(G,p)$
has the d-dimensional vector
$R(G,p)$
has the d-dimensional vector
![]() $p(u)-p(v)$
in the column-set corresponding to u and
$p(u)-p(v)$
in the column-set corresponding to u and
![]() $p(v)-p(u)$
in the column-set corresponding to u. All other entries of the row are zero.
$p(v)-p(u)$
in the column-set corresponding to u. All other entries of the row are zero.
When the affine span of
![]() $p(V(G))$
has dimension at least
$p(V(G))$
has dimension at least
![]() $d-1$
, the dimension of the space of trivial motions is
$d-1$
, the dimension of the space of trivial motions is
![]() $\binom {d+1}{2}$
, so
$\binom {d+1}{2}$
, so
![]() $(G,p)$
is infinitesimally rigid if and only if
$(G,p)$
is infinitesimally rigid if and only if
![]() $\operatorname {\mathrm {rank}} R(G,p)=d|V(G)|-\binom {d+1}{2}$
. In particular, if
$\operatorname {\mathrm {rank}} R(G,p)=d|V(G)|-\binom {d+1}{2}$
. In particular, if
![]() $(G,p)$
is infinitesimally rigid and G has at least d vertices, then
$(G,p)$
is infinitesimally rigid and G has at least d vertices, then
 $$ \begin{align} |E(G)|-d|V(G)|+\binom{d+1}{2}\geq 0. \end{align} $$
$$ \begin{align} |E(G)|-d|V(G)|+\binom{d+1}{2}\geq 0. \end{align} $$
Kalai [Reference Kalai10] and Gromov [Reference Gromov8] exploited the close relationship between (1.1) and (2.2) to use rigidity theory to prove their extensions of the Lower Bound Theorem. We will use a similar approach to obtain our lower bound theorem for
![]() ${\mathbb Z}_2$
-symmetric simplicial complexes.
${\mathbb Z}_2$
-symmetric simplicial complexes.
2.2 Rigidity under symmetry
A graph with a vertex pairing is a pair
![]() $(G,\ast )$
of a graph G and a free involution
$(G,\ast )$
of a graph G and a free involution
![]() $\ast $
acting on some
$\ast $
acting on some
![]() $X\subseteq V(G)$
. (Thus,
$X\subseteq V(G)$
. (Thus,
![]() $\ast : X\rightarrow X$
and satisfies
$\ast : X\rightarrow X$
and satisfies
![]() $\ast (\ast (u))=u$
and
$\ast (\ast (u))=u$
and
![]() $\ast (u)\neq u$
for all
$\ast (u)\neq u$
for all
![]() $u\in X$
.) We will denote
$u\in X$
.) We will denote
![]() $\ast (u)$
by
$\ast (u)$
by
![]() $u^*$
for each
$u^*$
for each
![]() $u\in X$
and put
$u\in X$
and put
![]() $Y^*=\{u^*: u\in Y\}$
for all
$Y^*=\{u^*: u\in Y\}$
for all
![]() $Y\subseteq X$
. In addition, for each
$Y\subseteq X$
. In addition, for each
![]() $W \subset V(G)$
, we put
$W \subset V(G)$
, we put
Then
![]() $\ast $
induces a free involution
$\ast $
induces a free involution
![]() $\ast _W: X_W \rightarrow X_W$
. We will simply denote
$\ast _W: X_W \rightarrow X_W$
. We will simply denote
![]() $\ast _W$
by
$\ast _W$
by
![]() $\ast $
when W is clear from the context. Similarly, for a subgraph H of G,
$\ast $
when W is clear from the context. Similarly, for a subgraph H of G,
![]() $(H,\ast _{V(H)})$
is simply denoted by
$(H,\ast _{V(H)})$
is simply denoted by
![]() $(H,\ast )$
.
$(H,\ast )$
.
We will use the free involution
![]() $\ast $
to force a symmetry on the point configuration in a possible realisation of G. Let
$\ast $
to force a symmetry on the point configuration in a possible realisation of G. Let
![]() $\Gamma $
be a point group of
$\Gamma $
be a point group of
![]() $\mathbb {R}^d$
of order two – that is, a subgroup of
$\mathbb {R}^d$
of order two – that is, a subgroup of
![]() $O(d)$
of order two. A
$O(d)$
of order two. A
![]() $\Gamma $
-framework is a triple
$\Gamma $
-framework is a triple
![]() $(G,\ast ,p)$
of a graph G, a free involution
$(G,\ast ,p)$
of a graph G, a free involution
![]() $\ast : X\rightarrow X$
for some
$\ast : X\rightarrow X$
for some
![]() $X \subseteq V(G)$
, and a point-configuration p such that
$X \subseteq V(G)$
, and a point-configuration p such that
![]() $p(u^*)=\gamma (p(u))$
for all
$p(u^*)=\gamma (p(u))$
for all
![]() $u\in X$
, where
$u\in X$
, where
![]() $\gamma $
is the non-identity element in
$\gamma $
is the non-identity element in
![]() $\Gamma $
. By ignoring
$\Gamma $
. By ignoring
![]() $\ast $
,
$\ast $
,
![]() $(G,\ast ,p)$
can be considered as a realisation of G, and hence, we can apply the terminology from Section 2.1 to
$(G,\ast ,p)$
can be considered as a realisation of G, and hence, we can apply the terminology from Section 2.1 to
![]() $(G,\ast ,p)$
. We will sometimes refer to a
$(G,\ast ,p)$
. We will sometimes refer to a
![]() $\Gamma $
-framework
$\Gamma $
-framework
![]() $(G,\ast ,p)$
as a
$(G,\ast ,p)$
as a
![]() $\Gamma $
-symmetric realisation of
$\Gamma $
-symmetric realisation of
![]() $(G,\ast )$
. We say that
$(G,\ast )$
. We say that
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid if
$\Gamma $
-rigid if
![]() $(G,\ast )$
has an infinitesimally rigid
$(G,\ast )$
has an infinitesimally rigid
![]() $\Gamma $
-symmetric realisation.
$\Gamma $
-symmetric realisation.
A
![]() $\Gamma $
-framework
$\Gamma $
-framework
![]() $(G,\ast ,p)$
is generic if the transcendence degree of the set of coordinates of all the points in
$(G,\ast ,p)$
is generic if the transcendence degree of the set of coordinates of all the points in
![]() $p(V)$
over
$p(V)$
over
![]() $\mathbb Q$
takes the maximum possible value
$\mathbb Q$
takes the maximum possible value
![]() $d(|V| - |X|/2)$
. Thus,
$d(|V| - |X|/2)$
. Thus,
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid if and only if every (or equivalently, some) generic
$\Gamma $
-rigid if and only if every (or equivalently, some) generic
![]() $\Gamma $
-symmetric realisation of
$\Gamma $
-symmetric realisation of
![]() $(G,\ast )$
is infinitesimally rigid.
$(G,\ast )$
is infinitesimally rigid.
Example 2.1. This example illustrates that the
![]() $\Gamma $
-rigidity of a fixed
$\Gamma $
-rigidity of a fixed
![]() $(G,\ast )$
may depend on the group
$(G,\ast )$
may depend on the group
![]() $\Gamma $
. Consider the case when
$\Gamma $
. Consider the case when
![]() $d=3$
. Then there are three different types of point groups of order two corresponding to point inversion, rotation and reflection. Suppose that G is the graph of the octahedron and
$d=3$
. Then there are three different types of point groups of order two corresponding to point inversion, rotation and reflection. Suppose that G is the graph of the octahedron and
![]() $\ast $
maps each vertex to its antipodal vertex. If
$\ast $
maps each vertex to its antipodal vertex. If
![]() $\Gamma $
is a rotation group, then any
$\Gamma $
is a rotation group, then any
![]() $\Gamma $
-framework
$\Gamma $
-framework
![]() $(G,\ast ,p)$
is the 1-skeleton of a Bricard octahedron, which is infinitesimally flexible; see Example 2.3 below. Conversely, we will show that every generic
$(G,\ast ,p)$
is the 1-skeleton of a Bricard octahedron, which is infinitesimally flexible; see Example 2.3 below. Conversely, we will show that every generic
![]() $\Gamma $
-framework
$\Gamma $
-framework
![]() $(G,\ast ,p)$
is infinitesimally rigid when
$(G,\ast ,p)$
is infinitesimally rigid when
![]() $\Gamma $
is a point inversion or reflection group.
$\Gamma $
is a point inversion or reflection group.
We will concentrate our attention on graphs G with a vertex pairing
![]() $*:X \rightarrow X$
with the property that
$*:X \rightarrow X$
with the property that
![]() $xx^* \not \in E$
for all
$xx^* \not \in E$
for all
![]() $x\in X$
. We will refer to such a vertex pairing as a non-adjacent vertex pairing. Note that if
$x\in X$
. We will refer to such a vertex pairing as a non-adjacent vertex pairing. Note that if
![]() $\ast : X \rightarrow X$
is a non-adjacent vertex pairing of G, then the induced bijection
$\ast : X \rightarrow X$
is a non-adjacent vertex pairing of G, then the induced bijection
![]() $*_W: X_W \rightarrow X_W$
is again a non-adjacent vertex pairing of
$*_W: X_W \rightarrow X_W$
is again a non-adjacent vertex pairing of
![]() $G[W]$
for all
$G[W]$
for all
![]() $W\subseteq V(G)$
.
$W\subseteq V(G)$
.
We emphasise that a non-adjacent vertex pairing
![]() $*:X\rightarrow X$
need not, in general, induce an involution on the edge set
$*:X\rightarrow X$
need not, in general, induce an involution on the edge set
![]() $E[X]$
. Our main concern, however, is the special case when
$E[X]$
. Our main concern, however, is the special case when
![]() $X=V(G)$
and
$X=V(G)$
and
![]() $\ast $
is an automorphism of G without fixed edges. In this case,
$\ast $
is an automorphism of G without fixed edges. In this case,
![]() $(G,\ast )$
is said to be a
$(G,\ast )$
is said to be a
![]() $\mathbb {Z}_2$
-symmetric graph. Since
$\mathbb {Z}_2$
-symmetric graph. Since
![]() $\ast $
is an automorphism,
$\ast $
is an automorphism,
![]() $\ast (e)$
is well defined, and we abbreviate
$\ast (e)$
is well defined, and we abbreviate
![]() $\ast (e)$
by
$\ast (e)$
by
![]() $e^*$
for each edge e. We consider the more general class of graphs with a non-adjacent vertex pairing because it arises naturally in our analysis of the
$e^*$
for each edge e. We consider the more general class of graphs with a non-adjacent vertex pairing because it arises naturally in our analysis of the
![]() ${\mathbb Z}_2$
-symmetric case.
${\mathbb Z}_2$
-symmetric case.
We next derive a stronger inequality than (2.2) for the number of edges in a
![]() $\Gamma $
-rigid
$\Gamma $
-rigid
![]() $\mathbb {Z}_2$
-symmetric graph. For integers
$\mathbb {Z}_2$
-symmetric graph. For integers
![]() $d \geq 1$
and
$d \geq 1$
and
![]() $0 \leq t \leq d$
, let
$0 \leq t \leq d$
, let
![]() $I_{t,d}$
be the the diagonal matrix of size d whose first t diagonal entries are 1 and remaining
$I_{t,d}$
be the the diagonal matrix of size d whose first t diagonal entries are 1 and remaining
![]() $d-t$
diagonal entries are
$d-t$
diagonal entries are
![]() $-1$
. Let
$-1$
. Let
![]() $\Gamma _{t,d}$
be the point group generated by
$\Gamma _{t,d}$
be the point group generated by
![]() $I_{t,d}$
. Observe that if
$I_{t,d}$
. Observe that if
![]() $\Gamma $
is a point group of order 2 in
$\Gamma $
is a point group of order 2 in
![]() $\mathbb R^d$
, then we can always choose a coordinate system so that
$\mathbb R^d$
, then we can always choose a coordinate system so that
![]() $\Gamma = \Gamma _{t,d}$
for some
$\Gamma = \Gamma _{t,d}$
for some
![]() $0\leq t \leq d-1$
.
$0\leq t \leq d-1$
.
Lemma 2.2. Let
![]() $\Gamma =\Gamma _{t,d}$
where
$\Gamma =\Gamma _{t,d}$
where
![]() $0 \leq t \leq d-1$
. Suppose that a
$0 \leq t \leq d-1$
. Suppose that a
![]() $\mathbb {Z}_2$
-symmetric graph
$\mathbb {Z}_2$
-symmetric graph
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid and
$\Gamma $
-rigid and
![]() $|V(G)|\geq 2d$
. Then
$|V(G)|\geq 2d$
. Then
 $$ \begin{align} |E(G)|\geq d|V(G)|-2\min\left\{\binom{t+1}{2}+\binom{d-t}{2}, \binom{d+1}{2} - \binom{t+1}{2}-\binom{d-t}{2}\right\}. \end{align} $$
$$ \begin{align} |E(G)|\geq d|V(G)|-2\min\left\{\binom{t+1}{2}+\binom{d-t}{2}, \binom{d+1}{2} - \binom{t+1}{2}-\binom{d-t}{2}\right\}. \end{align} $$
Proof. Let
![]() $n=|V(G)|$
and
$n=|V(G)|$
and
![]() $m=|E(G)|$
. Since
$m=|E(G)|$
. Since
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid, there is a
$\Gamma $
-rigid, there is a
![]() $\Gamma $
-symmetric infinitesimally rigid realisation
$\Gamma $
-symmetric infinitesimally rigid realisation
![]() $(G, \ast ,p)$
of
$(G, \ast ,p)$
of
![]() $(G,\ast )$
. Since
$(G,\ast )$
. Since
![]() $|V(G)|\geq 2d$
, we can take such a realisation so that the affine span of
$|V(G)|\geq 2d$
, we can take such a realisation so that the affine span of
![]() $p(V(G))$
is at least
$p(V(G))$
is at least
![]() $d-1$
. In particular, the space of trivial motions of
$d-1$
. In particular, the space of trivial motions of
![]() $(G,*,p)$
has dimension
$(G,*,p)$
has dimension
![]() $\binom {d+1}{2}$
.
$\binom {d+1}{2}$
.
Recall that the rigidity matrix
![]() $R(G,p)$
represents a linear map from
$R(G,p)$
represents a linear map from
![]() $\mathbb {R}^{dn}$
to
$\mathbb {R}^{dn}$
to
![]() $\mathbb {R}^m$
. We shall decompose
$\mathbb {R}^m$
. We shall decompose
![]() $\mathbb {R}^{dn}$
and
$\mathbb {R}^{dn}$
and
![]() $\mathbb {R}^m$
into two subspaces whose elements are either symmetric or anti-symmetric with respect to
$\mathbb {R}^m$
into two subspaces whose elements are either symmetric or anti-symmetric with respect to
![]() $\Gamma $
and
$\Gamma $
and
![]() $*$
. Specifically, let
$*$
. Specifically, let
 $$ \begin{align*} M_{\mathrm{sym}}&:=\{ \dot{p}:V(G)\rightarrow \mathbb{R}^d \mid \dot{p}(u^*)=I_{t,d} \dot{p}(u)\text{ for all } u\in V(G)\}, \\ M_{\mathrm{ant}}&:=\{ \dot{p}:V(G)\rightarrow \mathbb{R}^d \mid \dot{p}(u^*)=-I_{t,d} \dot{p}(u)\text{ for all } u\in V(G)\}, \\ S_{\mathrm{sym}}&:=\{ w:E(G)\rightarrow \mathbb{R} \mid w(e^*)=w(e) \text{ for all } e\in E(G)\} \text{ and} \\ S_{\mathrm{ant}}&:=\{ w:E(G)\rightarrow \mathbb{R} \mid w(e^*)=-w(e) \text{ for all } e\in E(G)\}. \end{align*} $$
$$ \begin{align*} M_{\mathrm{sym}}&:=\{ \dot{p}:V(G)\rightarrow \mathbb{R}^d \mid \dot{p}(u^*)=I_{t,d} \dot{p}(u)\text{ for all } u\in V(G)\}, \\ M_{\mathrm{ant}}&:=\{ \dot{p}:V(G)\rightarrow \mathbb{R}^d \mid \dot{p}(u^*)=-I_{t,d} \dot{p}(u)\text{ for all } u\in V(G)\}, \\ S_{\mathrm{sym}}&:=\{ w:E(G)\rightarrow \mathbb{R} \mid w(e^*)=w(e) \text{ for all } e\in E(G)\} \text{ and} \\ S_{\mathrm{ant}}&:=\{ w:E(G)\rightarrow \mathbb{R} \mid w(e^*)=-w(e) \text{ for all } e\in E(G)\}. \end{align*} $$
Then
![]() $\mathbb {R}^{dn}=M_{\mathrm {sym}}\oplus M_{\mathrm {ant}}$
and
$\mathbb {R}^{dn}=M_{\mathrm {sym}}\oplus M_{\mathrm {ant}}$
and
![]() $\mathbb {R}^m=S_{\mathrm {sym}}\oplus S_{\mathrm {ant}}$
. Observe further that the rigidity matrix maps
$\mathbb {R}^m=S_{\mathrm {sym}}\oplus S_{\mathrm {ant}}$
. Observe further that the rigidity matrix maps
![]() $M_{\mathrm {sym}}$
to
$M_{\mathrm {sym}}$
to
![]() $S_{\mathrm {sym}}$
and
$S_{\mathrm {sym}}$
and
![]() $M_{\mathrm {ant}}$
to
$M_{\mathrm {ant}}$
to
![]() $S_{\mathrm {ant}}$
. Indeed, if
$S_{\mathrm {ant}}$
. Indeed, if
![]() $\dot {p}\in M_{\mathrm {sym}}$
, then for any edge
$\dot {p}\in M_{\mathrm {sym}}$
, then for any edge
![]() $e=uv$
, we have
$e=uv$
, we have
 $$ \begin{align*} (p(u^*)-p(v^*))\cdot (\dot{p}(u^*)-\dot{p}(v^*))&= (I_{t,d}(p(u^*)-p(v^*)))\cdot I_{t,d}(\dot{p}(u^*)-\dot{p}(v^*)) \\ &=(p(u)-p(v))\cdot (\dot{p}(u)-\dot{p}(v)), \end{align*} $$
$$ \begin{align*} (p(u^*)-p(v^*))\cdot (\dot{p}(u^*)-\dot{p}(v^*))&= (I_{t,d}(p(u^*)-p(v^*)))\cdot I_{t,d}(\dot{p}(u^*)-\dot{p}(v^*)) \\ &=(p(u)-p(v))\cdot (\dot{p}(u)-\dot{p}(v)), \end{align*} $$
which implies that the image of
![]() $\dot {p}$
belongs to
$\dot {p}$
belongs to
![]() $S_{\mathrm {sym}}$
. A similar calculation shows the corresponding property for
$S_{\mathrm {sym}}$
. A similar calculation shows the corresponding property for
![]() $M_{\mathrm {ant}}$
.
$M_{\mathrm {ant}}$
.
Let T be the space of trivial infinitesimal motions of
![]() $(G,p)$
. A canonical basis of T consists of
$(G,p)$
. A canonical basis of T consists of
![]() $\binom {d}{2}$
infinitesimal rotations about the subspaces spanned by each set of
$\binom {d}{2}$
infinitesimal rotations about the subspaces spanned by each set of
![]() $(d-2)$
axes and d translations along each axis. Due to the structure of
$(d-2)$
axes and d translations along each axis. Due to the structure of
![]() $I_{t,d}$
, it follows that the
$I_{t,d}$
, it follows that the
![]() $\binom {t+1}{2}$
-dimensional space of isometries in the subspace spanned by the first t axes and the
$\binom {t+1}{2}$
-dimensional space of isometries in the subspace spanned by the first t axes and the
![]() $\binom {d-t}{2}$
-dimensional space of rotations rotating in the subspace spanned by the last
$\binom {d-t}{2}$
-dimensional space of rotations rotating in the subspace spanned by the last
![]() $d-t$
axes are contained in
$d-t$
axes are contained in
![]() $M_{\mathrm {sym}}$
. One can also directly check that the remaining
$M_{\mathrm {sym}}$
. One can also directly check that the remaining
![]() $\binom {d+1}{2} - \binom {t+1}{2}-\binom {d-t}{2}$
elements of the canonical basis belong to
$\binom {d+1}{2} - \binom {t+1}{2}-\binom {d-t}{2}$
elements of the canonical basis belong to
![]() $M_{\mathrm {ant}}$
. Hence,
$M_{\mathrm {ant}}$
. Hence,
 $$ \begin{align*} \dim T\cap M_{\mathrm{sym}}= \binom{t+1}{2}+\binom{d-t}{2} \text{ and } \dim T\cap M_{\mathrm{ant}} = \binom{d+1}{2} - \binom{t+1}{2}-\binom{d-t}{2}. \end{align*} $$
$$ \begin{align*} \dim T\cap M_{\mathrm{sym}}= \binom{t+1}{2}+\binom{d-t}{2} \text{ and } \dim T\cap M_{\mathrm{ant}} = \binom{d+1}{2} - \binom{t+1}{2}-\binom{d-t}{2}. \end{align*} $$
The infinitesimal rigidity of
![]() $(G,p)$
implies that
$(G,p)$
implies that
![]() $\ker R(G,p)=T$
. Since the rigidity matrix maps
$\ker R(G,p)=T$
. Since the rigidity matrix maps
![]() $M_{\mathrm {sym}}$
to
$M_{\mathrm {sym}}$
to
![]() $S_{\mathrm {sym}}$
and
$S_{\mathrm {sym}}$
and
![]() $M_{\mathrm {ant}}$
to
$M_{\mathrm {ant}}$
to
![]() $S_{\mathrm {ant}}$
, this gives
$S_{\mathrm {ant}}$
, this gives
 $$ \begin{align*} \frac{m}{2}&=\dim S_{\mathrm{sym}}\geq \dim M_{\mathrm{sym}}-\dim T\cap M_{\mathrm{sym}}=\frac{dn}{2}- \left(\binom{t+1}{2}+\binom{d-t}{2}\right) \text{ and}\\ \frac{m}{2}&=\dim S_{\mathrm{ant}}\geq \dim M_{\mathrm{ant}}-\dim T\cap M_{\mathrm{ant}}=\frac{dn}{2}- \left( \binom{d+1}{2} - \binom{t+1}{2}-\binom{d-t}{2}\right), \end{align*} $$
$$ \begin{align*} \frac{m}{2}&=\dim S_{\mathrm{sym}}\geq \dim M_{\mathrm{sym}}-\dim T\cap M_{\mathrm{sym}}=\frac{dn}{2}- \left(\binom{t+1}{2}+\binom{d-t}{2}\right) \text{ and}\\ \frac{m}{2}&=\dim S_{\mathrm{ant}}\geq \dim M_{\mathrm{ant}}-\dim T\cap M_{\mathrm{ant}}=\frac{dn}{2}- \left( \binom{d+1}{2} - \binom{t+1}{2}-\binom{d-t}{2}\right), \end{align*} $$
as required.
Example 2.3. Suppose a
![]() $\mathbb {Z}_2$
-symmetric graph
$\mathbb {Z}_2$
-symmetric graph
![]() $(G,*)$
is
$(G,*)$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() ${\mathbb R}^3$
. Then Lemma 2.2 implies
${\mathbb R}^3$
. Then Lemma 2.2 implies
 $$\begin{align*}|E(G)|\geq 3|V(G)|-\begin{cases} 6 & \text{ if } t=0\ \text{i.e.}\ \Gamma\ \text{is generated by a point inversion, } \\ 4 & \text{ if } t=1\ \text{i.e.}\ \Gamma\ \text{is generated by a half turn rotation, } \\ 6 & \text{ if } t=2\ \text{i.e.}\ \Gamma\ \text{is generated by a reflection}. \end{cases} \end{align*}$$
$$\begin{align*}|E(G)|\geq 3|V(G)|-\begin{cases} 6 & \text{ if } t=0\ \text{i.e.}\ \Gamma\ \text{is generated by a point inversion, } \\ 4 & \text{ if } t=1\ \text{i.e.}\ \Gamma\ \text{is generated by a half turn rotation, } \\ 6 & \text{ if } t=2\ \text{i.e.}\ \Gamma\ \text{is generated by a reflection}. \end{cases} \end{align*}$$
If G is the graph of the octahedron,
![]() $|E(G)|=12$
and
$|E(G)|=12$
and
![]() $|V(G)|=6$
. So it cannot be
$|V(G)|=6$
. So it cannot be
![]() $\Gamma $
-rigid if
$\Gamma $
-rigid if
![]() $\Gamma $
is generated by a half turn rotation, which is the case of the Bricard octahedron.
$\Gamma $
is generated by a half turn rotation, which is the case of the Bricard octahedron.
Note that the case when
![]() $d=3$
is exceptional since the right side of (2.3) is maximised at
$d=3$
is exceptional since the right side of (2.3) is maximised at
![]() $t=1$
when
$t=1$
when
![]() $d=3$
, and at
$d=3$
, and at
![]() $t=0$
when
$t=0$
when
![]() $d\geq 4$
.
$d\geq 4$
.
The infinitesimal rigidity of frameworks having a point group symmetry is an extensively studied topic in rigidity theory. See, for example, [Reference Schulze and Tanigawa15, Reference Schulze, Whiteley, Toth and O’Rourke16] for symmetric extensions of classical rigidity theorems.
2.3 Gluing properties
We write
![]() $\mathrm {aff}(Y)$
for the affine span of a subset Y of
$\mathrm {aff}(Y)$
for the affine span of a subset Y of
![]() $\mathbb R^d$
and
$\mathbb R^d$
and
![]() $\mathrm {lin}(Y)$
for its linear span. The gluing properties of rigid frameworks and graphs are important ingredients in the proof of Fogelsanger’s Rigidity Theorem. For completeness, and since we cannot find an authoritative source for these results in the literature, we include details of these gluing properties in the classical non-symmetric setting.
$\mathrm {lin}(Y)$
for its linear span. The gluing properties of rigid frameworks and graphs are important ingredients in the proof of Fogelsanger’s Rigidity Theorem. For completeness, and since we cannot find an authoritative source for these results in the literature, we include details of these gluing properties in the classical non-symmetric setting.
Theorem 2.4. Let
![]() $(G,p)$
be a framework in
$(G,p)$
be a framework in
![]() $\mathbb R^d$
. Suppose that
$\mathbb R^d$
. Suppose that
![]() $G_1, G_2$
are subgraphs of G such that
$G_1, G_2$
are subgraphs of G such that
![]() $(G_i,p|_{V(G_i)})$
is infinitesimally rigid for
$(G_i,p|_{V(G_i)})$
is infinitesimally rigid for
![]() $i=1,2$
and
$i=1,2$
and
![]() $\mathrm {aff}(p(V(G_1) \cap V(G_2)))$
has dimension at least
$\mathrm {aff}(p(V(G_1) \cap V(G_2)))$
has dimension at least
![]() $d-1$
. Then
$d-1$
. Then
![]() $(G,p)$
is infinitesimally rigid.
$(G,p)$
is infinitesimally rigid.
Proof. Suppose that
![]() $\dot {p}$
is an infinitesimal flex of
$\dot {p}$
is an infinitesimal flex of
![]() $(G,p)$
. By assumption, there exist skew symmetric matrices
$(G,p)$
. By assumption, there exist skew symmetric matrices
![]() $A_i$
of size d and
$A_i$
of size d and
![]() $t_i \in \mathbb R^d$
for
$t_i \in \mathbb R^d$
for
![]() $ i =1,2$
such that
$ i =1,2$
such that
![]() $\dot {p}(v) = A_ip(v) +t_i$
for
$\dot {p}(v) = A_ip(v) +t_i$
for
![]() $v \in V(G_i)$
. We can choose coordinates so that
$v \in V(G_i)$
. We can choose coordinates so that
![]() $p(w) = 0$
for some
$p(w) = 0$
for some
![]() $w \in V(G_1) \cap V(G_2)$
. It follows that
$w \in V(G_1) \cap V(G_2)$
. It follows that
![]() $A_1 0 +t_1 = \dot {p}(w) = A_2 0 + t_2$
. Therefore,
$A_1 0 +t_1 = \dot {p}(w) = A_2 0 + t_2$
. Therefore,
![]() $t_1 = t_2$
, and so
$t_1 = t_2$
, and so
![]() $A_1p(v) = A_2p(v)$
for all
$A_1p(v) = A_2p(v)$
for all
![]() $v \in V(G_1) \cap V(G_2)$
. Therefore, the skew symmetric matrix
$v \in V(G_1) \cap V(G_2)$
. Therefore, the skew symmetric matrix
![]() $A_1 - A_2$
vanishes on a space of dimension
$A_1 - A_2$
vanishes on a space of dimension
![]() $d-1$
, and so must be
$d-1$
, and so must be
![]() $0$
, as required.
$0$
, as required.
Corollary 2.5. Let
![]() $G_1$
and
$G_1$
and
![]() $G_2$
be graphs that are both rigid in
$G_2$
be graphs that are both rigid in
![]() $\mathbb R^d$
. Suppose that
$\mathbb R^d$
. Suppose that
![]() $|V(G_1) \cap V(G_1)| \geq d$
. Then
$|V(G_1) \cap V(G_1)| \geq d$
. Then
![]() $G_1 \cup G_2$
is rigid in
$G_1 \cup G_2$
is rigid in
![]() $\mathbb R^d$
.
$\mathbb R^d$
.
Now we extend Corollary 2.5 to
![]() $\Gamma $
-rigidity. First, we prove a lemma about the affine span of
$\Gamma $
-rigidity. First, we prove a lemma about the affine span of
![]() $\Gamma $
-symmetric subsets of
$\Gamma $
-symmetric subsets of
![]() $\mathbb R^d$
.
$\mathbb R^d$
.
Lemma 2.6. Let
![]() $\gamma = I_{t,d}$
for
$\gamma = I_{t,d}$
for
![]() $0 \leq t \leq d-1$
. Suppose that P is a generic set of points in
$0 \leq t \leq d-1$
. Suppose that P is a generic set of points in
![]() $\mathbb R^d$
and
$\mathbb R^d$
and
![]() $|P| = n$
. Then
$|P| = n$
. Then
![]() $\dim (\mathrm {aff}(P \cup \gamma (P))) =\min \{n,d-t\} +\min \{n-1,t\}$
.
$\dim (\mathrm {aff}(P \cup \gamma (P))) =\min \{n,d-t\} +\min \{n-1,t\}$
.
Proof. Let V, respectively W, be the eigenspace of
![]() $\gamma $
corresponding to the eigenvalue
$\gamma $
corresponding to the eigenvalue
![]() $1$
, respectively
$1$
, respectively
![]() $-1$
, and let
$-1$
, and let
![]() $\pi _V$
, respectively
$\pi _V$
, respectively
![]() $\pi _W$
, be the orthogonal projection from
$\pi _W$
, be the orthogonal projection from
![]() $\mathbb R^d$
onto V, respectively W. Since P is generic in
$\mathbb R^d$
onto V, respectively W. Since P is generic in
![]() $\mathbb R^d$
and
$\mathbb R^d$
and
![]() $\pi _V, \pi _W$
are projections onto coordinate subspaces, it follows that
$\pi _V, \pi _W$
are projections onto coordinate subspaces, it follows that
![]() $\pi _V(P)$
is generic in V and
$\pi _V(P)$
is generic in V and
![]() $\pi _W(P)$
is generic in W. Therefore,
$\pi _W(P)$
is generic in W. Therefore,
![]() $\dim (\mathrm {aff}(\pi _V(P))) = \min \{n-1,t\}$
and
$\dim (\mathrm {aff}(\pi _V(P))) = \min \{n-1,t\}$
and
![]() $\dim (\mathrm {lin}(\pi _W(P))) = \min \{n,d-t\}$
.
$\dim (\mathrm {lin}(\pi _W(P))) = \min \{n,d-t\}$
.
Claim 2.7.
![]() $\mathrm {aff}(P \cup \gamma (P)) = \mathrm {aff}(\pi _V(P)) + \mathrm {lin}(\pi _W(P))$
.
$\mathrm {aff}(P \cup \gamma (P)) = \mathrm {aff}(\pi _V(P)) + \mathrm {lin}(\pi _W(P))$
.
Proof of claim.
Suppose
![]() $x = \sum _{q \in P \cup \gamma (P)} c_q q \in \mathrm {aff}(P \cup \gamma (P)))$
for scalars
$x = \sum _{q \in P \cup \gamma (P)} c_q q \in \mathrm {aff}(P \cup \gamma (P)))$
for scalars
![]() $c_q$
with
$c_q$
with
![]() $\sum _q c_q=1$
. Now
$\sum _q c_q=1$
. Now
![]() $x = \pi _V(x) + \pi _W(x)$
and
$x = \pi _V(x) + \pi _W(x)$
and
![]() $\pi _V(x) = \sum _{p \in P} (c_p + c_{\gamma (p)})\pi _V(p)$
and
$\pi _V(x) = \sum _{p \in P} (c_p + c_{\gamma (p)})\pi _V(p)$
and
![]() $\pi _W(x) = \sum _{p \in P} (c_p - c_{\gamma (p)})\pi _W(p)$
. Since
$\pi _W(x) = \sum _{p \in P} (c_p - c_{\gamma (p)})\pi _W(p)$
. Since
![]() $\sum _{p \in P} (c_p+c_{\gamma (p)}) = \sum _{q \in P\cup \gamma (P)} c_q = 1$
, it follows that
$\sum _{p \in P} (c_p+c_{\gamma (p)}) = \sum _{q \in P\cup \gamma (P)} c_q = 1$
, it follows that
![]() $\mathrm {aff}(P \cup \gamma (P)) \subset \mathrm {aff}(\pi _V(P)) + \mathrm {lin}(\pi _W(P))$
.
$\mathrm {aff}(P \cup \gamma (P)) \subset \mathrm {aff}(\pi _V(P)) + \mathrm {lin}(\pi _W(P))$
.
To see the reverse containment holds, consider
![]() $\sum _{p \in P} d_p \pi _V(p) \in \mathrm {aff}(\pi _V(P))$
and
$\sum _{p \in P} d_p \pi _V(p) \in \mathrm {aff}(\pi _V(P))$
and
![]() $ \sum _{p \in P} b_p \pi _W(p) \in \mathrm {lin}(\pi _W(P)) $
. Set
$ \sum _{p \in P} b_p \pi _W(p) \in \mathrm {lin}(\pi _W(P)) $
. Set
![]() $c_p=\frac {d_p+b_p}{2}$
and
$c_p=\frac {d_p+b_p}{2}$
and
![]() $c_{\gamma (p)}=\frac {d_p-b_p}{2}$
for each
$c_{\gamma (p)}=\frac {d_p-b_p}{2}$
for each
![]() $p\in P$
. Then
$p\in P$
. Then
![]() $\sum _{q \in P \cup \gamma (P)} c_q = \sum _{p \in P} d_p = 1$
. It follows that
$\sum _{q \in P \cup \gamma (P)} c_q = \sum _{p \in P} d_p = 1$
. It follows that
![]() $\mathrm {aff}(\pi _V(P)) + \mathrm {lin}(\pi _W(P)) \subset \mathrm {aff}(P \cup \gamma (P))$
.
$\mathrm {aff}(\pi _V(P)) + \mathrm {lin}(\pi _W(P)) \subset \mathrm {aff}(P \cup \gamma (P))$
.
The facts that
![]() $\mathrm {aff}(\pi _V(P)) \subseteq V$
,
$\mathrm {aff}(\pi _V(P)) \subseteq V$
,
![]() $\mathrm {lin}(\pi _W(P))\subseteq W$
and
$\mathrm {lin}(\pi _W(P))\subseteq W$
and
![]() $V\cap W=\{{\mathbf {0}}\}$
(since
$V\cap W=\{{\mathbf {0}}\}$
(since
![]() $V,W$
are eigenspaces for distinct eigenvalues of
$V,W$
are eigenspaces for distinct eigenvalues of
![]() $\gamma $
) now give
$\gamma $
) now give
 $$ \begin{align*} \dim(\mathrm{aff}(P \cup \gamma(P))) = \dim (\mathrm{aff}(\pi_V(P)) + \mathrm{lin}(\pi_W(P)))&=\dim\mathrm{aff}(\pi_V(P)) + \dim\mathrm{lin}(\pi_W(P))\\ &= \min\{n,d-t\} +\min\{n-1,t\}, \end{align*} $$
$$ \begin{align*} \dim(\mathrm{aff}(P \cup \gamma(P))) = \dim (\mathrm{aff}(\pi_V(P)) + \mathrm{lin}(\pi_W(P)))&=\dim\mathrm{aff}(\pi_V(P)) + \dim\mathrm{lin}(\pi_W(P))\\ &= \min\{n,d-t\} +\min\{n-1,t\}, \end{align*} $$
as required.
Theorem 2.8 (Gluing Theorem).
Let
![]() $\Gamma = \Gamma _{t,d}$
for
$\Gamma = \Gamma _{t,d}$
for
![]() $0 \leq t \leq d-1$
. Let
$0 \leq t \leq d-1$
. Let
![]() $(G,\ast )$
be a graph with a vertex pairing
$(G,\ast )$
be a graph with a vertex pairing
![]() $\ast : X\rightarrow X$
. Suppose that
$\ast : X\rightarrow X$
. Suppose that
![]() $H_1=(V_1,E_1)$
and
$H_1=(V_1,E_1)$
and
![]() $H_2=(V_2,E_2)$
are subgraphs of G whose union is G and that, for
$H_2=(V_2,E_2)$
are subgraphs of G whose union is G and that, for
![]() $i=1,2$
,
$i=1,2$
,
![]() $(H_i,\ast )$
is
$(H_i,\ast )$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^d$
. Let
$\mathbb R^d$
. Let
![]() $m = |X_{V_1} \cap X_{V_2}|$
. Suppose that
$m = |X_{V_1} \cap X_{V_2}|$
. Suppose that
Then
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid.
$\Gamma $
-rigid.
Proof. Let
![]() $(G,\ast ,p)$
be a generic
$(G,\ast ,p)$
be a generic
![]() $\Gamma $
-framework. Then, for
$\Gamma $
-framework. Then, for
![]() $i=1,2$
,
$i=1,2$
,
![]() $(H_i, \ast , p|_{V_i})$
is generic and therefore infinitesimally rigid. Now we observe that, by Lemma 2.6, the dimension of
$(H_i, \ast , p|_{V_i})$
is generic and therefore infinitesimally rigid. Now we observe that, by Lemma 2.6, the dimension of
![]() $\mathrm {aff}(p(V_1 \cap V_2))$
is
$\mathrm {aff}(p(V_1 \cap V_2))$
is
![]() $\min \{|V_1\cap V_2| - m +\min \{m/2,d-t\} +\min \{m/2-1,t\},d\}$
. The theorem now follows by applying Theorem 2.4 to the frameworks
$\min \{|V_1\cap V_2| - m +\min \{m/2,d-t\} +\min \{m/2-1,t\},d\}$
. The theorem now follows by applying Theorem 2.4 to the frameworks
![]() $(H_i,p|_{V_i})$
,
$(H_i,p|_{V_i})$
,
![]() $i=1,2$
.
$i=1,2$
.
2.4 Vertex splitting
Whiteley’s Vertex Splitting Lemma [Reference Whiteley23, Proposition 1] is a fundamental result in rigidity theory and plays a key role in the proof of Fogelsanger’s Rigidity Theorem. We will derive a version of this lemma for
![]() $\Gamma $
-rigidity.
$\Gamma $
-rigidity.
First, we fix some terminology. Let G be a graph,
![]() $u \in V(G)$
,
$u \in V(G)$
,
![]() $C \subset N_G(u)$
and
$C \subset N_G(u)$
and
![]() $D\subset N_G(u) \setminus C$
. Let
$D\subset N_G(u) \setminus C$
. Let
![]() $G'$
be the graph obtained from G by deleting the edges
$G'$
be the graph obtained from G by deleting the edges
![]() $uw$
for all
$uw$
for all
![]() $w \in D$
, adding a new vertex
$w \in D$
, adding a new vertex
![]() $u'$
and adding edges
$u'$
and adding edges
![]() $u'z$
for all
$u'z$
for all
![]() $z \in C \cup D \cup \{u\}$
. We say that
$z \in C \cup D \cup \{u\}$
. We say that
![]() $G'$
is obtained from G by splitting
$G'$
is obtained from G by splitting
![]() $u'$
from u along C, or more succinctly, by vertex splitting at u.
$u'$
from u along C, or more succinctly, by vertex splitting at u.
The following theorem of is one of the central results in rigidity theory. We include details of Whiteley’s original proof [Reference Whiteley23] for the benefit of readers who may not be familiar with it, and since one of our later variations is proved using essentially the same method.
Theorem 2.9 (Whiteley’s Vertex Splitting Theorem).
Let
![]() $(G,p)$
be a framework in
$(G,p)$
be a framework in
![]() $\mathbb R^d$
such that
$\mathbb R^d$
such that
![]() $R(G,p)$
is row-independent. Also, let
$R(G,p)$
is row-independent. Also, let
![]() $u \in V(G)$
and
$u \in V(G)$
and
![]() $C \subset N_G(u)$
such that
$C \subset N_G(u)$
such that
![]() $|C| \leq d-1$
and
$|C| \leq d-1$
and
![]() $\{p(w) - p(u): w \in C\}$
is linearly independent. Let
$\{p(w) - p(u): w \in C\}$
is linearly independent. Let
![]() $G'$
be the graph obtained from G by splitting
$G'$
be the graph obtained from G by splitting
![]() $u'$
from u along C. Then there is some
$u'$
from u along C. Then there is some
![]() $z \in \mathbb R^d$
such that
$z \in \mathbb R^d$
such that
![]() $R(G',q)$
is row-independent, where
$R(G',q)$
is row-independent, where
![]() $q(w) = p(w)$
for all
$q(w) = p(w)$
for all
![]() $w \in V(G)$
and
$w \in V(G)$
and
![]() $q(u') = p(u)+z$
.
$q(u') = p(u)+z$
.
Proof. Since
![]() $|C| \leq d-1$
, we can choose
$|C| \leq d-1$
, we can choose
![]() $y \in \mathbb R^d$
so that
$y \in \mathbb R^d$
so that
![]() $y \not \in \mathrm {lin}\{p(w)-p(u):w \in C\}$
. Now, for each
$y \not \in \mathrm {lin}\{p(w)-p(u):w \in C\}$
. Now, for each
![]() $t \in \mathbb R$
, define
$t \in \mathbb R$
, define
![]() $q_t:V(G') \to \mathbb R^d$
by
$q_t:V(G') \to \mathbb R^d$
by
 $$ \begin{align*}q_t(v) = \left\{ \begin{array}{ll} p(v) &\text{if }v \in V(G), \\ p(u)+ty &\text{if } v = u'.\\ \end{array}\right. \end{align*} $$
$$ \begin{align*}q_t(v) = \left\{ \begin{array}{ll} p(v) &\text{if }v \in V(G), \\ p(u)+ty &\text{if } v = u'.\\ \end{array}\right. \end{align*} $$
It will suffice to show that for sufficiently small nonzero t,
![]() $R(G',q_t)$
is row-independent.
$R(G',q_t)$
is row-independent.
Let L be the matrix obtained by replacing the
![]() $uu'$
row of
$uu'$
row of
![]() $R(G,q_0)$
by the row vector that has y is the u column-set,
$R(G,q_0)$
by the row vector that has y is the u column-set,
![]() $-y$
is the
$-y$
is the
![]() $u'$
column-set and zeroes in all other entries.
$u'$
column-set and zeroes in all other entries.
Claim 2.10. L is row-independent.
Proof of claim.
Suppose that
![]() $\lambda $
is an element of the left kernel of L. We can think of
$\lambda $
is an element of the left kernel of L. We can think of
![]() $\lambda $
as a real valued function on
$\lambda $
as a real valued function on
![]() $E(G')$
. Define
$E(G')$
. Define
![]() $\pi : E(G) \to \mathbb R$
by
$\pi : E(G) \to \mathbb R$
by
 $$ \begin{align*}\pi(e) = \left\{ \begin{array}{ll} \lambda(e) &\text{if }e \not\in \{uw:w \in C\}, \\ \lambda(uw)+\lambda(u'w) &\text{if } e = uw, w \in C.\\ \end{array}\right. \end{align*} $$
$$ \begin{align*}\pi(e) = \left\{ \begin{array}{ll} \lambda(e) &\text{if }e \not\in \{uw:w \in C\}, \\ \lambda(uw)+\lambda(u'w) &\text{if } e = uw, w \in C.\\ \end{array}\right. \end{align*} $$
Now, using the facts that
![]() $q_0(u) = q_0(u') = p(u)$
,
$q_0(u) = q_0(u') = p(u)$
,
![]() $q_0(w) = p(w)$
for
$q_0(w) = p(w)$
for
![]() $w \in V(G)$
and
$w \in V(G)$
and
![]() $\lambda L = 0$
, we can readily show that
$\lambda L = 0$
, we can readily show that
![]() $\pi $
, considered as row vector with entries indexed by
$\pi $
, considered as row vector with entries indexed by
![]() $E(G)$
, is an element of the left kernel of
$E(G)$
, is an element of the left kernel of
![]() $ R(G,p)$
. Since
$ R(G,p)$
. Since
![]() $R(G,p)$
is row-independent, it follows that
$R(G,p)$
is row-independent, it follows that
![]() $\pi =0$
. Therefore,
$\pi =0$
. Therefore,
![]() $\lambda (e) = 0$
for all
$\lambda (e) = 0$
for all
![]() $e \not \in \{uw: w \in C\} \cup \{u'w:w \in C\}$
and
$e \not \in \{uw: w \in C\} \cup \{u'w:w \in C\}$
and
![]() $\lambda (uw)+\lambda (u'w) = 0$
for
$\lambda (uw)+\lambda (u'w) = 0$
for
![]() $w \in C$
. Now, using the fact that
$w \in C$
. Now, using the fact that
![]() $\lambda L = 0$
, and considering the uth column-set of L, we have
$\lambda L = 0$
, and considering the uth column-set of L, we have
Our choice of y and the fact that
![]() $\{p(u)-p(w):w \in C\}$
is linearly independent implies that
$\{p(u)-p(w):w \in C\}$
is linearly independent implies that
![]() $\lambda (uw) = 0$
for
$\lambda (uw) = 0$
for
![]() $w \in C$
and
$w \in C$
and
![]() $\lambda (uu') =0$
. So
$\lambda (uu') =0$
. So
![]() $\lambda = 0$
, and the claim is proved.
$\lambda = 0$
, and the claim is proved.
Finally, we consider, for
![]() $t\neq 0$
, the matrix
$t\neq 0$
, the matrix
![]() $M_t$
which is obtained by multiplying the
$M_t$
which is obtained by multiplying the
![]() $uu'$
row of
$uu'$
row of
![]() $R(G',q_t)$
by
$R(G',q_t)$
by
![]() $\frac 1t$
. It is clear that
$\frac 1t$
. It is clear that
![]() $\operatorname {\mathrm {rank}}(M_t) = \operatorname {\mathrm {rank}}(R(G',q_t))$
. It is also clear that
$\operatorname {\mathrm {rank}}(M_t) = \operatorname {\mathrm {rank}}(R(G',q_t))$
. It is also clear that
![]() $\lim _{t \to 0}(M_t) = L$
. Using the lower semicontinuity of the rank function and Claim 2.10, we see that, for sufficiently small nonzero t,
$\lim _{t \to 0}(M_t) = L$
. Using the lower semicontinuity of the rank function and Claim 2.10, we see that, for sufficiently small nonzero t,
![]() $\operatorname {\mathrm {rank}}(R(G,q_t)) = \operatorname {\mathrm {rank}}(M_t) \geq \operatorname {\mathrm {rank}}(L) = |E(G')|$
. This completes the proof of the theorem.
$\operatorname {\mathrm {rank}}(R(G,q_t)) = \operatorname {\mathrm {rank}}(M_t) \geq \operatorname {\mathrm {rank}}(L) = |E(G')|$
. This completes the proof of the theorem.
We remark that the inverse operation to vertex splitting is edge contraction. Given a graph G and an edge
![]() $uv\in E(G)$
, we use
$uv\in E(G)$
, we use
![]() $G/uv$
to denote the simple graph obtained from G by contracting v onto u. More precisely,
$G/uv$
to denote the simple graph obtained from G by contracting v onto u. More precisely,
![]() $G/uv = (G - v) \cup \{uz: z \in N_G(v)\}$
. Observe that G is obtained from
$G/uv = (G - v) \cup \{uz: z \in N_G(v)\}$
. Observe that G is obtained from
![]() $G/uv$
by splitting v from u along
$G/uv$
by splitting v from u along
![]() $N_G(u) \cap N_G(v)$
.
$N_G(u) \cap N_G(v)$
.
Note that if
![]() $*:X \rightarrow X$
is a non-adjacent vertex pairing and either
$*:X \rightarrow X$
is a non-adjacent vertex pairing and either
![]() $X \cap \{u,v\} = \emptyset $
, or
$X \cap \{u,v\} = \emptyset $
, or
![]() $u\in X$
,
$u\in X$
,
![]() $v \not \in X$
and
$v \not \in X$
and
![]() $u^*v \not \in E(G)$
, then
$u^*v \not \in E(G)$
, then
![]() $*$
is also a non-adjacent vertex pairing on
$*$
is also a non-adjacent vertex pairing on
![]() $G/uv$
.
$G/uv$
.
Now we will apply Theorem 2.9 to derive a sufficient condition that ensures that vertex splitting preserves
![]() $\Gamma $
-rigidity of a graph with a non-adjacent vertex pairing. We find it convenient to state this theorem in terms of edge contraction.
$\Gamma $
-rigidity of a graph with a non-adjacent vertex pairing. We find it convenient to state this theorem in terms of edge contraction.
Lemma 2.11. Suppose
![]() $\Gamma $
is a point group of
$\Gamma $
is a point group of
![]() $\mathbb R^d$
of order two. Let
$\mathbb R^d$
of order two. Let
![]() $(G,\ast )$
be a graph with a non-adjacent vertex pairing
$(G,\ast )$
be a graph with a non-adjacent vertex pairing
![]() $*:X \rightarrow X$
and
$*:X \rightarrow X$
and
![]() $uv \in E(G)$
with
$uv \in E(G)$
with
![]() $u,v \not \in X$
. Suppose that there is
$u,v \not \in X$
. Suppose that there is
![]() $C \subset N_G(u) \cap N_G(v)$
such that
$C \subset N_G(u) \cap N_G(v)$
such that
![]() $|C| = d-1$
and
$|C| = d-1$
and
![]() $|X_C| \leq 2$
. If
$|X_C| \leq 2$
. If
![]() $(G/uv,*)$
is
$(G/uv,*)$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^d$
, then
$\mathbb R^d$
, then
![]() $(G,*)$
is
$(G,*)$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^d$
.
$\mathbb R^d$
.
Proof. Observe that
![]() $X_{C \cup \{u\}} = X_C$
since
$X_{C \cup \{u\}} = X_C$
since
![]() $u \not \in X$
. If
$u \not \in X$
. If
![]() $|X_C| = 0$
, then for any
$|X_C| = 0$
, then for any
![]() $\Gamma $
-generic framework
$\Gamma $
-generic framework
![]() $(G/uv,\ast ,p)$
in
$(G/uv,\ast ,p)$
in
![]() $\mathbb R^d$
,
$\mathbb R^d$
,
![]() $p(C\cup \{u\})$
is a generic set of d points in
$p(C\cup \{u\})$
is a generic set of d points in
![]() $\mathbb R^d$
. If
$\mathbb R^d$
. If
![]() $|X_C| = 2$
, then
$|X_C| = 2$
, then
![]() $p(C \cup \{u\})$
is an affinely independent set of d-points in
$p(C \cup \{u\})$
is an affinely independent set of d-points in
![]() $\mathbb R^d$
. In both cases, it follows that
$\mathbb R^d$
. In both cases, it follows that
![]() $\{p(u) - p(z): z\in C\}$
is linearly independent, and so we can use Theorem 2.9 to construct a
$\{p(u) - p(z): z\in C\}$
is linearly independent, and so we can use Theorem 2.9 to construct a
![]() $\Gamma $
-framework
$\Gamma $
-framework
![]() $(G,\ast ,q)$
that is infinitesimally rigid in
$(G,\ast ,q)$
that is infinitesimally rigid in
![]() $\mathbb R^d$
.
$\mathbb R^d$
.
Lemma 2.11 deals with vertex splitting when the split vertex does not belong to X. We also will need a vertex splitting result for the situation where we simultaneously split a pair of vertices
![]() $u,u^\ast $
for some
$u,u^\ast $
for some
![]() $u \in X$
. In order to achieve this, we first derive a variation of Theorem 2.9, which involves simultaneously splitting two vertices of a framework in a carefully prescribed way.
$u \in X$
. In order to achieve this, we first derive a variation of Theorem 2.9, which involves simultaneously splitting two vertices of a framework in a carefully prescribed way.
The proof of Theorem 2.12 closely follows the proof of Theorem 2.9, so we only outline it, emphasising the few details which differ from the case of Theorem 2.9.
Theorem 2.12. Let
![]() $\tau :\mathbb R^d \rightarrow \mathbb R^d$
be a non-singular linear transformation. Suppose that
$\tau :\mathbb R^d \rightarrow \mathbb R^d$
be a non-singular linear transformation. Suppose that
![]() $(G,p)$
is a framework in
$(G,p)$
is a framework in
![]() $\mathbb R^d$
such that
$\mathbb R^d$
such that
![]() $R(G,p)$
is row-independent. Also, let
$R(G,p)$
is row-independent. Also, let
![]() $u,v \in V(G)$
be non-adjacent vertices,
$u,v \in V(G)$
be non-adjacent vertices,
![]() $C_1 \subset N_G(u), C_2 \subset N_G(v)$
such that
$C_1 \subset N_G(u), C_2 \subset N_G(v)$
such that
![]() $|C_1|,|C_2| \leq d-1$
, and the sets
$|C_1|,|C_2| \leq d-1$
, and the sets
![]() $\{p(w)-p(u):w \in C_1\}$
and
$\{p(w)-p(u):w \in C_1\}$
and
![]() $\{p(x) - p(v): x \in C_2\}$
are both linearly independent. Let
$\{p(x) - p(v): x \in C_2\}$
are both linearly independent. Let
![]() $G'$
be the graph obtained by splitting u from
$G'$
be the graph obtained by splitting u from
![]() $u'$
along
$u'$
along
![]() $C_1$
and then splitting v from
$C_1$
and then splitting v from
![]() $v'$
along
$v'$
along
![]() $C_2$
. Then there is some
$C_2$
. Then there is some
![]() $z \in \mathbb R^d$
such that
$z \in \mathbb R^d$
such that
![]() $R(G',q)$
is row-independent, where
$R(G',q)$
is row-independent, where
![]() $q(w) = p(w)$
for all
$q(w) = p(w)$
for all
![]() $w \in V(G)$
,
$w \in V(G)$
,
![]() $q(u') = p(u) +z$
and
$q(u') = p(u) +z$
and
![]() $q(v') = p(v) + \tau (z)$
.
$q(v') = p(v) + \tau (z)$
.
Proof. Choose
![]() $ y \in \mathbb R^d$
such that
$ y \in \mathbb R^d$
such that
![]() $y \not \in \mathrm {lin}\{p(u) - p(w): w \in C_1\}\cup \mathrm {lin}\{\tau ^{-1}(p(v) - p(x)): x \in C_2\}$
. For
$y \not \in \mathrm {lin}\{p(u) - p(w): w \in C_1\}\cup \mathrm {lin}\{\tau ^{-1}(p(v) - p(x)): x \in C_2\}$
. For
![]() $t \in \mathbb R$
, let
$t \in \mathbb R$
, let
![]() $q_t: V(G') \rightarrow \mathbb R^d$
be defined by
$q_t: V(G') \rightarrow \mathbb R^d$
be defined by
![]() $q_t(w) = p(w), w \in V(G)$
,
$q_t(w) = p(w), w \in V(G)$
,
![]() $q_t(u') = p(u)+ty$
,
$q_t(u') = p(u)+ty$
,
![]() $q_t(v') = p(v) +\tau (ty)$
. Let L be the matrix obtained from
$q_t(v') = p(v) +\tau (ty)$
. Let L be the matrix obtained from
![]() $R(G',q_0)$
by replacing the
$R(G',q_0)$
by replacing the
![]() $uu'$
row with the row that has y in the u column-set and
$uu'$
row with the row that has y in the u column-set and
![]() $-y$
in the
$-y$
in the
![]() $u'$
column-set, and replacing the the
$u'$
column-set, and replacing the the
![]() $vv'$
row with the row that has
$vv'$
row with the row that has
![]() $\tau (y)$
in the v column-set and
$\tau (y)$
in the v column-set and
![]() $-\tau (y)$
in the
$-\tau (y)$
in the
![]() $v'$
column-set.
$v'$
column-set.
Claim 2.13. L is row-independent.
Proof. This is proved in the same way as Claim 2.10, mutatis mutandis. In particular, note that the choice of y ensures that the sets
![]() $\{p(u)-p(w): w \in C_1\} \cup \{y\}$
and
$\{p(u)-p(w): w \in C_1\} \cup \{y\}$
and
![]() $\{p(v) - p(x):x \in C_2\}\cup \{\tau (y)\}$
are both linearly independent.
$\{p(v) - p(x):x \in C_2\}\cup \{\tau (y)\}$
are both linearly independent.
Now let
![]() $M_t$
be the matrix obtained from
$M_t$
be the matrix obtained from
![]() $R(G,q_t)$
by multiplying the
$R(G,q_t)$
by multiplying the
![]() $uu'$
and
$uu'$
and
![]() $vv'$
rows by
$vv'$
rows by
![]() $\frac 1t$
, and we complete the proof of the theorem in exactly the same way as the proof of Theorem 2.9.
$\frac 1t$
, and we complete the proof of the theorem in exactly the same way as the proof of Theorem 2.9.
We next apply Theorem 2.12 to the setting of
![]() $\Gamma $
-rigidity. Suppose that
$\Gamma $
-rigidity. Suppose that
![]() $G=(V,E)$
has a non-adjacent vertex pairing
$G=(V,E)$
has a non-adjacent vertex pairing
![]() $*:X \rightarrow X$
and
$*:X \rightarrow X$
and
![]() $x, y \in X$
with
$x, y \in X$
with
![]() $xy,x^*y^*\in E$
. If
$xy,x^*y^*\in E$
. If
![]() $x^*y, xy^* \not \in E$
, then the restriction of
$x^*y, xy^* \not \in E$
, then the restriction of
![]() $*$
to
$*$
to
![]() $X\setminus \{y,y^*\}$
is a non-adjacent vertex pairing of
$X\setminus \{y,y^*\}$
is a non-adjacent vertex pairing of
![]() $(G/xy)/x^*y^*$
. We will abuse notation and continue to use
$(G/xy)/x^*y^*$
. We will abuse notation and continue to use
![]() $*$
for this vertex pairing of
$*$
for this vertex pairing of
![]() $(G/xy)/x^*y^*$
.
$(G/xy)/x^*y^*$
.
Theorem 2.14. Let
![]() $\Gamma $
be a point group of order two in
$\Gamma $
be a point group of order two in
![]() $\mathbb {R}^d$
. Let
$\mathbb {R}^d$
. Let
![]() $(G,\ast )$
be a graph with a non-adjacent vertex pairing
$(G,\ast )$
be a graph with a non-adjacent vertex pairing
![]() $\ast :X\rightarrow X$
,
$\ast :X\rightarrow X$
,
![]() $x,y \in X$
such that
$x,y \in X$
such that
![]() $xy, x^*y^* \in E(G)$
and
$xy, x^*y^* \in E(G)$
and
![]() $xy^*, x^*y \not \in E(G)$
. Suppose that there exist
$xy^*, x^*y \not \in E(G)$
. Suppose that there exist
![]() $C \subset N_G(x)\cap N_G(y)$
and
$C \subset N_G(x)\cap N_G(y)$
and
![]() $D \subset N_G(x^*) \cap N_G(y^*)$
such that
$D \subset N_G(x^*) \cap N_G(y^*)$
such that
![]() $|C|, |D| = d-1$
and
$|C|, |D| = d-1$
and
![]() $|X_C|, |X_D| \leq 2$
. Let
$|X_C|, |X_D| \leq 2$
. Let
![]() $G' = (G/xy)/x^*y^*$
. If
$G' = (G/xy)/x^*y^*$
. If
![]() $(G',*)$
is
$(G',*)$
is
![]() $\Gamma $
-rigid, then
$\Gamma $
-rigid, then
![]() $(G,*)$
is
$(G,*)$
is
![]() $\Gamma $
-rigid.
$\Gamma $
-rigid.
Proof. Let
![]() $(G',\ast ,p)$
be a generic
$(G',\ast ,p)$
be a generic
![]() $\Gamma $
-framework. Then
$\Gamma $
-framework. Then
![]() $(G',p)$
is infinitesimally rigid by assumption. Let
$(G',p)$
is infinitesimally rigid by assumption. Let
![]() $I = \{xv: v\in C\} \cup \{x^*w: w \in D\}$
. Observe that
$I = \{xv: v\in C\} \cup \{x^*w: w \in D\}$
. Observe that
![]() $X_{C \cup \{x\}} = X_C$
and
$X_{C \cup \{x\}} = X_C$
and
![]() $X_{D \cup \{x^*\}} = X_D$
. Since
$X_{D \cup \{x^*\}} = X_D$
. Since
![]() $(G',\ast ,p)$
is a generic
$(G',\ast ,p)$
is a generic
![]() $\Gamma $
-framework and
$\Gamma $
-framework and
![]() $|X_C|, |X_D| \leq 2$
, it follows that both
$|X_C|, |X_D| \leq 2$
, it follows that both
![]() $\{p(w) - p(x): w \in C\}$
and
$\{p(w) - p(x): w \in C\}$
and
![]() $\{p(z) - p(x^*): z \in D\}$
are linearly independent. This also implies that the set of rows of
$\{p(z) - p(x^*): z \in D\}$
are linearly independent. This also implies that the set of rows of
![]() $R(G',p)$
labelled by I is linearly independent. Choose a maximal independent row-set that contains the row-set labelled by I and let J be the corresponding set of edges of G. Since
$R(G',p)$
labelled by I is linearly independent. Choose a maximal independent row-set that contains the row-set labelled by I and let J be the corresponding set of edges of G. Since
![]() $(G',p)$
is infinitesimally rigid, it follows that J spans
$(G',p)$
is infinitesimally rigid, it follows that J spans
![]() $V(G')$
and
$V(G')$
and
![]() $|J| = d|V(G')| - \binom {d+1}2$
. Let
$|J| = d|V(G')| - \binom {d+1}2$
. Let
![]() $G'[J]=(V(G'),J)$
. We apply Theorem 2.12 (with
$G'[J]=(V(G'),J)$
. We apply Theorem 2.12 (with
![]() $\tau $
being the non-identity element of
$\tau $
being the non-identity element of
![]() $\Gamma $
) to the framework
$\Gamma $
) to the framework
![]() $(G'[J],p)$
to obtain a
$(G'[J],p)$
to obtain a
![]() $\Gamma $
-framework
$\Gamma $
-framework
![]() $(G",\ast ,q)$
, where
$(G",\ast ,q)$
, where
![]() $G"$
is obtained from
$G"$
is obtained from
![]() $G'[J]$
by splitting x from y along C and then splitting
$G'[J]$
by splitting x from y along C and then splitting
![]() $x^*$
from
$x^*$
from
![]() $y^*$
along D. By Theorem 2.12,
$y^*$
along D. By Theorem 2.12,
![]() $(G",q)$
is infinitesimally rigid. Since
$(G",q)$
is infinitesimally rigid. Since
![]() $G"$
is a spanning subgraph of G,
$G"$
is a spanning subgraph of G,
![]() $(G,\ast , q)$
is the required infinitesimally rigid
$(G,\ast , q)$
is the required infinitesimally rigid
![]() $\Gamma $
-symmetric realisation of
$\Gamma $
-symmetric realisation of
![]() $(G,\ast )$
.
$(G,\ast )$
.
We emphasise again that for an arbitrary graph
![]() $G = (V,E)$
with a non-adjacent vertex pairing
$G = (V,E)$
with a non-adjacent vertex pairing
![]() $*:X \rightarrow X$
, the hypothesis that
$*:X \rightarrow X$
, the hypothesis that
![]() $xy \in E[X]$
does not imply that
$xy \in E[X]$
does not imply that
![]() $x^*y^* \in E$
. Hence, in order to apply Theorem 2.14 to G, we must check that
$x^*y^* \in E$
. Hence, in order to apply Theorem 2.14 to G, we must check that
![]() $xy,x^*y^*\in E$
and similarly that
$xy,x^*y^*\in E$
and similarly that
![]() $xy^*, x^*y\not \in E$
.
$xy^*, x^*y\not \in E$
.
3 Background on simplicial complexes
We now consider simplicial complexes. We summarise some notation and results from [Reference Cruickshank, Jackson and Tanigawa6] that we will need later. We refer the reader to [Reference Cruickshank, Jackson and Tanigawa6] for more details on this material.
Our main results will apply to a certain class of abstract simplicial k-complexes. However, as in [Reference Cruickshank, Jackson and Tanigawa6], it will be convenient for us to consider a larger family of complexes in which multiple copies of the same facet may exist. Thus, we define a simplicial k-multicomplex to be a multiset whose elements are
![]() $(k+1)$
-sets. Suppose that
$(k+1)$
-sets. Suppose that
![]() $\mathcal {S}$
is a simplicial k-multicomplex. For
$\mathcal {S}$
is a simplicial k-multicomplex. For
![]() $0\leq j\leq k$
, a j-face of
$0\leq j\leq k$
, a j-face of
![]() $\mathcal {S}$
is a
$\mathcal {S}$
is a
![]() $(j+1)$
-set F that is a subset of some element of
$(j+1)$
-set F that is a subset of some element of
![]() $\mathcal {S}$
. In the case that
$\mathcal {S}$
. In the case that
![]() $\mathcal {S}$
does not contain multiple copies of any k-face, we say that
$\mathcal {S}$
does not contain multiple copies of any k-face, we say that
![]() $\mathcal {S}$
is a simplicial k-complex. We justify this terminology by noting that a pure abstract simplicial complex of dimension k, in the usual sense of that term,Footnote
1
corresponds to a unique simplicial k-complex in our sense. For
$\mathcal {S}$
is a simplicial k-complex. We justify this terminology by noting that a pure abstract simplicial complex of dimension k, in the usual sense of that term,Footnote
1
corresponds to a unique simplicial k-complex in our sense. For
![]() $k \geq 1$
, the graph of
$k \geq 1$
, the graph of
![]() $\mathcal {S}$
, denoted
$\mathcal {S}$
, denoted
![]() $G(\mathcal {S})$
, is the simple graph whose vertex set,
$G(\mathcal {S})$
, is the simple graph whose vertex set,
![]() $V(\mathcal {S})$
, is the set of
$V(\mathcal {S})$
, is the set of
![]() $0$
-faces of
$0$
-faces of
![]() $\mathcal {S}$
and whose edge set,
$\mathcal {S}$
and whose edge set,
![]() $E(\mathcal {S})$
, is the set of
$E(\mathcal {S})$
, is the set of
![]() $1$
-faces of
$1$
-faces of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
The boundary of a simplicial k multicomplex
![]() $\mathcal {S}$
is given by
$\mathcal {S}$
is given by
By definition,
![]() $\partial \mathcal {S}$
is a simplicial
$\partial \mathcal {S}$
is a simplicial
![]() $(k-1)$
-complex. We say that
$(k-1)$
-complex. We say that
![]() $\mathcal {S}$
is a simplicial k-cycle if
$\mathcal {S}$
is a simplicial k-cycle if
![]() $\partial \mathcal {S} = \emptyset $
and that
$\partial \mathcal {S} = \emptyset $
and that
![]() $\mathcal {S}$
is a simplicial k-circuit if
$\mathcal {S}$
is a simplicial k-circuit if
![]() $\mathcal {S}$
is a nonempty simplicial k-cycle and no proper subset of
$\mathcal {S}$
is a nonempty simplicial k-cycle and no proper subset of
![]() $\mathcal {S}$
is a simplicial k-cycle. A trivial simplicial k-circuit is a simplicial k-multicomplex comprising two copies of the same k-face. Our use of the word ‘circuit’ here comes from matroid theory since the set of simplicial k-circuits contained within any simplicial k-multicomplex
$\mathcal {S}$
is a simplicial k-cycle. A trivial simplicial k-circuit is a simplicial k-multicomplex comprising two copies of the same k-face. Our use of the word ‘circuit’ here comes from matroid theory since the set of simplicial k-circuits contained within any simplicial k-multicomplex
![]() $\mathcal {S}$
forms the set of circuits of a matroid on
$\mathcal {S}$
forms the set of circuits of a matroid on
![]() $\mathcal {S}$
. In particular, the simplicial 1-circuits in a multigraph are the circuits of its graphic matroid. Note that if
$\mathcal {S}$
. In particular, the simplicial 1-circuits in a multigraph are the circuits of its graphic matroid. Note that if
![]() $\mathcal {S}$
is a simplicial k-multicomplex and
$\mathcal {S}$
is a simplicial k-multicomplex and
![]() $\mathcal {U} \subset \mathcal {S}$
is a simplicial k-cycle, then
$\mathcal {U} \subset \mathcal {S}$
is a simplicial k-cycle, then
![]() $\partial (\mathcal {S}\setminus \mathcal {U}) = \partial \mathcal {S}$
. This implies that a nonempty simplicial k-cycle can be partitioned into a disjoint union of simplicial k-circuits. We will frequently consider the symmetric difference
$\partial (\mathcal {S}\setminus \mathcal {U}) = \partial \mathcal {S}$
. This implies that a nonempty simplicial k-cycle can be partitioned into a disjoint union of simplicial k-circuits. We will frequently consider the symmetric difference
![]() $\mathcal {S} \triangle \mathcal {T}$
of two simplicial k-complexes
$\mathcal {S} \triangle \mathcal {T}$
of two simplicial k-complexes
![]() $\mathcal {S}, \mathcal {T}$
and use the fact that
$\mathcal {S}, \mathcal {T}$
and use the fact that
![]() $\partial (\mathcal {S} \triangle \mathcal {T}) = (\partial \mathcal {S}) \triangle (\partial \mathcal {T})$
.Footnote
2
$\partial (\mathcal {S} \triangle \mathcal {T}) = (\partial \mathcal {S}) \triangle (\partial \mathcal {T})$
.Footnote
2
We say that a simplicial k-multicomplex
![]() $\mathcal {S}$
is strongly connected if for any distinct
$\mathcal {S}$
is strongly connected if for any distinct
![]() $U,W \in \mathcal {S}$
, there is a sequence
$U,W \in \mathcal {S}$
, there is a sequence
![]() $U = U_1,\dots ,U_{\ell } = W$
in
$U = U_1,\dots ,U_{\ell } = W$
in
![]() $\mathcal {S}$
, such that
$\mathcal {S}$
, such that
![]() $|U_i \cap U_{i+1}| = k$
for
$|U_i \cap U_{i+1}| = k$
for
![]() $i = 1,\dots ,\ell -1$
. Observe that if
$i = 1,\dots ,\ell -1$
. Observe that if
![]() $\mathcal {T}$
is a maximal strongly connected subset of
$\mathcal {T}$
is a maximal strongly connected subset of
![]() $\mathcal {S}$
, then
$\mathcal {S}$
, then
![]() $\partial \mathcal {T} \subset \partial \mathcal {S}$
. In particular, it follows easily from this observation that any simplicial k-circuit is strongly connected.
$\partial \mathcal {T} \subset \partial \mathcal {S}$
. In particular, it follows easily from this observation that any simplicial k-circuit is strongly connected.
A k-pseudomanifold is a strongly connected simplicial k-complex in which every
![]() $(k-1)$
-face is contained in exactly two k-faces. It is not difficult to show that a k-pseudomanifold is a simplicial k-circuit [Reference Cruickshank, Jackson and Tanigawa6, Lemma 3.2]. We also note here that
$(k-1)$
-face is contained in exactly two k-faces. It is not difficult to show that a k-pseudomanifold is a simplicial k-circuit [Reference Cruickshank, Jackson and Tanigawa6, Lemma 3.2]. We also note here that
![]() $\mathcal {S}$
is a simplicial k-circuit if and only if it is a minimal homology cycle over
$\mathcal {S}$
is a simplicial k-circuit if and only if it is a minimal homology cycle over
![]() $\mathbb Z_2$
in the sense of Fogelsanger [Reference Fogelsanger7]. Fogelsanger’s Rigidity Theorem applies to minimal homology cycles over arbitrary abelian groups, and it might be interesting to investigate symmetric rigidity for arbitrary minimal homology cycles. We have not considered this extra generality in this paper since the class of simplicial k-circuits is already sufficiently general to include all pseudomanifolds.
$\mathbb Z_2$
in the sense of Fogelsanger [Reference Fogelsanger7]. Fogelsanger’s Rigidity Theorem applies to minimal homology cycles over arbitrary abelian groups, and it might be interesting to investigate symmetric rigidity for arbitrary minimal homology cycles. We have not considered this extra generality in this paper since the class of simplicial k-circuits is already sufficiently general to include all pseudomanifolds.
We next define a contraction operation for two vertices
![]() $u,v$
in a simplicial k-multicomplex
$u,v$
in a simplicial k-multicomplex
![]() $\mathcal {S}$
. Let
$\mathcal {S}$
. Let
![]() $\mathrm {Ast}(\{u,v\}) = \{U \in \mathcal {S}: \{u,v\} \not \subset U\}$
be the anti-star of
$\mathrm {Ast}(\{u,v\}) = \{U \in \mathcal {S}: \{u,v\} \not \subset U\}$
be the anti-star of
![]() $\{u,v\}$
in
$\{u,v\}$
in
![]() $\mathcal {S}$
. Then
$\mathcal {S}$
. Then
![]() $\mathcal {S}/uv$
is the simplicial k-multicomplex obtained from
$\mathcal {S}/uv$
is the simplicial k-multicomplex obtained from
![]() $\mathrm {Ast}(\{u,v\})$
by replacing every k-face U that contains v with
$\mathrm {Ast}(\{u,v\})$
by replacing every k-face U that contains v with
![]() $U-v+u$
. We say that
$U-v+u$
. We say that
![]() $\mathcal {S}/uv$
is obtained from
$\mathcal {S}/uv$
is obtained from
![]() $\mathcal {S}$
by contracting v onto u. Let
$\mathcal {S}$
by contracting v onto u. Let
![]() $\gamma :\mathrm {Ast}(\{u,v\}) \rightarrow \mathcal {S}/uv$
be the canonical bijection. Note that our contraction operation may create multiple copies of a k-face in
$\gamma :\mathrm {Ast}(\{u,v\}) \rightarrow \mathcal {S}/uv$
be the canonical bijection. Note that our contraction operation may create multiple copies of a k-face in
![]() $\mathcal {S}/uv$
even when
$\mathcal {S}/uv$
even when
![]() $\mathcal {S}$
is a simplicial complex. We allow this in order to have the useful property that the set of simplicial k-cycles is closed under the contraction operation. Note also that if every edge in
$\mathcal {S}$
is a simplicial complex. We allow this in order to have the useful property that the set of simplicial k-cycles is closed under the contraction operation. Note also that if every edge in
![]() $E(\mathcal {S}) \setminus \{u,v\}$
belongs to at least one k-face in
$E(\mathcal {S}) \setminus \{u,v\}$
belongs to at least one k-face in
![]() $\mathrm {Ast}(\{u,v\})$
, then
$\mathrm {Ast}(\{u,v\})$
, then
![]() $G(\mathcal {S}/uv) = G(\mathcal {S})/uv$
, where the right-hand side denotes the usual contraction operation on simple graphs.
$G(\mathcal {S}/uv) = G(\mathcal {S})/uv$
, where the right-hand side denotes the usual contraction operation on simple graphs.
We next describe the Fogelsanger decomposition of a simplicial k-circuit. Suppose that
![]() $\mathcal {S}$
is a nontrivial simplicial k-circuit and
$\mathcal {S}$
is a nontrivial simplicial k-circuit and
![]() $uv \in E(\mathcal {S})$
. Then
$uv \in E(\mathcal {S})$
. Then
![]() $\mathcal {S}/uv$
is a simplicial k-cycle, so we can express it as
$\mathcal {S}/uv$
is a simplicial k-cycle, so we can express it as
![]() $\mathcal {S}/uv = \mathcal {S}^{\prime }_1 \sqcup \dots \sqcup \mathcal {S}^{\prime }_m$
, where
$\mathcal {S}/uv = \mathcal {S}^{\prime }_1 \sqcup \dots \sqcup \mathcal {S}^{\prime }_m$
, where
![]() $\mathcal {S}^{\prime }_j$
is a simplicial k-circuit for
$\mathcal {S}^{\prime }_j$
is a simplicial k-circuit for
![]() $1\leq j \leq m$
(this partition is not necessarily unique). Let
$1\leq j \leq m$
(this partition is not necessarily unique). Let
 $$ \begin{align*} \mathcal{S}_j &= \gamma^{-1}(\mathcal{S}^{\prime}_j), \\ \mathcal{S}_j^\dagger &= \{K \subset V(\mathcal{S}): \{u,v\} \subset K, K-u, K-v \in \partial \mathcal{S}_j\}\text{ and} \\ \mathcal{S}_j^+ &= \mathcal{S}_j \cup \mathcal{S}_j^\dagger. \end{align*} $$
$$ \begin{align*} \mathcal{S}_j &= \gamma^{-1}(\mathcal{S}^{\prime}_j), \\ \mathcal{S}_j^\dagger &= \{K \subset V(\mathcal{S}): \{u,v\} \subset K, K-u, K-v \in \partial \mathcal{S}_j\}\text{ and} \\ \mathcal{S}_j^+ &= \mathcal{S}_j \cup \mathcal{S}_j^\dagger. \end{align*} $$
We say that
![]() $(\mathcal {S}_1^+,\dots ,\mathcal {S}_m^+)$
is a Fogelsanger decomposition for
$(\mathcal {S}_1^+,\dots ,\mathcal {S}_m^+)$
is a Fogelsanger decomposition for
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $uv$
. The properties of this decomposition are summarised in the following lemma, which is a restatement of [Reference Cruickshank, Jackson and Tanigawa6, Lemma 3.9].
$uv$
. The properties of this decomposition are summarised in the following lemma, which is a restatement of [Reference Cruickshank, Jackson and Tanigawa6, Lemma 3.9].
Lemma 3.1. Suppose
![]() $\mathcal {S}$
is a nontrivial simplicial k-circuit and
$\mathcal {S}$
is a nontrivial simplicial k-circuit and
![]() $uv\in E(\mathcal {S})$
. Let
$uv\in E(\mathcal {S})$
. Let
![]() $(\mathcal {S}_1^+,\mathcal {S}_2^+, \dots , \mathcal {S}_m^+)$
be a Fogelsanger decomposition of
$(\mathcal {S}_1^+,\mathcal {S}_2^+, \dots , \mathcal {S}_m^+)$
be a Fogelsanger decomposition of
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $uv$
. Then,
$uv$
. Then,
-
1.
 $\mathcal {S}_i^+/uv$
is a simplicial k-circuit for all
$\mathcal {S}_i^+/uv$
is a simplicial k-circuit for all
 $1\leq i\leq m$
;
$1\leq i\leq m$
; -
2.
 $\mathcal {S}_i^+$
is a nontrivial simplicial k-circuit for all
$\mathcal {S}_i^+$
is a nontrivial simplicial k-circuit for all
 $1\leq i\leq m$
, and each
$1\leq i\leq m$
, and each
 $K\in \mathcal {S}_i^+\setminus \mathcal {S}$
is a clique of
$K\in \mathcal {S}_i^+\setminus \mathcal {S}$
is a clique of
 $G(\mathcal {S})$
which contains
$G(\mathcal {S})$
which contains
 $\{u,v\}$
;
$\{u,v\}$
; -
3. each k-face of
 $\mathrm {Ast}(\{u,v\})$
is a k-face in a unique
$\mathrm {Ast}(\{u,v\})$
is a k-face in a unique
 $\mathcal {S}_i^+$
;
$\mathcal {S}_i^+$
; -
4.
 $\mathcal {S} = \triangle _{j=1}^m \mathcal {S}_{j}^+$
;
$\mathcal {S} = \triangle _{j=1}^m \mathcal {S}_{j}^+$
; -
5.
 $uv\in E(\mathcal {S}_i^+)$
for all
$uv\in E(\mathcal {S}_i^+)$
for all
 $1\leq i\leq m$
and
$1\leq i\leq m$
and
 $\bigcup _{i=1}^m E(\mathcal {S}_i^+)=E(\mathcal {S})$
;
$\bigcup _{i=1}^m E(\mathcal {S}_i^+)=E(\mathcal {S})$
; -
6. for all proper
 $ I\subset \{1,2,\ldots ,m\}$
, there exists
$ I\subset \{1,2,\ldots ,m\}$
, there exists
 $j\in \{1,2,\ldots ,m\}\setminus I$
and a
$j\in \{1,2,\ldots ,m\}\setminus I$
and a
 $(k+1)$
-clique K of
$(k+1)$
-clique K of
 $G(\mathcal {S})$
such that
$G(\mathcal {S})$
such that
 $K \not \in \mathcal {S}$
and
$K \not \in \mathcal {S}$
and
 $K\in (\triangle _{i\in I}\mathcal {S}_i ^+)\cap \mathcal {S}_{j}^+$
.
$K\in (\triangle _{i\in I}\mathcal {S}_i ^+)\cap \mathcal {S}_{j}^+$
.
4
 $\Gamma $
-rigidity of simplicial circuits with a non-adjacent vertex pairing
$\Gamma $
-rigidity of simplicial circuits with a non-adjacent vertex pairing
In this section, we will consider simplicial circuits with a non-adjacent vertex pairing and use the results of Section 2 to prove that their graphs are
![]() $\Gamma $
-rigid in certain cases. We begin with an analysis of the graph of a crosspolytope in this context. These graphs will serve as the base case in the inductive proof of our main theorem.
$\Gamma $
-rigid in certain cases. We begin with an analysis of the graph of a crosspolytope in this context. These graphs will serve as the base case in the inductive proof of our main theorem.
For
![]() $k \geq 0$
, let
$k \geq 0$
, let
![]() $e_1,e_2,\ldots , e_{k+1}$
be the standard basis for
$e_1,e_2,\ldots , e_{k+1}$
be the standard basis for
![]() ${\mathbb R}^{k+1}$
. The
${\mathbb R}^{k+1}$
. The
![]() $(k+1)$
-dimensional crosspolytope is the convex hull of the set of points
$(k+1)$
-dimensional crosspolytope is the convex hull of the set of points
![]() $\{\pm e_1,\pm e_2,\ldots , \pm e_{k+1}\}$
. We will use
$\{\pm e_1,\pm e_2,\ldots , \pm e_{k+1}\}$
. We will use
![]() $\mathcal {B}_{k}$
to denote the boundary complex of this polytope. It is well known that
$\mathcal {B}_{k}$
to denote the boundary complex of this polytope. It is well known that
![]() $\mathcal {B}_{k}$
is a simplicial k-complex whose vertex set is
$\mathcal {B}_{k}$
is a simplicial k-complex whose vertex set is
![]() $\{\pm e_i: 1\leq i \leq k+1\}$
. Moreover, the k-faces are precisely the transversals of
$\{\pm e_i: 1\leq i \leq k+1\}$
. Moreover, the k-faces are precisely the transversals of
![]() $\{ \{\pm e_1\}, \{\pm e_2\}, \dots ,\{\pm e_{k+1}\}\}$
. In particular, for any distinct vertices
$\{ \{\pm e_1\}, \{\pm e_2\}, \dots ,\{\pm e_{k+1}\}\}$
. In particular, for any distinct vertices
![]() $u,v$
of
$u,v$
of
![]() $\mathcal {B}_{k}$
,
$\mathcal {B}_{k}$
,
![]() $uv$
is an edge of
$uv$
is an edge of
![]() $\mathcal {B}_{k}$
if and only if
$\mathcal {B}_{k}$
if and only if
![]() $v \neq -u$
. Hence, there is the unique non-adjacent vertex pairing
$v \neq -u$
. Hence, there is the unique non-adjacent vertex pairing
![]() $\ast :V(\mathcal {B}_k)\rightarrow V(\mathcal {B}_k)$
that pairs the antipodal vertices of
$\ast :V(\mathcal {B}_k)\rightarrow V(\mathcal {B}_k)$
that pairs the antipodal vertices of
![]() $\mathcal {B}_k$
. Using this unique
$\mathcal {B}_k$
. Using this unique
![]() $\ast $
, the graph
$\ast $
, the graph
![]() $G(\mathcal {B}_k)$
of
$G(\mathcal {B}_k)$
of
![]() $\mathcal {B}_k$
is
$\mathcal {B}_k$
is
![]() $\mathbb {Z}_2$
-symmetric.
$\mathbb {Z}_2$
-symmetric.
We now check the
![]() $\Gamma _{t,k+1}$
-rigidity of
$\Gamma _{t,k+1}$
-rigidity of
![]() $(G(\mathcal {B}_{k}), \ast )$
. We need the following operation and result due to Whiteley [Reference Whiteley21]. Given a graph
$(G(\mathcal {B}_{k}), \ast )$
. We need the following operation and result due to Whiteley [Reference Whiteley21]. Given a graph
![]() $G=(V,E)$
, the cone of G is the graph
$G=(V,E)$
, the cone of G is the graph
![]() $G^v$
obtained by adding a new vertex v and all edges from v to V.
$G^v$
obtained by adding a new vertex v and all edges from v to V.
Lemma 4.1 (The Coning Lemma).
Suppose that
![]() $G=(V,E)$
is a graph,
$G=(V,E)$
is a graph,
![]() $G^v$
is the cone of G and p is a realisation of
$G^v$
is the cone of G and p is a realisation of
![]() $G^v$
in
$G^v$
in
![]() ${\mathbb R}^{k+1}$
such that
${\mathbb R}^{k+1}$
such that
![]() $p(V)$
is contained in a hyperplane H,
$p(V)$
is contained in a hyperplane H,
![]() $p(v)\not \in H$
and
$p(v)\not \in H$
and
![]() $(G,p|_V)$
is infinitesimally rigid in H (viewed as a copy of
$(G,p|_V)$
is infinitesimally rigid in H (viewed as a copy of
![]() ${\mathbb R}^{k}$
). Then
${\mathbb R}^{k}$
). Then
![]() $(G^v,p)$
is infinitesimally rigid in
$(G^v,p)$
is infinitesimally rigid in
![]() ${\mathbb R}^{k+1}$
.
${\mathbb R}^{k+1}$
.
Lemma 4.2. Suppose
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $\Gamma =\Gamma _{t,k+1}$
for some
$\Gamma =\Gamma _{t,k+1}$
for some
![]() $0 \leq t \leq k$
. Let
$0 \leq t \leq k$
. Let
![]() $G(\mathcal {B}_{k})$
be the graph of the
$G(\mathcal {B}_{k})$
be the graph of the
![]() $(k+1)$
-dimensional crosspolytope and
$(k+1)$
-dimensional crosspolytope and
![]() $\ast :V(\mathcal {B}_{k})\rightarrow V(\mathcal {B}_{k})$
be the non-adjacent vertex pairing on
$\ast :V(\mathcal {B}_{k})\rightarrow V(\mathcal {B}_{k})$
be the non-adjacent vertex pairing on
![]() $V(\mathcal {B}_{k})$
. Then
$V(\mathcal {B}_{k})$
. Then
![]() $(G(\mathcal {B}_{k}),\ast )$
is
$(G(\mathcal {B}_{k}),\ast )$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb {R}^{k+1}$
unless
$\mathbb {R}^{k+1}$
unless
![]() $k=2$
and
$k=2$
and
![]() $\Gamma $
is a rotation group of order two.
$\Gamma $
is a rotation group of order two.
Proof. Denote the set of vertices of
![]() $\mathcal {B}_{k}$
by
$\mathcal {B}_{k}$
by
![]() $\{x_1, x_1^*, \dots , x_{k+1}, x_{k+1}^*\}$
. We show by induction on k that
$\{x_1, x_1^*, \dots , x_{k+1}, x_{k+1}^*\}$
. We show by induction on k that
![]() $G(\mathcal {B}_k)$
has an infinitesimally rigid
$G(\mathcal {B}_k)$
has an infinitesimally rigid
![]() $\Gamma _{t,k+1}$
-symmetric realisation
$\Gamma _{t,k+1}$
-symmetric realisation
![]() $p_{t,k}$
in
$p_{t,k}$
in
![]() ${\mathbb R}^{k+1}$
. For the base case when
${\mathbb R}^{k+1}$
. For the base case when
![]() $k=2$
, it is straightforward to check that
$k=2$
, it is straightforward to check that
![]() $(G(\mathcal {B}_{2}),p_{0,2})$
is infinitesimally rigid when
$(G(\mathcal {B}_{2}),p_{0,2})$
is infinitesimally rigid when
![]() $p_{0,2}(x_i)=e_i$
and
$p_{0,2}(x_i)=e_i$
and
![]() $p_{0,2}(x_i^*)=-e_i$
for all
$p_{0,2}(x_i^*)=-e_i$
for all
![]() $1\leq i\leq 3$
;
$1\leq i\leq 3$
;
![]() $(G(\mathcal {B}_{2}),p_{2,2})$
is infinitesimally rigid when
$(G(\mathcal {B}_{2}),p_{2,2})$
is infinitesimally rigid when
![]() $p_{2,2}(x_i)=e_i+e_3$
and
$p_{2,2}(x_i)=e_i+e_3$
and
![]() $p_{2,2}(x_i^*)=e_i-e_3$
for all
$p_{2,2}(x_i^*)=e_i-e_3$
for all
![]() $1\leq i\leq 3$
. Hence, we may assume that
$1\leq i\leq 3$
. Hence, we may assume that
![]() $k\geq 3$
.
$k\geq 3$
.
The inductive step will follow immediately from the following:
Claim 4.3. Suppose
![]() $(G(\mathcal {B}_{k-1}),\ast )$
has an infinitesimally rigid
$(G(\mathcal {B}_{k-1}),\ast )$
has an infinitesimally rigid
![]() $\Gamma _{t,k}$
-symmetric realisation
$\Gamma _{t,k}$
-symmetric realisation
![]() $p_{t,k-1}$
in
$p_{t,k-1}$
in
![]() ${\mathbb R}^k$
for some
${\mathbb R}^k$
for some
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $0\leq t\leq k-1$
. Then
$0\leq t\leq k-1$
. Then
![]() $(G(\mathcal {B}_{k}),\ast )$
has both an infinitesimally rigid
$(G(\mathcal {B}_{k}),\ast )$
has both an infinitesimally rigid
![]() $\Gamma _{t,k+1}$
-symmetric realisation and an infinitesimally rigid
$\Gamma _{t,k+1}$
-symmetric realisation and an infinitesimally rigid
![]() $\Gamma _{t+1,k+1}$
-symmetric realisation in
$\Gamma _{t+1,k+1}$
-symmetric realisation in
![]() $\mathbb R^{k+1}$
.
$\mathbb R^{k+1}$
.
Proof. We may assume that
![]() $p_{t,k-1}$
is a generic
$p_{t,k-1}$
is a generic
![]() $\Gamma _{t,k}$
-symmetric realisation of
$\Gamma _{t,k}$
-symmetric realisation of
![]() $(G(\mathcal {B}_{k-1}),\ast )$
in
$(G(\mathcal {B}_{k-1}),\ast )$
in
![]() ${\mathbb R}^k$
and that
${\mathbb R}^k$
and that
![]() $V(\mathcal {B}_{k-1}) = \{x_1,x_1^*,\dots ,x_k,x_k^*\}$
.
$V(\mathcal {B}_{k-1}) = \{x_1,x_1^*,\dots ,x_k,x_k^*\}$
.
We first extend
![]() $p_{t,k-1}$
to an infinitesimally rigid
$p_{t,k-1}$
to an infinitesimally rigid
![]() $\Gamma _{t,k+1}$
-symmetric realisation
$\Gamma _{t,k+1}$
-symmetric realisation
![]() $p_{t,k}$
of
$p_{t,k}$
of
![]() $(G(\mathcal {B}_{k}),\ast )$
in
$(G(\mathcal {B}_{k}),\ast )$
in
![]() $\mathbb R^{k+1}$
by putting
$\mathbb R^{k+1}$
by putting
![]() $p_{t,k}(z) = (p_{t,k-1}(z),0)$
for all
$p_{t,k}(z) = (p_{t,k-1}(z),0)$
for all
![]() $ z\in V(\mathcal {B}_{k-1})$
and
$ z\in V(\mathcal {B}_{k-1})$
and
![]() $p_{t,k}(x_{k+1})=e_{k+1}=-p_{t,k}(x^*_{k+1})$
. Then the restrictions of
$p_{t,k}(x_{k+1})=e_{k+1}=-p_{t,k}(x^*_{k+1})$
. Then the restrictions of
![]() $p_{t,k}$
to both
$p_{t,k}$
to both
![]() $G(\mathcal {B}_{k})-x_{k+1}$
and
$G(\mathcal {B}_{k})-x_{k+1}$
and
![]() $G(\mathcal {B}_{k})-x_{k+1}^*$
are infinitesimally rigid by Lemma 4.1. We can now use Theorem 2.8 to deduce that
$G(\mathcal {B}_{k})-x_{k+1}^*$
are infinitesimally rigid by Lemma 4.1. We can now use Theorem 2.8 to deduce that
![]() $p_{t,k}$
is an infinitesimally rigid realisation of
$p_{t,k}$
is an infinitesimally rigid realisation of
![]() $G(\mathcal {B}_{k})$
.
$G(\mathcal {B}_{k})$
.
A similar proof works for
![]() $p_{t+1,k}$
. We construct a realisation
$p_{t+1,k}$
. We construct a realisation
![]() $p_{t+1,k}$
of
$p_{t+1,k}$
of
![]() $G(\mathcal {B}_{k})$
from
$G(\mathcal {B}_{k})$
from
![]() $p_{t,k-1}$
by putting
$p_{t,k-1}$
by putting
![]() $p_{t+1,k}(z) = (0,p_{t,k-1}(z))$
for all
$p_{t+1,k}(z) = (0,p_{t,k-1}(z))$
for all
![]() $ z\in V(\mathcal {B}_{k-1})$
and
$ z\in V(\mathcal {B}_{k-1})$
and
![]() $p_{t+1,k}(x_{k+1})=e_{1}=p_{t+1,k}(x^*_{k+1})$
. Then we can use Lemma 4.1 and Theorem 2.8 to deduce that
$p_{t+1,k}(x_{k+1})=e_{1}=p_{t+1,k}(x^*_{k+1})$
. Then we can use Lemma 4.1 and Theorem 2.8 to deduce that
![]() $(G(\mathcal {B}_{d}),p_{t+1,k})$
is infinitesimally rigid.
$(G(\mathcal {B}_{d}),p_{t+1,k})$
is infinitesimally rigid.
We next use Lemma 4.2 to analyse the case when
![]() $X\neq V(\mathcal {B}_k)$
.
$X\neq V(\mathcal {B}_k)$
.
Lemma 4.4. Let
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $X\subseteq V(\mathcal {B}_k)$
,
$X\subseteq V(\mathcal {B}_k)$
,
![]() $\ast :X\to X$
be a non-adjacent vertex pairing of
$\ast :X\to X$
be a non-adjacent vertex pairing of
![]() $G(\mathcal {B}_k)$
and
$G(\mathcal {B}_k)$
and
![]() $\Gamma $
be a point group of
$\Gamma $
be a point group of
![]() ${\mathbb R}^{k+1}$
of order two. Suppose that
${\mathbb R}^{k+1}$
of order two. Suppose that
![]() $|X|\leq 2k$
. Then
$|X|\leq 2k$
. Then
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^{k+1}$
.
$\mathbb R^{k+1}$
.
Proof. It will suffice to show that
![]() $(G(\mathcal {B}_k),\ast )$
has an infinitesimally rigid
$(G(\mathcal {B}_k),\ast )$
has an infinitesimally rigid
![]() $\Gamma $
-symmetric realisation in
$\Gamma $
-symmetric realisation in
![]() ${\mathbb R}^{k+1}$
. This follows immediately from Lemma 4.2 unless
${\mathbb R}^{k+1}$
. This follows immediately from Lemma 4.2 unless
![]() $k=2$
and
$k=2$
and
![]() $\Gamma $
is a rotation group. In the latter case, a realisation of
$\Gamma $
is a rotation group. In the latter case, a realisation of
![]() $G(\mathcal {B}_k)$
as the regular octahedron is a
$G(\mathcal {B}_k)$
as the regular octahedron is a
![]() $\Gamma $
-symmetric realisation of
$\Gamma $
-symmetric realisation of
![]() $(G(\mathcal {B}_k),\ast )$
since
$(G(\mathcal {B}_k),\ast )$
since
![]() $|X|\leq 4$
. Hence, the
$|X|\leq 4$
. Hence, the
![]() $\Gamma $
-rigidity of
$\Gamma $
-rigidity of
![]() $(G(\mathcal {B}_2),\ast )$
follows from the infinitesimal rigidity of the 1-skeleton of the regular octahedron.
$(G(\mathcal {B}_2),\ast )$
follows from the infinitesimal rigidity of the 1-skeleton of the regular octahedron.
We next show that Lemma 4.4 can be extended from
![]() $\mathcal {B}_k$
to arbitrary simplicial k-circuits. This result will be a key ingredient in the proof of our main theorem (Theorem 5.8).
$\mathcal {B}_k$
to arbitrary simplicial k-circuits. This result will be a key ingredient in the proof of our main theorem (Theorem 5.8).
Theorem 4.5. Let
![]() $G=(V,E)$
be the graph of a simplicial k-circuit
$G=(V,E)$
be the graph of a simplicial k-circuit
![]() $\mathcal {S}$
for some
$\mathcal {S}$
for some
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $X\subseteq V$
,
$X\subseteq V$
,
![]() $*:X\to X$
be a non-adjacent vertex pairing of G, and
$*:X\to X$
be a non-adjacent vertex pairing of G, and
![]() $\Gamma $
be a point group of
$\Gamma $
be a point group of
![]() ${\mathbb R}^{k+1}$
of order two. Suppose that
${\mathbb R}^{k+1}$
of order two. Suppose that
![]() $|X|\leq 2k$
. Then
$|X|\leq 2k$
. Then
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^{k+1}$
.
$\mathbb R^{k+1}$
.
Proof. Suppose, for a contradiction, that
![]() $\mathcal {S}$
is a counterexample with as few vertices as possible. Clearly,
$\mathcal {S}$
is a counterexample with as few vertices as possible. Clearly,
![]() $\mathcal {S}$
cannot be a trivial simplicial k-circuit. Let
$\mathcal {S}$
cannot be a trivial simplicial k-circuit. Let
![]() $(G,\ast ,p)$
be a generic
$(G,\ast ,p)$
be a generic
![]() $\Gamma $
-framework in
$\Gamma $
-framework in
![]() $\mathbb R^{k+1}$
. First, we record a useful observation. Suppose that
$\mathbb R^{k+1}$
. First, we record a useful observation. Suppose that
![]() $K \subset V$
is a clique in G. Then since
$K \subset V$
is a clique in G. Then since
![]() $xx^* \not \in E$
for all
$xx^* \not \in E$
for all
![]() $x \in X$
(as
$x \in X$
(as
![]() $\ast $
is non-adjacent), it follows that
$\ast $
is non-adjacent), it follows that
Claim 4.6. Every edge of G is incident to X.
Proof of claim.
Suppose, for a contradiction, that
![]() $uv \in E$
and
$uv \in E$
and
![]() $u,v \not \in X$
. Let
$u,v \not \in X$
. Let
![]() $(\mathcal {S}_1^+, \dots ,\mathcal {S}_m^+)$
be a Fogelsanger decomposition of
$(\mathcal {S}_1^+, \dots ,\mathcal {S}_m^+)$
be a Fogelsanger decomposition of
![]() $\mathcal {S}$
with respect to
$\mathcal {S}$
with respect to
![]() $uv$
. Put
$uv$
. Put
![]() $(V_i, E_i) = G_i = G(\mathcal {S}_i^+)$
and
$(V_i, E_i) = G_i = G(\mathcal {S}_i^+)$
and
![]() $X_i = X_{V_i} = (V_i \cap X) \cap (V_i \cap X)^*$
. Then
$X_i = X_{V_i} = (V_i \cap X) \cap (V_i \cap X)^*$
. Then
![]() $|X_i| \leq |X|$
for each i. Also,
$|X_i| \leq |X|$
for each i. Also,
![]() $\ast |_{X_i}$
is a non-adjacent vertex pairing for
$\ast |_{X_i}$
is a non-adjacent vertex pairing for
![]() $G_i$
by Lemma 3.1(e).
$G_i$
by Lemma 3.1(e).
Suppose
![]() $|V_i| < |V|$
for all
$|V_i| < |V|$
for all
![]() $i = 1,\dots ,m$
. Then, by the minimality of
$i = 1,\dots ,m$
. Then, by the minimality of
![]() $|V|$
,
$|V|$
,
![]() $(G_i,\ast |_{X_i})$
is
$(G_i,\ast |_{X_i})$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^{k+1}$
. It follows that
$\mathbb R^{k+1}$
. It follows that
![]() $(G_i,p|_{V_i})$
is infinitesimally rigid. Now, a straightforward induction argument using Lemma 3.1(6), Theorem 2.8(b) and (4.1) proves that
$(G_i,p|_{V_i})$
is infinitesimally rigid. Now, a straightforward induction argument using Lemma 3.1(6), Theorem 2.8(b) and (4.1) proves that
![]() $(G,p)$
is infinitesimally rigid, contradicting our choice of
$(G,p)$
is infinitesimally rigid, contradicting our choice of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Thus, we can assume without loss of generality that
![]() $V_1 = V$
. Since
$V_1 = V$
. Since
![]() $\mathcal {S}_1^+/uv$
is a simplicial k-circuit, it follows from the minimality of
$\mathcal {S}_1^+/uv$
is a simplicial k-circuit, it follows from the minimality of
![]() $|V|$
that
$|V|$
that
![]() $(G_1/uv,\ast )$
is
$(G_1/uv,\ast )$
is
![]() $\Gamma $
-rigid. By Lemma 3.1(b), we can choose
$\Gamma $
-rigid. By Lemma 3.1(b), we can choose
![]() $U \in \mathcal {S}_1^+$
such that
$U \in \mathcal {S}_1^+$
such that
![]() $u,v \in U$
. Since
$u,v \in U$
. Since
![]() $\mathcal {S}_1^+$
is a nontrivial simplicial circuit, there is some
$\mathcal {S}_1^+$
is a nontrivial simplicial circuit, there is some
![]() $w \not \in U$
such that
$w \not \in U$
such that
![]() $w \in N_{G_1}(u) \cap N_{G_1}(v)$
. Now
$w \in N_{G_1}(u) \cap N_{G_1}(v)$
. Now
![]() $C = U -\{u,v\}+w$
satisfies,
$C = U -\{u,v\}+w$
satisfies,
![]() $|C| = k$
, and
$|C| = k$
, and
![]() $|X_C| \leq 2$
. Lemma 2.11 now implies that
$|X_C| \leq 2$
. Lemma 2.11 now implies that
![]() $(G_1,\ast )$
is
$(G_1,\ast )$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^{k+1}$
and since
$\mathbb R^{k+1}$
and since
![]() $G_1$
is a spanning subgraph of G, that
$G_1$
is a spanning subgraph of G, that
![]() $(G,\ast )$
is also
$(G,\ast )$
is also
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() $\mathbb R^{k+1}$
. This contradicts our choice of
$\mathbb R^{k+1}$
. This contradicts our choice of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
For each
![]() $U\in \mathcal {S}$
, Claim 4.6 gives
$U\in \mathcal {S}$
, Claim 4.6 gives
![]() $|U\cap X|\geq k$
. Since
$|U\cap X|\geq k$
. Since
![]() $|X|\leq 2k$
and
$|X|\leq 2k$
and
![]() $xx^*\not \in E(\mathcal {S})$
for all
$xx^*\not \in E(\mathcal {S})$
for all
![]() $x\in X$
, we have
$x\in X$
, we have
Claim 4.7. Some subcomplex of
![]() $\mathcal {S}$
is isomorphic to
$\mathcal {S}$
is isomorphic to
![]() $\mathcal {B}_k$
.
$\mathcal {B}_k$
.
Proof. Choose
![]() $U\in \mathcal {S}$
. Since
$U\in \mathcal {S}$
. Since
![]() $xx^*\not \in E(\mathcal {S})$
for all
$xx^*\not \in E(\mathcal {S})$
for all
![]() $x\in X$
, (4.2) implies that we can label the elements of X as
$x\in X$
, (4.2) implies that we can label the elements of X as
![]() $x_1,x_1^*,x_2,x_2^*,\ldots , x_k,x_k^*$
with
$x_1,x_1^*,x_2,x_2^*,\ldots , x_k,x_k^*$
with
![]() $U\cap X=\{x_1,x_2,\ldots ,x_k\}$
. Let
$U\cap X=\{x_1,x_2,\ldots ,x_k\}$
. Let
![]() $U=\{x_1,x_2,\ldots ,x_k,u\}$
. Since
$U=\{x_1,x_2,\ldots ,x_k,u\}$
. Since
![]() $\mathcal {S}$
is a nontrivial simplicial k-circuit, (4.2) also implies that
$\mathcal {S}$
is a nontrivial simplicial k-circuit, (4.2) also implies that
![]() $U-x_i+x_i^*$
is a k-face of
$U-x_i+x_i^*$
is a k-face of
![]() $\mathcal {S}$
for all
$\mathcal {S}$
for all
![]() $1\leq i\leq k$
and hence that
$1\leq i\leq k$
and hence that
![]() $J+u$
is a k-face of
$J+u$
is a k-face of
![]() $\mathcal {S}$
for all transversals J of
$\mathcal {S}$
for all transversals J of
![]() $\{\{x_1,x_1^*\},\{x_2,x_2^*\},\ldots , \{x_k,x_k^*\}\}$
.
$\{\{x_1,x_1^*\},\{x_2,x_2^*\},\ldots , \{x_k,x_k^*\}\}$
.
These cannot be all of the k-faces of
![]() $\mathcal {S}$
since they do not form a simplicial k-circuit. Therefore, there is some
$\mathcal {S}$
since they do not form a simplicial k-circuit. Therefore, there is some
![]() $u' \in V(\mathcal {S})\setminus X$
such that
$u' \in V(\mathcal {S})\setminus X$
such that
![]() $u' \neq u$
, and the same argument as before shows that
$u' \neq u$
, and the same argument as before shows that
![]() $J+u'$
is a k-face of
$J+u'$
is a k-face of
![]() $\mathcal {S}$
for all transversals J of
$\mathcal {S}$
for all transversals J of
![]() $\{\{x_1,x_1^*\},\{x_2,x_2^*\},\ldots , \{x_k,x_k^*\}\}$
. Hence, every transversal of
$\{\{x_1,x_1^*\},\{x_2,x_2^*\},\ldots , \{x_k,x_k^*\}\}$
. Hence, every transversal of
![]() $\{\{x_1,x_1^*\},\{x_2,x_2^*\},\ldots , \{x_k,x_k^*\},\{u,u'\}\}$
is a k-face of
$\{\{x_1,x_1^*\},\{x_2,x_2^*\},\ldots , \{x_k,x_k^*\},\{u,u'\}\}$
is a k-face of
![]() $\mathcal {S}$
. These transversals induce a subcomplex of
$\mathcal {S}$
. These transversals induce a subcomplex of
![]() $\mathcal {S}$
which is isomorphic to
$\mathcal {S}$
which is isomorphic to
![]() $\mathcal {B}_k$
.
$\mathcal {B}_k$
.
Since both
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\mathcal {B}_k$
are simplicial k-circuits, Claim 4.7 implies that
$\mathcal {B}_k$
are simplicial k-circuits, Claim 4.7 implies that
![]() $\mathcal {S}\cong \mathcal {B}_k$
. We can now use Lemma 4.4 to deduce that
$\mathcal {S}\cong \mathcal {B}_k$
. We can now use Lemma 4.4 to deduce that
![]() $(G,\ast )$
is
$(G,\ast )$
is
![]() $\Gamma $
-rigid.
$\Gamma $
-rigid.
It is worth noting that the case
![]() $X = \emptyset $
in Theorem 4.5 is Fogelsanger’s theorem for simplicial k-circuits, so we can view Theorem 4.5 as a non-generic extension of this fundamental result in rigidity theory.
$X = \emptyset $
in Theorem 4.5 is Fogelsanger’s theorem for simplicial k-circuits, so we can view Theorem 4.5 as a non-generic extension of this fundamental result in rigidity theory.
The Bricard octahedron shows that the hypothesis
![]() $|X| \leq 2k$
in Theorem 4.5 is necessary when
$|X| \leq 2k$
in Theorem 4.5 is necessary when
![]() $k=2$
and
$k=2$
and
![]() $\Gamma $
is a half turn rotation group.
$\Gamma $
is a half turn rotation group.
5
 ${\mathbb Z}_2$
-symmetric simplicial complexes
${\mathbb Z}_2$
-symmetric simplicial complexes
Suppose that
![]() $\mathcal {S}$
is a simplicial k-multicomplex. Let
$\mathcal {S}$
is a simplicial k-multicomplex. Let
![]() $*:V(\mathcal {S}) \rightarrow V(\mathcal {S})$
be an involution. For
$*:V(\mathcal {S}) \rightarrow V(\mathcal {S})$
be an involution. For
![]() $X\subseteq V(\mathcal {S})$
and
$X\subseteq V(\mathcal {S})$
and
![]() $\mathcal {U} \subset \mathcal {S}$
, let
$\mathcal {U} \subset \mathcal {S}$
, let
![]() $X^*=\{x^*:x\in X\}$
and
$X^*=\{x^*:x\in X\}$
and
![]() $\mathcal {U}^* = \{K^*: K \in \mathcal {U}\}$
. The set X, respectively
$\mathcal {U}^* = \{K^*: K \in \mathcal {U}\}$
. The set X, respectively
![]() $\mathcal {U}$
, is
$\mathcal {U}$
, is
![]() $*$
-invariant if
$*$
-invariant if
![]() $X^*=X$
, respectively
$X^*=X$
, respectively
![]() $\mathcal {U}^*=\mathcal {U}$
. We say that
$\mathcal {U}^*=\mathcal {U}$
. We say that
![]() $*$
is a simplicial involution if for every facet F of
$*$
is a simplicial involution if for every facet F of
![]() $\mathcal {S}$
,
$\mathcal {S}$
,
![]() $F^*$
is a facet of
$F^*$
is a facet of
![]() $\mathcal {S}$
of the same multiplicity as F, and that
$\mathcal {S}$
of the same multiplicity as F, and that
![]() $*$
is free if
$*$
is free if
![]() $V(F^*) \neq V(F)$
for every face F of
$V(F^*) \neq V(F)$
for every face F of
![]() $\mathcal {S}$
. A
$\mathcal {S}$
. A
![]() $\mathbb {Z}_2$
-symmetric simplicial k-multicomplex is a pair
$\mathbb {Z}_2$
-symmetric simplicial k-multicomplex is a pair
![]() $(\mathcal {S},\ast )$
where
$(\mathcal {S},\ast )$
where
![]() $\mathcal {S}$
is a simplicial k-multicomplex and
$\mathcal {S}$
is a simplicial k-multicomplex and
![]() $*$
is a free simplicial involution on
$*$
is a free simplicial involution on
![]() $\mathcal {S}$
. This terminology is consistent with our terminology for graphs since if
$\mathcal {S}$
. This terminology is consistent with our terminology for graphs since if
![]() $(\mathcal {S},*)$
is a
$(\mathcal {S},*)$
is a
![]() $\mathbb {Z}_2$
-symmetric k-multicomplex, then
$\mathbb {Z}_2$
-symmetric k-multicomplex, then
![]() $(G(\mathcal {S}),\ast )$
is a
$(G(\mathcal {S}),\ast )$
is a
![]() $\mathbb {Z}_2$
-symmetric graph. We will often abuse notation by omitting explicit mention of the involution
$\mathbb {Z}_2$
-symmetric graph. We will often abuse notation by omitting explicit mention of the involution
![]() $\ast $
when it is obvious from the context.
$\ast $
when it is obvious from the context.
5.1
 $\mathbb {Z}_2$
-irreducible cycles and their structural properties
$\mathbb {Z}_2$
-irreducible cycles and their structural properties
We will refer to a
![]() $\mathbb {Z}_2$
-symmetric k-multicomplex, which is also a simplicial k-cycle, as a
$\mathbb {Z}_2$
-symmetric k-multicomplex, which is also a simplicial k-cycle, as a
![]() $\mathbb {Z}_2$
-symmetric k-cycle. A
$\mathbb {Z}_2$
-symmetric k-cycle. A
![]() $\mathbb Z_2$
-irreducible k-cycle is a nonempty
$\mathbb Z_2$
-irreducible k-cycle is a nonempty
![]() $\mathbb {Z}_2$
-symmetric k-cycle
$\mathbb {Z}_2$
-symmetric k-cycle
![]() $(\mathcal {S},*)$
which is minimal in the sense that for all
$(\mathcal {S},*)$
which is minimal in the sense that for all
![]() $\emptyset \neq \mathcal {T} \subsetneq \mathcal {S}$
,
$\emptyset \neq \mathcal {T} \subsetneq \mathcal {S}$
,
![]() $(\mathcal {T},*|_{V(\mathcal {T})})$
is not a
$(\mathcal {T},*|_{V(\mathcal {T})})$
is not a
![]() $\mathbb {Z}_2$
-symmetric k-cycle. We say that
$\mathbb {Z}_2$
-symmetric k-cycle. We say that
![]() $\mathcal {S}$
is a trivial
$\mathcal {S}$
is a trivial
![]() $\mathbb Z_2$
-irreducible k-cycle if it consists of two vertex disjoint copies of the trivial simplicial k-circuit and the involution interchanges the vertex sets of these two trivial simplicial k-circuits. Otherwise,
$\mathbb Z_2$
-irreducible k-cycle if it consists of two vertex disjoint copies of the trivial simplicial k-circuit and the involution interchanges the vertex sets of these two trivial simplicial k-circuits. Otherwise,
![]() $\mathcal {S}$
is a nontrivial
$\mathcal {S}$
is a nontrivial
![]() $\mathbb Z_2$
-irreducible k-cycle.
$\mathbb Z_2$
-irreducible k-cycle.
Suppose that
![]() $\mathcal {S}$
is a nonempty
$\mathcal {S}$
is a nonempty
![]() $\mathbb {Z}_2$
-symmetric k-cycle. It is straightforward to show that if
$\mathbb {Z}_2$
-symmetric k-cycle. It is straightforward to show that if
![]() $\mathcal {T}\subseteq \mathcal {S}$
is a
$\mathcal {T}\subseteq \mathcal {S}$
is a
![]() $\mathbb {Z}_2$
-symmetric k-cycle, then
$\mathbb {Z}_2$
-symmetric k-cycle, then
![]() $\mathcal {S}\setminus \mathcal {T}$
is a
$\mathcal {S}\setminus \mathcal {T}$
is a
![]() $\mathbb {Z}_2$
-symmetric k-cycle. This implies that there exists a partition
$\mathbb {Z}_2$
-symmetric k-cycle. This implies that there exists a partition
![]() $\mathcal {S} = \mathcal {S}_1 \sqcup \dots \sqcup \mathcal {S}_m$
where
$\mathcal {S} = \mathcal {S}_1 \sqcup \dots \sqcup \mathcal {S}_m$
where
![]() $\mathcal {S}_i$
is a
$\mathcal {S}_i$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle for
$\mathbb Z_2$
-irreducible k-cycle for
![]() $i = 1,\dots ,m$
. This partition is not necessarily unique (even up to permutations).
$i = 1,\dots ,m$
. This partition is not necessarily unique (even up to permutations).
An important class of examples is the following. Let P be a simplicial convex d-polytope. That is a convex polytope in
![]() $\mathbb R^d$
that has dimension d and such that every face in the boundary of P is a simplex. Suppose also that that P is centrally symmetric. The boundary complex
$\mathbb R^d$
that has dimension d and such that every face in the boundary of P is a simplex. Suppose also that that P is centrally symmetric. The boundary complex
![]() $B(P)$
is a simplicial
$B(P)$
is a simplicial
![]() $(d-1)$
-complex whose facets are the vertex sets of the
$(d-1)$
-complex whose facets are the vertex sets of the
![]() $(d-1)$
-dimensional faces of P. Then
$(d-1)$
-dimensional faces of P. Then
![]() $B(P)$
is a simplicial sphere and hence a simplicial
$B(P)$
is a simplicial sphere and hence a simplicial
![]() $(d-1)$
-circuit. Moreover, the involution
$(d-1)$
-circuit. Moreover, the involution
![]() $\ast : V(P) \to V(P)$
given by
$\ast : V(P) \to V(P)$
given by
![]() $v^\ast = -v$
makes
$v^\ast = -v$
makes
![]() $B(P)$
into a
$B(P)$
into a
![]() $\mathbb Z_2$
-irreducible (
$\mathbb Z_2$
-irreducible (
![]() $d-1$
)-cycle.
$d-1$
)-cycle.
More generally, if
![]() $\mathcal {S}$
is a simplicial k-circuit with a free simplicial involution, then since it does not properly contain any simplicial k-cycle (
$\mathcal {S}$
is a simplicial k-circuit with a free simplicial involution, then since it does not properly contain any simplicial k-cycle (
![]() $\ast $
-invariant or otherwise), it must also be a
$\ast $
-invariant or otherwise), it must also be a
![]() $\mathbb Z_2$
-irreducible k-cycle. However, there are
$\mathbb Z_2$
-irreducible k-cycle. However, there are
![]() $\mathbb Z_2$
-irreducible k-cycles that are not simplicial k-circuits – the trivial
$\mathbb Z_2$
-irreducible k-cycles that are not simplicial k-circuits – the trivial
![]() $\mathbb Z_2$
-irreducible k-cycle is an example. A nontrivial example is given in Figure 2. Since our main motivation is to understand simplicial k-circuits that have a free involution, the reader might wonder why we introduce the more general notion of a
$\mathbb Z_2$
-irreducible k-cycle is an example. A nontrivial example is given in Figure 2. Since our main motivation is to understand simplicial k-circuits that have a free involution, the reader might wonder why we introduce the more general notion of a
![]() $\mathbb Z_2$
-irreducible k-cycle. The reason is that
$\mathbb Z_2$
-irreducible k-cycle. The reason is that
![]() $\mathbb Z_2$
-irreducible k-cycles that are not simplicial k-circuits can arise naturally from the the
$\mathbb Z_2$
-irreducible k-cycles that are not simplicial k-circuits can arise naturally from the the
![]() $\mathbb Z_2$
-symmetric version of the Fogelsanger decomposition, even if we start with a simplicial k-circuit with a free involution.
$\mathbb Z_2$
-symmetric version of the Fogelsanger decomposition, even if we start with a simplicial k-circuit with a free involution.

Figure 2 The 1-skeleton of a
![]() $\mathbb Z_2$
-irreducible
$\mathbb Z_2$
-irreducible
![]() $2$
-cycle
$2$
-cycle
![]() $\mathcal {S}$
, which is not a simplicial 2-circuit. We have
$\mathcal {S}$
, which is not a simplicial 2-circuit. We have
![]() $\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
, where
$\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
, where
![]() $\mathcal {T}=\{\{v_1,v_2,v_3\},\{v_1,v_2,v_4\},\{v_1,v_3,v_4\},\{v_1^*,v_2,v_3\},\{v_1^*,v_2,v_4\},\{v_1^*,v_3,v_4\}\}$
is the simplicial 2-circuit given by the boundary complex of the hexahedron.
$\mathcal {T}=\{\{v_1,v_2,v_3\},\{v_1,v_2,v_4\},\{v_1,v_3,v_4\},\{v_1^*,v_2,v_3\},\{v_1^*,v_2,v_4\},\{v_1^*,v_3,v_4\}\}$
is the simplicial 2-circuit given by the boundary complex of the hexahedron.
Our first structural result on
![]() $\mathbb Z_2$
-irreducible k-cycles characterises those which are not simplicial k-circuits.
$\mathbb Z_2$
-irreducible k-cycles characterises those which are not simplicial k-circuits.
Lemma 5.1. Let
![]() $(\mathcal {S},*)$
be a nontrivial
$(\mathcal {S},*)$
be a nontrivial
![]() $\mathbb Z_2$
-irreducible k-cycle. Then either
$\mathbb Z_2$
-irreducible k-cycle. Then either
![]() $\mathcal {S}$
is a simplicial k-circuit or
$\mathcal {S}$
is a simplicial k-circuit or
![]() $\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
where
$\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
where
![]() $\mathcal {T}$
is a nontrivial simplicial k-circuit. Moreover, if the second alternative holds and
$\mathcal {T}$
is a nontrivial simplicial k-circuit. Moreover, if the second alternative holds and
![]() $\mathcal {U}$
is a simplicial k-circuit properly contained in
$\mathcal {U}$
is a simplicial k-circuit properly contained in
![]() $\mathcal {S}$
, then
$\mathcal {S}$
, then
![]() $\mathcal {U} = \mathcal {T}$
or
$\mathcal {U} = \mathcal {T}$
or
![]() $\mathcal {U} = \mathcal {T}^*$
.
$\mathcal {U} = \mathcal {T}^*$
.
Proof. Suppose that
![]() $\mathcal {S}$
is not a simplicial k-circuit. Then some simplicial k-circuit
$\mathcal {S}$
is not a simplicial k-circuit. Then some simplicial k-circuit
![]() $\mathcal {T}$
is properly contained in
$\mathcal {T}$
is properly contained in
![]() $\mathcal {S}$
. Since
$\mathcal {S}$
. Since
![]() $\mathcal {S}$
is a
$\mathcal {S}$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle,
$\mathbb Z_2$
-irreducible k-cycle,
![]() $\mathcal {T}^* \neq \mathcal {T}$
. It follows that
$\mathcal {T}^* \neq \mathcal {T}$
. It follows that
![]() $\mathcal {T} \triangle \mathcal {T}^*$
is a nonempty
$\mathcal {T} \triangle \mathcal {T}^*$
is a nonempty
![]() $*$
-invariant simplicial k-cycle contained in
$*$
-invariant simplicial k-cycle contained in
![]() $\mathcal {S}$
, so
$\mathcal {S}$
, so
![]() $\mathcal {T} \triangle \mathcal {T}^* = \mathcal {S}$
, whence
$\mathcal {T} \triangle \mathcal {T}^* = \mathcal {S}$
, whence
![]() $\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
. If
$\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
. If
![]() $\mathcal {T}$
is a trivial simplicial k-circuit, then
$\mathcal {T}$
is a trivial simplicial k-circuit, then
![]() $K = V(\mathcal {T}) \cap V(\mathcal {T}^*)$
is a face of
$K = V(\mathcal {T}) \cap V(\mathcal {T}^*)$
is a face of
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $K^* = K$
. Since
$K^* = K$
. Since
![]() $*$
is a free involution, it follows that
$*$
is a free involution, it follows that
![]() $K = \emptyset $
and so
$K = \emptyset $
and so
![]() $\mathcal {S}$
is a trivial
$\mathcal {S}$
is a trivial
![]() $\mathbb Z_2$
-irreducible k-cycle, contradicting the hypothesis. Hence,
$\mathbb Z_2$
-irreducible k-cycle, contradicting the hypothesis. Hence,
![]() $\mathcal {T}$
is nontrivial.
$\mathcal {T}$
is nontrivial.
Now suppose that the second alternative in the lemma holds and
![]() $\mathcal {U}$
is a simplicial k-circuit properly contained in
$\mathcal {U}$
is a simplicial k-circuit properly contained in
![]() $\mathcal {S}$
. Then
$\mathcal {S}$
. Then
![]() $\mathcal {S} = \mathcal {U} \sqcup \mathcal {U}^*$
by the same argument as the first paragraph, and
$\mathcal {S} = \mathcal {U} \sqcup \mathcal {U}^*$
by the same argument as the first paragraph, and
![]() $\mathcal {U} \triangle \mathcal {T} = (\mathcal {U}^* \cap \mathcal {T}) \cup (\mathcal {U} \cap \mathcal {T}^*)$
is a
$\mathcal {U} \triangle \mathcal {T} = (\mathcal {U}^* \cap \mathcal {T}) \cup (\mathcal {U} \cap \mathcal {T}^*)$
is a
![]() $*$
-invariant simplicial k-cycle contained in
$*$
-invariant simplicial k-cycle contained in
![]() $\mathcal {S}$
. Therefore, either
$\mathcal {S}$
. Therefore, either
![]() $\mathcal {U} \triangle \mathcal {T} = \emptyset $
and so
$\mathcal {U} \triangle \mathcal {T} = \emptyset $
and so
![]() $\mathcal {U} = \mathcal {T}$
or,
$\mathcal {U} = \mathcal {T}$
or,
![]() $\mathcal {U}\triangle \mathcal {T} = \mathcal {S}$
and so
$\mathcal {U}\triangle \mathcal {T} = \mathcal {S}$
and so
![]() $\mathcal {U} = \mathcal {S} \setminus \mathcal {T} = \mathcal {T}^*$
.
$\mathcal {U} = \mathcal {S} \setminus \mathcal {T} = \mathcal {T}^*$
.
An example illustrating the second alternative in Lemma 5.1 is given in Figure 2.
Lemma 5.2. Suppose that
![]() $(\mathcal {S},*)$
is a
$(\mathcal {S},*)$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle for some
$\mathbb Z_2$
-irreducible k-cycle for some
![]() $k \geq 1$
. Then
$k \geq 1$
. Then
![]() $|V(\mathcal {S})| \geq 2k+2$
with equality if and only if
$|V(\mathcal {S})| \geq 2k+2$
with equality if and only if
![]() $(\mathcal {S},*)$
is a trivial
$(\mathcal {S},*)$
is a trivial
![]() $\mathbb Z_2$
-irreducible k-cycle or
$\mathbb Z_2$
-irreducible k-cycle or
![]() $\mathcal {S}$
is isomorphic to
$\mathcal {S}$
is isomorphic to
![]() $\mathcal {B}_k$
.
$\mathcal {B}_k$
.
Proof. We have
![]() $|V(\mathcal {S})| \geq 2k+2$
since for any
$|V(\mathcal {S})| \geq 2k+2$
since for any
![]() $U \in \mathcal {S}$
, we have
$U \in \mathcal {S}$
, we have
![]() $U \cap U^* = \emptyset $
, and hence,
$U \cap U^* = \emptyset $
, and hence,
![]() $|V(\mathcal {S})| \geq |U \sqcup U^*|=2k+2$
.
$|V(\mathcal {S})| \geq |U \sqcup U^*|=2k+2$
.
Suppose that
![]() $|V(\mathcal {S})| = 2k+2$
. Let
$|V(\mathcal {S})| = 2k+2$
. Let
![]() $V(\mathcal {S})=\{x_i,x_i^*:1\leq i\leq k+1\}$
. If
$V(\mathcal {S})=\{x_i,x_i^*:1\leq i\leq k+1\}$
. If
![]() $\mathcal {S}$
contains two copies of some k-face W, then it follows easily that
$\mathcal {S}$
contains two copies of some k-face W, then it follows easily that
![]() $\mathcal {S} = \{\{ W , W, W^*, W^*\}\}$
, and so
$\mathcal {S} = \{\{ W , W, W^*, W^*\}\}$
, and so
![]() $\mathcal {S}$
is a trivial
$\mathcal {S}$
is a trivial
![]() $\mathbb Z_2$
-irreducible k-cycle. Thus, we may assume that each
$\mathbb Z_2$
-irreducible k-cycle. Thus, we may assume that each
![]() $W\in \mathcal {S}$
has multiplicity one. Then, for each
$W\in \mathcal {S}$
has multiplicity one. Then, for each
![]() $W \in \mathcal {S}$
and
$W \in \mathcal {S}$
and
![]() $w \in W$
, we have
$w \in W$
, we have
![]() $W-w+w^* \in \mathcal {S}$
since
$W-w+w^* \in \mathcal {S}$
since
![]() $W-w$
is contained in at least two k-faces of
$W-w$
is contained in at least two k-faces of
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $*$
is free. It follows that every transversal of
$*$
is free. It follows that every transversal of
![]() $\{ \{x_i,x_i^*\}: 1\leq i\leq k+1\}$
is a k-face of
$\{ \{x_i,x_i^*\}: 1\leq i\leq k+1\}$
is a k-face of
![]() $\mathcal {S}$
, and so,
$\mathcal {S}$
, and so,
![]() $\mathcal {S} \cong \mathcal {B}_k$
.
$\mathcal {S} \cong \mathcal {B}_k$
.
Lemma 5.3. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() $\mathbb Z_2$
-irreducible k-cycle for some
$\mathbb Z_2$
-irreducible k-cycle for some
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $X\subset V(\mathcal {S})$
be an inclusion-minimal
$X\subset V(\mathcal {S})$
be an inclusion-minimal
![]() $\ast $
-invariant vertex separator of
$\ast $
-invariant vertex separator of
![]() $G(\mathcal {S})$
. Suppose
$G(\mathcal {S})$
. Suppose
![]() $|X|\leq 2k$
. Then either
$|X|\leq 2k$
. Then either
![]() $\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
for some simplicial k-circuit
$\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
for some simplicial k-circuit
![]() $\mathcal {T}$
with
$\mathcal {T}$
with
![]() $V(\mathcal {T})\cap V(\mathcal {T}^*)=X$
, or
$V(\mathcal {T})\cap V(\mathcal {T}^*)=X$
, or
![]() $|X|=2k$
and the subgraph of
$|X|=2k$
and the subgraph of
![]() $G(\mathcal {S})$
induced by X is isomorphic to
$G(\mathcal {S})$
induced by X is isomorphic to
![]() $G(\mathcal {B}_{k-1})$
.
$G(\mathcal {B}_{k-1})$
.
Proof. Choose
![]() $V_1, V_2 \subset V(\mathcal {S})$
such that
$V_1, V_2 \subset V(\mathcal {S})$
such that
![]() $V_1 \cap V_2 = X$
,
$V_1 \cap V_2 = X$
,
![]() $G(\mathcal {S}) = G(\mathcal {S})[V_1] \cup G(\mathcal {S})[V_2]$
. Let
$G(\mathcal {S}) = G(\mathcal {S})[V_1] \cup G(\mathcal {S})[V_2]$
. Let
![]() $\mathcal {T}_i = \{W \in \mathcal {S}: W \subset V_i\}$
. Since X is a vertex separator of
$\mathcal {T}_i = \{W \in \mathcal {S}: W \subset V_i\}$
. Since X is a vertex separator of
![]() $G(\mathcal {S})$
, it follows that
$G(\mathcal {S})$
, it follows that
![]() $\mathcal {S} = \mathcal {T}_1 \cup \mathcal {T}_2$
and that
$\mathcal {S} = \mathcal {T}_1 \cup \mathcal {T}_2$
and that
![]() $\mathcal {T}_1, \mathcal {T}_2 \neq \mathcal {S}$
. The hypothesis that X is
$\mathcal {T}_1, \mathcal {T}_2 \neq \mathcal {S}$
. The hypothesis that X is
![]() $*$
-invariant and the fact that
$*$
-invariant and the fact that
![]() $|X| \leq 2k$
imply that, for any
$|X| \leq 2k$
imply that, for any
![]() $W\in \mathcal {S}$
,
$W\in \mathcal {S}$
,
![]() $W\not \subseteq X$
; hence,
$W\not \subseteq X$
; hence,
![]() $\mathcal {T}_1 \cap \mathcal {T}_2 = \emptyset $
. Thus,
$\mathcal {T}_1 \cap \mathcal {T}_2 = \emptyset $
. Thus,
![]() $\mathcal {S} = \mathcal {T}_1 \sqcup \mathcal {T}_2$
,
$\mathcal {S} = \mathcal {T}_1 \sqcup \mathcal {T}_2$
,
![]() $\partial \mathcal {T}_1 = \partial \mathcal {T}_2=:\mathcal {U}$
and
$\partial \mathcal {T}_1 = \partial \mathcal {T}_2=:\mathcal {U}$
and
![]() $V(\mathcal {U}) \subset X$
.
$V(\mathcal {U}) \subset X$
.
Suppose
![]() $\mathcal {U} = \emptyset $
. Then
$\mathcal {U} = \emptyset $
. Then
![]() $\mathcal {T}_i$
is a simplicial k-cycle for
$\mathcal {T}_i$
is a simplicial k-cycle for
![]() $i=1,2$
. Lemma 5.1 now implies that
$i=1,2$
. Lemma 5.1 now implies that
![]() $\mathcal {T}_1$
is a simplicial k-circuit,
$\mathcal {T}_1$
is a simplicial k-circuit,
![]() $\mathcal {T}_2=\mathcal {T}_1^*$
and
$\mathcal {T}_2=\mathcal {T}_1^*$
and
![]() $\mathcal {S}=\mathcal {T}_1\sqcup \mathcal {T}_1^*$
. The minimality of X now gives
$\mathcal {S}=\mathcal {T}_1\sqcup \mathcal {T}_1^*$
. The minimality of X now gives
![]() $V(\mathcal {T}_1)\cap V(\mathcal {T}_1^*)=X$
. Hence, we may assume that
$V(\mathcal {T}_1)\cap V(\mathcal {T}_1^*)=X$
. Hence, we may assume that
![]() $\mathcal {U} \neq \emptyset $
.
$\mathcal {U} \neq \emptyset $
.
The definition of the boundary operator implies that
![]() $\mathcal {U}$
is a simplicial
$\mathcal {U}$
is a simplicial
![]() $(k-1)$
-cycle and each of its facets has multiplicity one. Hence,
$(k-1)$
-cycle and each of its facets has multiplicity one. Hence,
![]() $\mathcal {U} \triangle \mathcal {U}^*$
is a
$\mathcal {U} \triangle \mathcal {U}^*$
is a
![]() $\mathbb {Z}_2$
-symmetric
$\mathbb {Z}_2$
-symmetric
![]() $(k-1)$
-cycle that does not contain a trivial simplicial
$(k-1)$
-cycle that does not contain a trivial simplicial
![]() $(k-1)$
-circuit. Since
$(k-1)$
-circuit. Since
![]() $V(\mathcal {U})\subseteq X$
and X is
$V(\mathcal {U})\subseteq X$
and X is
![]() $*$
-invariant,
$*$
-invariant,
![]() $\mathcal {V}:=\mathcal {U} \triangle \mathcal {U}^*\subseteq 2^X$
. We can now apply Lemma 5.2 and the hypothesis that
$\mathcal {V}:=\mathcal {U} \triangle \mathcal {U}^*\subseteq 2^X$
. We can now apply Lemma 5.2 and the hypothesis that
![]() $|X| \leq 2k$
to
$|X| \leq 2k$
to
![]() $\mathcal {V}$
to deduce that either
$\mathcal {V}$
to deduce that either
![]() $\mathcal {V} = \emptyset $
or
$\mathcal {V} = \emptyset $
or
![]() $\mathcal {V} \cong \mathcal {B}_{k-1}$
.
$\mathcal {V} \cong \mathcal {B}_{k-1}$
.
Suppose
![]() $\mathcal {V} \cong \mathcal {B}_{k-1}$
. Then
$\mathcal {V} \cong \mathcal {B}_{k-1}$
. Then
![]() $|X|=2k$
, and
$|X|=2k$
, and
![]() $\mathcal {V}$
is the
$\mathcal {V}$
is the
![]() $\mathbb Z_2$
-irreducible
$\mathbb Z_2$
-irreducible
![]() $(k-1)$
-cycle consisting of all transversals of the following partition of X:
$(k-1)$
-cycle consisting of all transversals of the following partition of X:
![]() $\{ \{x_1,x_1^*\},\dots ,\{x_k,x_k^*\}\}$
. Hence, every k-subset of X which contains no pair
$\{ \{x_1,x_1^*\},\dots ,\{x_k,x_k^*\}\}$
. Hence, every k-subset of X which contains no pair
![]() $\{x_i,x_i^*\}$
is contained in
$\{x_i,x_i^*\}$
is contained in
![]() $\mathcal {V}$
. Since
$\mathcal {V}$
. Since
![]() $*$
is free and
$*$
is free and
![]() $V(\mathcal {U})\subset X$
, this implies that
$V(\mathcal {U})\subset X$
, this implies that
![]() $\mathcal {U} \subset \mathcal {V}$
. Since
$\mathcal {U} \subset \mathcal {V}$
. Since
![]() $\mathcal {U}\subset \mathcal {V}$
and
$\mathcal {U}\subset \mathcal {V}$
and
![]() $\mathcal {V}=\mathcal {U}\triangle \mathcal {U}^*$
,
$\mathcal {V}=\mathcal {U}\triangle \mathcal {U}^*$
,
![]() $\mathcal {V} = \mathcal {U} \sqcup \mathcal {U}^*$
, and hence,
$\mathcal {V} = \mathcal {U} \sqcup \mathcal {U}^*$
, and hence,
![]() $\mathcal {V}$
is a trivial
$\mathcal {V}$
is a trivial
![]() $\mathbb Z_2$
-irreducible
$\mathbb Z_2$
-irreducible
![]() $(k-1)$
-cycle. This contradicts the assumption that
$(k-1)$
-cycle. This contradicts the assumption that
![]() $\mathcal {V} \cong \mathcal {B}_{k-1}$
.
$\mathcal {V} \cong \mathcal {B}_{k-1}$
.
Hence,
![]() $\mathcal {V}=\mathcal {U} \triangle \mathcal {U}^* = \emptyset $
so
$\mathcal {V}=\mathcal {U} \triangle \mathcal {U}^* = \emptyset $
so
![]() $\mathcal {U}=\mathcal {U}^*$
. Then
$\mathcal {U}=\mathcal {U}^*$
. Then
![]() $\mathcal {U}$
is a
$\mathcal {U}$
is a
![]() $\mathbb {Z}_2$
-symmetric
$\mathbb {Z}_2$
-symmetric
![]() $(k-1)$
-cycle with at most
$(k-1)$
-cycle with at most
![]() $2k$
vertices that does not contain a trivial
$2k$
vertices that does not contain a trivial
![]() $\mathbb Z_2$
-irreducible
$\mathbb Z_2$
-irreducible
![]() $(k-1)$
-cycle. Lemma 5.2 now implies that
$(k-1)$
-cycle. Lemma 5.2 now implies that
![]() $\mathcal {U} \cong \mathcal {B}_{k-1}$
, and hence,
$\mathcal {U} \cong \mathcal {B}_{k-1}$
, and hence,
![]() $G(\mathcal {S})[X]$
is isomorphic to
$G(\mathcal {S})[X]$
is isomorphic to
![]() $G(\mathcal {B}_{k-1})$
.
$G(\mathcal {B}_{k-1})$
.
5.2
 $\mathbb {Z}_2$
-symmetric Fogelsanger decomposition
$\mathbb {Z}_2$
-symmetric Fogelsanger decomposition
We next adapt Fogelsanger’s decomposition technique for simplicial k-circuits to the context of
![]() $\mathbb Z_2$
-irreducible k-cycles. Let
$\mathbb Z_2$
-irreducible k-cycles. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() $\mathbb Z_2$
-irreducible k-cycle and put
$\mathbb Z_2$
-irreducible k-cycle and put
![]() $G = (V,E)=G(\mathcal {S})$
. Suppose that
$G = (V,E)=G(\mathcal {S})$
. Suppose that
![]() $xy \in E$
and
$xy \in E$
and
![]() $xy^* \not \in E$
. Then
$xy^* \not \in E$
. Then
![]() $x^*y^* \in E$
,
$x^*y^* \in E$
,
![]() $x^*y \not \in E$
and
$x^*y \not \in E$
and
![]() $(\mathcal {S}/xy)/x^*y^*$
is a
$(\mathcal {S}/xy)/x^*y^*$
is a
![]() $\mathbb {Z}_2$
-symmetric k-cycle under the free simplicial involution induced by
$\mathbb {Z}_2$
-symmetric k-cycle under the free simplicial involution induced by
![]() $*$
on
$*$
on
![]() $V-y-y^*$
. Recall that, for a face F of
$V-y-y^*$
. Recall that, for a face F of
![]() $\mathcal {S}$
, the antistar of F in
$\mathcal {S}$
, the antistar of F in
![]() $\mathcal {S}$
is given by
$\mathcal {S}$
is given by
![]() $\mathrm {Ast}(F) = \{ U \in \mathcal {S}: F \not \subset U\}$
. Observe that there is a bijection
$\mathrm {Ast}(F) = \{ U \in \mathcal {S}: F \not \subset U\}$
. Observe that there is a bijection
![]() $\gamma : \mathrm {Ast}(\{x,y\}) \cap \mathrm {Ast}(\{x^*,y^*\}) \rightarrow (\mathcal {S}/xy)/x^*y^*$
given by
$\gamma : \mathrm {Ast}(\{x,y\}) \cap \mathrm {Ast}(\{x^*,y^*\}) \rightarrow (\mathcal {S}/xy)/x^*y^*$
given by
![]() $\gamma (U) = U$
if
$\gamma (U) = U$
if
![]() $y,y^* \not \in U$
,
$y,y^* \not \in U$
,
![]() $\gamma (U) = U -y+x$
if
$\gamma (U) = U -y+x$
if
![]() $ y \in U$
, and
$ y \in U$
, and
![]() $\gamma (U) = U -y^*+x^*$
if
$\gamma (U) = U -y^*+x^*$
if
![]() $ y^* \in U$
.
$ y^* \in U$
.
Choose a partition
![]() $\{\mathcal {S}_1',\mathcal {S}_2',\ldots ,\mathcal {S}_m'\}$
of
$\{\mathcal {S}_1',\mathcal {S}_2',\ldots ,\mathcal {S}_m'\}$
of
![]() $(\mathcal {S}/xy)/x^*y^*$
into
$(\mathcal {S}/xy)/x^*y^*$
into
![]() $\mathbb Z_2$
-irreducible k-cycles. For
$\mathbb Z_2$
-irreducible k-cycles. For
![]() $1\leq i \leq m$
, let
$1\leq i \leq m$
, let
![]() $\mathcal {S}_i = \gamma ^{-1}(\mathcal {S}^{\prime }_i)$
,
$\mathcal {S}_i = \gamma ^{-1}(\mathcal {S}^{\prime }_i)$
,
and
We say that
![]() $(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
is a
$(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
is a
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decomposition for
$\mathbb {Z}_2$
-symmetric Fogelsanger decomposition for
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $xy$
. Note that a
$xy$
. Note that a
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decomposition at
$\mathbb {Z}_2$
-symmetric Fogelsanger decomposition at
![]() $xy$
is defined only when
$xy$
is defined only when
![]() $xy^*\notin E$
.
$xy^*\notin E$
.
The
![]() $\mathbb Z_2$
-irreducible
$\mathbb Z_2$
-irreducible
![]() $2$
-cycle in Figure 2 can be used to illustrate this construction. We have
$2$
-cycle in Figure 2 can be used to illustrate this construction. We have
![]() $(\mathcal {S}/v_2v_4)/v_2^*v_4^*=\mathcal {S}_1'\sqcup \mathcal {S}_2'$
, where
$(\mathcal {S}/v_2v_4)/v_2^*v_4^*=\mathcal {S}_1'\sqcup \mathcal {S}_2'$
, where
![]() $\mathcal {S}_1'$
is a trivial
$\mathcal {S}_1'$
is a trivial
![]() $\mathbb Z_2$
-irreducible
$\mathbb Z_2$
-irreducible
![]() $2$
-cycle consisting of consisting of two copies of
$2$
-cycle consisting of consisting of two copies of
![]() $\{v_1,v_2,v_3\}$
and two copies of
$\{v_1,v_2,v_3\}$
and two copies of
![]() $\{v_1^*,v_2^*,v_3^*\}$
, and
$\{v_1^*,v_2^*,v_3^*\}$
, and
![]() $\mathcal {S}_2'$
is a trivial
$\mathcal {S}_2'$
is a trivial
![]() $\mathbb Z_2$
-irreducible
$\mathbb Z_2$
-irreducible
![]() $2$
-cycle consisting of consisting of two copies of
$2$
-cycle consisting of consisting of two copies of
![]() $\{v_1^*,v_2,v_3\}$
and two copies of
$\{v_1^*,v_2,v_3\}$
and two copies of
![]() $\{v_1,v_2^*,v_3^*\}$
. The above definitions now give
$\{v_1,v_2^*,v_3^*\}$
. The above definitions now give
![]() $\mathcal {S}_1=\mathcal {T}_1\cup \mathcal {T}_1^*$
, where
$\mathcal {S}_1=\mathcal {T}_1\cup \mathcal {T}_1^*$
, where
![]() $\mathcal {T}_1=\{\{v_1,v_2,v_3\},\{v_1,v_2,v_4\},\{v_1,v_3,v_4\}\}$
,
$\mathcal {T}_1=\{\{v_1,v_2,v_3\},\{v_1,v_2,v_4\},\{v_1,v_3,v_4\}\}$
,
![]() $\mathcal {S}_1^\dagger =\{\{v_2,v_3,v_4\}\}$
and
$\mathcal {S}_1^\dagger =\{\{v_2,v_3,v_4\}\}$
and
![]() $\mathcal {S}_1^+$
is the disjoint union of the boundary complexes of two tetrahedra on
$\mathcal {S}_1^+$
is the disjoint union of the boundary complexes of two tetrahedra on
![]() $\{v_1,v_2,v_3,v_4\}$
and
$\{v_1,v_2,v_3,v_4\}$
and
![]() $\{v_1^*,v_2^*,v_3^*,v_4^*\}$
, respectively. Similarly,
$\{v_1^*,v_2^*,v_3^*,v_4^*\}$
, respectively. Similarly,
![]() $\mathcal {S}_2^+$
is the disjoint union of the boundary complexes of two tetrahedra on
$\mathcal {S}_2^+$
is the disjoint union of the boundary complexes of two tetrahedra on
![]() $\{v_1^*,v_2,v_3,v_4\}$
and
$\{v_1^*,v_2,v_3,v_4\}$
and
![]() $\{v_1,v_2^*,v_3^*,v_4^*\}$
, respectively.
$\{v_1,v_2^*,v_3^*,v_4^*\}$
, respectively.
The properties of
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decompositions given in the following lemma are analogous to those for Fogelsanger decompositions given in Lemma 3.1.
$\mathbb {Z}_2$
-symmetric Fogelsanger decompositions given in the following lemma are analogous to those for Fogelsanger decompositions given in Lemma 3.1.
Lemma 5.4. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() $\mathbb Z_2$
-irreducible k-cycle for
$\mathbb Z_2$
-irreducible k-cycle for
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $xy\in E(\mathcal {S})$
with
$xy\in E(\mathcal {S})$
with
![]() $xy^*\not \in E(\mathcal {S})$
. Suppose that
$xy^*\not \in E(\mathcal {S})$
. Suppose that
![]() $(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
is a
$(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
is a
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decomposition for
$\mathbb {Z}_2$
-symmetric Fogelsanger decomposition for
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $xy$
. Let
$xy$
. Let
![]() $G(\mathcal {S}_i^+)=(V_i,E_i)$
for
$G(\mathcal {S}_i^+)=(V_i,E_i)$
for
![]() $1 \leq i \leq m$
. Then,
$1 \leq i \leq m$
. Then,
-
1.
 $xy, x^*y^* \in E_i$
for
$xy, x^*y^* \in E_i$
for
 $1 \leq i \leq m$
;
$1 \leq i \leq m$
; -
2.
 $\bigcup _{i=1}^m E_i = E$
and
$\bigcup _{i=1}^m E_i = E$
and
 $\bigcup _{i=1}^m V_i = V$
;
$\bigcup _{i=1}^m V_i = V$
; -
3.
 $(\mathcal {S}_i^+/xy)/x^*y^*$
is a
$(\mathcal {S}_i^+/xy)/x^*y^*$
is a
 $\mathbb Z_2$
-irreducible k-cycle for
$\mathbb Z_2$
-irreducible k-cycle for
 $1 \leq i \leq m$
;
$1 \leq i \leq m$
; -
4.
 $\mathcal {S}_i^+$
is a nontrivial
$\mathcal {S}_i^+$
is a nontrivial
 $\mathbb Z_2$
-irreducible k-cycle, and each
$\mathbb Z_2$
-irreducible k-cycle, and each
 $K \in \mathcal {S}_i^+\setminus \mathcal {S}$
is a clique of G that either contains
$K \in \mathcal {S}_i^+\setminus \mathcal {S}$
is a clique of G that either contains
 $\{x,y\}$
or contains
$\{x,y\}$
or contains
 $\{x^*,y^*\}$
;
$\{x^*,y^*\}$
; -
5. if
 $U\in \mathcal {S}$
and U contains neither
$U\in \mathcal {S}$
and U contains neither
 $\{x,y\}$
nor
$\{x,y\}$
nor
 $\{x^*,y^*\}$
, then U belongs to a unique
$\{x^*,y^*\}$
, then U belongs to a unique
 $\mathcal {S}_i^+$
;
$\mathcal {S}_i^+$
; -
6.
 $\mathcal {S} = \triangle _{k=1}^m \mathcal {S}_k^+$
;
$\mathcal {S} = \triangle _{k=1}^m \mathcal {S}_k^+$
; -
7. for all proper subsets I of
 $\{1,\dots ,m\}$
, there exists
$\{1,\dots ,m\}$
, there exists
 $j \in \{1,\dots ,m\} \setminus I$
such that
$j \in \{1,\dots ,m\} \setminus I$
such that
 $\mathcal {S}_{j}^+ \cap \triangle _{i \in I}\mathcal {S}_i^+$
is nonempty.
$\mathcal {S}_{j}^+ \cap \triangle _{i \in I}\mathcal {S}_i^+$
is nonempty.
Proof. We adopt the definitions of
![]() $\mathcal {S}^{\prime }_i$
,
$\mathcal {S}^{\prime }_i$
,
![]() $\mathcal {S}_i$
and
$\mathcal {S}_i$
and
![]() $\mathcal {S}_i^\dagger $
given in our description of a
$\mathcal {S}_i^\dagger $
given in our description of a
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decomposition. Note that for all
$\mathbb {Z}_2$
-symmetric Fogelsanger decomposition. Note that for all
![]() $1\leq i\leq m$
,
$1\leq i\leq m$
,
![]() $\mathcal {S}_i \neq \mathcal {S}$
since
$\mathcal {S}_i \neq \mathcal {S}$
since
![]() $xy \not \in E(\mathcal {S}_i)$
. Suppose
$xy \not \in E(\mathcal {S}_i)$
. Suppose
![]() $F \in \partial \mathcal {S}_i$
. Then
$F \in \partial \mathcal {S}_i$
. Then
![]() $F \cap \{x,y,x^*,y^*\} \neq \emptyset $
otherwise
$F \cap \{x,y,x^*,y^*\} \neq \emptyset $
otherwise
![]() $F \in \partial S$
, contradicting the fact that
$F \in \partial S$
, contradicting the fact that
![]() $\mathcal {S}$
is a simplicial k-cycle. For
$\mathcal {S}$
is a simplicial k-cycle. For
![]() $v \in \{x,y,x^*,y^*\}$
, let
$v \in \{x,y,x^*,y^*\}$
, let
![]() $\mathcal {U}_v = \{U \in \partial \mathcal {S}_i: v \in U\}$
. Since no edge in
$\mathcal {U}_v = \{U \in \partial \mathcal {S}_i: v \in U\}$
. Since no edge in
![]() $E(\mathcal {S}_i)$
joins two vertices of
$E(\mathcal {S}_i)$
joins two vertices of
![]() $\{x,y,x^*,y^*\}$
, we have
$\{x,y,x^*,y^*\}$
, we have
![]() $\partial \mathcal {S}_i = \mathcal {U}_x \sqcup \mathcal {U}_y \sqcup \mathcal {U}_{x^*} \sqcup \mathcal {U}_{y^*}$
. Furthermore, since
$\partial \mathcal {S}_i = \mathcal {U}_x \sqcup \mathcal {U}_y \sqcup \mathcal {U}_{x^*} \sqcup \mathcal {U}_{y^*}$
. Furthermore, since
![]() $\partial (\mathcal {S}_i/xy)/x^*y^* = \partial \mathcal {S}^{\prime }_i = \emptyset $
, it follows that
$\partial (\mathcal {S}_i/xy)/x^*y^* = \partial \mathcal {S}^{\prime }_i = \emptyset $
, it follows that
and
In particular,
Also,
![]() $*$
induces a bijection
$*$
induces a bijection
![]() $\mathcal {U}_x \rightarrow \mathcal {U}_{x^*}$
, and hence,
$\mathcal {U}_x \rightarrow \mathcal {U}_{x^*}$
, and hence,
Now if
![]() $xy \not \in \mathcal {S}_i^+$
, then
$xy \not \in \mathcal {S}_i^+$
, then
![]() $\mathcal {S}^\dagger _i =\emptyset $
, and it follows from (5.5) that
$\mathcal {S}^\dagger _i =\emptyset $
, and it follows from (5.5) that
![]() $\partial \mathcal {S}_i = \emptyset $
, contradicting the fact that
$\partial \mathcal {S}_i = \emptyset $
, contradicting the fact that
![]() $\mathcal {S}$
is a
$\mathcal {S}$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle and
$\mathbb Z_2$
-irreducible k-cycle and
![]() $\emptyset \neq \mathcal {S}_i \subsetneq \mathcal {S}$
. So
$\emptyset \neq \mathcal {S}_i \subsetneq \mathcal {S}$
. So
![]() $xy \in E(\mathcal {S}_i^+)$
, and since
$xy \in E(\mathcal {S}_i^+)$
, and since
![]() $\mathcal {S}_i^+$
is
$\mathcal {S}_i^+$
is
![]() $*$
-invariant,
$*$
-invariant,
![]() $x^*y^* \in E(\mathcal {S}_i^+)$
, proving (1).
$x^*y^* \in E(\mathcal {S}_i^+)$
, proving (1).
The definition of
![]() $\mathcal {S}_i^+$
implies that
$\mathcal {S}_i^+$
implies that
![]() $(\mathcal {S}_i^+/xy)/x^*y^* = \mathcal {S}^{\prime }_i$
. Since
$(\mathcal {S}_i^+/xy)/x^*y^* = \mathcal {S}^{\prime }_i$
. Since
![]() $\mathcal {S}_i'$
is a
$\mathcal {S}_i'$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle, this gives (3).
$\mathbb Z_2$
-irreducible k-cycle, this gives (3).
Claim 5.5.
![]() $\partial ( \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*) = \partial \mathcal {S}_i$
.
$\partial ( \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*) = \partial \mathcal {S}_i$
.
Proof of claim.
From (5.5) and the definition of
![]() $\mathcal {S}_i^\dagger $
, it follows that for
$\mathcal {S}_i^\dagger $
, it follows that for
![]() $0 \leq s \leq k-1$
, the map
$0 \leq s \leq k-1$
, the map
![]() $F \mapsto F+y$
is a bijection between the set of s-faces of
$F \mapsto F+y$
is a bijection between the set of s-faces of
![]() $\mathcal {U}_x$
that contain x and the set of
$\mathcal {U}_x$
that contain x and the set of
![]() $(s+1)$
-faces of
$(s+1)$
-faces of
![]() $\mathcal {S}^\dagger _i$
that contain
$\mathcal {S}^\dagger _i$
that contain
![]() $\{x,y\}$
. Since
$\{x,y\}$
. Since
![]() $\partial \mathcal {S}_i$
is a simplicial
$\partial \mathcal {S}_i$
is a simplicial
![]() $(k-1)$
-cycle, every
$(k-1)$
-cycle, every
![]() $(k-2)$
-face of
$(k-2)$
-face of
![]() $\mathcal {U}_x$
that contains x belongs to an even number of
$\mathcal {U}_x$
that contains x belongs to an even number of
![]() $(k-1)$
-faces of
$(k-1)$
-faces of
![]() $\mathcal {U}_x$
. Therefore, every
$\mathcal {U}_x$
. Therefore, every
![]() $(k-1)$
-face of
$(k-1)$
-face of
![]() $\mathcal {S}_i^\dagger $
that contains
$\mathcal {S}_i^\dagger $
that contains
![]() $\{x,y\}$
belongs to an even number of k-faces of
$\{x,y\}$
belongs to an even number of k-faces of
![]() $\mathcal {S}_i^\dagger $
. Hence,
$\mathcal {S}_i^\dagger $
. Hence,
![]() $\partial \mathcal {S}_i^\dagger = \{K-x: K \in \mathcal {S}_i^\dagger \} \cup \{K-y: K \in \mathcal {S}_i^\dagger \} = \mathcal {U}_y \sqcup \mathcal {U}_x$
. By symmetry,
$\partial \mathcal {S}_i^\dagger = \{K-x: K \in \mathcal {S}_i^\dagger \} \cup \{K-y: K \in \mathcal {S}_i^\dagger \} = \mathcal {U}_y \sqcup \mathcal {U}_x$
. By symmetry,
![]() $\partial ( (\mathcal {S}_i^\dagger )^*) = \mathcal {U}_{y^*} \sqcup \mathcal {U}_{x^*}$
. Therefore,
$\partial ( (\mathcal {S}_i^\dagger )^*) = \mathcal {U}_{y^*} \sqcup \mathcal {U}_{x^*}$
. Therefore,
![]() $\partial \mathcal {S}_i = \mathcal {U}_x \sqcup \mathcal {U}_y \sqcup \mathcal {U}_{x^*} \sqcup \mathcal {U}_{y^*}=\partial ( \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*) $
.
$\partial \mathcal {S}_i = \mathcal {U}_x \sqcup \mathcal {U}_y \sqcup \mathcal {U}_{x^*} \sqcup \mathcal {U}_{y^*}=\partial ( \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*) $
.
Since
![]() $\mathcal {S}_i^+ = \mathcal {S}_i \triangle ( \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*)$
, Claim 5.5 implies that
$\mathcal {S}_i^+ = \mathcal {S}_i \triangle ( \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*)$
, Claim 5.5 implies that
![]() $\partial \mathcal {S}_i^+ = \emptyset $
, and hence,
$\partial \mathcal {S}_i^+ = \emptyset $
, and hence,
![]() $\mathcal {S}_i^+$
is a
$\mathcal {S}_i^+$
is a
![]() ${\mathbb Z}_2$
-symmetric k-cycle.
${\mathbb Z}_2$
-symmetric k-cycle.
Suppose
![]() $\mathcal {T}\subseteq \mathcal {S}_i^+$
is a
$\mathcal {T}\subseteq \mathcal {S}_i^+$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle. If
$\mathbb Z_2$
-irreducible k-cycle. If
![]() $xy, x^*y^* \not \in E(\mathcal {T})$
, then
$xy, x^*y^* \not \in E(\mathcal {T})$
, then
![]() $\mathcal {T} \subsetneq \mathcal {S}$
, contradicting the fact that
$\mathcal {T} \subsetneq \mathcal {S}$
, contradicting the fact that
![]() $\mathcal {S}$
is a
$\mathcal {S}$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle. So
$\mathbb Z_2$
-irreducible k-cycle. So
![]() $xy,x^*y^* \in E(\mathcal {T})$
. Now
$xy,x^*y^* \in E(\mathcal {T})$
. Now
![]() $(\mathcal {T}/xy)/x^*y^*$
is a nonempty
$(\mathcal {T}/xy)/x^*y^*$
is a nonempty
![]() ${\mathbb Z}_2$
-symmetric k-cycle contained in the
${\mathbb Z}_2$
-symmetric k-cycle contained in the
![]() $\mathbb Z_2$
-irreducible k-cycle
$\mathbb Z_2$
-irreducible k-cycle
![]() $\mathcal {S}^{\prime }_i$
. Hence,
$\mathcal {S}^{\prime }_i$
. Hence,
![]() $(\mathcal {T}/xy)/x^*y^*=\mathcal {S}_i'$
and
$(\mathcal {T}/xy)/x^*y^*=\mathcal {S}_i'$
and
![]() $\mathcal {S}_i\subseteq \mathcal {T}$
. Since
$\mathcal {S}_i\subseteq \mathcal {T}$
. Since
![]() $\partial \mathcal {T} = \emptyset $
, it follows that
$\partial \mathcal {T} = \emptyset $
, it follows that
![]() $\mathcal {T} \supset \mathcal {S}_i^\dagger $
, and so
$\mathcal {T} \supset \mathcal {S}_i^\dagger $
, and so
![]() $\mathcal {T} = \mathcal {S}_i^+$
. Hence,
$\mathcal {T} = \mathcal {S}_i^+$
. Hence,
![]() $\mathcal {S}_i^+$
is a
$\mathcal {S}_i^+$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle, which is nontrivial by (3). Since
$\mathbb Z_2$
-irreducible k-cycle, which is nontrivial by (3). Since
![]() $\mathcal {S}_i^+\setminus \mathcal {S} \subset \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*$
, each
$\mathcal {S}_i^+\setminus \mathcal {S} \subset \mathcal {S}_i^\dagger \cup (\mathcal {S}_i^\dagger )^*$
, each
![]() $K \in \mathcal {S}_i^+\setminus \mathcal {S}$
is a clique of G that either contains
$K \in \mathcal {S}_i^+\setminus \mathcal {S}$
is a clique of G that either contains
![]() $\{x,y\}$
or contains
$\{x,y\}$
or contains
![]() $\{x^*,y^*\}$
. This completes the proof of (4).
$\{x^*,y^*\}$
. This completes the proof of (4).
If
![]() $U\in \mathcal {S}$
contains neither
$U\in \mathcal {S}$
contains neither
![]() $\{x,y\}$
nor
$\{x,y\}$
nor
![]() $\{x^*,y^*\}$
, then U is an element of
$\{x^*,y^*\}$
, then U is an element of
![]() $\mathcal {S}_i$
for a unique i, proving (5).
$\mathcal {S}_i$
for a unique i, proving (5).
We next prove (6). Suppose, for a contradiction, that
![]() $\mathcal {R}= \mathcal {S} \triangle \left (\triangle _{i=1}^m \mathcal {S}_i^+\right )\neq \emptyset $
and choose
$\mathcal {R}= \mathcal {S} \triangle \left (\triangle _{i=1}^m \mathcal {S}_i^+\right )\neq \emptyset $
and choose
![]() $U \in \mathcal {R}$
. By (5), either
$U \in \mathcal {R}$
. By (5), either
![]() $\{x,y\} \subset U$
or
$\{x,y\} \subset U$
or
![]() $\{x^*,y^*\} \subset U$
. Suppose
$\{x^*,y^*\} \subset U$
. Suppose
![]() $\{x,y\} \subset U$
(a similar argument works for the other case). Now
$\{x,y\} \subset U$
(a similar argument works for the other case). Now
![]() $\mathcal {R}$
is a simplicial k-cycle, and since
$\mathcal {R}$
is a simplicial k-cycle, and since
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\mathcal {S}_i^+, 1\leq i\leq m$
, are all nontrivial
$\mathcal {S}_i^+, 1\leq i\leq m$
, are all nontrivial
![]() $\mathbb Z_2$
-irreducible k-cycles,
$\mathbb Z_2$
-irreducible k-cycles,
![]() $\mathcal {R}$
does not contain any trivial simplicial k-circuit. It follows that there is some
$\mathcal {R}$
does not contain any trivial simplicial k-circuit. It follows that there is some
![]() $U' \in \mathcal {R}$
such that
$U' \in \mathcal {R}$
such that
![]() $U \cap U' = U -x$
. By (5),
$U \cap U' = U -x$
. By (5),
![]() $U'$
must contain
$U'$
must contain
![]() $\{x^*,y^*\}$
, and so
$\{x^*,y^*\}$
, and so
![]() $yy^* \in E(\mathcal {R}) \subset E(\mathcal {S})$
, contradicting the assumption that
$yy^* \in E(\mathcal {R}) \subset E(\mathcal {S})$
, contradicting the assumption that
![]() $*$
is a simplicial involution on
$*$
is a simplicial involution on
![]() $\mathcal {S}$
. Therefore,
$\mathcal {S}$
. Therefore,
![]() $\mathcal {R}$
must be empty – this proves (6).
$\mathcal {R}$
must be empty – this proves (6).
To verify (7), we suppose, for a contradiction, that there exists a proper subset I of
![]() $\{1,\dots ,m\}$
such that
$\{1,\dots ,m\}$
such that
![]() $\mathcal {S}_j^+ \cap \triangle _{i \in I} \mathcal {S}_i^+ = \emptyset $
for all
$\mathcal {S}_j^+ \cap \triangle _{i \in I} \mathcal {S}_i^+ = \emptyset $
for all
![]() $j \in J = \{1,\dots ,m\} \setminus I$
. Then, by (6),
$j \in J = \{1,\dots ,m\} \setminus I$
. Then, by (6),
![]() $\mathcal {S} = \triangle _{i=1}^m \mathcal {S}_i^+ = \triangle _{i \in I} \mathcal {S}_i^+ \sqcup \triangle _{j \in J} \mathcal {S}_j^+$
. This yields a partition of
$\mathcal {S} = \triangle _{i=1}^m \mathcal {S}_i^+ = \triangle _{i \in I} \mathcal {S}_i^+ \sqcup \triangle _{j \in J} \mathcal {S}_j^+$
. This yields a partition of
![]() $\mathcal {S}$
into two
$\mathcal {S}$
into two
![]() ${\mathbb Z}_2$
-symmetric k-cycles, contradicting the hypothesis that
${\mathbb Z}_2$
-symmetric k-cycles, contradicting the hypothesis that
![]() $\mathcal {S}$
is a
$\mathcal {S}$
is a
![]() $\mathbb Z_2$
-irreducible k-cycle. This proves (7).
$\mathbb Z_2$
-irreducible k-cycle. This proves (7).
We can now complete the proof of the lemma by verifying (2). Observe that if
![]() $uv \in E(\mathcal {S})$
and
$uv \in E(\mathcal {S})$
and
![]() $uv\not \in \{xy,x^*y^*\}$
, then since
$uv\not \in \{xy,x^*y^*\}$
, then since
![]() $\mathcal {S}$
is a nontrivial
$\mathcal {S}$
is a nontrivial
![]() $\mathbb Z_2$
-irreducible k-cycle and
$\mathbb Z_2$
-irreducible k-cycle and
![]() $xy^*,x^*y\not \in E(\mathcal {S})$
, there is some
$xy^*,x^*y\not \in E(\mathcal {S})$
, there is some
![]() $U \in \mathcal {S}$
such that
$U \in \mathcal {S}$
such that
![]() $u,v \in U$
and
$u,v \in U$
and
![]() $\{x,y\}, \{x^*,y^*\} \not \subset U$
. By (5),
$\{x,y\}, \{x^*,y^*\} \not \subset U$
. By (5),
![]() $uv \in E(\mathcal {S}_i^+)$
for some i. Using this, together with (1), we see that
$uv \in E(\mathcal {S}_i^+)$
for some i. Using this, together with (1), we see that
![]() $\bigcup _{i = 1}^m E(\mathcal {S}_i^+) = E$
. Since
$\bigcup _{i = 1}^m E(\mathcal {S}_i^+) = E$
. Since
![]() $G(\mathcal {S})$
has no isolated vertices, this implies that
$G(\mathcal {S})$
has no isolated vertices, this implies that
![]() $\bigcup _{i=1}^m V(\mathcal {S}_i^+) = V$
. This proves (2).
$\bigcup _{i=1}^m V(\mathcal {S}_i^+) = V$
. This proves (2).
We need one more additional property of
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decompositions.
$\mathbb {Z}_2$
-symmetric Fogelsanger decompositions.
Lemma 5.6. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() $\mathbb Z_2$
-irreducible k-cycle and
$\mathbb Z_2$
-irreducible k-cycle and
![]() $xy\in E(\mathcal {S})$
with
$xy\in E(\mathcal {S})$
with
![]() $xy^*\not \in E(\mathcal {S})$
. Let
$xy^*\not \in E(\mathcal {S})$
. Let
![]() $\{\mathcal {S}_1',\mathcal {S}_2',\ldots ,\mathcal {S}_m'\}$
be a partition of
$\{\mathcal {S}_1',\mathcal {S}_2',\ldots ,\mathcal {S}_m'\}$
be a partition of
![]() $(\mathcal {S}/xy)/x^*y^*$
into
$(\mathcal {S}/xy)/x^*y^*$
into
![]() $\mathbb Z_2$
-irreducible k-cycles and
$\mathbb Z_2$
-irreducible k-cycles and
![]() $(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
be the
$(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
be the
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decomposition for
$\mathbb {Z}_2$
-symmetric Fogelsanger decomposition for
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $xy$
corresponding to this partition. Suppose
$xy$
corresponding to this partition. Suppose
![]() $\mathcal {S}_j'=\mathcal {T}_j'\sqcup \mathcal {T}_j^{\prime *}$
for some simplicial k-circuit
$\mathcal {S}_j'=\mathcal {T}_j'\sqcup \mathcal {T}_j^{\prime *}$
for some simplicial k-circuit
![]() $\mathcal {T}_j'$
with
$\mathcal {T}_j'$
with
![]() $|V(\mathcal {T}_j')\cap V(\mathcal {T}_j^{\prime *})|\leq 2k-2$
. Then
$|V(\mathcal {T}_j')\cap V(\mathcal {T}_j^{\prime *})|\leq 2k-2$
. Then
![]() $\mathcal {S}_j^+=\mathcal {T}_j\sqcup \mathcal {T}_j^*$
for some simplicial k-circuit
$\mathcal {S}_j^+=\mathcal {T}_j\sqcup \mathcal {T}_j^*$
for some simplicial k-circuit
![]() $\mathcal {T}_j$
with
$\mathcal {T}_j$
with
![]() $|V(\mathcal {T}_j)\cap V(\mathcal {T}_j^*)|\leq |V(\mathcal {T}_j')\cap V(\mathcal {T}_j^{\prime *})|+2$
.
$|V(\mathcal {T}_j)\cap V(\mathcal {T}_j^*)|\leq |V(\mathcal {T}_j')\cap V(\mathcal {T}_j^{\prime *})|+2$
.
Proof. Since
![]() $\mathcal {S}_j'=(\mathcal {S}_j/xy)/x^*y^*$
, the hypothesis that
$\mathcal {S}_j'=(\mathcal {S}_j/xy)/x^*y^*$
, the hypothesis that
![]() $|V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})| \leq 2k-2$
implies that
$|V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})| \leq 2k-2$
implies that
![]() $G(\mathcal {S}_j^+)$
has a
$G(\mathcal {S}_j^+)$
has a
![]() $*$
-invariant vertex separator X with
$*$
-invariant vertex separator X with
![]() $V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})\subseteq X\subseteq V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})+y+y^*$
. In particular,
$V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})\subseteq X\subseteq V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})+y+y^*$
. In particular,
![]() $|X|\leq 2k$
. By Lemma 5.3, either
$|X|\leq 2k$
. By Lemma 5.3, either
![]() $\mathcal {S}_j^+=\mathcal {T}_j\sqcup \mathcal {T}_j^*$
for some simplicial k-circuit
$\mathcal {S}_j^+=\mathcal {T}_j\sqcup \mathcal {T}_j^*$
for some simplicial k-circuit
![]() $\mathcal {T}_j$
with
$\mathcal {T}_j$
with
![]() $V(\mathcal {T}_j)\cap V(\mathcal {T}_j^*)=X$
or
$V(\mathcal {T}_j)\cap V(\mathcal {T}_j^*)=X$
or
![]() $G(\mathcal {S}_j^+)[X]$
is isomorphic to
$G(\mathcal {S}_j^+)[X]$
is isomorphic to
![]() $G(\mathcal {B}_{k-1})$
. In the former case, we have the statement. So let us assume the latter case. Then we have
$G(\mathcal {B}_{k-1})$
. In the former case, we have the statement. So let us assume the latter case. Then we have
![]() $|X|=2k$
, and hence,
$|X|=2k$
, and hence,
![]() $|X|=|V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})|+2$
, so
$|X|=|V(\mathcal {T}') \cap V(\mathcal {T}^{\prime *})|+2$
, so
![]() $\{x,y,x^*,y^*\}\subseteq X$
. Together with
$\{x,y,x^*,y^*\}\subseteq X$
. Together with
![]() $G[X] \cong G(\mathcal {B}_{k-1})$
, this implies that
$G[X] \cong G(\mathcal {B}_{k-1})$
, this implies that
![]() $xy^* \in E$
, contradicting an hypothesis of the lemma.
$xy^* \in E$
, contradicting an hypothesis of the lemma.
5.3 Main rigidity theorem
We can now establish our main result. We begin with the following special case.
Lemma 5.7. Let
![]() $\Gamma =\Gamma _{t,k+1}$
for
$\Gamma =\Gamma _{t,k+1}$
for
![]() $0 \leq t \leq k$
. Let
$0 \leq t \leq k$
. Let
![]() $(\mathcal {S},\ast )$
be a
$(\mathcal {S},\ast )$
be a
![]() $\mathbb {Z}_2$
-irreducible k-cycle such that
$\mathbb {Z}_2$
-irreducible k-cycle such that
![]() $\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
for some simplicial k-circuit
$\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
for some simplicial k-circuit
![]() $\mathcal {T}$
with
$\mathcal {T}$
with
![]() $h:=|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq 2k$
. Then
$h:=|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq 2k$
. Then
![]() $(G(\mathcal {S}),\ast )$
is
$(G(\mathcal {S}),\ast )$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() ${\mathbb R}^{k+1}$
if and only if
${\mathbb R}^{k+1}$
if and only if
![]() $h\geq \max \{2(k-t),k+1,2t\}$
.
$h\geq \max \{2(k-t),k+1,2t\}$
.
Proof. To prove sufficiency, we suppose
![]() $h \geq \max \{2(k-t),k+1,2t\}$
. Let
$h \geq \max \{2(k-t),k+1,2t\}$
. Let
![]() $*_T$
be the non-adjacent vertex pairing induced on
$*_T$
be the non-adjacent vertex pairing induced on
![]() $V(\mathcal {T})\cap V(\mathcal {T}^*)$
by
$V(\mathcal {T})\cap V(\mathcal {T}^*)$
by
![]() $*$
. Since
$*$
. Since
![]() $h\leq 2k$
, we can apply Theorem 4.5 to
$h\leq 2k$
, we can apply Theorem 4.5 to
![]() $(G(\mathcal {T}),\ast _T)$
to deduce that
$(G(\mathcal {T}),\ast _T)$
to deduce that
![]() $(G(\mathcal {T}),\ast _T)$
is
$(G(\mathcal {T}),\ast _T)$
is
![]() $\Gamma $
-rigid. Symmetrically,
$\Gamma $
-rigid. Symmetrically,
![]() $(G(\mathcal {T}^*),\ast _T)$
is
$(G(\mathcal {T}^*),\ast _T)$
is
![]() $\Gamma $
-rigid. Now Theorem 2.8 (the gluing theorem) implies that the union of
$\Gamma $
-rigid. Now Theorem 2.8 (the gluing theorem) implies that the union of
![]() $(G(\mathcal {T}),\ast _T)$
and
$(G(\mathcal {T}),\ast _T)$
and
![]() $(G(\mathcal {T}^*),\ast _T)$
is
$(G(\mathcal {T}^*),\ast _T)$
is
![]() $\Gamma $
-rigid if
$\Gamma $
-rigid if
![]() $h\geq (k+1)+h-1-\min \{h/2,d-t\}-\min \{h/2-1,t\}$
, or equivalently,
$h\geq (k+1)+h-1-\min \{h/2,d-t\}-\min \{h/2-1,t\}$
, or equivalently,
![]() $\min \{h/2,k+1-t\}+ \min \{h/2-1,t\}\geq k$
. By an elementary calculation, one can check that this is equivalent to
$\min \{h/2,k+1-t\}+ \min \{h/2-1,t\}\geq k$
. By an elementary calculation, one can check that this is equivalent to
![]() $h\geq \max \{2(k-t),k+1,2t\}$
.
$h\geq \max \{2(k-t),k+1,2t\}$
.
To prove necessity, we suppose
![]() $h < \max \{2(k-t),k+1,2t\}$
and let
$h < \max \{2(k-t),k+1,2t\}$
and let
![]() $(G(\mathcal {S}),\ast ,p)$
be a generic
$(G(\mathcal {S}),\ast ,p)$
be a generic
![]() $\Gamma $
-symmetric framework. If
$\Gamma $
-symmetric framework. If
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^*$
are trivial simplicial k-circuits then, by Lemma 5.1,
$\mathcal {T}^*$
are trivial simplicial k-circuits then, by Lemma 5.1,
![]() $V(\mathcal {T}) \cap V(\mathcal {T}^*) = \emptyset $
, and it is clear that
$V(\mathcal {T}) \cap V(\mathcal {T}^*) = \emptyset $
, and it is clear that
![]() $G(\mathcal {S})$
is not
$G(\mathcal {S})$
is not
![]() $\Gamma $
-rigid. So we may assume that
$\Gamma $
-rigid. So we may assume that
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^*$
are nontrivial simplicial k-circuits. It follows easily that
$\mathcal {T}^*$
are nontrivial simplicial k-circuits. It follows easily that
However, the assumption
![]() $h < \max \{2(k-t),k+1,2t\}$
implies that
$h < \max \{2(k-t),k+1,2t\}$
implies that
![]() $H = \mathrm {aff}(p(V(\mathcal {T})\cap V(\mathcal {T}^*)))$
has dimension at most
$H = \mathrm {aff}(p(V(\mathcal {T})\cap V(\mathcal {T}^*)))$
has dimension at most
![]() $k-1$
, and so
$k-1$
, and so
![]() $(G(\mathcal {T}),\ast _T,p)$
has a nontrivial infinitesimal flex induced by rotation about H.
$(G(\mathcal {T}),\ast _T,p)$
has a nontrivial infinitesimal flex induced by rotation about H.
Theorem 5.8. Let
![]() $(\mathcal {S},*)$
be a nontrivial
$(\mathcal {S},*)$
be a nontrivial
![]() $\mathbb Z_2$
-irreducible k-cycle for some
$\mathbb Z_2$
-irreducible k-cycle for some
![]() $k \geq 2$
. Suppose that
$k \geq 2$
. Suppose that
![]() $\Gamma =\Gamma _{t,k+1}$
for some
$\Gamma =\Gamma _{t,k+1}$
for some
![]() $0\leq t \leq k$
and that
$0\leq t \leq k$
and that
![]() $\Gamma $
is not a rotation group when
$\Gamma $
is not a rotation group when
![]() $k=2$
. Then the following statements are equivalent.
$k=2$
. Then the following statements are equivalent.
-
(i)
 $(G(\mathcal {S}),\ast )$
is
$(G(\mathcal {S}),\ast )$
is
 $\Gamma $
-rigid in
$\Gamma $
-rigid in
 ${\mathbb R}^{k+1}$
;
${\mathbb R}^{k+1}$
; -
(ii)
 $\mathcal {S}$
is a simplicial k-circuit or
$\mathcal {S}$
is a simplicial k-circuit or
 $\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
for some simplicial k-circuit
$\mathcal {S}=\mathcal {T}\sqcup \mathcal {T}^*$
for some simplicial k-circuit
 $\mathcal {T}$
with
$\mathcal {T}$
with
 $|V(\mathcal {T})\cap V(\mathcal {T}^*)|\geq \max \{2(k-t),k+1,2t\}$
;
$|V(\mathcal {T})\cap V(\mathcal {T}^*)|\geq \max \{2(k-t),k+1,2t\}$
; -
(iii) for every
 $X \subset V(\mathcal {S})$
such that
$X \subset V(\mathcal {S})$
such that
 $X^* = X$
and
$X^* = X$
and
 $|X| < \max \{2(k-t),k+1,2t\}$
,
$|X| < \max \{2(k-t),k+1,2t\}$
,
 $G(\mathcal {S}) - X$
is connected.
$G(\mathcal {S}) - X$
is connected.
Proof. Let
![]() $c=\max \{2(k-t),k+1,2t\}$
.
$c=\max \{2(k-t),k+1,2t\}$
.
By Lemmas 5.1 and 5.7, (i) implies (ii). To see that (ii) and (iii) are equivalent, observe that
![]() $c\leq 2k$
since
$c\leq 2k$
since
![]() $0 \leq t\leq k$
. Also, if X is a
$0 \leq t\leq k$
. Also, if X is a
![]() $*$
-invariant subset of
$*$
-invariant subset of
![]() $V(\mathcal {S})$
of size less than
$V(\mathcal {S})$
of size less than
![]() $2k$
, then Lemma 5.3 implies that X is a vertex separator of
$2k$
, then Lemma 5.3 implies that X is a vertex separator of
![]() $G(\mathcal {T})$
if and only if
$G(\mathcal {T})$
if and only if
![]() $\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
for some simplicial k-circuit
$\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
for some simplicial k-circuit
![]() $\mathcal {T}$
with
$\mathcal {T}$
with
![]() $V(\mathcal {T}) \cap V(\mathcal {T}^*) \subseteq X$
. The equivalence between (ii) and (iii) now follows.
$V(\mathcal {T}) \cap V(\mathcal {T}^*) \subseteq X$
. The equivalence between (ii) and (iii) now follows.
It remains to prove that (ii) and (iii) imply (i). Suppose, for a contradiction, that
![]() $\mathcal {S}$
is a counterexample to this statement with
$\mathcal {S}$
is a counterexample to this statement with
![]() $|V(\mathcal {S})|$
minimal and let
$|V(\mathcal {S})|$
minimal and let
![]() $G(\mathcal {S})= G =(V,E) $
.
$G(\mathcal {S})= G =(V,E) $
.
Claim 5.9. There exists an edge
![]() $xy \in E$
such that
$xy \in E$
such that
![]() $x^*y \not \in E$
.
$x^*y \not \in E$
.
Proof of claim.
Suppose, for a contradiction, that
![]() $x^*y \in E$
whenever
$x^*y \in E$
whenever
![]() $xy \in E$
. Then, for every
$xy \in E$
. Then, for every
![]() $U \in \mathcal {S}$
,
$U \in \mathcal {S}$
,
![]() $G[U \sqcup U^*]$
can be obtained from the complete graph on
$G[U \sqcup U^*]$
can be obtained from the complete graph on
![]() $U\sqcup U^*$
by deleting the set of edges
$U\sqcup U^*$
by deleting the set of edges
![]() $\{xx^*:x\in U\}$
. Hence,
$\{xx^*:x\in U\}$
. Hence,
![]() $G[U \sqcup U^*]$
is isomorphic to
$G[U \sqcup U^*]$
is isomorphic to
![]() $G(\mathcal {B}_k)$
. We can now apply Lemma 4.2 to deduce that
$G(\mathcal {B}_k)$
. We can now apply Lemma 4.2 to deduce that
Suppose
![]() $\mathcal {S}$
is a simplicial k-circuit. Then
$\mathcal {S}$
is a simplicial k-circuit. Then
![]() $\mathcal {S}$
is a strongly connected simplicial k-complex so, for all
$\mathcal {S}$
is a strongly connected simplicial k-complex so, for all
![]() $U,U'\in \mathcal {S}$
, there exists a sequence of k-faces
$U,U'\in \mathcal {S}$
, there exists a sequence of k-faces
![]() $U_1,U_2,\ldots ,U_m$
of
$U_1,U_2,\ldots ,U_m$
of
![]() $\mathcal {S}$
such that
$\mathcal {S}$
such that
![]() $U_1=U$
,
$U_1=U$
,
![]() $U_m=U'$
and
$U_m=U'$
and
![]() $|U_i\cap U_{i+1}|=k$
for all
$|U_i\cap U_{i+1}|=k$
for all
![]() $1\leq i\leq m-1$
. Putting
$1\leq i\leq m-1$
. Putting
![]() $H=\bigcup _{i=1}^mG[U_i \cup U_i^*]$
, we can now use (5.6) and Theorem 2.8 to deduce that H is
$H=\bigcup _{i=1}^mG[U_i \cup U_i^*]$
, we can now use (5.6) and Theorem 2.8 to deduce that H is
![]() $\Gamma $
-rigid. This implies that every vertex of G belongs to the unique maximal
$\Gamma $
-rigid. This implies that every vertex of G belongs to the unique maximal
![]() $\Gamma $
-rigid subgraph of G which contains
$\Gamma $
-rigid subgraph of G which contains
![]() $U\sqcup U^*$
, and hence, G is
$U\sqcup U^*$
, and hence, G is
![]() $\Gamma $
-rigid. This contradicts the choice of
$\Gamma $
-rigid. This contradicts the choice of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Thus,
![]() $\mathcal {S}$
is not a simplicial k-circuit. Then
$\mathcal {S}$
is not a simplicial k-circuit. Then
![]() $\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
for some simplicial k-circuit
$\mathcal {S} = \mathcal {T} \sqcup \mathcal {T}^*$
for some simplicial k-circuit
![]() $\mathcal {T}$
with
$\mathcal {T}$
with
![]() $|V(\mathcal {T}) \cap V(\mathcal {T}^*)| \geq c$
by the assumption that (ii) holds for
$|V(\mathcal {T}) \cap V(\mathcal {T}^*)| \geq c$
by the assumption that (ii) holds for
![]() $\mathcal {S}$
. Then
$\mathcal {S}$
. Then
![]() $\mathcal {T}$
is strongly connected, so we can apply the argument in the previous paragraph to deduce that
$\mathcal {T}$
is strongly connected, so we can apply the argument in the previous paragraph to deduce that
![]() $V(\mathcal {T})$
is contained in a
$V(\mathcal {T})$
is contained in a
![]() $\Gamma $
-rigid subgraph of G. By symmetry,
$\Gamma $
-rigid subgraph of G. By symmetry,
![]() $V(\mathcal {T}^*)$
is also contained in a
$V(\mathcal {T}^*)$
is also contained in a
![]() $\Gamma $
-rigid subgraph of G. Since
$\Gamma $
-rigid subgraph of G. Since
![]() $V(G) = V(\mathcal {T}) \cup V(\mathcal {T})^*$
, we can now apply Theorem 2.8 to deduce that G is
$V(G) = V(\mathcal {T}) \cup V(\mathcal {T})^*$
, we can now apply Theorem 2.8 to deduce that G is
![]() $\Gamma $
-rigid, again a contradiction. This completes the proof of the claim.
$\Gamma $
-rigid, again a contradiction. This completes the proof of the claim.
Claim 5.9 tells us we can choose an edge
![]() $xy\in E$
such that
$xy\in E$
such that
![]() $xy^*\not \in E$
. Let
$xy^*\not \in E$
. Let
![]() $(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
be a
$(\mathcal {S}_1^+, \dots , \mathcal {S}_m^+)$
be a
![]() $\mathbb {Z}_2$
-symmetric Fogelsanger decomposition of
$\mathbb {Z}_2$
-symmetric Fogelsanger decomposition of
![]() $\mathcal {S}$
at
$\mathcal {S}$
at
![]() $xy$
, and put
$xy$
, and put
![]() $\mathcal {S}_i' = (\mathcal {S}_i^+/xy)/x^*y^*$
for all
$\mathcal {S}_i' = (\mathcal {S}_i^+/xy)/x^*y^*$
for all
![]() $1\leq i\leq m$
. By Lemma 5.4(3),
$1\leq i\leq m$
. By Lemma 5.4(3),
![]() $\mathcal {S}_i'$
is a
$\mathcal {S}_i'$
is a
![]() $\mathbb {Z}_2$
-irreducible k-cycle.
$\mathbb {Z}_2$
-irreducible k-cycle.
Claim 5.10. For all
![]() $1\leq i\leq m$
, either
$1\leq i\leq m$
, either
![]() $G(\mathcal {S}_i^+)$
is
$G(\mathcal {S}_i^+)$
is
![]() $\Gamma $
-rigid or
$\Gamma $
-rigid or
![]() $\mathcal {S}_i^+=\mathcal {T}_i\sqcup \mathcal {T}_i^*$
for some simplicial k-circuit
$\mathcal {S}_i^+=\mathcal {T}_i\sqcup \mathcal {T}_i^*$
for some simplicial k-circuit
![]() $\mathcal {T}_i$
with
$\mathcal {T}_i$
with
![]() $|V(\mathcal {T}_i)\cap V(\mathcal {T}_i^*)|\leq 2k$
.
$|V(\mathcal {T}_i)\cap V(\mathcal {T}_i^*)|\leq 2k$
.
Proof. The proof splits into two cases depending on the
![]() $\Gamma $
-rigidity of
$\Gamma $
-rigidity of
![]() $\mathcal {S}_i' = (\mathcal {S}_i^+/xy)/x^*y^*$
.
$\mathcal {S}_i' = (\mathcal {S}_i^+/xy)/x^*y^*$
.
Suppose
![]() $\mathcal {S}_i'$
is
$\mathcal {S}_i'$
is
![]() $\Gamma $
-rigid. Since
$\Gamma $
-rigid. Since
![]() $xy \in E(\mathcal {S}_i^+)$
and
$xy \in E(\mathcal {S}_i^+)$
and
![]() $\mathcal {S}_i^+$
is a nontrivial
$\mathcal {S}_i^+$
is a nontrivial
![]() $\mathbb Z_2$
-irreducible k-cycle by Lemma 5.4(a)(d), there exist
$\mathbb Z_2$
-irreducible k-cycle by Lemma 5.4(a)(d), there exist
![]() $U_1,U_2\in \mathcal {S}_i^+$
such that
$U_1,U_2\in \mathcal {S}_i^+$
such that
![]() $|U_1 \cap U_2| = k$
and
$|U_1 \cap U_2| = k$
and
![]() $\{x,y\} \subseteq U_1 \cap U_2$
. Let
$\{x,y\} \subseteq U_1 \cap U_2$
. Let
![]() $C = (U_1 \cup U_2)\setminus \{x,y\}$
. Then
$C = (U_1 \cup U_2)\setminus \{x,y\}$
. Then
![]() $C \subset N_{G(\mathcal {S}_i^+)}(x) \cap N_{G(\mathcal {S}_i^+)}(y)$
,
$C \subset N_{G(\mathcal {S}_i^+)}(x) \cap N_{G(\mathcal {S}_i^+)}(y)$
,
![]() $|C|=k$
and
$|C|=k$
and
![]() $|C \cap C^*| \leq 2$
. Similarly, we can choose
$|C \cap C^*| \leq 2$
. Similarly, we can choose
![]() ${D \subset N_{G(\mathcal {S}_i^+)}(x^*) \cap N_{G(\mathcal {S}_i^+)}(y^*)}$
such that
${D \subset N_{G(\mathcal {S}_i^+)}(x^*) \cap N_{G(\mathcal {S}_i^+)}(y^*)}$
such that
![]() $|D| = k$
and
$|D| = k$
and
![]() $|D \cap D^*| \leq 2$
. Theorem 2.14 now implies that
$|D \cap D^*| \leq 2$
. Theorem 2.14 now implies that
![]() $G(\mathcal {S}_i^+)$
is
$G(\mathcal {S}_i^+)$
is
![]() $\Gamma $
-rigid.
$\Gamma $
-rigid.
Next, suppose
![]() $\mathcal {S}_i'$
is not
$\mathcal {S}_i'$
is not
![]() $\Gamma $
-rigid. Then, by the minimality of
$\Gamma $
-rigid. Then, by the minimality of
![]() $|V(\mathcal {S})|$
,
$|V(\mathcal {S})|$
,
![]() $\mathcal {S}_i'$
does not satisfy (ii) in the statement of the theorem. Lemma 5.1 now implies that
$\mathcal {S}_i'$
does not satisfy (ii) in the statement of the theorem. Lemma 5.1 now implies that
![]() $\mathcal {S}_i'=\mathcal {T}'\sqcup \mathcal {T}^{\prime *}$
for some simplicial k-circuit
$\mathcal {S}_i'=\mathcal {T}'\sqcup \mathcal {T}^{\prime *}$
for some simplicial k-circuit
![]() $\mathcal {T}'$
with
$\mathcal {T}'$
with
![]() $|V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|<c$
. By Lemma 5.6, there is a simplicial k-circuit
$|V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|<c$
. By Lemma 5.6, there is a simplicial k-circuit
![]() $\mathcal {T}$
such that
$\mathcal {T}$
such that
![]() $\mathcal {S}_i^+=\mathcal {T}\sqcup \mathcal {T}^*$
with
$\mathcal {S}_i^+=\mathcal {T}\sqcup \mathcal {T}^*$
with
![]() $|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq |V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|+2$
. Suppose
$|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq |V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|+2$
. Suppose
![]() $1 \leq t \leq k-1$
. Then
$1 \leq t \leq k-1$
. Then
![]() $c=\max \{2(k-t),k+1,2t\}\leq 2k-1$
. Hence,
$c=\max \{2(k-t),k+1,2t\}\leq 2k-1$
. Hence,
![]() $|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq |V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|+2\leq c+1\leq 2k$
, as required. Hence, we may assume that
$|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq |V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|+2\leq c+1\leq 2k$
, as required. Hence, we may assume that
![]() $t=0$
or
$t=0$
or
![]() $t=k$
. Then
$t=k$
. Then
![]() $c=2k$
. Since
$c=2k$
. Since
![]() $|V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|$
and c are both even,
$|V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|$
and c are both even,
![]() $|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq |V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|+2\leq c=2k$
. This completes the proof.
$|V(\mathcal {T})\cap V(\mathcal {T}^*)|\leq |V(\mathcal {T}')\cap V(\mathcal {T}^{\prime *})|+2\leq c=2k$
. This completes the proof.
We next define a sequence of simplicial k-cycles
![]() $\mathcal {W}_1,\mathcal {W}_2,\ldots , \mathcal {W}_m$
. For each
$\mathcal {W}_1,\mathcal {W}_2,\ldots , \mathcal {W}_m$
. For each
![]() $1\leq i\leq m$
, we set
$1\leq i\leq m$
, we set
![]() $\mathcal {W}_i=\mathcal {S}_i^+$
if
$\mathcal {W}_i=\mathcal {S}_i^+$
if
![]() $G(\mathcal {S}_i^+)$
is
$G(\mathcal {S}_i^+)$
is
![]() $\Gamma $
-rigid. Otherwise, we put
$\Gamma $
-rigid. Otherwise, we put
![]() $\mathcal {W}_i=\mathcal {T}_i$
, where
$\mathcal {W}_i=\mathcal {T}_i$
, where
![]() $\mathcal {T}_i$
is the simplicial k-circuit given by Claim 5.10 for
$\mathcal {T}_i$
is the simplicial k-circuit given by Claim 5.10 for
![]() $\mathcal {S}_i^+$
. We will show that
$\mathcal {S}_i^+$
. We will show that
If
![]() $\mathcal {W}_i=\mathcal {S}_i^+$
, then
$\mathcal {W}_i=\mathcal {S}_i^+$
, then
![]() $G(\mathcal {W}_i)$
is
$G(\mathcal {W}_i)$
is
![]() $\Gamma $
-rigid by definition, and we have
$\Gamma $
-rigid by definition, and we have
![]() $\mathcal {W}_i^*=(\mathcal {S}_i^+)^*=\mathcal {S}_i^+$
because
$\mathcal {W}_i^*=(\mathcal {S}_i^+)^*=\mathcal {S}_i^+$
because
![]() $\mathcal {S}_i^+ $
is a
$\mathcal {S}_i^+ $
is a
![]() $\mathbb Z_2$
-irreducible k-cycle. Conversely, if
$\mathbb Z_2$
-irreducible k-cycle. Conversely, if
![]() $\mathcal {W}_i=\mathcal {T}_i$
, then we have
$\mathcal {W}_i=\mathcal {T}_i$
, then we have
![]() $|V(\mathcal {T}_i) \cap V(\mathcal {T}_i^*)| \leq 2k$
, and we can apply Theorem 4.5 to deduce that
$|V(\mathcal {T}_i) \cap V(\mathcal {T}_i^*)| \leq 2k$
, and we can apply Theorem 4.5 to deduce that
![]() $G(\mathcal {T}_i)$
and
$G(\mathcal {T}_i)$
and
![]() $G(\mathcal {T}_i^*)$
are both
$G(\mathcal {T}_i^*)$
are both
![]() $\Gamma $
-rigid. Thus, (5.7) holds.
$\Gamma $
-rigid. Thus, (5.7) holds.
We can now complete the proof of the theorem. Using Lemma 5.4(7) to reorder
![]() $(\mathcal {S}_1^+,\ldots ,\mathcal {S}_m^+)$
as necessary, and interchanging
$(\mathcal {S}_1^+,\ldots ,\mathcal {S}_m^+)$
as necessary, and interchanging
![]() $\mathcal {T}_i^*$
and
$\mathcal {T}_i^*$
and
![]() $\mathcal {T}_i$
where necessary, we can assume that
$\mathcal {T}_i$
where necessary, we can assume that
The hypothesis that
![]() $xx^*\not \in E$
for all
$xx^*\not \in E$
for all
![]() $x\in X$
implies that
$x\in X$
implies that
We can now apply a straightforward induction argument using (5.7), (5.8), (5.9) and Theorem 2.8 to deduce that
 $$ \begin{align} \bigcup_{i=1}^m G(\mathcal{W}_i)\ \text{and}\ \bigcup_{i=1}^m G(\mathcal{W}^*_i)\ \text{are both}\ \Gamma\text{-rigid.} \end{align} $$
$$ \begin{align} \bigcup_{i=1}^m G(\mathcal{W}_i)\ \text{and}\ \bigcup_{i=1}^m G(\mathcal{W}^*_i)\ \text{are both}\ \Gamma\text{-rigid.} \end{align} $$
If
![]() $\mathcal {W}_i=\mathcal {S}_i^+$
for some
$\mathcal {W}_i=\mathcal {S}_i^+$
for some
![]() $1\leq i\leq m$
, then
$1\leq i\leq m$
, then
![]() $\bigcup _{i=1}^m G(\mathcal {W}_i)$
and
$\bigcup _{i=1}^m G(\mathcal {W}_i)$
and
![]() $\bigcup _{i=1}^m G(\mathcal {W}^*_i)$
intersect in at least
$\bigcup _{i=1}^m G(\mathcal {W}^*_i)$
intersect in at least
![]() $2k$
vertices. By Theorem 2.8,
$2k$
vertices. By Theorem 2.8,
![]() $G(\mathcal {S}) = \left (\bigcup _{i=1}^m G(\mathcal {W}_i)\right ) \cup \left (\bigcup _{i=1}^m G(\mathcal {W}^*_i)\right )$
is
$G(\mathcal {S}) = \left (\bigcup _{i=1}^m G(\mathcal {W}_i)\right ) \cup \left (\bigcup _{i=1}^m G(\mathcal {W}^*_i)\right )$
is
![]() $\Gamma $
-rigid contradicting our choice of
$\Gamma $
-rigid contradicting our choice of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
So we can assume that for
![]() $i = 1,\dots ,m$
,
$i = 1,\dots ,m$
,
![]() $\mathcal {S}_i^+ = \mathcal {T}_i \sqcup \mathcal {T}_i^*$
, where
$\mathcal {S}_i^+ = \mathcal {T}_i \sqcup \mathcal {T}_i^*$
, where
![]() $\mathcal {T}_i$
is simplicial k-circuit properly contained in
$\mathcal {T}_i$
is simplicial k-circuit properly contained in
![]() $\mathcal {S}_i^+$
and
$\mathcal {S}_i^+$
and
![]() $\mathcal {W}_i = \mathcal {T}_i$
. If
$\mathcal {W}_i = \mathcal {T}_i$
. If
![]() $\mathcal {T}_i\cap \mathcal {T}_j^*\neq \emptyset $
for some distinct
$\mathcal {T}_i\cap \mathcal {T}_j^*\neq \emptyset $
for some distinct
![]() $i,j$
, then
$i,j$
, then
![]() $\bigcup _{i=1}^m G(\mathcal {T}_i)$
and
$\bigcup _{i=1}^m G(\mathcal {T}_i)$
and
![]() $\bigcup _{i=1}^m G(\mathcal {T}^*_i)$
intersect on a
$\bigcup _{i=1}^m G(\mathcal {T}^*_i)$
intersect on a
![]() $(k+1)$
-clique in
$(k+1)$
-clique in
![]() $G(\mathcal {S})$
. Hence, their union is
$G(\mathcal {S})$
. Hence, their union is
![]() $\Gamma $
-rigid by (5.9) and the gluing theorem (Theorem 2.8). Since the union is
$\Gamma $
-rigid by (5.9) and the gluing theorem (Theorem 2.8). Since the union is
![]() $G(\mathcal {S})$
by Lemma 5.4(b), this contradicts the choice of
$G(\mathcal {S})$
by Lemma 5.4(b), this contradicts the choice of
![]() $\mathcal {S}$
as a counterexample.
$\mathcal {S}$
as a counterexample.
Therefore,
![]() $\mathcal {T}_i\cap \mathcal {T}_j^*=\emptyset $
for all
$\mathcal {T}_i\cap \mathcal {T}_j^*=\emptyset $
for all
![]() $1\leq i, j\leq m$
. By Lemma 5.4(e),
$1\leq i, j\leq m$
. By Lemma 5.4(e),
![]() $\mathcal {T}_i^*$
contains a simplex
$\mathcal {T}_i^*$
contains a simplex
![]() $U\in \mathcal {S}$
that is not contained in any
$U\in \mathcal {S}$
that is not contained in any
![]() $\mathcal {S}_j^+$
for
$\mathcal {S}_j^+$
for
![]() $j\neq i$
. This, and the facts that
$j\neq i$
. This, and the facts that
![]() $\mathcal {T}_i\cap \mathcal {T}_j^*=\emptyset $
for all
$\mathcal {T}_i\cap \mathcal {T}_j^*=\emptyset $
for all
![]() $1\leq i,j\leq m$
and
$1\leq i,j\leq m$
and
![]() $\triangle _{i=1}^{m}\mathcal {S}_i^+=\mathcal {S}$
, imply that
$\triangle _{i=1}^{m}\mathcal {S}_i^+=\mathcal {S}$
, imply that
![]() $\triangle _{i=1}^{m}\mathcal {T}_i$
is a simplicial k-cycle that is properly contained in
$\triangle _{i=1}^{m}\mathcal {T}_i$
is a simplicial k-cycle that is properly contained in
![]() $\mathcal {S}$
, so
$\mathcal {S}$
, so
![]() $\mathcal {S}$
is not a simplicial k-circuit. Since
$\mathcal {S}$
is not a simplicial k-circuit. Since
![]() $\mathcal {S}$
satisfies (ii) from the statement of the theorem, it follows from Lemma 5.1 that
$\mathcal {S}$
satisfies (ii) from the statement of the theorem, it follows from Lemma 5.1 that
![]() $\mathcal {S}=\mathcal {T} \sqcup \mathcal {T}^*$
, where
$\mathcal {S}=\mathcal {T} \sqcup \mathcal {T}^*$
, where
![]() $\mathcal {T}=\triangle _{i=1}\mathcal {T}_i$
and
$\mathcal {T}=\triangle _{i=1}\mathcal {T}_i$
and
![]() $|V(\mathcal {T})\cap V(\mathcal {T}^*)|\geq \max \{2(k-t),k+1,2t\} =:c$
. Moreover, also by Lemma 5.1,
$|V(\mathcal {T})\cap V(\mathcal {T}^*)|\geq \max \{2(k-t),k+1,2t\} =:c$
. Moreover, also by Lemma 5.1,
![]() $\mathcal {T}$
must be a simplicial k-circuit.
$\mathcal {T}$
must be a simplicial k-circuit.
Note that
![]() $G(\mathcal {T})\subseteq \bigcup _{i=1}^m G(\mathcal {T}_i)$
and
$G(\mathcal {T})\subseteq \bigcup _{i=1}^m G(\mathcal {T}_i)$
and
![]() $G(\mathcal {T}^*)\subseteq \bigcup _{i=1}^m G(\mathcal {T}_i^*)$
, so
$G(\mathcal {T}^*)\subseteq \bigcup _{i=1}^m G(\mathcal {T}_i^*)$
, so
![]() $\bigcup _{i=1}^m G(\mathcal {T}_i)$
and
$\bigcup _{i=1}^m G(\mathcal {T}_i)$
and
![]() $\bigcup _{i=1}^m G(\mathcal {T}_i^*)$
also have at least c common vertices. We can now use (5.10), Theorem 2.8 and Lemma 5.4(b) to deduce that
$\bigcup _{i=1}^m G(\mathcal {T}_i^*)$
also have at least c common vertices. We can now use (5.10), Theorem 2.8 and Lemma 5.4(b) to deduce that
![]() $G(\mathcal {S})$
is
$G(\mathcal {S})$
is
![]() $\Gamma $
-rigid, contradicting our choice of
$\Gamma $
-rigid, contradicting our choice of
![]() $\mathcal {S}$
. This final contradiction completes the proof of the theorem.
$\mathcal {S}$
. This final contradiction completes the proof of the theorem.
Theorem 5.8 immediately gives the following sufficient condition for the
![]() $\Gamma $
-rigidity of
$\Gamma $
-rigidity of
![]() ${\mathbb Z}_2$
-symmetric simplicial circuits.
${\mathbb Z}_2$
-symmetric simplicial circuits.
Theorem 5.11. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() ${\mathbb Z}_2$
-symmetric simplicial k-circuit with
${\mathbb Z}_2$
-symmetric simplicial k-circuit with
![]() $k\geq 2$
. Then
$k\geq 2$
. Then
![]() $(G(\mathcal {S}),*)$
is
$(G(\mathcal {S}),*)$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() ${\mathbb R}^{k+1}$
if either
${\mathbb R}^{k+1}$
if either
![]() $k\geq 3$
or
$k\geq 3$
or
![]() $k=2$
and
$k=2$
and
![]() $\Gamma $
is not the half-turn rotation group.
$\Gamma $
is not the half-turn rotation group.
Since every pseudomanifold is a simplicial circuit, [Reference Klee, Nevo, Novik and Zheng11, Conjecture 8.3] follows immediately as a special case of Theorem 5.11.
6 The lower bound theorem
The lower bound theorem for
![]() $\mathbb Z_2$
-irreducible k-cycles is an immediate corollary of Theorem 5.8 and Lemma 2.2.
$\mathbb Z_2$
-irreducible k-cycles is an immediate corollary of Theorem 5.8 and Lemma 2.2.
Theorem 6.1. Let
![]() $(\mathcal {S},*)$
be a nontrivial simplicial
$(\mathcal {S},*)$
be a nontrivial simplicial
![]() $\mathbb Z_2$
-irreducible k-cycle for some
$\mathbb Z_2$
-irreducible k-cycle for some
![]() $k \geq 2$
. Suppose that
$k \geq 2$
. Suppose that
![]() $G(\mathcal {S}) - X$
is connected for all
$G(\mathcal {S}) - X$
is connected for all
![]() $X \subset V$
which satisfy
$X \subset V$
which satisfy
![]() $X^* = X$
and
$X^* = X$
and
![]() $|X| \leq 2k$
. Then
$|X| \leq 2k$
. Then
![]() $g_2( \mathcal {S}) = |E(\mathcal {S})| - (k+1)|V(\mathcal {S})| + \binom {k+2}2 \geq \binom {k+1}2 - (k+1)$
.
$g_2( \mathcal {S}) = |E(\mathcal {S})| - (k+1)|V(\mathcal {S})| + \binom {k+2}2 \geq \binom {k+1}2 - (k+1)$
.
Proof. We can apply Theorem 5.8 in the case when
![]() $\Gamma = \Gamma _{0,k+1}$
is a point inversion to deduce that
$\Gamma = \Gamma _{0,k+1}$
is a point inversion to deduce that
![]() $(G(\mathcal {S}),*)$
is
$(G(\mathcal {S}),*)$
is
![]() $\Gamma $
-rigid. The case
$\Gamma $
-rigid. The case
![]() $t=0$
of Lemma 2.2 now gives
$t=0$
of Lemma 2.2 now gives
![]() $g_2( \mathcal {S}) \geq \binom {k+1}2 - (k+1)$
.
$g_2( \mathcal {S}) \geq \binom {k+1}2 - (k+1)$
.
A similar argument using Theorem 5.11 and Lemma 2.2 gives the following:
Theorem 6.2. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() ${\mathbb Z}_2$
-symmetric simplicial k-circuit with
${\mathbb Z}_2$
-symmetric simplicial k-circuit with
![]() $k\geq 2$
. Then
$k\geq 2$
. Then
![]() $g_2(\mathcal {S}) \geq \binom {k+1}2 -(k+1)$
.
$g_2(\mathcal {S}) \geq \binom {k+1}2 -(k+1)$
.
Since every pseudomanifold is a simplicial circuit, this immediately gives the following lower bound result for pseudomanifolds and hence verifies the inequality part of [Reference Klee, Nevo, Novik and Zheng11, Conjecture 8.1]
Corollary 6.3. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() ${\mathbb Z}_2$
-symmetric k-pseudomanifold with
${\mathbb Z}_2$
-symmetric k-pseudomanifold with
![]() $k \geq 2$
. Then
$k \geq 2$
. Then
![]() $g_2(\mathcal {S}) \geq \binom {k+1}2 - (k+1)$
.
$g_2(\mathcal {S}) \geq \binom {k+1}2 - (k+1)$
.
7 Closing remarks
7.1 Characterising
 $\Gamma _{1,3}$
-rigid simplicial
$\Gamma _{1,3}$
-rigid simplicial
 $2$
-circuits
$2$
-circuits
Theorem 5.8 resolves the
![]() $\Gamma _{t,k+1}$
-rigidity question for
$\Gamma _{t,k+1}$
-rigidity question for
![]() ${\mathbb Z}_2$
-symmetric simplicial k-circuits in
${\mathbb Z}_2$
-symmetric simplicial k-circuits in
![]() ${\mathbb R}^{k+1}$
, except in the case when
${\mathbb R}^{k+1}$
, except in the case when
![]() $t=1$
and
$t=1$
and
![]() $k=2$
. In this case, Lemma 2.2 implies that the boundary complex of a
$k=2$
. In this case, Lemma 2.2 implies that the boundary complex of a
![]() ${\mathbb Z}_2$
-symmetric simplicial polyhedron cannot be
${\mathbb Z}_2$
-symmetric simplicial polyhedron cannot be
![]() $\Gamma _{1,3}$
-rigid in
$\Gamma _{1,3}$
-rigid in
![]() ${\mathbb R}^3$
. Other examples can be obtained from the boundary complex
${\mathbb R}^3$
. Other examples can be obtained from the boundary complex
![]() $\mathcal {P}$
of a
$\mathcal {P}$
of a
![]() ${\mathbb Z}_2$
-symmetric simplicial polyhedron by choosing a face F of
${\mathbb Z}_2$
-symmetric simplicial polyhedron by choosing a face F of
![]() $\mathcal {P}$
and ‘inserting’ an arbitrary simplicial
$\mathcal {P}$
and ‘inserting’ an arbitrary simplicial
![]() $2$
-circuit
$2$
-circuit
![]() $\mathcal {T}$
into both F and
$\mathcal {T}$
into both F and
![]() $F^*$
. More precisely, we choose a copy
$F^*$
. More precisely, we choose a copy
![]() $\mathcal {T}^*$
of
$\mathcal {T}^*$
of
![]() $\mathcal {T}$
, label the vertices of
$\mathcal {T}$
, label the vertices of
![]() $\mathcal {T}$
so that
$\mathcal {T}$
so that
![]() $F\in \mathcal {T}$
and
$F\in \mathcal {T}$
and
![]() $V(\mathcal {P})\cap V(\mathcal {T})=F$
, and then put
$V(\mathcal {P})\cap V(\mathcal {T})=F$
, and then put
![]() $\mathcal {S}=\mathcal {P}\triangle (\mathcal {T}\sqcup \mathcal {T}^*)$
.
$\mathcal {S}=\mathcal {P}\triangle (\mathcal {T}\sqcup \mathcal {T}^*)$
.
We believe that all examples of
![]() ${\mathbb Z}_2$
-symmetric simplicial
${\mathbb Z}_2$
-symmetric simplicial
![]() $2$
-circuits which are not
$2$
-circuits which are not
![]() $\Gamma _{1,3}$
-rigid in
$\Gamma _{1,3}$
-rigid in
![]() ${\mathbb R}^{3}$
can be obtained by recursively applying this insertion operation to the boundary complex of a
${\mathbb R}^{3}$
can be obtained by recursively applying this insertion operation to the boundary complex of a
![]() $Z_2$
-symmetric simplicial polyhedron. This would imply the following conjecture.
$Z_2$
-symmetric simplicial polyhedron. This would imply the following conjecture.
Conjecture 7.1. Suppose that
![]() $(\mathcal {S},*)$
is a
$(\mathcal {S},*)$
is a
![]() $\mathbb Z_2$
-symmetric simplicial 2-circuit such that
$\mathbb Z_2$
-symmetric simplicial 2-circuit such that
![]() $G(\mathcal {S})$
is 4-connected and non-planar. Then
$G(\mathcal {S})$
is 4-connected and non-planar. Then
![]() $G(\mathcal {S})$
is
$G(\mathcal {S})$
is
![]() $\Gamma _{1,3}$
-rigid in
$\Gamma _{1,3}$
-rigid in
![]() ${\mathbb R}^3$
.
${\mathbb R}^3$
.
A graph
![]() $G=(V,E)$
is redundantly rigid in
$G=(V,E)$
is redundantly rigid in
![]() ${\mathbb R}^d$
if
${\mathbb R}^d$
if
![]() $G-e$
is rigid in
$G-e$
is rigid in
![]() ${\mathbb R}^d$
for all
${\mathbb R}^d$
for all
![]() $e\in E$
. We showed in [Reference Cruickshank, Jackson and Tanigawa6] that if G is the graph of a simplicial k-circuit for some
$e\in E$
. We showed in [Reference Cruickshank, Jackson and Tanigawa6] that if G is the graph of a simplicial k-circuit for some
![]() $k\geq 3$
and G is
$k\geq 3$
and G is
![]() $(k+1)$
-connected, then G is redundantly rigid in
$(k+1)$
-connected, then G is redundantly rigid in
![]() ${\mathbb R}^{k+1}$
, and we used this to deduce that equality in the Lower Bound Theorem can only hold for simplicial k-circuits when they are stacked k-spheres. We believe that an analogous approach may work for
${\mathbb R}^{k+1}$
, and we used this to deduce that equality in the Lower Bound Theorem can only hold for simplicial k-circuits when they are stacked k-spheres. We believe that an analogous approach may work for
![]() $\Gamma $
-rigidity and our symmetric lower bound theorem.
$\Gamma $
-rigidity and our symmetric lower bound theorem.
7.2 Redundant
 $\Gamma $
-rigidity of simplicial circuits
$\Gamma $
-rigidity of simplicial circuits
Conjecture 7.2. Let
![]() $(\mathcal {S},*)$
be a
$(\mathcal {S},*)$
be a
![]() ${\mathbb Z}_2$
-symmetric simplicial k-circuit such that
${\mathbb Z}_2$
-symmetric simplicial k-circuit such that
![]() $k\geq 3$
,
$k\geq 3$
,
![]() $\mathcal {S}\neq \mathcal {B}_k$
and
$\mathcal {S}\neq \mathcal {B}_k$
and
![]() $G(\mathcal {S})$
is
$G(\mathcal {S})$
is
![]() $(k+1)$
-connected. Then, for all point groups
$(k+1)$
-connected. Then, for all point groups
![]() $\Gamma $
in
$\Gamma $
in
![]() ${\mathbb R}^{k+1}$
of order two and all
${\mathbb R}^{k+1}$
of order two and all
![]() $e\in E(\mathcal {S})$
,
$e\in E(\mathcal {S})$
,
![]() $(G(\mathcal {S})-e-e^*,*)$
is
$(G(\mathcal {S})-e-e^*,*)$
is
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() ${\mathbb R}^{k+1}$
.
${\mathbb R}^{k+1}$
.
Conjecture 7.2 would imply that equality can only hold in Theorem 6.2 when
![]() $\mathcal {S}$
is a symmetrically stacked sphere (see [Reference Klee, Nevo, Novik and Zheng11] for a definition) and would verify [Reference Klee, Nevo, Novik and Zheng11, Conjecture 8.1] as a special case.
$\mathcal {S}$
is a symmetrically stacked sphere (see [Reference Klee, Nevo, Novik and Zheng11] for a definition) and would verify [Reference Klee, Nevo, Novik and Zheng11, Conjecture 8.1] as a special case.
7.3 Non-adjacent vertex pairings
The Bricard octahedron shows that Theorem 4.5 will become false if we remove the hypothesis that
![]() $|X| \leq 2k$
. More generally, any
$|X| \leq 2k$
. More generally, any
![]() ${\mathbb Z}_2$
-symmetric boundary complex of a polyhedron will not be
${\mathbb Z}_2$
-symmetric boundary complex of a polyhedron will not be
![]() $\Gamma $
-rigid in
$\Gamma $
-rigid in
![]() ${\mathbb R}^3$
when
${\mathbb R}^3$
when
![]() $\Gamma $
is the half turn rotation group by Lemma 2.2. It is conceivable, however, that the hypothesis that
$\Gamma $
is the half turn rotation group by Lemma 2.2. It is conceivable, however, that the hypothesis that
![]() $|X| \leq 2k$
is not necessary in certain special cases. Indeed, [Reference Klee, Nevo, Novik and Zheng11, Conjecture 8.4] is precisely this statement in the case when
$|X| \leq 2k$
is not necessary in certain special cases. Indeed, [Reference Klee, Nevo, Novik and Zheng11, Conjecture 8.4] is precisely this statement in the case when
![]() $k=2$
,
$k=2$
,
![]() $\mathcal {S}$
is a simplicial sphere and
$\mathcal {S}$
is a simplicial sphere and
![]() $\Gamma $
is a point inversion group.
$\Gamma $
is a point inversion group.
7.4 More general group actions
Adin [Reference Adin1], and later Jorge [Reference Jorge9], extended Stanley’s lower bound theorem to rational polytopes with a cyclic linear symmetry group of prime power order. Their methods are very different from ours, relying on algebraic properties of the Stanley-Reisner ring of a simplicial complex.
It is natural to ask if the rigidity-based approach can be used to extend these results to simplicial circuits and/or other point groups. In this paper, we frequently use the fact that
![]() $*$
is free and
$*$
is free and
![]() $\Gamma $
is a point group of order two. Relaxing either of these restrictions in a rigidity-based approach remains an open problem.
$\Gamma $
is a point group of order two. Relaxing either of these restrictions in a rigidity-based approach remains an open problem.
7.5 The lower bound conjecture for higher dimensional faces
Let
![]() $\phi _j(n,k)$
be the number of j-faces of a symmetrically stacked k-sphere with n vertices. One can easily verify by induction on n that
$\phi _j(n,k)$
be the number of j-faces of a symmetrically stacked k-sphere with n vertices. One can easily verify by induction on n that
 $$\begin{align*}\phi_j(n,k) = \left\{ \begin{array}{ll} 2^{j+1}\binom{k+1}{j+1} + (n-2k-2)\binom{k+1}{j} & \text{ if } j \leq k-1 \\ 2^{k+1}+ k(n-2k-2) & \text{ if }j =k \end{array}\right. \end{align*}$$
$$\begin{align*}\phi_j(n,k) = \left\{ \begin{array}{ll} 2^{j+1}\binom{k+1}{j+1} + (n-2k-2)\binom{k+1}{j} & \text{ if } j \leq k-1 \\ 2^{k+1}+ k(n-2k-2) & \text{ if }j =k \end{array}\right. \end{align*}$$
For a simplicial complex
![]() $\mathcal {S}$
, let
$\mathcal {S}$
, let
![]() $f_j(\mathcal {S})$
be the number of j-faces of
$f_j(\mathcal {S})$
be the number of j-faces of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Conjecture 7.3. Suppose that
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $\mathcal {S}$
is a simplicial k-circuit with n vertices and
$\mathcal {S}$
is a simplicial k-circuit with n vertices and
![]() $*$
is a free simplicial involution on
$*$
is a free simplicial involution on
![]() $\mathcal {S}$
. Then
$\mathcal {S}$
. Then
![]() $f_j(\mathcal {S}) \geq \phi _n(n,k)$
for
$f_j(\mathcal {S}) \geq \phi _n(n,k)$
for
![]() $j = 1,\dots ,k$
. Moreover, if equality occurs for any j, then
$j = 1,\dots ,k$
. Moreover, if equality occurs for any j, then
![]() $\mathcal {S}$
must be a k-sphere and, in the case that
$\mathcal {S}$
must be a k-sphere and, in the case that
![]() $k\geq 3$
, must be a symmetrically stacked k-sphere.
$k\geq 3$
, must be a symmetrically stacked k-sphere.
In the non-symmetric setting, the analogous conjecture for simplicial manifolds can be derived from the case
![]() $j=1$
by an induction argument based on the fact that the link of any proper face in a simplicial manifold is a simplicial sphere of lower dimension (see [Reference Kalai10] for details). However, in the
$j=1$
by an induction argument based on the fact that the link of any proper face in a simplicial manifold is a simplicial sphere of lower dimension (see [Reference Kalai10] for details). However, in the
![]() $\mathbb Z_2$
-symmetric case, this argument does not generalise easily since the the link of F is not
$\mathbb Z_2$
-symmetric case, this argument does not generalise easily since the the link of F is not
![]() $\mathbb Z_2$
-symmetric. One might consider the union of the links of F and
$\mathbb Z_2$
-symmetric. One might consider the union of the links of F and
![]() $F^*$
, but that is not necessarily a simplicial manifold, even when
$F^*$
, but that is not necessarily a simplicial manifold, even when
![]() $\mathcal {S}$
is a simplicial sphere.
$\mathcal {S}$
is a simplicial sphere.
A further difficulty for Conjecture 7.3, and indeed for the non-symmetric version [Reference Cruickshank, Jackson and Tanigawa6, Conjecture 8.2], arises from the fact that the class of simplicial circuits is not link closed. In general, the link of a j-face in a nontrivial simplicial k-circuit will be a simplicial
![]() $(k-j-1)$
-cycle but not necessarily a simplicial
$(k-j-1)$
-cycle but not necessarily a simplicial
![]() $(k-j-1)$
-circuit.
$(k-j-1)$
-circuit.
Acknowledgements
We thank the anonymous referee for several suggestions that helped to improve the paper.
Competing interest
The authors have no competing interest to declare.
Financial support
This research was supported by JST PRESTO Grant Number JPMJPR2126, JSPS KAKENHI Grant Number 20H05961 and EPSRC overseas travel grant EP/T030461/1.