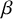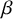1 Introduction
The Circular-
![]() $\beta $
ensemble (C
$\beta $
ensemble (C
![]() $\beta $
E) is a distribution on n points
$\beta $
E) is a distribution on n points
![]() $(e^{i\omega _1},e^{i\omega _2}, \dots , e^{i\omega _n})$
on the unit circle with a joint density given by
$(e^{i\omega _1},e^{i\omega _2}, \dots , e^{i\omega _n})$
on the unit circle with a joint density given by

In the special case of
![]() $\beta =2$
, this is the joint distribution of eigenvalues of a Haar-distributed unitary random matrix. The characteristic polynomial
$\beta =2$
, this is the joint distribution of eigenvalues of a Haar-distributed unitary random matrix. The characteristic polynomial ![]() of the C
of the C
![]() $\beta $
E has attracted a considerable interest, for its connections to the theories of logarithmically-correlated fields and (when
$\beta $
E has attracted a considerable interest, for its connections to the theories of logarithmically-correlated fields and (when
![]() $\beta =2$
) analytic number theory.
$\beta =2$
) analytic number theory.
A particular quantity of interest is ![]() . Let
. Let
The random matrix part of the Fyodorov–Hiary–Keating conjecture [Reference Fyodorov, Hiary and KeatingFHK12b] states that in the special case that
![]() $\beta =2$
,
$\beta =2$
,
![]() $M_n-m_n$
converges in distribution toward a limiting random variables
$M_n-m_n$
converges in distribution toward a limiting random variables
![]() $R_2$
, with
$R_2$
, with
It was later observed in [Reference Subag and ZeitouniSZ15] that the probability density in (1.3) is the law of the sum of two independent Gumbel random variables.
For general
![]() $\beta>0$
, an important step forward was obtained by [Reference Chhaibi, Madaule and NajnudelCMN18], who proved that
$\beta>0$
, an important step forward was obtained by [Reference Chhaibi, Madaule and NajnudelCMN18], who proved that
![]() $M_n-\sqrt {2/\beta }m_n$
is tight. One of our main results strengthens this to convergence in distribution and gives a description of the limiting law.
$M_n-\sqrt {2/\beta }m_n$
is tight. One of our main results strengthens this to convergence in distribution and gives a description of the limiting law.
Theorem 1.1. The sequence of random variables
![]() $M_n-\sqrt {2/\beta }m_n$
converges in distribution to a random variables
$M_n-\sqrt {2/\beta }m_n$
converges in distribution to a random variables
![]() $R_\beta $
. Further,
$R_\beta $
. Further,
 $$ \begin{align} R_\beta= C_\beta+G_\beta+\frac{1}{\sqrt{2\beta}}\log (\mathscr{B}_\infty(\beta)) , \end{align} $$
$$ \begin{align} R_\beta= C_\beta+G_\beta+\frac{1}{\sqrt{2\beta}}\log (\mathscr{B}_\infty(\beta)) , \end{align} $$
where
![]() $C_\beta $
is an (implicit) constant,
$C_\beta $
is an (implicit) constant,
![]() $G_\beta $
is Gumbel distributed with parameter
$G_\beta $
is Gumbel distributed with parameter
![]() $1/\sqrt {2\beta }$
, and
$1/\sqrt {2\beta }$
, and
![]() $\mathscr {B}_\infty (\beta )$
is a random variable that is independent of
$\mathscr {B}_\infty (\beta )$
is a random variable that is independent of
![]() $G_\beta $
.
$G_\beta $
.
Remark 1.2. We identify below (see Theorem 1.6)
![]() $\mathscr {B}_\infty (\beta )$
as the total mass of a certain derivative martingale. For a specific log-correlated field on the circle, [Reference RemyRem20] computes the law of the total mass of the associated GMC and confirms the Fyodorov-Bouchaud prediction [Reference Fyodorov and BouchaudFB08] for it. It is possible (and even anticipated, especially in light of [Reference Chhaibi and NajnudelCN19]) but not proved that the distribution of
$\mathscr {B}_\infty (\beta )$
as the total mass of a certain derivative martingale. For a specific log-correlated field on the circle, [Reference RemyRem20] computes the law of the total mass of the associated GMC and confirms the Fyodorov-Bouchaud prediction [Reference Fyodorov and BouchaudFB08] for it. It is possible (and even anticipated, especially in light of [Reference Chhaibi and NajnudelCN19]) but not proved that the distribution of
![]() $\mathscr {B}_\infty $
is also Gumbel. If true (even if only for
$\mathscr {B}_\infty $
is also Gumbel. If true (even if only for
![]() $\beta =2$
), Theorem 1.1 would then yield a proof of the random matrix side of the Fyodorov-Hiary-Keating conjecture [Reference Fyodorov, Hiary and KeatingFHK12b].
$\beta =2$
), Theorem 1.1 would then yield a proof of the random matrix side of the Fyodorov-Hiary-Keating conjecture [Reference Fyodorov, Hiary and KeatingFHK12b].
Theorem 1.1 is a consequence of a more general result, which gives the convergence of the distance between certain marked point processes built from a sequence of orthogonal polynomials and a sequence of (n-independent) decorated Poisson point process. This general result also applies to the imaginary part of
![]() $\log X_n(z)$
(and thus allows for control on maximal fluctuation of eigenvalue count on intervals). We postpone a discussion of Theorem 1.1 and a historical context of our results to after the introduction of the necessary preliminaries and the statement of our more general results.
$\log X_n(z)$
(and thus allows for control on maximal fluctuation of eigenvalue count on intervals). We postpone a discussion of Theorem 1.1 and a historical context of our results to after the introduction of the necessary preliminaries and the statement of our more general results.
1.1 OPUC preliminaries and formulation of main results
A major advance in the study of
![]() $M_n$
was achieved in [Reference Chhaibi, Madaule and NajnudelCMN18], who used the Orthogonal Polynomials on the Unit Circle (OPUC) representation of the C
$M_n$
was achieved in [Reference Chhaibi, Madaule and NajnudelCMN18], who used the Orthogonal Polynomials on the Unit Circle (OPUC) representation of the C
![]() $\beta $
E measure due to [Reference Killip and NenciuKN04]; we refer to [Reference SimonSim04] for an encyclopedic account of the OPUC theory. Let
$\beta $
E measure due to [Reference Killip and NenciuKN04]; we refer to [Reference SimonSim04] for an encyclopedic account of the OPUC theory. Let
![]() $\left \{ \gamma _k \right \}$
be independent, complex, rotationally invariant random variables for which
$\left \{ \gamma _k \right \}$
be independent, complex, rotationally invariant random variables for which
![]() $|\gamma _k|^2 = \operatorname {Beta}(1, \beta (k+1)/2)$
– that is, with density on
$|\gamma _k|^2 = \operatorname {Beta}(1, \beta (k+1)/2)$
– that is, with density on
![]() $[0,1]$
proportional to
$[0,1]$
proportional to
![]() $(1-x)^{\beta (k+1)/2-1}$
. The Szegő recurrence is, for all
$(1-x)^{\beta (k+1)/2-1}$
. The Szegő recurrence is, for all
![]() $k \geq 0,$
$k \geq 0,$

where ![]() and
and ![]() are polynomials of degree at most k. Define in terms of these coefficients the Prüfer phases
are polynomials of degree at most k. Define in terms of these coefficients the Prüfer phases
where here and below, we take the principal branch of the logarithm with discontinuity along the negative real line. Then, ![]() may be identified as a continuous version of the logarithm of
may be identified as a continuous version of the logarithm of ![]() (see [Reference Chhaibi, Madaule and NajnudelCMN18, Lemma 2.3]). These polynomials
(see [Reference Chhaibi, Madaule and NajnudelCMN18, Lemma 2.3]). These polynomials ![]() can be used to give an effective representation for the characteristic polynomial
can be used to give an effective representation for the characteristic polynomial
![]() $X_n$
by setting
$X_n$
by setting
![]() $\alpha $
to be a uniformly distributed element of the unit circle, independent of
$\alpha $
to be a uniformly distributed element of the unit circle, independent of
![]() $\left \{ \gamma _k : k \geq 0 \right \},$
and setting for any
$\left \{ \gamma _k : k \geq 0 \right \},$
and setting for any
![]() $\theta \in {\mathbb R},$
$\theta \in {\mathbb R},$
See [Reference Chhaibi, Madaule and NajnudelCMN18, (2.2)] for details of the demonstration, based on [Reference Killip and NenciuKN04, Proposition B.2], that this indeed has the law of the characteristic polynomial of C
![]() $\beta $
E.
$\beta $
E.
The polynomials ![]() satisfy the recurrence
satisfy the recurrence
We also recall the relative Prüfer phase [Reference Chhaibi, Madaule and NajnudelCMN18, Lemma 2.4] given by the recurrence
In law, ![]() is equal to
is equal to ![]()
We will be interested in the extreme values of the fluctuations of real and imaginary parts of ![]() for which reason we will formulate our results in terms of the recurrence
for which reason we will formulate our results in terms of the recurrence
where
![]() $\sigma $
is one of
$\sigma $
is one of ![]() Then, for
Then, for
![]() $\sigma =1$
,
$\sigma =1$
, ![]() , while for
, while for
![]() $\sigma =i$
,
$\sigma =i$
, ![]() . The entire analysis of
. The entire analysis of
![]() $\varphi $
occurs for a fixed
$\varphi $
occurs for a fixed
![]() $\sigma ,$
and so we shall not display the dependence on
$\sigma ,$
and so we shall not display the dependence on
![]() $\sigma .$
$\sigma .$
Formulation of main results
We already stated our main result concerning the maximum of the real part of the logarithm of the characteristic polynomial. In this section, we describe the rest of our results.
We recall the following, with
![]() $m_n = \log n - \tfrac {3}{4}\log \log n$
as in (1.2).
$m_n = \log n - \tfrac {3}{4}\log \log n$
as in (1.2).
Theorem 1.3 [Reference Chhaibi, Madaule and NajnudelCMN18].
For any ![]() the centered maximum max
θ∈[0, 2π]
φ
n
(θ) −8/β m
n
is tight. The same holds for the real and imaginary parts of the logarithm of the characteristic polynomial.
the centered maximum max
θ∈[0, 2π]
φ
n
(θ) −8/β m
n
is tight. The same holds for the real and imaginary parts of the logarithm of the characteristic polynomial.
We shall expand upon this result and show that, indeed, this maximum converges in distribution. Moreover, we shall show that the process of almost maxima converges. The following result, which complements Theorem 1.1, yields the convergence in law of the centered maxima of
![]() $\varphi _n$
.
$\varphi _n$
.
Theorem 1.4. For any ![]() the centered maximum max
θ∈[0, 2π]
φ
n
(θ) −8/β m
n
converges in law to a randomly shifted Gumbel of parameter
the centered maximum max
θ∈[0, 2π]
φ
n
(θ) −8/β m
n
converges in law to a randomly shifted Gumbel of parameter
![]() $\sqrt {2/\beta }$
. In the notation of Theorem 1.1, the limit is
$\sqrt {2/\beta }$
. In the notation of Theorem 1.1, the limit is
![]() $C_\beta ^\sigma +2G_\beta ^\sigma +\sqrt {2/\beta } \log \mathscr {B}_\infty $
, where
$C_\beta ^\sigma +2G_\beta ^\sigma +\sqrt {2/\beta } \log \mathscr {B}_\infty $
, where
![]() $G_\beta ^\sigma $
has the same law as
$G_\beta ^\sigma $
has the same law as
![]() $G_\beta $
and
$G_\beta $
and
![]() $C_\beta ^\sigma $
is an (implicit) constant.
$C_\beta ^\sigma $
is an (implicit) constant.
Remark 1.5. By the distributional identity,
which follows from the conjugation invariance of the law of
![]() $\gamma _k$
and the symmetry
$\gamma _k$
and the symmetry
![]() $-2\Im \log (1-z) = 2 \Im \log (1-\overline {z})$
, the case of
$-2\Im \log (1-z) = 2 \Im \log (1-\overline {z})$
, the case of
![]() $\sigma =-i$
in Theorem 1.4 follows similarly to the case of
$\sigma =-i$
in Theorem 1.4 follows similarly to the case of
![]() $\sigma =i$
.
$\sigma =i$
.
To describe the random shift, we need to introduce some machinery.
1.2 The derivative martingale
We will need the so-called derivative martingale. Define the random measure and its total mass

We equip the space of finite measures with the weak-* topology, and then we show that this measure converges almost surely. We recall (see (1.10)) that
![]() $\varphi _k(\cdot )$
coincides with either twice the real or imaginary parts of
$\varphi _k(\cdot )$
coincides with either twice the real or imaginary parts of ![]() (depending on
(depending on
![]() $\sigma $
).
$\sigma $
).
Theorem 1.6. For any ![]() and any
and any
![]() $\beta> 0,$
there is an almost surely finite random variable
$\beta> 0,$
there is an almost surely finite random variable
![]() $\mathscr {B}_\infty $
and an almost surely finite, nonatomic random measure
$\mathscr {B}_\infty $
and an almost surely finite, nonatomic random measure
![]() $\mathscr {D}_\infty $
so that
$\mathscr {D}_\infty $
so that
Furthermore, for any
![]() $\epsilon> 0$
, there is a compact
$\epsilon> 0$
, there is a compact
![]() $K \subset (0,\infty )$
so that with
$K \subset (0,\infty )$
so that with

it holds that for any
![]() $k \in {\mathbb N}$
,
$k \in {\mathbb N}$
,

This is shown in Section 9. We remark that
![]() $(\mathscr {B}_{2^j} : j \in {\mathbb N})$
is not in fact a martingale, but it is easily compared to a process
$(\mathscr {B}_{2^j} : j \in {\mathbb N})$
is not in fact a martingale, but it is easily compared to a process
![]() $(\widehat {\mathscr {B}_{2^j}} : j \in {\mathbb N})$
which is a martingale (see Section 9 for details).
$(\widehat {\mathscr {B}_{2^j}} : j \in {\mathbb N})$
which is a martingale (see Section 9 for details).
1.3 Sequential Poisson process approximation and extremal landscape
We introduce parameters
![]() $\{k_p : p \in {\mathbb N}\}$
which will be chosen large but independent of
$\{k_p : p \in {\mathbb N}\}$
which will be chosen large but independent of
![]() $n.$
These parameters will be taken large after n is sent to infinity. Moreover, they will be ordered in a decreasing fashion so that
$n.$
These parameters will be taken large after n is sent to infinity. Moreover, they will be ordered in a decreasing fashion so that
![]() $k_j \gg k_{j+1}.$
We shall not attempt to find any quantitative dependence of how these parameters are sent to infinity. All parameters will be assumed to be larger than
$k_j \gg k_{j+1}.$
We shall not attempt to find any quantitative dependence of how these parameters are sent to infinity. All parameters will be assumed to be larger than
![]() $1.$
$1.$
We formulate several sequential extremal processes approximation for the processes of near maxima; these extremal processes will be indexed by
![]() $k_1$
. Divide the unit circle into consecutive arcs
$k_1$
. Divide the unit circle into consecutive arcs
![]() $\{ \widehat {I_{j,n}}\}$
by the formula that for any
$\{ \widehat {I_{j,n}}\}$
by the formula that for any
![]() $j,n \in {\mathbb N},$
$j,n \in {\mathbb N},$
To avoid cumbersome notation, we suppress the n dependence in
![]() $\widehat {I_{j,n}}$
, writing
$\widehat {I_{j,n}}$
, writing
![]() $\widehat {I_j}$
instead, and we continue to do so in the forthcoming
$\widehat {I_j}$
instead, and we continue to do so in the forthcoming
![]() $D_{j,n},\theta _{j,n},\widehat {W}_{j,n}$
. Let
$D_{j,n},\theta _{j,n},\widehat {W}_{j,n}$
. Let
![]() ${\mathcal {D}}_{n/k_1}$
denote the collection of indices
${\mathcal {D}}_{n/k_1}$
denote the collection of indices
![]() $j=1,2,\dots ,\lceil \tfrac {n}{k_1}\rceil .$
We let
$j=1,2,\dots ,\lceil \tfrac {n}{k_1}\rceil .$
We let
![]() $\theta _j=\theta _{j,n}$
be the supremum of
$\theta _j=\theta _{j,n}$
be the supremum of
![]() $\widehat {I_{j,n}}.$
Over each of these intervals, we define the process
$\widehat {I_{j,n}}.$
Over each of these intervals, we define the process

This will serve as the decoration process, although we will not need to (and will not) prove their convergence as
![]() $k_1\to \infty $
.
$k_1\to \infty $
.
Remark 1.8. The choice of
![]() $D_j$
in the case of
$D_j$
in the case of
![]() $\sigma =1$
is motivated by the application to Theorem 1.1, which concerns the characteristic polynomial. While the characteristic polynomial
$\sigma =1$
is motivated by the application to Theorem 1.1, which concerns the characteristic polynomial. While the characteristic polynomial
![]() $X_n$
is coarsely approximated by the OPUC
$X_n$
is coarsely approximated by the OPUC ![]() , the coupling between them means the phase of
, the coupling between them means the phase of ![]() influences the modulus of
influences the modulus of
![]() $X_n$
. So, to prove Theorem 1.1, it is insufficient to record only the modulus of
$X_n$
. So, to prove Theorem 1.1, it is insufficient to record only the modulus of ![]() , whereas to prove Theorem 1.4, one could take the definition used in the case
, whereas to prove Theorem 1.4, one could take the definition used in the case
![]() $\sigma =i$
for both.
$\sigma =i$
for both.
We next define for all
![]() $j \in {\mathcal {D}}_{n/k_1}$
random variables
$j \in {\mathcal {D}}_{n/k_1}$
random variables
which is a local maximum, appropriately centered. We now define a random measure which we shall show is well-approximated by a Poisson process with random intensity. Define a measure on Borel subsets of
by

A central technical challenge will be to show that
![]() $\varphi _k$
and
$\varphi _k$
and ![]() are essentially constant on the interval
are essentially constant on the interval
![]() $\widehat {I_j}$
for
$\widehat {I_j}$
for
![]() $k \approx n/{k_1}$
, and that hence, it suffices to track both
$k \approx n/{k_1}$
, and that hence, it suffices to track both
![]() $\varphi _k$
and
$\varphi _k$
and ![]() only at the point
only at the point
![]() $\theta _j \in \widehat {I_j}.$
In this direction, it will be helpful to further decompose the local maximum
$\theta _j \in \widehat {I_j}.$
In this direction, it will be helpful to further decompose the local maximum
![]() $\widehat {W_j}.$
We define two new parameters
$\widehat {W_j}.$
We define two new parameters
![]() $k_1^+$
and
$k_1^+$
and
![]() $\widehat {k}_1$
as functions of
$\widehat {k}_1$
as functions of
![]() $k_1$
in such a way that
$k_1$
in such a way that
![]() $k_1^+/\widehat {k}_1, \widehat {k}_1/k_1 \to \infty ,$
specifically:
$k_1^+/\widehat {k}_1, \widehat {k}_1/k_1 \to \infty ,$
specifically:
We define
![]() $n_1 = \lfloor n/k_1\rfloor ,$
and we define
$n_1 = \lfloor n/k_1\rfloor ,$
and we define
![]() $\widehat {n}_1$
and
$\widehat {n}_1$
and
![]() $n_1^+$
analogously. Define
$n_1^+$
analogously. Define
Define for Borel subsets of ![]()

Note that the processes
![]() $\operatorname {Ex}_n$
and
$\operatorname {Ex}_n$
and
![]() $\operatorname {Ext}_n$
are closely related; see the proof of Theorem 1.11. Our goal will be to approximate the processes
$\operatorname {Ext}_n$
are closely related; see the proof of Theorem 1.11. Our goal will be to approximate the processes
![]() $\operatorname {Ext}_n$
(and
$\operatorname {Ext}_n$
(and
![]() $\operatorname {Ex}_n$
) by Poisson processes with random intensity.
$\operatorname {Ex}_n$
) by Poisson processes with random intensity.
Toward this end, recall that an important strategy used throughout the analysis of extrema of branching processes is effectively conditioning on the initial portion of the process, wherein the extrema gain a nontrivial correlation. We will do the same and condition on the first Verblunsky coefficients. We use the parameter
![]() $k_2,$
which we assume is a power of
$k_2,$
which we assume is a power of
![]() $2$
(to apply Theorem 1.6), to refer to how many Verblunsky coefficients on which we condition. We also use
$2$
(to apply Theorem 1.6), to refer to how many Verblunsky coefficients on which we condition. We also use
![]() $(\mathscr {F}_{k}: k \in {\mathbb N}_0)$
to refer to the natural
$(\mathscr {F}_{k}: k \in {\mathbb N}_0)$
to refer to the natural
![]() $\sigma $
-algebra generated by the sequence of Verblunsky coefficients
$\sigma $
-algebra generated by the sequence of Verblunsky coefficients
![]() $( \gamma _k : k \in {\mathbb N}_0).$
$( \gamma _k : k \in {\mathbb N}_0).$
We will compare
![]() $\operatorname {Ext}_n$
to the
$\operatorname {Ext}_n$
to the
![]() $\mathscr {F}_{k_2}$
-conditional Poisson random measures
$\mathscr {F}_{k_2}$
-conditional Poisson random measures ![]() ,
, ![]() ,
, ![]() with respective intensity measures
with respective intensity measures
 $$ \begin{align} &\mathscr{D}_{k_2}(\theta)d\theta \times I(v)dv \times \mathfrak{p}_{k_1}(v,df), \quad \mathscr{D}_{k_2}(\theta)d\theta \times I'(v)dv \times \mathfrak{p}_{k_1}(v,df), \quad \nonumber\\ &\qquad \mathscr{D}_{k_2}(\theta)d\theta \times I"(v)dv \times \mathfrak{p}_{k_1}(v,df), \end{align} $$
$$ \begin{align} &\mathscr{D}_{k_2}(\theta)d\theta \times I(v)dv \times \mathfrak{p}_{k_1}(v,df), \quad \mathscr{D}_{k_2}(\theta)d\theta \times I'(v)dv \times \mathfrak{p}_{k_1}(v,df), \quad \nonumber\\ &\qquad \mathscr{D}_{k_2}(\theta)d\theta \times I"(v)dv \times \mathfrak{p}_{k_1}(v,df), \end{align} $$
where

Here and in many places below, we slightly abuse notation by using
![]() $\times $
to denote also products of transition kernels (i.e., semidirect products). Thus,
$\times $
to denote also products of transition kernels (i.e., semidirect products). Thus,
![]() $I'$
is defined over a slightly longer interval than I, and
$I'$
is defined over a slightly longer interval than I, and
![]() $I"$
is defined over a slightly shorter interval than I. The law
$I"$
is defined over a slightly shorter interval than I. The law
![]() $\mathfrak {p}_{k_1}(v,\cdot )$
is that of a random function on
$\mathfrak {p}_{k_1}(v,\cdot )$
is that of a random function on ![]() which is related to the exponential of the solution of a family of coupled diffusions
which is related to the exponential of the solution of a family of coupled diffusions
![]() $\mathfrak {U}^o_{T_+}(\theta )$
in an auxiliary time parameter (see (2.78) and (2.52)).
$\mathfrak {U}^o_{T_+}(\theta )$
in an auxiliary time parameter (see (2.78) and (2.52)).
Remark 1.9. This process
![]() $\mathfrak {U}^o_{T_+}(\theta )$
consists of the terminal values of a coupled family of diffusions
$\mathfrak {U}^o_{T_+}(\theta )$
consists of the terminal values of a coupled family of diffusions
![]() $(t \mapsto \mathfrak {U}^o_t(\theta ))$
. This coupled family of diffusions can be related to the complex stochastic sine equation [Reference Valkó and VirágVV17] (see also the closely related stochastic sine equation [Reference Valkó and VirágVV09, Reference Killip and StoiciuKS+09]). The extreme values of this diffusion in
$(t \mapsto \mathfrak {U}^o_t(\theta ))$
. This coupled family of diffusions can be related to the complex stochastic sine equation [Reference Valkó and VirágVV17] (see also the closely related stochastic sine equation [Reference Valkó and VirágVV09, Reference Killip and StoiciuKS+09]). The extreme values of this diffusion in
![]() $\theta $
are then needed to describe
$\theta $
are then needed to describe
![]() $\mathfrak {p}_{k_1}$
, at least for how it appears here.
$\mathfrak {p}_{k_1}$
, at least for how it appears here.
Similarly, the measure
![]() $\operatorname {Ex}_n$
will be approximated by a Poisson random measure with a random intensity on the same space. This intensity on
$\operatorname {Ex}_n$
will be approximated by a Poisson random measure with a random intensity on the same space. This intensity on ![]() will take the form of a product measure
will take the form of a product measure
![]() $\mathscr{D}_\infty \times \widehat{\mathfrak{p}_{k_1}}$
, where
$\mathscr{D}_\infty \times \widehat{\mathfrak{p}_{k_1}}$
, where
![]() $(\widehat {\mathfrak {p}_{k_1}} :k_1 \in {\mathbb N})$
is a deterministic Radon measure on
$(\widehat {\mathfrak {p}_{k_1}} :k_1 \in {\mathbb N})$
is a deterministic Radon measure on ![]() , which is constructed as follows. Let
, which is constructed as follows. Let
be a map of ![]() to itself, and let
to itself, and let
We let ![]() be a Poisson random measure on
be a Poisson random measure on ![]() with intensity
with intensity
![]() $\mathscr{D}_\infty \times \widehat{\mathfrak{p}_{k_1}}$
. We may define similarly
$\mathscr{D}_\infty \times \widehat{\mathfrak{p}_{k_1}}$
. We may define similarly ![]() and
and ![]() .
.
To compare point processes on
![]() $\Gamma $
, we endow the latter with the distance
$\Gamma $
, we endow the latter with the distance
In terms of this, we define (compare with
![]() $d_1'$
from [Reference Chen and XiaCX11]) a Wasserstein distance on point configurations
$d_1'$
from [Reference Chen and XiaCX11]) a Wasserstein distance on point configurations
![]() $\xi _1 = \sum _{i=1}^m \delta _{y_i}$
and
$\xi _1 = \sum _{i=1}^m \delta _{y_i}$
and
![]() $\xi _2 = \sum _{i=1}^n \delta _{z_i}$
$\xi _2 = \sum _{i=1}^n \delta _{z_i}$

with the minimum being the distance over all permutations ![]() of
of
![]() $\{1,2,\dots ,n\}.$
Finally, for two point processes
$\{1,2,\dots ,n\}.$
Finally, for two point processes
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
, we define the pseudometric
$Q_2$
, we define the pseudometric
with the infimum over couplings
![]() $(\xi _1, \xi _2)$
in which
$(\xi _1, \xi _2)$
in which
![]() $\xi _1 \sim Q_1$
and
$\xi _1 \sim Q_1$
and
![]() $\xi _2 \sim Q_2.$
Note that this pseudometric only depends on the laws of the point processes. These distances are somewhat unorthodox; we develop Poisson approximations using these distances in Appendix A, as well as some comparisons of these distances to other more standard metrics used in Poisson approximation.
$\xi _2 \sim Q_2.$
Note that this pseudometric only depends on the laws of the point processes. These distances are somewhat unorthodox; we develop Poisson approximations using these distances in Appendix A, as well as some comparisons of these distances to other more standard metrics used in Poisson approximation.
To get a comparison between
![]() $\operatorname {Ext}_n$
and the point processes
$\operatorname {Ext}_n$
and the point processes ![]() , it is necessary to restrict to the case that the maximum of the modulus of the decoration
, it is necessary to restrict to the case that the maximum of the modulus of the decoration
![]() $|D_je^{\sqrt {4/\beta }V_j}|$
is sufficiently large. So, we set
$|D_je^{\sqrt {4/\beta }V_j}|$
is sufficiently large. So, we set

In what follows, for any measure (or point process)
![]() $\mathbf {Q}$
on
$\mathbf {Q}$
on
![]() $\Gamma $
, we write
$\Gamma $
, we write
![]() $\iota \# \mathbf {Q}$
for the push forward under the transformation that preserves the first coordinate and applies
$\iota \# \mathbf {Q}$
for the push forward under the transformation that preserves the first coordinate and applies
![]() $\iota $
of (1.22) to the last two. Note that under
$\iota $
of (1.22) to the last two. Note that under
![]() $\iota \#\mathbf {Q}$
, the second coordinate of the point process can always be recovered from the third. Our main result, which will imply Theorems 1.1 and 1.4, is the following convergence of marked processes. Here and in the sequel, for a point process
$\iota \#\mathbf {Q}$
, the second coordinate of the point process can always be recovered from the third. Our main result, which will imply Theorems 1.1 and 1.4, is the following convergence of marked processes. Here and in the sequel, for a point process ![]() and a set
and a set
![]() $B\subset \Gamma $
, we write
$B\subset \Gamma $
, we write ![]() for the restriction of
for the restriction of ![]() to B (i.e.,
to B (i.e., ![]() ).
).
Theorem 1.10. The restrictions of
![]() $\operatorname {Ext}_n^{k_1}$
and
$\operatorname {Ext}_n^{k_1}$
and ![]() to
to
![]() $\Gamma _{k_7}$
satisfy
$\Gamma _{k_7}$
satisfy
The same holds with ![]() or
or ![]() replacing
replacing ![]() in (1.25).
in (1.25).
The meaning of the
![]() $\limsup $
is that the parameters are taken to infinity in order, with n followed by
$\limsup $
is that the parameters are taken to infinity in order, with n followed by
![]() $k_1$
followed by
$k_1$
followed by
![]() $k_2.$
$k_2.$
Similarly, to make a comparison between ![]() and
and
![]() $\operatorname {Ex}_n^{k_1},$
we will only make a comparison in which their second coordinate is in a compact set. Hence, we shall further restrict the space
$\operatorname {Ex}_n^{k_1},$
we will only make a comparison in which their second coordinate is in a compact set. Hence, we shall further restrict the space
![]() ${\Gamma }$
from (1.16) to
${\Gamma }$
from (1.16) to
Theorems 1.10 and 1.6 lead directly to the following:
Theorem 1.11. For any
![]() $k_7> 0,$
the restrictions of the point processes to
$k_7> 0,$
the restrictions of the point processes to
![]() $\widehat {\Gamma }_{k_7}$
satisfy
$\widehat {\Gamma }_{k_7}$
satisfy
The same holds with ![]() or
or ![]() replacing
replacing ![]() in (1.27)
in (1.27)
Equipped with Theorem 1.11, we can now complete the proof of Theorems 1.1 and 1.4, assuming a technical estimate contained in Corollary 10.3.
Proof of Theorems 1.1 and 1.4.
We give first the details for Theorem 1.1 since its proof is more involved. Using (1.7), we have the representation for all
![]() $z \in {\mathbb C}$
$z \in {\mathbb C}$
where we recall
![]() $\alpha $
is uniformly distributed on the unit circle and independent of
$\alpha $
is uniformly distributed on the unit circle and independent of ![]() We begin by proving convergence. From Theorem 1.3, as
We begin by proving convergence. From Theorem 1.3, as
![]() $m_{n+1}-m_{n} \to 0$
as
$m_{n+1}-m_{n} \to 0$
as
![]() $n \to \infty ,$
the random variables
$n \to \infty ,$
the random variables
are tight. Let
![]() $R_*$
be any subsequential weak limit.
$R_*$
be any subsequential weak limit.
We recall that ![]() and hence on the unit circle, we have
and hence on the unit circle, we have
Thus, for
![]() $|z|=1$
, we have the representation of the log-modulus of the characteristic polynomial
$|z|=1$
, we have the representation of the log-modulus of the characteristic polynomial
Then using (1.14), we can represent
![]() $R_{n+1}$
by
$R_{n+1}$
by

By (1.28), the log-modulus of the characteristic polynomial can only increase by a
![]() $\log 2$
over the reversed OPUC
$\log 2$
over the reversed OPUC ![]() and so for any
and so for any
![]() $k_7$
sufficiently large,
$k_7$
sufficiently large,

Let ![]() for all
for all
![]() $x \in {\mathbb R}.$
Then, on the event
$x \in {\mathbb R}.$
Then, on the event
![]() $\max _j \widehat {W}_j>-k_7$
,
$\max _j \widehat {W}_j>-k_7$
,

We would like to apply Theorem 1.11 to establish the convergence of this statistic. For this, we need a Lipschitz bound on the mapping
with respect to the ![]() metric on point configurations. We note that there is n-dependence in the mapping (1.30) beyond the n dependence in the process
metric on point configurations. We note that there is n-dependence in the mapping (1.30) beyond the n dependence in the process
![]() $\operatorname {Ex}_n$
, which we would like to remove. It follows from the definition of the
$\operatorname {Ex}_n$
, which we would like to remove. It follows from the definition of the ![]() metric that (1.30) is
metric that (1.30) is
![]() $C(k_7)$
-Lipschitz. Moreover, the difference
$C(k_7)$
-Lipschitz. Moreover, the difference

Now the mapping ![]() has a Lipschitz constant with respect to the sup-norm that is bounded solely in terms of
has a Lipschitz constant with respect to the sup-norm that is bounded solely in terms of
![]() $k_7.$
Thus, if we define for each
$k_7.$
Thus, if we define for each
![]() $k_1$
a random variable by
$k_1$
a random variable by

then from Theorem 1.11 and the monotonicity of ![]()
with the supremum over all
![]() $1$
-Lipschitz real-valued functions
$1$
-Lipschitz real-valued functions
![]() $\vartheta $
. It follows that
$\vartheta $
. It follows that
Recall that
![]() $R_*$
is any subsequential limit point of
$R_*$
is any subsequential limit point of
![]() $\{R_n\},$
and hence, for any other subsequential limit
$\{R_n\},$
and hence, for any other subsequential limit
![]() $R_*',$
$R_*',$
As
![]() $k_7$
is arbitrary, it follows that
$k_7$
is arbitrary, it follows that
![]() $\{R_n\}$
has a unique weak-
$\{R_n\}$
has a unique weak-
![]() $*$
limit point (i.e., it converges in law). We also observe that since Theorem 1.11 also applies to
$*$
limit point (i.e., it converges in law). We also observe that since Theorem 1.11 also applies to ![]() or
or ![]() , in place of
, in place of ![]() , the same argument above holds if in the definition of
, the same argument above holds if in the definition of
![]() $\mathcal {R}^{k_1}$
, we replace
$\mathcal {R}^{k_1}$
, we replace ![]() by either of these. Hence, if we define
by either of these. Hence, if we define
![]() $\mathcal {R}^{k_1,'}$
and
$\mathcal {R}^{k_1,'}$
and
![]() $\mathcal {R}^{k_1,"}$
by making that replacement, then for all
$\mathcal {R}^{k_1,"}$
by making that replacement, then for all
![]() $k_7$
,
$k_7$
,
We next characterize the limit. For that, it is enough to evaluate for fixed
![]() $x\in {\mathbb R}$
the limit of the probability
$x\in {\mathbb R}$
the limit of the probability
![]() $\mathbb {P}(\mathcal {R}^{k_1}\leq x)$
as
$\mathbb {P}(\mathcal {R}^{k_1}\leq x)$
as
![]() $k_1\to \infty $
. Recall (1.29). For any
$k_1\to \infty $
. Recall (1.29). For any ![]() with
with ![]() , any
, any
![]() $x \in {\mathbb R}$
and any
$x \in {\mathbb R}$
and any ![]() introduce the Borel subset of
introduce the Borel subset of ![]()

From the definition of ![]() ,
,
and by approximation of the step function, we have for all x,
Using the fact that ![]() is Poisson of random intensity, the last probability can be written as
is Poisson of random intensity, the last probability can be written as ![]() , where
, where
Let
From Corollary 10.3, we have that uniformly on compact sets of
![]() $\alpha $
and y and uniformly in
$\alpha $
and y and uniformly in
![]() $|v| \leq (\log k_1)^{17/18}$
,
$|v| \leq (\log k_1)^{17/18}$
,

Note that due to the random phase in the definition of
![]() $\mathfrak {p}_{k_1}$
, the function
$\mathfrak {p}_{k_1}$
, the function ![]() is actually independent of
is actually independent of ![]() , and we can write
, and we can write ![]() . Then, using the change of variables
. Then, using the change of variables
![]() $v=w-\sqrt {\tfrac {\beta }{4}}x$
and setting
$v=w-\sqrt {\tfrac {\beta }{4}}x$
and setting
![]() $J=[(\log k_1^+)^{1/10}, (\log k_1^+)^{9/10}]$
,
$J=[(\log k_1^+)^{1/10}, (\log k_1^+)^{9/10}]$
,

In particular, ![]() does not depend on
does not depend on ![]() , and we can omit it from the notation. Since x is fixed, we obtain for w in the stated interval that
, and we can omit it from the notation. Since x is fixed, we obtain for w in the stated interval that
![]() $(w-\sqrt {\tfrac {\beta }{4}}x)/w=1+o_{k_1}(1)$
. Hence, if we let
$(w-\sqrt {\tfrac {\beta }{4}}x)/w=1+o_{k_1}(1)$
. Hence, if we let
![]() $\mathcal {I}_{x}'$
and
$\mathcal {I}_{x}'$
and
![]() $\mathcal {I}_{x}"$
to denote
$\mathcal {I}_{x}"$
to denote
![]() $\mathcal {I}_{x}$
with
$\mathcal {I}_{x}$
with
![]() $I',I"$
replacing I, respectively, we obtain
$I',I"$
replacing I, respectively, we obtain
Using that all of the distributions functions of
![]() $\mathcal {R}^{k_1}, \mathcal {R}^{k_1,'}, \mathcal {R}^{k_1,"}$
converge together in the limit, we conclude
$\mathcal {R}^{k_1}, \mathcal {R}^{k_1,'}, \mathcal {R}^{k_1,"}$
converge together in the limit, we conclude

where
is a constant that does depend on ![]() , and which takes values in
, and which takes values in
![]() $(0,\infty )$
due to tightness.
$(0,\infty )$
due to tightness.
The proof of Theorem 1.4 is identical, except that instead of working with
![]() $R_n$
as in (1.29), we can work directly with
$R_n$
as in (1.29), we can work directly with
![]() $\varphi _n$
, and in the right-hand side of (1.29), one replaces the expression by
$\varphi _n$
, and in the right-hand side of (1.29), one replaces the expression by
![]() $\log D_j(\theta )$
, resulting in a simplification of the proof.
$\log D_j(\theta )$
, resulting in a simplification of the proof.
Theorem 1.11 is a direct corollary of Theorem 1.10 and some estimates from Section 2 below.
Proof of Theorem 1.11.
Note first that from the data (θ
j
, V
j
, D
j
e
4/βV
j
), we can express the triple (θ
j
, W^
j
, D
j
) by a continuous transformation of the second two coordinates using
![]() $\iota $
, viz.
$\iota $
, viz.
![]() $ (\widehat {W}_j, D_j) =\iota ( V_j, D_je^{\sqrt {4/\beta }V_j}).$
Moreover, this maps
$ (\widehat {W}_j, D_j) =\iota ( V_j, D_je^{\sqrt {4/\beta }V_j}).$
Moreover, this maps
![]() $\Gamma _{k_7}$
to
$\Gamma _{k_7}$
to
![]() $\widehat {\Gamma }_{k_7}.$
Furthermore, the transformation
$\widehat {\Gamma }_{k_7}.$
Furthermore, the transformation
![]() $\iota $
is Lipschitz with some constant
$\iota $
is Lipschitz with some constant
![]() $L({k_7})$
when restricted to this set. Let
$L({k_7})$
when restricted to this set. Let ![]() and
and
![]() $Q = \operatorname {Ext}_n^{k_1} \cap \Gamma _{k_7}.$
Hence, for any
$Q = \operatorname {Ext}_n^{k_1} \cap \Gamma _{k_7}.$
Hence, for any
![]() $k_2$
,
$k_2$
,
where
![]() $\widehat {\iota }(P)$
is a Poisson point process on
$\widehat {\iota }(P)$
is a Poisson point process on
![]() $\widehat {\Gamma }_{k_7}$
with intensity
$\widehat {\Gamma }_{k_7}$
with intensity
![]() $\mathscr{D}_{k_2}(\theta)d\theta \times \widehat{\mathfrak{p}_{k_1}}$
and where we recall that
$\mathscr{D}_{k_2}(\theta)d\theta \times \widehat{\mathfrak{p}_{k_1}}$
and where we recall that
![]() $\widehat {\mathfrak {p}_{k_1}}$
is the pushforward of
$\widehat {\mathfrak {p}_{k_1}}$
is the pushforward of
![]() $I(t)dt \times \mathfrak {p}_{k_1}(t,df)$
under
$I(t)dt \times \mathfrak {p}_{k_1}(t,df)$
under
![]() $\iota $
, which is a Radon measure. The first term in (1.33) goes to
$\iota $
, which is a Radon measure. The first term in (1.33) goes to
![]() $0$
from Theorem 1.10.
$0$
from Theorem 1.10.
We now turn to the second term. Define for any two finite Borel measures on
![]() $\Gamma ,$
$\Gamma ,$

with the supremum over all g with both ![]() for all
for all
![]() $x,y \in \Gamma $
and
$x,y \in \Gamma $
and
![]() $|g(x)| \leq 1$
for all
$|g(x)| \leq 1$
for all
![]() $x \in \Gamma .$
We need the following bound:
$x \in \Gamma .$
We need the following bound:
which is shown in Lemma 2.24 (in the notation of that lemma, it is
![]() $\mathcal {H}$
). If
$\mathcal {H}$
). If
![]() $f : \widehat {\Gamma }_{k_7} \to {\mathbb R}$
is a
$f : \widehat {\Gamma }_{k_7} \to {\mathbb R}$
is a
![]() $1$
-bounded,
$1$
-bounded,
![]() $1$
-Lipschitz function with respect to
$1$
-Lipschitz function with respect to ![]() , we therefore have
, we therefore have

where g ranges over all the fibers
![]() $f( \cdot , y)$
over all
$f( \cdot , y)$
over all ![]() . These are all
. These are all
![]() $1$
-bounded and
$1$
-bounded and
![]() $1$
-Lipschitz with respect to the metric
$1$
-Lipschitz with respect to the metric
![]() $d(x,y) = (|x-y| \wedge 1).$
It follows from Arzelà-Ascoli and Theorem 1.6 (which gives almost sure weak-* convergence of
$d(x,y) = (|x-y| \wedge 1).$
It follows from Arzelà-Ascoli and Theorem 1.6 (which gives almost sure weak-* convergence of
![]() $\mathscr {D}_{k_2}$
to
$\mathscr {D}_{k_2}$
to
![]() $\mathscr {D}_{\infty }$
and the almost sure finiteness of
$\mathscr {D}_{\infty }$
and the almost sure finiteness of
![]() $\mathscr {D}_\infty $
) that
$\mathscr {D}_\infty $
) that
 $$\begin{align*}\limsup_{k_2,k_1 \to \infty} \bigg|\int_{\widehat{\Gamma}_{k_7}} f(x,y) \bigl(\mathscr{D}_{k_2}(dx) -\mathscr{D}_{\infty}(dx)\bigr)\widehat{\mathfrak{p}_{k_1}}(dy) \bigg| =0\quad \operatorname{a.s.} \end{align*}$$
$$\begin{align*}\limsup_{k_2,k_1 \to \infty} \bigg|\int_{\widehat{\Gamma}_{k_7}} f(x,y) \bigl(\mathscr{D}_{k_2}(dx) -\mathscr{D}_{\infty}(dx)\bigr)\widehat{\mathfrak{p}_{k_1}}(dy) \bigg| =0\quad \operatorname{a.s.} \end{align*}$$
Hence, again by Arzelà-Ascoli, taking supremum over all such f, we conclude
Hence, from Theorem A.2, ![]() as
as
![]() $k_1\to \infty $
followed by
$k_1\to \infty $
followed by
![]() $k_2 \to \infty ,$
which completes the proof for
$k_2 \to \infty ,$
which completes the proof for ![]() .
.
The proof for ![]() and
and ![]() is identical.
is identical.
1.4 Imaginary part of the log-determinant
The following corollary, which handles the imaginary part of the logarithm of the characteristic polynomial, follows from Theorems 1.10 and 1.11 in the same way that Theorem 1.1 followed from them; some adjustments are necessary because
![]() $\Im \log X_n(\theta )$
takes values on a (shifted) lattice; see (1.35) below.
$\Im \log X_n(\theta )$
takes values on a (shifted) lattice; see (1.35) below.
Corollary 1.12. There are deterministic constants ![]() and almost surely finite random variables
and almost surely finite random variables ![]() so that
so that

The adaptation of the proof needed to handle here the discreteness is somewhat simpler than that needed in the case of lattice valued branching random walks, as described in [Reference Bramson, Ding and ZeitouniBDZ16a, Section 5]; this is because the effects of discreteness here are only felt in the ‘decoration’ process.
The imaginary part of the logarithm of the characteristic polynomial is related to the eigenvalue counting process of the C
![]() $\beta $
E. Specifically, we take an increasing version of the map
$\beta $
E. Specifically, we take an increasing version of the map
(cf. Lemma 2.1 below) which in fact counts ![]() at all those
at all those
![]() $\theta $
except
$\theta $
except
![]() $\left \{ -\omega _1,-\omega _2,\dots ,-\omega _n \right \}.$
This has the same law (as a process in
$\left \{ -\omega _1,-\omega _2,\dots ,-\omega _n \right \}.$
This has the same law (as a process in
![]() $\theta $
) as
$\theta $
) as
As
![]() $\{\log X_n(1)/\sqrt {\log n}\}$
becomes a centered Gaussian (this follows from Proposition 2.2 with some minor adjustments) and
$\{\log X_n(1)/\sqrt {\log n}\}$
becomes a centered Gaussian (this follows from Proposition 2.2 with some minor adjustments) and
is tight, it follows that

is not tight, and in fact when scaled down by
![]() $\sqrt {\log n}$
converges in law to a centered nondegenerate Gaussian.
$\sqrt {\log n}$
converges in law to a centered nondegenerate Gaussian.
However, the maximum over all arcs of the centered counting function admits the representation

This motivates understanding the joint convergence of the maximum and the minimum of the imaginary part of the logarithm of the characteristic polynomial, which we do not pursue here.
Conjecture 1.13. The convergence in Corollary 1.12 holds jointly.
Note that in the model of Branching Brownian Motion, the analogue of Conjecture 1.13 was recently proved in [Reference Stasiński, Berestycki and MalleinSBM21]; see also [BKL+ Reference Chhaibi, Madaule and Najnudel24].
1.5 Related literature
The analysis in this paper falls within the topic of logarithmically correlated fields. Indeed, in the case of
![]() $\beta =2$
, it was shown in [Reference Hughes, Keating and O’ConnellHKO01] that the process
$\beta =2$
, it was shown in [Reference Hughes, Keating and O’ConnellHKO01] that the process
![]() $ Y_n(z)=\{\log |X_n(z)|\}_{|z|=1}$
is logarithmically correlated in the sense that for any smooth test function
$ Y_n(z)=\{\log |X_n(z)|\}_{|z|=1}$
is logarithmically correlated in the sense that for any smooth test function ![]() on
on
![]() $S^1$
with
$S^1$
with ![]() , the random variable
, the random variable ![]() converges in distribution to a centered Gaussian random variable with variance
converges in distribution to a centered Gaussian random variable with variance ![]() , where
, where ![]() is the k-th Fourier coefficient of
is the k-th Fourier coefficient of ![]() . See also [Reference Baker and ForresterBF97, Reference Keating and SnaithKS00, Reference WieandWie02] for related results. Note that the above variance expression corresponds to a generalized Gaussian field with correlation having singularity of the form
. See also [Reference Baker and ForresterBF97, Reference Keating and SnaithKS00, Reference WieandWie02] for related results. Note that the above variance expression corresponds to a generalized Gaussian field with correlation having singularity of the form
![]() $-\log |\theta -\theta '|$
.
$-\log |\theta -\theta '|$
.
For Gaussian logarithmically correlated fields, the study of the maximum has a long history, going back to the seminal work [Reference BramsonBra78, Reference BramsonBra83] concerning Branching Brownian motion (BBM). Bramson introduced the truncated second moment and barrier methods that are the core tools in all subsequential analysis (see [Reference RobertsRob13] for a modern perspective). Extremal processes for the BBM were constructed in [Reference Aïdékon, Berestycki, Brunet and ShiABBS13] and [Reference Arguin, Bovier and KistlerABK13]. Following some earlier work on tightness and rough structure of the extrema, the extension of the convergence of the maximum to the discrete Gaussian free field in the critical dimension
![]() $2$
was obtained in [Reference Bramson, Ding and ZeitouniBDZ16b] and (for the extremal process) in [Reference Biskup and LouidorBL18]. See [Reference BiskupBis20] for an updated account, and [Reference ZeitouniZei16] for an introduction. A convergence result for general log-correlated Gaussian field is presented in [Reference Ding, Roy and ZeitouniDRZ17]; see also [Reference MadauleMad15].
$2$
was obtained in [Reference Bramson, Ding and ZeitouniBDZ16b] and (for the extremal process) in [Reference Biskup and LouidorBL18]. See [Reference BiskupBis20] for an updated account, and [Reference ZeitouniZei16] for an introduction. A convergence result for general log-correlated Gaussian field is presented in [Reference Ding, Roy and ZeitouniDRZ17]; see also [Reference MadauleMad15].
In the physics literature, the notion of freezing in the context of extremal processes of logarithmically correlated fields arose in the seminal work [Reference Fyodorov and BouchaudFB08]. The link between the freezing phenomenon and extremal processes of the decorated, randomly shifted Poisson type was rigorously elucidated in [Reference Subag and ZeitouniSZ15]. The highly influential work [Reference Fyodorov, Hiary and KeatingFHK12b] (see also [Reference Fyodorov, Hiary and KeatingFHK12a]) applied the freezing paradigm to making predictions for the maximum of the logarithm of the modulus of the characteristic polynomial of CUE matrices (see (1.3)) and, using a conjectured dictionary going back to [Reference Keating and SnaithKS00], made predictions concerning the maximum of the Riemann
![]() $\zeta $
function over short intervals of the critical axis. This has stimulated much work, both on the random matrix side (which we will review shortly) and on the Riemann side, for which we refer to [Reference BramsonABB+19] and [Reference Arguin, Bourgade and RadziwiłłABR23] for the latest progress on verifying the FHK conjectures for the Riemann
$\zeta $
function over short intervals of the critical axis. This has stimulated much work, both on the random matrix side (which we will review shortly) and on the Riemann side, for which we refer to [Reference BramsonABB+19] and [Reference Arguin, Bourgade and RadziwiłłABR23] for the latest progress on verifying the FHK conjectures for the Riemann
![]() $\zeta $
function.
$\zeta $
function.
On the circular ensembles side, the first verification of the leading order in the FHK prediction was obtained in [Reference Arguin, Belius and BourgadeABB17], followed in short order by the verification of the second-order term [Reference Paquette and ZeitouniPZ18]; both works used explicit computations facilitated by dealing with
![]() $\beta =2$
and a decomposition of the log-determinant according to Fourier modes for the former or to spatial approximations for the latter. It was [Reference Chhaibi, Madaule and NajnudelCMN18] who introduced the use of Verblunsky coefficients and the Szegő recursions in (1.5) to not only handle arbitrary
$\beta =2$
and a decomposition of the log-determinant according to Fourier modes for the former or to spatial approximations for the latter. It was [Reference Chhaibi, Madaule and NajnudelCMN18] who introduced the use of Verblunsky coefficients and the Szegő recursions in (1.5) to not only handle arbitrary
![]() $\beta>0$
but also obtain the tightness of
$\beta>0$
but also obtain the tightness of
![]() $M_n-m_n$
. Along the way, [Reference Chhaibi, Madaule and NajnudelCMN18] derived various Gaussian approximations and barrier estimates that are fundamental for the current paper.
$M_n-m_n$
. Along the way, [Reference Chhaibi, Madaule and NajnudelCMN18] derived various Gaussian approximations and barrier estimates that are fundamental for the current paper.
The analysis for C
![]() $\beta $
E has natural analogues for Hermitian ensembles of the G
$\beta $
E has natural analogues for Hermitian ensembles of the G
![]() $\beta $
E type. We mention, in particular, [Reference Fyodorov and Le DoussalFD16] for an early application of the freezing scenario in that context. More recent work includes [Reference Lambert and PaquetteLP19, Reference Augeri, Butez and ZeitouniABZ23, Reference Claeys, Fahs, Lambert and WebbCFLW21, Reference Bourgade, Mody and PainBMP22, Reference Bourgade, Lopatto and ZeitouniBLZ23]. At this time, the results in the Hermitian setup are much less sharp than for circular ensembles.
$\beta $
E type. We mention, in particular, [Reference Fyodorov and Le DoussalFD16] for an early application of the freezing scenario in that context. More recent work includes [Reference Lambert and PaquetteLP19, Reference Augeri, Butez and ZeitouniABZ23, Reference Claeys, Fahs, Lambert and WebbCFLW21, Reference Bourgade, Mody and PainBMP22, Reference Bourgade, Lopatto and ZeitouniBLZ23]. At this time, the results in the Hermitian setup are much less sharp than for circular ensembles.
An important role in our analysis and results is played by the derivative martingale measure
![]() $\mathscr {D}_\infty (d\theta )$
and its total mass
$\mathscr {D}_\infty (d\theta )$
and its total mass
![]() $\mathscr {B}_\infty $
, both related to the theory of Gaussian Multiplicative Chaos (GMC); see [Reference Rhodes and VargasRV14] for a review. This is not surprising – the appearance of such martingales in the expression for the law of the maximum of the BBM was discovered already in [Reference Lalley and SellkeLS87]. Subsequentially, it appeared in the analogous studies for Branching Random Walks [Reference AïdékonAïd13], in the context of the Gaussian free field [Reference Duplantier, Rhodes, Sheffield and VargasDRSV14, Reference Biskup and LouidorBL18] and for more general log-correlated fields [Reference MadauleMad15]. As noted above, for a specific log-correlated field on the circle, [Reference RemyRem20] computes the law of the total mass of the associated GMC and confirms the Fyodorov-Bouchaud prediction [Reference Fyodorov and BouchaudFB08] for it.
$\mathscr {B}_\infty $
, both related to the theory of Gaussian Multiplicative Chaos (GMC); see [Reference Rhodes and VargasRV14] for a review. This is not surprising – the appearance of such martingales in the expression for the law of the maximum of the BBM was discovered already in [Reference Lalley and SellkeLS87]. Subsequentially, it appeared in the analogous studies for Branching Random Walks [Reference AïdékonAïd13], in the context of the Gaussian free field [Reference Duplantier, Rhodes, Sheffield and VargasDRSV14, Reference Biskup and LouidorBL18] and for more general log-correlated fields [Reference MadauleMad15]. As noted above, for a specific log-correlated field on the circle, [Reference RemyRem20] computes the law of the total mass of the associated GMC and confirms the Fyodorov-Bouchaud prediction [Reference Fyodorov and BouchaudFB08] for it.
We also mention that for a related model, [Reference Chhaibi and NajnudelCN19] provide a direct link with the relevant GMC. Their work implies convergence of the random measure ![]() when
when
![]() $\gamma =-2$
and
$\gamma =-2$
and
![]() $\beta \geq 2$
. After appropriate rescaling, this measure converges to the GMC of [Reference Fyodorov and BouchaudFB08, Reference RemyRem20, Reference Chhaibi and NajnudelCN19] rescaled to be a probability measure. Note that the exponent
$\beta \geq 2$
. After appropriate rescaling, this measure converges to the GMC of [Reference Fyodorov and BouchaudFB08, Reference RemyRem20, Reference Chhaibi and NajnudelCN19] rescaled to be a probability measure. Note that the exponent
![]() $\gamma =-2$
never quite appears in the problem we consider, and for any
$\gamma =-2$
never quite appears in the problem we consider, and for any
![]() $\beta $
, the relevant
$\beta $
, the relevant
![]() $\gamma $
is the positive critical point. When
$\gamma $
is the positive critical point. When
![]() $\beta =2$
, the full Fyodorov-Hiary-Keating conjecture would follow from convergence of
$\beta =2$
, the full Fyodorov-Hiary-Keating conjecture would follow from convergence of
![]() $\mathscr {D}_n(\theta )d\theta $
(which up to rescaling) to the same GMC; this is expected to have the same limit as
$\mathscr {D}_n(\theta )d\theta $
(which up to rescaling) to the same GMC; this is expected to have the same limit as ![]() (up to constants).
(up to constants).
Very recently, [Reference Lambert and NajnudelLN24] gave a proof of convergence of the random measure ![]() to the (subcritical) GMC whose total mass was evaluated in [Reference RemyRem20], for all
to the (subcritical) GMC whose total mass was evaluated in [Reference RemyRem20], for all
![]() $\gamma <\sqrt {2\beta }$
. Their techniques might be relevant to the evaluation of the law of
$\gamma <\sqrt {2\beta }$
. Their techniques might be relevant to the evaluation of the law of
![]() $\mathscr {D}_\infty $
, which corresponds to the case of critical GMC.
$\mathscr {D}_\infty $
, which corresponds to the case of critical GMC.
1.6 A high-level description of the proof
We now provide a high-level description of the proof that glosses over many important details. A detailed description of the proof that includes precise statements is provided in Section 2.
As in [Reference Chhaibi, Madaule and NajnudelCMN18], the key observation is that the recursion (1.10) contains all information needed in order to evaluate the determinant, due to (1.7). For fixed
![]() $\theta $
, the variable
$\theta $
, the variable
![]() $\varphi _k(\theta ), k=1,\ldots ,n$
can be well-approximated by a random walk, and further, for all k large, the increments of the random walk are essentially Gaussian.
$\varphi _k(\theta ), k=1,\ldots ,n$
can be well-approximated by a random walk, and further, for all k large, the increments of the random walk are essentially Gaussian.
We explain the strategy toward the proof of Theorem 1.4. We fix large constants
![]() $k_1,k_2$
(with
$k_1,k_2$
(with
![]() $k_1\gg k_2$
). Instead of directly studying the field
$k_1\gg k_2$
). Instead of directly studying the field ![]() , we consider a sublattice
, we consider a sublattice
![]() $\mathcal {D}_{n/k_1}$
of angles
$\mathcal {D}_{n/k_1}$
of angles
![]() $\theta _j$
of cardinality
$\theta _j$
of cardinality
![]() $\lceil n/k_1\rceil $
, and we associate to each an interval
$\lceil n/k_1\rceil $
, and we associate to each an interval
![]() $\widehat {I_{j,n}}$
as in (1.13). We write
$\widehat {I_{j,n}}$
as in (1.13). We write
and
We claim that the last expression can be approximated as
(This is not quite right, and in reality, we will need to consider an intermediate point
![]() $n/k_1^+$
with
$n/k_1^+$
with
![]() $k_1^+>k_1$
, but we gloss over this detail at this high-level description.)
$k_1^+>k_1$
, but we gloss over this detail at this high-level description.)
To analyze the maximum in (1.36), we introduce the field ![]() , with
, with ![]() and
and
![]() $\Delta $
defined above (1.36), and write (1.36) as
$\Delta $
defined above (1.36), and write (1.36) as
The main contribution to the maximum comes from js with
![]() $\Delta _{k_2,n/k_1}(\theta _j)$
large, of the order of
$\Delta _{k_2,n/k_1}(\theta _j)$
large, of the order of
![]() $\sqrt {8/\beta }(m_n-\log (k_1k_2))$
. However, the
$\sqrt {8/\beta }(m_n-\log (k_1k_2))$
. However, the
![]() $\Delta _{k_2,n/k_1}(j)$
are far from independent for different j. In order to begin controlling this, we introduce two ‘good events’: a global good event
$\Delta _{k_2,n/k_1}(j)$
are far from independent for different j. In order to begin controlling this, we introduce two ‘good events’: a global good event
![]() $\mathscr {G}_n$
, which allows us to replace the recursion by one driven by Gaussian variables (called
$\mathscr {G}_n$
, which allows us to replace the recursion by one driven by Gaussian variables (called
![]() $\mathfrak {z}_t(\theta )$
and taken for convenience in continuous time) and also impose an a priori upper limit on the recursion, and a barrier event
$\mathfrak {z}_t(\theta )$
and taken for convenience in continuous time) and also impose an a priori upper limit on the recursion, and a barrier event
![]() $\widehat {\mathscr {R}}$
, which ensures that the Gaussian-driven recursion
$\widehat {\mathscr {R}}$
, which ensures that the Gaussian-driven recursion
![]() $\mathfrak {z}_t(\theta )$
stays within a certain entropic envelope. We will also insist that
$\mathfrak {z}_t(\theta )$
stays within a certain entropic envelope. We will also insist that
![]() $\mathfrak {z}_{n/k_1}(\theta _j)$
stays within an appropriate window. These steps are similar to what is done in [Reference Chhaibi, Madaule and NajnudelCMN18], and they prepare the ground for the application of the second moment method.
$\mathfrak {z}_{n/k_1}(\theta _j)$
stays within an appropriate window. These steps are similar to what is done in [Reference Chhaibi, Madaule and NajnudelCMN18], and they prepare the ground for the application of the second moment method.
We next claim that the fields
![]() $f_{n,j}(\eta )$
converge in distribution to the solution of a system of coupled stochastic differential equations as in (2.52) (again, this is not literally the case and requires some pre-processing in the form of restriction to appropriate events and using
$f_{n,j}(\eta )$
converge in distribution to the solution of a system of coupled stochastic differential equations as in (2.52) (again, this is not literally the case and requires some pre-processing in the form of restriction to appropriate events and using
![]() $k_1^+$
as before). In particular, the laws of those fields are determined by the Markov kernel
$k_1^+$
as before). In particular, the laws of those fields are determined by the Markov kernel
![]() $\mathfrak {p}_{k_1}$
. Further and crucially, the fields
$\mathfrak {p}_{k_1}$
. Further and crucially, the fields
![]() $f_{n,j}$
can be constructed so that for well-separated js, they are independent. This analysis is contained in Sections 5 and 6.
$f_{n,j}$
can be constructed so that for well-separated js, they are independent. This analysis is contained in Sections 5 and 6.
As in many applications of the second moment method, to allow for some decoupling, it is necessary to condition on
![]() $\mathscr {F}_{k_2}$
. We need to find high points of the right side of (1.37). The basic estimate, for a given j, is that with
$\mathscr {F}_{k_2}$
. We need to find high points of the right side of (1.37). The basic estimate, for a given j, is that with
![]() $w_j=\sqrt {8/\beta } \log k_2-\varphi _{k_2}(\theta _j)$
,
$w_j=\sqrt {8/\beta } \log k_2-\varphi _{k_2}(\theta _j)$
,
 $$ \begin{align} \mathbb{P}\Big(\Delta_{k_2,n/k_1}(\theta_j)\sim \sqrt{8/\beta}(m_n-\log (k_1k_2)-v)\mid \mathscr{F}_{k_2}\Big) \sim C \frac{ve^{2v} w_j e^{-2w_j}}{n}.\end{align} $$
$$ \begin{align} \mathbb{P}\Big(\Delta_{k_2,n/k_1}(\theta_j)\sim \sqrt{8/\beta}(m_n-\log (k_1k_2)-v)\mid \mathscr{F}_{k_2}\Big) \sim C \frac{ve^{2v} w_j e^{-2w_j}}{n}.\end{align} $$
This estimate (after some pre-processing) is taken from [Reference Chhaibi, Madaule and NajnudelCMN18]; see Appendix B.
If the variables ![]() were an independent family, we would be at this point done, for then we would have that
were an independent family, we would be at this point done, for then we would have that

Hence, we have using independence over different j that

which would then yield Theorem 1.4.
Unfortunately, different js are not independent. We handle that through several Poisson approximations. First, we condition on
![]() $\mathscr {F}_{n/k_1}$
and use the ‘two moments suffice’ method of [Reference Arratia, Goldstein and GordonAGG89] to show that the process of near maxima (together with the shape
$\mathscr {F}_{n/k_1}$
and use the ‘two moments suffice’ method of [Reference Arratia, Goldstein and GordonAGG89] to show that the process of near maxima (together with the shape
![]() $(\varphi _n(\theta )-\varphi _{n/k_1}(\theta ), \theta \in \widehat {I_{j,n}})$
) can be well-approximated, as
$(\varphi _n(\theta )-\varphi _{n/k_1}(\theta ), \theta \in \widehat {I_{j,n}})$
) can be well-approximated, as
![]() $k_1\to \infty $
, by a Poisson point process of intensity
$k_1\to \infty $
, by a Poisson point process of intensity
![]() $\mathfrak {m}$
which depends still on
$\mathfrak {m}$
which depends still on
![]() $k_1$
; see (2.59) and Proposition 2.22. In the proof, the independence for well-separated js and the second moment computations play a crucial role. (As mentioned above, we need to replace
$k_1$
; see (2.59) and Proposition 2.22. In the proof, the independence for well-separated js and the second moment computations play a crucial role. (As mentioned above, we need to replace
![]() $k_1$
by
$k_1$
by
![]() $k_1^+\gg k_1$
to make the argument work; for this reason, we introduce a second Poisson approximation; see Section 2.6.)
$k_1^+\gg k_1$
to make the argument work; for this reason, we introduce a second Poisson approximation; see Section 2.6.)
This is close to the statement of Theorem 1.10, except that the Poisson process we obtained so far has a random intensity, measurable on
![]() $\mathscr {F}_{n/k_1^+}$
. Our final step is another standard use of the second moment method to show that this random intensity concentrates; see Section 2.9. As proved earlier in Section 1.3, all our theorems, and in particular Theorem 1.4, follow from Theorem 1.10.
$\mathscr {F}_{n/k_1^+}$
. Our final step is another standard use of the second moment method to show that this random intensity concentrates; see Section 2.9. As proved earlier in Section 1.3, all our theorems, and in particular Theorem 1.4, follow from Theorem 1.10.
2 The arc of the proof
In this (long) section, we will give a proof of the main theorem, in which we defer many of the major technical arguments to later sections. Each subsection, save for the first which contains preliminaries, carries one of the major steps in the proof of Theorem 1.10.
2.1 Soft properties of the Prüfer phases
We make here some elementary and important observations about the Prüfer phases. The Prüfer phases have that ![]() and
and ![]() are increasing functions of
are increasing functions of
![]() $\theta \in {\mathbb R}$
(see the discussion in [Reference Killip and StoiciuKS+09, Section 2]). Furthermore, for any
$\theta \in {\mathbb R}$
(see the discussion in [Reference Killip and StoiciuKS+09, Section 2]). Furthermore, for any
![]() $\theta \in {\mathbb R}$
and
$\theta \in {\mathbb R}$
and ![]()
It follows that the relative Prüfer phase ![]() for all
for all
![]() $\theta \geq 0$
and all
$\theta \geq 0$
and all
![]() $k \in {\mathbb N}.$
However, more is true. For any real number
$k \in {\mathbb N}.$
However, more is true. For any real number
![]() $x,$
let
$x,$
let ![]() be the largest element of
be the largest element of ![]() which is less than or equal to
which is less than or equal to
![]() $x.$
Also, let
$x.$
Also, let ![]() Then, we have the following:
Then, we have the following:
Lemma 2.1. For ![]() is a nondecreasing sequence in
is a nondecreasing sequence in
![]() $k.$
Also, for any
$k.$
Also, for any
![]() $k \geq 0, $
$k \geq 0, $
![]() .
.
Proof. We claim that the function
defined on ![]() is nonnegative. Observe that the function is harmonic in z for fixed
is nonnegative. Observe that the function is harmonic in z for fixed ![]() and bounded below for all
and bounded below for all
![]() $|z| < 1$
. Hence, by the Lindelöf maximum principle [Reference Garnett and MarshallGM08, Lemma 1.1], the infimum of this function over
$|z| < 1$
. Hence, by the Lindelöf maximum principle [Reference Garnett and MarshallGM08, Lemma 1.1], the infimum of this function over
![]() $|z| < 1$
is bounded below by its infimum over
$|z| < 1$
is bounded below by its infimum over
![]() $\{|z|=1\} \setminus F$
for any finite set F. However,
$\{|z|=1\} \setminus F$
for any finite set F. However, ![]() for
for ![]() and hence for
and hence for
![]() $|z|=1,$
the function takes values in
$|z|=1,$
the function takes values in ![]() except for when
except for when ![]()
Next we decompose, for any
![]() $k \geq 0$
and any
$k \geq 0$
and any
![]() $\theta \geq 0,$
$\theta \geq 0,$

Hence, the claim follows.
2.2 Marginally Gaussian approximations
We follow [Reference Chhaibi, Madaule and NajnudelCMN18] in introducing a family of processes with Gaussian marginals that well approximate the OPUC recurrence. We recall that the Prüfer phases can be expressed in terms of
![]() $\operatorname {Gamma}$
distributed random variables as
$\operatorname {Gamma}$
distributed random variables as

with all variables independent. We define the variables
Then
![]() $\left \{ \{X_j,Y_j\}\!:\! j \geq 0 \right \}$
are jointly iid
$\left \{ \{X_j,Y_j\}\!:\! j \geq 0 \right \}$
are jointly iid
![]() $N(0,\tfrac 12)$
and independent of
$N(0,\tfrac 12)$
and independent of
![]() $\left \{ \Gamma ^a_j\! :\! j \geq 0\right \}.$
Set
$\left \{ \Gamma ^a_j\! :\! j \geq 0\right \}.$
Set ![]() noting that
noting that
![]() $\mathbb {E} \Gamma ^a_j = \beta _j^2.$
$\mathbb {E} \Gamma ^a_j = \beta _j^2.$
We will also introduce a continuous time marginally Gaussian process
![]() $(\mathfrak {Z}_t^{\mathbb C} : t \geq 0),$
which we shall use for some comparisons. As
$(\mathfrak {Z}_t^{\mathbb C} : t \geq 0),$
which we shall use for some comparisons. As
![]() $\left \{ Z_k \right \}$
are independent standard complex Gaussians with
$\left \{ Z_k \right \}$
are independent standard complex Gaussians with
![]() $\mathbb {E} |Z_k|^2 = 1,$
we may enlarge the probability space to include a complex Brownian motion
$\mathbb {E} |Z_k|^2 = 1,$
we may enlarge the probability space to include a complex Brownian motion
![]() $(\mathfrak {W}_t : t \geq 0)$
such that
$(\mathfrak {W}_t : t \geq 0)$
such that
with
 $$ \begin{align} H_k = \sum_{j=1}^k \frac{1}{j} \end{align} $$
$$ \begin{align} H_k = \sum_{j=1}^k \frac{1}{j} \end{align} $$
the k-th harmonic number (and
![]() $H_0=0$
). In terms of
$H_0=0$
). In terms of
![]() $\mathfrak {W}$
, we define
$\mathfrak {W}$
, we define
![]() $\mathfrak {Z}^{\mathbb C}(\theta )$
by
$\mathfrak {Z}^{\mathbb C}(\theta )$
by

where for each
![]() $k \geq 0, k(s) = k$
on
$k \geq 0, k(s) = k$
on
![]() $s \in [ H_k,H_{k+1} ).$
Then by construction, we have the relationship
$s \in [ H_k,H_{k+1} ).$
Then by construction, we have the relationship

We also define
![]() $\mathfrak {Z}_t = \Re \bigl (\sigma \mathfrak {Z}_t^{{\mathbb C}}\bigr )$
for all
$\mathfrak {Z}_t = \Re \bigl (\sigma \mathfrak {Z}_t^{{\mathbb C}}\bigr )$
for all
![]() $t \geq H_{k_2},$
which therefore satisfies that
$t \geq H_{k_2},$
which therefore satisfies that
![]() $(\mathfrak {Z}_{t+H_{k_2}}-\mathfrak {Z}_{H_{k_2}} : t \geq 0)$
is a standard real Brownian motion.
$(\mathfrak {Z}_{t+H_{k_2}}-\mathfrak {Z}_{H_{k_2}} : t \geq 0)$
is a standard real Brownian motion.
In [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 3.1], it is shown that we can approximate ![]() by
by
![]() $\mathfrak {Z}_{H_k}^{\mathbb C}$
.
$\mathfrak {Z}_{H_k}^{\mathbb C}$
.
Proposition 2.2.
This is proven in [Reference Chhaibi, Madaule and NajnudelCMN18] though not explicitly stated as such. A careful reading of [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 3.1] (in which
![]() $\left \{ \mathfrak {Z}_{H_k}^{\mathbb C}(\theta ) \right \}$
is denoted
$\left \{ \mathfrak {Z}_{H_k}^{\mathbb C}(\theta ) \right \}$
is denoted
![]() $\left \{ Z_k(\theta ) \right \}$
) shows that their proof gives the statement in Proposition 2.2, which is stronger than what is claimed in [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 3.1]. We shall notate, where convenient, the coupled Gaussian random walks
$\left \{ Z_k(\theta ) \right \}$
) shows that their proof gives the statement in Proposition 2.2, which is stronger than what is claimed in [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 3.1]. We shall notate, where convenient, the coupled Gaussian random walks
Truncation
We will frequently need to truncate these variables. We let
![]() $M \in {\mathbb N}$
be a fixed large parameter and define an event
$M \in {\mathbb N}$
be a fixed large parameter and define an event
![]() $\mathscr {T}_M$
on which
$\mathscr {T}_M$
on which
By the construction of
![]() $\mathfrak {W},$
this event controls the magnitude of
$\mathfrak {W},$
this event controls the magnitude of
![]() $E_j = |X_j+i Y_j|^2.$
By adjusting the cutoffs for
$E_j = |X_j+i Y_j|^2.$
By adjusting the cutoffs for
![]() $\Gamma ^a_j$
, we may assume that on
$\Gamma ^a_j$
, we may assume that on ![]() We may further do this truncation in such a way that
We may further do this truncation in such a way that
![]() $\mathbb {P}(\mathscr {T}_M) \to 1$
as
$\mathbb {P}(\mathscr {T}_M) \to 1$
as
![]() $M \to \infty .$
$M \to \infty .$
2.3 First moment simplifications
In this section, we will show that near-maxima typically arise with many simplifying features. All the estimates in this section will use first-moment type estimates, which is to say that we will control the expected number of
![]() $j \in \mathcal {D}_{n/k_1}$
such that
$j \in \mathcal {D}_{n/k_1}$
such that
![]() $W_j$
is large without some other simplifying properties taking place.
$W_j$
is large without some other simplifying properties taking place.
2.3.1 The upsloping barriers
We will use the same barrier functions employed in [Reference Chhaibi, Madaule and NajnudelCMN18], so as to reuse as much of the machinery developed there. We begin by introducing a high barrier
![]() $A_k^{\ll }$
, which can be used to give a priori bounds on the growth of the processes
$A_k^{\ll }$
, which can be used to give a priori bounds on the growth of the processes
![]() $n \mapsto \varphi _n(\theta )$
:
$n \mapsto \varphi _n(\theta )$
:

where we recall that
![]() $H_k = \sum _{j=1}^k \frac {1}{j}$
is the k-th harmonic number; see (2.4).
$H_k = \sum _{j=1}^k \frac {1}{j}$
is the k-th harmonic number; see (2.4).
We let
![]() $\mathscr {B}_{n,k_2,k_6}$
be the event that the process is below this barrier at all
$\mathscr {B}_{n,k_2,k_6}$
be the event that the process is below this barrier at all ![]() at dyadic time points and at the final time; that is, for some
at dyadic time points and at the final time; that is, for some
![]() $k_6$
and with
$k_6$
and with
![]() $\log _2$
denoting the logarithm on basis
$\log _2$
denoting the logarithm on basis
![]() $2$
,
$2$
,

In the definition, we use only integer
![]() $k,$
and we recall that
$k,$
and we recall that
![]() $k_2 \in 2^{{\mathbb N}}.$
Then, the event that the barrier is exceeded satisfies:
$k_2 \in 2^{{\mathbb N}}.$
Then, the event that the barrier is exceeded satisfies:
Lemma 2.3.
Note that this barrier curves above the straight barrier (and further the function
![]() $H_k \mapsto A_{k}^{\ll }$
is piecewise concave). We will also use barriers that curve below, but the previous statement is not true for such barriers.
$H_k \mapsto A_{k}^{\ll }$
is piecewise concave). We will also use barriers that curve below, but the previous statement is not true for such barriers.
Proof. By Proposition 2.2, it is enough to prove the statement with
![]() $\varphi _{j}{(\theta )},$
replaced by
$\varphi _{j}{(\theta )},$
replaced by
![]() $\{G_j(\theta )\}$
. For the
$\{G_j(\theta )\}$
. For the
![]() $\{G_j(\theta )\}$
process, this is [Reference Chhaibi, Madaule and NajnudelCMN18, (4.4)].
$\{G_j(\theta )\}$
process, this is [Reference Chhaibi, Madaule and NajnudelCMN18, (4.4)].
Besides using an priori upper bound on the growth of the process
![]() $\varphi _n,$
we will also only work on the event that the processes
$\varphi _n,$
we will also only work on the event that the processes
![]() $G_k(\theta )$
and
$G_k(\theta )$
and
![]() $\varphi _k(\theta )$
are close, and so we define
$\varphi _k(\theta )$
are close, and so we define

We shall want to work on the event that for some
![]() $k_2,k_6 \in {\mathbb N},$
$k_2,k_6 \in {\mathbb N},$
where we recall that the truncation event
![]() $\mathscr {T}_{k_2}$
is defined in (2.8) and emphasize that this is indeed a typical event due to Proposition 2.2:
$\mathscr {T}_{k_2}$
is defined in (2.8) and emphasize that this is indeed a typical event due to Proposition 2.2:
Lemma 2.4. If we take n large followed by
![]() $k_2$
and
$k_2$
and
![]() $k_6,$
$k_6,$
2.3.2 Downsloping barriers and the banana
We shall use that extremal statistics are well-approximated by restricting the
![]() $\{\varphi _n(\theta )\}$
to a fine mesh in
$\{\varphi _n(\theta )\}$
to a fine mesh in
![]() $\theta $
. We let
$\theta $
. We let
![]() $k_5 \in {\mathbb N}$
be a parameter we use to control the mesh size, which will be
$k_5 \in {\mathbb N}$
be a parameter we use to control the mesh size, which will be ![]() . We introduce the near-leader event
. We introduce the near-leader event
![]() $\mathscr {L}(\theta ),$
which is simply that
$\mathscr {L}(\theta ),$
which is simply that
![]() $\varphi _n(\theta )$
is large:
$\varphi _n(\theta )$
is large:
We also introduce further barrier functions ![]() for any
for any
![]() $p \in {\mathbb N}$
,
$p \in {\mathbb N}$
,

A random walk conditioned to lie below the barrier
![]() $A_{(\cdot )}^{\ll }$
and conditioned to end near the barrier will tend to stay in the banana-like envelope
$A_{(\cdot )}^{\ll }$
and conditioned to end near the barrier will tend to stay in the banana-like envelope ![]() (and hence also,
(and hence also, ![]() for any
for any
![]() $p \geq 1$
).
$p \geq 1$
).
We introduce the barriers as it will be convenient over the course of the argument to change between barrier functions (all of which functionally play the same role). To aid in this changing of barriers, it is convenient if we further restrict the process at the entrance time
![]() $H_{k_2}$
to be in an even more restrained window. Recall that
$H_{k_2}$
to be in an even more restrained window. Recall that ![]() and define
and define
For fixed
![]() $\theta , (\mathfrak {Z}_t(\theta ) : t)$
has the law of a standard Brownian motion. This motivates the introduction of the following event:
$\theta , (\mathfrak {Z}_t(\theta ) : t)$
has the law of a standard Brownian motion. This motivates the introduction of the following event:
 $$ \begin{align} \widehat{\mathscr{R}}(\theta) &= \mathscr{U}(\theta) \cap \left\{ \forall~t \in [H_{k_2},H_n-k_4] : \sqrt{\tfrac{8}{\beta}}A_{t}^{1,-} \leq \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_t(\theta) \leq \sqrt{\tfrac{8}{\beta}}A_{t}^{1,+} \right\} \\ &\quad \bigcap \left\{ \forall t \in [H_n-k_4,H_n] \! : \! \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_t(\theta) \leq \sqrt{\tfrac{8}{\beta}}\bigl(t-\tfrac{3}{4}\log\log n + \tfrac{1}{\sqrt{2}}\bigl( \tfrac{t (H_n - t + (\log k_5)^{50})}{H_n}\bigr)^{1/50}\bigr) \right\}.\nonumber \end{align} $$
$$ \begin{align} \widehat{\mathscr{R}}(\theta) &= \mathscr{U}(\theta) \cap \left\{ \forall~t \in [H_{k_2},H_n-k_4] : \sqrt{\tfrac{8}{\beta}}A_{t}^{1,-} \leq \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_t(\theta) \leq \sqrt{\tfrac{8}{\beta}}A_{t}^{1,+} \right\} \\ &\quad \bigcap \left\{ \forall t \in [H_n-k_4,H_n] \! : \! \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_t(\theta) \leq \sqrt{\tfrac{8}{\beta}}\bigl(t-\tfrac{3}{4}\log\log n + \tfrac{1}{\sqrt{2}}\bigl( \tfrac{t (H_n - t + (\log k_5)^{50})}{H_n}\bigr)^{1/50}\bigr) \right\}.\nonumber \end{align} $$
We end the barrier
![]() $k_4$
time steps early, which is relatively early in the sense that
$k_4$
time steps early, which is relatively early in the sense that
![]() $k_4 \gg k_5.$
In some instances, we need barrier information which continues all the way to the end, for which reason we include the second part. We note that this is essentially provided to us by the good event
$k_4 \gg k_5.$
In some instances, we need barrier information which continues all the way to the end, for which reason we include the second part. We note that this is essentially provided to us by the good event
![]() $\mathscr {B}_{n,k_2,k_6}$
in (2.10), and it is a small argument to simply include the continuous part.
$\mathscr {B}_{n,k_2,k_6}$
in (2.10), and it is a small argument to simply include the continuous part.
We now show by a first moment argument that we may restrict attention to those angles for which this event occurs.
Proposition 2.5. For all
![]() $k_6$
,
$k_6$
,

Proof of Proposition 2.5.
On the event
![]() $\mathscr {G}_{n}$
(see (2.10) and (2.11)), we have that for any
$\mathscr {G}_{n}$
(see (2.10) and (2.11)), we have that for any ![]() ,
,
for integer k and for
![]() $k= \log _2 n.$
However, on the event
$k= \log _2 n.$
However, on the event
![]() $\mathscr {L}(\theta ) \cap \mathscr {G}_{n},$
we have
$\mathscr {L}(\theta ) \cap \mathscr {G}_{n},$
we have
We recall that ![]() It is a classical estimate on Gaussian random walk that when (2.16) and (2.17) and
It is a classical estimate on Gaussian random walk that when (2.16) and (2.17) and
![]() $\mathscr {U}(\theta )$
occur, the entropic envelope condition
$\mathscr {U}(\theta )$
occur, the entropic envelope condition
![]() $\widehat {\mathscr {R}}(\theta )$
is typical. Indeed, for
$\widehat {\mathscr {R}}(\theta )$
is typical. Indeed, for
![]() $\varphi _{k_2}(\theta ) \in [s_{k_2}^{-},s_{k_2}^{+}]$
(i.e., when
$\varphi _{k_2}(\theta ) \in [s_{k_2}^{-},s_{k_2}^{+}]$
(i.e., when
![]() $\mathscr {U}(\theta )$
occurs), we show in Lemma 4.3 that there are constants
$\mathscr {U}(\theta )$
occurs), we show in Lemma 4.3 that there are constants
![]() $C,c$
so that for all
$C,c$
so that for all
![]() $n \gg k_2 \gg k_4$
sufficiently large,
$n \gg k_2 \gg k_4$
sufficiently large,
 $$ \begin{align} \mathbb{P}(\widehat{\mathscr{R}}(\theta)^c \cap (2.17) \cap (2.16) \vert \mathfrak{Z}_{H_n}(\theta), \mathscr{F}_{k_2}) \leq C \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}(\theta)) e^{-(\log k_5)^{2}} }{\log n}. \end{align} $$
$$ \begin{align} \mathbb{P}(\widehat{\mathscr{R}}(\theta)^c \cap (2.17) \cap (2.16) \vert \mathfrak{Z}_{H_n}(\theta), \mathscr{F}_{k_2}) \leq C \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}(\theta)) e^{-(\log k_5)^{2}} }{\log n}. \end{align} $$
Now as we still have that the increment
it follows from integrating the Gaussian density that
 $$ \begin{align} \begin{aligned} &\mathbb{P}(\widehat{\mathscr{R}}(\theta)^c \cap (2.17) \cap (2.16)\cap \mathscr{G}_n \vert \mathscr{F}_{k_2}) \\ &\leq C \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}(\theta)) e^{-(\log k_5)^{2}} k_6}{\log n (H_n - H_{k_2})^{1/2}}\exp\left( -\frac{(\sqrt{2}m_n-\mathfrak{Z}_{H_{k_2}}(\theta) - 2k_6)^2}{2(H_n - H_{k_2})} \right). \\ &\leq C \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}(\theta)) e^{-(\log k_5)^{2}} k_6}{ n}\exp\left( 2\sqrt{2}k_6 + \sqrt{2}\mathfrak{Z}_{H_{k_2}}(\theta)- \log k_2 \right). \\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathbb{P}(\widehat{\mathscr{R}}(\theta)^c \cap (2.17) \cap (2.16)\cap \mathscr{G}_n \vert \mathscr{F}_{k_2}) \\ &\leq C \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}(\theta)) e^{-(\log k_5)^{2}} k_6}{\log n (H_n - H_{k_2})^{1/2}}\exp\left( -\frac{(\sqrt{2}m_n-\mathfrak{Z}_{H_{k_2}}(\theta) - 2k_6)^2}{2(H_n - H_{k_2})} \right). \\ &\leq C \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}(\theta)) e^{-(\log k_5)^{2}} k_6}{ n}\exp\left( 2\sqrt{2}k_6 + \sqrt{2}\mathfrak{Z}_{H_{k_2}}(\theta)- \log k_2 \right). \\ \end{aligned} \end{align} $$
We conclude that on the event
![]() $\varphi _{k_2}(\theta ) \in [s_{k_2}^{-},s_{k_2}^{+}],$
$\varphi _{k_2}(\theta ) \in [s_{k_2}^{-},s_{k_2}^{+}],$
 $$ \begin{align} \begin{aligned} \mathbb{P}( \mathscr{L}(\theta) \cap \widehat{\mathscr{R}}(\theta)^c \cap \mathscr{G}_n \vert \mathscr{F}_{k_2}) &\leq C_\beta \frac{ (\sqrt{2}\log k_2 -\mathfrak{Z}_{H_{k_2}}(\theta)) k_6 e^{-(\log k_5)^{2}} }{ n} e^{6k_6 + \sqrt{\tfrac{\beta}{2}}\varphi_{k_2}(\theta)- \log k_2 }. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbb{P}( \mathscr{L}(\theta) \cap \widehat{\mathscr{R}}(\theta)^c \cap \mathscr{G}_n \vert \mathscr{F}_{k_2}) &\leq C_\beta \frac{ (\sqrt{2}\log k_2 -\mathfrak{Z}_{H_{k_2}}(\theta)) k_6 e^{-(\log k_5)^{2}} }{ n} e^{6k_6 + \sqrt{\tfrac{\beta}{2}}\varphi_{k_2}(\theta)- \log k_2 }. \end{aligned} \end{align} $$
We must also give a relatively sharp bound when
![]() $\varphi _{k_2}(\theta )$
is outside this good range. These estimates are already given in [Reference Chhaibi, Madaule and NajnudelCMN18] but are essentially standard Gaussian random walk estimates going back to [Reference BramsonBra83]. As we work on the event
$\varphi _{k_2}(\theta )$
is outside this good range. These estimates are already given in [Reference Chhaibi, Madaule and NajnudelCMN18] but are essentially standard Gaussian random walk estimates going back to [Reference BramsonBra83]. As we work on the event
![]() $\mathscr {G}_n,$
(2.16) is given to us. The process
$\mathscr {G}_n,$
(2.16) is given to us. The process
![]() $k \mapsto G_{2^k}(\theta ) - G_{k_2}(\theta )$
is a Gaussian random walk whose increments have (nearly) variance
$k \mapsto G_{2^k}(\theta ) - G_{k_2}(\theta )$
is a Gaussian random walk whose increments have (nearly) variance
![]() ${\frac {4}{\beta }}\log 2$
started from
${\frac {4}{\beta }}\log 2$
started from
![]() $0.$
From (2.16), this process stays below the barrier
$0.$
From (2.16), this process stays below the barrier
![]() $k\mapsto \sqrt {\frac {8 \log 2}{\beta }}(k +g(k))$
with g controlled by
$k\mapsto \sqrt {\frac {8 \log 2}{\beta }}(k +g(k))$
with g controlled by
![]() $({k \wedge (\log _2 n-k)})^{1/100}.$
The probability of (2.17) happening is thus uniformly bounded from the appropriate ballot theorem (see, for example, [Reference Belius, Rosen and ZeitouniBRZ19, Lemma 2.1])
$({k \wedge (\log _2 n-k)})^{1/100}.$
The probability of (2.17) happening is thus uniformly bounded from the appropriate ballot theorem (see, for example, [Reference Belius, Rosen and ZeitouniBRZ19, Lemma 2.1])
 $$ \begin{align*} & \mathbb{P}((2.17) \cap \mathscr{G}_n \vert (2.16), \mathscr{F}_{k_2})\\ & \leq C_\beta \exp\left(-\frac{(\sqrt{\tfrac{8}{\beta}}m_n - \varphi_{k_2}(\theta) - 3k_6)^2}{\frac{8}{\beta}\log(n/k_2)}\right) \frac{ (\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)+ 2k_6) k_6}{(\log(n/k_2))^{3/2}}, \end{align*} $$
$$ \begin{align*} & \mathbb{P}((2.17) \cap \mathscr{G}_n \vert (2.16), \mathscr{F}_{k_2})\\ & \leq C_\beta \exp\left(-\frac{(\sqrt{\tfrac{8}{\beta}}m_n - \varphi_{k_2}(\theta) - 3k_6)^2}{\frac{8}{\beta}\log(n/k_2)}\right) \frac{ (\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)+ 2k_6) k_6}{(\log(n/k_2))^{3/2}}, \end{align*} $$
for some constant
![]() $C_\beta .$
On sending
$C_\beta .$
On sending
![]() $n \to \infty ,$
we therefore have (after increasing
$n \to \infty ,$
we therefore have (after increasing
![]() $C_\beta $
) that the left side of the last display is bounded above by the bound
$C_\beta $
) that the left side of the last display is bounded above by the bound
 $$ \begin{align} & \mathbb{P}((2.17)\cap \mathscr{G}_n \vert (2.16), \mathscr{F}_{k_2})\\ & \nonumber \leq C_\beta k_6^2 \exp\left( -\log( n k_2) + \sqrt{\tfrac{\beta}{2}}( \varphi_{k_2}(\theta) + c_\beta k_6)(1+o_n(1)) \right) \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)+ 2k_6\bigr). \end{align} $$
$$ \begin{align} & \mathbb{P}((2.17)\cap \mathscr{G}_n \vert (2.16), \mathscr{F}_{k_2})\\ & \nonumber \leq C_\beta k_6^2 \exp\left( -\log( n k_2) + \sqrt{\tfrac{\beta}{2}}( \varphi_{k_2}(\theta) + c_\beta k_6)(1+o_n(1)) \right) \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)+ 2k_6\bigr). \end{align} $$
We can now return to the summation we wish to bound:

We emphasize that in the events (2.17) and (2.16), we have taken ![]()
From the almost sure continuity of
![]() $\varphi _{k_2}(\theta )$
, we get convergence of these sums to integrals, and using (2.21) and (2.20),
$\varphi _{k_2}(\theta )$
, we get convergence of these sums to integrals, and using (2.21) and (2.20),

Hence, by Theorem 1.6, the convergence follows.
2.3.3 Meshing
We define for each
![]() $j \in {\mathcal {D}}_{n/k_1}$
the set
$j \in {\mathcal {D}}_{n/k_1}$
the set
![]() $I_j$
of
$I_j$
of ![]() which is at least distance
which is at least distance ![]() from the complement of
from the complement of
![]() $\widehat {I_j}$
; that is,
$\widehat {I_j}$
; that is,
For any
![]() $j\in {\mathbb Z},$
define
$j\in {\mathbb Z},$
define
Deterministically, it is possible to bound the error of
![]() $\widehat {W}_j$
(recall (1.15)) and the maximum of
$\widehat {W}_j$
(recall (1.15)) and the maximum of
![]() $\varphi _n$
over
$\varphi _n$
over ![]() (for example, as in [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 4.5]). We shall expand upon this by showing that, in fact, we can guarantee
(for example, as in [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 4.5]). We shall expand upon this by showing that, in fact, we can guarantee
![]() $\widehat {W}_j$
is large implies
$\widehat {W}_j$
is large implies
![]() $W_j$
is large, except with a negligible probability, as a consequence of interpolation.
$W_j$
is large, except with a negligible probability, as a consequence of interpolation.
Proposition 2.6. Any interval in which
![]() $\widehat {W}_j$
is large must also have
$\widehat {W}_j$
is large must also have
![]() $W_j$
is large in the sense that for any
$W_j$
is large in the sense that for any
![]() $k_7$
,
$k_7$
,

We delay the proof to the end of Section 3 until after introducing the relevant interpolation tools.
2.3.4 A canonical trunk with small oscillations
Tightness of
![]() $\max _j \widehat {W}_j$
and Proposition 2.6 guarantee that we can find choices of
$\max _j \widehat {W}_j$
and Proposition 2.6 guarantee that we can find choices of
![]() $\theta $
in the sufficiently fine mesh that are close to maximum. Combining this with Proposition 2.5, we conclude that all leading
$\theta $
in the sufficiently fine mesh that are close to maximum. Combining this with Proposition 2.5, we conclude that all leading
![]() $\theta $
behave like leading particles in a branching random walk in the sense that they are confined to the banana-like region. We would like to be able to say that for each interval
$\theta $
behave like leading particles in a branching random walk in the sense that they are confined to the banana-like region. We would like to be able to say that for each interval
![]() $I_j,$
for which
$I_j,$
for which
![]() $W_j \in [-k_6,k_6],$
all the random walks
$W_j \in [-k_6,k_6],$
all the random walks
![]() $(\varphi _{k}(\theta ) : k)$
for all
$(\varphi _{k}(\theta ) : k)$
for all
![]() $\theta \in I_j$
behave like a single random walk, at least for
$\theta \in I_j$
behave like a single random walk, at least for
![]() $k \leq {n}_1^+$
(which is long before the effective branching time).
$k \leq {n}_1^+$
(which is long before the effective branching time).
Recall that
![]() $\theta _j$
is the largest point of
$\theta _j$
is the largest point of
![]() $\widehat {I}_j.$
We proceed to define the events for
$\widehat {I}_j.$
We proceed to define the events for
![]() $j \in \mathcal {D}_{n/k_1}$
:
$j \in \mathcal {D}_{n/k_1}$
:

In the imaginary case
![]() $\sigma = i$
, we only use the event
$\sigma = i$
, we only use the event ![]() ; in the real case, we use the event
; in the real case, we use the event
![]() $\mathscr {O}_j$
, which of course implies the event
$\mathscr {O}_j$
, which of course implies the event
![]() $\mathscr {O}_j^+$
.
$\mathscr {O}_j^+$
.
These events control the oscillation of the respective functions on an interval of
![]() $\theta $
which is much smaller than the natural smoothness scale of
$\theta $
which is much smaller than the natural smoothness scale of
![]() $\varphi _{n_1^+}(\theta )$
is small. We are interested in controlling this oscillation when the random walk
$\varphi _{n_1^+}(\theta )$
is small. We are interested in controlling this oscillation when the random walk
![]() $(\varphi _{k}{(\theta _j)} : k)$
is a near-leader. Indeed, to that end, for
$(\varphi _{k}{(\theta _j)} : k)$
is a near-leader. Indeed, to that end, for
![]() $j \in \mathcal {D}_{n/k_1},$
define the good ray events
$j \in \mathcal {D}_{n/k_1},$
define the good ray events
 $$ \begin{align} \begin{aligned} &\mathscr{R}^p_{j}(m) = \mathscr{U}(\theta_j) \cap \left\{ \forall~ H_{k_2} \leq t \leq H_m : \sqrt{\tfrac{8}{\beta}}A_{t}^{p,-} \leq \sqrt{\tfrac{4}{\beta}} \mathfrak{Z}_t(\theta_j) \leq \sqrt{\tfrac{8}{\beta}}A_{t}^{p,+} \right\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathscr{R}^p_{j}(m) = \mathscr{U}(\theta_j) \cap \left\{ \forall~ H_{k_2} \leq t \leq H_m : \sqrt{\tfrac{8}{\beta}}A_{t}^{p,-} \leq \sqrt{\tfrac{4}{\beta}} \mathfrak{Z}_t(\theta_j) \leq \sqrt{\tfrac{8}{\beta}}A_{t}^{p,+} \right\}. \end{aligned} \end{align} $$
This differs from the previous (2.15) in that we specialize to the angle
![]() $\theta _j$
and that it only bounds the behavior of the walk up to time
$\theta _j$
and that it only bounds the behavior of the walk up to time
![]() $\log m.$
We have also slightly increased the barrier sizes from (2.15).
$\log m.$
We have also slightly increased the barrier sizes from (2.15).
Our main strategy for this estimate in the
![]() $\sigma =1$
case is to use the a priori bounds which ultimately follow from
$\sigma =1$
case is to use the a priori bounds which ultimately follow from ![]() being a polynomial of degree
being a polynomial of degree
![]() $k.$
This is contained in the following:
$k.$
This is contained in the following:
Proposition 2.7. (Real case
![]() $\sigma =1$
) For any
$\sigma =1$
) For any
![]() $k_5,k_6$
and all
$k_5,k_6$
and all
![]() $n \gg k_1$
sufficiently large, on the event
$n \gg k_1$
sufficiently large, on the event
![]() $\mathscr {G}_n$
, for any j for which there is a
$\mathscr {G}_n$
, for any j for which there is a
![]() $\theta ' \in I_j$
satisfying
$\theta ' \in I_j$
satisfying
also
![]() $\mathscr {O}_j$
holds.
$\mathscr {O}_j$
holds.
Proof. Recall that in the real case
![]() $(\sigma = 1)$
,
$(\sigma = 1)$
, ![]() Here, we will show that almost surely on the events in question, there is a deterministic error
Here, we will show that almost surely on the events in question, there is a deterministic error
![]() $\varepsilon _{k_1,n}$
so that for all
$\varepsilon _{k_1,n}$
so that for all
![]() $k_1$
sufficiently large,
$k_1$
sufficiently large,
 $$\begin{align*}\max_{\theta \in I_j} \max_{k_2 \leq k \leq \widehat{n}_1} |\varphi_k(\theta) - \varphi_k(\theta')| \leq \varepsilon_{k_1,n} \quad \text{where} \quad \limsup_{n\to \infty} \varepsilon_{k_1,n} \leq \sqrt{\tfrac{{k_1}}{\widehat{k}_1 }}. \end{align*}$$
$$\begin{align*}\max_{\theta \in I_j} \max_{k_2 \leq k \leq \widehat{n}_1} |\varphi_k(\theta) - \varphi_k(\theta')| \leq \varepsilon_{k_1,n} \quad \text{where} \quad \limsup_{n\to \infty} \varepsilon_{k_1,n} \leq \sqrt{\tfrac{{k_1}}{\widehat{k}_1 }}. \end{align*}$$
This will show that
![]() $\mathscr {O}_j$
holds for all n and
$\mathscr {O}_j$
holds for all n and
![]() $k_1$
large.
$k_1$
large.
On
![]() $\mathscr {G}_{n},$
we have that for any
$\mathscr {G}_{n},$
we have that for any
![]() $k_2\leq k \leq \widehat {n}_1$
and
$k_2\leq k \leq \widehat {n}_1$
and
![]() $|z| = 1$
,
$|z| = 1$
,
(A priori, we only have this bound on dyadic integers; however, the event
![]() $\mathscr {T}_{k_2}$
, which forms part of
$\mathscr {T}_{k_2}$
, which forms part of
![]() $\mathscr {G}_{k_2}$
, yields together with the latter that one can interpolate the bound to all integers in the indicated range.) From Bernstein’s inequality (see Theorem 8.1) for any
$\mathscr {G}_{k_2}$
, yields together with the latter that one can interpolate the bound to all integers in the indicated range.) From Bernstein’s inequality (see Theorem 8.1) for any
![]() $k \leq \widehat {n}_1$
and
$k \leq \widehat {n}_1$
and
![]() $|z| = 1,$
$|z| = 1,$
By construction, ![]() for all
for all
![]() $\theta \in I_j.$
Hence, for any
$\theta \in I_j.$
Hence, for any
![]() $\theta \in I_j,$
using the lower bound assumption on
$\theta \in I_j,$
using the lower bound assumption on
![]() $\varphi _{k}(\theta ')$
,
$\varphi _{k}(\theta ')$
,

The mapping
![]() $x \mapsto -\log x + C(\log x)^{17/18}$
is decreasing for all x bigger than some
$x \mapsto -\log x + C(\log x)^{17/18}$
is decreasing for all x bigger than some
![]() $x_0$
depending only on
$x_0$
depending only on
![]() $C,$
and therefore as
$C,$
and therefore as
![]() $k \leq \widehat {n}_1$
, we have that for all
$k \leq \widehat {n}_1$
, we have that for all
![]() $\widehat {k}_1$
sufficiently large,
$\widehat {k}_1$
sufficiently large,

which tends to
![]() $0$
for any
$0$
for any
![]() $\{k_p : p \geq 2\}.$
Moreover, recalling that from how
$\{k_p : p \geq 2\}.$
Moreover, recalling that from how
![]() $\widehat {k}_1$
is chosen,
$\widehat {k}_1$
is chosen,
![]() $\log (\tfrac {k_1}{\widehat {k}_1}) = \log (\widehat {k}_1)^{19/20}(1+o_{k_1})$
. Hence, we conclude that for all
$\log (\tfrac {k_1}{\widehat {k}_1}) = \log (\widehat {k}_1)^{19/20}(1+o_{k_1})$
. Hence, we conclude that for all
![]() $k_1$
sufficiently large,
$k_1$
sufficiently large,

This implies that
![]() $\mathscr {O}_j$
occurs.
$\mathscr {O}_j$
occurs.
Corollary 2.8. (Real case
![]() $\sigma =1$
) For any
$\sigma =1$
) For any
![]() $k_5,k_6$
,
$k_5,k_6$
,

Proof. Recall the ray event
![]() $\widehat {\mathscr {R}}(\theta )$
(cf. (2.15)). We further define the event
$\widehat {\mathscr {R}}(\theta )$
(cf. (2.15)). We further define the event
![]() $\widehat {\mathscr {R}}_j$
as the event that all almost-leaders in
$\widehat {\mathscr {R}}_j$
as the event that all almost-leaders in
![]() $I_j$
satisfy the ray event
$I_j$
satisfy the ray event
![]() $\widehat {\mathscr {R}}(\theta )$
:
$\widehat {\mathscr {R}}(\theta )$
:
 $$ \begin{align} \widehat{\mathscr{R}}_j = \bigcap_{ \theta \in I_j} (\mathscr{L}(\theta)^c \cup \widehat{\mathscr{R}}(\theta)). \end{align} $$
$$ \begin{align} \widehat{\mathscr{R}}_j = \bigcap_{ \theta \in I_j} (\mathscr{L}(\theta)^c \cup \widehat{\mathscr{R}}(\theta)). \end{align} $$
We note that using Proposition 2.5, with high probability at any mesh point
![]() $\theta $
at which
$\theta $
at which
![]() $\mathscr {L}(\theta )$
holds, the ray event
$\mathscr {L}(\theta )$
holds, the ray event
![]() $\widehat {\mathscr {R}}(\theta )$
holds as well. Hence, it suffices to show
$\widehat {\mathscr {R}}(\theta )$
holds as well. Hence, it suffices to show

Note that on the event
![]() $\{W_{j} \in [-k_6,k_6]\} \cap \widehat {\mathscr {R}}_j$
(from the definition (2.28)), we have that there is a
$\{W_{j} \in [-k_6,k_6]\} \cap \widehat {\mathscr {R}}_j$
(from the definition (2.28)), we have that there is a
![]() $\theta ' \in I_j$
for which
$\theta ' \in I_j$
for which
![]() $\mathscr {L}(\theta ') \cap \widehat { \mathscr {R}}(\theta ')$
holds. On
$\mathscr {L}(\theta ') \cap \widehat { \mathscr {R}}(\theta ')$
holds. On
![]() $\mathscr {G}_n$
, we have the uniform bound for all
$\mathscr {G}_n$
, we have the uniform bound for all
![]() $\theta \in I_j$
,
$\theta \in I_j$
,
and hence, at
![]() $\theta '$
, for all
$\theta '$
, for all
![]() $k_2 \leq k \leq \widehat {n}_1$
,
$k_2 \leq k \leq \widehat {n}_1$
,
Thus, from Proposition 2.7,
![]() $\mathscr {O}_j$
holds for all
$\mathscr {O}_j$
holds for all
![]() $k_1 \gg k_2$
sufficiently large.
$k_1 \gg k_2$
sufficiently large.
We must still show that
![]() $\mathscr {R}_j^2(\widehat {n}_1)$
occurs. As the event
$\mathscr {R}_j^2(\widehat {n}_1)$
occurs. As the event
![]() $\widehat {\mathscr {R}}(\theta ')$
holds and on
$\widehat {\mathscr {R}}(\theta ')$
holds and on
![]() $\mathscr {O}_j$
we can bound
$\mathscr {O}_j$
we can bound
![]() $|\varphi _{\widehat {n}_1}(\theta ')-\varphi _{\widehat {n}_1}(\theta _j)|=o_{k_2}(1)$
, then when
$|\varphi _{\widehat {n}_1}(\theta ')-\varphi _{\widehat {n}_1}(\theta _j)|=o_{k_2}(1)$
, then when
![]() $t=H_k$
for integer k with
$t=H_k$
for integer k with
![]() $\log _2 k_2 \leq k \leq \log _2 \widehat {n}_1$
,
$\log _2 k_2 \leq k \leq \log _2 \widehat {n}_1$
,
Now the oscillations of
![]() $\mathfrak {Z}_t(\theta ')$
for
$\mathfrak {Z}_t(\theta ')$
for
![]() $t \in [H_{k},H_{k+1}]$
are controlled, on
$t \in [H_{k},H_{k+1}]$
are controlled, on
![]() $\mathscr {G}_n$
(see (2.8)), by something which is
$\mathscr {G}_n$
(see (2.8)), by something which is
![]() $o_{k_2}(1).$
Thus, the conclusion holds with
$o_{k_2}(1).$
Thus, the conclusion holds with
![]() $p = 2$
, which absorbs the extra
$p = 2$
, which absorbs the extra
![]() $k_6$
term.
$k_6$
term.
This does not complete the analysis of the real case. We will also need that the Prüfer phases do not oscillate much. This we reduce to a conditional first moment estimate on ![]() .
.
Proposition 2.9. (Real case
![]() $\sigma =1$
) For any
$\sigma =1$
) For any
![]() $k_2,k_4,k_5,k_6$
and for any
$k_2,k_4,k_5,k_6$
and for any
![]() $p \leq 4$
,
$p \leq 4$
,

We note that the factor
![]() $(\log k_1)^{25}$
should be considered as a rate in this statement: the remainder of the constants would correctly balance the sum if the
$(\log k_1)^{25}$
should be considered as a rate in this statement: the remainder of the constants would correctly balance the sum if the ![]() term were removed. Indeed, our first application of this will be to show the following:
term were removed. Indeed, our first application of this will be to show the following:
Corollary 2.10. (Real case
![]() $\sigma =1$
) For any
$\sigma =1$
) For any
![]() $k_2,k_4,k_5,k_6$
and for any
$k_2,k_4,k_5,k_6$
and for any
![]() $p \leq 4$
,
$p \leq 4$
,

Proof of Corollary 2.10.
On the event
![]() $\mathscr {O}_j \cap \mathscr {G}_n,$
for all n sufficiently large, the event
$\mathscr {O}_j \cap \mathscr {G}_n,$
for all n sufficiently large, the event
![]() $W_j \in [-k_6,k_6]$
is contained in the event that for one of the
$W_j \in [-k_6,k_6]$
is contained in the event that for one of the
![]() $C k_5 k_1$
elements
$C k_5 k_1$
elements
![]() $\theta \in I_j$
and a constant
$\theta \in I_j$
and a constant
![]() $C(\beta ,k_6)$
sufficiently large,
$C(\beta ,k_6)$
sufficiently large,
Thus, conditioning on
![]() $\mathscr {F}_{\widehat {n}_1}$
and using the standard Gaussian tail bound,
$\mathscr {F}_{\widehat {n}_1}$
and using the standard Gaussian tail bound,

By how
![]() $\widehat {n}_1$
is defined (see (1.18)) and how the barrier is defined (2.13), this tends to
$\widehat {n}_1$
is defined (see (1.18)) and how the barrier is defined (2.13), this tends to
![]() $0$
with
$0$
with
![]() $k_1 \ll n$
(deterministically). Thus, the result follows from Proposition 2.9.
$k_1 \ll n$
(deterministically). Thus, the result follows from Proposition 2.9.
Proof of Proposition 2.9.
Using the bound on the difference of
![]() $\sqrt {\tfrac {\beta }{2}}\varphi _{\widehat {n}_1}(\theta _j)$
and
$\sqrt {\tfrac {\beta }{2}}\varphi _{\widehat {n}_1}(\theta _j)$
and
![]() $\sqrt {2}\mathfrak {Z}_{H_{\widehat {n}_1}}$
, it suffices to show
$\sqrt {2}\mathfrak {Z}_{H_{\widehat {n}_1}}$
, it suffices to show

Let
![]() $\theta _{j}^{\mp }$
be the largest and smallest element of
$\theta _{j}^{\mp }$
be the largest and smallest element of
![]() $\widehat {I}_j$
, respectively. Introduce the event
$\widehat {I}_j$
, respectively. Introduce the event

We emphasize the ray event
![]() $\mathscr {R}^p_j(\widehat {n}_1)$
runs to a much later time (when
$\mathscr {R}^p_j(\widehat {n}_1)$
runs to a much later time (when
![]() $k_1$
is large) than the oscillation event
$k_1$
is large) than the oscillation event
![]() $\widehat {\mathscr {O}}_j.$
$\widehat {\mathscr {O}}_j.$
Our main task will be to show that conditionally on
![]() $\mathfrak {Z}_{H_{\widehat {n}_1}}(\theta _j), \mathscr {F}_{k_2},$
and
$\mathfrak {Z}_{H_{\widehat {n}_1}}(\theta _j), \mathscr {F}_{k_2},$
and
![]() $\mathscr {R}^p_j(\widehat {n}_1),$
the probability of the event
$\mathscr {R}^p_j(\widehat {n}_1),$
the probability of the event
![]() $\bigl (\widehat {\mathscr {O}_j}\bigr )^c$
is controlled. We show in Corollary 4.7 (recall (2.7) for the change in notation) that there is a constant
$\bigl (\widehat {\mathscr {O}_j}\bigr )^c$
is controlled. We show in Corollary 4.7 (recall (2.7) for the change in notation) that there is a constant
![]() $C_\beta> 0$
sufficiently large that for all
$C_\beta> 0$
sufficiently large that for all
![]() $n,k_1$
large, uniformly in
$n,k_1$
large, uniformly in
![]() $\theta _j$
,
$\theta _j$
,
 $$ \begin{align} & \mathbb{P}[ \widehat{ \mathscr{O}_j}^c \cap \mathscr{R}_j^p(\widehat{n}_1) \cap \mathscr{G}_n ~\vert~ \mathscr{F}_{k_2}, \mathfrak{Z}_{H_{\widehat{n}_1}}(\theta_j)]\nonumber\\ & \qquad \leq C_\beta \frac{ \left( \sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta_j)+k_6 \right)_+ \left( \sqrt{2}m_n - \mathfrak{Z}_{H_{\widehat{n}_1}}(\theta_j) \right)_+ }{(\log k_1)^{50}\log(\widehat{n}_1/k_2)}. \end{align} $$
$$ \begin{align} & \mathbb{P}[ \widehat{ \mathscr{O}_j}^c \cap \mathscr{R}_j^p(\widehat{n}_1) \cap \mathscr{G}_n ~\vert~ \mathscr{F}_{k_2}, \mathfrak{Z}_{H_{\widehat{n}_1}}(\theta_j)]\nonumber\\ & \qquad \leq C_\beta \frac{ \left( \sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta_j)+k_6 \right)_+ \left( \sqrt{2}m_n - \mathfrak{Z}_{H_{\widehat{n}_1}}(\theta_j) \right)_+ }{(\log k_1)^{50}\log(\widehat{n}_1/k_2)}. \end{align} $$
We can now return to (2.31) and substitute in the left-hand side the last estimate. We can treat the exponential of
![]() $\sqrt {2}(\mathfrak {Z}_{H_{\widehat {n}_1}} - \mathfrak {Z}_{H_{k_2}}) - \log (\widehat {n}_1/k_2)$
as a change of measure. Under this tilted measure
$\sqrt {2}(\mathfrak {Z}_{H_{\widehat {n}_1}} - \mathfrak {Z}_{H_{k_2}}) - \log (\widehat {n}_1/k_2)$
as a change of measure. Under this tilted measure
![]() ${\mathbb Q}$
, the increment
${\mathbb Q}$
, the increment
![]() $\mathfrak {Z}_{H_{\widehat {n}_1}} - \mathfrak {Z}_{H_{k_2}}$
has mean
$\mathfrak {Z}_{H_{\widehat {n}_1}} - \mathfrak {Z}_{H_{k_2}}$
has mean
![]() $\sqrt {2}\log (\widehat {n}_1/k_2).$
Then recalling the definition of
$\sqrt {2}\log (\widehat {n}_1/k_2).$
Then recalling the definition of
![]() $\widehat {n}_1$
(see (1.18)) for all n sufficiently large,
$\widehat {n}_1$
(see (1.18)) for all n sufficiently large,

Thus, we conclude for all n sufficiently large using the Brownian Bridge ballot theorem [Reference Karatzas and ShreveKS91, (3.40)],

Hence, summing over
![]() $j \in \mathcal {D}_{n/k_1}$
and sending
$j \in \mathcal {D}_{n/k_1}$
and sending
![]() $n\to \infty ,$
$n\to \infty ,$

Hence, this tends to
![]() $0$
on multiplying by
$0$
on multiplying by
![]() $(\log k_1)^{25}$
and sending
$(\log k_1)^{25}$
and sending
![]() $k_1 \to \infty .$
$k_1 \to \infty .$
Proposition 2.11 (Imaginary case
 $\sigma =i$
).
$\sigma =i$
).
For any
![]() $k_5,k_6$
and
$k_5,k_6$
and
![]() $p = 2$
,
$p = 2$
,

Furthermore, for all
![]() $k_2$
sufficiently large and
$k_2$
sufficiently large and
![]() $p = 2$
,
$p = 2$
,

Proof. When ![]() for all
for all
![]() $k,\theta .$
The proof of the first claim is identical to the real case Proposition 2.9.
$k,\theta .$
The proof of the first claim is identical to the real case Proposition 2.9.
We turn to the second claim. From Proposition 2.5, we may assume that whenever ![]() occurs for some j, then so does
occurs for some j, then so does ![]() . We will further show now that whenever
. We will further show now that whenever ![]() occurs, so does the event
occurs, so does the event

In particular, in a manner similar to Proposition 2.9, we can derive

We comment briefly on the proof of (2.36) at the end, and we turn to deriving the second claim of this proposition. The event
![]() $\widehat {\mathscr {O}}(\theta )$
, for any
$\widehat {\mathscr {O}}(\theta )$
, for any
![]() $\theta \in I_j$
, directly implies
$\theta \in I_j$
, directly implies ![]() (recalling (2.26)), from the monotonicity of the Prüfer phases. However, on the event
(recalling (2.26)), from the monotonicity of the Prüfer phases. However, on the event
![]() $W_j \in [-k_6,k_6]$
, we have a
$W_j \in [-k_6,k_6]$
, we have a
![]() $\theta \in I_j$
so that
$\theta \in I_j$
so that
![]() $\widehat {\mathscr {R}}(\theta ) \cap \widehat {\mathscr {O}}(\theta )$
holds. Using monotonicity of the Prüfer phases and
$\widehat {\mathscr {R}}(\theta ) \cap \widehat {\mathscr {O}}(\theta )$
holds. Using monotonicity of the Prüfer phases and
![]() $\widehat {\mathscr {O}}(\theta )$
, for any k with
$\widehat {\mathscr {O}}(\theta )$
, for any k with
![]() $k_2 \leq k \leq n_1^+$
,
$k_2 \leq k \leq n_1^+$
,
Furthermore, trivially by monotonicity, ![]() , and so
, and so ![]() . Subtracting the mean behavior from
. Subtracting the mean behavior from ![]() for
for
![]() $\theta $
in this range also is vanishing; that is,
$\theta $
in this range also is vanishing; that is,
![]() $\max _{k_2\leq k \leq n_1^+} |\varphi _k(\theta _j) - \varphi _k(\theta )| = o_{k_1}(1)$
. As the oscillations of
$\max _{k_2\leq k \leq n_1^+} |\varphi _k(\theta _j) - \varphi _k(\theta )| = o_{k_1}(1)$
. As the oscillations of
![]() $\mathfrak {Z}_t$
for
$\mathfrak {Z}_t$
for
![]() $t \in [H_k,H_{k+1}]$
are
$t \in [H_k,H_{k+1}]$
are
![]() $o_{k_2}(1)$
on
$o_{k_2}(1)$
on
![]() $\mathscr {G}_n$
and
$\mathscr {G}_n$
and
![]() $|\sqrt {\tfrac {4}{\beta }}\mathfrak {Z}_{H_k}-\varphi _k|\leq k_6$
, we conclude for all
$|\sqrt {\tfrac {4}{\beta }}\mathfrak {Z}_{H_k}-\varphi _k|\leq k_6$
, we conclude for all
![]() $H_{k_2} \leq t \leq H_{n_1^+}$
,
$H_{k_2} \leq t \leq H_{n_1^+}$
,
 $$\begin{align*}\begin{aligned} &\sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta_j) \leq \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta) + o_{k_2}(1) + 2k_6 \leq \sqrt{\tfrac{8}{\beta}}A_t^{1,+} + o_{k_2}(1)+2k_6, \\ &\sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta_j) \geq \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta) - o_{k_2}(1) - 2k_6 \geq \sqrt{\tfrac{8}{\beta}}A_t^{1,-} - o_{k_2}(1) - 2k_6, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta_j) \leq \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta) + o_{k_2}(1) + 2k_6 \leq \sqrt{\tfrac{8}{\beta}}A_t^{1,+} + o_{k_2}(1)+2k_6, \\ &\sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta_j) \geq \sqrt{\tfrac{4}{\beta}}\mathfrak{Z}_{t}(\theta) - o_{k_2}(1) - 2k_6 \geq \sqrt{\tfrac{8}{\beta}}A_t^{1,-} - o_{k_2}(1) - 2k_6, \end{aligned} \end{align*}$$
which hence implies the event
![]() $\mathscr {R}^{1.1}_{j}({n}_1^+)$
for all
$\mathscr {R}^{1.1}_{j}({n}_1^+)$
for all
![]() $k_2$
sufficiently large. Thus, we have reduced the second claim to showing
$k_2$
sufficiently large. Thus, we have reduced the second claim to showing

We separately consider the events that
![]() $\mathscr {R}^2_{j}(\widehat {n}_1)$
fails due to 4βℨ
t
(θ
j
) ≥8βA
t
p, + or due to 8βA
t
p, −≥4βℨ
t
(θ
j
) for some t in
$\mathscr {R}^2_{j}(\widehat {n}_1)$
fails due to 4βℨ
t
(θ
j
) ≥8βA
t
p, + or due to 8βA
t
p, −≥4βℨ
t
(θ
j
) for some t in
![]() $[H_{n_1^+}, H_{\widehat {n}_1}],$
which we call
$[H_{n_1^+}, H_{\widehat {n}_1}],$
which we call
![]() $\operatorname {REsc}_j^+$
and
$\operatorname {REsc}_j^+$
and
![]() $\operatorname {REsc}_j^-$
, respectively. We start with the failure event
$\operatorname {REsc}_j^-$
, respectively. We start with the failure event
![]() $\operatorname {REsc}_j^+$
. For any
$\operatorname {REsc}_j^+$
. For any
![]() $\theta \in I_j$
, on the event
$\theta \in I_j$
, on the event
![]() $\mathscr {L}(\theta )$
, we must have
$\mathscr {L}(\theta )$
, we must have
Thus, conditioning on
![]() $\mathscr {F}_{{n}_1}$
and using the standard Gaussian tail bound,
$\mathscr {F}_{{n}_1}$
and using the standard Gaussian tail bound,

From monotonicity of the Prüfer phases, for
![]() $\theta \in I_j$
φ
n^1
(θ) ≤ φ
n^1
(θ
j
) + o
k
1
(1), and hence on
$\theta \in I_j$
φ
n^1
(θ) ≤ φ
n^1
(θ
j
) + o
k
1
(1), and hence on
![]() $\mathscr {G}_n$
, we have the same estimate for
$\mathscr {G}_n$
, we have the same estimate for
![]() $\mathfrak {Z}$
up to a constant depending on
$\mathfrak {Z}$
up to a constant depending on
![]() $k_6$
. Thus,
$k_6$
. Thus,

Hence, it suffices to estimate above the
![]() $\mathscr {F}_{n_1^+}$
-conditional probability of
$\mathscr {F}_{n_1^+}$
-conditional probability of
![]() $\operatorname {REsc}_j^+$
, which requires that the Brownian motion
$\operatorname {REsc}_j^+$
, which requires that the Brownian motion
![]() $\mathfrak {Z}_t$
for
$\mathfrak {Z}_t$
for
![]() $t \in [H_{n_1^+}, H_{\widehat {n}_1}]$
exceeds a barrier. This barrier can be bounded below by the linear barrier
$t \in [H_{n_1^+}, H_{\widehat {n}_1}]$
exceeds a barrier. This barrier can be bounded below by the linear barrier
with
![]() $p=2.$
We also have that
$p=2.$
We also have that
![]() $\mathfrak {Z}_t$
cannot exceed the barrier
$\mathfrak {Z}_t$
cannot exceed the barrier
which is implied by the event
![]() $\mathscr {G}_n$
for all
$\mathscr {G}_n$
for all
![]() $k_1$
sufficiently large.
$k_1$
sufficiently large.
The
![]() $\mathscr {F}_{n_1^+}\vee \sigma (\mathfrak {Z}_{H_{n_1}})$
-conditional probability that
$\mathscr {F}_{n_1^+}\vee \sigma (\mathfrak {Z}_{H_{n_1}})$
-conditional probability that
![]() $\mathfrak {Z}_{H_{\widehat {n}_1}}> \sqrt {2} A_{H_{\widehat {n}_1}}^{1,+}$
is vanishingly small as the variance of the Brownian bridge is at least
$\mathfrak {Z}_{H_{\widehat {n}_1}}> \sqrt {2} A_{H_{\widehat {n}_1}}^{1,+}$
is vanishingly small as the variance of the Brownian bridge is at least
![]() $\tfrac 12(\log k_1)^{19/20}$
at this time. Moreover, for a standard Brownian bridge, the probability that it stays below a straight line with intercepts
$\tfrac 12(\log k_1)^{19/20}$
at this time. Moreover, for a standard Brownian bridge, the probability that it stays below a straight line with intercepts
![]() $a,b> 0$
is
$a,b> 0$
is
![]() $1-e^{-2ab}$
[Reference Karatzas and ShreveKS91, (3.40)]. It follows that
$1-e^{-2ab}$
[Reference Karatzas and ShreveKS91, (3.40)]. It follows that
 $$\begin{align*}\mathbb{P}( ({2.39}) \mid \mathscr{F}_{n_1^+}\vee \sigma(\mathfrak{Z}_{H_{\widehat{n}_1}})) = 1-\exp\bigg(-2 \tfrac{(\sqrt{2}m_{n_1^+}-\mathfrak{Z}_{H_{n_1^+}}-(\log k_1)^{\tfrac{19}{20}\tfrac{1}{10}})(\sqrt{2}m_{\widehat{n}_1}-\mathfrak{Z}_{H_{\widehat{n}_1}}-(\log k_1)^{\tfrac{19}{20}\tfrac{1}{10}})}{H_{\widehat{n}_1}-H_{{n}_1^+}}\bigg). \end{align*}$$
$$\begin{align*}\mathbb{P}( ({2.39}) \mid \mathscr{F}_{n_1^+}\vee \sigma(\mathfrak{Z}_{H_{\widehat{n}_1}})) = 1-\exp\bigg(-2 \tfrac{(\sqrt{2}m_{n_1^+}-\mathfrak{Z}_{H_{n_1^+}}-(\log k_1)^{\tfrac{19}{20}\tfrac{1}{10}})(\sqrt{2}m_{\widehat{n}_1}-\mathfrak{Z}_{H_{\widehat{n}_1}}-(\log k_1)^{\tfrac{19}{20}\tfrac{1}{10}})}{H_{\widehat{n}_1}-H_{{n}_1^+}}\bigg). \end{align*}$$
Uniformly over allowed
![]() $\mathfrak {Z}_{H_{n_1}^+}$
(which are restricted by the event
$\mathfrak {Z}_{H_{n_1}^+}$
(which are restricted by the event
![]() $\mathscr {R}^{(1.1)}_j(n_1^+)$
) and uniformly over
$\mathscr {R}^{(1.1)}_j(n_1^+)$
) and uniformly over
![]() $\mathfrak {Z}_{H_{\widehat {n}_1}} \in [\sqrt {2} A_{H_{\widehat {n}_1}}^{1,-},\sqrt {2} A_{H_{\widehat {n}_1}}^{1,+}]$
,
$\mathfrak {Z}_{H_{\widehat {n}_1}} \in [\sqrt {2} A_{H_{\widehat {n}_1}}^{1,-},\sqrt {2} A_{H_{\widehat {n}_1}}^{1,+}]$
,
 $$\begin{align*}\mathbb{P}( ({2.39}) \mid \mathscr{F}_{n_1^+}\vee \sigma(\mathfrak{Z}_{H_{\widehat{n}_1}})) = 1-\exp\bigg(-2 \tfrac{(\sqrt{2}m_{n_1^+}-\mathfrak{Z}_{H_{n_1^+}})(\sqrt{2}m_{\widehat{n}_1}-\mathfrak{Z}_{H_{\widehat{n}_1}})}{H_{\widehat{n}_1}-H_{{n}_1^+}}(1+o_{k_1}(1))\bigg). \end{align*}$$
$$\begin{align*}\mathbb{P}( ({2.39}) \mid \mathscr{F}_{n_1^+}\vee \sigma(\mathfrak{Z}_{H_{\widehat{n}_1}})) = 1-\exp\bigg(-2 \tfrac{(\sqrt{2}m_{n_1^+}-\mathfrak{Z}_{H_{n_1^+}})(\sqrt{2}m_{\widehat{n}_1}-\mathfrak{Z}_{H_{\widehat{n}_1}})}{H_{\widehat{n}_1}-H_{{n}_1^+}}(1+o_{k_1}(1))\bigg). \end{align*}$$
The same holds for
![]() $\mathbb {P}( ({2.40}) \mid \mathscr {F}_{n_1^+}\vee \sigma (\mathfrak {Z}_{H_{\widehat {n}_1}}))$
, and so we conclude that
$\mathbb {P}( ({2.40}) \mid \mathscr {F}_{n_1^+}\vee \sigma (\mathfrak {Z}_{H_{\widehat {n}_1}}))$
, and so we conclude that
as either both probabilities are close to
![]() $1$
(and so no cancellation within the exponentials is needed), or they cancel. We conclude that
$1$
(and so no cancellation within the exponentials is needed), or they cancel. We conclude that

so that we have shown

This conditional expectation we then evaluate, giving

Hence, on sending
![]() $k_1 \to \infty $
and using Theorem 1.6, this tends to
$k_1 \to \infty $
and using Theorem 1.6, this tends to
![]() $0$
.
$0$
.
Recalling the definition below (2.37), we turn to the case of
![]() $\operatorname {REsc}_j^-$
. On this event, for some
$\operatorname {REsc}_j^-$
. On this event, for some
![]() $t \in [H_{n_1^+}, H_{\widehat {n}_1}]$
, we have
$t \in [H_{n_1^+}, H_{\widehat {n}_1}]$
, we have
![]() $\mathfrak {Z}_t(\theta _j) \leq \sqrt {2}(t - \tfrac 34 \log \log n - (\log n - t)^{\tfrac {9}{10}}).$
From monotonicity, it follows that for all
$\mathfrak {Z}_t(\theta _j) \leq \sqrt {2}(t - \tfrac 34 \log \log n - (\log n - t)^{\tfrac {9}{10}}).$
From monotonicity, it follows that for all
![]() $\theta \in I_j$
and some
$\theta \in I_j$
and some
![]() $t \in [H_{n_1^+}, H_{\widehat {n}_1}]$
,
$t \in [H_{n_1^+}, H_{\widehat {n}_1}]$
,
However, on the event
![]() $\widehat {R}(\theta ),$
we have
$\widehat {R}(\theta ),$
we have
Hence, these are incompatible, and so we have that trivially,

We finish by briefly commenting on the proof of (2.36). We begin by taking a conditional probability of the event ![]() . From Corollary 4.7,
. From Corollary 4.7,

This is the same control that we had in the real part (compare to (2.33)), and so the proof can be completed in a similar way to Proposition 2.9.
2.4 Decoupling and a diffusion approximation
Our main tool for showing a Poisson approximation will be to modify the process
![]() $\varphi _k$
for
$\varphi _k$
for
![]() $k \geq n_1^+$
which shows both that in a sense,
$k \geq n_1^+$
which shows both that in a sense,
![]() $\varphi _k(\theta )-\varphi _{n_1^+}(\theta )$
stabilizes as
$\varphi _k(\theta )-\varphi _{n_1^+}(\theta )$
stabilizes as
![]() $n\to \infty $
and simultaneously gives actual
$n\to \infty $
and simultaneously gives actual
![]() $(\mathscr {F}_{n_1^+})$
-conditional independence of these processes for sufficiently separated
$(\mathscr {F}_{n_1^+})$
-conditional independence of these processes for sufficiently separated
![]() $\theta .$
Set
$\theta .$
Set
![]() $T_{+} = \log k_1$
and
$T_{+} = \log k_1$
and
![]() $T_- = \log (k_1/k_1^+).$
We shall construct a family of standard complex Brownian motions
$T_- = \log (k_1/k_1^+).$
We shall construct a family of standard complex Brownian motions
which will have the property that they are independent from one another when the relevant arcs are separated by a small power of
![]() $n.$
Now with respect to these Brownian motions, we define the complex diffusions
$n.$
Now with respect to these Brownian motions, we define the complex diffusions
![]() $(\mathfrak {L}^j_t : t \in [T_-,T_+], \theta \in {\mathbb R},j \in \mathcal {D}_{n/k_1})$
as the (strong) solution of the stochastic differential equation
$(\mathfrak {L}^j_t : t \in [T_-,T_+], \theta \in {\mathbb R},j \in \mathcal {D}_{n/k_1})$
as the (strong) solution of the stochastic differential equation

The diffusion
![]() $\mathfrak {L}^j(\theta )$
will serve as a proxy for the evolution of
$\mathfrak {L}^j(\theta )$
will serve as a proxy for the evolution of ![]() , where
, where
![]() $k(t) \approx n_1 e^t$
up to rounding errors, and in particular, its imaginary part will mimick the evolution of the Prüfer phases. When
$k(t) \approx n_1 e^t$
up to rounding errors, and in particular, its imaginary part will mimick the evolution of the Prüfer phases. When
![]() $\sigma =1$
, the diffusion
$\sigma =1$
, the diffusion
![]() $\mathfrak {U}^j_t(\theta )$
is designed to be a proxy for
$\mathfrak {U}^j_t(\theta )$
is designed to be a proxy for ![]() .
.
Later, we shall consider different initial conditions for the SDE in (2.43), which will be enforced at
![]() $t=T_-$
; Namely, we shall enforce constant initial conditions (the latter process will be denoted
$t=T_-$
; Namely, we shall enforce constant initial conditions (the latter process will be denoted
![]() $\mathfrak {L}_t^{o,j}$
or
$\mathfrak {L}_t^{o,j}$
or
![]() $\mathfrak {L}_t^o$
; see, for example, (2.52) below). We note that if the initial conditions do not depend on n, then the law of the process in (2.43) does not depend on n; moreover if the initial conditions are constant in
$\mathfrak {L}_t^o$
; see, for example, (2.52) below). We note that if the initial conditions do not depend on n, then the law of the process in (2.43) does not depend on n; moreover if the initial conditions are constant in
![]() $\theta $
, then the law of this diffusion is just a translation of a
$\theta $
, then the law of this diffusion is just a translation of a
![]() $0$
-initial condition process by the initialization.
$0$
-initial condition process by the initialization.
Proposition 2.12. Fix
![]() $C>0$
. Then, there exists
$C>0$
. Then, there exists
![]() $\delta _0>0$
so that for any
$\delta _0>0$
so that for any
![]() $\delta \in (0,\delta _0)$
, there exists a family of Brownian motions
$\delta \in (0,\delta _0)$
, there exists a family of Brownian motions
![]() $\{ \mathfrak {W}_{t}^j : T_- \leq t \leq T_+, j \in \mathcal {D}_{n/k_1}\}$
so that the following holds. Let
$\{ \mathfrak {W}_{t}^j : T_- \leq t \leq T_+, j \in \mathcal {D}_{n/k_1}\}$
so that the following holds. Let
![]() $j \in \mathcal {D}_{n/k_1}.$
Let
$j \in \mathcal {D}_{n/k_1}.$
Let
![]() $(\mathfrak {L}^j_t : t \in [T_-,T_+])$
solve (2.43). For all n sufficiently large (with respect to
$(\mathfrak {L}^j_t : t \in [T_-,T_+])$
solve (2.43). For all n sufficiently large (with respect to
![]() $k_1$
),
$k_1$
),

where
![]() $\log k(t)= \log k_n(t)$
is a linear function with
$\log k(t)= \log k_n(t)$
is a linear function with
![]() $k(T_-) = n_1^+$
and
$k(T_-) = n_1^+$
and
![]() $k(T_+) = n.$
Moreover, for any
$k(T_+) = n.$
Moreover, for any
![]() $j \in \mathcal {D}_{n/k_1}$
,
$j \in \mathcal {D}_{n/k_1}$
,
are conditionally independent given
![]() $\mathscr {F}_{n_1^+}.$
$\mathscr {F}_{n_1^+}.$
This allows the comparison of ![]() to different
to different
![]() $\mathfrak {L}^{j'}$
(for
$\mathfrak {L}^{j'}$
(for
![]() $j'\neq j$
) provided that
$j'\neq j$
) provided that
![]() $|\theta _j-\theta _{j'}|$
is small enough. We give the proof in Section 5.
$|\theta _j-\theta _{j'}|$
is small enough. We give the proof in Section 5.
2.4.1 Simplifying the decoration
Now, since the probability is so high that
![]() $|\mathfrak {U}^j_t(\theta ) - \varphi _{k(t)}(\theta _j + \tfrac {\theta }{n}) +\sqrt {\tfrac {8}{\beta }}m_n| < n^{-\delta }$
for all
$|\mathfrak {U}^j_t(\theta ) - \varphi _{k(t)}(\theta _j + \tfrac {\theta }{n}) +\sqrt {\tfrac {8}{\beta }}m_n| < n^{-\delta }$
for all
![]() $t \in [T_-,T_+]$
, we may just work on the event
$t \in [T_-,T_+]$
, we may just work on the event

We will also introduce another barrier event, now specific to
![]() $\mathfrak {U}^j$
and only concerning
$\mathfrak {U}^j$
and only concerning
![]() $k \geq n_1^+.$
We define a decoration ray event with a (once more) enlarged barrier function. These are given by, for
$k \geq n_1^+.$
We define a decoration ray event with a (once more) enlarged barrier function. These are given by, for
![]() $t \in [T_-,T_+]$
,
$t \in [T_-,T_+]$
,
Note the exponents coincide with those of ![]() . So we introduce a decoration ray event
. So we introduce a decoration ray event

the latter of which states that all lattice-point near-leaders (
![]() $\theta \in I_j$
for which
$\theta \in I_j$
for which
![]() $\mathfrak {U}^j_{T_+}(\theta )$
is large) reached that height by staying within (an enlarged) banana-like tube. On the event
$\mathfrak {U}^j_{T_+}(\theta )$
is large) reached that height by staying within (an enlarged) banana-like tube. On the event
![]() $\mathscr {G}^1_n \cap \mathscr {G}_n,$
if the event
$\mathscr {G}^1_n \cap \mathscr {G}_n,$
if the event
![]() $\widehat {\mathscr {R}_j}$
holds (see (2.28) and (2.15)), then deterministically,
$\widehat {\mathscr {R}_j}$
holds (see (2.28) and (2.15)), then deterministically,
![]() $\mathscr {P}_j'$
holds as well (once
$\mathscr {P}_j'$
holds as well (once
![]() $k_1$
and
$k_1$
and
![]() $k_4$
are sufficiently large).
$k_4$
are sufficiently large).
Instead of looking at the local maximum of
![]() $\varphi _n$
, we may look at the local maximum of
$\varphi _n$
, we may look at the local maximum of
![]() $\mathfrak {U}^j_{T^+}.$
Moreover, we define the analogues of
$\mathfrak {U}^j_{T^+}.$
Moreover, we define the analogues of
![]() $W_j$
and
$W_j$
and
![]() $V_j$
(see (2.25) and (1.19)) for this new process
$V_j$
(see (2.25) and (1.19)) for this new process

We also define a new decoration process
![]() $D_j'$
by first defining it on a mesh by the formula
$D_j'$
by first defining it on a mesh by the formula

We extend
![]() $D_j'$
to be piecewise linear between the mesh points.
$D_j'$
to be piecewise linear between the mesh points.
2.4.2 Continuity of the decoration processes around near maxima
We need to show that near local maxima, the decoration process is well-behaved and, moreover, that the meshing accurately captures the continuum process. Define the good event:
Definition 2.13. We let
![]() ${\mathscr {N}}_j$
be the event that the following holds.
${\mathscr {N}}_j$
be the event that the following holds.
-
1. The maximum over the grid,
 $W_j,$
is in
$W_j,$
is in
 $[-k_6,k_6].$
$[-k_6,k_6].$
-
2. For some
 $\epsilon _\beta $
(to be specified), in the neighborhood of a near-maximal grid point
$\epsilon _\beta $
(to be specified), in the neighborhood of a near-maximal grid point
 $\theta \in I_j$
, the field
$\theta \in I_j$
, the field
 $\varphi _n(\theta )$
does not vary too much. Specifically, at any point
$\varphi _n(\theta )$
does not vary too much. Specifically, at any point
 $\theta \in I_j$
at which
$\theta \in I_j$
at which
 $\varphi _n(\theta ) \in \sqrt {\tfrac {8}{\beta }}m_{n} + [-k_6,\infty )$
(i.e.,
$\varphi _n(\theta ) \in \sqrt {\tfrac {8}{\beta }}m_{n} + [-k_6,\infty )$
(i.e.,
 $\mathscr {L}(\theta )$
holds), all points
$\mathscr {L}(\theta )$
holds), all points
 $\theta '$
with
$\theta '$
with  satisfy
satisfy
 $|\varphi _n(\theta )-\varphi _n(\theta ')| \leq k_5^{-\epsilon _\beta }.$
$|\varphi _n(\theta )-\varphi _n(\theta ')| \leq k_5^{-\epsilon _\beta }.$
-
3. For any point
 $\theta \in \widehat {I}_j$
at which
$\theta \in \widehat {I}_j$
at which
 $\varphi _n(\theta ) \geq \sqrt {\tfrac {8}{\beta }}m_{n} - k_6$
, there is a point
$\varphi _n(\theta ) \geq \sqrt {\tfrac {8}{\beta }}m_{n} - k_6$
, there is a point
 $\theta ' \in I_j$
with
$\theta ' \in I_j$
with  at which
at which
 $|\varphi _n(\theta )-\varphi _n(\theta ')| \leq k_5^{-\epsilon _\beta }.$
$|\varphi _n(\theta )-\varphi _n(\theta ')| \leq k_5^{-\epsilon _\beta }.$
By a combination of a first moment argument and interpolation theorems for polynomials, we show that in any arc where
![]() $\widehat {W}_j$
is large, we also have
$\widehat {W}_j$
is large, we also have
![]() $\mathscr {N}_j.$
$\mathscr {N}_j.$
Proposition 2.14. Any interval in which
![]() $\widehat {W}_j$
is large must also have
$\widehat {W}_j$
is large must also have
![]() $\mathscr {N}_j$
occur in that
$\mathscr {N}_j$
occur in that

We give the proof in Section 3.
2.5 Summary of first-moment reductions
The reductions made in Section 2.3 will now be summarized. Define for
![]() $j \in \mathcal {D}_{n/k_1}$
,
$j \in \mathcal {D}_{n/k_1}$
,
Using these events, define for Borel subsets of ![]() the following approximation:
the following approximation:

Proposition 2.15. For any
![]() $k_7$
, the restrictions of
$k_7$
, the restrictions of
![]() $\operatorname {Extr}_n$
and
$\operatorname {Extr}_n$
and
![]() $\operatorname {Ext}_n$
to
$\operatorname {Ext}_n$
to
![]() $\Gamma _{k_7}$
satisfy
$\Gamma _{k_7}$
satisfy
Proof. By definition of the metric ![]() , we may restrict the point processes to good events and conclude
, we may restrict the point processes to good events and conclude
and hence, from Lemma 2.4 and Proposition 2.12, this tends to
![]() $0$
in that
$0$
in that
The same holds for
![]() $\operatorname {Extr}_n$
replaced by
$\operatorname {Extr}_n$
replaced by
![]() $\operatorname {Ext}_n,$
and so we may as well restrict to the event
$\operatorname {Ext}_n,$
and so we may as well restrict to the event
![]() ${\mathscr {G}^1_n \cap \mathscr {G}_n}.$
${\mathscr {G}^1_n \cap \mathscr {G}_n}.$
The point process
![]() $\operatorname {Ext}_n$
we then further thin by defining
$\operatorname {Ext}_n$
we then further thin by defining

and

We have that as point processes
![]() $ \operatorname {Ext}_n \geq \operatorname {Ext}_n' \geq \operatorname {Ext}_n". $
Hence, from the definition of the
$ \operatorname {Ext}_n \geq \operatorname {Ext}_n' \geq \operatorname {Ext}_n". $
Hence, from the definition of the ![]() -distance, it suffices to show that
-distance, it suffices to show that ![]() as it then follows that all of these point processes are close on restriction to
as it then follows that all of these point processes are close on restriction to
![]() $\Gamma _{k_7}$
.
$\Gamma _{k_7}$
.
Recall that the events
![]() $\mathscr {R}_{j}^2(\widehat {n}_1) \subseteq \mathscr {R}_{j}^2({n}_1^+)$
and
$\mathscr {R}_{j}^2(\widehat {n}_1) \subseteq \mathscr {R}_{j}^2({n}_1^+)$
and
![]() $\mathscr {O}_j \subseteq \mathscr {O}_j^+.$
We claim that the combination of Propositions 2.6, 2.7, 2.11 and 2.14 together with Corollary 2.10 show that on the good event
$\mathscr {O}_j \subseteq \mathscr {O}_j^+.$
We claim that the combination of Propositions 2.6, 2.7, 2.11 and 2.14 together with Corollary 2.10 show that on the good event
![]() ${\mathscr {G}^1_n \cap \mathscr {G}_n}$
, the expected number of points lost by performing this thinning tends to
${\mathscr {G}^1_n \cap \mathscr {G}_n}$
, the expected number of points lost by performing this thinning tends to
![]() $0$
; that is,
$0$
; that is,
Proposition 2.6 implies that for any triple
![]() $(\theta _j,V_j,D_je^{\sqrt {4/\beta }V_j}) \in \Gamma _{k_7}$
, we may include the good event that
$(\theta _j,V_j,D_je^{\sqrt {4/\beta }V_j}) \in \Gamma _{k_7}$
, we may include the good event that
![]() ${W_j} \in [-k_6,k_6]$
. Proposition 2.7 implies for
${W_j} \in [-k_6,k_6]$
. Proposition 2.7 implies for
![]() $\sigma =1$
(the real case) that for any
$\sigma =1$
(the real case) that for any
![]() ${W_j} \in [-k_6,k_6]$
, we may include the good events both
${W_j} \in [-k_6,k_6]$
, we may include the good events both
![]() $\mathscr {R}_{j}^2(\widehat {n}_1)$
and
$\mathscr {R}_{j}^2(\widehat {n}_1)$
and
![]() $\mathscr {O}_j$
. Corollary 2.10 implies for
$\mathscr {O}_j$
. Corollary 2.10 implies for
![]() $\sigma =1$
(the real case) that we may further add the good event that
$\sigma =1$
(the real case) that we may further add the good event that ![]() occurs. Proposition 2.11 implies the analogue of the previous two statements in the imaginary case. Proposition 2.14 finally adds the
occurs. Proposition 2.11 implies the analogue of the previous two statements in the imaginary case. Proposition 2.14 finally adds the
![]() $\mathscr {N}_j$
event.
$\mathscr {N}_j$
event.
We also introduce a thinning

On the events
![]() $\mathscr {G}^1_n \cap \mathscr {G}_n$
, we have
$\mathscr {G}^1_n \cap \mathscr {G}_n$
, we have
In particular,
Finally, we undo the thinning on
![]() $\operatorname {Extr}_n.$
We just note that since on the event
$\operatorname {Extr}_n.$
We just note that since on the event
![]() $\mathscr {G}^1_n \cap \mathscr {G}_n$
, the processes
$\mathscr {G}^1_n \cap \mathscr {G}_n$
, the processes
![]() $(V_j',V_j)$
and
$(V_j',V_j)$
and
![]() $(D_j', D_j)$
are sufficiently close, we have that
$(D_j', D_j)$
are sufficiently close, we have that
As (2.51) holds for any
![]() $k_7$
, the result follows.
$k_7$
, the result follows.
2.6 Second approximation: removing the oscillations at level
 $n_1^+$
$n_1^+$
The first-moment reductions allow us to assume that the profile at level
![]() $n_1^+$
in the neighborhoods of high decorations are flat. However, they still carry n-dependence, and we still need to show that these small oscillations at level
$n_1^+$
in the neighborhoods of high decorations are flat. However, they still carry n-dependence, and we still need to show that these small oscillations at level
![]() $n_1^+$
propagate to small oscillations at the level
$n_1^+$
propagate to small oscillations at the level
![]() $n.$
So, we introduce a new diffusion which solves (2.43) after an intermediate time
$n.$
So, we introduce a new diffusion which solves (2.43) after an intermediate time
![]() $T_\dagger = \log (k_1/\widehat {k}_1)$
, has
$T_\dagger = \log (k_1/\widehat {k}_1)$
, has
![]() $0$
initial conditions at time
$0$
initial conditions at time
![]() $T_{-}$
, and between
$T_{-}$
, and between
![]() $[T_-,T_\dagger ]$
, it is a single Brownian motion.
$[T_-,T_\dagger ]$
, it is a single Brownian motion.

These initial conditions are flat in that they do not vary over the interval ![]() (note that the value of the initial condition, when flat, does not change the law of the increments). We note that there is a fixed phase
(note that the value of the initial condition, when flat, does not change the law of the increments). We note that there is a fixed phase
![]() $\Im \mathfrak {L}^{j}_{T_-}(0)$
that appears in the diffusion, which does not affect the law of the process as it rotates the complex white noise. We shall show that
$\Im \mathfrak {L}^{j}_{T_-}(0)$
that appears in the diffusion, which does not affect the law of the process as it rotates the complex white noise. We shall show that
![]() $\mathfrak {L}^{o,j}_t(\theta ) + \mathfrak {L}^{j}_{T_-}(0)$
is a good approximation for
$\mathfrak {L}^{o,j}_t(\theta ) + \mathfrak {L}^{j}_{T_-}(0)$
is a good approximation for
![]() $\mathfrak {L}^j_{t}(\theta )$
, and so we need to carry this
$\mathfrak {L}^j_{t}(\theta )$
, and so we need to carry this
![]() $\mathscr {F}_{T_-}$
-measurable constant
$\mathscr {F}_{T_-}$
-measurable constant
![]() $\mathfrak {L}^{j}_{T_-}(0)$
whenever we make a comparison.
$\mathfrak {L}^{j}_{T_-}(0)$
whenever we make a comparison.
We also change the barrier event by dropping the barrier on
![]() $[T_-,T_\dagger ]$
; we also include a shift h, which measures the additional (positive) amount the process
$[T_-,T_\dagger ]$
; we also include a shift h, which measures the additional (positive) amount the process
![]() $\mathfrak {U}_t^{o,j}$
will need to climb (recall (2.45)):
$\mathfrak {U}_t^{o,j}$
will need to climb (recall (2.45)):

In analogy with (2.48), we define a decoration process in which we replace the
![]() $\mathfrak {L}^{j}_t$
by
$\mathfrak {L}^{j}_t$
by
![]() $\mathfrak {L}^{o,j}_t$
,
$\mathfrak {L}^{o,j}_t$
,

and where we linearly interpolate between these
![]() $\theta $
to give continuous functions on
$\theta $
to give continuous functions on ![]() We introduce
We introduce
![]() $W_j^o$
as
$W_j^o$
as
 $$\begin{align*}W_j^o = \max_\theta \log | D_j^o(\theta)| - \sqrt{\frac{4}{\beta}}V_j', \end{align*}$$
$$\begin{align*}W_j^o = \max_\theta \log | D_j^o(\theta)| - \sqrt{\frac{4}{\beta}}V_j', \end{align*}$$
which plays the same role as
![]() $W_j'$
. We also define the Markov kernel
$W_j'$
. We also define the Markov kernel
![]() $\mathfrak {s}(\cdot ,\cdot )=\mathfrak {s}_{k_1,k_5}(\cdot ,\cdot )$
$\mathfrak {s}(\cdot ,\cdot )=\mathfrak {s}_{k_1,k_5}(\cdot ,\cdot )$

which is deterministic and depends neither on j nor on n.
Remark 2.16. By construction, the decoration takes as input at time
![]() $T_\dagger $
the process
$T_\dagger $
the process
![]() $\mathfrak {L}^{o,j}_{T_\dagger }$
, which is flat. The time
$\mathfrak {L}^{o,j}_{T_\dagger }$
, which is flat. The time
![]() $T_\dagger $
is negative by a sublogarithmic time in
$T_\dagger $
is negative by a sublogarithmic time in
![]() $k_1$
. This we show to be interchangeable with a decoration that uses a process that solves (2.43) with flat initial condition at time
$k_1$
. This we show to be interchangeable with a decoration that uses a process that solves (2.43) with flat initial condition at time
![]() $T_-.$
Indeed, we could as well start the initial condition at
$T_-.$
Indeed, we could as well start the initial condition at
![]() $-\infty $
, but we do not pursue this.
$-\infty $
, but we do not pursue this.
Remark 2.17. The effect of restricting the processes to a grid is for technical convenience. In fact, we could now remove the linear interpolation at this stage of the proof if we so desire; see Remark 4.9. However, this is not necessary to complete the main results, and so we do not pursue it.
We introduce a new point process in which the decoration has been replaced by this one, and unnecessary events have been dropped:

Here, we use the shorthand
![]() $D_j^o = D_j^o(V_j').$
$D_j^o = D_j^o(V_j').$
Proposition 2.18. For any
![]() $k_7$
, the restrictions of
$k_7$
, the restrictions of
![]() $\operatorname {Extr}_n$
and
$\operatorname {Extr}_n$
and
![]() $\operatorname {Extre}_n$
to
$\operatorname {Extre}_n$
to
![]() $\Gamma _{k_7}$
satisfy
$\Gamma _{k_7}$
satisfy
Proof. Recall (2.48) and let
![]() $E_j$
be the event that
$E_j$
be the event that
This event is typical in that for
![]() $\theta $
for which both
$\theta $
for which both
![]() $D_j^oe^{-\sqrt {4/\beta }V_j'}$
and
$D_j^oe^{-\sqrt {4/\beta }V_j'}$
and
![]() $D_j'$
are below
$D_j'$
are below
![]() $e^{-(\log k_1)^{1/100}}$
, it holds trivially, whereas if a single one is above this level, we do control the difference (and moreover, the difference is much smaller). By Proposition 6.1, by a simple union bound, on the event
$e^{-(\log k_1)^{1/100}}$
, it holds trivially, whereas if a single one is above this level, we do control the difference (and moreover, the difference is much smaller). By Proposition 6.1, by a simple union bound, on the event ![]() (recall (1.10)), for all
(recall (1.10)), for all
![]() $k_1$
sufficiently large,
$k_1$
sufficiently large,
 $$\begin{align*}\begin{aligned} &\mathbb{P}( E_j \cap \bigl\{\delta_{(\theta_j,V_j',D_j'e^{\sqrt{4/\beta}V_j'})}(\Gamma_{k_7}^+)> 0\bigr\} ~|\mathscr{F}_{n_1^+}) \leq Ck_5(k_1/k_1^+) e^{-\delta(\log k_1)^{19/20}}, \\ &\mathbb{P}( E_j \cap \bigl\{\delta_{(\theta_j,V_j',D_j^o)}(\Gamma_{k_7}^+) > 0\bigr\} ~|\mathscr{F}_{n_1^+}) \leq Ck_5(k_1/k_1^+) e^{-\delta(\log k_1)^{19/20}}. \\ \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\mathbb{P}( E_j \cap \bigl\{\delta_{(\theta_j,V_j',D_j'e^{\sqrt{4/\beta}V_j'})}(\Gamma_{k_7}^+)> 0\bigr\} ~|\mathscr{F}_{n_1^+}) \leq Ck_5(k_1/k_1^+) e^{-\delta(\log k_1)^{19/20}}, \\ &\mathbb{P}( E_j \cap \bigl\{\delta_{(\theta_j,V_j',D_j^o)}(\Gamma_{k_7}^+) > 0\bigr\} ~|\mathscr{F}_{n_1^+}) \leq Ck_5(k_1/k_1^+) e^{-\delta(\log k_1)^{19/20}}. \\ \end{aligned} \end{align*}$$
The probability that
![]() $E_j^c$
is sufficiently high that we can essentially assume it always holds. In other words, if we define the process
$E_j^c$
is sufficiently high that we can essentially assume it always holds. In other words, if we define the process

then
To see this, just note using the estimate Lemma 4.4 and the control on
![]() $\varphi _{n_1^+}$
given by
$\varphi _{n_1^+}$
given by
![]() $\mathscr {R}_j^2(n_1^+)$
,
$\mathscr {R}_j^2(n_1^+)$
,
 $$\begin{align*}\begin{aligned} \mathbb{E} [\operatorname{Extre}_n^*(\Gamma_{k_7}^+) ~|~ \mathscr{F}_{k_2}] \leq \frac{c(k_5)}{n_1} \sum_{j \in \mathcal{D}_{n/k_1}} &e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr) \\ &\times \exp\bigl(O( (\log k_1)^{\tfrac{9}{10}})-\delta (\log k_1)^{19/20} \bigr). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathbb{E} [\operatorname{Extre}_n^*(\Gamma_{k_7}^+) ~|~ \mathscr{F}_{k_2}] \leq \frac{c(k_5)}{n_1} \sum_{j \in \mathcal{D}_{n/k_1}} &e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr) \\ &\times \exp\bigl(O( (\log k_1)^{\tfrac{9}{10}})-\delta (\log k_1)^{19/20} \bigr). \end{aligned} \end{align*}$$
This tends to
![]() $0$
almost surely on taking
$0$
almost surely on taking
![]() $n \to \infty $
followed by
$n \to \infty $
followed by
![]() $k_1 \to \infty .$
$k_1 \to \infty .$
As in the proof of Proposition 2.15, we introduce comparison point processes,

We note that all of these processes are thinnings of one another in that
and so if we show that the number of points in
![]() $\Gamma _{k_7}$
that are thinned tends to
$\Gamma _{k_7}$
that are thinned tends to
![]() $0$
in probability between each of these. We justify each of these thinnings below.
$0$
in probability between each of these. We justify each of these thinnings below.
The first thinning.
Note that since
![]() $\operatorname {Extre}_n^*(\Gamma _{k_7})$
converges to
$\operatorname {Extre}_n^*(\Gamma _{k_7})$
converges to
![]() $0$
, we may assume that
$0$
, we may assume that
![]() $E_j^c$
whenever
$E_j^c$
whenever
![]() $\delta _{(\theta _j, V_j', D_j^o)}(\Gamma _{k_7}) = 1$
. On the event
$\delta _{(\theta _j, V_j', D_j^o)}(\Gamma _{k_7}) = 1$
. On the event
![]() $\mathscr {G}_n \cap \mathscr {G}_n^1 \cap E_j^c$
, if
$\mathscr {G}_n \cap \mathscr {G}_n^1 \cap E_j^c$
, if
![]() $\delta _{(\theta _j, V_j', D_j^o)}(\Gamma _{k_7}) = 1,$
then it follows that for some
$\delta _{(\theta _j, V_j', D_j^o)}(\Gamma _{k_7}) = 1,$
then it follows that for some
![]() $\theta \in I_j$
,
$\theta \in I_j$
,
![]() $\mathscr {P}_j(\theta ,V_j')$
held (because, if not, by definition,
$\mathscr {P}_j(\theta ,V_j')$
held (because, if not, by definition,
![]() $D_j^o$
is identically
$D_j^o$
is identically
![]() $0$
, contradicting the
$0$
, contradicting the
![]() $\Gamma _{k_7}$
condition). As
$\Gamma _{k_7}$
condition). As
![]() $E_j^c$
holds, we also have that
$E_j^c$
holds, we also have that
![]() $\mathscr {P}_j'(\theta )$
holds. By Proposition 2.7 and the fact that
$\mathscr {P}_j'(\theta )$
holds. By Proposition 2.7 and the fact that
![]() $\mathscr {R}^2_j(n_1^+)$
holds, we therefore have that deterministically,
$\mathscr {R}^2_j(n_1^+)$
holds, we therefore have that deterministically,
![]() $\mathscr {R}_j^4(\widehat {n}_1) \cap \mathscr {O}_j$
holds.
$\mathscr {R}_j^4(\widehat {n}_1) \cap \mathscr {O}_j$
holds.
The second thinning.
We have that the difference

We can dominate the event

As we work on
![]() ${\mathscr {G}_n \cap \mathscr {G}_n^1}$
, for one of these rays to succeed, we must have that a Gaussian of variance
${\mathscr {G}_n \cap \mathscr {G}_n^1}$
, for one of these rays to succeed, we must have that a Gaussian of variance
![]() $\log (n/\widehat {n}_1)$
climbs distance
$\log (n/\widehat {n}_1)$
climbs distance
Using that
![]() $\log (n/\widehat {n}_1)=\log \widehat {k}_1\gg \sqrt {\tfrac {\beta }{8}}\varphi _{\widehat {n}_1}(\theta _j) - m_{\widehat {n}_1}+O_{k_4}(1)$
on our event, the probability of the Gaussian exceedance is bounded above by
$\log (n/\widehat {n}_1)=\log \widehat {k}_1\gg \sqrt {\tfrac {\beta }{8}}\varphi _{\widehat {n}_1}(\theta _j) - m_{\widehat {n}_1}+O_{k_4}(1)$
on our event, the probability of the Gaussian exceedance is bounded above by
 $$\begin{align*}\exp\bigl({-\bigl( -\sqrt{\tfrac{\beta}{4}}\varphi_{\widehat{n}_1}(\theta_j)\! +\!\sqrt{2}m_{\widehat{n}_1} \! +\!\sqrt{2}\log(n/\widehat{n}_1)\!+\!O_{k_4}(1)\bigr)^2/2\log \widehat{ k}_1}\bigr)\!\leq \!\frac{C(k_4)}{\widehat{k}_1}\exp\bigl( \sqrt{\tfrac{\beta}{2}}\varphi_{\widehat{n}_1}(\theta_j) - 2m_{\widehat{n}_1} \bigr). \end{align*}$$
$$\begin{align*}\exp\bigl({-\bigl( -\sqrt{\tfrac{\beta}{4}}\varphi_{\widehat{n}_1}(\theta_j)\! +\!\sqrt{2}m_{\widehat{n}_1} \! +\!\sqrt{2}\log(n/\widehat{n}_1)\!+\!O_{k_4}(1)\bigr)^2/2\log \widehat{ k}_1}\bigr)\!\leq \!\frac{C(k_4)}{\widehat{k}_1}\exp\bigl( \sqrt{\tfrac{\beta}{2}}\varphi_{\widehat{n}_1}(\theta_j) - 2m_{\widehat{n}_1} \bigr). \end{align*}$$
There are
![]() $O_{k_5}(k_1)$
of these Gaussians, and so by a union bound,
$O_{k_5}(k_1)$
of these Gaussians, and so by a union bound,
 $$\begin{align*}\mathbb{P}({(\theta_j, V_j', D_j^o) \in (\Gamma_{k_7})}~|~\mathscr{F}_{\widehat{n}_1}) \leq C(k_4) \frac{ k_1}{\widehat{k}_1} \times \exp\bigl( \sqrt{\tfrac{\beta}{2}}\varphi_{\widehat{n}_1}(\theta_j) - 2m_{\widehat{n}_1} \bigr). \end{align*}$$
$$\begin{align*}\mathbb{P}({(\theta_j, V_j', D_j^o) \in (\Gamma_{k_7})}~|~\mathscr{F}_{\widehat{n}_1}) \leq C(k_4) \frac{ k_1}{\widehat{k}_1} \times \exp\bigl( \sqrt{\tfrac{\beta}{2}}\varphi_{\widehat{n}_1}(\theta_j) - 2m_{\widehat{n}_1} \bigr). \end{align*}$$
The claim now follows from Proposition 2.9 (or 2.11 in the imaginary case).
The third thinning.
If we introduce now

then we have that on
![]() $\Gamma _{k_7}$
,
$\Gamma _{k_7}$
,
and so
Finally, by direct computation on the event
![]() $\operatorname {Extre}_n^*(\Gamma _{k_7})=0$
$\operatorname {Extre}_n^*(\Gamma _{k_7})=0$
as this holds with probability tending to
![]() $1,$
the proof is complete.
$1,$
the proof is complete.
2.7 Initial Poisson approximation
We are now in a position to introduce the first Poisson process approximation that we make. Define the
![]() $(\mathscr {F}_{n_1^+})$
-measurable random measures on
$(\mathscr {F}_{n_1^+})$
-measurable random measures on ![]()

This is the intensity of
![]() $\operatorname {Extre}_n$
conditioned on
$\operatorname {Extre}_n$
conditioned on
![]() $\mathscr {F}_{n_1^+}$
. We show that
$\mathscr {F}_{n_1^+}$
. We show that
![]() $\operatorname {Extre}_n$
can be compared to a Poisson process of the same intensity. Here and throughout, we write
$\operatorname {Extre}_n$
can be compared to a Poisson process of the same intensity. Here and throughout, we write ![]() for a Poisson process of intensity
for a Poisson process of intensity
![]() $\Lambda $
.
$\Lambda $
.
To execute the proof, we will need to use some second moment machinery for events depending on the behavior of pairs of rays between times
![]() $k_2$
and
$k_2$
and
![]() $n_1^+$
. To do this, we leverage an important technical tool from [Reference Chhaibi, Madaule and NajnudelCMN18]. Specifically, [Reference Chhaibi, Madaule and NajnudelCMN18] introduces another auxiliary Gaussian process
$n_1^+$
. To do this, we leverage an important technical tool from [Reference Chhaibi, Madaule and NajnudelCMN18]. Specifically, [Reference Chhaibi, Madaule and NajnudelCMN18] introduces another auxiliary Gaussian process
![]() $k\mapsto {Z}_{2^k}^{k_2}(\theta )$
, defined for each
$k\mapsto {Z}_{2^k}^{k_2}(\theta )$
, defined for each
![]() $k_2$
, which is shown to be close to
$k_2$
, which is shown to be close to
![]() $\varphi $
. The process
$\varphi $
. The process
![]() ${Z}_{2^k}^{k_2}(\theta )$
is similar to the Gaussian random walk
${Z}_{2^k}^{k_2}(\theta )$
is similar to the Gaussian random walk
![]() $G_k$
, albeit with some changes to make the process simpler on short blocks. We will not need the exact form of the process; it is given by [Reference Chhaibi, Madaule and NajnudelCMN18, (5.2)]. Define the event
$G_k$
, albeit with some changes to make the process simpler on short blocks. We will not need the exact form of the process; it is given by [Reference Chhaibi, Madaule and NajnudelCMN18, (5.2)]. Define the event

Using results of [Reference Chhaibi, Madaule and NajnudelCMN18], this event is typical:
Lemma 2.19. For any
![]() $k_3$
,
$k_3$
,
Proof. See [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 5.2] (note that the notation differs in that their
![]() $\left \{ Z_k \right \}$
is our
$\left \{ Z_k \right \}$
is our
![]() $\left \{ G_k \right \}$
and their process
$\left \{ G_k \right \}$
and their process
![]() $\{Z^{(2^r,\Delta )}_k\}$
is our
$\{Z^{(2^r,\Delta )}_k\}$
is our
![]() ${Z}_{2^k}^r(\theta )$
)
${Z}_{2^k}^r(\theta )$
)
Using this process, [Reference Chhaibi, Madaule and NajnudelCMN18] are able to get good two-ray estimates that mimic branching random walk behavior. We need slightly different estimates, but at its heart, they are small (albeit not easily verified) modifications to the estimates of [Reference Chhaibi, Madaule and NajnudelCMN18]. We summarize the estimates we need in the following. Define a function, with
![]() $x_j = \sqrt {2}H_{k_2}-\mathfrak {Z}_{H_{k_2}}(\theta _j)$
,
$x_j = \sqrt {2}H_{k_2}-\mathfrak {Z}_{H_{k_2}}(\theta _j)$
,
 $$ \begin{align} \begin{aligned} &\mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) =\mathscr{Q}^{(k_2,k_3,n_1^+)}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \\ &= \mathbb{P}( \mathscr{Z}_{k_2} \cap {\mathscr{R}^2_j({n}_1^+)} \cap {\mathscr{R}^2_\ell({n}_1^+)} \cap \operatorname{EP}_j \cap \operatorname{EP}_l ~\vert~ \mathscr{F}_{k_2}), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) =\mathscr{Q}^{(k_2,k_3,n_1^+)}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \\ &= \mathbb{P}( \mathscr{Z}_{k_2} \cap {\mathscr{R}^2_j({n}_1^+)} \cap {\mathscr{R}^2_\ell({n}_1^+)} \cap \operatorname{EP}_j \cap \operatorname{EP}_l ~\vert~ \mathscr{F}_{k_2}), \end{aligned} \end{align} $$
where we define the event
The second moment estimates we import in the following. We show how these can be derived from modifications of [Reference Chhaibi, Madaule and NajnudelCMN18] in Appendix B.
Proposition 2.20. The two-ray estimate satisfies the three following upper bounds. Let
![]() ${\mathtt k}$
be the time of branching between
${\mathtt k}$
be the time of branching between
![]() $\theta _j$
and
$\theta _j$
and
![]() $\theta _\ell ,$
which we can take to be
$\theta _\ell ,$
which we can take to be ![]() Let
Let
![]() ${\mathtt k}_+={\mathtt k}_+(k_2,n)$
be defined by
${\mathtt k}_+={\mathtt k}_+(k_2,n)$
be defined by

The following second moment estimates hold:
-
1. (Time of branching
 ${\mathtt k} \leq (\log _2 k_2)/2$
) For any
${\mathtt k} \leq (\log _2 k_2)/2$
) For any
 $k_3$
and all
$k_3$
and all
 $k_2$
large enough if
$k_2$
large enough if
 ${\mathtt k} \leq (\log _2 k_2)/2,$
where
${\mathtt k} \leq (\log _2 k_2)/2,$
where
 $\eta _{k_2,k_3} \to 0$
as
$\eta _{k_2,k_3} \to 0$
as
 $k_2 \to \infty $
followed by
$k_2 \to \infty $
followed by
 $k_3$
. See Appendix Lemma B.5.
$k_3$
. See Appendix Lemma B.5.
-
2. (Time of branching
 ${\mathtt k} \leq (\log _2 n)/2$
) For all
${\mathtt k} \leq (\log _2 n)/2$
) For all
 $k_2$
sufficiently large and all
$k_2$
sufficiently large and all
 $n \gg k_2$
,
$n \gg k_2$
,  $$ \begin{align*} \mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \leq c(k_3) \begin{cases} \frac{z_jx_j k_2}{n_1^+} \frac{z_\ell x_\ell k_2}{n_1^+} \exp\bigl(\sqrt{2}(z_j-x_j + z_\ell-x_\ell)\bigr) &\text{if } {\mathtt k}_+ \leq \log_2 k_2, \\ \frac{z_j z_\ell x_j k_2}{n_1^+} \frac{2^{{\mathtt k}}}{n_1^+} \exp\bigl(\sqrt{2}(z_j-x_j + z_\ell)\bigr) e^{-c({\mathtt k}_+)^{1/10}} &\text{if } {\mathtt k}_+ \geq \log_2 k_2. \end{cases} \end{align*} $$
$$ \begin{align*} \mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \leq c(k_3) \begin{cases} \frac{z_jx_j k_2}{n_1^+} \frac{z_\ell x_\ell k_2}{n_1^+} \exp\bigl(\sqrt{2}(z_j-x_j + z_\ell-x_\ell)\bigr) &\text{if } {\mathtt k}_+ \leq \log_2 k_2, \\ \frac{z_j z_\ell x_j k_2}{n_1^+} \frac{2^{{\mathtt k}}}{n_1^+} \exp\bigl(\sqrt{2}(z_j-x_j + z_\ell)\bigr) e^{-c({\mathtt k}_+)^{1/10}} &\text{if } {\mathtt k}_+ \geq \log_2 k_2. \end{cases} \end{align*} $$
See Appendix Lemma B.4.
-
3. (Time of branching
 $(\log _2 n)/2 \leq {\mathtt k} \leq \log _2 n_1^+$
) For all
$(\log _2 n)/2 \leq {\mathtt k} \leq \log _2 n_1^+$
) For all
 $k_2$
sufficiently large and all
$k_2$
sufficiently large and all
 $n \gg k_2$
,
$n \gg k_2$
,  $$\begin{align*}\mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \leq c(k_3) \frac{ x_jz_j k_2}{n_1^+} \frac{2^{{\mathtt k}}}{n_1^+} e^{\sqrt{2}(z_j-x_j+z_\ell)} e^{-c(\log_2 n - {\mathtt k}_+)^{1/10}}. \end{align*}$$
$$\begin{align*}\mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \leq c(k_3) \frac{ x_jz_j k_2}{n_1^+} \frac{2^{{\mathtt k}}}{n_1^+} e^{\sqrt{2}(z_j-x_j+z_\ell)} e^{-c(\log_2 n - {\mathtt k}_+)^{1/10}}. \end{align*}$$
See Appendix Lemma B.6.
-
4. (Time of branching
 ${\mathtt k} \geq \log _2 n_1^+$
) While useful for the range of
${\mathtt k} \geq \log _2 n_1^+$
) While useful for the range of
 ${\mathtt k}$
described, this holds for all
${\mathtt k}$
described, this holds for all
 ${\mathtt k}$
:
${\mathtt k}$
:  $$\begin{align*}\mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \leq c(k_3) \frac{z_jx_j k_2}{n_1^+} \exp\bigl(\sqrt{2}(z_j-x_j)\bigr). \end{align*}$$
$$\begin{align*}\mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \leq c(k_3) \frac{z_jx_j k_2}{n_1^+} \exp\bigl(\sqrt{2}(z_j-x_j)\bigr). \end{align*}$$
This is a triviality which follows from Lemma 4.4 and bounding above the two-ray event by a one-ray event.
Remark 2.21. All these upper bounds also hold if in
![]() $\mathscr {Q}$
, we replace the ray event
$\mathscr {Q}$
, we replace the ray event
![]() $\mathscr {R}_j^p(n_1^+)$
by one which only holds at times
$\mathscr {R}_j^p(n_1^+)$
by one which only holds at times
![]() $H_{2^k}$
(instead of a continuous barrier); see (2.71). Likewise, if we further replace the process
$H_{2^k}$
(instead of a continuous barrier); see (2.71). Likewise, if we further replace the process
![]() $\mathfrak {Z}_{H_{2^k}}$
by
$\mathfrak {Z}_{H_{2^k}}$
by
![]() $Z_{2^k}^{k_2} + \mathfrak {Z}_{H_{k_2}}$
, in the discrete barrier event, the bound holds. In this case, we no longer need to work on the good event
$Z_{2^k}^{k_2} + \mathfrak {Z}_{H_{k_2}}$
, in the discrete barrier event, the bound holds. In this case, we no longer need to work on the good event
![]() $\mathscr {Z}_{k_2}.$
$\mathscr {Z}_{k_2}.$
Using these second moment estimates, we turn to the first Poisson approximation.
Proposition 2.22. For any
![]() $k_4,\dots ,k_7$
, the restrictions of
$k_4,\dots ,k_7$
, the restrictions of
![]() $\operatorname {Extre}_n$
and
$\operatorname {Extre}_n$
and ![]() to
to
![]() $\Gamma _{k_7}$
satisfy
$\Gamma _{k_7}$
satisfy
To give the proof, we need to develop some first and second moment estimates for the process near the end of the ray.
2.8 Decoration Process estimates
We turn to giving some conditional first and second moment estimates for rays.
Lemma 2.23 (Coarse intensity bound).
The intensity measure
![]() $\mathfrak {m}_j$
satisfies
$\mathfrak {m}_j$
satisfies
 $$\begin{align*}\mathfrak{m}_j(\Gamma_{k_7}) \leq \mathfrak{m}_j(\Gamma_{k_7}^+) = c(k_4)(1+o_{k_4}) e^{T_-} \frac{V_j'}{(T_+-T_-)^{3/2}} e^{-\sqrt{2}V_j' -(V_j')^2/2(T_+-T_-)}. \end{align*}$$
$$\begin{align*}\mathfrak{m}_j(\Gamma_{k_7}) \leq \mathfrak{m}_j(\Gamma_{k_7}^+) = c(k_4)(1+o_{k_4}) e^{T_-} \frac{V_j'}{(T_+-T_-)^{3/2}} e^{-\sqrt{2}V_j' -(V_j')^2/2(T_+-T_-)}. \end{align*}$$
Proof. To estimate
![]() $\mathfrak {m}_j$
, we first observe that (recalling
$\mathfrak {m}_j$
, we first observe that (recalling
![]() $W_j^o$
from (2.54))
$W_j^o$
from (2.54))
Define the first moment

Hence, we can bound by first moment on the event
![]() $\mathscr {R}_j^2(n_1^+)$
,
$\mathscr {R}_j^2(n_1^+)$
,

We then apply Lemma 10.1 to each of these summands. Hence, we arrive at
 $$\begin{align*}m_1=(1+o_{k_4}) k_1k_5 e^{-(T_+-T_-)} \frac{c(k_7,\infty) V_j' \sqrt{k_4}}{(T_+-T_-)^{3/2}} e^{-\sqrt{2}V_j' -(V_j')^2/2(T_+-T_-)}, \end{align*}$$
$$\begin{align*}m_1=(1+o_{k_4}) k_1k_5 e^{-(T_+-T_-)} \frac{c(k_7,\infty) V_j' \sqrt{k_4}}{(T_+-T_-)^{3/2}} e^{-\sqrt{2}V_j' -(V_j')^2/2(T_+-T_-)}, \end{align*}$$
which simplifies to the claimed result.
Proof of Proposition 2.22.
We shall use the Poisson process machinery stated in Theorem A.1, which we shall translate into this context. Due to the nature of the Poisson approximation, we shall use the nonatomicity of the derivative martingale proved in Theorem 1.6. We let
![]() $\eta> 0$
be a parameter which shall be taken to
$\eta> 0$
be a parameter which shall be taken to
![]() $0$
after
$0$
after
![]() $k_2$
to establish the convergence in probability.
$k_2$
to establish the convergence in probability.
Step 1: Restricting the measures.
As the measure
![]() $\mathscr {D}_\infty $
is finite and nonatomic, we have that there is
$\mathscr {D}_\infty $
is finite and nonatomic, we have that there is
![]() $m \in {\mathbb N}$
sufficiently large that
$m \in {\mathbb N}$
sufficiently large that
where for the case
![]() $j=m$
, we consider the arc as part of the torus. Hence, for all
$j=m$
, we consider the arc as part of the torus. Hence, for all
![]() $k_2$
sufficiently large, we have
$k_2$
sufficiently large, we have
Let
![]() $\mathcal {E}$
denote the event that there exists a
$\mathcal {E}$
denote the event that there exists a
![]() $j=1,\dots ,m$
such that
$j=1,\dots ,m$
such that
From (2.62), we have that
As we can relate ![]() to intensity of both point processes, this in effect is saying that neither point process has any points. Indeed, for either process
to intensity of both point processes, this in effect is saying that neither point process has any points. Indeed, for either process
![]() $\Xi = \operatorname {Extre}_n$
or
$\Xi = \operatorname {Extre}_n$
or ![]() ,
,
 $$\begin{align*}\mathbb{E} (\mathfrak{m}(\Gamma_{k_7}^+~|~\mathscr{F}_{k_2})) \leq \frac{c(k_4)}{n_1} \sum_{j \in \mathcal{D}_{n/k_1}} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta_j)\bigr)_+. \end{align*}$$
$$\begin{align*}\mathbb{E} (\mathfrak{m}(\Gamma_{k_7}^+~|~\mathscr{F}_{k_2})) \leq \frac{c(k_4)}{n_1} \sum_{j \in \mathcal{D}_{n/k_1}} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta_j)\bigr)_+. \end{align*}$$
On taking
![]() $n \to \infty $
, we conclude
$n \to \infty $
, we conclude
And hence, we conclude
Hence, it suffices to work on the event
![]() $\mathcal {E}^c$
.
$\mathcal {E}^c$
.
Step 2: Setting up the Poisson approximation.
We let
![]() $\delta> 0$
be the same constant as in (2.44) (so that Proposition 2.12 applies), and define for
$\delta> 0$
be the same constant as in (2.44) (so that Proposition 2.12 applies), and define for
![]() $j \in \mathcal {D}_{n/k_1}$
,
$j \in \mathcal {D}_{n/k_1}$
,
with
![]() $d_{\mathbb T}$
the distance in the quotient space
$d_{\mathbb T}$
the distance in the quotient space ![]() Recall (2.47) and (2.54). By construction, for all
Recall (2.47) and (2.54). By construction, for all
![]() $j \in \mathcal {D}_{n/k_1}$
,
$j \in \mathcal {D}_{n/k_1}$
,
Define for any
![]() $j \in \mathcal {D}_{n/k_1},$
$j \in \mathcal {D}_{n/k_1},$

We note that
![]() $\mathbb {E}( P_i ~|~ \mathscr {F}_{n_1^+}) = \mathfrak {m}_i(\Gamma _{k_7}^+).$
Theorem A.1 shows that there is a numerical constant
$\mathbb {E}( P_i ~|~ \mathscr {F}_{n_1^+}) = \mathfrak {m}_i(\Gamma _{k_7}^+).$
Theorem A.1 shows that there is a numerical constant
![]() $C>0$
so that with
$C>0$
so that with ![]()

We also note that the left-hand side of (2.63) is bounded by
![]() $1,$
and hence, it suffices to bound the right-hand side of (2.63) on any
$1,$
and hence, it suffices to bound the right-hand side of (2.63) on any
![]() $\bigl (\mathscr {F}_{{n}_1^+}\bigr )$
-measurable event with probability tending to
$\bigl (\mathscr {F}_{{n}_1^+}\bigr )$
-measurable event with probability tending to
![]() $1$
. Nonetheless, as input, we need estimates for the
$1$
. Nonetheless, as input, we need estimates for the
![]() $\bigl (\mathscr {F}_{n_1^+}\bigr )$
-conditional expectation of
$\bigl (\mathscr {F}_{n_1^+}\bigr )$
-conditional expectation of
![]() $P_j$
and for pairs
$P_j$
and for pairs
![]() $P_j$
and
$P_j$
and
![]() $P_i$
where
$P_i$
where
![]() $i \in \mathcal {B}_j.$
We note that
$i \in \mathcal {B}_j.$
We note that
![]() $\mathbb {E}[ P_j ~|~\mathscr {F}_{n_1^+}] = \mathfrak {m}_j( \Gamma _{k_7}^+).$
$\mathbb {E}[ P_j ~|~\mathscr {F}_{n_1^+}] = \mathfrak {m}_j( \Gamma _{k_7}^+).$
To complete the proof of the proposition, we claim that there are events
![]() $\mathcal {F}=\mathcal {F}(n,(k_j))$
so that on
$\mathcal {F}=\mathcal {F}(n,(k_j))$
so that on
![]() $\mathcal {F} \cap \mathcal {E}^c$
, the following hold:
$\mathcal {F} \cap \mathcal {E}^c$
, the following hold:
-
1.
 $\mathfrak {m}(\Gamma _{k_7}^+) = O_{k_2}(1)$
,
$\mathfrak {m}(\Gamma _{k_7}^+) = O_{k_2}(1)$
, -
2.
 $\operatorname {Var}(\operatorname {Extr}_n ( \Gamma _{k_7}^+)~|~ \mathscr {F}_{n_1^+}) = O_{k_2}(1)$
,
$\operatorname {Var}(\operatorname {Extr}_n ( \Gamma _{k_7}^+)~|~ \mathscr {F}_{n_1^+}) = O_{k_2}(1)$
, -
3.
 $L_j^2 \geq c(k_4)\eta ^2$
,
$L_j^2 \geq c(k_4)\eta ^2$
,
and so that ![]() .
.
Step 3: Completing the proof on the good event
 $\mathcal {F}$
.
$\mathcal {F}$
.
Assuming the claim holds, we have reduced the problem to showing that on the event
![]() $\mathcal {F}$
,
$\mathcal {F}$
,

For the term
![]() $(iii),$
we note that
$(iii),$
we note that
![]() $\mathfrak {m}_j(\Gamma _{k_7}^+),$
which goes to
$\mathfrak {m}_j(\Gamma _{k_7}^+),$
which goes to
![]() $0$
uniformly in j faster than any power of
$0$
uniformly in j faster than any power of
![]() $\log k_1$
(from Lemma 2.23). Hence, by the boundededness of
$\log k_1$
(from Lemma 2.23). Hence, by the boundededness of
![]() $\mathfrak {m}(\Gamma _{k_7}^+)$
on
$\mathfrak {m}(\Gamma _{k_7}^+)$
on
![]() $\mathcal {F}$
, this term tends to
$\mathcal {F}$
, this term tends to
![]() $0.$
$0.$
For term
![]() $(i),$
we will use the second moment machinery. To prepare for it, we use Lemma 2.23 and, bounding the sum on
$(i),$
we will use the second moment machinery. To prepare for it, we use Lemma 2.23 and, bounding the sum on
![]() $z_j,z_\ell $
by an integral, which holds up to a constant depending on
$z_j,z_\ell $
by an integral, which holds up to a constant depending on
![]() $k_3$
, arrive at
$k_3$
, arrive at
 $$ \begin{align} \mathbb{E}[~ (i) ~|~ \mathscr{F}_{k_2}] \leq c(k_3) \bigl(\frac{k_1}{k_1^+}\bigr)^2 \sum_{\ell \in \mathcal{B}_j} \int_{z_j,z_\ell} \mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \frac{z_j z_\ell}{(\log k_1)^3} e^{-\sqrt{2}(z_j+z_\ell)} dz_jdz_\ell. \end{align} $$
$$ \begin{align} \mathbb{E}[~ (i) ~|~ \mathscr{F}_{k_2}] \leq c(k_3) \bigl(\frac{k_1}{k_1^+}\bigr)^2 \sum_{\ell \in \mathcal{B}_j} \int_{z_j,z_\ell} \mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \frac{z_j z_\ell}{(\log k_1)^3} e^{-\sqrt{2}(z_j+z_\ell)} dz_jdz_\ell. \end{align} $$
We divide the angles
![]() $\theta _\ell $
according to whether or not
$\theta _\ell $
according to whether or not
![]() $(\log _2 n_1^+-{\mathtt k}_+) \geq q$
or
$(\log _2 n_1^+-{\mathtt k}_+) \geq q$
or
![]() $(\log _2 n_1^+-{\mathtt k}_+) \leq q$
for a q chosen below as
$(\log _2 n_1^+-{\mathtt k}_+) \leq q$
for a q chosen below as
![]() $(\log k_1)^{1/100}$
. For the former case, we use the third case of Proposition 2.20. For the latter case, we just bound
$(\log k_1)^{1/100}$
. For the former case, we use the third case of Proposition 2.20. For the latter case, we just bound
![]() $\mathscr {Q}(\theta _j,x_j,z_j;\theta _\ell ,x_\ell ,z_\ell )$
by the probability of the
$\mathscr {Q}(\theta _j,x_j,z_j;\theta _\ell ,x_\ell ,z_\ell )$
by the probability of the
![]() $\theta _j$
-ray event. We also note that the number of
$\theta _j$
-ray event. We also note that the number of
![]() $\theta _j$
in this latter case is
$\theta _j$
in this latter case is
![]() $(k_1^+/k_1)e^{q + 100(\log \log k_1)^2}$
. Applying the bound from this case, we arrive at
$(k_1^+/k_1)e^{q + 100(\log \log k_1)^2}$
. Applying the bound from this case, we arrive at
 $$ \begin{align} \begin{aligned} \mathbb{E}[~ (i) ~|~ \mathscr{F}_{k_2}] &\leq \frac{c(k_2)}{n_1} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr) \\ &\times (\log k_1)^3 \bigg\{ \sum_{\varkappa = q}^{\delta \log n} \bigl\{ \exp\bigl(-c \varkappa^{1/10}\bigr) \bigr\} + \exp\bigl(q+ C(\log\log k_1)^2-c (\log k_1)^{1/10}\bigr) \bigg\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbb{E}[~ (i) ~|~ \mathscr{F}_{k_2}] &\leq \frac{c(k_2)}{n_1} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr) \\ &\times (\log k_1)^3 \bigg\{ \sum_{\varkappa = q}^{\delta \log n} \bigl\{ \exp\bigl(-c \varkappa^{1/10}\bigr) \bigr\} + \exp\bigl(q+ C(\log\log k_1)^2-c (\log k_1)^{1/10}\bigr) \bigg\}. \end{aligned} \end{align} $$
Note that the stretched exponential gain in the second term is simply from the entropic envelope. As the event we consider restricts the location of
![]() $\varphi _{k_2}(\theta _j)$
to be positive, we may use that
$\varphi _{k_2}(\theta _j)$
to be positive, we may use that
 $$\begin{align*}\sum_{j \in \mathcal{D}_{n/k_1}} \frac{1}{n_1} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr)_+ \end{align*}$$
$$\begin{align*}\sum_{j \in \mathcal{D}_{n/k_1}} \frac{1}{n_1} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr)_+ \end{align*}$$
converges on taking
![]() $n \to \infty $
. Taking
$n \to \infty $
. Taking
![]() $q = (\log k_1)^{1/100}$
, the sum is on the order of
$q = (\log k_1)^{1/100}$
, the sum is on the order of
![]() $e^{-\Omega ( (\log k_1)^{1/1000})}$
. Hence, on taking
$e^{-\Omega ( (\log k_1)^{1/1000})}$
. Hence, on taking
![]() $k_1\to \infty $
,
$k_1\to \infty $
,

The analysis for
![]() $\mathbb {E}[~ (ii) ~|~ \mathscr {F}_{k_2}]$
is similar, but with one important modification. For ‘bushes’
$\mathbb {E}[~ (ii) ~|~ \mathscr {F}_{k_2}]$
is similar, but with one important modification. For ‘bushes’
![]() $\theta _j$
and
$\theta _j$
and
![]() $\theta _\ell $
that branch at or before
$\theta _\ell $
that branch at or before
![]() $n_1^+$
(i.e.,
$n_1^+$
(i.e.,
![]() ${\mathtt k} \leq \log _2 n_1^+$
), we claim that the bound in (2.65) holds as well: we bound each indicator
${\mathtt k} \leq \log _2 n_1^+$
), we claim that the bound in (2.65) holds as well: we bound each indicator ![]() above by a sum of indicators of ray event and then use Lemma 10.1. For
above by a sum of indicators of ray event and then use Lemma 10.1. For
![]() $\theta _\ell $
which are close to
$\theta _\ell $
which are close to
![]() $\theta _j$
, we use the same strategy, although we instead lose the precise dependence on
$\theta _j$
, we use the same strategy, although we instead lose the precise dependence on
![]() $z_\ell $
and instead have just the factor
$z_\ell $
and instead have just the factor
![]() $e^{-\Omega ( \log k_1)^{1/10}}.$
For
$e^{-\Omega ( \log k_1)^{1/10}}.$
For
![]() $\ell $
so that
$\ell $
so that
![]() ${\mathtt k} \geq \log _2 n_1^+$
, this produces the bound:
${\mathtt k} \geq \log _2 n_1^+$
, this produces the bound:
 $$\begin{align*}\sum_{j \in \mathcal{D}_{n/k_1}} c(k_3) \bigl(\frac{k_1}{k_1^+}\bigr)^2 \sum_{\ell} \mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \frac{z_j} {(\log k_1)^{3/2}} e^{-\sqrt{2}(z_j) -c(\log k_1)^{1/10}}. \end{align*}$$
$$\begin{align*}\sum_{j \in \mathcal{D}_{n/k_1}} c(k_3) \bigl(\frac{k_1}{k_1^+}\bigr)^2 \sum_{\ell} \mathscr{Q}(\theta_j,x_j,z_j;\theta_\ell,x_\ell,z_\ell) \frac{z_j} {(\log k_1)^{3/2}} e^{-\sqrt{2}(z_j) -c(\log k_1)^{1/10}}. \end{align*}$$
Using the final case of Proposition 2.20 gives an estimate which is
![]() $e^{-\Omega ( (\log k_1)^{1/10})}$
.
$e^{-\Omega ( (\log k_1)^{1/10})}$
.
Step 4: Proof of claim.
Point 1. We have that
 $$\begin{align*}\mathfrak{m}(\Gamma_{k_7}^+) = \sum_{j \in \mathcal{D}_{n/k_1}} \mathfrak{m}_j(\Gamma_{k_7}^+), \end{align*}$$
$$\begin{align*}\mathfrak{m}(\Gamma_{k_7}^+) = \sum_{j \in \mathcal{D}_{n/k_1}} \mathfrak{m}_j(\Gamma_{k_7}^+), \end{align*}$$
and so using Lemmas 2.23 and 4.4,
 $$\begin{align*}\mathbb{E}[\mathfrak{m}(\Gamma_{k_7}^+)~|~\mathscr{F}_{k_2}] \leq \frac{c(k_4)}{n_1} \sum_{j \in \mathcal{D}_{n/k_1}} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr)_+. \end{align*}$$
$$\begin{align*}\mathbb{E}[\mathfrak{m}(\Gamma_{k_7}^+)~|~\mathscr{F}_{k_2}] \leq \frac{c(k_4)}{n_1} \sum_{j \in \mathcal{D}_{n/k_1}} e^{\sqrt{\tfrac{\beta}{2}}(\varphi_{k_2}(\theta_j)) -\log(k_2)} \bigl(\sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta)\bigr)_+. \end{align*}$$
This converges on taking
![]() $n\to \infty $
almost surely to
$n\to \infty $
almost surely to

and so remains bounded almost surely by Theorem 1.6.
Point 2. It suffices to bound the conditional second moment, which is to say
We then have
 $$\begin{align*}\mathbb{E}[ \operatorname{Extre}_n^2 ( \Gamma_{k_7}^+)~|~ \mathscr{F}_{n_1^+} ] \leq \sum_{j \in \mathcal{D}_{n/k_1}} \mathfrak{m}_j( \Gamma_{k_7}^+) + \sum_{j \in \mathcal{D}_{n/k_1}} \mathbb{E}[ P_jS_j ~|~ \mathscr{F}_{n_1^+}] + \sum_{j \in \mathcal{D}_{n/k_1}} \sum_{\ell \not\in \mathcal{B}_j} \mathfrak{m}_j( \Gamma_{k_7}^+) \mathfrak{m}_\ell( \Gamma_{k_7}^+). \end{align*}$$
$$\begin{align*}\mathbb{E}[ \operatorname{Extre}_n^2 ( \Gamma_{k_7}^+)~|~ \mathscr{F}_{n_1^+} ] \leq \sum_{j \in \mathcal{D}_{n/k_1}} \mathfrak{m}_j( \Gamma_{k_7}^+) + \sum_{j \in \mathcal{D}_{n/k_1}} \mathbb{E}[ P_jS_j ~|~ \mathscr{F}_{n_1^+}] + \sum_{j \in \mathcal{D}_{n/k_1}} \sum_{\ell \not\in \mathcal{B}_j} \mathfrak{m}_j( \Gamma_{k_7}^+) \mathfrak{m}_\ell( \Gamma_{k_7}^+). \end{align*}$$
The first term is nothing but
![]() $\mathfrak {m}(\Gamma _{k_7}^+)$
, which we have already controlled. The second term we controlled earlier in part
$\mathfrak {m}(\Gamma _{k_7}^+)$
, which we have already controlled. The second term we controlled earlier in part
![]() $(ii)$
above. The third term we estimate in the same fashion as
$(ii)$
above. The third term we estimate in the same fashion as
![]() $(i)$
in (2.66).
$(i)$
in (2.66).
Point 3. We let
![]() $\text {Arc}_{i}$
for
$\text {Arc}_{i}$
for
![]() $i=1,\dots ,m$
be a Lipschitz function of the torus
$i=1,\dots ,m$
be a Lipschitz function of the torus ![]() , which is
, which is
![]() $1$
on the complement of
$1$
on the complement of ![]() and
and
![]() $0$
on
$0$
on ![]() . Extend
. Extend
![]() $\text {Arc}_{i}$
to a function of
$\text {Arc}_{i}$
to a function of
![]() $\Gamma _{k_7}^+$
by setting
$\Gamma _{k_7}^+$
by setting
![]() $\text {Arc}_{i}(x,y,z)=\text {Arc}_{i}(x).$
Then, for each
$\text {Arc}_{i}(x,y,z)=\text {Arc}_{i}(x).$
Then, for each
![]() $j \in \mathcal {D}_{n/k_1}$
, for all n sufficiently large, there is an
$j \in \mathcal {D}_{n/k_1}$
, for all n sufficiently large, there is an
![]() $i\in 1,\dots ,m$
so that L
j
≥ 𝔪(Arc
i
). Hence, it suffices to show that each of these
$i\in 1,\dots ,m$
so that L
j
≥ 𝔪(Arc
i
). Hence, it suffices to show that each of these
![]() $\mathfrak {m}( \text {Arc}_{i} )$
satisfies the claimed bound.
$\mathfrak {m}( \text {Arc}_{i} )$
satisfies the claimed bound.
Now we claim that, in fact, 𝔪(Arc
i
) concentrates around its
![]() $\mathscr {F}_{k_2}$
-conditional mean and that its conditional mean has the claimed lower bound. In fact, we shall need this concentration argument at a later point as well, and so we formulate a general statement here.
$\mathscr {F}_{k_2}$
-conditional mean and that its conditional mean has the claimed lower bound. In fact, we shall need this concentration argument at a later point as well, and so we formulate a general statement here.
Lemma 2.24. Let f be a nonnegative, Lipschitz function from the torus ![]() bounded above by
bounded above by
![]() $1$
. Extend it to a function of
$1$
. Extend it to a function of ![]() by setting
by setting
![]() $f(x,y,z) = f(x)$
. Then there is positive constant
$f(x,y,z) = f(x)$
. Then there is positive constant
![]() $\mathcal {H}=\mathcal {H}(k_1,k_4,k_5,k_7)$
which is bounded (above and away from
$\mathcal {H}=\mathcal {H}(k_1,k_4,k_5,k_7)$
which is bounded (above and away from
![]() $0$
, for
$0$
, for
![]() $k_7$
large), uniformly in
$k_7$
large), uniformly in
![]() $k_1$
, so that
$k_1$
, so that
The constant
![]() $\mathcal {H}$
is given in (2.68).
$\mathcal {H}$
is given in (2.68).
This completes the proof of the proposition.
Proof of Lemma 2.24.
If
![]() $\mathscr {D}_\infty (f) = 0$
, then it suffices to show
$\mathscr {D}_\infty (f) = 0$
, then it suffices to show
![]() $\mathfrak {m}(f)$
tends to
$\mathfrak {m}(f)$
tends to
![]() $0$
. This follows directly from (2.67), and so it suffices to consider the case that
$0$
. This follows directly from (2.67), and so it suffices to consider the case that
![]() $\mathscr {D}_\infty (f)> 0.$
$\mathscr {D}_\infty (f)> 0.$
The proof follows from a second moment method, restricted to the event
![]() $\mathscr {Z}_{k_2}$
, which complicates the first moment estimate. We first compute the first moment without the restriction to
$\mathscr {Z}_{k_2}$
, which complicates the first moment estimate. We first compute the first moment without the restriction to
![]() $\mathscr {Z}_{k_2}$
. The conditional first moment of
$\mathscr {Z}_{k_2}$
. The conditional first moment of
![]() $\mathfrak {m}(f)$
is given by
$\mathfrak {m}(f)$
is given by
 $$\begin{align*}\mathbb{E}[ \mathfrak{m}(f) ~|~ \mathscr{F}_{k_2}] =\sum_{j \in \mathcal{D}_{n/k_1}} f(\theta_j) \mathbb{E}[ ~ \mathscr{R}_{j}^2(n_1^+) p_{j} ~|~ \mathscr{F}_{k_2}], \end{align*}$$
$$\begin{align*}\mathbb{E}[ \mathfrak{m}(f) ~|~ \mathscr{F}_{k_2}] =\sum_{j \in \mathcal{D}_{n/k_1}} f(\theta_j) \mathbb{E}[ ~ \mathscr{R}_{j}^2(n_1^+) p_{j} ~|~ \mathscr{F}_{k_2}], \end{align*}$$
where
![]() $p_j = p(V_j') = \mathbb {P}( W_j^o \in [-k_7,\infty )~|~\mathscr {F}_{n_1^+}).$
The function p is inexplicit and depends on
$p_j = p(V_j') = \mathbb {P}( W_j^o \in [-k_7,\infty )~|~\mathscr {F}_{n_1^+}).$
The function p is inexplicit and depends on
![]() $k_4,k_5,k_7$
. Using Lemma 4.4,
$k_4,k_5,k_7$
. Using Lemma 4.4,

The interval J is
![]() $[(\log k_1^+)^{1/10}, (\log k_1^+)^{9/10}]$
. The constant
$[(\log k_1^+)^{1/10}, (\log k_1^+)^{9/10}]$
. The constant
![]() $\mathcal {H}$
is given by
$\mathcal {H}$
is given by

Note that the density that appears is bounded by Lemma 2.23 (using
![]() $T_-=\log (k_1/k_1^+)$
and
$T_-=\log (k_1/k_1^+)$
and
![]() $T_+=\log k_1$
), and we obtain
$T_+=\log k_1$
), and we obtain
 $$ \begin{align} \mathcal{H} = c(k_4)(1+o_{k_4}) \int_J e^{-z^2/(2\log k_1^+)} \frac{z^2 dz}{(\log k_1^+)^{3/2}} \leq c'(k_4). \end{align} $$
$$ \begin{align} \mathcal{H} = c(k_4)(1+o_{k_4}) \int_J e^{-z^2/(2\log k_1^+)} \frac{z^2 dz}{(\log k_1^+)^{3/2}} \leq c'(k_4). \end{align} $$
We return to this bound in a moment, but note that by combining the above, we have the upper bound for the conditional first moment:

Before proceeding, we show that
![]() $\mathcal {H}$
is bounded below uniformly in
$\mathcal {H}$
is bounded below uniformly in
![]() $n,k_1$
, at least for
$n,k_1$
, at least for
![]() $k_7$
large enough. Assume not. Take
$k_7$
large enough. Assume not. Take
![]() $f=1$
. Then necessarily,
$f=1$
. Then necessarily,
![]() $\liminf _{k_1\to \infty } \limsup _{n\to \infty } \mathfrak {m}(f)=0$
, in probability. Using Proposition 2.15, we conclude then that, at least for
$\liminf _{k_1\to \infty } \limsup _{n\to \infty } \mathfrak {m}(f)=0$
, in probability. Using Proposition 2.15, we conclude then that, at least for
![]() $k_7$
large,
$k_7$
large,
But this contradicts the tightness in Theorem 1.3.
To produce a lower bound for the first moment, we introduce two comparison measures
![]() $\mathfrak {m}_j'$
and
$\mathfrak {m}_j'$
and
![]() $\mathfrak {m}_j"$
, which serve as comparisons to
$\mathfrak {m}_j"$
, which serve as comparisons to
![]() $\mathfrak {m}_j$
, and which are modified by slightly adjusting the ray event
$\mathfrak {m}_j$
, and which are modified by slightly adjusting the ray event
![]() $\mathscr {R}_j^2(n_1^+)$
. We introduce two-ray events, which will only be used for this argument,
$\mathscr {R}_j^2(n_1^+)$
. We introduce two-ray events, which will only be used for this argument,
 $$ \begin{align} \begin{aligned} &\mathscr{V}_j' = \mathscr{U}(\theta_j) \bigcap \{ \forall~t \in [H_{k_2},H_{n_1^+}] \cap \{H_{2^k} : k \in {\mathbb N}\}, ~:~ \mathfrak{Z}_t(\theta_j) \in \sqrt{2}[A_{t}^{5/2,-},A_{t}^{5/2,+}] \} \\ &\qquad\qquad\bigcap \{ -V_j' \in [ (\log k_1)^{0.49},(\log k_1)^{0.51} \},\quad \text{ and }\\ &\mathscr{V}_j" = \mathscr{U}(\theta_j) \bigcap \{ \forall~t \in [H_{k_2},H_{n_1^+}] \cap \{H_{2^k} : k \in {\mathbb N}\}, ~:~ Z^{k_2}_{2^n}(\theta_j) \in \sqrt{2}[A_{t}^{2,-},A_{t}^{2,+}] \} \\ &\qquad\qquad\bigcap \{ -V_j' \in [ (\log k_1)^{0.49},(\log k_1)^{0.51} \}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathscr{V}_j' = \mathscr{U}(\theta_j) \bigcap \{ \forall~t \in [H_{k_2},H_{n_1^+}] \cap \{H_{2^k} : k \in {\mathbb N}\}, ~:~ \mathfrak{Z}_t(\theta_j) \in \sqrt{2}[A_{t}^{5/2,-},A_{t}^{5/2,+}] \} \\ &\qquad\qquad\bigcap \{ -V_j' \in [ (\log k_1)^{0.49},(\log k_1)^{0.51} \},\quad \text{ and }\\ &\mathscr{V}_j" = \mathscr{U}(\theta_j) \bigcap \{ \forall~t \in [H_{k_2},H_{n_1^+}] \cap \{H_{2^k} : k \in {\mathbb N}\}, ~:~ Z^{k_2}_{2^n}(\theta_j) \in \sqrt{2}[A_{t}^{2,-},A_{t}^{2,+}] \} \\ &\qquad\qquad\bigcap \{ -V_j' \in [ (\log k_1)^{0.49},(\log k_1)^{0.51} \}. \end{aligned} \end{align} $$
Let
![]() $\mathfrak {m}'$
and
$\mathfrak {m}'$
and
![]() $\mathfrak {m}"$
be the sum of all the
$\mathfrak {m}"$
be the sum of all the
![]() $\mathfrak {m}_j'$
and
$\mathfrak {m}_j'$
and
![]() $\mathfrak {m}_j"$
, respectively (see (2.59)). From Lemma 4.4 and a direct first moment estimate
$\mathfrak {m}_j"$
, respectively (see (2.59)). From Lemma 4.4 and a direct first moment estimate
and hence on taking
![]() $k_2 \to \infty ,$
this tends to
$k_2 \to \infty ,$
this tends to
![]() $0$
almost surely. Moreover, on the event
$0$
almost surely. Moreover, on the event
![]() $\mathscr {Z}_{k_2}$
, we have that
$\mathscr {Z}_{k_2}$
, we have that
![]() $\mathfrak {m}' \geq \mathfrak {m}"$
, and hence, combining this with the display above,
$\mathfrak {m}' \geq \mathfrak {m}"$
, and hence, combining this with the display above,
To evaluate this expectation, we lower bound the expectation without the restriction to the event
![]() $\mathscr {Z}_{k_2}$
and then argue the event can be removed.
$\mathscr {Z}_{k_2}$
and then argue the event can be removed.
Using Lemma C.1 and the Girsanov transformation, we also can give a sharp estimate for the ray probability. However, this is not given as a density estimate, but rather with a restriction of the endpoint
![]() $V_j'$
to land in an interval of length
$V_j'$
to land in an interval of length
![]() $1/\sqrt {k_3}$
(as in Proposition 2.20). Hence, we partition the interval J into a grid
$1/\sqrt {k_3}$
(as in Proposition 2.20). Hence, we partition the interval J into a grid
![]() $\bar J$
of separation
$\bar J$
of separation
![]() $1/\sqrt {k_3}$
, whose elements are parametrized by z:
$1/\sqrt {k_3}$
, whose elements are parametrized by z:

where the factor
![]() $\eta _{k_2,k_3} \to 0$
as
$\eta _{k_2,k_3} \to 0$
as
![]() $k_2 \to \infty $
followed by
$k_2 \to \infty $
followed by
![]() $k_3\to \infty $
. In Lemma 10.2, we show that the function
$k_3\to \infty $
. In Lemma 10.2, we show that the function
![]() $p(z)$
satisfies the estimate
$p(z)$
satisfies the estimate
Hence, we can uniformly approximate the sum over z by an integral and arrive at

This is exactly
![]() $\mathcal {H}$
, and so we have
$\mathcal {H}$
, and so we have

To complete the first moment analysis, it suffices to show that
as then from (2.73) and (2.70),

We shall show using the second moment machinery in Proposition 2.20 (and see Remark 2.21) that
And hence, it follows by Cauchy–Schwarz and Lemma 2.19
We turn to the conditional second moment, and note that this argument will give the same upper bound as was needed for the second moment of
![]() $\mathfrak {m}"$
in (2.75) (see Remark 2.21):
$\mathfrak {m}"$
in (2.75) (see Remark 2.21):

where
![]() $p_j = p(V_j') = \mathbb {P}( W_j^o \in [-k_7,\infty )~|~\mathscr {F}_{n_1^+})$
and the sum is over all
$p_j = p(V_j') = \mathbb {P}( W_j^o \in [-k_7,\infty )~|~\mathscr {F}_{n_1^+})$
and the sum is over all
![]() $j,\ell \in \mathcal {D}_{n/k_1}.$
We divide the angle pairs
$j,\ell \in \mathcal {D}_{n/k_1}.$
We divide the angle pairs
![]() $(\theta _j,\theta _\ell )$
into two classes
$(\theta _j,\theta _\ell )$
into two classes
![]() $\operatorname {NR}$
and
$\operatorname {NR}$
and
![]() $\operatorname {FR}$
, where the latter means
$\operatorname {FR}$
, where the latter means
![]() $\theta _{j}$
and
$\theta _{j}$
and
![]() $\theta _{\ell }$
have branchpoint
$\theta _{\ell }$
have branchpoint
![]() ${\mathtt k}$
(in the notation of Proposition 2.20) less than
${\mathtt k}$
(in the notation of Proposition 2.20) less than
![]() $\tfrac 12 \log _2 k_2$
. We let
$\tfrac 12 \log _2 k_2$
. We let
![]() $\operatorname {NR}$
be all other pairs. For the well-separated angles
$\operatorname {NR}$
be all other pairs. For the well-separated angles
![]() $\operatorname {FR}$
, we can afford only multiplicative errors of the form
$\operatorname {FR}$
, we can afford only multiplicative errors of the form
![]() $1+o_{k_3}$
. Now Proposition 2.20 gives such an estimate, albeit only after asking the endpoint to be in a bin of size
$1+o_{k_3}$
. Now Proposition 2.20 gives such an estimate, albeit only after asking the endpoint to be in a bin of size
![]() $(1/\sqrt {k_3})$
.
$(1/\sqrt {k_3})$
.
Thus, by partitioning the two-ray expectation in (2.76) according to the values of
![]() $V_{j}'$
and
$V_{j}'$
and
![]() $V_{\ell }'$
(using bins of size
$V_{\ell }'$
(using bins of size
![]() $(1/\sqrt {k_3})$
so to apply Proposition 2.20), we have that for
$(1/\sqrt {k_3})$
so to apply Proposition 2.20), we have that for
![]() $(\theta _j,\theta _\ell ) \in \operatorname {FR}$
, the contribution to (2.76) is bounded above by
$(\theta _j,\theta _\ell ) \in \operatorname {FR}$
, the contribution to (2.76) is bounded above by
 $$\begin{align*}\sum_{z_j,z_\ell} \mathscr{Q}(\theta_j,x_j,z_j; \theta_\ell,x_\ell,z_{\ell}) \times \max_{u_j,u_{\ell} \leq 1/\sqrt{k_3}} p(z_j+u_j)p(z_\ell+u_\ell). \end{align*}$$
$$\begin{align*}\sum_{z_j,z_\ell} \mathscr{Q}(\theta_j,x_j,z_j; \theta_\ell,x_\ell,z_{\ell}) \times \max_{u_j,u_{\ell} \leq 1/\sqrt{k_3}} p(z_j+u_j)p(z_\ell+u_\ell). \end{align*}$$
By (2.72), the maximum value of p over a short interval of length
![]() $1/\sqrt {k_3}$
is its average value over the same interval up to an error
$1/\sqrt {k_3}$
is its average value over the same interval up to an error
![]() $o_{k_3}$
. Using the first case of Proposition 2.20, we conclude with that notation
$o_{k_3}$
. Using the first case of Proposition 2.20, we conclude with that notation

where the sum is over all
![]() $\theta _j,\theta _\ell $
in the arc and J is as before. Thus, on taking
$\theta _j,\theta _\ell $
in the arc and J is as before. Thus, on taking
![]() $n\to \infty ,$
$n\to \infty ,$

For the near terms, we need to use all the cases of the two-ray bound Proposition 2.20:

We then partition these near terms into which case of Proposition 2.20 the pairs land. That is, we define the sets:
-
1.
 $\operatorname {NR}_1(\theta _j)$
are all those
$\operatorname {NR}_1(\theta _j)$
are all those
 $\ell $
so that
$\ell $
so that
 ${\mathtt k} \geq (\log _2 k_2)/2$
but
${\mathtt k} \geq (\log _2 k_2)/2$
but
 ${\mathtt k}_+ \leq \log _2 k_2$
.
${\mathtt k}_+ \leq \log _2 k_2$
. -
2.
 $\operatorname {NR}_2(\theta _j)$
are all those
$\operatorname {NR}_2(\theta _j)$
are all those
 $\ell $
not in
$\ell $
not in
 $\operatorname {NR}_1(\theta _j)$
but so that
$\operatorname {NR}_1(\theta _j)$
but so that
 ${\mathtt k} \leq (\log _2 n)/2$
.
${\mathtt k} \leq (\log _2 n)/2$
. -
3.
 $\operatorname {NR}_3(\theta _j)$
are all those
$\operatorname {NR}_3(\theta _j)$
are all those
 $\ell $
not in
$\ell $
not in
 $\operatorname {NR}_i(\theta _j)$
for
$\operatorname {NR}_i(\theta _j)$
for
 $i\in \{1,2\}$
but so that
$i\in \{1,2\}$
but so that
 ${\mathtt k} \leq \log _2 n_1^+$
.
${\mathtt k} \leq \log _2 n_1^+$
. -
4.
 $\operatorname {NR}_4(\theta _j)$
are all those
$\operatorname {NR}_4(\theta _j)$
are all those
 $\ell $
not in
$\ell $
not in
 $\operatorname {NR}_i(\theta _j)$
for
$\operatorname {NR}_i(\theta _j)$
for
 $i\in \{1,2,3\}$
.
$i\in \{1,2,3\}$
.
In all cases, we have sharp dependence on
![]() $x_j$
and
$x_j$
and
![]() $z_j$
, and so we can integrate over
$z_j$
, and so we can integrate over
![]() $z_j$
to give exactly
$z_j$
to give exactly
![]() $\mathcal {H}$
up to an error depending on
$\mathcal {H}$
up to an error depending on
![]() $k_3$
. For the terms in
$k_3$
. For the terms in
![]() $\operatorname {NR}_1(\theta _j)$
, we also have sharp dependence on
$\operatorname {NR}_1(\theta _j)$
, we also have sharp dependence on
![]() $x_\ell $
and
$x_\ell $
and
![]() $z_\ell $
up to a multiplicative error, and hence, we have
$z_\ell $
up to a multiplicative error, and hence, we have

By nonatomicity of
![]() $\mathscr {D}_\infty $
,
$\mathscr {D}_\infty $
,
For the terms of the second type, the bound in Proposition 2.20 loses the dependence in
![]() $x_\ell ,$
but we gain a factor due to the entropic barrier, which is summable
$x_\ell ,$
but we gain a factor due to the entropic barrier, which is summable

The same bound holds for terms of the third type, using the entropic barrier gain, but now gaining a factor
![]() $e^{-c(\log k_1)^{1/10}}$
. Finally, for the terms of fourth type, we use Lemma 2.23, due to which we gain the same
$e^{-c(\log k_1)^{1/10}}$
. Finally, for the terms of fourth type, we use Lemma 2.23, due to which we gain the same
![]() $e^{-c(\log k_1)^{1/10}}$
. In all, we have that the sum over all
$e^{-c(\log k_1)^{1/10}}$
. In all, we have that the sum over all
![]() $\operatorname {NR}$
pairs satisfies
$\operatorname {NR}$
pairs satisfies

Combining this with (2.77), we have that
This together with (2.74) proves the lemma.
2.9 Third Poisson approximation: concentration of the intensity
The final Poisson approximation replaces the intensity
![]() $\mathfrak {m}$
by (essentially) its
$\mathfrak {m}$
by (essentially) its
![]() $\mathscr {F}_{k_2}$
-conditional expectation. This is done by a first and second moment computation. The measure to which we compare
$\mathscr {F}_{k_2}$
-conditional expectation. This is done by a first and second moment computation. The measure to which we compare
![]() $\mathfrak {m}$
is the one given in the introduction (1.21) – namely, with
$\mathfrak {m}$
is the one given in the introduction (1.21) – namely, with
![]() $I(v)$
as in (1.21) and
$I(v)$
as in (1.21) and
![]() $\mathfrak {s}$
as in (2.55):
$\mathfrak {s}$
as in (2.55):

Proposition 2.25. For any
![]() $k_7$
, the restrictions of
$k_7$
, the restrictions of ![]() and
and ![]() to
to
![]() $\Gamma _{k_7}$
satisfy
$\Gamma _{k_7}$
satisfy
Proof. In the first step, we replace the measure
![]() $\mathfrak {m}$
by one in which the decoration is averaged; that is, we compare to
$\mathfrak {m}$
by one in which the decoration is averaged; that is, we compare to

Note that this is identical to
![]() $\mathfrak {m}$
in the case
$\mathfrak {m}$
in the case
![]() $\sigma = i$
. The intensities
$\sigma = i$
. The intensities
![]() $\mathfrak {m}(\Gamma _{k_7})$
and
$\mathfrak {m}(\Gamma _{k_7})$
and
![]() $\overline {\mathfrak {m}}(\Gamma _{k_7})$
are tight in all parameters (see (2.67))
$\overline {\mathfrak {m}}(\Gamma _{k_7})$
are tight in all parameters (see (2.67))
![]() $\{n,k_1,\dots ,k_6\}$
. Using Theorem A.2, it thus suffices to show
$\{n,k_1,\dots ,k_6\}$
. Using Theorem A.2, it thus suffices to show
![]() $d_{\operatorname {BL}}(\mathfrak {m},\overline {\mathfrak {m}}) \to 0$
to conclude that
$d_{\operatorname {BL}}(\mathfrak {m},\overline {\mathfrak {m}}) \to 0$
to conclude that
Letting F be the functions in ![]() with max modulus in
with max modulus in
![]() $[e^{-k_7},e^{k_7}]$
, we can bound
$[e^{-k_7},e^{k_7}]$
, we can bound

where ![]() and the bounded Lipschitz norm is restricted to F. We show in Corollary 10.5 that this distance is bounded by
and the bounded Lipschitz norm is restricted to F. We show in Corollary 10.5 that this distance is bounded by
![]() $\mathcal {O}(e^{-(\log k_1)^{19/20}})p(V_j')$
, where
$\mathcal {O}(e^{-(\log k_1)^{19/20}})p(V_j')$
, where
![]() $p(V_j') = \mathbb {P}( W_j^o \in [-k_7,\infty )~|~\mathscr {F}_{n_1^+}).$
Thus, like in (2.67),
$p(V_j') = \mathbb {P}( W_j^o \in [-k_7,\infty )~|~\mathscr {F}_{n_1^+}).$
Thus, like in (2.67),
For the final step, we show
We again use Theorem A.2 to reduce this to controlling the bounded Lipschitz norm on
![]() $\Gamma _{k_7}$
. Let
$\Gamma _{k_7}$
. Let
![]() $\bar \iota \#\mathfrak {n}$
and
$\bar \iota \#\mathfrak {n}$
and
![]() $\bar \iota \#\overline {\mathfrak {m}}$
be the restriction of
$\bar \iota \#\overline {\mathfrak {m}}$
be the restriction of
![]() $\iota \#(\mathfrak {n}\cap \Gamma _{k_7})$
and
$\iota \#(\mathfrak {n}\cap \Gamma _{k_7})$
and
![]() $ \iota \# (\overline {\mathfrak {m}}\cap \Gamma _{k_7})$
to
$ \iota \# (\overline {\mathfrak {m}}\cap \Gamma _{k_7})$
to ![]() , and note that the restriction to
, and note that the restriction to ![]() is identical for both processes except for a additive random variable, taking value in a compact (
is identical for both processes except for a additive random variable, taking value in a compact (
![]() $k_7$
-dependent) set. From Corollary A.3 and the fact that after the push forward by
$k_7$
-dependent) set. From Corollary A.3 and the fact that after the push forward by
![]() $\iota $
, the second coordinate in
$\iota $
, the second coordinate in
![]() $\Gamma $
is continuously determined by the third, there is a finite list of nonnegative Lipschitz functions
$\Gamma $
is continuously determined by the third, there is a finite list of nonnegative Lipschitz functions
![]() $\{f_j\}$
, depending on
$\{f_j\}$
, depending on
![]() $k_7$
, for which it suffices to show that
$k_7$
, for which it suffices to show that
(We note that the use of
![]() $\iota $
was precisely to reduce the collections of functions
$\iota $
was precisely to reduce the collections of functions
![]() $\{f_j\}$
to a collection that does not depend on
$\{f_j\}$
to a collection that does not depend on
![]() $k_1$
.) Now, (2.80) follows from Lemma 2.24.
$k_1$
.) Now, (2.80) follows from Lemma 2.24.
3 Interpolation-based regularity arguments
In this section, we give proofs of Proposition 2.6 and Proposition 2.14; both rely on certain a priori regularity properties of
![]() $\varphi _n,$
but the second one additionally uses a substantial probabilistic input – Proposition 4.8 in the case
$\varphi _n,$
but the second one additionally uses a substantial probabilistic input – Proposition 4.8 in the case
![]() $\sigma =1$
. The
$\sigma =1$
. The
![]() $\sigma =i$
case is substantially simpler; in effect, the regularity is much better for imaginary
$\sigma =i$
case is substantially simpler; in effect, the regularity is much better for imaginary
![]() $\sigma $
owing to the monotonicity of the Prüfer phases. We introduce the following notation for working with the case of real
$\sigma $
owing to the monotonicity of the Prüfer phases. We introduce the following notation for working with the case of real
![]() $\sigma .$
For any
$\sigma .$
For any
![]() $\theta \in {\mathbb R},$
define (with
$\theta \in {\mathbb R},$
define (with
![]() $\delta _\beta $
given by half of
$\delta _\beta $
given by half of
![]() $\delta $
from Proposition 4.8)
$\delta $
from Proposition 4.8)

The deterministic result we need is the following:
Lemma 3.1. For
![]() $\sigma = i,$
and any
$\sigma = i,$
and any
![]() $\theta ' \leq \theta $
,
$\theta ' \leq \theta $
,
For
![]() $\sigma = 1$
if
$\sigma = 1$
if
![]() $\sup _{\theta } \varphi _n(\theta ) \leq \sqrt {\tfrac {8}{\beta }}m_n+k_6,$
then there is an absolute constant C so that for all
$\sup _{\theta } \varphi _n(\theta ) \leq \sqrt {\tfrac {8}{\beta }}m_n+k_6,$
then there is an absolute constant C so that for all
![]() $n,k_5$
sufficiently large with respect to
$n,k_5$
sufficiently large with respect to
![]() $k_6,$
and all
$k_6,$
and all ![]() ,
,

Proof. For the first claim, we use that the Prüfer phases ![]() are monotone increasing in
are monotone increasing in
![]() $\theta $
; see the discussion in the beginning of Section 2.1, and recall that
$\theta $
; see the discussion in the beginning of Section 2.1, and recall that ![]() . For the second claim, we apply Theorem 8.2 to the polynomial Q such that
. For the second claim, we apply Theorem 8.2 to the polynomial Q such that
![]() $|Q(e^{i\theta })|^2 = e^{\varphi _n(\theta )}$
for all real
$|Q(e^{i\theta })|^2 = e^{\varphi _n(\theta )}$
for all real
![]() $\theta $
. This has degree n, and the theorem applies with
$\theta $
. This has degree n, and the theorem applies with
![]() $m=2k_5$
and
$m=2k_5$
and
![]() $b\asymp k_5^{1-\delta _\beta }.$
$b\asymp k_5^{1-\delta _\beta }.$
To take advantage of this deterministic result, we then use some first and second moment estimates which when combined with Lemma 3.1 imply Proposition 2.14. The first of these is essentially a triviality that shows that we can disregard near maxima that occur near the boundary of an interval
![]() $\widehat {I}_j,$
more specifically those mesh points that are not contained in
$\widehat {I}_j,$
more specifically those mesh points that are not contained in
![]() $K = \cup _{j \in \mathcal {D}_{n/k_1}} I_j$
(recall the definition of
$K = \cup _{j \in \mathcal {D}_{n/k_1}} I_j$
(recall the definition of
![]() $I_j$
in (2.24)).
$I_j$
in (2.24)).
Lemma 3.2. For all
![]() $k_2,k_4,k_5,k_6$
,
$k_2,k_4,k_5,k_6$
,

Proof. For any
![]() $I_j$
, the fraction of angles
$I_j$
, the fraction of angles
![]() $\theta \in I_j$
so that
$\theta \in I_j$
so that
![]() $\theta \not \in K$
vanishes like
$\theta \not \in K$
vanishes like
![]() $\tfrac {\log k_1}{k_1}$
as
$\tfrac {\log k_1}{k_1}$
as
![]() $k_1 \to \infty .$
In particular, the left-hand-side of the display tends to
$k_1 \to \infty .$
In particular, the left-hand-side of the display tends to
![]() $0$
like
$0$
like
![]() $O_{k_p, p \geq 2}( (\log k_1)/k_1)$
(compare with the proof of Proposition 2.5).
$O_{k_p, p \geq 2}( (\log k_1)/k_1)$
(compare with the proof of Proposition 2.5).
From here, we can also give a quick proof of Proposition 2.6:
Proof of Proposition 2.6.
We focus on the harder case
![]() $\sigma =1$
, since the proof for
$\sigma =1$
, since the proof for
![]() $\sigma =i$
is immediate. We first observe that on the event
$\sigma =i$
is immediate. We first observe that on the event
![]() $\mathscr {G}_{n},$
globally
$\mathscr {G}_{n},$
globally
![]() $\theta \mapsto \varphi _n(\theta )$
is bounded by
$\theta \mapsto \varphi _n(\theta )$
is bounded by
![]() $k_6$
, and hence, we always have
$k_6$
, and hence, we always have
![]() $W_j \leq k_6$
for any
$W_j \leq k_6$
for any
![]() $j \in \mathcal {D}_{n/k_1}.$
$j \in \mathcal {D}_{n/k_1}.$
Suppose that
![]() $\widehat {W}_j \geq -k_7$
, and hence, there is a
$\widehat {W}_j \geq -k_7$
, and hence, there is a
![]() $\theta $
in a neighborhood of
$\theta $
in a neighborhood of
![]() $\widehat {I}_j$
at which
$\widehat {I}_j$
at which
![]() $\varphi _n(\theta ) - \sqrt {\tfrac {8}{\beta }}m_n \geq -k_7.$
Using the first conclusion of Lemma 3.1, there must be a
$\varphi _n(\theta ) - \sqrt {\tfrac {8}{\beta }}m_n \geq -k_7.$
Using the first conclusion of Lemma 3.1, there must be a
![]() $\theta ' \in J(\theta )$
at which
$\theta ' \in J(\theta )$
at which
 $$\begin{align*}e^{\varphi_n(\theta') - \sqrt{\tfrac{8}{\beta}}m_n} \geq \bigg(\frac{2k_5-1}{2k_5}\bigg) \bigg( e^{-k_7} - \frac{Ce^{k_6} }{k_5^{\delta_\beta}} \bigg). \end{align*}$$
$$\begin{align*}e^{\varphi_n(\theta') - \sqrt{\tfrac{8}{\beta}}m_n} \geq \bigg(\frac{2k_5-1}{2k_5}\bigg) \bigg( e^{-k_7} - \frac{Ce^{k_6} }{k_5^{\delta_\beta}} \bigg). \end{align*}$$
By virtue of Lemma 3.2, we may assume that
![]() $\theta ' \in I_j.$
Making
$\theta ' \in I_j.$
Making
![]() $k_5$
large, we conclude
$k_5$
large, we conclude
As
![]() $k_6$
is much larger than
$k_6$
is much larger than
![]() $k_7,$
this concludes the proof.
$k_7,$
this concludes the proof.
The second probabilistic input we need in order to prove Proposition 2.14 is that on the finite sets
![]() $J(\theta )$
for
$J(\theta )$
for
![]() $\theta \in I_j$
at which
$\theta \in I_j$
at which
![]() $\mathscr {L}(\theta )$
occurs, the process
$\mathscr {L}(\theta )$
occurs, the process
![]() $\varphi $
can be taken nearly constant (or more specifically its oscillation is no more than
$\varphi $
can be taken nearly constant (or more specifically its oscillation is no more than
![]() $k_5^{-\delta _\beta }$
) simultaneously for all
$k_5^{-\delta _\beta }$
) simultaneously for all
![]() $\theta $
for which
$\theta $
for which
![]() $\mathscr {L}(\theta )$
holds. Define the event
$\mathscr {L}(\theta )$
holds. Define the event

Thus we show the following:
Lemma 3.3. For all
![]() $k_6$
,
$k_6$
,

Proposition 2.14 follows immediately from Lemmas 3.3 and 3.1 in the case
![]() $\sigma =1$
.
$\sigma =1$
.
Proof. We may additionally work on the event
![]() $\mathscr {G}_n^1,$
using which we may replace
$\mathscr {G}_n^1,$
using which we may replace
![]() $\varphi _n(\theta _\ell + \tfrac {\theta }{n})$
by
$\varphi _n(\theta _\ell + \tfrac {\theta }{n})$
by
![]() $\mathfrak {U}_{T_+}(\theta )$
. The main technical work is contained in Proposition 4.8. Under this proposition, we have an estimate
$\mathfrak {U}_{T_+}(\theta )$
. The main technical work is contained in Proposition 4.8. Under this proposition, we have an estimate

We have used here that ![]() , the initial conditions from (2.43). Bounding above the probability, which proceeds in the same fashion as (2.19)–(2.23), we have
, the initial conditions from (2.43). Bounding above the probability, which proceeds in the same fashion as (2.19)–(2.23), we have

Using Theorem 1.6 we have on sending
![]() $k_2 \to \infty $
that this upper bound converges almost surely. On afterward sending
$k_2 \to \infty $
that this upper bound converges almost surely. On afterward sending
![]() $k_5$
to infinity, the result follows.
$k_5$
to infinity, the result follows.
4 Bessel bridges
In what follows,
![]() $\theta _0$
will be a fixed angle in
$\theta _0$
will be a fixed angle in ![]() Recall from (2.7) that for
Recall from (2.7) that for
![]() $\sigma \in \left \{ 1, i \right \},$
$\sigma \in \left \{ 1, i \right \},$
Recall further (see (2.5), (2.7)) the complex Brownian motion
![]() $\mathfrak {Z}^{\mathbb C}_t(\theta _0)$
with the normalization
$\mathfrak {Z}^{\mathbb C}_t(\theta _0)$
with the normalization
![]() $[\mathfrak {Z}_t^{\mathbb C}(\theta _0),\overline {\mathfrak {Z}_t^{\mathbb C}(\theta _0)}] = 2t$
and the standard real Brownian motion
$[\mathfrak {Z}_t^{\mathbb C}(\theta _0),\overline {\mathfrak {Z}_t^{\mathbb C}(\theta _0)}] = 2t$
and the standard real Brownian motion
![]() $\mathfrak {Z}_t=\Re (\sigma \mathfrak {Z}_t^{\mathbb C}(\theta _0))$
for any
$\mathfrak {Z}_t=\Re (\sigma \mathfrak {Z}_t^{\mathbb C}(\theta _0))$
for any
![]() $t \geq 0,$
so that
$t \geq 0,$
so that
![]() $G_k(\theta _0) = \sqrt {\tfrac {4}{\beta }}\mathfrak {Z}_{H_k}(\theta _0)$
for any
$G_k(\theta _0) = \sqrt {\tfrac {4}{\beta }}\mathfrak {Z}_{H_k}(\theta _0)$
for any
![]() $k \geq 0.$
$k \geq 0.$
We shall work conditionally on the endpoints
![]() $\mathfrak {Z}_t$
of various intervals
$\mathfrak {Z}_t$
of various intervals
![]() $[t_0,t_1]$
, after which the process is a standard Brownian bridge. Further conditioning this bridge to lie below the line
$[t_0,t_1]$
, after which the process is a standard Brownian bridge. Further conditioning this bridge to lie below the line
![]() $t\mapsto \alpha t,$
on the interval
$t\mapsto \alpha t,$
on the interval
![]() $[t_0, t_1]$
, the process
$[t_0, t_1]$
, the process
![]() $\alpha t - \mathfrak {Z}_t$
has the law of a
$\alpha t - \mathfrak {Z}_t$
has the law of a
![]() $3$
-dimensional Bessel process bridge. It remains a semimartingale after this conditioning (with respect to the appropriate augmented filtration), and moreover, it is a strong solution to an SDE. We record these facts and some distributional facts about this Bessel bridge in the following lemma.
$3$
-dimensional Bessel process bridge. It remains a semimartingale after this conditioning (with respect to the appropriate augmented filtration), and moreover, it is a strong solution to an SDE. We record these facts and some distributional facts about this Bessel bridge in the following lemma.
Lemma 4.1. Let
![]() $(B_t : t \geq 0)$
be a standard real Brownian motion. For any
$(B_t : t \geq 0)$
be a standard real Brownian motion. For any
![]() $\alpha , c_0,c_1> 0$
and any
$\alpha , c_0,c_1> 0$
and any
![]() $ 0 < t_0 < t_1,$
let
$ 0 < t_0 < t_1,$
let
![]() $(\mathfrak {X}_t : t \in [t_0,t_1])$
be the strong solution of
$(\mathfrak {X}_t : t \in [t_0,t_1])$
be the strong solution of
 $$\begin{align*}\mathfrak{X}_t - \mathfrak{X}_{t_0} = \alpha (t-t_0) + (B_t - B_{t_0}) + \int_{t_0}^t \left( \frac{1}{\mathfrak{X}_s-\alpha s} - \frac{\mathfrak{X}_s-(\alpha s-c_1)}{t_1-s} \right)\,ds, \quad \mathfrak{X}_{t_0} = \alpha t_0 - c_0. \end{align*}$$
$$\begin{align*}\mathfrak{X}_t - \mathfrak{X}_{t_0} = \alpha (t-t_0) + (B_t - B_{t_0}) + \int_{t_0}^t \left( \frac{1}{\mathfrak{X}_s-\alpha s} - \frac{\mathfrak{X}_s-(\alpha s-c_1)}{t_1-s} \right)\,ds, \quad \mathfrak{X}_{t_0} = \alpha t_0 - c_0. \end{align*}$$
Then,
![]() $(\mathfrak {Z}_t : t \in [t_0,t_1])$
has the same law as
$(\mathfrak {Z}_t : t \in [t_0,t_1])$
has the same law as
![]() $(\mathfrak {X}_t : t \in [t_0,t_1])$
when conditioning on
$(\mathfrak {X}_t : t \in [t_0,t_1])$
when conditioning on
For any
![]() $t \in (t_0,t_1),$
the density of
$t \in (t_0,t_1),$
the density of
![]() $y_t = \alpha t-\mathfrak {X}_t$
is given by
$y_t = \alpha t-\mathfrak {X}_t$
is given by
 $$\begin{align*}f(u) = Z(t_1-t_0,c_0,c_1) \sinh\bigg( \frac{c_0 u}{t-t_0} \bigg) \sinh\bigg( \frac{u c_1}{t_1-t} \bigg) \exp\bigg( -\frac{u^2}{2(t-t_0)} -\frac{u^2}{2(t_1-t)} \bigg), \quad u \geq 0, \end{align*}$$
$$\begin{align*}f(u) = Z(t_1-t_0,c_0,c_1) \sinh\bigg( \frac{c_0 u}{t-t_0} \bigg) \sinh\bigg( \frac{u c_1}{t_1-t} \bigg) \exp\bigg( -\frac{u^2}{2(t-t_0)} -\frac{u^2}{2(t_1-t)} \bigg), \quad u \geq 0, \end{align*}$$
where
![]() $Z(\cdot ,\cdot ,\cdot )$
is a normalizing constant (given explicitly in the proof text). Provided
$Z(\cdot ,\cdot ,\cdot )$
is a normalizing constant (given explicitly in the proof text). Provided
![]() $(c_0^2+c_1^2) \leq (t_1 - t_0)$
, we therefore have the estimates, with
$(c_0^2+c_1^2) \leq (t_1 - t_0)$
, we therefore have the estimates, with
![]() $s=\min \{t-t_0,t_1-t\}$
, for some absolute constant C
$s=\min \{t-t_0,t_1-t\}$
, for some absolute constant C
Furthermore, with
![]() $i \in \{0,1\}$
depending on whichever achieves the minimum of
$i \in \{0,1\}$
depending on whichever achieves the minimum of
![]() $\min \{|t-t_i|\}$
in the definition of s,
$\min \{|t-t_i|\}$
in the definition of s,
Proof. See [Reference Revuz and YorRY99, Chapter XI] for a good exposition. Setting
![]() $X_t = \alpha t - \mathfrak {Z}_t,$
the SDE reduces to a standard result on a Brownian motion conditioned to stay positive (cf. [Reference Revuz and YorRY99, Exercise XI.3.11.2], [Reference RobertsRob13]). The density f is given in [Reference Revuz and YorRY99, Chapter XI.3]. The normalizing constant Z is given by
$X_t = \alpha t - \mathfrak {Z}_t,$
the SDE reduces to a standard result on a Brownian motion conditioned to stay positive (cf. [Reference Revuz and YorRY99, Exercise XI.3.11.2], [Reference RobertsRob13]). The density f is given in [Reference Revuz and YorRY99, Chapter XI.3]. The normalizing constant Z is given by

Under the assumption on
![]() $c_0^2+c_1^2$
and using the numerical inequality
$c_0^2+c_1^2$
and using the numerical inequality
![]() $x \leq \sinh (x)$
for all
$x \leq \sinh (x)$
for all
![]() $x \geq 0$
, we may bound above the normalizing constant Z
$x \geq 0$
, we may bound above the normalizing constant Z
 $$\begin{align*}Z \leq C\bigg( \frac{t_1-t_0}{c_0c_1}\bigg) \bigg(\frac{t_1-t_0}{(t-t_0)(t_1-t)}\bigg)^{1/2} \exp\bigg( -\frac{c_0^2}{2(t-t_0)} -\frac{c_1^2}{2(t_1-t)} \bigg). \end{align*}$$
$$\begin{align*}Z \leq C\bigg( \frac{t_1-t_0}{c_0c_1}\bigg) \bigg(\frac{t_1-t_0}{(t-t_0)(t_1-t)}\bigg)^{1/2} \exp\bigg( -\frac{c_0^2}{2(t-t_0)} -\frac{c_1^2}{2(t_1-t)} \bigg). \end{align*}$$
Using
![]() $\sinh (x) \leq xe^x$
for all
$\sinh (x) \leq xe^x$
for all
![]() $x \geq 0$
, we arrive at the density bound for another absolute constant
$x \geq 0$
, we arrive at the density bound for another absolute constant
![]() $C>0$
:
$C>0$
:
 $$\begin{align*}f(u) \leq Cu^2\bigg(\frac{t_1-t_0}{(t-t_0)(t_1-t)}\bigg)^{3/2} \exp\bigg( -\frac{(u-c_0)^2}{2(t-t_0)} -\frac{(u-c_1)^2}{2(t_1-t)} \bigg). \end{align*}$$
$$\begin{align*}f(u) \leq Cu^2\bigg(\frac{t_1-t_0}{(t-t_0)(t_1-t)}\bigg)^{3/2} \exp\bigg( -\frac{(u-c_0)^2}{2(t-t_0)} -\frac{(u-c_1)^2}{2(t_1-t)} \bigg). \end{align*}$$
Hence, with the same constant C, we have
The final conclusion follows similarly.
We also note that a Bessel bridge has good oscillation properties on short time windows, provided its endpoints are not brought close to the barrier:
Lemma 4.2. Suppose that
![]() $(\mathfrak {X}_t : t \in [0,1])$
has the law of a
$(\mathfrak {X}_t : t \in [0,1])$
has the law of a
![]() $3$
-dimensional Bessel bridge with
$3$
-dimensional Bessel bridge with
![]() $\mathfrak {X}_0 = x_0$
and
$\mathfrak {X}_0 = x_0$
and
![]() $\mathfrak {X}_1 = x_1$
. Then, if
$\mathfrak {X}_1 = x_1$
. Then, if
![]() $x_1,x_0 \geq 1$
, there is an absolute constant
$x_1,x_0 \geq 1$
, there is an absolute constant
![]() $c> 0$
so that
$c> 0$
so that
 $$\begin{align*}\mathbb{P}\bigg( \sup_{t \in [0,1]} |\mathfrak{X}_t - (x_1-x_0)t - x_0| \geq s+c \bigg) \leq \exp(-s^2/c). \end{align*}$$
$$\begin{align*}\mathbb{P}\bigg( \sup_{t \in [0,1]} |\mathfrak{X}_t - (x_1-x_0)t - x_0| \geq s+c \bigg) \leq \exp(-s^2/c). \end{align*}$$
Proof. We can realize the Bessel bridge by taking a Brownian Bridge
![]() $\mathfrak {Z}_t$
with the same endpoints and conditioning it to remain positive. Let
$\mathfrak {Z}_t$
with the same endpoints and conditioning it to remain positive. Let
![]() $\mathcal {H}$
be the event that this Brownian bridge is positive. It then suffices to prove that
$\mathcal {H}$
be the event that this Brownian bridge is positive. It then suffices to prove that
 $$\begin{align*}\mathbb{P}\bigg( \bigg\{ \sup_{t \in [0,1]} |\mathfrak{Z}_t - (x_1-x_0)t - x_0| \geq s+c \bigg\} ~\vert~ \mathcal{H} \bigg) \leq \exp(-s^2/c). \end{align*}$$
$$\begin{align*}\mathbb{P}\bigg( \bigg\{ \sup_{t \in [0,1]} |\mathfrak{Z}_t - (x_1-x_0)t - x_0| \geq s+c \bigg\} ~\vert~ \mathcal{H} \bigg) \leq \exp(-s^2/c). \end{align*}$$
This is a standard fact for
![]() $\mathfrak {Z}_t$
without the conditioning; that is, there is a
$\mathfrak {Z}_t$
without the conditioning; that is, there is a
![]() $c>0$
sufficiently large that
$c>0$
sufficiently large that
 $$\begin{align*}\mathbb{P}\bigg( \bigg\{ \sup_{t \in [0,1]} |\mathfrak{Z}_t - (x_1-x_0)t - x_0| \geq s+c \bigg\} \bigg) \leq \exp(-s^2/c). \end{align*}$$
$$\begin{align*}\mathbb{P}\bigg( \bigg\{ \sup_{t \in [0,1]} |\mathfrak{Z}_t - (x_1-x_0)t - x_0| \geq s+c \bigg\} \bigg) \leq \exp(-s^2/c). \end{align*}$$
The event
![]() $\mathcal {H}$
has probability bounded below by some absolute constant (indeed, it is possible to compute it), but note that by monotonicity, it is bounded below by the same probability where we take
$\mathcal {H}$
has probability bounded below by some absolute constant (indeed, it is possible to compute it), but note that by monotonicity, it is bounded below by the same probability where we take
![]() $x_1=x_0=1,$
which in any case is some number
$x_1=x_0=1,$
which in any case is some number
![]() $p> 0$
, and so
$p> 0$
, and so
 $$\begin{align*}\mathbb{P}\bigg( \bigg\{ \sup_{t \in [0,1]} |\mathfrak{Z}_t - (x_1-x_0)t - x_0| \geq s+c \bigg\} ~\vert~ \mathcal{H} \bigg) \leq \exp(-s^2/c)/p. \end{align*}$$
$$\begin{align*}\mathbb{P}\bigg( \bigg\{ \sup_{t \in [0,1]} |\mathfrak{Z}_t - (x_1-x_0)t - x_0| \geq s+c \bigg\} ~\vert~ \mathcal{H} \bigg) \leq \exp(-s^2/c)/p. \end{align*}$$
Then increasing c, the claimed bound follows.
As our first application, we show that conditionally on the process lying slightly below a concave barrier, the process in fact tends to stay in the entropic envelope. Recall the event
![]() $\mathscr {G}_n$
from Lemma 2.4, and the event
$\mathscr {G}_n$
from Lemma 2.4, and the event
![]() $ \widehat {\mathscr {R}}(\theta )$
from (2.15).
$ \widehat {\mathscr {R}}(\theta )$
from (2.15).
Lemma 4.3. On the event that
![]() $\mathfrak {Z}_{H_{k_2}} \in \sqrt {2}(\log k_2 - [(\log k_2)^{0.49}, (\log k_2)^{0.51}])$
and that
$\mathfrak {Z}_{H_{k_2}} \in \sqrt {2}(\log k_2 - [(\log k_2)^{0.49}, (\log k_2)^{0.51}])$
and that
![]() $\mathfrak {Z}_{H_n} \in \sqrt {2}m_n + [-k_6,k_6],$
there is a constant
$\mathfrak {Z}_{H_n} \in \sqrt {2}m_n + [-k_6,k_6],$
there is a constant
![]() $c> 0$
sufficiently small so that for all
$c> 0$
sufficiently small so that for all
![]() $n \gg k_2 \gg k_4 \gg k_5$
sufficiently large,
$n \gg k_2 \gg k_4 \gg k_5$
sufficiently large,
 $$\begin{align*}\mathbb{P}( \widehat{\mathscr{R}}(\theta)^c \cap \mathscr{G}_n ~\vert~ \mathfrak{Z}_{H_{k_2}},\mathfrak{Z}_{H_{n}} ) \leq \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}) e^{-c(\log k_5)^{2}} }{\log n}. \end{align*}$$
$$\begin{align*}\mathbb{P}( \widehat{\mathscr{R}}(\theta)^c \cap \mathscr{G}_n ~\vert~ \mathfrak{Z}_{H_{k_2}},\mathfrak{Z}_{H_{n}} ) \leq \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}}) e^{-c(\log k_5)^{2}} }{\log n}. \end{align*}$$
Proof. We will work conditionally on
![]() $\mathfrak {Z}_{H_{k_2}}$
and
$\mathfrak {Z}_{H_{k_2}}$
and
![]() $\mathfrak {Z}_{H_{n}}$
throughout the proof, and we will work on the
$\mathfrak {Z}_{H_{n}}$
throughout the proof, and we will work on the
![]() $\sigma (\mathfrak {Z}_{H_{k_2}},\mathfrak {Z}_{H_{n}})$
-measurable event in the statement of the lemma.
$\sigma (\mathfrak {Z}_{H_{k_2}},\mathfrak {Z}_{H_{n}})$
-measurable event in the statement of the lemma.
We recall that on the event
![]() $\mathscr {G}_n$
, we have (see (2.9))
$\mathscr {G}_n$
, we have (see (2.9))
From [Reference Chhaibi, Madaule and NajnudelCMN18, Lemma A.5], the probability of this event is bounded above by
 $$ \begin{align} \mathbb{P} ( (4.3) | \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}}) \leq C_\beta \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}})_+ k_6 }{\log(n/k_2)}. \end{align} $$
$$ \begin{align} \mathbb{P} ( (4.3) | \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}}) \leq C_\beta \frac{ (\sqrt{2}\log k_2 - \mathfrak{Z}_{H_{k_2}})_+ k_6 }{\log(n/k_2)}. \end{align} $$
We can fill in this barrier and slightly increase its height and define the event

By a simple union bound estimate over each interval
![]() $[H_{2^{k-1}},H_{2^k}]$
for all
$[H_{2^{k-1}},H_{2^k}]$
for all
![]() $k_5$
sufficiently large,
$k_5$
sufficiently large,
Note that we therefore have
![]() $\mathbb {P} ( (4.5)^c \cap (4.3) \vert \mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}})$
is the same order as the bound claimed in the lemma, and it suffices to, going forward, bound
$\mathbb {P} ( (4.5)^c \cap (4.3) \vert \mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}})$
is the same order as the bound claimed in the lemma, and it suffices to, going forward, bound
![]() $\mathbb {P} (\widehat {\mathscr {R}}(\theta )^c \cap (4.5) \vert \mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}})$
(which will be lower order for
$\mathbb {P} (\widehat {\mathscr {R}}(\theta )^c \cap (4.5) \vert \mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}})$
(which will be lower order for
![]() $k_4 \gg k_5$
).
$k_4 \gg k_5$
).
Recall that under
![]() $\mathbb {P},$
conditional on
$\mathbb {P},$
conditional on
![]() $\mathfrak {Z}_{H_{k_2}},\mathfrak {Z}_{H_{n}},$
the process
$\mathfrak {Z}_{H_{k_2}},\mathfrak {Z}_{H_{n}},$
the process
 $$\begin{align*}\mathfrak{B}_t = \mathfrak{Z}_t - \mathfrak{Z}_{H_{k_2}} - \frac{\mathfrak{Z}_{H_{n}}- \mathfrak{Z}_{H_{k_2}}} {H_n - H_{k_2}}(t-H_{k_2}) \end{align*}$$
$$\begin{align*}\mathfrak{B}_t = \mathfrak{Z}_t - \mathfrak{Z}_{H_{k_2}} - \frac{\mathfrak{Z}_{H_{n}}- \mathfrak{Z}_{H_{k_2}}} {H_n - H_{k_2}}(t-H_{k_2}) \end{align*}$$
is a bridge starting and ending an
![]() $0.$
Define a change of measure by
$0.$
Define a change of measure by

for some (linear) functional
![]() $F.$
Then, without conditioning on its endpoints, under
$F.$
Then, without conditioning on its endpoints, under
![]() ${\mathbb Q},$
the process ℨ
t
− g(t) is a standard Brownian motion for
${\mathbb Q},$
the process ℨ
t
− g(t) is a standard Brownian motion for
![]() $t \in [H_{k_2},H_n]$
and, after conditioning, this process is a Brownian bridge. Moreover, we see that the conditional Radon–Nikodym derivative is just given by (4.7) with
$t \in [H_{k_2},H_n]$
and, after conditioning, this process is a Brownian bridge. Moreover, we see that the conditional Radon–Nikodym derivative is just given by (4.7) with
![]() $F=0.$
$F=0.$
Estimating the probability
![]() ${\mathbb Q}( \widehat {\mathscr {R}}^c(\theta ) ~|~ (4.5))$
is straightforward, given that there is an explicit probabilistic description for the conditional process. So, our goal is to show that
${\mathbb Q}( \widehat {\mathscr {R}}^c(\theta ) ~|~ (4.5))$
is straightforward, given that there is an explicit probabilistic description for the conditional process. So, our goal is to show that
![]() $\mathbb {P}( \widehat {\mathscr {R}}^c(\theta ) \cap (4.5))$
is not much larger.
$\mathbb {P}( \widehat {\mathscr {R}}^c(\theta ) \cap (4.5))$
is not much larger.

Conditioning on (4.5),
![]() $\mathfrak {Z}_{H_{k_2}},$
and
$\mathfrak {Z}_{H_{k_2}},$
and
![]() $\mathfrak {Z}_{H_{n}}, \mathfrak {Z}_t-g(t)$
has the law of a Bessel bridge under
$\mathfrak {Z}_{H_{n}}, \mathfrak {Z}_t-g(t)$
has the law of a Bessel bridge under
![]() ${\mathbb Q}$
. Thus, under
${\mathbb Q}$
. Thus, under
![]() ${\mathbb Q}$
, we can use the estimates in Lemma 4.1 to estimate the probability of
${\mathbb Q}$
, we can use the estimates in Lemma 4.1 to estimate the probability of
![]() $\widehat {\mathscr {R}}(\theta )$
under
$\widehat {\mathscr {R}}(\theta )$
under
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
We first establish that under the conditional measure
![]() ${\mathbb Q}(\cdot ~|~(4.5), \mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}})$
, the process
${\mathbb Q}(\cdot ~|~(4.5), \mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}})$
, the process
![]() $\mathfrak {Z}_t$
is not outside the entropic barrier of half the size at integer times up to
$\mathfrak {Z}_t$
is not outside the entropic barrier of half the size at integer times up to
![]() $H_n-k_4+1$
(cf. (2.13)),
$H_n-k_4+1$
(cf. (2.13)),

For bounding the event of exceeding the entropic barrier, we use the summability of the powers in Lemma 4.1 to conclude
 $$ \begin{align*} & {\mathbb Q}( \mathfrak{Z}_t \notin [\tilde{A}_t^{n,-},\tilde{A}_t^{n,+}] \text{ for some integer }t \leq H_n-k_4+1~|~(4.5), \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}})\\ & \leq C\bigl( (\log k_2)^{-1/5} + k_4^{-1/5}\bigr). \end{align*} $$
$$ \begin{align*} & {\mathbb Q}( \mathfrak{Z}_t \notin [\tilde{A}_t^{n,-},\tilde{A}_t^{n,+}] \text{ for some integer }t \leq H_n-k_4+1~|~(4.5), \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}})\\ & \leq C\bigl( (\log k_2)^{-1/5} + k_4^{-1/5}\bigr). \end{align*} $$
We may then fill in the gaps by again using union bound together with the oscillation estimate Lemma 4.2 over each interval to conclude for some larger constant
![]() $C>0$
,
$C>0$
,
for all
![]() $k_2, k_4$
sufficiently large. We will show that we can reduce to this case by bounding the expression ℚ[(dℙdℚ)2 | (4.5), ℨ
H
k
2
, ℨ
H
n
]. Let
$k_2, k_4$
sufficiently large. We will show that we can reduce to this case by bounding the expression ℚ[(dℙdℚ)2 | (4.5), ℨ
H
k
2
, ℨ
H
n
]. Let
![]() $\alpha = \sqrt {2}(1-\tfrac {3}{4}\tfrac {\log \log n}{\log n}) - \frac {\mathfrak {Z}_{H_{n}}- \mathfrak {Z}_{H_{k_2}}} {H_n - H_{k_2}}=O(\tfrac {(\log k_2)^{0.51} + k_6} {\log n}),$
and which is positive for all
$\alpha = \sqrt {2}(1-\tfrac {3}{4}\tfrac {\log \log n}{\log n}) - \frac {\mathfrak {Z}_{H_{n}}- \mathfrak {Z}_{H_{k_2}}} {H_n - H_{k_2}}=O(\tfrac {(\log k_2)^{0.51} + k_6} {\log n}),$
and which is positive for all
![]() $k_2$
and n sufficiently large. Under
$k_2$
and n sufficiently large. Under
![]() ${\mathbb Q}$
and conditioned on
${\mathbb Q}$
and conditioned on
![]() $\mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}}$
, the process
$\mathfrak {Z}_{H_{k_2}}, \mathfrak {Z}_{H_{n}}$
, the process
 $$\begin{align*}\begin{aligned} \mathfrak{X}_t &= -\mathfrak{B}_t + g(t) + \alpha (t-H_{k_2}) +\sqrt{2}(1-\tfrac{3}{4}\tfrac{\log\log n}{\log n})H_{k_2} -\mathfrak{Z}_{H_{k_2}} \\ &= -\mathfrak{Z}_t + g(t) + \sqrt{2}(1-\tfrac{3}{4}\tfrac{\log\log n}{\log n})t \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathfrak{X}_t &= -\mathfrak{B}_t + g(t) + \alpha (t-H_{k_2}) +\sqrt{2}(1-\tfrac{3}{4}\tfrac{\log\log n}{\log n})H_{k_2} -\mathfrak{Z}_{H_{k_2}} \\ &= -\mathfrak{Z}_t + g(t) + \sqrt{2}(1-\tfrac{3}{4}\tfrac{\log\log n}{\log n})t \end{aligned} \end{align*}$$
is a Brownian bridge, and the event (4.5) becomes
Thus, conditionally on (4.5),
![]() $(\mathfrak {X}_t : t \in [H_{k_2},H_n])$
has the law of a Bessel bridge (cf. Lemma 4.1).
$(\mathfrak {X}_t : t \in [H_{k_2},H_n])$
has the law of a Bessel bridge (cf. Lemma 4.1).
The conditional Radon–Nikodym derivative can be expressed in terms of
![]() $\mathfrak {X}$
by
$\mathfrak {X}$
by
 $$ \begin{align} \frac{d\mathbb{P}}{d{\mathbb Q}} = \exp\left( \int_{H_{k_2}}^{H_{n}} \bigl\{-g"(t) \mathfrak{X}_t +g"(t)(\alpha(t- H_{k_2})+\sqrt{2}(1-\tfrac{3}{4}\tfrac{\log\log n}{\log n})H_{k_2} -\mathfrak{Z}_{H_{k_2}}) -\tfrac{(g'(t))^2}{2}\bigr\} dt \right). \end{align} $$
$$ \begin{align} \frac{d\mathbb{P}}{d{\mathbb Q}} = \exp\left( \int_{H_{k_2}}^{H_{n}} \bigl\{-g"(t) \mathfrak{X}_t +g"(t)(\alpha(t- H_{k_2})+\sqrt{2}(1-\tfrac{3}{4}\tfrac{\log\log n}{\log n})H_{k_2} -\mathfrak{Z}_{H_{k_2}}) -\tfrac{(g'(t))^2}{2}\bigr\} dt \right). \end{align} $$
We can estimate the function g for a sufficiently large absolute constant
![]() $L>0,$
$L>0,$
and we also observe that g is concave; recall (4.5). From the concavity of g and the convexity of the exponential, we can therefore bound
 $$ \begin{align} \bigg(\frac{d\mathbb{P}}{d{\mathbb Q}}\bigg)^2 \leq \exp\left( \int_{H_{k_2}}^{H_{n}} -2 g"(t)\mathfrak{X}_t dt \right). \end{align} $$
$$ \begin{align} \bigg(\frac{d\mathbb{P}}{d{\mathbb Q}}\bigg)^2 \leq \exp\left( \int_{H_{k_2}}^{H_{n}} -2 g"(t)\mathfrak{X}_t dt \right). \end{align} $$
From Lemma 4.1, we have a subgaussian estimate on
![]() $\mathfrak {X}_t$
. Recall the subgaussian norm
$\mathfrak {X}_t$
. Recall the subgaussian norm
such that

Hence, using Jensen’s inequality,

Splitting the integral and using the bound on
![]() $g"$
and
$g"$
and ![]() , we have
, we have

In summary, we conclude that for all
![]() $k_4$
and
$k_4$
and
![]() $k_2$
sufficiently large, there is an absolute constant
$k_2$
sufficiently large, there is an absolute constant
![]() $C>0$
so that
$C>0$
so that
 $$ \begin{align} {\mathbb Q}\bigg(\bigg(\frac{d\mathbb{P}}{d{\mathbb Q}}\bigg)^2~\vert~(4.5), \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}} \bigg) \leq e^{C k_4^{-24/25} + C(\log k_2)^{-47/50} }. \end{align} $$
$$ \begin{align} {\mathbb Q}\bigg(\bigg(\frac{d\mathbb{P}}{d{\mathbb Q}}\bigg)^2~\vert~(4.5), \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}} \bigg) \leq e^{C k_4^{-24/25} + C(\log k_2)^{-47/50} }. \end{align} $$
Hence, using Cauchy-Schwarz, we get that for all
![]() $k_2$
and
$k_2$
and
![]() $k_4$
sufficiently large,
$k_4$
sufficiently large,
Finally, the
![]() ${\mathbb Q}$
probability of (4.5), conditionally on
${\mathbb Q}$
probability of (4.5), conditionally on
![]() $\mathfrak {Z}_{H_{k_2}},\mathfrak {Z}_{H_{n}},$
is the probability that the Brownian bridge
$\mathfrak {Z}_{H_{k_2}},\mathfrak {Z}_{H_{n}},$
is the probability that the Brownian bridge
![]() $\mathfrak {X}_t$
stays positive for all time. This probability is, in fact, explicit [Reference Karatzas and ShreveKS91, (3.40)]:
$\mathfrak {X}_t$
stays positive for all time. This probability is, in fact, explicit [Reference Karatzas and ShreveKS91, (3.40)]:
 $$ \begin{align} {\mathbb Q}( (4.5) | \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}}) &= 1-\exp\left(-\frac{2\mathfrak{X}_{H_{k_2}}\mathfrak{X}_{H_{n}}}{H_{n} - H_{k_2}} \right) \leq C \frac{(\sqrt{2}\log k_2- \mathfrak{Z}_{H_{k_2}})\log k_5}{\log n }, \end{align} $$
$$ \begin{align} {\mathbb Q}( (4.5) | \mathfrak{Z}_{H_{k_2}}, \mathfrak{Z}_{H_{n}}) &= 1-\exp\left(-\frac{2\mathfrak{X}_{H_{k_2}}\mathfrak{X}_{H_{n}}}{H_{n} - H_{k_2}} \right) \leq C \frac{(\sqrt{2}\log k_2- \mathfrak{Z}_{H_{k_2}})\log k_5}{\log n }, \end{align} $$
for all
![]() $n,k_2$
sufficiently large and some
$n,k_2$
sufficiently large and some
![]() $C>0$
. For n large, this contribution is negligible in comparison to (4.6). Hence, by (4.8) and (4.15), the proof is complete.
$C>0$
. For n large, this contribution is negligible in comparison to (4.6). Hence, by (4.8) and (4.15), the proof is complete.
By a similar argument, we can actually estimate the density of the Bessel process endpoint killed when it exits an entropic envelope.
Lemma 4.4. For notational convenience, let
![]() $s = H_{n_1^+}$
. Fix
$s = H_{n_1^+}$
. Fix
![]() $p \geq 2$
. On the event that
$p \geq 2$
. On the event that
![]() $\mathfrak {Z}_{H_{k_2}} \in \sqrt {2}(\log k_2 - [(\log k_2)^{0.49}, (\log k_2)^{0.51}])$
and
$\mathfrak {Z}_{H_{k_2}} \in \sqrt {2}(\log k_2 - [(\log k_2)^{0.49}, (\log k_2)^{0.51}])$
and
![]() $y \in \sqrt {2}(s-\frac {3}{4}\log \log n - [A_{s}^{p-1,-}, A_{s}^{p-1,+}]),$
$y \in \sqrt {2}(s-\frac {3}{4}\log \log n - [A_{s}^{p-1,-}, A_{s}^{p-1,+}]),$

Furthermore, for all
![]() $y \in \sqrt {2}(s-\frac {3}{4}\log \log n-[A_{s}^{p,-}, A_{s}^{p,+}])$
, the density is upper bounded by the right-hand side. With
$y \in \sqrt {2}(s-\frac {3}{4}\log \log n-[A_{s}^{p,-}, A_{s}^{p,+}])$
, the density is upper bounded by the right-hand side. With
![]() $y \in \sqrt {2}(s-\frac {3}{4}\log \log n-[A_{s}^{p-1,-}, A_{s}^{p-1,+}])$
, if we introduce
$y \in \sqrt {2}(s-\frac {3}{4}\log \log n-[A_{s}^{p-1,-}, A_{s}^{p-1,+}])$
, if we introduce
![]() $\mathscr {V}_j'$
(see (2.71)) as the alteration of (2.27), where we only put the entropic envelope restriction at t in the set
$\mathscr {V}_j'$
(see (2.71)) as the alteration of (2.27), where we only put the entropic envelope restriction at t in the set
![]() $\{H_{2^k} : k \in {\mathbb N}\}$
, we furthermore have
$\{H_{2^k} : k \in {\mathbb N}\}$
, we furthermore have

In the lemma and also below, we write
![]() $P(dy)\leq fdy$
for a (sub)-probability measure P when we mean that the density of P with respect to Lebesgue measure is bounded by f.
$P(dy)\leq fdy$
for a (sub)-probability measure P when we mean that the density of P with respect to Lebesgue measure is bounded by f.
Proof. Define the event
![]() $\mathscr {E}$
that
$\mathscr {E}$
that
and note that
![]() $\mathscr {R}^p_{j}(n_1^+) \subset \mathscr {E}$
.
$\mathscr {R}^p_{j}(n_1^+) \subset \mathscr {E}$
.
Define the change of measure
Under
![]() ${\mathbb Q}$
,
${\mathbb Q}$
,
![]() $\mathfrak {X}_t$
is a standard Brownian motion. Therefore,
$\mathfrak {X}_t$
is a standard Brownian motion. Therefore,
 $$ \begin{align} \begin{aligned} &\mathbb{P}( \mathscr{R}^p_{j}(n_1^+) \cap \{\sqrt{2}m_{n_1^+} - \mathfrak{Z}_{s} \in [y,y+dy]\} ~\vert~ \mathfrak{Z}_{H_{k_2}} ) \\ &= {\mathbb Q}( \mathscr{R}^p_{j}(n_1^+) \cap \{\mathfrak{X}_s \in [y,y+dy]\} ~\vert~ \mathfrak{Z}_{H_{k_2}} ) \\ &\times \exp\bigl(-s + \tfrac32 \log s+\sqrt{2}y + \sqrt{2}\mathfrak{Z}_{H_{k_2}} - H_{k_2} + o_n\bigr). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathbb{P}( \mathscr{R}^p_{j}(n_1^+) \cap \{\sqrt{2}m_{n_1^+} - \mathfrak{Z}_{s} \in [y,y+dy]\} ~\vert~ \mathfrak{Z}_{H_{k_2}} ) \\ &= {\mathbb Q}( \mathscr{R}^p_{j}(n_1^+) \cap \{\mathfrak{X}_s \in [y,y+dy]\} ~\vert~ \mathfrak{Z}_{H_{k_2}} ) \\ &\times \exp\bigl(-s + \tfrac32 \log s+\sqrt{2}y + \sqrt{2}\mathfrak{Z}_{H_{k_2}} - H_{k_2} + o_n\bigr). \end{aligned} \end{align} $$
Define for convenience
![]() $t = s-H_{k_2}$
and
$t = s-H_{k_2}$
and
![]() $x = \sqrt {2}\bigl (1-\tfrac {3}{4}\tfrac {\log s}{s}\bigr )H_{k_2}-\mathfrak {Z}_{H_{k_2}}.$
Under
$x = \sqrt {2}\bigl (1-\tfrac {3}{4}\tfrac {\log s}{s}\bigr )H_{k_2}-\mathfrak {Z}_{H_{k_2}}.$
Under
![]() ${\mathbb Q}((\cdot )~\vert ~\mathfrak {Z}_{H_{k_2}})$
,
${\mathbb Q}((\cdot )~\vert ~\mathfrak {Z}_{H_{k_2}})$
,
![]() $\mathfrak {X}_t$
has a gaussian density of mean
$\mathfrak {X}_t$
has a gaussian density of mean
![]() $\mathfrak {X}_{H_{k_2}}$
and variance t. However, by the restriction on y, the gaussian trivializes, and so
$\mathfrak {X}_{H_{k_2}}$
and variance t. However, by the restriction on y, the gaussian trivializes, and so

To produce the upper bound on the density in (4.17), we use the inclusion
![]() $\mathscr {R}^p_{j}(n_1^+) \subset \mathscr {E}$
and then bound, using (4.16),
$\mathscr {R}^p_{j}(n_1^+) \subset \mathscr {E}$
and then bound, using (4.16),
Hence we conclude, from combining everything with (4.20),

For the lower bound in (4.17), we condition on
![]() $\mathscr {E}$
and express
$\mathscr {E}$
and express
Thus, it suffices to give a vanishing upper bound on
Conditionally on
![]() $\mathscr {E}$
,
$\mathscr {E}$
,
![]() $\mathfrak {Z}_{H_{k_2}}$
and
$\mathfrak {Z}_{H_{k_2}}$
and
![]() $ \mathfrak {X}_s = y$
,
$ \mathfrak {X}_s = y$
,
![]() $\mathfrak {X}_t$
is a Bessel-3 bridge on
$\mathfrak {X}_t$
is a Bessel-3 bridge on
![]() $[H_{k_2},s]$
. As this determines the Radon–Nikodym derivative, and using the extra assumption from the statement of the lemma that y is far from the edge of the entropic window, the argument is now similar to what is shown in Lemma 4.3: one starts by bounding the probability that the Bessel bridge escapes the entropic envelope at times in
$[H_{k_2},s]$
. As this determines the Radon–Nikodym derivative, and using the extra assumption from the statement of the lemma that y is far from the edge of the entropic window, the argument is now similar to what is shown in Lemma 4.3: one starts by bounding the probability that the Bessel bridge escapes the entropic envelope at times in
![]() $H_{2^k}$
with
$H_{2^k}$
with
![]() $k \in {\mathbb N}$
, and then between two integer times use a gaussian tail bound for the oscillation from Lemma 4.2. We omit further details.
$k \in {\mathbb N}$
, and then between two integer times use a gaussian tail bound for the oscillation from Lemma 4.2. We omit further details.
To see (4.18), note that the same oscillation lemma shows that with
![]() $p=2$
,
$p=2$
,
which implies the claim (4.18) since
 $$\begin{align*}\begin{aligned} &{\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c \cap \mathscr{V}_j' ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr) \\ &= {\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c \cap \mathscr{V}_j' \cap \mathscr{E} ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr) +{\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c \cap \mathscr{V}_j' \cap \mathscr{E}^c ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr)\\ &\leq {\mathbb Q}\bigl(\mathscr{E} ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr)\cdot {\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y, \mathscr{E} \bigr) +{\mathbb Q}\bigl( \mathscr{V}_j' \cap \mathscr{E}^c ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr)\\ &\leq o_{k_2} {\mathbb Q}\bigl(\mathscr{E} ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &{\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c \cap \mathscr{V}_j' ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr) \\ &= {\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c \cap \mathscr{V}_j' \cap \mathscr{E} ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr) +{\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c \cap \mathscr{V}_j' \cap \mathscr{E}^c ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr)\\ &\leq {\mathbb Q}\bigl(\mathscr{E} ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr)\cdot {\mathbb Q}\bigl( \bigl(\mathscr{R}^{2}_{j}(n_1^+)\bigr)^c ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y, \mathscr{E} \bigr) +{\mathbb Q}\bigl( \mathscr{V}_j' \cap \mathscr{E}^c ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr)\\ &\leq o_{k_2} {\mathbb Q}\bigl(\mathscr{E} ~\vert~ \mathfrak{Z}_{H_{k_2}}, \mathfrak{X}_s = y \bigr), \end{aligned} \end{align*}$$
where we used (4.22) and (4.23) in the last inequality. The conclusion follow from the explicit expression for the right-hand side; see, for example, (4.21).
4.1 The coarse oscillation bound
In this section, we consider a single
![]() $j \in \mathcal {D}_{n/k_1}$
, and hence, we write simply the barrier event
$j \in \mathcal {D}_{n/k_1}$
, and hence, we write simply the barrier event
 $$ \begin{align} \begin{aligned} {\mathscr{R}} &= \left\{ \forall~ \log k_2 \leq t \leq \log \widehat{n}_1 : \sqrt{\tfrac{8}{\beta}}A_{t}^{4,-} \leq \sqrt{\tfrac{4}{\beta}} \mathfrak{Z}_t(\theta_0) \leq \sqrt{\tfrac{8}{\beta}}A_{t}^{4,+} \right\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\mathscr{R}} &= \left\{ \forall~ \log k_2 \leq t \leq \log \widehat{n}_1 : \sqrt{\tfrac{8}{\beta}}A_{t}^{4,-} \leq \sqrt{\tfrac{4}{\beta}} \mathfrak{Z}_t(\theta_0) \leq \sqrt{\tfrac{8}{\beta}}A_{t}^{4,+} \right\}. \end{aligned} \end{align} $$
In this section, our goal is to estimate the probability of the oscillation event

with ![]() when we condition on
when we condition on
![]() $\mathscr {R}.$
Let
$\mathscr {R}.$
Let
![]() $(\mathscr {H}_t : t \geq 0)$
be the join of the filtrations (recalling (2.2))
$(\mathscr {H}_t : t \geq 0)$
be the join of the filtrations (recalling (2.2))
where we further augment by
![]() $\mathfrak {Z}_{\log {\widehat {n}_1}}.$
Note that
$\mathfrak {Z}_{\log {\widehat {n}_1}}.$
Note that
![]() $G_k$
and
$G_k$
and ![]() are adapted to
are adapted to
![]() $\mathscr {H}_{H_k}$
for any
$\mathscr {H}_{H_k}$
for any
![]() $k \in {\mathbb N}.$
Let
$k \in {\mathbb N}.$
Let
![]() $\tau $
be any
$\tau $
be any
![]() $\mathscr {H}$
stopping time such that for all
$\mathscr {H}$
stopping time such that for all
![]() $\log k_2 \leq t \leq \tau , \mathfrak {Z}_t$
satisfies
$\log k_2 \leq t \leq \tau , \mathfrak {Z}_t$
satisfies
Then (see (4.24)), if
![]() $\tau $
is just the first time (4.26) fails, then on
$\tau $
is just the first time (4.26) fails, then on
![]() $\mathscr {R}$
, it follows
$\mathscr {R}$
, it follows
![]() $\tau> \log \widehat {n}_1.$
$\tau> \log \widehat {n}_1.$
We will let
![]() $\mathcal {B}$
be the event that
$\mathcal {B}$
be the event that
![]() $\mathfrak {Z}_t \leq \sqrt {2}t$
for all
$\mathfrak {Z}_t \leq \sqrt {2}t$
for all
![]() $t \geq H_{k_2}$
and
$t \geq H_{k_2}$
and
![]() $\mathfrak {Z}_{\log {\widehat {n}_1}} \in [ \mathcal {A}_{\log \widehat {n_1}}^{4,-}, \mathcal {A}_{\log \widehat {n}_1}^{4,+} ].$
Then conditionally on
$\mathfrak {Z}_{\log {\widehat {n}_1}} \in [ \mathcal {A}_{\log \widehat {n_1}}^{4,-}, \mathcal {A}_{\log \widehat {n}_1}^{4,+} ].$
Then conditionally on
![]() $\mathcal {B},$
we can use Lemma 4.1 to compute the behavior of increments of
$\mathcal {B},$
we can use Lemma 4.1 to compute the behavior of increments of
![]() $\mathfrak {Z}.$
$\mathfrak {Z}.$
Lemma 4.5. Set Δ
k+1:= ℨ
τ∧H
k+1
− ℨ
τ∧H
k
. For
![]() $k_2 \leq k \leq \log n_1^+,$
there is a constant
$k_2 \leq k \leq \log n_1^+,$
there is a constant
![]() $C>0$
so that for all
$C>0$
so that for all
![]() $k_2$
and
$k_2$
and
![]() $k_1$
sufficiently large,
$k_1$
sufficiently large,

where the meaning of the first line is that the LHS is bounded above and below by the RHS, choosing signs appropriately, and where
for some constant
![]() $C>0.$
$C>0.$
Proof. We can express the increment
![]() $\Delta _{k+1},$
using Lemma 4.1, as
$\Delta _{k+1},$
using Lemma 4.1, as

and
![]() $B_{(\cdot )}$
is a
$B_{(\cdot )}$
is a
![]() $\mathscr {H}$
-adapted standard Brownian motion. The increment
$\mathscr {H}$
-adapted standard Brownian motion. The increment
![]() $\Delta _{k+1}'$
we can control using the barriers. By construction, for
$\Delta _{k+1}'$
we can control using the barriers. By construction, for
![]() $s \leq \tau $
for all
$s \leq \tau $
for all
![]() $k_1$
and n sufficiently large,
$k_1$
and n sufficiently large,
For
![]() $\tau \geq s \geq \frac {1}{2} \log n,$
we can also bound
$\tau \geq s \geq \frac {1}{2} \log n,$
we can also bound
In particular, for
![]() $k \leq \log n_1^+$
and all n sufficiently large,
$k \leq \log n_1^+$
and all n sufficiently large,
 $$ \begin{align} |\Delta_{k+1}'| \leq (\tau \wedge H_{k+1} - \tau \wedge H_{k}) \bigg( (\log k_2)^{-1/18} + 2(\log k_1)^{-1/100}\bigg). \end{align} $$
$$ \begin{align} |\Delta_{k+1}'| \leq (\tau \wedge H_{k+1} - \tau \wedge H_{k}) \bigg( (\log k_2)^{-1/18} + 2(\log k_1)^{-1/100}\bigg). \end{align} $$
As
![]() $B_{\tau \wedge (\cdot )}$
is a martingale,
$B_{\tau \wedge (\cdot )}$
is a martingale,
and using the bound (4.28), the claim concerning the first moment follows. For the second moment, we use
 $$ \begin{align} \left| \sqrt{\mathbb{E}[ \Delta_{k+1}^2 \vert \mathscr{H}_{H_k},\mathcal{B} ]} - \sqrt{\mathbb{E}[ (\Delta_{k+1}-\Delta_{k+1}')^2 \vert \mathscr{H}_{H_k},\mathcal{B}]} \right| \leq \sqrt{\mathbb{E}[ (\Delta_{k+1}')^2 \vert \mathscr{H}_{H_k},\mathcal{B} ]}. \end{align} $$
$$ \begin{align} \left| \sqrt{\mathbb{E}[ \Delta_{k+1}^2 \vert \mathscr{H}_{H_k},\mathcal{B} ]} - \sqrt{\mathbb{E}[ (\Delta_{k+1}-\Delta_{k+1}')^2 \vert \mathscr{H}_{H_k},\mathcal{B}]} \right| \leq \sqrt{\mathbb{E}[ (\Delta_{k+1}')^2 \vert \mathscr{H}_{H_k},\mathcal{B} ]}. \end{align} $$
Meanwhile, we have the exact formula
Hence, using (4.28) and (4.29), the bound for the second moment follows.
Proposition 4.6. There is a deterministic constant
![]() $C_\beta $
so that for all
$C_\beta $
so that for all
![]() $k_1$
sufficiently large, depending on
$k_1$
sufficiently large, depending on
![]() $k_2,$
and all n sufficiently large, depending on
$k_2,$
and all n sufficiently large, depending on
![]() $k_1$
, it holds uniformly in
$k_1$
, it holds uniformly in
![]() $\theta _0$
that
$\theta _0$
that
As the conditional probability of
![]() $\mathcal {B}$
is explicit, we conclude the following:
$\mathcal {B}$
is explicit, we conclude the following:
Corollary 4.7. There is a constant
![]() $C_\beta $
so that for all
$C_\beta $
so that for all
![]() $n,k_1$
sufficiently large, it holds uniformly in
$n,k_1$
sufficiently large, it holds uniformly in
![]() $\theta _0$
that
$\theta _0$
that
 $$\begin{align*}\mathbb{P}[ \widehat{ \mathscr{O}}^c \cap \mathscr{R} \cap \mathscr{G}_n ~\vert~ \mathscr{H}_{H_{k_2}}] \leq C_\beta \frac{ \left( \sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta_0)+k_6 \right)_+ \left( \sqrt{\tfrac{8}{\beta}}m_n - G_{\widehat{n}_1}(\theta_0) \right)_+ }{(\log k_1)^{50}\log(\widehat{n}_1/k_2)}, \quad a.s. \end{align*}$$
$$\begin{align*}\mathbb{P}[ \widehat{ \mathscr{O}}^c \cap \mathscr{R} \cap \mathscr{G}_n ~\vert~ \mathscr{H}_{H_{k_2}}] \leq C_\beta \frac{ \left( \sqrt{2}\log k_2 - \sqrt{\tfrac{\beta}{4}} \varphi_{k_2}(\theta_0)+k_6 \right)_+ \left( \sqrt{\tfrac{8}{\beta}}m_n - G_{\widehat{n}_1}(\theta_0) \right)_+ }{(\log k_1)^{50}\log(\widehat{n}_1/k_2)}, \quad a.s. \end{align*}$$
Proof. We multiply the result of Proposition 4.6 by ℙ[B | H H k 2 ], which is the probability that a Brownian bridge stays below a straight barrier (see (4.16)).
Proof of Proposition 4.6.
With some abuse of notation, let ![]() for any
for any
![]() $k\in {\mathbb N}$
for any
$k\in {\mathbb N}$
for any
![]() $\theta \geq \theta _0.$
We will show that for all
$\theta \geq \theta _0.$
We will show that for all
![]() $k_1$
and n sufficiently large (depending on
$k_1$
and n sufficiently large (depending on
![]() $k_2$
), there is a constant
$k_2$
), there is a constant
![]() $C_\beta $
so that
$C_\beta $
so that
The analogous bound for |ψ n 1 + (θ −− θ 0)| = −ψ n 1 + (θ −− θ 0) holds by the same argument after making appropriate sign changes. We just show (4.30). The proof will use tail estimates and computations contained in Section 7.
We will just write
![]() $\theta $
for
$\theta $
for
![]() $\theta _+ - \theta _0.$
Further, since our estimates will not depend on
$\theta _+ - \theta _0.$
Further, since our estimates will not depend on
![]() $\theta _0$
, in the rest of the proof, we take
$\theta _0$
, in the rest of the proof, we take
![]() $\theta _0=0$
. Let
$\theta _0=0$
. Let
![]() $\tau $
be the first time
$\tau $
be the first time
![]() $t \geq \log k_2$
that either (4.26) fails, or for some
$t \geq \log k_2$
that either (4.26) fails, or for some
![]() $H_k \leq t$
where
$H_k \leq t$
where
![]() $k_2 \leq k$
, either
$k_2 \leq k$
, either ![]() or
or
recall (2.1). Define

For any
![]() $\theta> 0,$
let
$\theta> 0,$
let ![]() solve (cf. (1.9))
solve (cf. (1.9))

and ![]() Then, on the event
Then, on the event
![]() $\mathscr {R} \cap \mathscr {G}_n$
(compare with (2.8)) if
$\mathscr {R} \cap \mathscr {G}_n$
(compare with (2.8)) if ![]() , we must actually have
, we must actually have
![]() $\tau> H_{ n_1^+}.$
Thus, for any
$\tau> H_{ n_1^+}.$
Thus, for any
![]() $t> 0$
,
$t> 0$
,
On the event ![]() By construction,
By construction, ![]() almost surely (see Lemma 2.1).
almost surely (see Lemma 2.1).
From Lemma 7.2, we have that for
![]() $k_2$
sufficiently large, the relative Prüfer phases (recall (1.9)) satisfy for some absolute constant C and any
$k_2$
sufficiently large, the relative Prüfer phases (recall (1.9)) satisfy for some absolute constant C and any
![]() $H_k < \tau $
,
$H_k < \tau $
,

The case
![]() $\sigma =1:$
We will estimate the conditional expectation of (4.33) given
$\sigma =1:$
We will estimate the conditional expectation of (4.33) given
![]() $\mathscr {H}_{H_k}$
using Lemma 4.5. We note using Lemma 4.5, we have for
$\mathscr {H}_{H_k}$
using Lemma 4.5. We note using Lemma 4.5, we have for
![]() $H_k < \tau $
,
$H_k < \tau $
,
 $$\begin{align*}\mathbb{E}[ Z^\tau_k ~\vert~\mathscr{H}_{H_k}, \mathcal{B}] = \frac{(-\sqrt{2} + O( (\log k_2)^{-1/18} + (\log k_1)^{-1/100}))}{\sqrt{k+1}}, \end{align*}$$
$$\begin{align*}\mathbb{E}[ Z^\tau_k ~\vert~\mathscr{H}_{H_k}, \mathcal{B}] = \frac{(-\sqrt{2} + O( (\log k_2)^{-1/18} + (\log k_1)^{-1/100}))}{\sqrt{k+1}}, \end{align*}$$
and moreover, the imaginary part of the expectation is
![]() $0$
. In the same way,
$0$
. In the same way,
Hence, using that ![]() for some
for some
![]() $C_\beta>0$
, which implies that the
$C_\beta>0$
, which implies that the
![]() $O(1/k)$
terms have a negative sign,
$O(1/k)$
terms have a negative sign,

The remainder of the real case will be covered by the argument for the imaginary cases, but the argument for the real case is simpler and given below. If we define the increasing function
![]() $k \mapsto P_k$
by the recurrence
$k \mapsto P_k$
by the recurrence

then ![]() is a supermartingale started at
is a supermartingale started at
![]() $0.$
Hence, for all
$0.$
Hence, for all
![]() $t \geq 0,$
$t \geq 0,$

with the final inequality following from the same argument as Doob’s inequality applied to the super-martingale ![]() . The recurrence for
. The recurrence for
![]() $P_k$
(4.35) is easily solved, and it can be checked that
$P_k$
(4.35) is easily solved, and it can be checked that
for some other sufficiently large
![]() $C_\beta .$
Hence, as
$C_\beta .$
Hence, as
![]() $\theta \leq Cn_1^{-1},$
we have
$\theta \leq Cn_1^{-1},$
we have
![]() $P_{n_1^+} \leq C_\beta e^{-(\log k_1)^{(29/30)}}.$
Thus, (4.36) and (4.32) imply (4.30).
$P_{n_1^+} \leq C_\beta e^{-(\log k_1)^{(29/30)}}.$
Thus, (4.36) and (4.32) imply (4.30).
The imaginary case ![]() In this case, to estimate (4.33) for
In this case, to estimate (4.33) for
![]() $H_k < \tau $
, we note using Lemma 4.5,
$H_k < \tau $
, we note using Lemma 4.5,

and moreover, the real part of the expectation is
![]() $0$
; the
$0$
; the ![]() depends on the sign of
depends on the sign of
![]() $\sigma .$
In the same way,
$\sigma .$
In the same way,
We note that there will also be a sign change in the
![]() $(1-\cos )$
term. For either of
$(1-\cos )$
term. For either of ![]() , it will be necessary to consider the (less advantageous) case considered on account of needing to consider the case
, it will be necessary to consider the (less advantageous) case considered on account of needing to consider the case
![]() $\theta _{-}$
(in which
$\theta _{-}$
(in which
![]() $\theta < 0$
).
$\theta < 0$
).
Applying Lemma 4.5 and bounding the cosine,

Let
![]() $\eta (x) = (\log \tfrac {1}{x})^{-100}e^{(\log \tfrac {1}{x})^{29/30}}$
for
$\eta (x) = (\log \tfrac {1}{x})^{-100}e^{(\log \tfrac {1}{x})^{29/30}}$
for
![]() $x \in (0,1)$
and define a stopping time
$x \in (0,1)$
and define a stopping time
![]() $\vartheta $
as the first
$\vartheta $
as the first
![]() $k \geq k_2$
such that
$k \geq k_2$
such that
Then, the stopped process ![]() satisfies for
satisfies for
![]() $k_2 \leq k \leq n_1^+$
,
$k_2 \leq k \leq n_1^+$
,

If we define the increasing function
![]() $k \mapsto P_k$
by the recurrence
$k \mapsto P_k$
by the recurrence

then ![]() is a supermartingale started at
is a supermartingale started at
![]() $0.$
The recurrence for
$0.$
The recurrence for
![]() $P_k$
is easily solved explicitly, and in particular, there is a constant
$P_k$
is easily solved explicitly, and in particular, there is a constant
![]() $C_\beta $
sufficiently large that for any
$C_\beta $
sufficiently large that for any
![]() $0 \leq k \leq n_1^+,$
$0 \leq k \leq n_1^+,$
 $$ \begin{align} k \theta \leq P_{k}-P_0 \leq C_\beta \sum_{\ell=0}^{k-1} \bigl\{ \theta + \eta^2( \tfrac{\ell+1}{n_1}) (\ell+1) \theta^2 \bigr\} \end{align} $$
$$ \begin{align} k \theta \leq P_{k}-P_0 \leq C_\beta \sum_{\ell=0}^{k-1} \bigl\{ \theta + \eta^2( \tfrac{\ell+1}{n_1}) (\ell+1) \theta^2 \bigr\} \end{align} $$
for all
![]() $k_1$
sufficiently large. If we take c as the maximum of
$k_1$
sufficiently large. If we take c as the maximum of
![]() $x \eta ^2(x)$
on
$x \eta ^2(x)$
on
![]() $[0,1],$
then we can further bound
$[0,1],$
then we can further bound
Moreover, for all
![]() $t \geq 0$
and any
$t \geq 0$
and any
![]() $m \leq n_1^+,$
by the same argument as in Doob’s inequality,
$m \leq n_1^+,$
by the same argument as in Doob’s inequality,

We can use this bound to control the probability that
![]() $\vartheta \in [2^{\ell -1},2^{\ell }].$
For this to happen for some
$\vartheta \in [2^{\ell -1},2^{\ell }].$
For this to happen for some
![]() $\ell \geq \log _2 k_2$
, we must have for some
$\ell \geq \log _2 k_2$
, we must have for some
![]() $c_\beta $
sufficiently small
$c_\beta $
sufficiently small
Hence, summing over
![]() $\log _2 k_2 \leq \ell \leq \log _2 n_1^+$
and using (4.42) and (4.43) and increasing
$\log _2 k_2 \leq \ell \leq \log _2 n_1^+$
and using (4.42) and (4.43) and increasing
![]() $C_\beta $
as needed between the inequalities,
$C_\beta $
as needed between the inequalities,

On the event
![]() $\{\vartheta> n_1^+\} \cap \mathscr {G}_n,$
we thus have that
$\{\vartheta> n_1^+\} \cap \mathscr {G}_n,$
we thus have that
![]() $\tau> n_1^+$
and
$\tau> n_1^+$
and
Hence, if we apply (4.43) again with
![]() $t = (\log k_1)^{50}P_{n_1^+},$
we conclude that for all
$t = (\log k_1)^{50}P_{n_1^+},$
we conclude that for all
![]() $k_1$
sufficiently large,
$k_1$
sufficiently large,

To conclude the proof, we observe that ![]() is a continuously differentiable function, and
is a continuously differentiable function, and
Hence, on taking
![]() $n\to \infty $
, the
$n\to \infty $
, the ![]() terms tend to
terms tend to
![]() $0$
almost surely, and we conclude
$0$
almost surely, and we conclude

which completes the proof by how
![]() $\eta $
was chosen.
$\eta $
was chosen.
4.2 The fine oscillation bound
In this section, we develop an estimate of continuity for the real part of the field, where we consider a high value of the field
![]() $\mathfrak {U}^j_{T_+}(\theta ')$
and then give a continuity estimate for
$\mathfrak {U}^j_{T_+}(\theta ')$
and then give a continuity estimate for
![]() $\mathfrak {U}^j_{T_+}(\theta )$
for
$\mathfrak {U}^j_{T_+}(\theta )$
for
![]() $\theta \in [\theta ',\theta '+\theta _0]$
for small
$\theta \in [\theta ',\theta '+\theta _0]$
for small
![]() $\theta _0.$
Without loss of generality, we will take
$\theta _0.$
Without loss of generality, we will take
![]() $\theta '=0.$
$\theta '=0.$
Proposition 4.8. (
![]() $\sigma =1$
). We suppose that for
$\sigma =1$
). We suppose that for
![]() $\alpha>4,\theta _0 > 0$
are given and satisfy
$\alpha>4,\theta _0 > 0$
are given and satisfy
where the constant
![]() $\varepsilon $
is a small positive constant, to be determined, that depends on
$\varepsilon $
is a small positive constant, to be determined, that depends on
![]() $\beta> 0$
. We will condition on
$\beta> 0$
. We will condition on
![]() $(\mathfrak {L}_{T_-}(\theta ): \theta )$
. We assume that the oscillations of the initial conditions are small in that
$(\mathfrak {L}_{T_-}(\theta ): \theta )$
. We assume that the oscillations of the initial conditions are small in that
We consider large endpoints in the sense that
Then there is
![]() $\delta =\delta (\beta )>0$
and a constant
$\delta =\delta (\beta )>0$
and a constant
![]() $C_\beta $
sufficiently large so that for any fixed set S in
$C_\beta $
sufficiently large so that for any fixed set S in
![]() $[0,\theta _0]$
of cardinality at most
$[0,\theta _0]$
of cardinality at most
![]() $e^{\theta _0^{-\delta }}$
, the event
$e^{\theta _0^{-\delta }}$
, the event
satisfies, on the event (4.45),
 $$\begin{align*}\begin{aligned} &\mathbb{P}\bigl( \mathscr{O}_{*}^c \cap \mathscr{P}_j'(0) \cap (4.46) ~\vert~ (\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr) \\ &\qquad\leq C_\beta(k_6) \frac{ \theta_0^{1+\delta} (\log k_5)\bigl( -\sqrt{\tfrac{8}{\beta}}(T_+-T_-) - \mathfrak{U}_{T_-}^j(0) \bigr) \exp\bigl(\sqrt{\tfrac{\beta}{2}} \mathfrak{U}_{T_-}^j(0) +2(T_+-T_-) \bigr) }{k_1^+(\log k_1)^{3/2}}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\mathbb{P}\bigl( \mathscr{O}_{*}^c \cap \mathscr{P}_j'(0) \cap (4.46) ~\vert~ (\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr) \\ &\qquad\leq C_\beta(k_6) \frac{ \theta_0^{1+\delta} (\log k_5)\bigl( -\sqrt{\tfrac{8}{\beta}}(T_+-T_-) - \mathfrak{U}_{T_-}^j(0) \bigr) \exp\bigl(\sqrt{\tfrac{\beta}{2}} \mathfrak{U}_{T_-}^j(0) +2(T_+-T_-) \bigr) }{k_1^+(\log k_1)^{3/2}}. \end{aligned} \end{align*}$$
Remark 4.9. An extension of the argument shows that in the case that
![]() $\alpha =\infty $
(which is to say the initial conditions are
$\alpha =\infty $
(which is to say the initial conditions are
![]() $0$
), we may, in fact, bound the
$0$
), we may, in fact, bound the
![]() $\delta $
-Hölder exponent on the interval by a constant with the same probability (up to constants). This is by applying a chaining argument, and effectively applying this proposition repeatedly to control the process on intervals of size
$\delta $
-Hölder exponent on the interval by a constant with the same probability (up to constants). This is by applying a chaining argument, and effectively applying this proposition repeatedly to control the process on intervals of size
![]() $\theta _0 {2^{-k}}$
for
$\theta _0 {2^{-k}}$
for
![]() $k=0,1,2,\dots $
. Step
$k=0,1,2,\dots $
. Step
![]() $1$
would remain the same (albeit with
$1$
would remain the same (albeit with
![]() $\mathscr {O}_*$
being the Hölder continuity event). Steps 2–5 (control on the difference of the imaginary part) should be generalized from the difference of the imaginary part over the interval
$\mathscr {O}_*$
being the Hölder continuity event). Steps 2–5 (control on the difference of the imaginary part) should be generalized from the difference of the imaginary part over the interval
![]() $[0,\theta _0]$
to the interval
$[0,\theta _0]$
to the interval
![]() $[\theta _1,\theta _2]$
, but essentially no details change. Step
$[\theta _1,\theta _2]$
, but essentially no details change. Step
![]() $6$
would change similarly. Finally, the chaining would be done.
$6$
would change similarly. Finally, the chaining would be done.
Proof. We let
![]() $d\mathfrak {X}_t = \sqrt {\tfrac {4}{\beta }}\Re (e^{i \Im \mathfrak {L}^{j}_t(0)} d \mathfrak {W}_t^j)$
and let
$d\mathfrak {X}_t = \sqrt {\tfrac {4}{\beta }}\Re (e^{i \Im \mathfrak {L}^{j}_t(0)} d \mathfrak {W}_t^j)$
and let
![]() $d\mathfrak {B}_t = \sqrt {\tfrac {4}{\beta }}\Im (e^{i \Im \mathfrak {L}_t^{j}(0)} d \mathfrak {W}_t^j),$
for
$d\mathfrak {B}_t = \sqrt {\tfrac {4}{\beta }}\Im (e^{i \Im \mathfrak {L}_t^{j}(0)} d \mathfrak {W}_t^j),$
for
![]() $t \in [T_-,T_+]$
. We also set the initial conditions
$t \in [T_-,T_+]$
. We also set the initial conditions
![]() $\mathfrak {B}_{T_-} =0$
and
$\mathfrak {B}_{T_-} =0$
and
![]() $\mathfrak {X}_{T_-}=\mathfrak {-U}_{T_-}^{j}(0)$
. Hence, the process
$\mathfrak {X}_{T_-}=\mathfrak {-U}_{T_-}^{j}(0)$
. Hence, the process
![]() $\mathfrak {X}$
equals
$\mathfrak {X}$
equals
![]() $-\mathfrak {U}^j$
.
$-\mathfrak {U}^j$
.
We let
![]() $\mathscr {H}$
be the filtration generated by
$\mathscr {H}$
be the filtration generated by
![]() $\mathfrak {X}$
and
$\mathfrak {X}$
and
![]() $\mathfrak {B}$
with
$\mathfrak {B}$
with
![]() $\mathfrak {X}_{T_+}$
and
$\mathfrak {X}_{T_+}$
and
![]() $(\mathfrak {L}^j_{T_-}{(\theta )} : \theta )$
adjoined. For a large integer absolute constant
$(\mathfrak {L}^j_{T_-}{(\theta )} : \theta )$
adjoined. For a large integer absolute constant
![]() $k_*$
, we set
$k_*$
, we set
![]() $T_* = T_+-k_*$
and we condition on the event that we remain below the concave barrier
$T_* = T_+-k_*$
and we condition on the event that we remain below the concave barrier
This barrier is above the concave barrier in
![]() $\mathscr {P}_j'(0).$
$\mathscr {P}_j'(0).$
As in the definitions and manipulations between (4.7) and (4.13) from Lemma 4.3, we define a measure
![]() $\mathbb {Q}$
which is mutually absolutely continuous with respect to
$\mathbb {Q}$
which is mutually absolutely continuous with respect to
![]() $\mathbb {P}$
and which flattens the curvature in (4.47). For this measure, there is a
$\mathbb {P}$
and which flattens the curvature in (4.47). For this measure, there is a
![]() $(\mathbb {Q}, \mathscr {H})$
-Brownian motion
$(\mathbb {Q}, \mathscr {H})$
-Brownian motion
![]() $(X_t:t \in [T_-,T_+])$
such that
$(X_t:t \in [T_-,T_+])$
such that

In the above, we have extended the definition of
![]() $\ell $
for
$\ell $
for
![]() $t \geq T_*$
by taking it constant and equal to
$t \geq T_*$
by taking it constant and equal to
![]() $\ell (T_*)$
. Under
$\ell (T_*)$
. Under
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\mathfrak {B}$
remains a
$\mathfrak {B}$
remains a
![]() $(\mathbb {Q}, \mathscr {H})$
-Brownian motion. Moreover, from (4.13), we have a bound on the Radon–Nikodym derivative
$(\mathbb {Q}, \mathscr {H})$
-Brownian motion. Moreover, from (4.13), we have a bound on the Radon–Nikodym derivative
 $$ \begin{align} \frac{d \mathbb{P}}{d \mathbb{Q}} \leq \exp \bigg( \int_{T_-}^{T_*} \!\!\!\!\!\! -\ell"(t)(\ell(t) + \mathfrak{X}_t) dt \bigg). \end{align} $$
$$ \begin{align} \frac{d \mathbb{P}}{d \mathbb{Q}} \leq \exp \bigg( \int_{T_-}^{T_*} \!\!\!\!\!\! -\ell"(t)(\ell(t) + \mathfrak{X}_t) dt \bigg). \end{align} $$
We also introduce
![]() $\mathfrak {D}_t = \ell (t \wedge T_*)+\mathfrak {X}_t$
, which under
$\mathfrak {D}_t = \ell (t \wedge T_*)+\mathfrak {X}_t$
, which under
![]() $\mathbb {Q}$
is an
$\mathbb {Q}$
is an
![]() $\mathscr {H}$
-adapted Bessel bridge with endpoints
$\mathscr {H}$
-adapted Bessel bridge with endpoints
The process
![]() $\mathfrak {D}$
describes the distance of
$\mathfrak {D}$
describes the distance of
![]() $\mathfrak {X}$
from the barrier.
$\mathfrak {X}$
from the barrier.
Step 1: Reduction to a conditional probability.
We will show in this section that the problem can be reduced to showing
for some
![]() $\delta> 0$
(note that
$\delta> 0$
(note that
![]() $\delta $
also hides in the definition of
$\delta $
also hides in the definition of
![]() $\mathscr {O}_{*}$
) depending on
$\mathscr {O}_{*}$
) depending on
![]() $\beta $
and all
$\beta $
and all
![]() $k_4,k_5$
bigger than some constant also depending only
$k_4,k_5$
bigger than some constant also depending only
![]() $\beta $
. Suppose we have established (4.50). Using the change of measure, we have
$\beta $
. Suppose we have established (4.50). Using the change of measure, we have

Applying Hölder’s inequality, there is
![]() $\lambda> 1$
sufficiently large that
$\lambda> 1$
sufficiently large that
 $$\begin{align*}\mathbb{P}\bigl( \mathscr{O}_{*}^c \cap \mathscr{P}_j'(0) ~\vert~ \mathfrak{U}^j_{T_+}(0),(\mathfrak{L}^j_{T_-}(\theta): \theta), (4.47)\bigr) \leq {\mathbb Q}\ \left( \exp \bigg( \int_{T_-}^{T_*} \!\!\!\!\!\! -\lambda \ell"(t)\mathfrak{D}_t dt \bigg) \right)^{1/\lambda} \theta_0^{1+\delta/2}. \end{align*}$$
$$\begin{align*}\mathbb{P}\bigl( \mathscr{O}_{*}^c \cap \mathscr{P}_j'(0) ~\vert~ \mathfrak{U}^j_{T_+}(0),(\mathfrak{L}^j_{T_-}(\theta): \theta), (4.47)\bigr) \leq {\mathbb Q}\ \left( \exp \bigg( \int_{T_-}^{T_*} \!\!\!\!\!\! -\lambda \ell"(t)\mathfrak{D}_t dt \bigg) \right)^{1/\lambda} \theta_0^{1+\delta/2}. \end{align*}$$
Controlling the Radon–Nikodym derivative is the same argument as the argument between (4.13) and (4.14). We have for some absolute constant
![]() $L>0$
,
$L>0$
,
and from Lemma 4.1 for some constant
![]() $C_\beta $
,
$C_\beta $
,
where ![]() is the subgaussian norm with respect to the conditional probability measure given as
is the subgaussian norm with respect to the conditional probability measure given as
![]() $\mathbb {Q}( \cdot ~|~\mathfrak {U}^j_{T_+}(0),(\mathfrak {L}^j_{T_-}(\theta ): \theta ), (4.47))$
. Hence, by convexity of the norm,
$\mathbb {Q}( \cdot ~|~\mathfrak {U}^j_{T_+}(0),(\mathfrak {L}^j_{T_-}(\theta ): \theta ), (4.47))$
. Hence, by convexity of the norm,

Thus, we have after increasing
![]() $C_\beta $
for all
$C_\beta $
for all
![]() $\lambda \geq 1$
,
$\lambda \geq 1$
,
 $$\begin{align*}{\mathbb Q}\ \left( \exp \bigg( \int_{T_-}^{T_*} \!\!\!\!\!\! -\lambda \ell"(t)\mathfrak{D}_t dt \bigg) \right)^{1/\lambda} \leq \exp\bigl( \lambda C_\beta (\log k_5)^{-24} \bigr), \end{align*}$$
$$\begin{align*}{\mathbb Q}\ \left( \exp \bigg( \int_{T_-}^{T_*} \!\!\!\!\!\! -\lambda \ell"(t)\mathfrak{D}_t dt \bigg) \right)^{1/\lambda} \leq \exp\bigl( \lambda C_\beta (\log k_5)^{-24} \bigr), \end{align*}$$
which is bounded by
![]() $2$
for all
$2$
for all
![]() $k_5$
small (depending on
$k_5$
small (depending on
![]() $\lambda $
, which in turn depends only on
$\lambda $
, which in turn depends only on
![]() $\beta $
).
$\beta $
).
Thus, we have shown
for some constant
![]() $\delta> 0$
depending only on
$\delta> 0$
depending only on
![]() $\beta $
and all
$\beta $
and all
![]() $k_4,k_5$
bigger than some constant depending only on
$k_4,k_5$
bigger than some constant depending only on
![]() $\beta $
. The event (4.47) contains
$\beta $
. The event (4.47) contains
![]() $\mathscr {P}_j'(0)$
, and so
$\mathscr {P}_j'(0)$
, and so
We then take expectation on both sides of the equation over
![]() $\mathfrak {U}^j_{T_+}(0)$
satisfying (4.46). Let
$\mathfrak {U}^j_{T_+}(0)$
satisfying (4.46). Let
![]() $\mathbb {M}$
be the change of measure that flattens the linear part of
$\mathbb {M}$
be the change of measure that flattens the linear part of
![]() $\ell $
(with respect to the conditional measure
$\ell $
(with respect to the conditional measure
![]() $\mathbb {P}( \cdot ~|~(\mathfrak {L}^j_{T_-}(\theta ): \theta ))$
)
$\mathbb {P}( \cdot ~|~(\mathfrak {L}^j_{T_-}(\theta ): \theta ))$
)
 $$\begin{align*}\frac{d\mathbb{M}}{d\mathbb{P}} = \exp \bigg( \sqrt{\tfrac{\beta}{2}} (\mathfrak{U}_{T_+}^j(0) - \mathfrak{U}_{T_-}^j(0)) - (T_+-T_-) \bigg), \end{align*}$$
$$\begin{align*}\frac{d\mathbb{M}}{d\mathbb{P}} = \exp \bigg( \sqrt{\tfrac{\beta}{2}} (\mathfrak{U}_{T_+}^j(0) - \mathfrak{U}_{T_-}^j(0)) - (T_+-T_-) \bigg), \end{align*}$$
under which
is a speed-
![]() $(\tfrac {4}{\beta })$
Brownian motion. Note that on (4.46), the change of measure
$(\tfrac {4}{\beta })$
Brownian motion. Note that on (4.46), the change of measure
![]() $\frac {d\mathbb {M}}{d\mathbb {P}}$
is controlled up to constants by
$\frac {d\mathbb {M}}{d\mathbb {P}}$
is controlled up to constants by
 $$\begin{align*}\frac{d\mathbb{M}}{d\mathbb{P}} \geq C(k_6) \exp \bigg( -\sqrt{\tfrac{\beta}{2}} \mathfrak{U}_{T_-}^j(0) -(T_+-T_-) \bigg). \end{align*}$$
$$\begin{align*}\frac{d\mathbb{M}}{d\mathbb{P}} \geq C(k_6) \exp \bigg( -\sqrt{\tfrac{\beta}{2}} \mathfrak{U}_{T_-}^j(0) -(T_+-T_-) \bigg). \end{align*}$$
In particular, we have (using
![]() $T_+ - T_- = \log k_1^+$
)
$T_+ - T_- = \log k_1^+$
)
 $$ \begin{align*} & \mathbb{P}\bigl( (4.47) \cap (4.46) ~\vert~(\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr)\\ & \quad \leq \frac{ C(k_6)} {k_1^+ } \exp\bigg(\sqrt{\tfrac{\beta}{2}} \mathfrak{U}_{T_-}^j(0) +2(T_+-T_-) \bigg) \mathbb{M}\bigl( (4.47) \cap (4.46) ~\vert~ (\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr). \end{align*} $$
$$ \begin{align*} & \mathbb{P}\bigl( (4.47) \cap (4.46) ~\vert~(\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr)\\ & \quad \leq \frac{ C(k_6)} {k_1^+ } \exp\bigg(\sqrt{\tfrac{\beta}{2}} \mathfrak{U}_{T_-}^j(0) +2(T_+-T_-) \bigg) \mathbb{M}\bigl( (4.47) \cap (4.46) ~\vert~ (\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr). \end{align*} $$
Using barrier estimates as in [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6], we can bound the
![]() $\mathbb {M}$
-probability for values of
$\mathbb {M}$
-probability for values of
![]() $\mathfrak {U}^j_{T_-}(0)$
given by
$\mathfrak {U}^j_{T_-}(0)$
given by
![]() $\mathscr {P}_j'(0)$
$\mathscr {P}_j'(0)$
 $$\begin{align*}\mathbb{M}\bigl( (4.47) \cap (4.46) ~\vert~ (\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr) \leq \frac{C(k_6)(\log k_5) \bigl( -\mathfrak{U}_{T_-}^j(0) -\sqrt{\tfrac{8}{\beta}}(T_+-T_-) \bigr) }{(\log k_1)^{3/2}}. \end{align*}$$
$$\begin{align*}\mathbb{M}\bigl( (4.47) \cap (4.46) ~\vert~ (\mathfrak{L}^j_{T_-}(\theta): \theta)\bigr) \leq \frac{C(k_6)(\log k_5) \bigl( -\mathfrak{U}_{T_-}^j(0) -\sqrt{\tfrac{8}{\beta}}(T_+-T_-) \bigr) }{(\log k_1)^{3/2}}. \end{align*}$$
This concludes the reduction of the lemma to (4.50).
Step 2: Finding a good event on which the slope of the Bessel bridge is tame.
We introduce a random variable to control the slopes of the Bessel bridge:

Conditioning on
![]() $\mathfrak {D}_{T_*}$
, by the Gaussian tail bound for the Brownian bridge increment
$\mathfrak {D}_{T_*}$
, by the Gaussian tail bound for the Brownian bridge increment
![]() $\mathfrak {D}_{T_+} - \mathfrak {D}_{T_*}$
and the Gaussian tail bound for the Bessel bridge increment (cf. Lemma 4.1)
$\mathfrak {D}_{T_+} - \mathfrak {D}_{T_*}$
and the Gaussian tail bound for the Bessel bridge increment (cf. Lemma 4.1)
![]() $\mathfrak {D}_{T_*} - \mathfrak {D}_{T_+-k}$
, there is a Gaussian tail bound for
$\mathfrak {D}_{T_*} - \mathfrak {D}_{T_+-k}$
, there is a Gaussian tail bound for
![]() $\mathfrak {u}$
of the form
$\mathfrak {u}$
of the form
 $$\begin{align*}\mathbb{Q} \left( \bigg| \frac{ \mathfrak{D}_{T_+} - \mathfrak{D}_{T_+-k} } {k} \bigg|> C\sqrt{\tfrac{4}{\beta}}(1+x) ~\middle\vert~ \mathscr{H}_{T_-} \right) \leq Ce^{-k x^2} \end{align*}$$
$$\begin{align*}\mathbb{Q} \left( \bigg| \frac{ \mathfrak{D}_{T_+} - \mathfrak{D}_{T_+-k} } {k} \bigg|> C\sqrt{\tfrac{4}{\beta}}(1+x) ~\middle\vert~ \mathscr{H}_{T_-} \right) \leq Ce^{-k x^2} \end{align*}$$
for some C sufficiently large and all
![]() $k \geq k_*.$
Thus, summing in k, we may assume that the event
$k \geq k_*.$
Thus, summing in k, we may assume that the event
occurs with
![]() $(\mathbb {Q}~|~\mathscr {H}_{T_-})$
-conditional probability at least
$(\mathbb {Q}~|~\mathscr {H}_{T_-})$
-conditional probability at least
![]() $1-C_{\beta } e^{-c_\beta \widehat {\delta }^2(\log (1/\theta _0))^{1.01}}$
for all
$1-C_{\beta } e^{-c_\beta \widehat {\delta }^2(\log (1/\theta _0))^{1.01}}$
for all
![]() $\widehat {\delta }, \theta _0> 0$
sufficiently small.
$\widehat {\delta }, \theta _0> 0$
sufficiently small.
Step 3: Finding a good event with small oscillations.
The oscillations of
![]() $\mathfrak {X}_t$
must be controlled, especially near the endpoint
$\mathfrak {X}_t$
must be controlled, especially near the endpoint
![]() $t=T_+,$
to control their contribution to the diffusions
$t=T_+,$
to control their contribution to the diffusions
![]() $d\mathfrak {X}_t +i d\mathfrak {B}_t.$
These oscillations are ultimately controlled by those of the underlying Brownian motion
$d\mathfrak {X}_t +i d\mathfrak {B}_t.$
These oscillations are ultimately controlled by those of the underlying Brownian motion
![]() ${X}_t$
. Define the event
${X}_t$
. Define the event
![]() $E_{1}$
, for
$E_{1}$
, for
![]() $\widehat {\delta }$
to be determined as a function of
$\widehat {\delta }$
to be determined as a function of
![]() $\beta $
,
$\beta $
,
 $$\begin{align*}\max \bigg\{ \frac{|X_u-X_s|}{|u-s|^{1/4}} , \frac{|\mathfrak{X}_{u}-\mathfrak{X}_s|}{|u-s|^{1/4}} \bigg\} \leq \tfrac{\widehat{\delta}}{3} \bigl( \log(1/\theta_0)^{0.51} (T_+-u+1)^{0.49} \bigr), \forall~ T_+ \geq u \geq s \geq T_-, |u-s| \leq 1. \end{align*}$$
$$\begin{align*}\max \bigg\{ \frac{|X_u-X_s|}{|u-s|^{1/4}} , \frac{|\mathfrak{X}_{u}-\mathfrak{X}_s|}{|u-s|^{1/4}} \bigg\} \leq \tfrac{\widehat{\delta}}{3} \bigl( \log(1/\theta_0)^{0.51} (T_+-u+1)^{0.49} \bigr), \forall~ T_+ \geq u \geq s \geq T_-, |u-s| \leq 1. \end{align*}$$
We may bound this probability by reducing the statement to a union bound over sets
for integer
![]() $k.$
$k.$
First, we will need a basic input: from oscillation theory of Brownian motion, there is an absolute constant
![]() $C>0$
so that for all
$C>0$
so that for all
![]() $x>0,$
$x>0,$
 $$ \begin{align} \mathbb{Q}\bigg( \sup_{ (u,s) \in \operatorname{CP}_k} \frac{|X_u-X_s|}{|u-s|^{1/4}}> \sqrt{\tfrac{4}{\beta}}C(1+x) ~\bigg\vert~ \mathscr{H}_{T_-} \bigg) \leq e^{-x^2}. \end{align} $$
$$ \begin{align} \mathbb{Q}\bigg( \sup_{ (u,s) \in \operatorname{CP}_k} \frac{|X_u-X_s|}{|u-s|^{1/4}}> \sqrt{\tfrac{4}{\beta}}C(1+x) ~\bigg\vert~ \mathscr{H}_{T_-} \bigg) \leq e^{-x^2}. \end{align} $$
This follows, for example, from the Borel-Tsirelson-Ibragimov-Sudakov inequality, together with [Reference Revuz and YorRY99, Theorem I.2.1]. Taking a union bound over k, we conclude that with
![]() $(\mathbb {Q}~|~\mathscr {H}_{T_-})$
-conditional probability
$(\mathbb {Q}~|~\mathscr {H}_{T_-})$
-conditional probability
![]() $1-C_{\beta } e^{-c_\beta \widehat {\delta }^2 (\log (1/\theta _0))^2}$
for all
$1-C_{\beta } e^{-c_\beta \widehat {\delta }^2 (\log (1/\theta _0))^2}$
for all
![]() $\widehat {\delta }, \theta _0> 0$
sufficiently small,
$\widehat {\delta }, \theta _0> 0$
sufficiently small,
To control the oscillations of
![]() $\mathfrak {X},$
it suffices to control the oscillations of
$\mathfrak {X},$
it suffices to control the oscillations of
![]() $\mathfrak {D}$
in its place, as for any
$\mathfrak {D}$
in its place, as for any
![]() $T_+ \geq u \geq s \geq T_-$
with
$T_+ \geq u \geq s \geq T_-$
with
![]() $|u-s| \leq 1$
,
$|u-s| \leq 1$
,
and
![]() $\ell '$
remains bounded.
$\ell '$
remains bounded.
For the control on
![]() $\mathfrak {D}$
, we consider separately the cases of
$\mathfrak {D}$
, we consider separately the cases of
![]() $k \leq k_*-2$
and
$k \leq k_*-2$
and
![]() $k \geq k_*-2$
. In the former case, if we condition on the value of
$k \geq k_*-2$
. In the former case, if we condition on the value of
![]() $\mathfrak {X}_{T_*}$
, then the process
$\mathfrak {X}_{T_*}$
, then the process
![]() $\bigl (\mathfrak {X}_{t} : t \in [T_*,T_+]\bigr )$
is a speed-
$\bigl (\mathfrak {X}_{t} : t \in [T_*,T_+]\bigr )$
is a speed-
![]() $({\tfrac {4}{\beta }})$
Brownian bridge. Its slope can be controlled by
$({\tfrac {4}{\beta }})$
Brownian bridge. Its slope can be controlled by
![]() $\mathfrak {u}$
, and after removing its slope, the same bound (4.53) holds, with possibly different constants, and so taking a union bound over k, we control the probability of
$\mathfrak {u}$
, and after removing its slope, the same bound (4.53) holds, with possibly different constants, and so taking a union bound over k, we control the probability of
![]() $E_1$
failing for these k.
$E_1$
failing for these k.
For
![]() $k \geq k_*-2$
, integrating the differential representation for
$k \geq k_*-2$
, integrating the differential representation for
![]() $\mathfrak {D}_t$
, we have that for
$\mathfrak {D}_t$
, we have that for
![]() $(u,s) \in \operatorname {CP}_k$
,
$(u,s) \in \operatorname {CP}_k$
,

On the event
![]() $\mathscr {P}_j'(\theta )$
, we may bound
$\mathscr {P}_j'(\theta )$
, we may bound
![]() $\mathfrak {D}_t \geq \sqrt {\tfrac {8}{\beta }}(\log k_5)$
(which is due to the concave barrier in
$\mathfrak {D}_t \geq \sqrt {\tfrac {8}{\beta }}(\log k_5)$
(which is due to the concave barrier in
![]() $\mathscr {P}_j'(\theta )$
being shifted by a constant factor from the conditioning (4.47)), for all
$\mathscr {P}_j'(\theta )$
being shifted by a constant factor from the conditioning (4.47)), for all
![]() $t \in (s,u)$
for which
$t \in (s,u)$
for which
![]() $t \leq T_*$
. To the second integral, we add and subtract
$t \leq T_*$
. To the second integral, we add and subtract
![]() $\mathfrak {D}_{T_+-k+2}$
in the following way:
$\mathfrak {D}_{T_+-k+2}$
in the following way:
 $$\begin{align*}\int_s^u \bigg( \frac{\mathfrak{D}_{T_+}-\mathfrak{D}_t}{T_+-t} \bigg) dt = \int_s^u \bigg( \frac{\mathfrak{D}_{T_+}-\mathfrak{D}_{T_+-k+2}}{T_+-t} \bigg) dt + \int_s^u \bigg( \frac{\mathfrak{D}_{T_+-k+2}-\mathfrak{D}_t}{T_+-t} \bigg) dt. \end{align*}$$
$$\begin{align*}\int_s^u \bigg( \frac{\mathfrak{D}_{T_+}-\mathfrak{D}_t}{T_+-t} \bigg) dt = \int_s^u \bigg( \frac{\mathfrak{D}_{T_+}-\mathfrak{D}_{T_+-k+2}}{T_+-t} \bigg) dt + \int_s^u \bigg( \frac{\mathfrak{D}_{T_+-k+2}-\mathfrak{D}_t}{T_+-t} \bigg) dt. \end{align*}$$
The first part we control in the same way as above. As for the second, we may bound it above to create the following implicit bound:
 $$ \begin{align*} & \sup_{ (u,s) \in \operatorname{CP}_k} \frac{|\mathfrak{D}_u -\mathfrak{D}_s|}{|u-s|^{1/4}}\\ & \quad \leq \sup_{ (u,s) \in \operatorname{CP}_k} \frac{|X_u-X_s|}{|u-s|^{1/4}} + (\mathfrak{u}+C_\beta) + \frac{C}{k_*-4} \bigg( \max_{\kappa=k_*-2, \dots, k_*+2} \sup_{ (u,s) \in \operatorname{CP}_\kappa} \frac{|\mathfrak{D}_u -\mathfrak{D}_s|}{|u-s|^{1/4}} \bigg). \end{align*} $$
$$ \begin{align*} & \sup_{ (u,s) \in \operatorname{CP}_k} \frac{|\mathfrak{D}_u -\mathfrak{D}_s|}{|u-s|^{1/4}}\\ & \quad \leq \sup_{ (u,s) \in \operatorname{CP}_k} \frac{|X_u-X_s|}{|u-s|^{1/4}} + (\mathfrak{u}+C_\beta) + \frac{C}{k_*-4} \bigg( \max_{\kappa=k_*-2, \dots, k_*+2} \sup_{ (u,s) \in \operatorname{CP}_\kappa} \frac{|\mathfrak{D}_u -\mathfrak{D}_s|}{|u-s|^{1/4}} \bigg). \end{align*} $$
Here,
![]() $C_\beta $
controls the Bessel generator term and C is an absolute constant. Hence, on taking maxima over both sides, we conclude for all
$C_\beta $
controls the Bessel generator term and C is an absolute constant. Hence, on taking maxima over both sides, we conclude for all
![]() $k_*$
larger than an absolute constant,
$k_*$
larger than an absolute constant,
 $$\begin{align*}\sup_{ (u,s) \in \operatorname{CP}_k} \frac{|\mathfrak{D}_u -\mathfrak{D}_s|}{|u-s|^{1/4}} \leq 2 \bigg( \max_{\kappa=k_*-2, \dots, k_*+2} \sup_{ (u,s) \in \operatorname{CP}_\kappa} \frac{|{X}_u -{X}_s|}{|u-s|^{1/4}} +\mathfrak{u}+C_\beta \bigg). \end{align*}$$
$$\begin{align*}\sup_{ (u,s) \in \operatorname{CP}_k} \frac{|\mathfrak{D}_u -\mathfrak{D}_s|}{|u-s|^{1/4}} \leq 2 \bigg( \max_{\kappa=k_*-2, \dots, k_*+2} \sup_{ (u,s) \in \operatorname{CP}_\kappa} \frac{|{X}_u -{X}_s|}{|u-s|^{1/4}} +\mathfrak{u}+C_\beta \bigg). \end{align*}$$
Using (4.54) and (4.52), we conclude that there is some
![]() $C_\beta , c_\beta> 0$
such that for all sufficiently small
$C_\beta , c_\beta> 0$
such that for all sufficiently small
![]() $\theta _0$
and
$\theta _0$
and
![]() $\widehat {\delta }$
,
$\widehat {\delta }$
,
Step 4: Finding a good event on which the imaginary part can not explode.
This will turn out to be the most probabilistically expensive part. Let
![]() $E_{2}$
be the event, for
$E_{2}$
be the event, for
![]() $C_\beta , \delta _\beta $
to be determined,
$C_\beta , \delta _\beta $
to be determined,
 $$ \begin{align} \mathfrak{X}_t -\mathfrak{X}_s \leq \left( 1+\frac{2}{\beta} - 3\widehat{\delta}\right) (t-s) - \delta_\beta \bigl( \log(\theta_0) \bigr) + \log_+(T_+ - t) , \quad \forall\, T_+ \geq t \geq s \geq T_-. \end{align} $$
$$ \begin{align} \mathfrak{X}_t -\mathfrak{X}_s \leq \left( 1+\frac{2}{\beta} - 3\widehat{\delta}\right) (t-s) - \delta_\beta \bigl( \log(\theta_0) \bigr) + \log_+(T_+ - t) , \quad \forall\, T_+ \geq t \geq s \geq T_-. \end{align} $$
As we will work on the event
![]() $E_1$
, it suffices to control the above on integer-valued points; hence, it instead suffices to bound the probability
$E_1$
, it suffices to control the above on integer-valued points; hence, it instead suffices to bound the probability
 $$\begin{align*}\begin{aligned} \mathfrak{X}_t -\mathfrak{X}_s &\leq \left( 1+\frac{2}{\beta} - 3\widehat{\delta}\right) (t-s) - (\delta_\beta-2\widehat{\delta}) \bigl( \log(\theta_0) \bigr) + (1-2\widehat{\delta})\log_+(T_+ - t), \\ &\forall\ T_+ \geq t \geq s \geq T_- \quad\text{for which} \quad t,s \in {\mathbb Z}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathfrak{X}_t -\mathfrak{X}_s &\leq \left( 1+\frac{2}{\beta} - 3\widehat{\delta}\right) (t-s) - (\delta_\beta-2\widehat{\delta}) \bigl( \log(\theta_0) \bigr) + (1-2\widehat{\delta})\log_+(T_+ - t), \\ &\forall\ T_+ \geq t \geq s \geq T_- \quad\text{for which} \quad t,s \in {\mathbb Z}. \end{aligned} \end{align*}$$
We can furthermore formulate a sufficient bound in terms of
![]() $\mathfrak {D}$
using that
$\mathfrak {D}$
using that
![]() $|\ell '(t) - \sqrt {\tfrac {8}{\beta }}| \leq \widehat {\delta }$
(which holds provided
$|\ell '(t) - \sqrt {\tfrac {8}{\beta }}| \leq \widehat {\delta }$
(which holds provided
![]() $k_5$
is chosen sufficiently large with respect to
$k_5$
is chosen sufficiently large with respect to
![]() $\widehat {\delta }$
), so that
$\widehat {\delta }$
), so that
 $$ \begin{align} \begin{aligned} \mathfrak{D}_t -\mathfrak{D}_s &\leq \left( 1 +\frac{2}{\beta} +\sqrt{\frac{8}{\beta}} - 4\widehat{\delta}\right) (t-s) - (\delta_\beta-2\widehat{\delta}) \bigl( \log(\theta_0) \bigr) + (1-2\widehat{\delta})\log_+(T_+ - t), \\ &\forall\ T_+ \geq t \geq s \geq T_- \quad\text{for which} \quad t,s \in {\mathbb Z}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathfrak{D}_t -\mathfrak{D}_s &\leq \left( 1 +\frac{2}{\beta} +\sqrt{\frac{8}{\beta}} - 4\widehat{\delta}\right) (t-s) - (\delta_\beta-2\widehat{\delta}) \bigl( \log(\theta_0) \bigr) + (1-2\widehat{\delta})\log_+(T_+ - t), \\ &\forall\ T_+ \geq t \geq s \geq T_- \quad\text{for which} \quad t,s \in {\mathbb Z}. \end{aligned} \end{align} $$
If
![]() $s\geq T_*$
, then as in the lead-up to (4.52), conditioning on the value of
$s\geq T_*$
, then as in the lead-up to (4.52), conditioning on the value of
![]() $\mathfrak {D}_{T_*}$
the process
$\mathfrak {D}_{T_*}$
the process
![]() $ (\mathfrak {D}_t -\mathfrak {D}_{T_*} : t \in [T_*,T_+]) $
is a speed-
$ (\mathfrak {D}_t -\mathfrak {D}_{T_*} : t \in [T_*,T_+]) $
is a speed-
![]() $({\tfrac {4}{\beta }})$
Brownian bridge under
$({\tfrac {4}{\beta }})$
Brownian bridge under
![]() ${\mathbb Q}$
with slope at most
${\mathbb Q}$
with slope at most
![]() $\mathfrak {u}$
. Hence, we have a tail bound that for any
$\mathfrak {u}$
. Hence, we have a tail bound that for any
![]() $t \geq s$
with
$t \geq s$
with
![]() $s \geq T_*$
,
$s \geq T_*$
,
 $$ \begin{align} \begin{aligned} &{\mathbb Q}\ \left( \bigl\{ \mathfrak{D}_t - \mathfrak{D}_s> \delta +\tfrac{\widehat{\delta}}{3}(t-s) \bigr\} \cap E_0 ~\middle\vert~ \mathscr{H}_{T_-} \right) \leq \exp\left( - \frac{\beta \widehat{\delta}^2}{8(t-s)} \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &{\mathbb Q}\ \left( \bigl\{ \mathfrak{D}_t - \mathfrak{D}_s> \delta +\tfrac{\widehat{\delta}}{3}(t-s) \bigr\} \cap E_0 ~\middle\vert~ \mathscr{H}_{T_-} \right) \leq \exp\left( - \frac{\beta \widehat{\delta}^2}{8(t-s)} \right). \end{aligned} \end{align} $$
Using this, we have that the portion of (4.57) for which
![]() $t,s$
with
$t,s$
with
![]() $T_* \leq s \leq t \leq T_+$
can be controlled by
$T_* \leq s \leq t \leq T_+$
can be controlled by
![]() $\widehat {\delta }\log (1/\theta _0)$
, which is less than the bound stated in (4.57), with probability
$\widehat {\delta }\log (1/\theta _0)$
, which is less than the bound stated in (4.57), with probability
![]() $1-C_{\beta } e^{-c_\beta \widehat {\delta }^2 (\log (1/\theta _0))^2}$
for all
$1-C_{\beta } e^{-c_\beta \widehat {\delta }^2 (\log (1/\theta _0))^2}$
for all
![]() $\widehat {\delta }, \theta _0> 0$
sufficiently small. Hence, we may reduce the problem to showing
$\widehat {\delta }, \theta _0> 0$
sufficiently small. Hence, we may reduce the problem to showing
 $$ \begin{align} \begin{aligned} \mathfrak{D}_t -\mathfrak{D}_s &\leq \left( 1 +\frac{2}{\beta} +\sqrt{\frac{8}{\beta}} - 4\widehat{\delta}\right) (t-s) - (\delta_\beta-3\widehat{\delta}) \bigl( \log(\theta_0) \bigr) + (1-2\widehat{\delta})\log_+(T_+ - t), \\ &\forall\ T_* \geq t \geq s \geq T_- \quad\text{for which} \quad t,s \in {\mathbb Z}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathfrak{D}_t -\mathfrak{D}_s &\leq \left( 1 +\frac{2}{\beta} +\sqrt{\frac{8}{\beta}} - 4\widehat{\delta}\right) (t-s) - (\delta_\beta-3\widehat{\delta}) \bigl( \log(\theta_0) \bigr) + (1-2\widehat{\delta})\log_+(T_+ - t), \\ &\forall\ T_* \geq t \geq s \geq T_- \quad\text{for which} \quad t,s \in {\mathbb Z}. \end{aligned} \end{align} $$
For all
![]() $s \leq t \leq T_*$
, we begin by recalling that the Bessel bridge SDE has strong solutions:
$s \leq t \leq T_*$
, we begin by recalling that the Bessel bridge SDE has strong solutions:

For all
![]() $k_5$
sufficiently large (with respect to
$k_5$
sufficiently large (with respect to
![]() $\widehat {\delta }$
) on
$\widehat {\delta }$
) on
![]() $\mathscr {P}_j'(0)$
, we may bound above the Bessel generator term by
$\mathscr {P}_j'(0)$
, we may bound above the Bessel generator term by
![]() $\widehat {\delta }$
. The slope we bound on
$\widehat {\delta }$
. The slope we bound on
![]() $E_0 \cap E_1 \cap \mathscr {P}_j'(0)$
by comparing t to its (integer) ceiling
$E_0 \cap E_1 \cap \mathscr {P}_j'(0)$
by comparing t to its (integer) ceiling
 $$ \begin{align} \bigg| \frac{\mathfrak{D}_{T_+}-\mathfrak{D}_t}{T_+-t} \bigg| \leq \frac{2\widehat{\delta}}{3} \frac{ \log(1/\theta_0)^{0.51}} {(T_+-t)^{0.51}}. \end{align} $$
$$ \begin{align} \bigg| \frac{\mathfrak{D}_{T_+}-\mathfrak{D}_t}{T_+-t} \bigg| \leq \frac{2\widehat{\delta}}{3} \frac{ \log(1/\theta_0)^{0.51}} {(T_+-t)^{0.51}}. \end{align} $$
When
![]() $T_+-t \geq \log (1/\theta _0)$
, we can just as well bound the above by
$T_+-t \geq \log (1/\theta _0)$
, we can just as well bound the above by
![]() $\frac {2\widehat {\delta }}{3}$
. We conclude that we have the bound on
$\frac {2\widehat {\delta }}{3}$
. We conclude that we have the bound on
![]() $E_0 \cap E_1 \cap \mathscr {P}_j'(0)$
$E_0 \cap E_1 \cap \mathscr {P}_j'(0)$
 $$ \begin{align} \mathfrak{D}_t - \mathfrak{D}_s \leq X_t - X_s + \frac{5\widehat{\delta}}{3} (t-s) + \frac{5\widehat{\delta}}{3} \log(1/\theta_0) \quad \text{for all} \quad T_- \leq s \leq t \leq T_*. \end{align} $$
$$ \begin{align} \mathfrak{D}_t - \mathfrak{D}_s \leq X_t - X_s + \frac{5\widehat{\delta}}{3} (t-s) + \frac{5\widehat{\delta}}{3} \log(1/\theta_0) \quad \text{for all} \quad T_- \leq s \leq t \leq T_*. \end{align} $$
Thus, for any
![]() $t \leq T_*$
and
$t \leq T_*$
and
![]() $w>0$
, we have the bound, using the probability that Brownian motion hits a line,
$w>0$
, we have the bound, using the probability that Brownian motion hits a line,
 $$\begin{align*}\begin{aligned} & {\mathbb Q}\ \left( \exists~s \in [T_-,t]: \mathfrak{D}_t - \mathfrak{D}_s> w + \bigg(1 + \frac{2}{\beta}+\sqrt{\frac{8}{\beta}} - 4\widehat{\delta} \bigg)(t-s) ~\bigg\vert~ \mathscr{H}_{T_{-}} \right) \\ &\quad \leq \exp\,\left( - \frac{\beta}{2} \bigg(1 + \frac{2}{\beta} +\sqrt{\frac{8}{\beta}} - \frac{17\widehat{\delta}}{3}\bigg) \bigg(w - \frac{5\widehat{\delta}}{3}\log(1/\theta_0)\bigg) \right). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} & {\mathbb Q}\ \left( \exists~s \in [T_-,t]: \mathfrak{D}_t - \mathfrak{D}_s> w + \bigg(1 + \frac{2}{\beta}+\sqrt{\frac{8}{\beta}} - 4\widehat{\delta} \bigg)(t-s) ~\bigg\vert~ \mathscr{H}_{T_{-}} \right) \\ &\quad \leq \exp\,\left( - \frac{\beta}{2} \bigg(1 + \frac{2}{\beta} +\sqrt{\frac{8}{\beta}} - \frac{17\widehat{\delta}}{3}\bigg) \bigg(w - \frac{5\widehat{\delta}}{3}\log(1/\theta_0)\bigg) \right). \end{aligned} \end{align*}$$
We pick a
![]() $\delta _\beta \in (0,1)$
and an
$\delta _\beta \in (0,1)$
and an
![]() $\eta _\beta $
so that
$\eta _\beta $
so that
 $$ \begin{align} \frac{\beta}{2}\bigg(1 + \frac{2}{\beta} + \sqrt{\frac{8}{\beta}}\bigg)\delta_\beta> \eta_\beta >1. \end{align} $$
$$ \begin{align} \frac{\beta}{2}\bigg(1 + \frac{2}{\beta} + \sqrt{\frac{8}{\beta}}\bigg)\delta_\beta> \eta_\beta >1. \end{align} $$
We apply the tail bound just above with
![]() $w =(\delta _\beta - 3\widehat {\delta }) \bigl ( \log (1/(\theta _0)) \bigr ) + \bigl (1 - 2\widehat {\delta }\bigr )\log _+(T_+ - t),$
from which it follows that for all
$w =(\delta _\beta - 3\widehat {\delta }) \bigl ( \log (1/(\theta _0)) \bigr ) + \bigl (1 - 2\widehat {\delta }\bigr )\log _+(T_+ - t),$
from which it follows that for all
![]() $\widehat {\delta }$
sufficiently small (as a function of
$\widehat {\delta }$
sufficiently small (as a function of
![]() $\beta $
),
$\beta $
),
 $$\begin{align*}\begin{aligned} & {\mathbb Q}\ \left( \bigg\{\exists~s \in [T_-,t]: \text{ (4.59) fails } \bigg\} \cap E_0 \cap E_1 \cap \mathscr{P}_j'(0) ~\bigg\vert~ \mathscr{H}_{T_{-}} \right) \leq (T_+ - t)^{-(1/2)\log(1/\theta_0)} \theta_0^{\eta_\beta + \widehat{\delta}}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} & {\mathbb Q}\ \left( \bigg\{\exists~s \in [T_-,t]: \text{ (4.59) fails } \bigg\} \cap E_0 \cap E_1 \cap \mathscr{P}_j'(0) ~\bigg\vert~ \mathscr{H}_{T_{-}} \right) \leq (T_+ - t)^{-(1/2)\log(1/\theta_0)} \theta_0^{\eta_\beta + \widehat{\delta}}. \end{aligned} \end{align*}$$
Summing in t, it is seen that for
![]() $\widehat {\delta }$
sufficiently small and
$\widehat {\delta }$
sufficiently small and
![]() $\theta _0$
sufficiently small to absorb the constants,
$\theta _0$
sufficiently small to absorb the constants,
Step 5: A tail bound for the change in the imaginary part.
We estimate the imaginary part of
This satisfies the SDE
 $$\begin{align*}d\Delta_t = \theta_0 e^t k_1^{-1} dt + \sqrt{\tfrac{4}{\beta}} \Im \bigg((e^{i \Delta_t}-1)e^{i \Im \mathfrak{L}_t(0)} d \mathfrak{W}_t^j\bigg), \end{align*}$$
$$\begin{align*}d\Delta_t = \theta_0 e^t k_1^{-1} dt + \sqrt{\tfrac{4}{\beta}} \Im \bigg((e^{i \Delta_t}-1)e^{i \Im \mathfrak{L}_t(0)} d \mathfrak{W}_t^j\bigg), \end{align*}$$
which has almost surely nonnegative solutions. Then we express
where
![]() $\xi _1(x)$
and
$\xi _1(x)$
and
![]() $\xi _2(x)$
are bounded by
$\xi _2(x)$
are bounded by
![]() $C_\beta x^2.$
$C_\beta x^2.$
Let
![]() $M_t = \exp \left ( \mathfrak {X}_t - \tfrac {2}{\beta }t \right ).$
Then we have from Itô’s Lemma
$M_t = \exp \left ( \mathfrak {X}_t - \tfrac {2}{\beta }t \right ).$
Then we have from Itô’s Lemma
 $$ \begin{align} d\bigg( \frac{ \Delta_t } {M_t} \bigg) = \frac{1}{M_t} \bigg( \theta_0 e^tk_1^{-1} dt + \xi_1(\Delta_t) (d\mathfrak{X}_t-\tfrac{4}{\beta}dt) + \xi_2(\Delta_t) d\mathfrak{B}_t\bigg). \end{align} $$
$$ \begin{align} d\bigg( \frac{ \Delta_t } {M_t} \bigg) = \frac{1}{M_t} \bigg( \theta_0 e^tk_1^{-1} dt + \xi_1(\Delta_t) (d\mathfrak{X}_t-\tfrac{4}{\beta}dt) + \xi_2(\Delta_t) d\mathfrak{B}_t\bigg). \end{align} $$
This we can integrate to conclude for
![]() $t \in [T_-,T_+],$
$t \in [T_-,T_+],$
 $$ \begin{align} \Delta_{t} = \frac{M_t}{M_{T_-}} \Delta_{T_-} + \int_{T_{-}}^{t} \frac{M_t}{M_s} \bigl(\theta_0 e^s k_1^{-1}ds + \xi_1(\Delta_s) (d\mathfrak{X}_s-\tfrac{4}{\beta} ds) + \xi_2(\Delta_s) d\mathfrak{B}_s\bigr). \end{align} $$
$$ \begin{align} \Delta_{t} = \frac{M_t}{M_{T_-}} \Delta_{T_-} + \int_{T_{-}}^{t} \frac{M_t}{M_s} \bigl(\theta_0 e^s k_1^{-1}ds + \xi_1(\Delta_s) (d\mathfrak{X}_s-\tfrac{4}{\beta} ds) + \xi_2(\Delta_s) d\mathfrak{B}_s\bigr). \end{align} $$
Now by definition we have
 $$ \begin{align} \frac{M_t}{M_s} = \exp\left( \mathfrak{X}_t -\mathfrak{X}_s -\frac{2}{\beta}(t-s) \right). \end{align} $$
$$ \begin{align} \frac{M_t}{M_s} = \exp\left( \mathfrak{X}_t -\mathfrak{X}_s -\frac{2}{\beta}(t-s) \right). \end{align} $$
Recalling (4.56), on the event
![]() $E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
,
$E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
,
Let
 $$\begin{align*}L_t = \int_{T_-}^{t} \frac{ M_t }{M_s} \theta_0 e^s k_1^{-1} ds, \quad \text{for any} \quad t\in [T_-,T_+]. \end{align*}$$
$$\begin{align*}L_t = \int_{T_-}^{t} \frac{ M_t }{M_s} \theta_0 e^s k_1^{-1} ds, \quad \text{for any} \quad t\in [T_-,T_+]. \end{align*}$$
On the event
![]() $E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0),$
we have from (4.67) the bound
$E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0),$
we have from (4.67) the bound
for
![]() $t \in [T_-,T_+].$
$t \in [T_-,T_+].$
Let
![]() $\tau $
be the first time s greater than
$\tau $
be the first time s greater than
![]() $T_-$
that
$T_-$
that
and note that from (4.68), for all
![]() $t \in [T_-,T_+],$
and on the event
$t \in [T_-,T_+],$
and on the event
![]() $E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
and the conditions on
$E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
and the conditions on
![]() $\alpha , \theta _0$
((4.45) and (4.44)),
$\alpha , \theta _0$
((4.45) and (4.44)),
 $$ \begin{align} \begin{aligned} \Delta_{t\wedge \tau} = |\Delta_{t\wedge \tau}| &\leq |\Delta_{t\wedge \tau}-L_{t\wedge \tau} - M_{t\wedge \tau} M_{T_-}^{-1}\Delta_{T_-}| +|M_{t\wedge \tau} M_{T_-}^{-1}\Delta_{T_-}| +|L_{t\wedge \tau}| \\ &\leq 2 (\theta_0)^{1-\delta_\beta} \bigl( \mathcal{W}(t \wedge \tau) + (\log k_1)^{-\alpha/2} \bigr). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Delta_{t\wedge \tau} = |\Delta_{t\wedge \tau}| &\leq |\Delta_{t\wedge \tau}-L_{t\wedge \tau} - M_{t\wedge \tau} M_{T_-}^{-1}\Delta_{T_-}| +|M_{t\wedge \tau} M_{T_-}^{-1}\Delta_{T_-}| +|L_{t\wedge \tau}| \\ &\leq 2 (\theta_0)^{1-\delta_\beta} \bigl( \mathcal{W}(t \wedge \tau) + (\log k_1)^{-\alpha/2} \bigr). \end{aligned} \end{align} $$
Returning to the SDE for
![]() $\Delta ,$
we now write
$\Delta ,$
we now write
Letting
![]() $N_t = \exp \bigl (U_t - \tfrac 12 \langle U_t \rangle \bigr )$
, we therefore have
$N_t = \exp \bigl (U_t - \tfrac 12 \langle U_t \rangle \bigr )$
, we therefore have
 $$ \begin{align} \Delta_t -L_t - \frac{M_{t}} {M_{T_-}} \Delta_{T_-} = \bigg( \frac{N_t}{N_{T_-}} -\frac{M_t}{M_{T_-}} \bigg) \Delta_{T_-} + \int_{T_{-}}^{t} \bigg( \frac{N_t}{N_s} -\frac{M_t}{M_s} \bigg) \bigl(\theta_0 e^s k_1^{-1}ds\bigr). \end{align} $$
$$ \begin{align} \Delta_t -L_t - \frac{M_{t}} {M_{T_-}} \Delta_{T_-} = \bigg( \frac{N_t}{N_{T_-}} -\frac{M_t}{M_{T_-}} \bigg) \Delta_{T_-} + \int_{T_{-}}^{t} \bigg( \frac{N_t}{N_s} -\frac{M_t}{M_s} \bigg) \bigl(\theta_0 e^s k_1^{-1}ds\bigr). \end{align} $$
This essentially reduces the problem to an estimate on the ratios of integrating factors that holds up to the stopping time. First, we observe that we have the representation
 $$\begin{align*}\log\bigg( \frac{N_t}{N_{T_-}} \frac{M_{T_-}}{M_t} \bigg) = \int_{T_-}^t \bigl(\tfrac{\xi_1(\Delta_u)}{\Delta_u} d\mathfrak{X}_u + \tfrac{\xi_2(\Delta_u)}{\Delta_u} d\mathfrak{B}_u\bigr) - \frac2\beta \int_{T_-}^t \bigl( 2\tfrac{\xi_1(\Delta_u)}{\Delta_u} + \bigl(\tfrac{\xi_1(\Delta_u)}{\Delta_u}\bigr)^2 + \bigl(\tfrac{\xi_2(\Delta_u)}{\Delta_u}\bigr)^2 \bigr) \,du. \end{align*}$$
$$\begin{align*}\log\bigg( \frac{N_t}{N_{T_-}} \frac{M_{T_-}}{M_t} \bigg) = \int_{T_-}^t \bigl(\tfrac{\xi_1(\Delta_u)}{\Delta_u} d\mathfrak{X}_u + \tfrac{\xi_2(\Delta_u)}{\Delta_u} d\mathfrak{B}_u\bigr) - \frac2\beta \int_{T_-}^t \bigl( 2\tfrac{\xi_1(\Delta_u)}{\Delta_u} + \bigl(\tfrac{\xi_1(\Delta_u)}{\Delta_u}\bigr)^2 + \bigl(\tfrac{\xi_2(\Delta_u)}{\Delta_u}\bigr)^2 \bigr) \,du. \end{align*}$$
We bound the right-hand side uniformly over
![]() $T_{-} \leq t \leq \tau $
. There are three types of terms to control: the finite variation terms in the second integral
$T_{-} \leq t \leq \tau $
. There are three types of terms to control: the finite variation terms in the second integral
![]() $(i)$
, the martingale terms in the first integral
$(i)$
, the martingale terms in the first integral
![]() $(ii)$
and the finite variation terms in the first integral
$(ii)$
and the finite variation terms in the first integral
![]() $(iii)$
. Then for the first terms, using the bound on
$(iii)$
. Then for the first terms, using the bound on
![]() $\Delta $
in (4.69),
$\Delta $
in (4.69),

For the second terms, we need a stochastic control, and we have by bounding the quadratic variation for some constant
 $$\begin{align*}\begin{aligned} &{\mathbb Q}\ \left( \bigg\{ \max_{s \leq T_+ \wedge \tau} \bigg| \int_{T_-}^{s} \tfrac{\xi_1(\Delta_u)}{\Delta_u} d{X}_u + \tfrac{\xi_2(\Delta_u)}{\Delta_u} d\mathfrak{B}_u \bigg|> x \bigg\} \cap E_0 \cap E_1 \cap E_2 \cap \mathscr{P}_j'(0) ~\middle\vert~ \mathscr{H}_{T_-} \right) \\ &\leq \exp\bigg(-\frac{x^2} {C(\beta, \widehat{\delta}) (\theta_0)^{4(1-\delta_\beta)}} \bigg). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &{\mathbb Q}\ \left( \bigg\{ \max_{s \leq T_+ \wedge \tau} \bigg| \int_{T_-}^{s} \tfrac{\xi_1(\Delta_u)}{\Delta_u} d{X}_u + \tfrac{\xi_2(\Delta_u)}{\Delta_u} d\mathfrak{B}_u \bigg|> x \bigg\} \cap E_0 \cap E_1 \cap E_2 \cap \mathscr{P}_j'(0) ~\middle\vert~ \mathscr{H}_{T_-} \right) \\ &\leq \exp\bigg(-\frac{x^2} {C(\beta, \widehat{\delta}) (\theta_0)^{4(1-\delta_\beta)}} \bigg). \end{aligned} \end{align*}$$
In particular, we may assume with probability
![]() $1-e^{O( \theta _0^{-2(1-\delta _\beta )})}$
that
$1-e^{O( \theta _0^{-2(1-\delta _\beta )})}$
that

Finally, for the third terms,

On the event
![]() $\mathscr {P}_j'(0),$
$\mathscr {P}_j'(0),$

On the event
![]() $E_0 \cap E_1 \cap \mathscr {P}_j'(0),$
using (4.60) and the control for
$E_0 \cap E_1 \cap \mathscr {P}_j'(0),$
using (4.60) and the control for
![]() $\ell '$
, we have
$\ell '$
, we have
 $$ \begin{align} \bigg| \frac{\mathfrak{X}_{T_+}-\mathfrak{X}_s}{T_+ - s} \bigg| \leq \widehat{\delta} \log(1/\theta_0). \end{align} $$
$$ \begin{align} \bigg| \frac{\mathfrak{X}_{T_+}-\mathfrak{X}_s}{T_+ - s} \bigg| \leq \widehat{\delta} \log(1/\theta_0). \end{align} $$
Hence, applying these bounds, we have for some
![]() $C(\beta ,\widehat {\delta })$
sufficiently large,
$C(\beta ,\widehat {\delta })$
sufficiently large,
Combining all of these, we conclude that for some
![]() $C(\beta ,\widehat {\delta })$
sufficiently large,
$C(\beta ,\widehat {\delta })$
sufficiently large,
 $$ \begin{align} \max_{T_- \leq s \leq t \leq T_+\wedge \tau} \bigg| \log\bigg( \frac{N_t}{N_{s}} \frac{M_{s}}{M_t} \bigg) \bigg| \leq C(\beta,\widehat{\delta})\theta_0^{1-\delta_\beta} \log(1/\theta_0). \end{align} $$
$$ \begin{align} \max_{T_- \leq s \leq t \leq T_+\wedge \tau} \bigg| \log\bigg( \frac{N_t}{N_{s}} \frac{M_{s}}{M_t} \bigg) \bigg| \leq C(\beta,\widehat{\delta})\theta_0^{1-\delta_\beta} \log(1/\theta_0). \end{align} $$
Hence, we conclude from (4.70) that for
![]() $t \leq \tau $
, for some
$t \leq \tau $
, for some
![]() $C(\beta ,\widehat {\delta })$
and all
$C(\beta ,\widehat {\delta })$
and all
![]() $\theta _0$
sufficiently small (depending on
$\theta _0$
sufficiently small (depending on
![]() $\beta , \widehat {\delta }$
),
$\beta , \widehat {\delta }$
),
 $$\begin{align*}|\Delta_{t} -L_t - \frac{M_{t}} {M_{T_-}} \Delta_{T_-} | \leq \bigg( \exp\bigl( C\theta_0^{1-\delta_\beta} \log(1/\theta_0) \bigr)-1\bigg) \cdot \bigg( \frac{M_t}{M_{T_-}} \Delta_{T_-} + \int_{T_{-}}^{t} \frac{M_t}{M_s} \bigl(\theta_0 e^s k_1^{-1}ds\bigr) \bigg). \end{align*}$$
$$\begin{align*}|\Delta_{t} -L_t - \frac{M_{t}} {M_{T_-}} \Delta_{T_-} | \leq \bigg( \exp\bigl( C\theta_0^{1-\delta_\beta} \log(1/\theta_0) \bigr)-1\bigg) \cdot \bigg( \frac{M_t}{M_{T_-}} \Delta_{T_-} + \int_{T_{-}}^{t} \frac{M_t}{M_s} \bigl(\theta_0 e^s k_1^{-1}ds\bigr) \bigg). \end{align*}$$
We conclude as in (4.69) that for some
![]() $C=C(\beta ,\widehat {\delta })$
,
$C=C(\beta ,\widehat {\delta })$
,
By the definition of
![]() $\tau ,$
we conclude that on the events considered,
$\tau ,$
we conclude that on the events considered,
![]() $E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
, as well as on the event in which (4.71) holds, that
$E_0 \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
, as well as on the event in which (4.71) holds, that
![]() $\tau> T_+$
, and hence (4.69) holds for all
$\tau> T_+$
, and hence (4.69) holds for all
![]() $t \in [T_-,T_+].$
In summary, we conclude there is an
$t \in [T_-,T_+].$
In summary, we conclude there is an
![]() $\eta _\beta>1$
(see (4.62)), a
$\eta _\beta>1$
(see (4.62)), a
![]() $\delta _\beta \in (0,1)$
, a
$\delta _\beta \in (0,1)$
, a
![]() $C_\beta> 0$
and an
$C_\beta> 0$
and an
![]() $\epsilon>0$
so that for all
$\epsilon>0$
so that for all
![]() $\theta _0$
sufficiently small,
$\theta _0$
sufficiently small,
 $$ \begin{align} &{\mathbb Q}\Big( \{ \exists~t \in [T_-,T_+] ~:~\\ &\nonumber\qquad |\Delta_t|> C_\beta (\theta_0)^{1-\delta_\beta}\bigl(e^{-(1-\widehat{\delta})(T_+-t)} +\log^{-\alpha/2} (k_1) \bigr) \} \cap E_0 \cap E_1 \cap E_2 \cap \mathscr{P}_j'(0) ~\vert~ \mathscr{H}_{T_-} \Big ) \leq \theta_0^{\eta_\beta + \widehat{\delta}}. \end{align} $$
$$ \begin{align} &{\mathbb Q}\Big( \{ \exists~t \in [T_-,T_+] ~:~\\ &\nonumber\qquad |\Delta_t|> C_\beta (\theta_0)^{1-\delta_\beta}\bigl(e^{-(1-\widehat{\delta})(T_+-t)} +\log^{-\alpha/2} (k_1) \bigr) \} \cap E_0 \cap E_1 \cap E_2 \cap \mathscr{P}_j'(0) ~\vert~ \mathscr{H}_{T_-} \Big ) \leq \theta_0^{\eta_\beta + \widehat{\delta}}. \end{align} $$
Step 6: Control for the real part.
Going forward, we work on the event
![]() $F_{\theta _0}$
on which
$F_{\theta _0}$
on which
the probability of which is estimated in (4.74). The real part of
![]() $\mathfrak {L}_t$
we will represent by
$\mathfrak {L}_t$
we will represent by
Using the SDE for
![]() $\mathfrak {L}$
in (2.43),
$\mathfrak {L}$
in (2.43),
Since
![]() $0 \leq \Delta _t(\theta ) \leq \Delta _t(\theta _0)$
, we can estimate the finite variation parts on
$0 \leq \Delta _t(\theta ) \leq \Delta _t(\theta _0)$
, we can estimate the finite variation parts on
![]() $F_{\theta _0} \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
using a similar analysis as in (4.73) by
$F_{\theta _0} \cap E_1 \cap E_2 \cap \mathscr {P}_j'(0)$
using a similar analysis as in (4.73) by

The quadratic variation is dominated on the event
![]() $F_{\theta _0}$
by, for some sufficiently large
$F_{\theta _0}$
by, for some sufficiently large
![]() $C_\beta ,$
$C_\beta ,$
 $$\begin{align*}\langle \Delta_{T_+}^r(\theta) \rangle \leq C_\beta \int_{T_-}^{T_+} \Delta_t^2(\theta_0) dt \leq C_\beta^2 \bigl(\theta_0\bigr)^{2-2\delta_\beta}. \end{align*}$$
$$\begin{align*}\langle \Delta_{T_+}^r(\theta) \rangle \leq C_\beta \int_{T_-}^{T_+} \Delta_t^2(\theta_0) dt \leq C_\beta^2 \bigl(\theta_0\bigr)^{2-2\delta_\beta}. \end{align*}$$
Therefore, we have a tail bound that for some
![]() $C_\beta $
sufficiently large and for all
$C_\beta $
sufficiently large and for all
![]() $x> 0,$
$x> 0,$
Thus, taking
![]() $x = \theta _0^{-\varepsilon }$
for
$x = \theta _0^{-\varepsilon }$
for
![]() $\varepsilon < 1-\delta _\beta $
, we conclude that
$\varepsilon < 1-\delta _\beta $
, we conclude that
which finally, using (4.52),(4.55),(4.63) and (4.74), concludes (4.50).
5 The diffusion approximation
In this section, we prove Proposition 2.12. The proof is given by a series of short lemmas. A summary proof is given in the penultimate section. In the final section, we develop a general tail bound which we use at multiple points in the development.
It is convenient in this section to work conditionally on the event
![]() $\mathscr {T}_{n_1^+}$
from (2.8). We let, for the event
$\mathscr {T}_{n_1^+}$
from (2.8). We let, for the event
![]() $\mathscr {T}_{n_1^+}$
and filtration
$\mathscr {T}_{n_1^+}$
and filtration
![]() $\mathscr {F}_{n_1^+}$
,
$\mathscr {F}_{n_1^+}$
,
and let
![]() $\mathbb {E}_M$
denote the associated expectation. Under the law
$\mathbb {E}_M$
denote the associated expectation. Under the law
![]() $\mathbb {P}_M, (X_j,Y_j)$
(see (2.2)) are no longer independent of one another for
$\mathbb {P}_M, (X_j,Y_j)$
(see (2.2)) are no longer independent of one another for
![]() $j \geq n_1^+$
. They do, however, still satisfy uniform Gaussian integrability, in that
$j \geq n_1^+$
. They do, however, still satisfy uniform Gaussian integrability, in that
for all Lipschitz F on the (convex) support of
![]() $(X_j,Y_j)$
; see [Reference Bobkov and LedouxBL00, Proposition 3.1]. We will use this subgaussian concentration for the family of functions that appear in the definitions of
$(X_j,Y_j)$
; see [Reference Bobkov and LedouxBL00, Proposition 3.1]. We will use this subgaussian concentration for the family of functions that appear in the definitions of ![]() and, in particular, to control the linearization error.
and, in particular, to control the linearization error.
5.1 Locally linear processes
In a similar fashion to [Reference Chhaibi, Madaule and NajnudelCMN18], we introduce a process which in short windows of k evolves linearly. Let
![]() $\varkappa $
be a parameter, to be chosen later as a power of n, which will be the block length within which
$\varkappa $
be a parameter, to be chosen later as a power of n, which will be the block length within which ![]() will evolve linearly. Define a new recurrence, recalling
will evolve linearly. Define a new recurrence, recalling
![]() $\beta _j = \sqrt {\frac {\beta }{2}(j+1)}$
for all
$\beta _j = \sqrt {\frac {\beta }{2}(j+1)}$
for all
![]() $j \geq 0$
,
$j \geq 0$
,

As we will see below, the variables
![]() $\lambda _k(\theta )$
are good approximations for
$\lambda _k(\theta )$
are good approximations for ![]() .
.
We begin with a simple observation that for
![]() $\varkappa $
sufficiently small with respect to
$\varkappa $
sufficiently small with respect to
![]() ${n_1^+},$
the difference between
${n_1^+},$
the difference between
![]() $\lambda _k$
and
$\lambda _k$
and
![]() $\lambda _k^*$
can be controlled.
$\lambda _k^*$
can be controlled.
Lemma 5.1. For all
![]() $C>0$
, there is constant
$C>0$
, there is constant
![]() $D>0$
so that for all
$D>0$
so that for all
![]() ${n_1^+}$
sufficiently large (depending on
${n_1^+}$
sufficiently large (depending on
![]() $\beta $
and M),
$\beta $
and M),
 $$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k < n} |\lambda_k(\theta) - \lambda_k^*(\theta)| \geq D \sqrt{\tfrac{\varkappa \log n}{\beta {n_1^+}}} \right] \leq n^{-C}. \end{align*}$$
$$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k < n} |\lambda_k(\theta) - \lambda_k^*(\theta)| \geq D \sqrt{\tfrac{\varkappa \log n}{\beta {n_1^+}}} \right] \leq n^{-C}. \end{align*}$$
Proof. We show the proof for
![]() ${n_1^+} \leq k < {n_1^+} + \varkappa .$
For larger
${n_1^+} \leq k < {n_1^+} + \varkappa .$
For larger
![]() $k,$
we have the same estimate (and indeed it only improves). We have that
$k,$
we have the same estimate (and indeed it only improves). We have that
 $$\begin{align*}\lambda_k(\theta) - \lambda_k^*(\theta) = \sum_{j = {n_1^+}}^{k-1} \frac{Z_j e^{i\Im\lambda^*_j(\theta)}}{\beta_j}. \end{align*}$$
$$\begin{align*}\lambda_k(\theta) - \lambda_k^*(\theta) = \sum_{j = {n_1^+}}^{k-1} \frac{Z_j e^{i\Im\lambda^*_j(\theta)}}{\beta_j}. \end{align*}$$
Under
![]() $\mathbb {P}$
, this is Gaussian with variance
$\mathbb {P}$
, this is Gaussian with variance
![]() $\tfrac {4}{\beta }\sum _{j={n_1^+}}^{k-1} \frac {1}{j+1} \leq \tfrac {4 \varkappa }{\beta {n_1^+}}.$
Hence, there is an absolute constant so that for all
$\tfrac {4}{\beta }\sum _{j={n_1^+}}^{k-1} \frac {1}{j+1} \leq \tfrac {4 \varkappa }{\beta {n_1^+}}.$
Hence, there is an absolute constant so that for all
![]() $t \geq 0$
and all
$t \geq 0$
and all
![]() $\theta $
,
$\theta $
,
 $$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k < n_1^++\varkappa} |\lambda_k(\theta) - \lambda_k^*(\theta)| \geq t \right] \leq \frac{2}{\mathbb{P}(\mathscr{T}_{{n_1^+}})} \exp\left( -\beta (n_1^+ t)^2/(C\varkappa) \right). \end{align*}$$
$$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k < n_1^++\varkappa} |\lambda_k(\theta) - \lambda_k^*(\theta)| \geq t \right] \leq \frac{2}{\mathbb{P}(\mathscr{T}_{{n_1^+}})} \exp\left( -\beta (n_1^+ t)^2/(C\varkappa) \right). \end{align*}$$
In particular, for
![]() $t = D\sqrt {\tfrac {\varkappa \log n}{\beta {n_1^+}}}$
with D sufficiently large, the claim follows.
$t = D\sqrt {\tfrac {\varkappa \log n}{\beta {n_1^+}}}$
with D sufficiently large, the claim follows.
We turn to comparing the differences ![]() (for real-valued R and
(for real-valued R and
![]() $\Delta $
). We begin by observing that the difference satisfies a recurrence for
$\Delta $
). We begin by observing that the difference satisfies a recurrence for
![]() $k \geq {n_1^+}$
:
$k \geq {n_1^+}$
:

where
![]() $\left \{ (\tilde {\gamma _k},\tilde {Z_k}) \right \}$
have the same law as
$\left \{ (\tilde {\gamma _k},\tilde {Z_k}) \right \}$
have the same law as
![]() $\left \{ (\gamma _k,Z_k) \right \}.$
The proof of the following lemma uses calculus computations contained in Section 7.
$\left \{ (\gamma _k,Z_k) \right \}.$
The proof of the following lemma uses calculus computations contained in Section 7.
Lemma 5.2. Suppose
![]() $\varkappa \geq \sqrt {{n_1^+}}.$
For all
$\varkappa \geq \sqrt {{n_1^+}}.$
For all
![]() $\delta> 0$
and all
$\delta> 0$
and all
![]() $C>0$
,
$C>0$
,
 $$\begin{align*}\mathbb{P}_M\bigg[ \max_{{n_1^+} \leq k \leq n} |R_k+i\Delta_k| \geq n^{\delta} \sqrt{\varkappa/{n_1^+}} \bigg] \leq n^{-C} \end{align*}$$
$$\begin{align*}\mathbb{P}_M\bigg[ \max_{{n_1^+} \leq k \leq n} |R_k+i\Delta_k| \geq n^{\delta} \sqrt{\varkappa/{n_1^+}} \bigg] \leq n^{-C} \end{align*}$$
for all n sufficiently large.
Proof. We show the bound for the imaginary part. We can express
where in the notation of Lemma 7.1,
Hence, by (5.1) and Lemma 7.1, there is a constant
![]() $C>0$
so that for any
$C>0$
so that for any
![]() $k \geq {n_1^+},$
and any
$k \geq {n_1^+},$
and any
![]() $\mu \in {\mathbb R}$
,
$\mu \in {\mathbb R}$
,
 $$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta_{k+1}} \middle \vert \mathscr{F}_k \right] \leq \exp\left(\mu \Delta_k + \frac{C\mu^2| e^{i\Delta_k(\theta)+i\Im(\lambda_k(\theta)-\lambda_k^*(\theta))} - 1|^2}{\beta_k^2} + \frac{C\mu^2\log k}{\beta_k^3}\right). \end{align*}$$
$$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta_{k+1}} \middle \vert \mathscr{F}_k \right] \leq \exp\left(\mu \Delta_k + \frac{C\mu^2| e^{i\Delta_k(\theta)+i\Im(\lambda_k(\theta)-\lambda_k^*(\theta))} - 1|^2}{\beta_k^2} + \frac{C\mu^2\log k}{\beta_k^3}\right). \end{align*}$$
Let T be the first
![]() $k \geq {n_1^+}$
such that
$k \geq {n_1^+}$
such that
![]() $|\Im (\lambda _k(\theta ) - \lambda _{k}^*(\theta ))|$
is larger than
$|\Im (\lambda _k(\theta ) - \lambda _{k}^*(\theta ))|$
is larger than
![]() $D\sqrt {\tfrac {\varkappa \log n}{\beta {n_1^+}}}$
for some
$D\sqrt {\tfrac {\varkappa \log n}{\beta {n_1^+}}}$
for some
![]() $D> \sqrt {\beta }.$
Let
$D> \sqrt {\beta }.$
Let
![]() $\Delta _k^T=\Delta _{k\wedge T}$
. We have supposed that
$\Delta _k^T=\Delta _{k\wedge T}$
. We have supposed that
![]() $\varkappa \geq \sqrt {{n_1^+}},$
and therefore, there is an absolute constant
$\varkappa \geq \sqrt {{n_1^+}},$
and therefore, there is an absolute constant
![]() $C>0$
so that for any
$C>0$
so that for any
![]() $k \geq {n_1^+}$
and any
$k \geq {n_1^+}$
and any
![]() $\mu \in {\mathbb R},$
$\mu \in {\mathbb R},$
 $$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta^T_{k+1}} \middle \vert \mathscr{F}_k \right] \leq \exp\left(\mu \Delta^T_k + \frac{C\mu^2((\Delta^T_k)^2+ D^2\tfrac{\varkappa \log n}{\beta {n_1^+}})}{\beta k}\right). \end{align*}$$
$$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta^T_{k+1}} \middle \vert \mathscr{F}_k \right] \leq \exp\left(\mu \Delta^T_k + \frac{C\mu^2((\Delta^T_k)^2+ D^2\tfrac{\varkappa \log n}{\beta {n_1^+}})}{\beta k}\right). \end{align*}$$
In preparation to use Proposition 5.6, we observe from (5.3) and Lemma 7.1 that there is an absolute constant
![]() $C>0$
so that for all
$C>0$
so that for all
![]() ${n_1^+}$
sufficiently large,
${n_1^+}$
sufficiently large,
 $$\begin{align*}\Delta^T_{k+1}(\theta)-\Delta^T_k(\theta) \leq C\Delta^T_k\sqrt{ \frac{\log({n_1^+})}{\beta {n_1^+}}} + CD\sqrt{\frac{\varkappa \log n}{\beta {n_1^+}}}. \end{align*}$$
$$\begin{align*}\Delta^T_{k+1}(\theta)-\Delta^T_k(\theta) \leq C\Delta^T_k\sqrt{ \frac{\log({n_1^+})}{\beta {n_1^+}}} + CD\sqrt{\frac{\varkappa \log n}{\beta {n_1^+}}}. \end{align*}$$
Hence, by Proposition 5.6, there is an absolute constant
![]() $C>0$
so that for all
$C>0$
so that for all
![]() $x \geq C\log (n/{n_1^+})/\beta + C,$
$x \geq C\log (n/{n_1^+})/\beta + C,$
 $$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k \leq n} \Delta^T_k \geq x D\sqrt{\varkappa \log(n)/(\beta {n_1^+})} \right] \leq \exp\left( -\frac{1}{C}\frac{\log(x)^2}{\log(n/{n_1^+})} \right). \end{align*}$$
$$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k \leq n} \Delta^T_k \geq x D\sqrt{\varkappa \log(n)/(\beta {n_1^+})} \right] \leq \exp\left( -\frac{1}{C}\frac{\log(x)^2}{\log(n/{n_1^+})} \right). \end{align*}$$
The same bound holds for
![]() $-\Delta _k^T,$
and therefore, by Lemma 5.1, the lemma follows.
$-\Delta _k^T,$
and therefore, by Lemma 5.1, the lemma follows.
To control the real part
![]() $R_k$
, we again use Lemma 7.1, although there is no longer a need for the ladder. We suppress the details.
$R_k$
, we again use Lemma 7.1, although there is no longer a need for the ladder. We suppress the details.
5.2 Band-resampled approximation
Recall from (2.2) that
![]() $Z_\ell = \sqrt {E_\ell } e^{i\Theta _\ell }$
is a complex Gaussian for each
$Z_\ell = \sqrt {E_\ell } e^{i\Theta _\ell }$
is a complex Gaussian for each
![]() $\ell .$
For any
$\ell .$
For any
![]() $r \in {\mathbb N},$
define
$r \in {\mathbb N},$
define
![]() $k_r = {n_1^+} + r\varkappa .$
The family of Gaussians
$k_r = {n_1^+} + r\varkappa .$
The family of Gaussians
![]() $\left \{ Z_\ell : k_{r-1} \leq \ell < k_r \right \}$
are i.i.d. Hence, we can represent, for any
$\left \{ Z_\ell : k_{r-1} \leq \ell < k_r \right \}$
are i.i.d. Hence, we can represent, for any
![]() $r \in {\mathbb N}$
, these Gaussians through their discrete Fourier transform:
$r \in {\mathbb N}$
, these Gaussians through their discrete Fourier transform:
 $$ \begin{align} Z_{\ell+k_{r-1}} = \frac{1}{\sqrt{\varkappa}}\sum_{p=1}^{\varkappa} e(\tfrac{-p\ell}{\varkappa}) \hat{Z}_{p}^{(r)}, \quad \text{for } 0 \leq \ell \leq \varkappa-1, \end{align} $$
$$ \begin{align} Z_{\ell+k_{r-1}} = \frac{1}{\sqrt{\varkappa}}\sum_{p=1}^{\varkappa} e(\tfrac{-p\ell}{\varkappa}) \hat{Z}_{p}^{(r)}, \quad \text{for } 0 \leq \ell \leq \varkappa-1, \end{align} $$
where ![]() and
and
![]() $\left \{ \hat Z_p^{(r)} : r \in {\mathbb N}, 1 \leq p \leq \varkappa \right \}$
are another family of i.i.d. complex Gaussians.
$\left \{ \hat Z_p^{(r)} : r \in {\mathbb N}, 1 \leq p \leq \varkappa \right \}$
are another family of i.i.d. complex Gaussians.
We shall estimate the effect on the recurrence
![]() $\lambda _k(\theta )$
wherein we resample some of the
$\lambda _k(\theta )$
wherein we resample some of the
![]() $\{\hat Z_p\}$
corresponding to modes that are far from
$\{\hat Z_p\}$
corresponding to modes that are far from
![]() $\theta .$
Let
$\theta .$
Let
![]() $\omega \leq \varkappa $
be a positive integer parameter, which will be the bandwidth. For a fixed
$\omega \leq \varkappa $
be a positive integer parameter, which will be the bandwidth. For a fixed
![]() $j \in {\mathcal {D}}_{n/k_1},$
define for any
$j \in {\mathcal {D}}_{n/k_1},$
define for any
![]() $r \in {\mathbb N}$
,
$r \in {\mathbb N}$
,

where
![]() $\left \{ \check Z_p^{(r,j)} : r \in {\mathbb N}, 1 \leq p \leq \varkappa ,j \in {\mathcal {D}}_{n/k_1} \right \}$
is another family of standard complex Gaussians.
$\left \{ \check Z_p^{(r,j)} : r \in {\mathbb N}, 1 \leq p \leq \varkappa ,j \in {\mathcal {D}}_{n/k_1} \right \}$
is another family of standard complex Gaussians.
We also define locally linear processes driven by these band-resampled Gaussians:
 $$ \begin{align} \begin{aligned} &\lambda_{k+1}^{(j)}(\theta)=\lambda_{k}^{(j)}(\theta) + i\theta + 2 \frac{Z_k^{(j)} e^{i\Im \lambda^{*,(j)}_k(\theta)}}{\beta_k} \quad \text{for all } k \geq {n_1^+}, \quad \text{where}\\ &\lambda_{{n_1^+}}^{(j)}(\theta) = \lambda_{n_1^+}(\theta), \quad \text{ and } \quad \lambda^{*,(j)}_k(\theta) = \lambda^{(j)}_{n^*(k)}(\theta) +i (k-n^*(k))\theta \quad \text{for all } k \geq {n_1^+}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\lambda_{k+1}^{(j)}(\theta)=\lambda_{k}^{(j)}(\theta) + i\theta + 2 \frac{Z_k^{(j)} e^{i\Im \lambda^{*,(j)}_k(\theta)}}{\beta_k} \quad \text{for all } k \geq {n_1^+}, \quad \text{where}\\ &\lambda_{{n_1^+}}^{(j)}(\theta) = \lambda_{n_1^+}(\theta), \quad \text{ and } \quad \lambda^{*,(j)}_k(\theta) = \lambda^{(j)}_{n^*(k)}(\theta) +i (k-n^*(k))\theta \quad \text{for all } k \geq {n_1^+}. \end{aligned} \end{align} $$
We then define ![]()
Lemma 5.3. Suppose that
![]() $j \in \mathcal {D}_{n/k_1}$
and that
$j \in \mathcal {D}_{n/k_1}$
and that
![]() $\theta \in {\mathbb R}$
satisfies
$\theta \in {\mathbb R}$
satisfies
There is an absolute constant
![]() $C>0$
so that for any
$C>0$
so that for any
![]() $r \in {\mathbb N}$
and all
$r \in {\mathbb N}$
and all
![]() $\mu \in {\mathbb R}$
,
$\mu \in {\mathbb R}$
,
 $$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta_{k_r}^{(j)}} \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq \exp\left( \mu \Delta_{k_{r-1}}^{(j)} +\frac{\mu^2 C\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta k_{r-1}} + \frac{\mu^2 C\varkappa }{ \beta \omega k_{r-1}} \right), \end{align*}$$
$$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta_{k_r}^{(j)}} \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq \exp\left( \mu \Delta_{k_{r-1}}^{(j)} +\frac{\mu^2 C\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta k_{r-1}} + \frac{\mu^2 C\varkappa }{ \beta \omega k_{r-1}} \right), \end{align*}$$
and so that for all
![]() $t \geq 0$
,
$t \geq 0$
,
 $$\begin{align*}\mathbb{P}_M\left[ \max_{k_{r-1} \leq k < k_r} | \Delta_k^{(j)}-\Delta_{k_{r-1}}^{(j)} | \geq t \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq 2\exp\left( -\frac{t^2k_{r-1}\omega \beta}{C\varkappa(\omega |\Delta_{k_{r-1}}^{(j)}|^2 + 1) } \right). \end{align*}$$
$$\begin{align*}\mathbb{P}_M\left[ \max_{k_{r-1} \leq k < k_r} | \Delta_k^{(j)}-\Delta_{k_{r-1}}^{(j)} | \geq t \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq 2\exp\left( -\frac{t^2k_{r-1}\omega \beta}{C\varkappa(\omega |\Delta_{k_{r-1}}^{(j)}|^2 + 1) } \right). \end{align*}$$
Proof. For any
![]() $r \in {\mathbb N},$
we have that conditionally on
$r \in {\mathbb N},$
we have that conditionally on
![]() $\mathscr {F}_{k_{r-1}}, \left \{ \Delta _k^{(j)} : k_{r-1} \leq k < k_r \right \}$
are jointly Gaussian under
$\mathscr {F}_{k_{r-1}}, \left \{ \Delta _k^{(j)} : k_{r-1} \leq k < k_r \right \}$
are jointly Gaussian under
![]() $\mathbb {P}.$
Moreover, for such
$\mathbb {P}.$
Moreover, for such
![]() $k,$
we can write
$k,$
we can write
 $$\begin{align*}\Delta_k^{(j)} -\Delta_{k_{r-1}}^{(j)} = 2\Im \sum_{\ell=0}^{k-k_{r-1}} \left\{ \frac{Z_{\ell+k_{r-1}}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} -\frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda^{(j)}_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} \right\}. \end{align*}$$
$$\begin{align*}\Delta_k^{(j)} -\Delta_{k_{r-1}}^{(j)} = 2\Im \sum_{\ell=0}^{k-k_{r-1}} \left\{ \frac{Z_{\ell+k_{r-1}}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} -\frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda^{(j)}_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} \right\}. \end{align*}$$
We give an upper bound for the variance of
![]() $\Delta _k^{(j)}-\Delta _{k_{r-1}}^{(j)},$
which we do by separately bounding the variance of
$\Delta _k^{(j)}-\Delta _{k_{r-1}}^{(j)},$
which we do by separately bounding the variance of
 $$\begin{align*}A= 2\Im\sum_{\ell=0}^{k-k_{r-1}} \left\{ \frac{Z_{\ell+k_{r-1}}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} -\frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} \right\} \end{align*}$$
$$\begin{align*}A= 2\Im\sum_{\ell=0}^{k-k_{r-1}} \left\{ \frac{Z_{\ell+k_{r-1}}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} -\frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} \right\} \end{align*}$$
and of
 $$\begin{align*}B= 2\Im\sum_{\ell=0}^{k-k_{r-1}} \left\{ \frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} -\frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda^{(j)}_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} \right\}. \end{align*}$$
$$\begin{align*}B= 2\Im\sum_{\ell=0}^{k-k_{r-1}} \left\{ \frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} -\frac{Z_{\ell+k_{r-1}}^{(j)}e^{i\ell\theta + i\lambda^{(j)}_{k_{r-1}}}}{\beta_{\ell+k_{r-1}}} \right\}. \end{align*}$$
For the second one, we observe that
 $$ \begin{align} \operatorname{Var}(B \vert \mathscr{F}_{k_{r-1}} ) \leq \frac{8\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta \cdot {k_{r-1}}}. \end{align} $$
$$ \begin{align} \operatorname{Var}(B \vert \mathscr{F}_{k_{r-1}} ) \leq \frac{8\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta \cdot {k_{r-1}}}. \end{align} $$
The main work is to control the variance of
![]() $A.$
By rotation invariance, we may drop the
$A.$
By rotation invariance, we may drop the
![]() $e^{i\lambda _{k_{r-1}}}$
from both terms and write
$e^{i\lambda _{k_{r-1}}}$
from both terms and write

where we have set

Moreover,

and so it remains to estimate
![]() $|c_p|^2.$
Note that we have the simple bound
$|c_p|^2.$
Note that we have the simple bound

We have that under the assumptions on
![]() $\theta $
, when
$\theta $
, when ![]() , then
, then ![]() Hence, using summation-by-parts, there is an absolute constant
Hence, using summation-by-parts, there is an absolute constant
![]() $C>0$
so that
$C>0$
so that

Thus, turning to (5.8), we can bound for some absolute constant
![]() $C>0$
,
$C>0$
,
 $$\begin{align*}\operatorname{Var}(A \vert \mathscr{F}_{k_{r-1}}) \leq \frac{C}{\beta_{k_{r-1}}^2} + \sum_{p=\omega}^\infty \frac{C\varkappa}{p^2\beta_{k_{r-1}}^2}. \end{align*}$$
$$\begin{align*}\operatorname{Var}(A \vert \mathscr{F}_{k_{r-1}}) \leq \frac{C}{\beta_{k_{r-1}}^2} + \sum_{p=\omega}^\infty \frac{C\varkappa}{p^2\beta_{k_{r-1}}^2}. \end{align*}$$
Hence, we conclude from this equation and (5.7) that there is an absolute constant
![]() $C>0$
so that
$C>0$
so that
 $$\begin{align*}\operatorname{Var}(\Delta_k^{(j)}-\Delta_{k_{r-1}}^{(j)} \vert \mathscr{F}_{k_{r-1}}) \leq \frac{C\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta k_{r-1}} + \frac{C\varkappa }{ \beta \omega k_{r-1}}. \end{align*}$$
$$\begin{align*}\operatorname{Var}(\Delta_k^{(j)}-\Delta_{k_{r-1}}^{(j)} \vert \mathscr{F}_{k_{r-1}}) \leq \frac{C\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta k_{r-1}} + \frac{C\varkappa }{ \beta \omega k_{r-1}}. \end{align*}$$
As we condition on an event of probability at least
![]() $1/2$
for M sufficiently large, it follows that
$1/2$
for M sufficiently large, it follows that
![]() $\Delta _k^{(j)}$
remains subgaussian conditionally on
$\Delta _k^{(j)}$
remains subgaussian conditionally on
![]() $\mathscr {F}_{k_{r-1}},$
with subgaussian constant only an absolute constant more than the unconditioned standard deviation of
$\mathscr {F}_{k_{r-1}},$
with subgaussian constant only an absolute constant more than the unconditioned standard deviation of
![]() $\Delta _{k}^{(j)}$
given
$\Delta _{k}^{(j)}$
given
![]() $\mathscr {F}_{k_{r-1}}.$
As
$\mathscr {F}_{k_{r-1}}.$
As
![]() $\Delta _k^{(j)}$
remains centered under
$\Delta _k^{(j)}$
remains centered under
![]() $\mathbb {P}_M,$
using standard manipulations (see, for example, [Reference VershyninVer18, Proposition 2.5.2]), it follows that there is another absolute constant
$\mathbb {P}_M,$
using standard manipulations (see, for example, [Reference VershyninVer18, Proposition 2.5.2]), it follows that there is another absolute constant
![]() $C>0$
so that for all
$C>0$
so that for all
![]() $\mu \in {\mathbb R}$
,
$\mu \in {\mathbb R}$
,
 $$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta_{k_r}^{(j)}} \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq \exp\left( \mu \Delta_{k_{r-1}}^{(j)} +\frac{\mu^2 C\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta k_{r-1}} + \frac{\mu^2 C\varkappa }{ \beta \omega k_{r-1}} \right). \end{align*}$$
$$\begin{align*}\mathbb{E}_M\left[ e^{\mu \Delta_{k_r}^{(j)}} \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq \exp\left( \mu \Delta_{k_{r-1}}^{(j)} +\frac{\mu^2 C\varkappa |\Delta^{(j)}_{k_{r-1}}|^2}{\beta k_{r-1}} + \frac{\mu^2 C\varkappa }{ \beta \omega k_{r-1}} \right). \end{align*}$$
Likewise, the desired concentration inequality follows for the maximum.
Lemma 5.4. Suppose that
![]() $j \in \mathcal {D}_{n/k_1}$
and that
$j \in \mathcal {D}_{n/k_1}$
and that
![]() $\theta \in {\mathbb R}$
satisfies
$\theta \in {\mathbb R}$
satisfies
For all
![]() $\delta $
sufficiently small and all
$\delta $
sufficiently small and all
![]() $C>0$
, if
$C>0$
, if
![]() $n_1^+/\varkappa \geq n^{\delta }$
and
$n_1^+/\varkappa \geq n^{\delta }$
and
![]() $\omega \geq n^{\delta }$
, then for all n sufficiently large,
$\omega \geq n^{\delta }$
, then for all n sufficiently large,
 $$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k \leq n} |R_{k}^{(j)}(\theta)+i\Delta_{k}^{(j)}(\theta)| \geq n^{\delta}/\sqrt{\omega} \right] \leq n^{-C}. \end{align*}$$
$$\begin{align*}\mathbb{P}_M\left[ \max_{{n_1^+} \leq k \leq n} |R_{k}^{(j)}(\theta)+i\Delta_{k}^{(j)}(\theta)| \geq n^{\delta}/\sqrt{\omega} \right] \leq n^{-C}. \end{align*}$$
Proof. Using Lemma 5.3, for any
![]() $t \geq 0$
,
$t \geq 0$
,
 $$\begin{align*}\mathbb{P}_M\left[ \max_{k_{r-1} \leq k < k_r} | \Delta_k^{(j)}-\Delta_{k_{r-1}}^{(j)} | \geq t\bigl(\sqrt{\omega} |\Delta_{k_{r-1}}^{(j)}| +1\bigr) \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq 2\exp\left( -\frac{t^2k_{r-1}\omega \beta}{C\varkappa} \right). \end{align*}$$
$$\begin{align*}\mathbb{P}_M\left[ \max_{k_{r-1} \leq k < k_r} | \Delta_k^{(j)}-\Delta_{k_{r-1}}^{(j)} | \geq t\bigl(\sqrt{\omega} |\Delta_{k_{r-1}}^{(j)}| +1\bigr) \middle \vert \mathscr{F}_{k_{r-1}} \right] \leq 2\exp\left( -\frac{t^2k_{r-1}\omega \beta}{C\varkappa} \right). \end{align*}$$
Hence, taking
![]() $t=1/\sqrt {\omega }$
, if we let
$t=1/\sqrt {\omega }$
, if we let
![]() $\mathcal {E}$
be the event that
$\mathcal {E}$
be the event that
then this event holds with probability
![]() $1-e^{-\Omega (n^{\delta })}$
. We turn to controlling
$1-e^{-\Omega (n^{\delta })}$
. We turn to controlling
![]() $\Delta _{k_{r}}^{(j)}$
on the event
$\Delta _{k_{r}}^{(j)}$
on the event
![]() $\mathcal {E}$
using Proposition 5.6. From Lemma 5.3,
$\mathcal {E}$
using Proposition 5.6. From Lemma 5.3,
![]() $A_{r+\lfloor {n_1^+}/\varkappa \rfloor } = \Delta _{k_{r-1}}^{(j)}$
satisfies (5.13) with
$A_{r+\lfloor {n_1^+}/\varkappa \rfloor } = \Delta _{k_{r-1}}^{(j)}$
satisfies (5.13) with
![]() $V=C/\beta $
,
$V=C/\beta $
,
![]() $W = C/(\beta \omega )$
,
$W = C/(\beta \omega )$
,
![]() $\epsilon = 1$
and
$\epsilon = 1$
and
![]() $E=1/\sqrt {\omega }$
.
$E=1/\sqrt {\omega }$
.
 $$\begin{align*}\mathbb{P}\left[ \bigl\{ \max_{r : k_{r-1} \leq n} |A_{r+\lfloor {n_1^+}/\varkappa \rfloor}| \geq x\sqrt{1/\omega} \bigr\} \cap \mathcal{E} \right] \leq 2\exp\left( -\frac{1}{C}\frac{\beta(\log x)^2}{\log(n/{n_1^+})} \right). \end{align*}$$
$$\begin{align*}\mathbb{P}\left[ \bigl\{ \max_{r : k_{r-1} \leq n} |A_{r+\lfloor {n_1^+}/\varkappa \rfloor}| \geq x\sqrt{1/\omega} \bigr\} \cap \mathcal{E} \right] \leq 2\exp\left( -\frac{1}{C}\frac{\beta(\log x)^2}{\log(n/{n_1^+})} \right). \end{align*}$$
Hence, taking
![]() $x = n^{\delta }$
completes the proof for the imaginary part.
$x = n^{\delta }$
completes the proof for the imaginary part.
Once more, for the real part, the proof is simpler: having controlled the difference of imaginary parts, the difference of real parts admits a block martingale structure. We suppress the details.
5.3 Coupling to Brownian motions
We augment the probability space by creating a family of complex Brownian motions
![]() $\{\widehat {(\mathfrak {W}}_t^j : t \geq 0) : j \in \mathcal {D}_{n/k_1}\}$
having
$\{\widehat {(\mathfrak {W}}_t^j : t \geq 0) : j \in \mathcal {D}_{n/k_1}\}$
having
for all
![]() $k \geq n_1^+$
. They may be constructed so that conditionally on all
$k \geq n_1^+$
. They may be constructed so that conditionally on all
![]() $\{Z_k^{(j)} : k,j\}$
, the bridges
$\{Z_k^{(j)} : k,j\}$
, the bridges
 $$\begin{align*}\bigg\{ (\widehat{\mathfrak{W}}^j_{t} -\widehat{\mathfrak{W}}^j_{H_{k}} : t \in [H_k,H_{k+1}]), j \in \mathcal{D}_{n/k_1}, k \geq n_1^+ \bigg\} \end{align*}$$
$$\begin{align*}\bigg\{ (\widehat{\mathfrak{W}}^j_{t} -\widehat{\mathfrak{W}}^j_{H_{k}} : t \in [H_k,H_{k+1}]), j \in \mathcal{D}_{n/k_1}, k \geq n_1^+ \bigg\} \end{align*}$$
are independent. By construction, we may extend
![]() $\lambda ^{(j)}$
to a continuous function of time by setting (cf. (5.6))
$\lambda ^{(j)}$
to a continuous function of time by setting (cf. (5.6))
and where
![]() $H_t = H_k + \tfrac {t-k}{k+1}.$
We make a time change by setting
$H_t = H_k + \tfrac {t-k}{k+1}.$
We make a time change by setting
 $$\begin{align*}k_n(t) = n_1^+\exp\bigg( \frac{\log(n/n_1^+)}{T+-T_-} \bigl(t-T_-\bigr)\bigg) \quad t \in [T_-,T_+]. \end{align*}$$
$$\begin{align*}k_n(t) = n_1^+\exp\bigg( \frac{\log(n/n_1^+)}{T+-T_-} \bigl(t-T_-\bigr)\bigg) \quad t \in [T_-,T_+]. \end{align*}$$
In terms of this time change, we set
Finally, we define the Brownian motion
![]() $\mathfrak {W}_t^j$
by the identity
$\mathfrak {W}_t^j$
by the identity
 $$ \begin{align} d\mathfrak{W}_t^j = \frac{ e^{i(k_n(t)+1)\theta_j} d\widehat{\mathfrak{W}}_{H_{k_n(t)}}^j }{\sqrt{\tfrac{d}{dt} (H_{k_n(t)})}} \quad \text{on} \quad t \in [T_-,T_+]. \end{align} $$
$$ \begin{align} d\mathfrak{W}_t^j = \frac{ e^{i(k_n(t)+1)\theta_j} d\widehat{\mathfrak{W}}_{H_{k_n(t)}}^j }{\sqrt{\tfrac{d}{dt} (H_{k_n(t)})}} \quad \text{on} \quad t \in [T_-,T_+]. \end{align} $$
Recall
![]() $\mathfrak {L}_t^j$
which solves (2.43). The function
$\mathfrak {L}_t^j$
which solves (2.43). The function
![]() $\widehat {\mathfrak {L}}^j_t(\theta )$
is an approximate solution of the same equation, and we can compare the two solutions.
$\widehat {\mathfrak {L}}^j_t(\theta )$
is an approximate solution of the same equation, and we can compare the two solutions.
Lemma 5.5. For any
![]() $C>0$
and any
$C>0$
and any
![]() $\delta> 0$
sufficiently small, for all n sufficiently large,
$\delta> 0$
sufficiently small, for all n sufficiently large,
Proof. We begin by posing a stochastic differential equation for
![]() $\widehat {\mathfrak {L}}^j_t(\theta )$
. We have that it is a strong solution of the differential equation
$\widehat {\mathfrak {L}}^j_t(\theta )$
. We have that it is a strong solution of the differential equation
We note the derivative
![]() $k_n'(t)$
satisfies
$k_n'(t)$
satisfies
Similarly, almost everywhere,
Thus, we can express the SDE as
for deterministic errors
![]() $E_1,E_2$
which are
$E_1,E_2$
which are
![]() $O_{k_1}(1/n)$
and a random error
$O_{k_1}(1/n)$
and a random error
![]() $E_3(t)$
which is controlled by Lemma 5.1.
$E_3(t)$
which is controlled by Lemma 5.1.
Hence, if we form the difference ![]() , we have that
, we have that
We can furthermore check that
![]() $f_t = \log (1 + n^{2\delta } |D_t|^2)$
has both drift and diffusion coefficient which are bounded above by
$f_t = \log (1 + n^{2\delta } |D_t|^2)$
has both drift and diffusion coefficient which are bounded above by
![]() $O_{k_1}(1)$
uniformly in
$O_{k_1}(1)$
uniformly in
![]() $\theta $
with probability at least
$\theta $
with probability at least
![]() $1-n^{-C}$
by Lemma 5.1. It follows that we have a Gaussian tail bound for the difference with a variance which is
$1-n^{-C}$
by Lemma 5.1. It follows that we have a Gaussian tail bound for the difference with a variance which is
![]() $O_{k_1}(1)$
, which implies the claim.
$O_{k_1}(1)$
, which implies the claim.
The lemmas assembled give a proof of Proposition 2.12.
Proof of Proposition 2.12.
We briefly survey the role of each lemma and combine them for the proof of the Proposition. We suppose C is given and let
![]() $\delta> 0$
be as in the Proposition. We apply these lemmas with
$\delta> 0$
be as in the Proposition. We apply these lemmas with
![]() $\varkappa = n^{1-4\delta }$
and
$\varkappa = n^{1-4\delta }$
and
![]() $\omega = 2n^{4\delta }$
. Lemma 5.5 connects the SDE
$\omega = 2n^{4\delta }$
. Lemma 5.5 connects the SDE
![]() $\mathfrak {L}_t^j(\theta )$
to an approximate solution 𝔏^
t
j
(θ) = λ
k
n
(t)
(j)(θ
j
+θn) − i(k
n
(t)+ 1)θ
j
: for all
$\mathfrak {L}_t^j(\theta )$
to an approximate solution 𝔏^
t
j
(θ) = λ
k
n
(t)
(j)(θ
j
+θn) − i(k
n
(t)+ 1)θ
j
: for all
![]() $\delta>0$
sufficiently small,
$\delta>0$
sufficiently small,
This approximate solution is a time-changed and spatially scaled version of the process
![]() $\lambda _k^{(j)}(\theta )$
. Lemma 5.4 bounds the difference between
$\lambda _k^{(j)}(\theta )$
. Lemma 5.4 bounds the difference between
![]() $\lambda _k^{(j)}$
and
$\lambda _k^{(j)}$
and
![]() $\lambda _k$
(and all n sufficiently large and
$\lambda _k$
(and all n sufficiently large and
![]() $\delta < \tfrac 18$
) as
$\delta < \tfrac 18$
) as
 $$\begin{align*}\sup_{|\theta| \leq n^{8\delta}} \mathbb{P}_M\left[ \max_{{n_1^+} \leq k \leq n} |\lambda_k^{(j)}(\theta_j + \tfrac{\theta}{n})-\lambda_k(\theta_j + \tfrac{\theta}{n})| \geq n^{\delta-2\delta} \right] \leq n^{-C}/3,\quad \operatorname{a.s.} \end{align*}$$
$$\begin{align*}\sup_{|\theta| \leq n^{8\delta}} \mathbb{P}_M\left[ \max_{{n_1^+} \leq k \leq n} |\lambda_k^{(j)}(\theta_j + \tfrac{\theta}{n})-\lambda_k(\theta_j + \tfrac{\theta}{n})| \geq n^{\delta-2\delta} \right] \leq n^{-C}/3,\quad \operatorname{a.s.} \end{align*}$$
This shows that we can replace the driving Gaussian noise by band-resampled Gaussians, for which Fourier modes that are far from those
![]() $\theta _j$
are resampled. Note that if we take
$\theta _j$
are resampled. Note that if we take
![]() $\delta < \tfrac {1}{10}$
, the constraint on
$\delta < \tfrac {1}{10}$
, the constraint on
![]() $\theta $
that
$\theta $
that
![]() $|\theta | \leq n^{8\delta }$
is more restrictive than
$|\theta | \leq n^{8\delta }$
is more restrictive than
![]() $|\theta | \leq n^{1-2\delta }.$
$|\theta | \leq n^{1-2\delta }.$
Lemma 5.2 now shows that
![]() $\lambda _k(\theta )$
, which is a locally linearized (in time) version of a shift of
$\lambda _k(\theta )$
, which is a locally linearized (in time) version of a shift of ![]() , is indeed close to it; that is, for all
, is indeed close to it; that is, for all
![]() $\delta> 0$
sufficiently small, n sufficiently large,
$\delta> 0$
sufficiently small, n sufficiently large,

Finally, this construction holds for every j, and for
![]() $j_1$
and
$j_1$
and
![]() $j_2$
, if the sets
$j_2$
, if the sets
![]() $\{ \theta : |e(\theta _{j_p}) - e(\theta )| \leq 2n^{8\delta -1}\}$
are disjoint for
$\{ \theta : |e(\theta _{j_p}) - e(\theta )| \leq 2n^{8\delta -1}\}$
are disjoint for
![]() $p\in \{1,2\}$
, then the processes
$p\in \{1,2\}$
, then the processes
![]() $\mathfrak {L}_t^{j_p}$
are
$\mathfrak {L}_t^{j_p}$
are
![]() $\mathbb {P}_M$
-independent.
$\mathbb {P}_M$
-independent.
5.4 Logarithmic ladder
We suppose that
![]() $\left \{ A_k \right \}$
is a sequence of random variables which roughly has the type of multiplicative recurrence structure of the Prüfer phases. This is to say, we let
$\left \{ A_k \right \}$
is a sequence of random variables which roughly has the type of multiplicative recurrence structure of the Prüfer phases. This is to say, we let
![]() $\mathscr {F}_k = \sigma (A_1,A_2, \dots , A_k)$
and we suppose there are constants V and W so that for all
$\mathscr {F}_k = \sigma (A_1,A_2, \dots , A_k)$
and we suppose there are constants V and W so that for all
![]() $\lambda \in {\mathbb R}$
and all
$\lambda \in {\mathbb R}$
and all
![]() $k \geq {n_1^+}$
for some
$k \geq {n_1^+}$
for some
![]() ${n_1^+} \in {\mathbb N},$
${n_1^+} \in {\mathbb N},$
Proposition 5.6. Let
![]() $\epsilon ,E> 0$
be given and suppose that
$\epsilon ,E> 0$
be given and suppose that
![]() $E \leq \sqrt {W/V}.$
Let
$E \leq \sqrt {W/V}.$
Let
![]() $\mathcal {E}$
be the event such that
$\mathcal {E}$
be the event such that
There is an absolute constant
![]() $C>0$
so that for all
$C>0$
so that for all
![]() $x \geq \max \{(2+\epsilon )^2,CV(2+\epsilon )^3\log (2+\epsilon )\log (n/{n_1^+})\},$
$x \geq \max \{(2+\epsilon )^2,CV(2+\epsilon )^3\log (2+\epsilon )\log (n/{n_1^+})\},$
Proof. Set
![]() $\eta = 1+\epsilon $
. We define stopping times
$\eta = 1+\epsilon $
. We define stopping times
![]() $\{\tau _p\}$
, for
$\{\tau _p\}$
, for
![]() $p \in {\mathbb N}$
, as the first times
$p \in {\mathbb N}$
, as the first times
![]() $k \geq {n_1^+}$
that
$k \geq {n_1^+}$
that
![]() $A_{k}$
exceeds
$A_{k}$
exceeds
![]() $\eta ^p E$
or that
$\eta ^p E$
or that
![]() $k=n$
. Then, it follows that on
$k=n$
. Then, it follows that on
![]() $\mathcal {E}$
,
$\mathcal {E}$
,
Define, for any
![]() $p \in {\mathbb N}$
, the process
$p \in {\mathbb N}$
, the process
 $$\begin{align*}M_j = e^{\lambda A_{j}(\theta) - \lambda^2 (V\eta^{2p+2}E^2+W)H_j}, \quad\quad \text{where } H_j = \sum_{k=1}^j \frac{1}{k}. \end{align*}$$
$$\begin{align*}M_j = e^{\lambda A_{j}(\theta) - \lambda^2 (V\eta^{2p+2}E^2+W)H_j}, \quad\quad \text{where } H_j = \sum_{k=1}^j \frac{1}{k}. \end{align*}$$
When stopped at
![]() $\tau _{p+1}, \left \{ M_j \right \}$
is a supermartingale, and so
$\tau _{p+1}, \left \{ M_j \right \}$
is a supermartingale, and so
It follows that
Now,
![]() $H_{\tau _{p+1}} - H_{\tau _p} \leq \log ( \tau _{p+1}/\tau _p).$
On the event that
$H_{\tau _{p+1}} - H_{\tau _p} \leq \log ( \tau _{p+1}/\tau _p).$
On the event that
![]() $\tau _{p+1}/\tau _p \leq t_p$
for some
$\tau _{p+1}/\tau _p \leq t_p$
for some
![]() $t_p \geq 1,$
we conclude that
$t_p \geq 1,$
we conclude that
Finally, optimizing in
![]() $\lambda ,$
it follows that
$\lambda ,$
it follows that
 $$ \begin{align*} \mathbb{P}\left[ \{\tau_{p+1}/\tau_p \leq t_p\} \cap \mathcal{E} \middle\vert \mathscr{F}_{\tau_p} \right] & \leq \exp\left( -\frac{(\eta^{p}(\eta-1-\epsilon) - 1)^2E^2}{4\log(t_p)(V\eta^{2p+2}E^2+W)} \right)\\ & \leq \exp\left( -\frac{\eta^{2p-1}E^2}{4\log(t_p)(V\eta^{2p+2}E^2+W)} \right), \end{align*} $$
$$ \begin{align*} \mathbb{P}\left[ \{\tau_{p+1}/\tau_p \leq t_p\} \cap \mathcal{E} \middle\vert \mathscr{F}_{\tau_p} \right] & \leq \exp\left( -\frac{(\eta^{p}(\eta-1-\epsilon) - 1)^2E^2}{4\log(t_p)(V\eta^{2p+2}E^2+W)} \right)\\ & \leq \exp\left( -\frac{\eta^{2p-1}E^2}{4\log(t_p)(V\eta^{2p+2}E^2+W)} \right), \end{align*} $$
where in the final equality, we have used that
![]() $\eta = 2+\epsilon $
and
$\eta = 2+\epsilon $
and
![]() $p \geq 1.$
$p \geq 1.$
Let
![]() $r_0 \geq {n_1^+}$
be the smallest integer such that
$r_0 \geq {n_1^+}$
be the smallest integer such that
![]() $V \eta ^{2r_0}E^2 \geq W.$
Then by iterating the previous conditional expectation,
$V \eta ^{2r_0}E^2 \geq W.$
Then by iterating the previous conditional expectation,
 $$\begin{align*}\begin{aligned} \mathbb{P}\left[ \cap_{p=r_0}^r \{\tau_{p+1}/\tau_p \leq t_p\} \cap \mathcal{E} \middle\vert \mathscr{F}_{\tau_{r_0}} \right] &\leq \exp\left( -\sum_{p=r_0}^r\frac{\eta^{2p-1}E^2}{4\log(t_p)(V\eta^{2p+2}E^2+W)} \right) \\ &\leq \exp\left( -\sum_{p=r_0}^r\frac{1}{8V\eta^3\log(t_p)} \right) \\ &\leq \mathbb{P}\left[ \cap_{p=r_0}^r \bigg\{ \tfrac{1}{8V\eta^3 X_p} \leq \log( t_p ) \bigg\} \right], \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathbb{P}\left[ \cap_{p=r_0}^r \{\tau_{p+1}/\tau_p \leq t_p\} \cap \mathcal{E} \middle\vert \mathscr{F}_{\tau_{r_0}} \right] &\leq \exp\left( -\sum_{p=r_0}^r\frac{\eta^{2p-1}E^2}{4\log(t_p)(V\eta^{2p+2}E^2+W)} \right) \\ &\leq \exp\left( -\sum_{p=r_0}^r\frac{1}{8V\eta^3\log(t_p)} \right) \\ &\leq \mathbb{P}\left[ \cap_{p=r_0}^r \bigg\{ \tfrac{1}{8V\eta^3 X_p} \leq \log( t_p ) \bigg\} \right], \end{aligned} \end{align*}$$
where
![]() $\left \{ X_p \right \}$
are a family of independent
$\left \{ X_p \right \}$
are a family of independent
![]() $\operatorname {Exp}(1)$
random variables. Hence, we may couple
$\operatorname {Exp}(1)$
random variables. Hence, we may couple
![]() $\left \{ \tau _p\! :\! p \geq r_0 \right \}$
with
$\left \{ \tau _p\! :\! p \geq r_0 \right \}$
with
![]() $\left \{ X_p \right \}$
in such a way that on
$\left \{ X_p \right \}$
in such a way that on
![]() $\mathcal {E}$
,
$\mathcal {E}$
,
Moreover, we conclude that for any
![]() $t \geq 0,$
$t \geq 0,$
Using the harmonic-mean–arithmetic-mean inequality,
 $$\begin{align*}\frac{r-r_0}{ \sum_{p=r_0}^{r-1} X_p} \leq \frac{1}{r-r_0} \sum_{p=r_0}^{r-1} \tfrac{1}{X_p}. \end{align*}$$
$$\begin{align*}\frac{r-r_0}{ \sum_{p=r_0}^{r-1} X_p} \leq \frac{1}{r-r_0} \sum_{p=r_0}^{r-1} \tfrac{1}{X_p}. \end{align*}$$
Hence, we arrive at, under the assumption that
![]() $\tfrac { (r-r_0)^2}{8V\eta ^3 \log (t)} \geq 2(r-r_0),$
$\tfrac { (r-r_0)^2}{8V\eta ^3 \log (t)} \geq 2(r-r_0),$
 $$ \begin{align} \mathbb{P}\left[ \{\tau_r/\tau_{r_0} \leq t\} \cap \mathcal{E} \right] \leq \mathbb{P}\left[ {\textstyle \sum_{p=r_0}^{r-1} X_p} \geq \tfrac{ (r-r_0)^2}{8V\eta^3 \log(t)} \right] \leq \exp\left( -\frac{1}{C} \min \left\{ \tfrac{ (r-r_0)^2}{V\eta^3 \log(t)}, \tfrac{ (r-r_0)^3}{V^2\eta^6 \log(t)^2} \right\} \right), \end{align} $$
$$ \begin{align} \mathbb{P}\left[ \{\tau_r/\tau_{r_0} \leq t\} \cap \mathcal{E} \right] \leq \mathbb{P}\left[ {\textstyle \sum_{p=r_0}^{r-1} X_p} \geq \tfrac{ (r-r_0)^2}{8V\eta^3 \log(t)} \right] \leq \exp\left( -\frac{1}{C} \min \left\{ \tfrac{ (r-r_0)^2}{V\eta^3 \log(t)}, \tfrac{ (r-r_0)^3}{V^2\eta^6 \log(t)^2} \right\} \right), \end{align} $$
using Bernstein’s inequality for subexponential random variables [Reference VershyninVer18, Theorem 2.8.1]. Observe that under the assumption, the minimum is always attained by the first term.
Finally, we observe that for r such that
![]() $V \eta ^{2r}E^2 \geq W,$
$V \eta ^{2r}E^2 \geq W,$
provided
![]() $r-r_0 \geq 16V \eta ^3 \log (n/{n_1^+}).$
Moreover, for
$r-r_0 \geq 16V \eta ^3 \log (n/{n_1^+}).$
Moreover, for
![]() $x \geq 1,$
if we take
$x \geq 1,$
if we take
![]() $r = r_0 + \lfloor \log (x)/\log (\eta )\rfloor - 1$
,
$r = r_0 + \lfloor \log (x)/\log (\eta )\rfloor - 1$
,
 $$\begin{align*}\begin{aligned} \mathbb{P}\bigl[ \bigl\{ \max_{{n_1^+} \leq k \leq n} A_k \geq x \sqrt{W/V} \bigr\} \cap \mathcal{E} \bigr] &\leq \mathbb{P}\bigl[ \bigl\{ \max_{{n_1^+} \leq k \leq n} A_k \geq \eta^{r-r_0+1}\sqrt{W/V} \bigr\} \cap \mathcal{E} \bigr]\\ &\leq \mathbb{P}\bigl[ \bigl\{ \max_{{n_1^+} \leq k \leq n} A_k \geq \eta^{r}E \bigr\} \cap \mathcal{E} \bigr]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathbb{P}\bigl[ \bigl\{ \max_{{n_1^+} \leq k \leq n} A_k \geq x \sqrt{W/V} \bigr\} \cap \mathcal{E} \bigr] &\leq \mathbb{P}\bigl[ \bigl\{ \max_{{n_1^+} \leq k \leq n} A_k \geq \eta^{r-r_0+1}\sqrt{W/V} \bigr\} \cap \mathcal{E} \bigr]\\ &\leq \mathbb{P}\bigl[ \bigl\{ \max_{{n_1^+} \leq k \leq n} A_k \geq \eta^{r}E \bigr\} \cap \mathcal{E} \bigr]. \end{aligned} \end{align*}$$
Hence, for
![]() $x \geq \eta ^2,$
we conclude there is an absolute constant
$x \geq \eta ^2,$
we conclude there is an absolute constant
![]() $C>0$
such that
$C>0$
such that
provided
![]() $\log (x) \geq \log (\eta )+16V\eta ^3\log (\eta ) \log (n/{n_1^+}).$
This completes the proof.
$\log (x) \geq \log (\eta )+16V\eta ^3\log (\eta ) \log (n/{n_1^+}).$
This completes the proof.
6 Changing the initial condition
In our application, we will want to consider changing the initial conditions of
![]() $\mathfrak {L}_{T_-}.$
The real part of
$\mathfrak {L}_{T_-}.$
The real part of
![]() $(\mathfrak {L}_t : t)$
does not influence the evolution of the diffusion, and therefore, any initial condition specified for
$(\mathfrak {L}_t : t)$
does not influence the evolution of the diffusion, and therefore, any initial condition specified for
![]() $\Re \mathfrak {L}_{T_{-}}$
will simply appear as an additive perturbation to solution of
$\Re \mathfrak {L}_{T_{-}}$
will simply appear as an additive perturbation to solution of
![]() $(\mathfrak {L}_t : t)$
with
$(\mathfrak {L}_t : t)$
with
![]() $\Re \mathfrak {L}_{T_{-}}(\theta )=0.$
However, we wish to show that for the imaginary part, the probability that a small perturbation of initial condition grows in magnitude and the random walk performs an unusual growth (as is needed to be relevant for the maximum) is small. In fact, it will be important in the real case
$\Re \mathfrak {L}_{T_{-}}(\theta )=0.$
However, we wish to show that for the imaginary part, the probability that a small perturbation of initial condition grows in magnitude and the random walk performs an unusual growth (as is needed to be relevant for the maximum) is small. In fact, it will be important in the real case
![]() $\sigma =1$
that having a large real part tends to compress the relative Prüfer phase.
$\sigma =1$
that having a large real part tends to compress the relative Prüfer phase.
Proposition 6.1. Fix some
![]() $j \in \mathcal {D}_{n/k_1}$
and some
$j \in \mathcal {D}_{n/k_1}$
and some ![]() Let
Let
![]() $(\mathfrak {L}_t:t \in [T_-,T_+])$
solve (2.43) and let
$(\mathfrak {L}_t:t \in [T_-,T_+])$
solve (2.43) and let
![]() $(\mathfrak {L}_t^o:t \in [T_-,T_+])$
solve (2.52). Suppose
$(\mathfrak {L}_t^o:t \in [T_-,T_+])$
solve (2.52). Suppose
![]() $|\Im (\mathfrak {L}_{T_-}(\theta )-\mathfrak {L}_{T_-}(0))| \leq \frac {k_1(\log k_1)^{50}}{k_1^+}.$
Set
$|\Im (\mathfrak {L}_{T_-}(\theta )-\mathfrak {L}_{T_-}(0))| \leq \frac {k_1(\log k_1)^{50}}{k_1^+}.$
Set ![]() On the event
On the event
there is a
![]() $\delta>0$
so that for all
$\delta>0$
so that for all
![]() $k_1$
sufficiently large,
$k_1$
sufficiently large,
 $$\begin{align*}\mathbb{P}( |\Delta_{T_+}|> \sqrt{\tfrac{k_1}{\hat{k}_1}}, \left\{ \mathfrak{U}_{T_+}(\theta) \in [-(\log k_1)^{1/100},3k_6] \right\} ~\vert~ \mathscr{F}_{n_1^+}) \leq \frac{1}{k_1^+} e^{-\delta(\log k_1)^{19/20}}. \end{align*}$$
$$\begin{align*}\mathbb{P}( |\Delta_{T_+}|> \sqrt{\tfrac{k_1}{\hat{k}_1}}, \left\{ \mathfrak{U}_{T_+}(\theta) \in [-(\log k_1)^{1/100},3k_6] \right\} ~\vert~ \mathscr{F}_{n_1^+}) \leq \frac{1}{k_1^+} e^{-\delta(\log k_1)^{19/20}}. \end{align*}$$
The same holds if we replace
![]() $\mathfrak {U}$
by
$\mathfrak {U}$
by
![]() $\mathfrak {U}^o+\mathfrak {U}(0)$
in the above two equations. If
$\mathfrak {U}^o+\mathfrak {U}(0)$
in the above two equations. If
![]() $\sigma =1$
, we also have the conclusion in the last display with
$\sigma =1$
, we also have the conclusion in the last display with ![]() replacing
replacing
![]() $\Delta _t$
.
$\Delta _t$
.
Proof. We show the case
![]() $\sigma =1$
first. We shall show how to modify the argument for
$\sigma =1$
first. We shall show how to modify the argument for
![]() $\sigma =i$
after completing the
$\sigma =i$
after completing the
![]() $\sigma =1$
case.
$\sigma =1$
case.
Step 1: Change of measure.
In this case, we have d𝔘
t
= 4βℜ(e
iℑ𝔏
t
(θ)
d𝔚
t
j
). Let
![]() $d\mathfrak {B}_t = \sqrt {\tfrac {4}{\beta }} \Im ( e^{i \Im \mathfrak {L}_t(\theta )} d \mathfrak {W}_t^j ),$
which (for fixed
$d\mathfrak {B}_t = \sqrt {\tfrac {4}{\beta }} \Im ( e^{i \Im \mathfrak {L}_t(\theta )} d \mathfrak {W}_t^j ),$
which (for fixed
![]() $\theta $
) is an independent Brownian motion of
$\theta $
) is an independent Brownian motion of
![]() $\mathfrak {U}$
. Define a change of measure
$\mathfrak {U}$
. Define a change of measure
 $$\begin{align*}\frac{d{\mathbb Q}}{d\mathbb{P}} = \exp\left( \sqrt{\frac{\beta}{2}} (\mathfrak{U}_{T_+}(\theta)-\mathfrak{U}_{T_-}(\theta)) - (T_+-T_-) \right). \end{align*}$$
$$\begin{align*}\frac{d{\mathbb Q}}{d\mathbb{P}} = \exp\left( \sqrt{\frac{\beta}{2}} (\mathfrak{U}_{T_+}(\theta)-\mathfrak{U}_{T_-}(\theta)) - (T_+-T_-) \right). \end{align*}$$
Then, under
![]() ${\mathbb Q}, d\mathfrak {U}_t = d\mathfrak {X}_t + \sqrt {\tfrac {8}{\beta }}dt$
on
${\mathbb Q}, d\mathfrak {U}_t = d\mathfrak {X}_t + \sqrt {\tfrac {8}{\beta }}dt$
on
![]() $[T_-,T_+]$
for a
$[T_-,T_+]$
for a
![]() ${\mathbb Q}$
-Brownian motion
${\mathbb Q}$
-Brownian motion
![]() $(\mathfrak {X}_t: t \in [T_-,T_+])$
(with quadratic variation
$(\mathfrak {X}_t: t \in [T_-,T_+])$
(with quadratic variation
![]() $\tfrac {4}{\beta }(t-T_{-})$
). Under
$\tfrac {4}{\beta }(t-T_{-})$
). Under
![]() ${\mathbb Q}, \mathfrak {B}$
remains an independent Brownian motion with the same quadratic variation as
${\mathbb Q}, \mathfrak {B}$
remains an independent Brownian motion with the same quadratic variation as
![]() $\mathfrak {X}.$
$\mathfrak {X}.$
On the event given for
![]() $\mathfrak {U}_{T_+}(\theta )$
in the statement of the Lemma, this Radon–Nikodym derivative is also in control and is given by
$\mathfrak {U}_{T_+}(\theta )$
in the statement of the Lemma, this Radon–Nikodym derivative is also in control and is given by
![]() $e^{(\log k_1^+) + O( \log k_1)^{9/10}}.$
Hence, it suffices to show that
$e^{(\log k_1^+) + O( \log k_1)^{9/10}}.$
Hence, it suffices to show that
To prove the statements with
![]() $\mathfrak {U}^o$
, we instead need to use the change of measure
$\mathfrak {U}^o$
, we instead need to use the change of measure
 $$\begin{align*}\frac{d{\mathbb Q}^o}{d\mathbb{P}} = \exp\left( \sqrt{\frac{\beta}{2}} (\mathfrak{U}^o_{T_+}(\theta)-\mathfrak{U}^o_{T_-}(\theta)) - (T_+-T_-) \right), \end{align*}$$
$$\begin{align*}\frac{d{\mathbb Q}^o}{d\mathbb{P}} = \exp\left( \sqrt{\frac{\beta}{2}} (\mathfrak{U}^o_{T_+}(\theta)-\mathfrak{U}^o_{T_-}(\theta)) - (T_+-T_-) \right), \end{align*}$$
but everything proceeds with obvious changes. We continue with the case
![]() $\mathfrak {U}.$
$\mathfrak {U}.$
The difference
![]() $\Delta _t$
satisfies the SDE
$\Delta _t$
satisfies the SDE

In the case that
![]() $\Delta _{T-}> 0$
, the process remains nonnegative for all time.
$\Delta _{T-}> 0$
, the process remains nonnegative for all time.
Step 2: No movement before
 $T_\dagger $
.
$T_\dagger $
.
Recall that
![]() $T_\dagger =-(\log k_1)^{19/20}<0$
. Set
$T_\dagger =-(\log k_1)^{19/20}<0$
. Set
![]() $\mathfrak {e}(t) = \exp (\sqrt {\tfrac {8}{\beta }}(t-T_-)).$
Note that
$\mathfrak {e}(t) = \exp (\sqrt {\tfrac {8}{\beta }}(t-T_-)).$
Note that

Let
![]() $\vartheta $
be the first time in
$\vartheta $
be the first time in
![]() $[T_-,T_\dagger ]$
that
$[T_-,T_\dagger ]$
that
![]() $|\Delta _{t}|> 10\exp (T_\dagger )$
. Then,
$|\Delta _{t}|> 10\exp (T_\dagger )$
. Then,
 $$\begin{align*}\Delta_t = \frac{\Delta_{T_-}}{\mathfrak{e}(t)} +\frac{\theta}{k_1 \mathfrak{e}(t)}\int_{T_-}^t \mathfrak{e}(s)e^s\,ds + \frac{1}{\mathfrak{e}(t)} \bigl(M(t) + \mathcal{Y}(t) \bigr) \end{align*}$$
$$\begin{align*}\Delta_t = \frac{\Delta_{T_-}}{\mathfrak{e}(t)} +\frac{\theta}{k_1 \mathfrak{e}(t)}\int_{T_-}^t \mathfrak{e}(s)e^s\,ds + \frac{1}{\mathfrak{e}(t)} \bigl(M(t) + \mathcal{Y}(t) \bigr) \end{align*}$$
for a martingale M and a finite variation term
![]() $\mathcal {Y}$
. The first two terms, prior to
$\mathcal {Y}$
. The first two terms, prior to
![]() $T_\dagger $
, are bounded by
$T_\dagger $
, are bounded by
![]() $7\exp (T_\dagger )$
. The final term is bounded, before
$7\exp (T_\dagger )$
. The final term is bounded, before
![]() $T_\dagger \wedge \vartheta $
, by
$T_\dagger \wedge \vartheta $
, by
![]() $Ce^{3T_\dagger }$
. The martingale, up to time
$Ce^{3T_\dagger }$
. The martingale, up to time
![]() $T_\dagger \wedge \vartheta $
, has quadratic variation bounded above by
$T_\dagger \wedge \vartheta $
, has quadratic variation bounded above by
![]() $\mathfrak {e}^2(t)e^{4T_\dagger }$
. Thus, summing over integer times between
$\mathfrak {e}^2(t)e^{4T_\dagger }$
. Thus, summing over integer times between
![]() $[T_-,T_\dagger ]$
, the
$[T_-,T_\dagger ]$
, the
![]() $\mathbb {Q}$
-probability that it reaches height
$\mathbb {Q}$
-probability that it reaches height
![]() $\mathfrak {e}(t)e^{1.9T_\dagger }$
is at most
$\mathfrak {e}(t)e^{1.9T_\dagger }$
is at most
![]() $\exp (-c\exp (-cT_\dagger ))$
for some
$\exp (-c\exp (-cT_\dagger ))$
for some
![]() $c> 0$
. As
$c> 0$
. As
![]() $\Delta _t$
is continuous, we conclude that with probability
$\Delta _t$
is continuous, we conclude that with probability
![]() $1-\exp (-c\exp (-cT_\dagger ))$
,
$1-\exp (-c\exp (-cT_\dagger ))$
,
![]() $\vartheta = \infty ,$
which is to say
$\vartheta = \infty ,$
which is to say
![]() $|\Delta (T_\dagger )| \leq 10\exp (T_\dagger ).$
$|\Delta (T_\dagger )| \leq 10\exp (T_\dagger ).$
Step 3: Self-stabilizing after
 $T_\dagger $
.
$T_\dagger $
.
From time
![]() $t> T_\dagger $
, the SDE (6.1) becomes
$t> T_\dagger $
, the SDE (6.1) becomes
From the vanishing of the drift and diffusion terms, this equation cannot cross any multiple of ![]() . By passing to its negative if necessary, we may assume
. By passing to its negative if necessary, we may assume ![]() We let
We let
![]() $\tau $
be the first hitting time of
$\tau $
be the first hitting time of
![]() $\Delta _{t}$
to
$\Delta _{t}$
to ![]() Then by comparison, before
Then by comparison, before
![]() $\tau , \Delta _{t}$
for any
$\tau , \Delta _{t}$
for any
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $\delta> 0$
sufficiently small that
$\delta> 0$
sufficiently small that
![]() $\Delta _t$
is dominated by the solution to
$\Delta _t$
is dominated by the solution to
for all
![]() $t \leq \tau $
, where
$t \leq \tau $
, where
![]() $\Delta _{T_\dagger }'=\Delta _{T_\dagger }$
. Taking logarithms, we have from Itô’s Lemma,
$\Delta _{T_\dagger }'=\Delta _{T_\dagger }$
. Taking logarithms, we have from Itô’s Lemma,

The stopped martingale part has uniformly bounded quadratic variation. The drift is bounded as well, using
![]() $\cos (x) \leq 1 - x^2(\tfrac 12-\epsilon )$
before the stopping time
$\cos (x) \leq 1 - x^2(\tfrac 12-\epsilon )$
before the stopping time
![]() $\tau ',$
the first time
$\tau ',$
the first time
![]() $\Delta _t'$
reaches
$\Delta _t'$
reaches ![]() for
for
![]() $\delta '$
sufficiently small. In particular, for
$\delta '$
sufficiently small. In particular, for
![]() $t \leq \tau '$
,
$t \leq \tau '$
,
 $$\begin{align*}d \log(\Delta_t') \leq dM_t - \left( \sqrt{\frac{8}{\beta}}-(1+\frac4\beta)\epsilon+\frac{2}{\beta} \right) dt, \end{align*}$$
$$\begin{align*}d \log(\Delta_t') \leq dM_t - \left( \sqrt{\frac{8}{\beta}}-(1+\frac4\beta)\epsilon+\frac{2}{\beta} \right) dt, \end{align*}$$
for a martingale
![]() $M_t$
with
$M_t$
with
![]() $d\langle M \rangle _t \leq \frac {C}{\beta }dt$
and
$d\langle M \rangle _t \leq \frac {C}{\beta }dt$
and
![]() $M_{T_\dagger }=0.$
Hence, to bound the
$M_{T_\dagger }=0.$
Hence, to bound the
![]() ${\mathbb Q}$
-probability that
${\mathbb Q}$
-probability that
![]() $\log (\Delta _{T_+}') \geq \log (\Delta _{T_\dagger }') +0.4 (\log k_1)^{19/20},$
we can instead bound the probability that there is a
$\log (\Delta _{T_+}') \geq \log (\Delta _{T_\dagger }') +0.4 (\log k_1)^{19/20},$
we can instead bound the probability that there is a
![]() $t \leq \tau '$
such that
$t \leq \tau '$
such that
 $$\begin{align*}M_t \geq 0.4(\log k_1)^{19/20} +(1-\epsilon)\left( \sqrt{\frac{8}{\beta}}-(1+\frac4\beta)\epsilon+\frac{2}{\beta} \right) (t-T_\dagger), \end{align*}$$
$$\begin{align*}M_t \geq 0.4(\log k_1)^{19/20} +(1-\epsilon)\left( \sqrt{\frac{8}{\beta}}-(1+\frac4\beta)\epsilon+\frac{2}{\beta} \right) (t-T_\dagger), \end{align*}$$
noting that on the complement of this event,
![]() $\tau '> (T_+-T_\dagger )$
, and so also,
$\tau '> (T_+-T_\dagger )$
, and so also,
![]() $\tau> T_+-T_\dagger .$
From a time change, this probability is dominated above by the probability that a
$\tau> T_+-T_\dagger .$
From a time change, this probability is dominated above by the probability that a
![]() $\frac {\beta }{C}t$
-quadratic variation Brownian motion crosses the same linear barrier, and so
$\frac {\beta }{C}t$
-quadratic variation Brownian motion crosses the same linear barrier, and so
 $$\begin{align*}\begin{aligned} {\mathbb Q}(\log(\Delta_{T_+\wedge \tau'}') \geq \log(\Delta_{T_\dagger}')+ 0.4(\log k_1)^{19/20}) &\leq \exp\left( -(\log k_1)^{19/20}\frac{0.4\sqrt{\beta}}{\sqrt{C}}\left( \sqrt{\frac{8}{\beta}}-(1+\frac4\beta)\epsilon+\frac{2}{\beta} \right) \right)\\ &=e^{-c (\log k_1)^{19/20}}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} {\mathbb Q}(\log(\Delta_{T_+\wedge \tau'}') \geq \log(\Delta_{T_\dagger}')+ 0.4(\log k_1)^{19/20}) &\leq \exp\left( -(\log k_1)^{19/20}\frac{0.4\sqrt{\beta}}{\sqrt{C}}\left( \sqrt{\frac{8}{\beta}}-(1+\frac4\beta)\epsilon+\frac{2}{\beta} \right) \right)\\ &=e^{-c (\log k_1)^{19/20}}. \end{aligned} \end{align*}$$
for some
![]() $c(\beta )>0$
and for all
$c(\beta )>0$
and for all
![]() $k_1$
sufficiently large.
$k_1$
sufficiently large.
Step 4: Control of the real part.
Having controlled the difference of imaginary parts, we can then control the difference of real parts
![]() $\Delta ^r.$
We derive the diffusion for
$\Delta ^r.$
We derive the diffusion for
![]() $\Delta ^r,$
whose behavior is determined entirely by that of
$\Delta ^r,$
whose behavior is determined entirely by that of
![]() $\Delta :$
$\Delta :$
 $$ \begin{align*} \begin{aligned} d\Delta_t^r &= \sqrt{\tfrac{4}{\beta}} \Re \bigg((e^{i \Im \mathfrak{L}_t(\theta)}-e^{i \Im (\mathfrak{L}_t^o(\theta) + \mathfrak{L}_{T_-}^j(\theta_j) )}) d \mathfrak{W}_t^j \bigg) \\ &= \sqrt{\tfrac{4}{\beta}} \bigg( \Re ( e^{i \Im \mathfrak{L}_t(\theta)} d \mathfrak{W}_t^j ) (1-\cos \Delta_t) - \Im ( e^{i \Im \mathfrak{L}_t(\theta)} d \mathfrak{W}_t^j ) \sin \Delta_t \bigg) \\ &= d\mathfrak{U}_t (1-\cos \Delta_t) - d\mathfrak{B}_t \sin \Delta_t \\ &= dt \sqrt{\tfrac{8}{\beta}} (1-\cos \Delta_t) + d\mathfrak{X}_t (1-\cos \Delta_t) - d\mathfrak{B}_t \sin \Delta_t. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d\Delta_t^r &= \sqrt{\tfrac{4}{\beta}} \Re \bigg((e^{i \Im \mathfrak{L}_t(\theta)}-e^{i \Im (\mathfrak{L}_t^o(\theta) + \mathfrak{L}_{T_-}^j(\theta_j) )}) d \mathfrak{W}_t^j \bigg) \\ &= \sqrt{\tfrac{4}{\beta}} \bigg( \Re ( e^{i \Im \mathfrak{L}_t(\theta)} d \mathfrak{W}_t^j ) (1-\cos \Delta_t) - \Im ( e^{i \Im \mathfrak{L}_t(\theta)} d \mathfrak{W}_t^j ) \sin \Delta_t \bigg) \\ &= d\mathfrak{U}_t (1-\cos \Delta_t) - d\mathfrak{B}_t \sin \Delta_t \\ &= dt \sqrt{\tfrac{8}{\beta}} (1-\cos \Delta_t) + d\mathfrak{X}_t (1-\cos \Delta_t) - d\mathfrak{B}_t \sin \Delta_t. \end{aligned} \end{align*} $$
The
![]() ${\mathbb Q}$
-probability of the event that
${\mathbb Q}$
-probability of the event that
![]() $|\Delta _t| \leq e^{-0.51(\log k_1)^{19/20} - \epsilon (t-T_-)}$
for all
$|\Delta _t| \leq e^{-0.51(\log k_1)^{19/20} - \epsilon (t-T_-)}$
for all
![]() $t \in [T_-,T_+]$
is
$t \in [T_-,T_+]$
is
![]() $1-e^{-\delta (\log k_1)^{19/20}}$
for some
$1-e^{-\delta (\log k_1)^{19/20}}$
for some
![]() $\delta ,\epsilon> 0$
and all
$\delta ,\epsilon> 0$
and all
![]() $k_1$
sufficiently large. On that event, both the drift and the quadratic variation of the martingale part of
$k_1$
sufficiently large. On that event, both the drift and the quadratic variation of the martingale part of
![]() $\Delta _t^r$
are bounded by
$\Delta _t^r$
are bounded by
![]() $O( e^{- 1.01(\log k_1)^{19/20}})$
for all
$O( e^{- 1.01(\log k_1)^{19/20}})$
for all
![]() $k_1$
sufficiently large. Thus, the probability that this reaches
$k_1$
sufficiently large. Thus, the probability that this reaches
![]() $e^{-0.5(\log k_1)^{19/20}}$
has the claimed probability.
$e^{-0.5(\log k_1)^{19/20}}$
has the claimed probability.
Step 5: The imaginary case.
We now have
and we let
which again is an independent Brownian motion. The difference
![]() $\Delta _t$
satisfies the SDE (see the first two lines of (6.1))
$\Delta _t$
satisfies the SDE (see the first two lines of (6.1))
Step 1 and 2 proceed in exactly the same way. For step 3, after the change of measure, we have the SDE for
![]() $t \geq T_\dagger $
,
$t \geq T_\dagger $
,
In the case
![]() $\sigma =i$
, the drift is positive but weak (as it is quadratic in
$\sigma =i$
, the drift is positive but weak (as it is quadratic in
![]() $\Delta _t$
). In particular, before
$\Delta _t$
). In particular, before
![]() $\tau ,$
we can dominate the solution by
$\tau ,$
we can dominate the solution by
The proof now continues the same way as in the real case.
7 Calculus estimates for the Prüfer phases
Lemma 7.1. Let
![]() $\lambda _1,\lambda _2 \in \mathbb {C}$
and let
$\lambda _1,\lambda _2 \in \mathbb {C}$
and let
![]() $\alpha ,\Gamma \in {\mathbb R}$
with
$\alpha ,\Gamma \in {\mathbb R}$
with
![]() $\Gamma> 1$
be fixed real numbers, and define, for
$\Gamma> 1$
be fixed real numbers, and define, for
![]() $z=x+iy$
with
$z=x+iy$
with
![]() $x,y \in \mathbb {R},$
$x,y \in \mathbb {R},$
 $$\begin{align*}\begin{aligned} &F(x,y)=F(z) = \Re\left\{ \lambda_1\log(1-u(z)e^{i\alpha}) - \lambda_1\log(1-u(z)) +\lambda_2\log(1-u(z)) \right\}, \\ &\text{where} \quad u=u(z) = \frac{z}{\sqrt{ |z|^2 + \Gamma}}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &F(x,y)=F(z) = \Re\left\{ \lambda_1\log(1-u(z)e^{i\alpha}) - \lambda_1\log(1-u(z)) +\lambda_2\log(1-u(z)) \right\}, \\ &\text{where} \quad u=u(z) = \frac{z}{\sqrt{ |z|^2 + \Gamma}}. \end{aligned} \end{align*}$$
Then, there is an absolute constant
![]() $C> 0$
so that for
$C> 0$
so that for
![]() $x^2+y^2 = r^2 \leq \Gamma /2$
,
$x^2+y^2 = r^2 \leq \Gamma /2$
,

Proof. We begin by computing the partial of F with respect to
![]() $u,$
giving
$u,$
giving
 $$ \begin{align} \frac{d}{du}F = - \Re\left\{ \lambda_1\frac{e^{i\alpha}-1}{(1-ue^{i\alpha})(1-u)} +\lambda_2\frac{1}{1-u} \right\}. \end{align} $$
$$ \begin{align} \frac{d}{du}F = - \Re\left\{ \lambda_1\frac{e^{i\alpha}-1}{(1-ue^{i\alpha})(1-u)} +\lambda_2\frac{1}{1-u} \right\}. \end{align} $$
Further,

We have that ![]() is nearly real, as is
is nearly real, as is ![]() nearly imaginary, when x and y are much smaller than
nearly imaginary, when x and y are much smaller than
![]() $\Gamma :$
$\Gamma :$
As for the principal terms, using
![]() $r^2 \leq \Gamma ,$
$r^2 \leq \Gamma ,$

Likewise,
Hence, using
![]() $|u(x+iy)| \leq r\Gamma ^{-1/2} \leq \frac {1}{\sqrt {2}}$
, we conclude (7.1) for an absolute constant
$|u(x+iy)| \leq r\Gamma ^{-1/2} \leq \frac {1}{\sqrt {2}}$
, we conclude (7.1) for an absolute constant
![]() $C>0$
by combining the previous displays.
$C>0$
by combining the previous displays.
By a similar second order expansion, we arrive at the following:
Lemma 7.2. Let
![]() $\lambda _1,\lambda _2 \in \mathbb {C}$
, let
$\lambda _1,\lambda _2 \in \mathbb {C}$
, let
![]() $\alpha ,\Gamma \in {\mathbb R}$
with
$\alpha ,\Gamma \in {\mathbb R}$
with
![]() $\Gamma> 1$
and let F be as in Lemma 7.1. Then there is an absolute constant
$\Gamma> 1$
and let F be as in Lemma 7.1. Then there is an absolute constant
![]() $C> 0$
so that for
$C> 0$
so that for
![]() $x^2+y^2 = r^2 \leq \Gamma /2$
,
$x^2+y^2 = r^2 \leq \Gamma /2$
,
 $$\begin{align*} & \left| F(x+iy) + \Re\left\{ (\lambda_1(e^{i\alpha}-1) + \lambda_2) \frac{x+iy}{\Gamma^{1/2}} + (\lambda_1(e^{2i\alpha}-1) + \lambda_2) \frac{(x+iy)^2}{2\Gamma} \right\} \right| \\ &\quad \leq \frac{C(|\lambda_1(e^{i\alpha}-1)| + |\lambda_2|)r^3}{\Gamma^{3/2}}. \end{align*}$$
$$\begin{align*} & \left| F(x+iy) + \Re\left\{ (\lambda_1(e^{i\alpha}-1) + \lambda_2) \frac{x+iy}{\Gamma^{1/2}} + (\lambda_1(e^{2i\alpha}-1) + \lambda_2) \frac{(x+iy)^2}{2\Gamma} \right\} \right| \\ &\quad \leq \frac{C(|\lambda_1(e^{i\alpha}-1)| + |\lambda_2|)r^3}{\Gamma^{3/2}}. \end{align*}$$
Proof. Differentiating (7.2) and composing with
![]() $u(x+iy)$
and its derivatives, the claimed bound is easily checked.
$u(x+iy)$
and its derivatives, the claimed bound is easily checked.
8 Polynomial interpolation
We will use some results for the a priori stability of polynomials. The first of these is a classical inequality due to Bernstein:
Theorem 8.1. For any polynomial Q of degree
![]() $k \geq 1,$
$k \geq 1,$
See [Reference Rahman and SchmeisserRS02, Chapter 14].
We also need a quantitative interpolation result for polynomials of a given degree. The following is in some sense a generalization of [Reference Chhaibi, Madaule and NajnudelCMN18, Lemma 4.3]. Related inequalities have been published before; see especially [Reference Rakhmanov and ShekhtmanRS06] and [Reference Frappier, Rahman and RuscheweyhFRR85, Theorem 8].
Theorem 8.2. For any polynomial Q of degree
![]() $k \geq 1,$
and any natural number
$k \geq 1,$
and any natural number
![]() $m \geq 2,$
$m \geq 2,$
Furthermore, if for any
![]() $b> 0$
we partition the
$b> 0$
we partition the
![]() $(2mk)$
-th roots of unity into
$(2mk)$
-th roots of unity into
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {F}$
so that
$\mathcal {F}$
so that
![]() $\mathcal {N}$
are all those roots of unity
$\mathcal {N}$
are all those roots of unity
![]() $\omega $
so that
$\omega $
so that
![]() $|\omega -1| \leq \frac {2b}{k},$
then there is an absolute constant
$|\omega -1| \leq \frac {2b}{k},$
then there is an absolute constant
![]() $C>0$
so that
$C>0$
so that
 $$\begin{align*}\begin{aligned} &\max_{\substack{|z-1|\leq \frac{b}{k},\\ |z|=1}} |Q(z)|^2 \leq \frac{m}{m-1}\cdot \max_{\omega \in \mathcal{N}} |Q(\omega)|^2 + \frac{C}{b(m-1)}\cdot\max_{\omega \in \mathcal{F}} |Q(\omega)|^2 \quad\text{and}\\ &\min_{\substack{|z-1|\leq \frac{b}{k}, \\ |z|=1}} |Q(z)|^2 \geq \frac{m}{m-1}\cdot \min_{\omega \in \mathcal{N}} |Q(\omega)|^2 - \bigg(1+\frac{C}{b}\bigg)\frac{1}{(m-1)}\cdot\max_{\omega : \omega^{2mk}=1} |Q(\omega)|^2. \\ \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\max_{\substack{|z-1|\leq \frac{b}{k},\\ |z|=1}} |Q(z)|^2 \leq \frac{m}{m-1}\cdot \max_{\omega \in \mathcal{N}} |Q(\omega)|^2 + \frac{C}{b(m-1)}\cdot\max_{\omega \in \mathcal{F}} |Q(\omega)|^2 \quad\text{and}\\ &\min_{\substack{|z-1|\leq \frac{b}{k}, \\ |z|=1}} |Q(z)|^2 \geq \frac{m}{m-1}\cdot \min_{\omega \in \mathcal{N}} |Q(\omega)|^2 - \bigg(1+\frac{C}{b}\bigg)\frac{1}{(m-1)}\cdot\max_{\omega : \omega^{2mk}=1} |Q(\omega)|^2. \\ \end{aligned} \end{align*}$$
We give a proof of this fact. For any
![]() $m \in {\mathbb N}$
, let
$m \in {\mathbb N}$
, let
![]() $F_m$
be the Fejér kernel, which for
$F_m$
be the Fejér kernel, which for
![]() $|z|=1$
has the representation
$|z|=1$
has the representation
 $$ \begin{align} F_m(z) =\frac{1}{m}\sum_{r=0}^{m-1}\sum_{s=-r}^r z^s =\frac{1}{m} \bigg[\sum_{s=0}^{m-1} z^s \bigg] \bigg[\sum_{s=0}^{m-1} z^{-s} \bigg] =\frac{1}{m}\frac{|1-z^m|^2}{|1-z|^2}. \end{align} $$
$$ \begin{align} F_m(z) =\frac{1}{m}\sum_{r=0}^{m-1}\sum_{s=-r}^r z^s =\frac{1}{m} \bigg[\sum_{s=0}^{m-1} z^s \bigg] \bigg[\sum_{s=0}^{m-1} z^{-s} \bigg] =\frac{1}{m}\frac{|1-z^m|^2}{|1-z|^2}. \end{align} $$
We will need the following identity. In what follows, we use the shorthand notation ![]() .
.
Lemma 8.3. For all
![]() $m,r \in {\mathbb N}$
and all
$m,r \in {\mathbb N}$
and all
![]() $t \in {\mathbb R},$
$t \in {\mathbb R},$
 $$\begin{align*}\sum_{j=1}^{rm} F_{m}(e(t+j/(rm)) =rm. \end{align*}$$
$$\begin{align*}\sum_{j=1}^{rm} F_{m}(e(t+j/(rm)) =rm. \end{align*}$$
See [Reference HofbauerHof02] for a discussion of this. We give a proof below:
Proof. Observe that using (8.1), we can write

We use the well-known identity that for any ![]() ,
,

By continuity, it suffices to establish the identity for irrational
![]() $t.$
We have, by grouping the terms in the sum over j according to their residue class
$t.$
We have, by grouping the terms in the sum over j according to their residue class
![]() $\ell $
modulo r,
$\ell $
modulo r,

In the penultimate display, we have extracted a factor of m and again applied (8.2).
We can now give a proof of Theorem 8.2.
Proof. Define for any
![]() $m \in {\mathbb N}$
with
$m \in {\mathbb N}$
with
![]() $m> 1$
,
$m> 1$
,
Then, we can write
 $$\begin{align*}R(z) = \frac{1}{2mk} \sum_{s=-km}^{km} \lambda_s z^s, \end{align*}$$
$$\begin{align*}R(z) = \frac{1}{2mk} \sum_{s=-km}^{km} \lambda_s z^s, \end{align*}$$
where
![]() $\lambda _s = 1$
for
$\lambda _s = 1$
for
![]() $-k \leq s \leq k.$
In particular, for any
$-k \leq s \leq k.$
In particular, for any
![]() $0 \leq r < km$
,
$0 \leq r < km$
,
 $$\begin{align*}\sum_{ \omega:\omega^{2mk}=1} \omega^r R(z \bar{\omega}) = \frac{1}{2mk} \sum_{s=-km}^{km} \lambda_s z^s \cdot \bigg[ \sum_{ \omega:\omega^{2mk}=1} \omega^r \bar{\omega}^s \bigg] = \lambda_r z^r, \end{align*}$$
$$\begin{align*}\sum_{ \omega:\omega^{2mk}=1} \omega^r R(z \bar{\omega}) = \frac{1}{2mk} \sum_{s=-km}^{km} \lambda_s z^s \cdot \bigg[ \sum_{ \omega:\omega^{2mk}=1} \omega^r \bar{\omega}^s \bigg] = \lambda_r z^r, \end{align*}$$
and so it follows that for any polynomial
![]() $Q(z)$
of degree k and z on the unit circle,
$Q(z)$
of degree k and z on the unit circle,

where the first equality follows as
![]() $|Q(z)|^2$
for
$|Q(z)|^2$
for
![]() $|z|=1$
can be represented as a Laurent polynomial with Fourier support contained in
$|z|=1$
can be represented as a Laurent polynomial with Fourier support contained in
![]() $[-k,k]$
, and the inequality follows from the positivity of the Fejér kernel.
$[-k,k]$
, and the inequality follows from the positivity of the Fejér kernel.
Using Lemma 8.3, we have
 $$\begin{align*}\sum_{ \omega:\omega^{2mk} = 1} \frac{F_{km}(z \bar \omega)}{2k(m-1)} =\frac{m}{m-1}, \end{align*}$$
$$\begin{align*}\sum_{ \omega:\omega^{2mk} = 1} \frac{F_{km}(z \bar \omega)}{2k(m-1)} =\frac{m}{m-1}, \end{align*}$$
and hence, for all
![]() $|z|=1,$
$|z|=1,$
If we further partition the roots of unity into
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {F}$
as in the statement of the theorem, we can bound
$\mathcal {F}$
as in the statement of the theorem, we can bound
![]() $X(z)$
using (8.1) by
$X(z)$
using (8.1) by
 $$\begin{align*}X(z) \leq \frac{m}{m-1}\cdot \max_{\omega \in \mathcal{N}}|Q(\omega)|^2 + \max_{\omega \in \mathcal{F}}|Q(\omega)|^2 \cdot \sum_{\omega \in \mathcal{F}} \frac{2}{km(m-1)|1-z\bar{\omega}|^2}. \end{align*}$$
$$\begin{align*}X(z) \leq \frac{m}{m-1}\cdot \max_{\omega \in \mathcal{N}}|Q(\omega)|^2 + \max_{\omega \in \mathcal{F}}|Q(\omega)|^2 \cdot \sum_{\omega \in \mathcal{F}} \frac{2}{km(m-1)|1-z\bar{\omega}|^2}. \end{align*}$$
If z satisfies that
![]() $|z-1| \leq \frac {b}{k},$
then
$|z-1| \leq \frac {b}{k},$
then
![]() $|\omega - z| \geq \frac {b}{k}$
, and there is therefore an absolute constant
$|\omega - z| \geq \frac {b}{k}$
, and there is therefore an absolute constant
![]() $C> 0$
so that
$C> 0$
so that
 $$ \begin{align} \sum_{\omega \in \mathcal{F}} \frac{2}{km(m-1)|1-z\bar{\omega}|^2} \leq \frac{C}{b(m-1)}, \end{align} $$
$$ \begin{align} \sum_{\omega \in \mathcal{F}} \frac{2}{km(m-1)|1-z\bar{\omega}|^2} \leq \frac{C}{b(m-1)}, \end{align} $$
which completes the proof of the upper bound.
For the lower bound, starting from (8.3),
 $$\begin{align*}\begin{aligned} |Q(z)|^2 &= \sum_{ \omega:\omega^{2mk} = 1} |Q(\omega)|^2 R(z \bar{\omega}) \\ &\geq \sum_{ \omega:\omega^{2mk} = 1} |Q(\omega)|^2 \frac{F_{km}(z\bar{\omega})}{2k(m-1)} - \max_{\omega:\omega^{2mk}=1} |Q(\omega)|^2 \cdot \sum_{ \omega:\omega^{2mk} = 1} \frac{F_{k}(z\bar{\omega})}{2mk(m-1)}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} |Q(z)|^2 &= \sum_{ \omega:\omega^{2mk} = 1} |Q(\omega)|^2 R(z \bar{\omega}) \\ &\geq \sum_{ \omega:\omega^{2mk} = 1} |Q(\omega)|^2 \frac{F_{km}(z\bar{\omega})}{2k(m-1)} - \max_{\omega:\omega^{2mk}=1} |Q(\omega)|^2 \cdot \sum_{ \omega:\omega^{2mk} = 1} \frac{F_{k}(z\bar{\omega})}{2mk(m-1)}. \end{aligned} \end{align*}$$
Using Lemma 8.3, we conclude
Furthermore,
 $$\begin{align*}X(z) \geq \min_{\omega \in \mathcal{N}} |Q(\omega)|^2 \cdot \sum_{\omega \in \mathcal{N}} \frac{F_{km}(z\bar{\omega})}{2k(m-1)} \geq \min_{\omega \in \mathcal{N}} |Q(\omega)|^2 \bigg(\frac{m}{m-1} - \frac{C}{b(m-1)}\bigg), \end{align*}$$
$$\begin{align*}X(z) \geq \min_{\omega \in \mathcal{N}} |Q(\omega)|^2 \cdot \sum_{\omega \in \mathcal{N}} \frac{F_{km}(z\bar{\omega})}{2k(m-1)} \geq \min_{\omega \in \mathcal{N}} |Q(\omega)|^2 \bigg(\frac{m}{m-1} - \frac{C}{b(m-1)}\bigg), \end{align*}$$
using (8.4).
9 Convergence of the derivative martingale
We recall from (1.10)
for
![]() $\sigma \in \left \{ 1, i \right \}.$
$\sigma \in \left \{ 1, i \right \}.$
We also recall (from (2.1)) that
![]() $\gamma _j$
are independent, rotationally invariant in law, and have
$\gamma _j$
are independent, rotationally invariant in law, and have
![]() $|\gamma _j|^2$
distributed as
$|\gamma _j|^2$
distributed as
![]() $\operatorname {Beta}(1, \beta _j)$
, where
$\operatorname {Beta}(1, \beta _j)$
, where
![]() $\beta _j^2 = \tfrac {\beta }{2}(j+1)$
. Hence, we have an explicit expression for the moment generating functions of
$\beta _j^2 = \tfrac {\beta }{2}(j+1)$
. Hence, we have an explicit expression for the moment generating functions of
![]() $\varphi ,$
given by (see [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 2.5] or [Reference Bourgade, Hughes, Nikeghbali and YorBHNY08, Lemma 2.3]).
$\varphi ,$
given by (see [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 2.5] or [Reference Bourgade, Hughes, Nikeghbali and YorBHNY08, Lemma 2.3]).
Lemma 9.1. For any
![]() $s,t \in {\mathbb C}$
with
$s,t \in {\mathbb C}$
with
![]() $\Re s \geq -1$
,
$\Re s \geq -1$
,
 $$\begin{align*}\mathbb{E}[ e^{s \Re( \log(1-\gamma_j))+ t \Im( \log(1-\gamma_j))}] = \frac{\Gamma(1+\beta_j^2)\Gamma(1+s+\beta_j^2)}{\Gamma(1+\beta_j^2 + (s+it)/2)\Gamma(1+\beta_j^2 + (s-it)/2)}. \end{align*}$$
$$\begin{align*}\mathbb{E}[ e^{s \Re( \log(1-\gamma_j))+ t \Im( \log(1-\gamma_j))}] = \frac{\Gamma(1+\beta_j^2)\Gamma(1+s+\beta_j^2)}{\Gamma(1+\beta_j^2 + (s+it)/2)\Gamma(1+\beta_j^2 + (s-it)/2)}. \end{align*}$$
For
![]() $s \geq 0$
and
$s \geq 0$
and
![]() $t \in {\mathbb R},$
$t \in {\mathbb R},$
 $$\begin{align*}\mathbb{E}[ e^{s \Re( \log(1-\gamma_j))+ t \Im( \log(1-\gamma_j))}] \leq \exp\left( \frac{s^2+t^2}{2}\frac{1}{1+\beta(j+1)} \right). \end{align*}$$
$$\begin{align*}\mathbb{E}[ e^{s \Re( \log(1-\gamma_j))+ t \Im( \log(1-\gamma_j))}] \leq \exp\left( \frac{s^2+t^2}{2}\frac{1}{1+\beta(j+1)} \right). \end{align*}$$
We define for any
![]() $j\in {\mathbb N}$
and any
$j\in {\mathbb N}$
and any ![]() Define
Define
which is a martingale. Set ![]() and define
and define

which is also a martingale. Define

We need an elementary computation of the asymptotic behavior of the sums of
![]() $H_k.$
$H_k.$
Lemma 9.2. The following limits exist and are finite:
 $$\begin{align*}\lim_{j\to \infty} \sum_{k=1}^j H_k(s_\beta) -\log j = \mathfrak{g}_\beta, \quad \text{and} \quad \lim_{j\to \infty} \sum_{k=1}^j H_k'(s_\beta) - \sqrt{\frac{8}{\beta}}\log j = \mathfrak{h}_\beta. \end{align*}$$
$$\begin{align*}\lim_{j\to \infty} \sum_{k=1}^j H_k(s_\beta) -\log j = \mathfrak{g}_\beta, \quad \text{and} \quad \lim_{j\to \infty} \sum_{k=1}^j H_k'(s_\beta) - \sqrt{\frac{8}{\beta}}\log j = \mathfrak{h}_\beta. \end{align*}$$
Proof. We recall the ratio asymptotic for the
![]() $\Gamma $
function (see [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClainOOL+
, 5.11])
$\Gamma $
function (see [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClainOOL+
, 5.11])
 $$\begin{align*}\frac{\Gamma(\beta_k^2 + x)} {\Gamma(\beta_k^2+y)} =\beta_k^{2(x-y)}\left( 1+ \frac{\tfrac12(x-y)(x+y-1)}{\beta_k^2} + O(\beta_k^{-4}) \right). \end{align*}$$
$$\begin{align*}\frac{\Gamma(\beta_k^2 + x)} {\Gamma(\beta_k^2+y)} =\beta_k^{2(x-y)}\left( 1+ \frac{\tfrac12(x-y)(x+y-1)}{\beta_k^2} + O(\beta_k^{-4}) \right). \end{align*}$$
Then, for any
![]() $s,t \in {\mathbb C},$
$s,t \in {\mathbb C},$
 $$\begin{align*}\mathbb{E}[ e^{s \Re( \log(1-\gamma_k))+ t \Im( \log(1-\gamma_k))}] = 1 + \frac{s^2+t^2}{4\beta_k^2} + O(\beta_k^{-4}), \end{align*}$$
$$\begin{align*}\mathbb{E}[ e^{s \Re( \log(1-\gamma_k))+ t \Im( \log(1-\gamma_k))}] = 1 + \frac{s^2+t^2}{4\beta_k^2} + O(\beta_k^{-4}), \end{align*}$$
and the asymptotic can be differentiated on both sides with respect to s and t as well. Thus,
 $$\begin{align*}H_k(s) = \frac{s^2}{\beta_k^2} + O(\beta_k^{-4}). \end{align*}$$
$$\begin{align*}H_k(s) = \frac{s^2}{\beta_k^2} + O(\beta_k^{-4}). \end{align*}$$
For
![]() $H_k(s_\beta )$
, we therefore have
$H_k(s_\beta )$
, we therefore have
which leads directly to the claimed asymptotic. For the derivative, we have that
 $$\begin{align*}H_k'(s_\beta) = \frac{2s_\beta}{\beta_k^2} + O(\beta_{k}^{-4}) = \sqrt{\frac{8}{\beta}} \frac{1}{k+1}+ O(\beta_{k}^{-4}). \end{align*}$$
$$\begin{align*}H_k'(s_\beta) = \frac{2s_\beta}{\beta_k^2} + O(\beta_{k}^{-4}) = \sqrt{\frac{8}{\beta}} \frac{1}{k+1}+ O(\beta_{k}^{-4}). \end{align*}$$
We observe that the field
![]() $\{\sqrt {\frac {8}{\beta }}\log j - \varphi _j(\theta )\}$
is rarely very negative and is, in fact, almost surely positive for all j sufficiently large (but random).
$\{\sqrt {\frac {8}{\beta }}\log j - \varphi _j(\theta )\}$
is rarely very negative and is, in fact, almost surely positive for all j sufficiently large (but random).
Lemma 9.3.

Proof. We use Proposition [Reference Chhaibi, Madaule and NajnudelCMN18, Propositions 3.1, 4.5], due to which

Using [Reference Chhaibi, Madaule and NajnudelCMN18, (4.6) and the display following with
![]() $C=t$
] for any j and any
$C=t$
] for any j and any
![]() $t \geq 1$
(we take
$t \geq 1$
(we take
![]() $t = (\tfrac 12+\epsilon )\log \log j$
),
$t = (\tfrac 12+\epsilon )\log \log j$
),
for some constant
![]() $C_\beta>0.$
By Borel–Cantelli applied to the sequence
$C_\beta>0.$
By Borel–Cantelli applied to the sequence
![]() $j \in 2^{\mathbb N},$
we have for any
$j \in 2^{\mathbb N},$
we have for any
![]() $\epsilon> 0$
and for all such
$\epsilon> 0$
and for all such
![]() $j\in 2^{\mathbb N}$
sufficiently large,
$j\in 2^{\mathbb N}$
sufficiently large,
With the control provided by the proof of Lemma 9.3 and Lemma 2.4, we may work on an event
![]() $\mathcal {E}_\kappa $
$\mathcal {E}_\kappa $

On the event
![]() $\mathcal {E}_\kappa $
, we can use Girsanov and the ballot theorem for the Gaussian random walk
$\mathcal {E}_\kappa $
, we can use Girsanov and the ballot theorem for the Gaussian random walk
![]() $j \mapsto G_j(\theta )$
to conclude for any
$j \mapsto G_j(\theta )$
to conclude for any
![]() $\delta>0$
any
$\delta>0$
any ![]()
 $$ \begin{align} \mathbb{P}[ \mathcal{E}_\kappa, \log j + \kappa - \sqrt{\tfrac{\beta}{8}} \varphi_j \in [{k-1},k] ] \leq \begin{cases} \frac{C_{\beta,\kappa,\delta}k}{(\log j)^{3/2}}{\exp\left( -\frac{(\log j - k)^2}{\log j} \right)}, & k \leq (1-\delta)\log j, \\ \frac{C_{\beta,\kappa,\delta}}{(\log j)^{1/2}}{\exp\left( -\frac{(\log j - k)^2}{\log j} \right)}, & k> (1-\delta)\log j. \end{cases} \end{align} $$
$$ \begin{align} \mathbb{P}[ \mathcal{E}_\kappa, \log j + \kappa - \sqrt{\tfrac{\beta}{8}} \varphi_j \in [{k-1},k] ] \leq \begin{cases} \frac{C_{\beta,\kappa,\delta}k}{(\log j)^{3/2}}{\exp\left( -\frac{(\log j - k)^2}{\log j} \right)}, & k \leq (1-\delta)\log j, \\ \frac{C_{\beta,\kappa,\delta}}{(\log j)^{1/2}}{\exp\left( -\frac{(\log j - k)^2}{\log j} \right)}, & k> (1-\delta)\log j. \end{cases} \end{align} $$
We begin with the observation that the improperly normalized mass tends almost surely to
![]() $0$
at the critical
$0$
at the critical
![]() $s=s_\beta .$
$s=s_\beta .$
Lemma 9.4. For any
![]() $\sigma \in \left \{ 1, i \right \}$
and any
$\sigma \in \left \{ 1, i \right \}$
and any
![]() $\beta> 0,$
$\beta> 0,$

Furthermore, {Z
j
logj: j ∈ ℕ} is tight, and for any
![]() $\epsilon> 0,$
there is a compact
$\epsilon> 0,$
there is a compact
![]() $K\subset (0,\infty )$
so that if
$K\subset (0,\infty )$
so that if

then for any
![]() $j \in {\mathbb N}$
,
$j \in {\mathbb N}$
,

Proof. The process
![]() $Z_j$
is a positive martingale, and so it converges almost surely. After establishing the claimed tightness, it follows that
$Z_j$
is a positive martingale, and so it converges almost surely. After establishing the claimed tightness, it follows that ![]() Hence, along some subsequence, it converges almost surely to
Hence, along some subsequence, it converges almost surely to
![]() $0.$
The almost sure convergence of
$0.$
The almost sure convergence of
![]() $Z_j$
then completes the proof of the first point.
$Z_j$
then completes the proof of the first point.
The remaining statements now follow by taking expectations of
![]() $Z_j$
on the event
$Z_j$
on the event
![]() $\mathcal {E}_\kappa .$
In particular, using (9.3), we have (with
$\mathcal {E}_\kappa .$
In particular, using (9.3), we have (with
![]() $\log j - \sqrt {\tfrac {8}{\beta }} \varphi _j = {u}{\sqrt {\log j}}$
) and
$\log j - \sqrt {\tfrac {8}{\beta }} \varphi _j = {u}{\sqrt {\log j}}$
) and
![]() $t=(1-\delta )\sqrt {\log j}$
$t=(1-\delta )\sqrt {\log j}$

This simplifies to

In particular, we conclude that

is tight, and as
![]() $\cup _{\kappa \in {\mathbb N}} \mathcal {E}_\kappa $
has probability
$\cup _{\kappa \in {\mathbb N}} \mathcal {E}_\kappa $
has probability
![]() $1$
, the tightness without the indicator holds.
$1$
, the tightness without the indicator holds.
Essentially, the same computation shows the claimed estimates for the final display of the lemma. With
![]() $K = [\eta /2, 2\eta ^{-1}],$
for all j sufficiently large,
$K = [\eta /2, 2\eta ^{-1}],$
for all j sufficiently large,

This may be made as small as desired by picking
![]() $\eta $
small.
$\eta $
small.
We will use this convergence to compare
![]() $\widehat {\mathscr {B}}_j$
and
$\widehat {\mathscr {B}}_j$
and
![]() ${\mathscr {B}_j},$
and
${\mathscr {B}_j},$
and
![]() $\widehat {\mathscr {D}}_j$
and
$\widehat {\mathscr {D}}_j$
and
![]() ${\mathscr {D}_j}$
. Before doing this comparison, we will show the convergence of
${\mathscr {D}_j}$
. Before doing this comparison, we will show the convergence of
![]() $\widehat {\mathscr {B}}_j$
and of
$\widehat {\mathscr {B}}_j$
and of
![]() $\int \widehat {\mathscr {D}}_j (\theta ) f(\theta ) d\theta $
for positive bounded test functions f. Similar ideas appear in [Reference Duplantier, Rhodes, Sheffield and VargasDRSV14].
$\int \widehat {\mathscr {D}}_j (\theta ) f(\theta ) d\theta $
for positive bounded test functions f. Similar ideas appear in [Reference Duplantier, Rhodes, Sheffield and VargasDRSV14].
Lemma 9.5. There is an almost surely nonnegative finite random variable
![]() $\widehat {\mathscr {B}}_\infty $
and nonnegative measure
$\widehat {\mathscr {B}}_\infty $
and nonnegative measure
![]() $\widehat {\mathscr {D}}_\infty $
so that for any bounded positive deterministic test function f,
$\widehat {\mathscr {D}}_\infty $
so that for any bounded positive deterministic test function f,

Proof. Define the positive and negative parts

and define

Define
We will show
![]() $\sum _{\ell =1}^\infty Y_{2^\ell } < \infty $
almost surely. Having done so, the lemma will follow, as we now explain. Observe
$\sum _{\ell =1}^\infty Y_{2^\ell } < \infty $
almost surely. Having done so, the lemma will follow, as we now explain. Observe
It follows that both ![]() are supermartingales with respect to the filtration
are supermartingales with respect to the filtration
![]() $(\mathscr {F}_{2^\ell } : \ell \in {\mathbb N})$
. Letting
$(\mathscr {F}_{2^\ell } : \ell \in {\mathbb N})$
. Letting
![]() $\tau $
be the stopping time that
$\tau $
be the stopping time that
![]() $\ell \mapsto \sum _{k=1}^{\ell } Y_{2^k}$
exceeds
$\ell \mapsto \sum _{k=1}^{\ell } Y_{2^k}$
exceeds
![]() $R,$
then
$R,$
then ![]() is a supermartingale bounded below by
is a supermartingale bounded below by
![]() $-R$
(by predictability) which converges almost surely. As this holds for any
$-R$
(by predictability) which converges almost surely. As this holds for any
![]() $R \in {\mathbb N}$
, it follows that
$R \in {\mathbb N}$
, it follows that ![]() converges almost surely. As the sum of
converges almost surely. As the sum of
![]() $Y_{2^k}$
converges almost surely as well,
$Y_{2^k}$
converges almost surely as well, ![]() converges almost surely. Hence, so does their difference.
converges almost surely. Hence, so does their difference.
Remark 9.6. From Lemma 9.3, it follows that, in fact,
![]() $\widehat {\mathscr {B}}_{j}^{-}$
is eventually
$\widehat {\mathscr {B}}_{j}^{-}$
is eventually
![]() $0$
for all j sufficiently large, almost surely.
$0$
for all j sufficiently large, almost surely.
The statement concerning ![]() follows similarly: instead of (9.4), use that
follows similarly: instead of (9.4), use that

and the rest follows as in the treatment of
![]() $\widehat {\mathscr {B}}_{2^\ell }$
.
$\widehat {\mathscr {B}}_{2^\ell }$
.
So, it remains to show
![]() $\sum _{j=1}^\infty Y_{2^j} < \infty $
almost surely. There is a
$\sum _{j=1}^\infty Y_{2^j} < \infty $
almost surely. There is a
![]() $C_\beta $
so that for all j sufficiently large,
$C_\beta $
so that for all j sufficiently large,

The increment
![]() $\sqrt {\beta /2}\bigl (\varphi _{2^{j+1}}(\theta )-\varphi _{2^{j}}(\theta )\bigr )$
is uniformly subgaussian over all j (from Lemma 9.1). Hence, on the event
$\sqrt {\beta /2}\bigl (\varphi _{2^{j+1}}(\theta )-\varphi _{2^{j}}(\theta )\bigr )$
is uniformly subgaussian over all j (from Lemma 9.1). Hence, on the event
![]() $\mathcal {E}_\kappa ,$
the restriction that
$\mathcal {E}_\kappa ,$
the restriction that
implies that there is a constant
![]() $c_{\beta ,\kappa }> 0$
so that for all
$c_{\beta ,\kappa }> 0$
so that for all
![]() $j \in {\mathbb N}$
,
$j \in {\mathbb N}$
,
 $$\begin{align*}\mathbb{E}\left[ e^{ \sqrt{\beta/2}\left( \varphi_{2^{j+1}}(\theta)-\varphi_{2^{j}}(\theta)\right) -\log 2 } \bigl( \varphi_{2^{j+1}} - \sqrt{\tfrac{8}{\beta}}\log 2^{j+1} \bigr)_+ ~\vert~ \mathscr{F}_{2^{j}} \right] \leq e^{-c_{\beta,\kappa} (\log j)^2}. \end{align*}$$
$$\begin{align*}\mathbb{E}\left[ e^{ \sqrt{\beta/2}\left( \varphi_{2^{j+1}}(\theta)-\varphi_{2^{j}}(\theta)\right) -\log 2 } \bigl( \varphi_{2^{j+1}} - \sqrt{\tfrac{8}{\beta}}\log 2^{j+1} \bigr)_+ ~\vert~ \mathscr{F}_{2^{j}} \right] \leq e^{-c_{\beta,\kappa} (\log j)^2}. \end{align*}$$
Hence, we arrive at the conclusion that almost surely,

From Lemma 9.4, this is finite almost surely, which completes the proof as the
![]() $(\mathcal {E}_\kappa : \kappa \in {\mathbb N})$
exhaust the probability space.
$(\mathcal {E}_\kappa : \kappa \in {\mathbb N})$
exhaust the probability space.
We conclude with the proof of Theorem 1.6.
Proof of Theorem 1.6.
We begin by noting that
![]() $\widehat {\mathscr {D}}_j$
and
$\widehat {\mathscr {D}}_j$
and
![]() $\mathscr {D}_j$
are exactly related by the identity
$\mathscr {D}_j$
are exactly related by the identity
 $$\begin{align*}\sqrt{\tfrac{4}{\beta}} \mathscr{D}_j(\theta) e^{\log j - \sum_{k=1}^j H_k(s_\beta)} -\widehat{\mathscr{D}_j}(\theta) = \mathscr{M}_j(\theta,s_\beta) \bigg(\sum_{k=1}^j H_k'(s_\beta) - \sqrt{\tfrac{8}{\beta}} \log j\bigg). \end{align*}$$
$$\begin{align*}\sqrt{\tfrac{4}{\beta}} \mathscr{D}_j(\theta) e^{\log j - \sum_{k=1}^j H_k(s_\beta)} -\widehat{\mathscr{D}_j}(\theta) = \mathscr{M}_j(\theta,s_\beta) \bigg(\sum_{k=1}^j H_k'(s_\beta) - \sqrt{\tfrac{8}{\beta}} \log j\bigg). \end{align*}$$
Hence, integrating against a positive bounded test function f, from Lemma 9.2, Lemma 9.4 and Lemma 9.5,

It remains to prove the nonatomicity of
![]() $\widehat {\mathscr {D}}_\infty $
. Mimicking Lemma 9.4, with
$\widehat {\mathscr {D}}_\infty $
. Mimicking Lemma 9.4, with
![]() $\epsilon \in (0,1/3)$
, introduce the interval
$\epsilon \in (0,1/3)$
, introduce the interval
![]() $K_k=[k^{-\epsilon }, k^\epsilon ]$
and, for
$K_k=[k^{-\epsilon }, k^\epsilon ]$
and, for
![]() $j_0$
fixed, the function
$j_0$
fixed, the function

The same argument as in Lemma 9.4 shows that
 $$\begin{align*}\int \mathscr{M}_{2^j}(\theta,s_\beta) \bigg|\bigg( \varphi_{2^j}(\theta) - \sqrt{\tfrac{8}{\beta}} j\log 2\bigg)\bigg| (1-\widehat{\chi}_{j_0,j}(\theta)) d\theta\leq C \sum_{k=j_0}^j \frac{1}{k^{3\epsilon}}\leq \frac{C'}{j_0^{3\epsilon-1}}.\end{align*}$$
$$\begin{align*}\int \mathscr{M}_{2^j}(\theta,s_\beta) \bigg|\bigg( \varphi_{2^j}(\theta) - \sqrt{\tfrac{8}{\beta}} j\log 2\bigg)\bigg| (1-\widehat{\chi}_{j_0,j}(\theta)) d\theta\leq C \sum_{k=j_0}^j \frac{1}{k^{3\epsilon}}\leq \frac{C'}{j_0^{3\epsilon-1}}.\end{align*}$$
Taking
![]() $j_0$
large, it thus suffices to prove the nonatomicity of the limit of the positive measures
$j_0$
large, it thus suffices to prove the nonatomicity of the limit of the positive measures
 $\mathscr {M}_{2^j}(\theta ,s_\beta ) \bigg |\bigg (\varphi _{2^j}(\theta ) - \sqrt {\tfrac {8}{\beta }} j\log 2\bigg )\bigg | \widehat {\chi }_{j_0,j}(\theta ) d\theta $
for large fixed
$\mathscr {M}_{2^j}(\theta ,s_\beta ) \bigg |\bigg (\varphi _{2^j}(\theta ) - \sqrt {\tfrac {8}{\beta }} j\log 2\bigg )\bigg | \widehat {\chi }_{j_0,j}(\theta ) d\theta $
for large fixed
![]() $j_0$
. Toward this end, divide
$j_0$
. Toward this end, divide ![]() to intervals
to intervals
![]() $\Delta _i$
of length
$\Delta _i$
of length
![]() $\delta $
. Using Lemma 2.19, we can replace
$\delta $
. Using Lemma 2.19, we can replace
![]() $\varphi _{2^k}(\theta )-\varphi _{2^{j_0}}(\theta )$
by
$\varphi _{2^k}(\theta )-\varphi _{2^{j_0}}(\theta )$
by
![]() $Z_{2^k}^{2^{j_0}}(\theta )$
.
$Z_{2^k}^{2^{j_0}}(\theta )$
.
Let
 $A_{i,j}=\int _{\Delta _i} \mathscr {M}_{2^j}(\theta ,s_\beta ) \bigg |\bigg (\varphi _{2^j}(\theta ) - \sqrt {\tfrac {8}{\beta }} j\log 2\bigg )\bigg | \widehat {\chi }_{j_0,j}(\theta ) d\theta $
. Using Lemma B.2, we have that
$A_{i,j}=\int _{\Delta _i} \mathscr {M}_{2^j}(\theta ,s_\beta ) \bigg |\bigg (\varphi _{2^j}(\theta ) - \sqrt {\tfrac {8}{\beta }} j\log 2\bigg )\bigg | \widehat {\chi }_{j_0,j}(\theta ) d\theta $
. Using Lemma B.2, we have that
where
![]() $\max _i C_{i,j_0}<\infty $
is a random variable independent of
$\max _i C_{i,j_0}<\infty $
is a random variable independent of
![]() $\Delta $
or j. Using Lemmas B.4 and B.5 as in Proposition 2.20, we obtain that
$\Delta $
or j. Using Lemmas B.4 and B.5 as in Proposition 2.20, we obtain that
where
![]() $\max _i C_{i,j_0}'<\infty $
is a random variable independent of
$\max _i C_{i,j_0}'<\infty $
is a random variable independent of
![]() $\Delta $
or j. Hence, for any
$\Delta $
or j. Hence, for any
![]() $\delta>0$
, ℙ(A
i, j
> δ∣F
2
j
0
) ≤ max
i
C
i, j
0
′Δo(Δ)δ
2, and therefore,
$\delta>0$
, ℙ(A
i, j
> δ∣F
2
j
0
) ≤ max
i
C
i, j
0
′Δo(Δ)δ
2, and therefore,
 $$\begin{align*}\mathbb{P} (\exists i: A_{i,j}>\delta\mid \mathscr{F}_{2^{j_0}})\leq \frac{\max_i C_{i,j_0}' o(\Delta)}{\delta^2}.\end{align*}$$
$$\begin{align*}\mathbb{P} (\exists i: A_{i,j}>\delta\mid \mathscr{F}_{2^{j_0}})\leq \frac{\max_i C_{i,j_0}' o(\Delta)}{\delta^2}.\end{align*}$$
Since this is true uniformly in j, taking the limit as first
![]() $j\to \infty $
and then
$j\to \infty $
and then
![]() $\Delta \to 0$
gives the claim of nonatomiticity of
$\Delta \to 0$
gives the claim of nonatomiticity of
![]() $\widehat {\mathscr {D}}_\infty $
.
$\widehat {\mathscr {D}}_\infty $
.
10 Decoration process technical estimates
In this section, we collect other estimates about the decoration. In all, we need a relatively sharp upper estimate on a single ray of the decoration being high (that is sharp up to constants
![]() $c(k_4)$
). We also provide a weak upper estimate on two rays being high which is sharp up to a power of
$c(k_4)$
). We also provide a weak upper estimate on two rays being high which is sharp up to a power of
![]() $(\log k_1)$
.
$(\log k_1)$
.
We also need a few technical estimates of a different nature. Due to the technical nature of the two-ray estimates we produce up to level
![]() $n_1^+$
, we show a continuity estimate for the Markov kernel
$n_1^+$
, we show a continuity estimate for the Markov kernel
![]() $(x,df)\mapsto \mathfrak {s}(x,e^x df)$
in the parameter x. Finally, we show a mixing estimate of the decoration measure comparing
$(x,df)\mapsto \mathfrak {s}(x,e^x df)$
in the parameter x. Finally, we show a mixing estimate of the decoration measure comparing
![]() $\mathfrak {s}(x,e^{i\alpha +x} df)$
in the case of
$\mathfrak {s}(x,e^{i\alpha +x} df)$
in the case of
![]() $\sigma =1$
to the same with uniformly random
$\sigma =1$
to the same with uniformly random
![]() $\alpha $
.
$\alpha $
.
10.1 Moment estimates
The following are needed to produce estimates for
![]() $\mathfrak {s}$
. These concern the diffusions
$\mathfrak {s}$
. These concern the diffusions
![]() $\mathfrak {U}^{o,j}$
and the events
$\mathfrak {U}^{o,j}$
and the events
![]() $\mathscr {P}_j$
; see (2.53). As the estimates have no dependence on j, we suppress the j.
$\mathscr {P}_j$
; see (2.53). As the estimates have no dependence on j, we suppress the j.
Lemma 10.1. For some
![]() $0 < c(k_7,x) < c(k_7,\infty )$
which is a continuous function of
$0 < c(k_7,x) < c(k_7,\infty )$
which is a continuous function of
![]() $k_7$
,
$k_7$
,
 $$ \begin{align} \mathbb{P}\bigg( \bigl\{ \mathfrak{U}^o_{T_+}(\theta)-\sqrt{\tfrac{4}{\beta}}h \in [-k_7,x] \bigr\} \cap \mathscr{P}(\theta,h) ~\big\vert~\mathscr{F}_{n_1^+} \bigg) = (1+o_{k_4})\frac{c(k_7,x) h \sqrt{k_4}}{(T_+-T_-)^{3/2}} e^{-(T_+-T_-)} e^{-\sqrt{2}h -h^2/2(T_+-T_-)} , \end{align} $$
$$ \begin{align} \mathbb{P}\bigg( \bigl\{ \mathfrak{U}^o_{T_+}(\theta)-\sqrt{\tfrac{4}{\beta}}h \in [-k_7,x] \bigr\} \cap \mathscr{P}(\theta,h) ~\big\vert~\mathscr{F}_{n_1^+} \bigg) = (1+o_{k_4})\frac{c(k_7,x) h \sqrt{k_4}}{(T_+-T_-)^{3/2}} e^{-(T_+-T_-)} e^{-\sqrt{2}h -h^2/2(T_+-T_-)} , \end{align} $$
for all
Further, the upper bound in (10.1) holds for all
![]() $h \geq 0.$
Next, if
$h \geq 0.$
Next, if
![]() $\theta _1,\theta _2$
are such that
$\theta _1,\theta _2$
are such that
![]() $|\theta _1|,|\theta _2| \leq 3n^{8\delta }$
and
$|\theta _1|,|\theta _2| \leq 3n^{8\delta }$
and
![]() $h_1,h_2$
are as in (10.2), then, for some
$h_1,h_2$
are as in (10.2), then, for some
![]() $c(k_7)>0$
, with
$c(k_7)>0$
, with
![]() $|\theta _1-\theta _2|e^{T_*}=k_1$
and
$|\theta _1-\theta _2|e^{T_*}=k_1$
and
![]() $h=(h_1\vee h_2)$
,
$h=(h_1\vee h_2)$
,
 $$ \begin{align} &\mathbb{P}\bigg( \bigcap_{i\in \{1,2\}} \bigl\{ \mathfrak{U}^o_{T_+}(\theta_i) -\sqrt{\tfrac{4}{\beta}}h_i \in [-k_7,\infty) \bigr\} \cap \mathscr{P}(\theta_i,h_i) ~\big\vert~\mathscr{F}_{n_1^+} \bigg) \\ &\leq\! \begin{cases} c(k_7)h\frac{(T_+-T_*)\wedge (T_*-T_-)}{(T_*-T_-+1)^{3/2}}\exp\bigg(\! -S(T_-,T_+,h)\!-\! \Big(T_+-T_*+(T_+-T_*)^{1/14}\Big)\! -\!{h^2/2(T_+-T_-)} \bigg), &\\ \qquad\qquad\qquad\qquad\qquad\qquad \qquad\qquad\qquad\qquad\qquad\qquad \text{if } e^{k_4}\leq |\theta_1-\theta_2| \leq k_1e^{-T_-}, &\\ c(k_7)\exp \bigg( -S(T_-,T_+,h_1)-S(T_-,T_+,h_2)-(h_1^2+h_2^2)/2(T_+-T_-)\bigg), \\ \qquad\qquad\qquad\qquad\qquad\qquad \qquad\qquad\qquad\qquad\qquad\qquad \text{if } |\theta_1-\theta_2| \geq k_1e^{-T_-}, & \end{cases} \nonumber \end{align} $$
$$ \begin{align} &\mathbb{P}\bigg( \bigcap_{i\in \{1,2\}} \bigl\{ \mathfrak{U}^o_{T_+}(\theta_i) -\sqrt{\tfrac{4}{\beta}}h_i \in [-k_7,\infty) \bigr\} \cap \mathscr{P}(\theta_i,h_i) ~\big\vert~\mathscr{F}_{n_1^+} \bigg) \\ &\leq\! \begin{cases} c(k_7)h\frac{(T_+-T_*)\wedge (T_*-T_-)}{(T_*-T_-+1)^{3/2}}\exp\bigg(\! -S(T_-,T_+,h)\!-\! \Big(T_+-T_*+(T_+-T_*)^{1/14}\Big)\! -\!{h^2/2(T_+-T_-)} \bigg), &\\ \qquad\qquad\qquad\qquad\qquad\qquad \qquad\qquad\qquad\qquad\qquad\qquad \text{if } e^{k_4}\leq |\theta_1-\theta_2| \leq k_1e^{-T_-}, &\\ c(k_7)\exp \bigg( -S(T_-,T_+,h_1)-S(T_-,T_+,h_2)-(h_1^2+h_2^2)/2(T_+-T_-)\bigg), \\ \qquad\qquad\qquad\qquad\qquad\qquad \qquad\qquad\qquad\qquad\qquad\qquad \text{if } |\theta_1-\theta_2| \geq k_1e^{-T_-}, & \end{cases} \nonumber \end{align} $$
where
We emphasize that in (10.1), we implicitly used that
![]() $k_{i+1}\ll k_i$
in the o notation. We also recall that
$k_{i+1}\ll k_i$
in the o notation. We also recall that
![]() $T_-<0$
, so that the bottom inequality in (10.3) represents separation of angles much larger than
$T_-<0$
, so that the bottom inequality in (10.3) represents separation of angles much larger than
![]() $k_1$
.
$k_1$
.
Proof. We write the proof for
![]() $\sigma =1$
, the case
$\sigma =1$
, the case
![]() $\sigma =i$
being similar but simpler. To alleviate notation, we introduce a useful change of variables. Recall that
$\sigma =i$
being similar but simpler. To alleviate notation, we introduce a useful change of variables. Recall that
Let
![]() $(W_t^1,W_t^2)=(\Re \mathfrak {W}_t,\Im \mathfrak {W}_t)$
and set
$(W_t^1,W_t^2)=(\Re \mathfrak {W}_t,\Im \mathfrak {W}_t)$
and set
 $$ \begin{align} d\left(\begin{array}{l} V_t^1\\ V_t^2 \end{array}\right)= \left(\begin{array}{cc} \cos(\Im L_t(0)) & -\sin(\Im L_t(0))\\ \sin(\Im L_t(0)) & \cos (\Im L_t(0)) \end{array} \right)d\left(\begin{array}{l} W_t^1\\ W_t^2 \end{array} \right). \end{align} $$
$$ \begin{align} d\left(\begin{array}{l} V_t^1\\ V_t^2 \end{array}\right)= \left(\begin{array}{cc} \cos(\Im L_t(0)) & -\sin(\Im L_t(0))\\ \sin(\Im L_t(0)) & \cos (\Im L_t(0)) \end{array} \right)d\left(\begin{array}{l} W_t^1\\ W_t^2 \end{array} \right). \end{align} $$
Note that the pair of processes
![]() $V_t^1,V_t^2$
are independent standard Brownian motions. Let
$V_t^1,V_t^2$
are independent standard Brownian motions. Let
![]() $(R_t(\theta ),I_t(\theta )) = (\Re \mathfrak {L}_t(\theta ), \Im \mathfrak {L}_t(\theta ))$
, and set
$(R_t(\theta ),I_t(\theta )) = (\Re \mathfrak {L}_t(\theta ), \Im \mathfrak {L}_t(\theta ))$
, and set
![]() $(R_t,I_t)=(R_t(0),I_t(0))$
. We then have, with
$(R_t,I_t)=(R_t(0),I_t(0))$
. We then have, with
![]() $\hat I_t(\theta )=I_t(\theta )-I_t$
, that
$\hat I_t(\theta )=I_t(\theta )-I_t$
, that
and
 $$ \begin{align} dR_t(\theta)&=\sqrt{\tfrac{4}{\beta}}(\cos(\hat I_t(\theta)) dV_t^1+ \sin(\hat I_t(\theta)) dV_t^2),\\ d\hat I_t(\theta)&=\theta e^t k_1^{-1} dt+\sqrt{\tfrac{4}{\beta}}(\sin(\hat I_t(\theta)) dV_t^1-(1- \cos(\hat I_t(\theta)) dV_t^2). \nonumber \end{align} $$
$$ \begin{align} dR_t(\theta)&=\sqrt{\tfrac{4}{\beta}}(\cos(\hat I_t(\theta)) dV_t^1+ \sin(\hat I_t(\theta)) dV_t^2),\\ d\hat I_t(\theta)&=\theta e^t k_1^{-1} dt+\sqrt{\tfrac{4}{\beta}}(\sin(\hat I_t(\theta)) dV_t^1-(1- \cos(\hat I_t(\theta)) dV_t^2). \nonumber \end{align} $$
We begin with the proof of (10.1). Note that for any
![]() $\theta $
, we have
$\theta $
, we have
![]() $t\mapsto \mathfrak {U}^o_t(\theta )=R_t(\theta )$
has the same law as that of
$t\mapsto \mathfrak {U}^o_t(\theta )=R_t(\theta )$
has the same law as that of
![]() $t\mapsto R_t$
, and further,
$t\mapsto R_t$
, and further,
![]() $R_t$
is a
$R_t$
is a
![]() $\sqrt {4/\beta }$
multiple of a standard Brownian motion. Thus, by standard barrier estimates and the Markov property (see, for example, [Reference Belius, Rosen and ZeitouniBRZ19, Proof of Lemma 5.3]), we obtain, with
$\sqrt {4/\beta }$
multiple of a standard Brownian motion. Thus, by standard barrier estimates and the Markov property (see, for example, [Reference Belius, Rosen and ZeitouniBRZ19, Proof of Lemma 5.3]), we obtain, with
![]() $h'$
as in (10.2), that
$h'$
as in (10.2), that

where
![]() $J_{k_4}=[-k_4^{13/14}, -k_4^{1/14}]$
. We then obtain (recalling that
$J_{k_4}=[-k_4^{13/14}, -k_4^{1/14}]$
. We then obtain (recalling that
![]() $k_i\gg k_{i+1}$
)
$k_i\gg k_{i+1}$
)

We turn to the two-ray estimates; note that we are shooting for a rough bound only, essentially accurate at the exponential scale. We may and will take
![]() $\theta _1=0$
and write
$\theta _1=0$
and write
![]() $\theta =\theta _2$
. Set
$\theta =\theta _2$
. Set
![]() $ L_t= e^{\lambda (R_t+R_t(\theta ))}$
and
$ L_t= e^{\lambda (R_t+R_t(\theta ))}$
and
![]() $\theta _t= \theta e^{t} k_1^{-1}$
. We emphasize that the estimates we will obtain will be uniform with respect to the initial condition
$\theta _t= \theta e^{t} k_1^{-1}$
. We emphasize that the estimates we will obtain will be uniform with respect to the initial condition
![]() $\hat I_{T_-}(\theta )$
. Fix
$\hat I_{T_-}(\theta )$
. Fix
![]() $\tilde I_t=\hat I_t-\theta _t$
. We have from (10.7) that
$\tilde I_t=\hat I_t-\theta _t$
. We have from (10.7) that
and therefore, setting
![]() $\ell _t=\mathbb {E} L_t$
,
$\ell _t=\mathbb {E} L_t$
,
![]() $\ell _t^c= \mathbb {E}(\cos (\tilde I_t) L_t)$
,
$\ell _t^c= \mathbb {E}(\cos (\tilde I_t) L_t)$
,
![]() $\ell _t^s= \mathbb {E}(\sin (\tilde I_t) L_t)$
, we obtain that
$\ell _t^s= \mathbb {E}(\sin (\tilde I_t) L_t)$
, we obtain that
However, for some explicit martingale
![]() $M_t$
,
$M_t$
,
 $$ \begin{align*} d(\cos(\tilde I_t) L_t)&= dM_t + \tfrac{4\lambda^2}{\beta}(1+\cos(\theta_t+\tilde I_t))\cos(\tilde I_t)L_t dt- \tfrac{4}{\beta}\cos(\tilde I_t) (1-\cos(\theta_t+\tilde I_t))L_t dt\\ &\quad - \tfrac{4\lambda}{\beta} \sin(2(\theta_t+\tilde I_t))\sin(\tilde I_t)L_t dt, \end{align*} $$
$$ \begin{align*} d(\cos(\tilde I_t) L_t)&= dM_t + \tfrac{4\lambda^2}{\beta}(1+\cos(\theta_t+\tilde I_t))\cos(\tilde I_t)L_t dt- \tfrac{4}{\beta}\cos(\tilde I_t) (1-\cos(\theta_t+\tilde I_t))L_t dt\\ &\quad - \tfrac{4\lambda}{\beta} \sin(2(\theta_t+\tilde I_t))\sin(\tilde I_t)L_t dt, \end{align*} $$
with a similar expression for
![]() $d(\sin (\tilde I_t) L_t)$
. Therefore, there exists a constant
$d(\sin (\tilde I_t) L_t)$
. Therefore, there exists a constant
![]() $\alpha =\alpha (\lambda ,\beta )$
so that
$\alpha =\alpha (\lambda ,\beta )$
so that
From now on, we take
![]() $4\lambda ^2/\beta =a$
(
$4\lambda ^2/\beta =a$
(
![]() $a\sim 2$
is the exponent we will need for Chebychev’s inequality). Define
$a\sim 2$
is the exponent we will need for Chebychev’s inequality). Define
![]() $\hat \ell _t =\ell _t e^{-a (t-T_-)}$
, and similarly,
$\hat \ell _t =\ell _t e^{-a (t-T_-)}$
, and similarly,
![]() $\hat \ell _t^c,\hat \ell _t^s$
. Then,
$\hat \ell _t^c,\hat \ell _t^s$
. Then,
and therefore, with
![]() $t\geq T_{-}$
,
$t\geq T_{-}$
,
 $$ \begin{align*}\hat \ell_{t}-\hat \ell_{T_-}=a \int_{T_-}^t \big(\cos(\theta_u)\hat \ell_u^c-\sin(\theta_u) \hat \ell_u^s\big)du.\end{align*} $$
$$ \begin{align*}\hat \ell_{t}-\hat \ell_{T_-}=a \int_{T_-}^t \big(\cos(\theta_u)\hat \ell_u^c-\sin(\theta_u) \hat \ell_u^s\big)du.\end{align*} $$
Using the change of variables
![]() $e^{u}=s$
, we have that
$e^{u}=s$
, we have that
![]() $\theta _u=\theta s/k_1$
, and thus, we obtain that
$\theta _u=\theta s/k_1$
, and thus, we obtain that
 $$ \begin{align} \hat \ell_t-\hat \ell_{T_-}= a \int_{e^{T_-}}^{e^{t}} s^{-1}\big(\cos(\theta s/k_1) \hat\ell^c_{\log s}-\sin(\theta s/k_1) \hat \ell^s_{\log s}\big) ds. \end{align} $$
$$ \begin{align} \hat \ell_t-\hat \ell_{T_-}= a \int_{e^{T_-}}^{e^{t}} s^{-1}\big(\cos(\theta s/k_1) \hat\ell^c_{\log s}-\sin(\theta s/k_1) \hat \ell^s_{\log s}\big) ds. \end{align} $$
Consider first the case
![]() $\theta e^{T_-}/k_1> c$
for some fixed constant
$\theta e^{T_-}/k_1> c$
for some fixed constant
![]() $c>1$
– that is,
$c>1$
– that is,
![]() $T_*\leq T_--\log c$
. Set
$T_*\leq T_--\log c$
. Set
![]() $T_{\ell }=T_-+\ell $
,
$T_{\ell }=T_-+\ell $
,
![]() $\ell \geq 0$
. We consider first
$\ell \geq 0$
. We consider first ![]() . Let
. Let
Then, for
![]() $s\in I_\ell $
, we have (using integration by parts) that
$s\in I_\ell $
, we have (using integration by parts) that
Performing in (10.11) integration by parts and using (10.10) and that
![]() $|\hat \ell _t^c|,|\hat \ell _t^s|\leq \hat \ell _t$
, we obtain (using that
$|\hat \ell _t^c|,|\hat \ell _t^s|\leq \hat \ell _t$
, we obtain (using that
![]() $4ab_\ell \ll 1$
for
$4ab_\ell \ll 1$
for
![]() $\lambda $
bounded by say
$\lambda $
bounded by say
![]() $4$
if c is chosen large enough) that for
$4$
if c is chosen large enough) that for
![]() $e^t\in I_\ell $
,
$e^t\in I_\ell $
,
 $$ \begin{align*}\hat \ell_t \leq \hat \ell_{T_\ell}+4ab_\ell \hat \ell_t+4\alpha ab_\ell \int_{e^{T_\ell}}^{e^t} s^{-1}\hat \ell_{\log s} ds =\hat \ell_{T_\ell}+4ab_\ell \hat \ell_t+ 4\alpha ab_\ell \int_{T_\ell}^t \hat \ell_u du .\end{align*} $$
$$ \begin{align*}\hat \ell_t \leq \hat \ell_{T_\ell}+4ab_\ell \hat \ell_t+4\alpha ab_\ell \int_{e^{T_\ell}}^{e^t} s^{-1}\hat \ell_{\log s} ds =\hat \ell_{T_\ell}+4ab_\ell \hat \ell_t+ 4\alpha ab_\ell \int_{T_\ell}^t \hat \ell_u du .\end{align*} $$
An application of Gronwall’s inequality then gives that for such t,
Unravelling the definitions, we have obtained that for
![]() $e^t\in I_\ell $
,
$e^t\in I_\ell $
,

uniformly in the initial conditions of
![]() $\hat I_{T_-}(\theta )$
, where C is a universal constant independent of
$\hat I_{T_-}(\theta )$
, where C is a universal constant independent of
![]() $\ell $
and we used that
$\ell $
and we used that
![]() $\sum _{j=1}^\ell a b_j \alpha (T_{j+1}-T_j)/(1-4ab_j)$
is uniformly bounded. In particular, for
$\sum _{j=1}^\ell a b_j \alpha (T_{j+1}-T_j)/(1-4ab_j)$
is uniformly bounded. In particular, for
![]() $\theta _1,\theta _2$
with
$\theta _1,\theta _2$
with
![]() $|\theta _1-\theta _2|\geq c k_1 e^{-T_-}$
, using Chebycheff’s inequality with
$|\theta _1-\theta _2|\geq c k_1 e^{-T_-}$
, using Chebycheff’s inequality with
![]() $\lambda \sim 2$
, we obtain that
$\lambda \sim 2$
, we obtain that
 $$ \begin{align} \mathbb{P} (R_{{T_+}}(\theta_i) &\geq \sqrt{8/\beta} ((h_i-k_7)/\sqrt{2}+(T_+-T_-)), i=1,2) \nonumber \\ &\leq C e^{- \sum_{i=1}^2 \big(\sqrt{2} (T_+-T_-)+(h_1-k_7)\big)^2/2(T_+-T_-) }, \end{align} $$
$$ \begin{align} \mathbb{P} (R_{{T_+}}(\theta_i) &\geq \sqrt{8/\beta} ((h_i-k_7)/\sqrt{2}+(T_+-T_-)), i=1,2) \nonumber \\ &\leq C e^{- \sum_{i=1}^2 \big(\sqrt{2} (T_+-T_-)+(h_1-k_7)\big)^2/2(T_+-T_-) }, \end{align} $$
which yields the bottom inequality in (10.3).
We next turn to the case
![]() $T_+-k_4\geq T_*>T_- -\log c$
. In that case, we apply the barrier estimate for time
$T_+-k_4\geq T_*>T_- -\log c$
. In that case, we apply the barrier estimate for time
![]() $(T_*-T_- -\log c)_+$
and the same computation as above for larger times. That is, assuming without loss of generality that
$(T_*-T_- -\log c)_+$
and the same computation as above for larger times. That is, assuming without loss of generality that
![]() $h=h_1$
, we write
$h=h_1$
, we write
![]() $T_*'=(T_*\vee T_-)$
and, with
$T_*'=(T_*\vee T_-)$
and, with
![]() $\mathscr {P}(\theta _i,h_i)^{T_*'}$
the part of the barrier event
$\mathscr {P}(\theta _i,h_i)^{T_*'}$
the part of the barrier event
![]() $\mathscr {P}(\theta _i,h_i)$
up to time
$\mathscr {P}(\theta _i,h_i)$
up to time
![]() $T_*'$
,
$T_*'$
,
 $$ \begin{align} \mathbb{P} (R_{{T_+}}(\theta_i) &\geq \sqrt{8/\beta} ((h_i-k_7)/\sqrt{2}+(T_+-T_-))\cap \mathscr{P}(\theta_i,h_i), i=1,2) \\ &\leq \int \mathbb{P}(\sqrt{\beta/8}R_{{T_*'}}(\theta_1)\in dz\cap\mathscr{P}(\theta_1,h_1)^{T_*'} )\nonumber\\ &\quad \times\mathbb{P}\Big(R_{T_+}(\theta_1)-R_{T_*'}(\theta_1)\geq \sqrt{8/\beta} ((h_1-k_7)/\sqrt{2}+(T_+-T_-)-z),\nonumber\\ &\qquad\qquad R_{T_+}(\theta_2)-R_{T_*'}(\theta_2)\geq \sqrt{8/\beta} (-k_7/\sqrt{2}+(T_+-T_*)+T_*^{1/14}\Big). \nonumber \end{align} $$
$$ \begin{align} \mathbb{P} (R_{{T_+}}(\theta_i) &\geq \sqrt{8/\beta} ((h_i-k_7)/\sqrt{2}+(T_+-T_-))\cap \mathscr{P}(\theta_i,h_i), i=1,2) \\ &\leq \int \mathbb{P}(\sqrt{\beta/8}R_{{T_*'}}(\theta_1)\in dz\cap\mathscr{P}(\theta_1,h_1)^{T_*'} )\nonumber\\ &\quad \times\mathbb{P}\Big(R_{T_+}(\theta_1)-R_{T_*'}(\theta_1)\geq \sqrt{8/\beta} ((h_1-k_7)/\sqrt{2}+(T_+-T_-)-z),\nonumber\\ &\qquad\qquad R_{T_+}(\theta_2)-R_{T_*'}(\theta_2)\geq \sqrt{8/\beta} (-k_7/\sqrt{2}+(T_+-T_*)+T_*^{1/14}\Big). \nonumber \end{align} $$
Note that the integration over the variable z in the right side of (10.14) is restricted in particular to the range
![]() $z\in [(T_+-T_*')^{1/14},(T_+-T_*')^{13/14}]$
. We control the second probability in the right-hand side of (10.14) as in the case
$z\in [(T_+-T_*')^{1/14},(T_+-T_*')^{13/14}]$
. We control the second probability in the right-hand side of (10.14) as in the case
![]() $T_*\leq T_--\log c$
, while the first probability is controlled by a standard Gaussian bound. This yields the top inequality in (10.3). Further details are omitted.
$T_*\leq T_--\log c$
, while the first probability is controlled by a standard Gaussian bound. This yields the top inequality in (10.3). Further details are omitted.
10.2 Regularity of the kernel
Lemma 10.2. Let F be the subset of ![]() for which
for which
![]() $\max _\theta |f(\theta )|> e^{-k_7}$
(which corresponds to those decorations in
$\max _\theta |f(\theta )|> e^{-k_7}$
(which corresponds to those decorations in
![]() $\Gamma _{k_7}^+$
). Let
$\Gamma _{k_7}^+$
). Let
![]() $\mathfrak {r}(x,\alpha ,f)$
be the Radon–Nikodym derivative of the measure
$\mathfrak {r}(x,\alpha ,f)$
be the Radon–Nikodym derivative of the measure
![]() $\mathfrak {s}(\alpha +x, e^{\sqrt {4/\beta }(\alpha +x)}df)$
with respect to
$\mathfrak {s}(\alpha +x, e^{\sqrt {4/\beta }(\alpha +x)}df)$
with respect to
![]() $\mathfrak {s}(x,e^{\sqrt {4/\beta }x}df)$
on F. Then, uniformly in
$\mathfrak {s}(x,e^{\sqrt {4/\beta }x}df)$
on F. Then, uniformly in
![]() $|x|\leq (\log k_1)^{17/18}$
and
$|x|\leq (\log k_1)^{17/18}$
and
![]() $|\alpha | \leq 1$
,
$|\alpha | \leq 1$
,
The same holds for
![]() $\mathfrak {p}$
trivially by integrating over the random phase:
$\mathfrak {p}$
trivially by integrating over the random phase:
Corollary 10.3. Using the same F, and for the same set of
![]() $|x| \leq (\log k_1)^{17/18}$
, the Radon-Nikodym derivative
$|x| \leq (\log k_1)^{17/18}$
, the Radon-Nikodym derivative
![]() $\mathfrak {t}(x,\alpha ,f)$
of
$\mathfrak {t}(x,\alpha ,f)$
of
![]() $\mathfrak {p}(\alpha +x, e^{\sqrt {4/\beta }(\alpha +x)}df)$
with respect to
$\mathfrak {p}(\alpha +x, e^{\sqrt {4/\beta }(\alpha +x)}df)$
with respect to
![]() $\mathfrak {p}(x,e^{\sqrt {4/\beta }x}df)$
satisfies
$\mathfrak {p}(x,e^{\sqrt {4/\beta }x}df)$
satisfies
Proof of Lemma 10.2.
We recall the definition of
![]() $\mathfrak {U}_t^{o,j}(h)$
from below (2.54). In particular, we have a decomposition
$\mathfrak {U}_t^{o,j}(h)$
from below (2.54). In particular, we have a decomposition
 $$ \begin{align} \begin{aligned} &\mathfrak{U}_{T_+}^{o}(\theta) =\mathfrak{U}_{T_\dagger}^o(0) +(\mathfrak{U}_{T_+}^o(\theta)-\mathfrak{U}_{T_\dagger}^o(0)), \\ &\mathfrak{L}_{T_+}^{o}(\theta) =\mathfrak{L}_{T_\dagger}^o(0) +(\mathfrak{L}_{T_+}^o(\theta)-\mathfrak{L}_{T_\dagger}^o(0)), \\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathfrak{U}_{T_+}^{o}(\theta) =\mathfrak{U}_{T_\dagger}^o(0) +(\mathfrak{U}_{T_+}^o(\theta)-\mathfrak{U}_{T_\dagger}^o(0)), \\ &\mathfrak{L}_{T_+}^{o}(\theta) =\mathfrak{L}_{T_\dagger}^o(0) +(\mathfrak{L}_{T_+}^o(\theta)-\mathfrak{L}_{T_\dagger}^o(0)), \\ \end{aligned} \end{align} $$
where the entire process
![]() $\{(\mathfrak {L}_{T_+}^o(\theta )-\mathfrak {L}_{T_\dagger }^o(0)) : \theta \}$
is independent of
$\{(\mathfrak {L}_{T_+}^o(\theta )-\mathfrak {L}_{T_\dagger }^o(0)) : \theta \}$
is independent of
![]() $\mathfrak {L}_{T_\dagger }^o(0)$
(and hence also
$\mathfrak {L}_{T_\dagger }^o(0)$
(and hence also
![]() $\mathfrak {U}_{T_\dagger }^o(0)$
). Then
$\mathfrak {U}_{T_\dagger }^o(0)$
). Then
![]() $D_j^o$
can be decomposed as
$D_j^o$
can be decomposed as
which makes
![]() $\widehat {D}(x)$
independent of
$\widehat {D}(x)$
independent of
![]() $\mathfrak {U}_{T_\dagger }^o(0)$
. Let
$\mathfrak {U}_{T_\dagger }^o(0)$
. Let
![]() $\widehat {\mathfrak {s}}(x,\cdot )$
be the law of
$\widehat {\mathfrak {s}}(x,\cdot )$
be the law of
![]() $\widehat {D}(x)$
. Note to have
$\widehat {D}(x)$
. Note to have
![]() $D_j^o(x) \in e^{\sqrt {4/\beta }x}F$
, we must have
$D_j^o(x) \in e^{\sqrt {4/\beta }x}F$
, we must have
as if not, then by definition,
![]() $D_j^o \equiv 0$
. Define the interval
$D_j^o \equiv 0$
. Define the interval
which has width which is at most
![]() $O( (\log k_1^+)^{13/14})$
and allows us to write the previous display as
$O( (\log k_1^+)^{13/14})$
and allows us to write the previous display as
![]() $x+\sqrt {\tfrac {\beta }{4}}\mathfrak {U}_{T_\dagger }^{o}(0) + \sqrt {2}(T_\dagger - T_-) \in J$
. Thus, we have a representation for
$x+\sqrt {\tfrac {\beta }{4}}\mathfrak {U}_{T_\dagger }^{o}(0) + \sqrt {2}(T_\dagger - T_-) \in J$
. Thus, we have a representation for
![]() $f \in F$
, with
$f \in F$
, with
![]() $T=T_\dagger -T_-$
, and where integrate over the law of
$T=T_\dagger -T_-$
, and where integrate over the law of
![]() $y = x+\sqrt {\tfrac {\beta }{4}}\mathfrak {U}_{T_\dagger }^{o}(0) + \sqrt {2}T$
,
$y = x+\sqrt {\tfrac {\beta }{4}}\mathfrak {U}_{T_\dagger }^{o}(0) + \sqrt {2}T$
,
Hence, this probability is differentiable in x, and, in fact,
On the assumptions on
![]() $x,y$
, the factor
$x,y$
, the factor
![]() $(\sqrt {2}-(x-y)/T)$
is bounded uniformly over the x and y considered by
$(\sqrt {2}-(x-y)/T)$
is bounded uniformly over the x and y considered by
![]() $\sqrt {2} + (\log k_1)^{-\delta }$
for some
$\sqrt {2} + (\log k_1)^{-\delta }$
for some
![]() $\delta>0,$
and hence, we conclude
$\delta>0,$
and hence, we conclude
Hence, from Gronwall’s inequality, we conclude the claimed estimate.
10.3 Mixing of phase
The final technical estimate that must be done for the decoration, which only concerns the case
![]() $\sigma =1$
, is the mixing of phase. Specifically, we must estimate the statistical difference between
$\sigma =1$
, is the mixing of phase. Specifically, we must estimate the statistical difference between
where
![]() $U \overset {\mathscr {L}}{=} \operatorname {Unif}([0,1])$
. This is the measure that appears in
$U \overset {\mathscr {L}}{=} \operatorname {Unif}([0,1])$
. This is the measure that appears in
![]() $\overline {\mathfrak {m}}$
in (2.79). Once more, we let F be the subset of
$\overline {\mathfrak {m}}$
in (2.79). Once more, we let F be the subset of ![]() for which
for which
![]() $\max _\theta |f(\theta )|> e^{-k_7}$
.
$\max _\theta |f(\theta )|> e^{-k_7}$
.
We use a representation that is similar to (10.16) – namely, that
where W is a centered Gaussian variable, independent of ![]() of variance
of variance
![]() $\tfrac {4}{\beta }(T_\dagger -T_-)$
, corresponding to the imaginary part of the increment of
$\tfrac {4}{\beta }(T_\dagger -T_-)$
, corresponding to the imaginary part of the increment of
![]() $\mathfrak {L}_{T_\dagger } - \mathfrak {L}_{T_-}$
. Now by virtue of the variance being large, we can make a total variation comparison of
$\mathfrak {L}_{T_\dagger } - \mathfrak {L}_{T_-}$
. Now by virtue of the variance being large, we can make a total variation comparison of
![]() $e^{i(\alpha + W)}$
to
$e^{i(\alpha + W)}$
to
![]() $e^{iU}$
.
$e^{iU}$
.
Lemma 10.4. With
![]() $\operatorname {dtv}$
the total variance distance, for a real Gaussian Z of variance V and a uniform variable U on
$\operatorname {dtv}$
the total variance distance, for a real Gaussian Z of variance V and a uniform variable U on
![]() $[0,1]$
, there is an absolute constant
$[0,1]$
, there is an absolute constant
![]() $C>0$
so that
$C>0$
so that
Proof. By periodicity, we may take ![]() . We compute the Fourier coefficients of the law of
. We compute the Fourier coefficients of the law of
![]() $e^{i(\alpha + Z)}$
. Note that the k-th coefficient is given by
$e^{i(\alpha + Z)}$
. Note that the k-th coefficient is given by
As the total variation distance is given by integrating the
![]() $\text {L}^1$
-distance of the densities, we have
$\text {L}^1$
-distance of the densities, we have
This leads to the following:
Corollary 10.5. Over any subset ![]() for which
for which
![]() $e^{i\alpha }F = F$
for any
$e^{i\alpha }F = F$
for any
![]() $\alpha \in {\mathbb R}$
,
$\alpha \in {\mathbb R}$
,
Proof. Rescaling both sides of the equation by
![]() $\mathfrak {s}(e^{x}F),$
we then have a bound for the bounded variation distance of two probability measures,
$\mathfrak {s}(e^{x}F),$
we then have a bound for the bounded variation distance of two probability measures,
From (10.17), we have that the phase
![]() $e^{iW}$
is independent of
$e^{iW}$
is independent of ![]() , and hence, we have a coupling of these two measures that holds with probability
, and hence, we have a coupling of these two measures that holds with probability ![]() . By the definition of bounded-Lipschitz metric, the claimed bound follows.
. By the definition of bounded-Lipschitz metric, the claimed bound follows.
Appendices
Appendix A Point Processes
We record some elementary properties about point processes and, in particular, approximation of point processes by Poisson processes. We will let
![]() $\Gamma $
be a complete separable metric space, with a metric
$\Gamma $
be a complete separable metric space, with a metric ![]() which is bounded by
which is bounded by
![]() $1.$
We will use the metrics
$1.$
We will use the metrics ![]() and
and ![]() from the introduction. We also define two metrics over finite point measures on
from the introduction. We also define two metrics over finite point measures on
![]() $\Gamma $
and their laws: for any finite point measures
$\Gamma $
and their laws: for any finite point measures
![]() $\xi _1 = \sum _{i=1}^m \delta _{y_i}$
and
$\xi _1 = \sum _{i=1}^m \delta _{y_i}$
and
![]() $\xi _2 = \sum _{i=1}^n \delta _{z_i}$
on
$\xi _2 = \sum _{i=1}^n \delta _{z_i}$
on
![]() $\Gamma $
,
$\Gamma $
,

with the minimum being over all permutations of
![]() $\{1,2,\dots ,n\}.$
Finally, for two laws on point processes
$\{1,2,\dots ,n\}.$
Finally, for two laws on point processes
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
, we let
$Q_2$
, we let
We note that it is possible to bound ∂
1(ξ
1, ξ
2) ≤ d
1(ξ
1, ξ
2)max{|ξ
1|, |ξ
2|}, where
![]() $|\xi _j|$
is the cardinality of the point set for
$|\xi _j|$
is the cardinality of the point set for
![]() $j=1,2$
, and hence,
$j=1,2$
, and hence,

We will formulate a corollary of [Reference Chen and XiaCX11] for Poisson process approximation with local dependency structure. We let
![]() $\left \{ \Xi _i : i \in \mathcal {I} \right \}$
be a set of Bernoulli point processes, so that
$\left \{ \Xi _i : i \in \mathcal {I} \right \}$
be a set of Bernoulli point processes, so that
![]() $\Xi _i(\Gamma ) \in \{0,1\}.$
We will suppose that elements of this set have local dependence, in that for each
$\Xi _i(\Gamma ) \in \{0,1\}.$
We will suppose that elements of this set have local dependence, in that for each
![]() $i \in \mathcal {I}$
, there are sets
$i \in \mathcal {I}$
, there are sets
![]() $A_i \subseteq B_i \subseteq \mathcal {I}$
with
$A_i \subseteq B_i \subseteq \mathcal {I}$
with
![]() $i \in A_i$
so that
$i \in A_i$
so that
For all
![]() $i \in \mathcal {I}$
, we let
$i \in \mathcal {I}$
, we let
![]() ${\lambda }_i$
be the intensity measure of
${\lambda }_i$
be the intensity measure of
![]() $\Xi _i$
, and we set
$\Xi _i$
, and we set
![]() $\Xi := \sum _{i \in \mathcal {I}} \Xi _i$
,
$\Xi := \sum _{i \in \mathcal {I}} \Xi _i$
, ![]() and
and ![]()
Theorem A.1. Suppose
![]() $\left \{ \Xi _i : i \in \mathcal {I} \right \}$
satisfy (A.2), and define for any
$\left \{ \Xi _i : i \in \mathcal {I} \right \}$
satisfy (A.2), and define for any
![]() $i \in \mathcal {I},$
$i \in \mathcal {I},$

Then there is a numerical constant
![]() $C>0$
so that for a Poisson process
$C>0$
so that for a Poisson process ![]() with intensity
with intensity
![]() $\lambda ,$
$\lambda ,$

Proof. We start by using [Reference Chen and XiaCX11, (2.6)] to establish that there is a numerical constant
![]() $C>0$
so that
$C>0$
so that

We note that in the notation of that equation,
![]() $|V_i| = T_i,$
and their
$|V_i| = T_i,$
and their
![]() $\lambda $
are our
$\lambda $
are our
![]() $\lambda .$
Finally, we bound their
$\lambda .$
Finally, we bound their
![]() $\kappa _i$
by Var(|Ξ(Γ)|)/L
i
, and we bound
$\kappa _i$
by Var(|Ξ(Γ)|)/L
i
, and we bound
![]() $\sqrt {\kappa _i}$
by
$\sqrt {\kappa _i}$
by
![]() $1+\kappa _i.$
$1+\kappa _i.$
We also note that [Reference Chen and XiaCX11] requires that
![]() $\Gamma $
is a locally compact metric space. As
$\Gamma $
is a locally compact metric space. As
![]() $\lambda $
is a finite Borel measure on
$\lambda $
is a finite Borel measure on
![]() $\Gamma ,$
it is tight. Hence, there are compact sets
$\Gamma ,$
it is tight. Hence, there are compact sets
![]() $K_i$
so that with
$K_i$
so that with
![]() $\tilde {\Gamma } =\cup _{i=1}^\infty K_i, \lambda ( \Gamma \setminus \tilde {\Gamma } ) = 0.$
The space
$\tilde {\Gamma } =\cup _{i=1}^\infty K_i, \lambda ( \Gamma \setminus \tilde {\Gamma } ) = 0.$
The space
![]() $\tilde {\Gamma }$
is locally compact, and both point processes
$\tilde {\Gamma }$
is locally compact, and both point processes
![]() $\Xi $
and
$\Xi $
and ![]() put
put
![]() $0$
mass on
$0$
mass on
![]() $\Gamma \setminus \tilde {\Gamma }$
with probability
$\Gamma \setminus \tilde {\Gamma }$
with probability
![]() $1.$
Hence, we may apply the Theorem of [Reference Chen and XiaCX11] to
$1.$
Hence, we may apply the Theorem of [Reference Chen and XiaCX11] to
![]() $\Xi $
and
$\Xi $
and ![]() considered as point processes on
considered as point processes on
![]() $\tilde {\Gamma }$
with the same metrics
$\tilde {\Gamma }$
with the same metrics ![]() and
and
![]() $d_2$
. Furthermore, coupling the point processes as random measures on
$d_2$
. Furthermore, coupling the point processes as random measures on
![]() $\tilde {\Gamma }$
gives a coupling of the point processes as random measures on
$\tilde {\Gamma }$
gives a coupling of the point processes as random measures on
![]() $\Gamma ,$
and hence, (A.3) follows.
$\Gamma ,$
and hence, (A.3) follows.
From (A.1), and using that
![]() $d_1$
is bounded by
$d_1$
is bounded by
![]() $1,$
$1,$
As
![]() $L_i \leq \Lambda ,$
the claim follows.
$L_i \leq \Lambda ,$
the claim follows.
We also formulate a change-of-intensity lemma that controls the distance between two Poisson processes of similar intensity. Define for any two finite Borel measures ![]() and
and
![]() $\lambda $
on
$\lambda $
on
![]() $\Gamma ,$
$\Gamma ,$

with the supremum over all f with both ![]() for all
for all
![]() $x,y \in \Gamma $
and
$x,y \in \Gamma $
and
![]() $|f(x)| \leq 1$
for all
$|f(x)| \leq 1$
for all
![]() $x \in \Gamma .$
Then, we have the following:
$x \in \Gamma .$
Then, we have the following:
Theorem A.2. Let ![]() and
and
![]() $\lambda $
be two finite measures on
$\lambda $
be two finite measures on
![]() $\Gamma .$
Let
$\Gamma .$
Let ![]() Then,
Then,
Proof. The first is nearly a corollary of [Reference Brown and XiaBX95, Theorem 1.2]. To derive it, apply Lemma 2.6 directly to the second line of the displayed equation at the top of [Reference Brown and XiaBX95, p.259]. The second follows from the first by using (A.1).
Corollary A.3. For any compact
![]() $\Gamma $
, and for any
$\Gamma $
, and for any
![]() $\epsilon> 0$
, there is a finite list
$\epsilon> 0$
, there is a finite list
![]() $f_1,f_2, \dots , f_n$
of nonnegative functions
$f_1,f_2, \dots , f_n$
of nonnegative functions
![]() $f_j$
with
$f_j$
with ![]() and
and
![]() $|f_j(x)| \leq 1$
for all
$|f_j(x)| \leq 1$
for all
![]() $x,y \in \Gamma $
and a
$x,y \in \Gamma $
and a
![]() $\delta $
so that if
$\delta $
so that if

then ∂ 2(Π(π), Π(λ)) ≤ ϵ.
Proof. By Arzelà–Ascoli, we can find a list
![]() $\{g_j\}$
for
$\{g_j\}$
for
![]() $j=1,\dots ,n$
so that for all
$j=1,\dots ,n$
so that for all
![]() $1$
-Lipschitz, 1-bounded f,
$1$
-Lipschitz, 1-bounded f,
Let
![]() $\{f_j\}$
be all the positive and negative parts of the functions in this list. We may also assume the constant-1 function is in the list. Now suppose that
$\{f_j\}$
be all the positive and negative parts of the functions in this list. We may also assume the constant-1 function is in the list. Now suppose that

Then, ![]() , and so by Theorem A.2,
, and so by Theorem A.2,
If ![]() there was nothing to prove in the first place. Otherwise, by taking
there was nothing to prove in the first place. Otherwise, by taking
![]() $\delta $
sufficiently small, we conclude the claim.
$\delta $
sufficiently small, we conclude the claim.
B Auxilliary one- and two-rays estimates
We collect in this appendix the key two-rays estimates used in the bulk of the evolution. The argument was developed in details in [Reference Chhaibi, Madaule and NajnudelCMN18], and, in fact, even our tex file is based on theirs. The hurried reader may skip the content of the appendix, keeping only the statements of Propositions B.2, B.3 and Lemmas B.4, B.5, B.6, B.8 and B.9 in mind.
Throughout, we adopt exactly, for ease of reference, the notation of [Reference Chhaibi, Madaule and NajnudelCMN18].
Further notation:
For any
![]() $n\geq p$
,
$n\geq p$
, ![]() , we define
, we define

We stress that
![]() $Z_n^{(p)}$
depends implicitly of
$Z_n^{(p)}$
depends implicitly of
![]() $\beta $
because of the Prüfer phase. Similarly, we define
$\beta $
because of the Prüfer phase. Similarly, we define

where
More generally, for any family of quantities depending on an index k, we will denote the difference of the quantities indexed by k and p by the same notation, with k as an index and p as an superscript.
In the following, it will be convenient to study the field at times which are powers of
![]() $2$
.
$2$
.
B.1 The Chhaibi-Madaule-Najnudel coupling
As in [Reference Chhaibi, Madaule and NajnudelCMN18], we introduce a new process in order to gain more independence. Recall that
![]() $N=\log _2 n$
.
$N=\log _2 n$
.
A more independent field:
For each fixed
![]() $\theta $
,
$\theta $
,
![]() $(Z_{2^k}(\theta ))_{k\geq 0}$
is a complex Gaussian random walk. Moreover, we could compute the correlations of
$(Z_{2^k}(\theta ))_{k\geq 0}$
is a complex Gaussian random walk. Moreover, we could compute the correlations of
![]() $Z_{2^k}(\theta )$
and
$Z_{2^k}(\theta )$
and
![]() $Z_{2^k}(\theta ')$
and observe that they behave logarithmically with respect to the distance between
$Z_{2^k}(\theta ')$
and observe that they behave logarithmically with respect to the distance between
![]() $\theta $
and
$\theta $
and
![]() $\theta '$
modulo
$\theta '$
modulo ![]() . However, Z is not globally Gaussian, so we cannot directly apply known results on the maximum of Gaussian fields, but we will still provide its approximative branching structure. To achieve this aim, we will gain some independence by making small changes on Z.
. However, Z is not globally Gaussian, so we cannot directly apply known results on the maximum of Gaussian fields, but we will still provide its approximative branching structure. To achieve this aim, we will gain some independence by making small changes on Z.
Let us fix some integer r, which will be assumed to be larger than some suitable universal constant. For
![]() $l \geq r$
, we denote
$l \geq r$
, we denote ![]() . Observe that for any
. Observe that for any
![]() $N \geq r$
, we can rewrite formula [Reference Chhaibi, Madaule and NajnudelCMN18, (3.3)] as
$N \geq r$
, we can rewrite formula [Reference Chhaibi, Madaule and NajnudelCMN18, (3.3)] as

Note that
![]() $\Delta ^{(l)}$
and
$\Delta ^{(l)}$
and
![]() $l - \Delta ^{(l)} $
are strictly positive if
$l - \Delta ^{(l)} $
are strictly positive if
![]() $l \geq r$
and r is large enough. Now, let
$l \geq r$
and r is large enough. Now, let
![]() $Z^{(2^r,\Delta )}$
be the process defined by
$Z^{(2^r,\Delta )}$
be the process defined by

Observe that
![]() $Z_{2^{N}}^{(2^r)}(\theta )$
and
$Z_{2^{N}}^{(2^r)}(\theta )$
and
![]() $Z_{2^{N}}^{(2^r,\Delta )}(\theta )$
only differ by the change in the square root of the denominator and by the replacement of some increments of the Prüfer phases by their mean. The following is a slight variation of [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 5.2]; the additional statement (B.4) actually follows from the proof in [Reference Chhaibi, Madaule and NajnudelCMN18].
$Z_{2^{N}}^{(2^r,\Delta )}(\theta )$
only differ by the change in the square root of the denominator and by the replacement of some increments of the Prüfer phases by their mean. The following is a slight variation of [Reference Chhaibi, Madaule and NajnudelCMN18, Proposition 5.2]; the additional statement (B.4) actually follows from the proof in [Reference Chhaibi, Madaule and NajnudelCMN18].
Proposition B.1. For r large enough,

In particular, as
![]() $\sum _{l\geq r } 2 l^{-2}<+\infty $
, we have that almost surely,
$\sum _{l\geq r } 2 l^{-2}<+\infty $
, we have that almost surely,
and
In the proof of Proposition B.1, [Reference Chhaibi, Madaule and NajnudelCMN18] introduce the variables, for any
![]() $l\geq 0$
,
$l\geq 0$
, ![]() ,
,

with
The main steps in the proof consist of the estimates
and, for
![]() $\lambda \in {\mathbb R}$
,
$\lambda \in {\mathbb R}$
,

(see [Reference Chhaibi, Madaule and NajnudelCMN18, (5.6), (5.8)].)
B.2 One- and two-ray estimates
In the sequel, for all fields denoted by Z with some indices and superscripts, we write R with the same indices and superscripts for the real part of
![]() $\sigma $
times the initial field (recall that
$\sigma $
times the initial field (recall that
![]() $\sigma \in \{1,i,-i\}$
).
$\sigma \in \{1,i,-i\}$
).
An envelope for the paths of
 $R_{2^{N}}^{(2^r,\Delta )}(\theta ) $
:
$R_{2^{N}}^{(2^r,\Delta )}(\theta ) $
:
For
![]() $j \geq r$
, let
$j \geq r$
, let

where
![]() $(\lambda _j^{(r)})_{j\geq r}$
is a nonnegative and increasing sequence, tending, when
$(\lambda _j^{(r)})_{j\geq r}$
is a nonnegative and increasing sequence, tending, when
![]() $j \rightarrow \infty $
, to a limit
$j \rightarrow \infty $
, to a limit
![]() $\lambda _{\infty }^{(r)}$
such that
$\lambda _{\infty }^{(r)}$
such that
 $$ \begin{align*}\lambda_\infty^{(r)} < \sum_{l\geq r} 2^{-\Delta^{(l)}} \leq 2^{-e^{\sqrt{\log r}}} \sum_{l=1}^{\infty} 2^{- 100 \lfloor \log^2 l \rfloor } \ll 2^{-e^{\sqrt{\log r}}} \to 0\end{align*} $$
$$ \begin{align*}\lambda_\infty^{(r)} < \sum_{l\geq r} 2^{-\Delta^{(l)}} \leq 2^{-e^{\sqrt{\log r}}} \sum_{l=1}^{\infty} 2^{- 100 \lfloor \log^2 l \rfloor } \ll 2^{-e^{\sqrt{\log r}}} \to 0\end{align*} $$
when r goes to
![]() $\infty $
. Let
$\infty $
. Let ![]() and
and ![]() , and for
, and for
![]() $N \geq 2r$
,
$N \geq 2r$
,
![]() $k \in [|r, N|]$
, define
$k \in [|r, N|]$
, define

and

We then define an envelope by its lower bound and its upper bound at each
![]() $k\in [|r,N|]$
:
$k\in [|r,N|]$
:
Fix
![]() $x<0$
(depending on
$x<0$
(depending on
![]() $k_2$
),
$k_2$
),
![]() $z<0$
(depending on
$z<0$
(depending on
![]() $k_1^+$
), and
$k_1^+$
), and
![]() $\upsilon \in (0,1)$
. Set
$\upsilon \in (0,1)$
. Set
![]() $N_+=\log n_1^+$
. The basic event we need to consider is, for
$N_+=\log n_1^+$
. The basic event we need to consider is, for ![]() ,
,

We will consider
![]() $x\in [- r^{1/20},- r^{19/20}]$
and
$x\in [- r^{1/20},- r^{19/20}]$
and
![]() $z\in [-(k_1^+)^{1/20},-(k_1^+)^{19/20}]$
. The walk
$z\in [-(k_1^+)^{1/20},-(k_1^+)^{19/20}]$
. The walk
![]() $(R_{2^k}^{(2^r,\Delta )}(\theta ))_{r \leq k \leq N}$
is a Gaussian random walk whose distribution is the same as
$(R_{2^k}^{(2^r,\Delta )}(\theta ))_{r \leq k \leq N}$
is a Gaussian random walk whose distribution is the same as
![]() $\sqrt {\frac {1}{2}} (W_{\tau _j^{(r)}})_{r \leq k \leq N}$
. In the case where an event
$\sqrt {\frac {1}{2}} (W_{\tau _j^{(r)}})_{r \leq k \leq N}$
. In the case where an event
![]() $\mathfrak I_N(\theta )$
occurs for some
$\mathfrak I_N(\theta )$
occurs for some ![]() , it means that
, it means that
![]() $x+R_{2^k}^{(2^r,\Delta )}(\theta )$
is around
$x+R_{2^k}^{(2^r,\Delta )}(\theta )$
is around
![]() $\tau _k^{(r)}$
for
$\tau _k^{(r)}$
for
![]() $r \leq k \leq N$
(i.e., the Brownian motion W is roughly growing linearly with rate
$r \leq k \leq N$
(i.e., the Brownian motion W is roughly growing linearly with rate
![]() $\sqrt {2}$
). For this reason, in the sequel of this part of the paper, we will often compare the probability of an event
$\sqrt {2}$
). For this reason, in the sequel of this part of the paper, we will often compare the probability of an event
![]() $Ev$
concerning the random walk
$Ev$
concerning the random walk
![]() $(R_{2^k}^{(2^r,\Delta )}(\theta ))_{r \leq k \leq N}$
to the probability of a similar event
$(R_{2^k}^{(2^r,\Delta )}(\theta ))_{r \leq k \leq N}$
to the probability of a similar event
![]() $GEv$
, where a linear function
$GEv$
, where a linear function
![]() $t \mapsto t \sqrt {2}$
has been subtracted from the possible trajectories of the underlying Brownian motion W for which the event
$t \mapsto t \sqrt {2}$
has been subtracted from the possible trajectories of the underlying Brownian motion W for which the event
![]() $Ev$
is satisfied. If
$Ev$
is satisfied. If
![]() $Ev$
depends only on the trajectory of W up to a certain time T, we get, by using the Girsanov transfomation, an equality of the form
$Ev$
depends only on the trajectory of W up to a certain time T, we get, by using the Girsanov transfomation, an equality of the form
and then the inequality
where
![]() $\mu $
denotes the smallest possible value of
$\mu $
denotes the smallest possible value of
![]() $W_T$
for which the event
$W_T$
for which the event
![]() $GEv$
can occur.
$GEv$
can occur.
The following proposition gives a lower bound for the first moment of
![]() $\mathfrak I_N$
.
$\mathfrak I_N$
.
Proposition B.2 (First moment of
 $\mathfrak I_N$
).
$\mathfrak I_N$
).
For any
![]() $\upsilon \in (0,1)$
,
$\upsilon \in (0,1)$
,
![]() $r\in {\mathbb N}$
large enough and N large enough depending on r,
$r\in {\mathbb N}$
large enough and N large enough depending on r,
where, with W being a standard Brownian motion,

Further, for
![]() $x,z$
as above, the asymptotics of
$x,z$
as above, the asymptotics of
![]() $\mathbb{P} (Event_{r,N})$
are given in Lemma C.1 below.
$\mathbb{P} (Event_{r,N})$
are given in Lemma C.1 below.
Proof. Since
![]() $(R_{2^j}^{(2^r, \Delta )}(\theta ))_{r \leq j \leq N_+}$
is a Gaussian random walk whose distribution does not depend on
$(R_{2^j}^{(2^r, \Delta )}(\theta ))_{r \leq j \leq N_+}$
is a Gaussian random walk whose distribution does not depend on
![]() $\theta $
, we have
$\theta $
, we have
 $$ \begin{align*} &\mathbb{P}\left( \mathfrak I_N (\theta)\right) =\\ &\quad \mathbb{P}\left( \forall j\in [|r,N_+|],\, L_j^{(N)} \leq x+R_{2^j}^{(2^r,\Delta)}(0) \leq U_j^{(N)}, x+R_{2^{N_+}}^{(2^r,\Delta)} (0)\in \tau^{(r)}_{N_+}-\frac34 \log N+[z,z+\upsilon) \right). \end{align*} $$
$$ \begin{align*} &\mathbb{P}\left( \mathfrak I_N (\theta)\right) =\\ &\quad \mathbb{P}\left( \forall j\in [|r,N_+|],\, L_j^{(N)} \leq x+R_{2^j}^{(2^r,\Delta)}(0) \leq U_j^{(N)}, x+R_{2^{N_+}}^{(2^r,\Delta)} (0)\in \tau^{(r)}_{N_+}-\frac34 \log N+[z,z+\upsilon) \right). \end{align*} $$
More precisely, we know that
![]() $(R_{2^j}^{(2^r,\Delta )}(0))_{j\geq r}$
is distributed like
$(R_{2^j}^{(2^r,\Delta )}(0))_{j\geq r}$
is distributed like
![]() $ \sqrt {\frac {1}{2}} (W_{ \tau ^{(r)}_j})_{j\geq r} $
. By Girsanov’s transform, with density
$ \sqrt {\frac {1}{2}} (W_{ \tau ^{(r)}_j})_{j\geq r} $
. By Girsanov’s transform, with density
![]() $ e^{\sqrt {2}W_{\tau ^{(r)}_{N_+} }- \tau ^{(r)}_{N_+}} $
, we have
$ e^{\sqrt {2}W_{\tau ^{(r)}_{N_+} }- \tau ^{(r)}_{N_+}} $
, we have

with a similar upper bound replacing
![]() $- 2\upsilon -\lambda _\infty ^{(r)} $
by
$- 2\upsilon -\lambda _\infty ^{(r)} $
by
![]() $ 2\upsilon +\lambda _\infty ^{(r)}$
. Using Lemma C.1 completes the proof of the right inequality in (B.12).
$ 2\upsilon +\lambda _\infty ^{(r)}$
. Using Lemma C.1 completes the proof of the right inequality in (B.12).
We will also need a similar estimate for shorter times. Let
![]() $t<N/4$
and set
$t<N/4$
and set
 $$ \begin{align*} \mathfrak I_{t,f}(\theta) &=\mathfrak I_{N,t}(\theta,x,z)\\ &:={\{ \forall k\in [|r,t|],\, L_k^{(N)} \leq x+R_{2^k}^{(2^r,\Delta)}(\theta) \leq U_k^{(N)}, x+R_{2^{t}}^{(2^r,\Delta)} (\theta)\in \tau^{(r)}_{t}+[z,z+\upsilon)\}}.\end{align*} $$
$$ \begin{align*} \mathfrak I_{t,f}(\theta) &=\mathfrak I_{N,t}(\theta,x,z)\\ &:={\{ \forall k\in [|r,t|],\, L_k^{(N)} \leq x+R_{2^k}^{(2^r,\Delta)}(\theta) \leq U_k^{(N)}, x+R_{2^{t}}^{(2^r,\Delta)} (\theta)\in \tau^{(r)}_{t}+[z,z+\upsilon)\}}.\end{align*} $$
Note that because of our choice of t, only the first part of the barrier is employed in
![]() $\mathfrak I_{t,f}$
, and therefore,
$\mathfrak I_{t,f}$
, and therefore,
![]() $\mathfrak I_{t,f}(\theta )$
does not depend on N. We have the following analogue of Proposition B.2.
$\mathfrak I_{t,f}(\theta )$
does not depend on N. We have the following analogue of Proposition B.2.
Proposition B.3 (First moment of
 $\mathfrak I_{N,t}$
).
$\mathfrak I_{N,t}$
).
For any
![]() $\upsilon \in (0,1)$
,
$\upsilon \in (0,1)$
,
![]() $C>0$
,
$C>0$
,
![]() $r\in {\mathbb N}$
large enough, x as above,
$r\in {\mathbb N}$
large enough, x as above,
![]() $z\in [-\sqrt {t}/C, -C\sqrt {t}]$
and t large enough depending on r,
$z\in [-\sqrt {t}/C, -C\sqrt {t}]$
and t large enough depending on r,
where, with W being a standard Brownian motion,
 $$ \begin{align*} Event_{r,t,f} &= Event_{r,N,t}(x,z)\\ &:= \left\{ \forall j\in [|r,t|],\, l_j^{(N)} \leq x+ \sqrt{\frac{1}{2}} W_{\tau^{(r)}_j} \leq u_j^{(N)} , x+ \sqrt{\frac{1}{2}} W_{\tau^{(r)}_{t}}\in \tau^{(r)}_{t}+[z,z+\upsilon)\right\}.\end{align*} $$
$$ \begin{align*} Event_{r,t,f} &= Event_{r,N,t}(x,z)\\ &:= \left\{ \forall j\in [|r,t|],\, l_j^{(N)} \leq x+ \sqrt{\frac{1}{2}} W_{\tau^{(r)}_j} \leq u_j^{(N)} , x+ \sqrt{\frac{1}{2}} W_{\tau^{(r)}_{t}}\in \tau^{(r)}_{t}+[z,z+\upsilon)\right\}.\end{align*} $$
The proof is similar to that of Proposition B.2 and is omitted.
B.3 Two-rays estimate
We will bound here
(For the sake of shortness of notation, when no confusion occurs, we write ![]() , omitting the
, omitting the
![]() $x,z,x',z'$
from the notation.) This study, which is technical, is based on the fact that the random walks
$x,z,x',z'$
from the notation.) This study, which is technical, is based on the fact that the random walks
![]() $(R_{2^j}^{(2^r,\Delta )}(\theta ))_{r \leq j \leq N}$
and
$(R_{2^j}^{(2^r,\Delta )}(\theta ))_{r \leq j \leq N}$
and
![]() $(R_{2^j}^{(2^r,\Delta )}(\theta '))_{r \leq j \leq N}$
are Gaussian random walks whose increments are approximately independent after some branching time which is roughly minus the logarithm in base
$(R_{2^j}^{(2^r,\Delta )}(\theta '))_{r \leq j \leq N}$
are Gaussian random walks whose increments are approximately independent after some branching time which is roughly minus the logarithm in base
![]() $2$
of the distance modulo
$2$
of the distance modulo ![]() between
between
![]() $\theta $
and
$\theta $
and
![]() $\theta '$
.
$\theta '$
.
The general idea is as follows. For given
![]() $\theta , \theta '$
, we will consider the integer
$\theta , \theta '$
, we will consider the integer
![]() ${\mathtt k}$
such that
${\mathtt k}$
such that ![]() ,
,
![]() $|| \cdot ||$
denoting the distance on the set
$|| \cdot ||$
denoting the distance on the set ![]() . One can understand
. One can understand
![]() ${\mathtt k}$
as the time of (approximate) branching between the field at
${\mathtt k}$
as the time of (approximate) branching between the field at
![]() $\theta $
and at
$\theta $
and at
![]() $\theta ' $
. We will show that after some time
$\theta ' $
. We will show that after some time
![]() ${\mathtt k}_+ = {\mathtt k}_+({\mathtt k}) $
‘slightly larger’ than
${\mathtt k}_+ = {\mathtt k}_+({\mathtt k}) $
‘slightly larger’ than
![]() ${\mathtt k}$
, we are able to bring out independence between the increments of
${\mathtt k}$
, we are able to bring out independence between the increments of
![]() $(R_{2^k}^{(2^r,\Delta )}(\theta ))_{k\geq r} $
and
$(R_{2^k}^{(2^r,\Delta )}(\theta ))_{k\geq r} $
and
![]() $ (R_{2^k}^{(2^r,\Delta )}(\theta '))_{k\geq r}$
. By analogy with the Gaussian field, we will see this time as a time of decorrelation. It is defined as follows:
$ (R_{2^k}^{(2^r,\Delta )}(\theta '))_{k\geq r}$
. By analogy with the Gaussian field, we will see this time as a time of decorrelation. It is defined as follows:
-
• For
 ${\mathtt k} \leq N/2$
, the time of decorrelation is
${\mathtt k} \leq N/2$
, the time of decorrelation is
 ${\mathtt k}_+ := {\mathtt k} + 3 \Delta ^{({\mathtt k})}$
. Recall that In particular, for
${\mathtt k}_+ := {\mathtt k} + 3 \Delta ^{({\mathtt k})}$
. Recall that In particular, for $$ \begin{align*}\Delta^{({\mathtt k})}:= e^{\sqrt{\log r}} + 100\lfloor \log^2 {\mathtt k} \rfloor.\end{align*} $$
$$ \begin{align*}\Delta^{({\mathtt k})}:= e^{\sqrt{\log r}} + 100\lfloor \log^2 {\mathtt k} \rfloor.\end{align*} $$
 ${\mathtt k} \leq r/2$
and r large enough, the walks
${\mathtt k} \leq r/2$
and r large enough, the walks
 $(R_{2^k}^{(2^r,\Delta )}(\theta ))_{k\geq r} $
and
$(R_{2^k}^{(2^r,\Delta )}(\theta ))_{k\geq r} $
and
 $ (R_{2^k}^{(2^r,\Delta )}(\theta '))_{k\geq r}$
will have ‘almost independent increments’ from the starting time r, since
$ (R_{2^k}^{(2^r,\Delta )}(\theta '))_{k\geq r}$
will have ‘almost independent increments’ from the starting time r, since
 $r \leq {\mathtt k}_+$
.
$r \leq {\mathtt k}_+$
.
-
• For
 $N/2 < {\mathtt k} \leq N _+$
, we will require a faster decorrelation. We take
$N/2 < {\mathtt k} \leq N _+$
, we will require a faster decorrelation. We take
 ${\mathtt k}_+ := {\mathtt k} + 3 \kappa ^{({\mathtt k})}$
, where However, the price to pay is that we will have to modify our field
${\mathtt k}_+ := {\mathtt k} + 3 \kappa ^{({\mathtt k})}$
, where However, the price to pay is that we will have to modify our field $$ \begin{align*}\kappa^{({\mathtt k})} := \lfloor r/100 \rfloor + 100 \lfloor \log (N-{\mathtt k}) \rfloor^2.\end{align*} $$
$$ \begin{align*}\kappa^{({\mathtt k})} := \lfloor r/100 \rfloor + 100 \lfloor \log (N-{\mathtt k}) \rfloor^2.\end{align*} $$
 $(R_{2^j}^{(2^r,\Delta )}(\theta ))_{r \leq j \leq N}$
in the spirit of subsection B.1.
$(R_{2^j}^{(2^r,\Delta )}(\theta ))_{r \leq j \leq N}$
in the spirit of subsection B.1.
Our two-rays estimates are divided to three lemmas, numbered B.4, B.5 and B.6. The statement of each of these lemmas gives a suitable majorization of ![]() , for a given range of values of
, for a given range of values of
![]() ${\mathtt k}$
.
${\mathtt k}$
.
Lemma B.4 (Time of branching
 ${\mathtt k} \leq N/2$
).
${\mathtt k} \leq N/2$
).
For any
![]() $\upsilon \in (0,1)$
, r large enough, N large enough depending on r,
$\upsilon \in (0,1)$
, r large enough, N large enough depending on r,
![]() ${\mathtt k} \leq \frac {N}{2}$
and
${\mathtt k} \leq \frac {N}{2}$
and ![]() , we have
, we have
 $$ \begin{align} \mathbb{P}_N(\theta, \theta')&\ll \left\{ \begin{array}{ll} |zz' xx'| 2^{2r-2N_+ +2(x-z+x'-z')} ,\qquad &\text{when } {\mathtt k}_+ \leq r,\\ |zz'x| e^{2(x-z-z')}2^{r-N_+} 2^{{\mathtt k}_+-N_+} e^{- {\mathtt k}_+^{\alpha_-}} ,\qquad &\text{when } {\mathtt k}_+ \geq r. \end{array} \right. \end{align} $$
$$ \begin{align} \mathbb{P}_N(\theta, \theta')&\ll \left\{ \begin{array}{ll} |zz' xx'| 2^{2r-2N_+ +2(x-z+x'-z')} ,\qquad &\text{when } {\mathtt k}_+ \leq r,\\ |zz'x| e^{2(x-z-z')}2^{r-N_+} 2^{{\mathtt k}_+-N_+} e^{- {\mathtt k}_+^{\alpha_-}} ,\qquad &\text{when } {\mathtt k}_+ \geq r. \end{array} \right. \end{align} $$
The following lemma studies pairs whose time of branching happen before
![]() $r/2$
. It refines the estimate obtained in the previous lemma.
$r/2$
. It refines the estimate obtained in the previous lemma.
Lemma B.5 (Time of branching
 ${\mathtt k} \leq r/2$
).
${\mathtt k} \leq r/2$
).
For any
![]() $\upsilon \in (0,1)$
,
$\upsilon \in (0,1)$
,
![]() $r\in {\mathbb N}$
large enough,
$r\in {\mathbb N}$
large enough,
![]() $ {\mathtt k} \leq \frac {r}{2}$
,
$ {\mathtt k} \leq \frac {r}{2}$
, ![]() and N large enough depending on r, we have
and N large enough depending on r, we have
where
Lemma B.6 (Time of branching
 $N/2 < {\mathtt k} \leq N_+$
).
$N/2 < {\mathtt k} \leq N_+$
).
For
![]() $\upsilon \in (0,1)$
,
$\upsilon \in (0,1)$
,
![]() $r\in {\mathbb N}$
large enough, N large enough depending on r,
$r\in {\mathbb N}$
large enough, N large enough depending on r,
![]() $N/2 < {\mathtt k} \leq N_+$
and
$N/2 < {\mathtt k} \leq N_+$
and ![]() , we have
, we have
![]() ${\mathtt k}_+ < N$
and
${\mathtt k}_+ < N$
and
Remark B.7. The proof of the Lemma B.6 is the unique place where we use
![]() $(l_j^{(N)})_{r \leq j\leq N}$
, the lower part of the envelope.
$(l_j^{(N)})_{r \leq j\leq N}$
, the lower part of the envelope.
B.3.1 Dyadic case
We start by assuming ![]() and prove Lemmas B.4 and B.6 in this dyadic case. This part is mainly for pedagogical purposes while laying the ground for the general case. It illustrates perfectly the machinery of the proof in a simpler setting.
and prove Lemmas B.4 and B.6 in this dyadic case. This part is mainly for pedagogical purposes while laying the ground for the general case. It illustrates perfectly the machinery of the proof in a simpler setting.
It will be convenient to denote, for any
![]() $l\in [|r,N_+|]$
,
$l\in [|r,N_+|]$
,
![]() $p\in [|0,2^{\Delta ^{(l)}}-1|]$
,
$p\in [|0,2^{\Delta ^{(l)}}-1|]$
,
 $$ \begin{align} I_{l,p}(\theta) := \frac{ \sum_{j=0}^{2^{l-\Delta^{(l)}}-1} {\mathcal N}^{\mathbb C}_{2^{l}+p 2^{l-\Delta^{(l)}} + j} e^{i \theta j} } { \sqrt{{ 2^{l}+p 2^{l-\Delta^{(l)}} }} } \operatorname{{\stackrel{{\mathcal L}}{=}}} {\mathcal N}^{{\mathbb C}}\left(0, (2^{\Delta^{(l)}}+ p)^{-1} \right). \end{align} $$
$$ \begin{align} I_{l,p}(\theta) := \frac{ \sum_{j=0}^{2^{l-\Delta^{(l)}}-1} {\mathcal N}^{\mathbb C}_{2^{l}+p 2^{l-\Delta^{(l)}} + j} e^{i \theta j} } { \sqrt{{ 2^{l}+p 2^{l-\Delta^{(l)}} }} } \operatorname{{\stackrel{{\mathcal L}}{=}}} {\mathcal N}^{{\mathbb C}}\left(0, (2^{\Delta^{(l)}}+ p)^{-1} \right). \end{align} $$
Recall that
![]() $R_{2^N}^{(2^r,\Delta )}(\theta )$
and
$R_{2^N}^{(2^r,\Delta )}(\theta )$
and
![]() $R_{2^N}^{(2^r, \Delta )}(\theta ')$
can be written as
$R_{2^N}^{(2^r, \Delta )}(\theta ')$
can be written as


The crucial observation is that for any
![]() $ l \in [|{\mathtt k}_+,N_+|] $
(we easily check that
$ l \in [|{\mathtt k}_+,N_+|] $
(we easily check that
![]() ${\mathtt k}_+ <N_+$
if r is large enough,
${\mathtt k}_+ <N_+$
if r is large enough,
![]() $N \geq r$
and
$N \geq r$
and
![]() ${\mathtt k} \leq N/2$
) and any
${\mathtt k} \leq N/2$
) and any
![]() $p\leq 2^{\Delta ^{(l)}}-1$
, the random variables
$p\leq 2^{\Delta ^{(l)}}-1$
, the random variables
![]() $ I_{l,p}(\theta )$
and
$ I_{l,p}(\theta )$
and
![]() $ I_{l,p}(\theta ')$
are independent and identically distributed. Indeed, they form a complex Gaussian vector, and they are uncorrelated, since for
$ I_{l,p}(\theta ')$
are independent and identically distributed. Indeed, they form a complex Gaussian vector, and they are uncorrelated, since for
![]() $l \geq {\mathtt k}_+$
, one has
$l \geq {\mathtt k}_+$
, one has
![]() $l - \Delta ^{(l)} \geq {\mathtt k}$
if
$l - \Delta ^{(l)} \geq {\mathtt k}$
if
![]() $l \geq r $
and r is large enough, and then
$l \geq r $
and r is large enough, and then

We deduce that the increments of
![]() $R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
and
$R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
and
![]() $R_{2^{j}}^{(2^r,\Delta )}(\theta ') $
after the time
$R_{2^{j}}^{(2^r,\Delta )}(\theta ') $
after the time
![]() ${\mathtt k}_+$
are independent and identically distributed. Recalling the definition of
${\mathtt k}_+$
are independent and identically distributed. Recalling the definition of
![]() $\tau ^{(r)}$
in (B.9) and (B.18), it follows that
$\tau ^{(r)}$
in (B.9) and (B.18), it follows that
 $$ \begin{align*} (R_{2^{j}}^{(2^r,\Delta)}(\theta))_{j\geq r} \operatorname{{\stackrel{{\mathcal L}}{=}}} (R_{2^{j}}^{(2^r,\Delta)}(\theta'))_{j\geq r} \operatorname{{\stackrel{{\mathcal L}}{=}}} \sqrt{\frac{1}{2}} ( W_{\tau_j^{(r)}})_{j\geq r}. \end{align*} $$
$$ \begin{align*} (R_{2^{j}}^{(2^r,\Delta)}(\theta))_{j\geq r} \operatorname{{\stackrel{{\mathcal L}}{=}}} (R_{2^{j}}^{(2^r,\Delta)}(\theta'))_{j\geq r} \operatorname{{\stackrel{{\mathcal L}}{=}}} \sqrt{\frac{1}{2}} ( W_{\tau_j^{(r)}})_{j\geq r}. \end{align*} $$
For any
![]() $k \in [|r, N_+|]$
,
$k \in [|r, N_+|]$
,
![]() $x, z<0$
, we introduce the events
$x, z<0$
, we introduce the events
 $$ \begin{align} \nonumber Ev(k,x,z)&:= \left\{ \forall j\in [|k,N_+|],\, l_j^{(N)} \leq\sqrt{\frac{1}{2}}W_{\tau_j^{(k)}}- \tau^{(k)}_j +x \leq u_j^{(N)}, \right.\nonumber\\ &\qquad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}}- \tau^{(k)}_{N_+} +x\in -\frac34 \log N +[z,z+\upsilon) \right\},\nonumber \\ GEv(k,x,z)&:=\left\{ \forall j\in [|k,N_+|],\, l_j^{(N)} \leq\sqrt{\frac{1}{2}}W_{\tau_j^{(k)}} +x \leq u_j^{(N)}, \right.\nonumber\\ &\qquad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}}+x\in -\frac34 \log N +[z,z+\upsilon) \right\}. \end{align} $$
$$ \begin{align} \nonumber Ev(k,x,z)&:= \left\{ \forall j\in [|k,N_+|],\, l_j^{(N)} \leq\sqrt{\frac{1}{2}}W_{\tau_j^{(k)}}- \tau^{(k)}_j +x \leq u_j^{(N)}, \right.\nonumber\\ &\qquad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}}- \tau^{(k)}_{N_+} +x\in -\frac34 \log N +[z,z+\upsilon) \right\},\nonumber \\ GEv(k,x,z)&:=\left\{ \forall j\in [|k,N_+|],\, l_j^{(N)} \leq\sqrt{\frac{1}{2}}W_{\tau_j^{(k)}} +x \leq u_j^{(N)}, \right.\nonumber\\ &\qquad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}}+x\in -\frac34 \log N +[z,z+\upsilon) \right\}. \end{align} $$
Note that
![]() $GEv(r,x,z)=Event_{r,N}(x,z)$
from Proposition B.2; we only keep the separate notation for compatibility with [Reference Chhaibi, Madaule and NajnudelCMN18]. Furthermore, note that
$GEv(r,x,z)=Event_{r,N}(x,z)$
from Proposition B.2; we only keep the separate notation for compatibility with [Reference Chhaibi, Madaule and NajnudelCMN18]. Furthermore, note that
![]() $GEv(k,x,z)$
is equal to the event obtained from
$GEv(k,x,z)$
is equal to the event obtained from
![]() $Ev(k,x,z)$
after Girsanov transform with density
$Ev(k,x,z)$
after Girsanov transform with density
 $ \exp \left ( \sqrt {2}W_{\tau ^{(k)}_{N_+} }- \tau ^{(k)}_{N_+} \right ) $
. Performing the transform yields
$ \exp \left ( \sqrt {2}W_{\tau ^{(k)}_{N_+} }- \tau ^{(k)}_{N_+} \right ) $
. Performing the transform yields

where in the last inequality, we used the definition (B.9) of
![]() $\tau _{N_+}^{(k)}$
and the fact that
$\tau _{N_+}^{(k)}$
and the fact that
![]() $e^{-\sqrt {2} W_{\tau ^{(k)}_{N_+} } }\leq N^{\frac {3}{2}} e^{2(x-z+\upsilon )} $
on
$e^{-\sqrt {2} W_{\tau ^{(k)}_{N_+} } }\leq N^{\frac {3}{2}} e^{2(x-z+\upsilon )} $
on
![]() $GEv(k,x,z)$
.
$GEv(k,x,z)$
.
In order to allow for more flexibility and for later use, let us record the following analogous events. For
![]() $k \in [|r,N_+|]$
,
$k \in [|r,N_+|]$
,
![]() $a\geq 0$
,
$a\geq 0$
,
![]() $E=(E_j)_{j\geq k}$
a sequence of reals such that
$E=(E_j)_{j\geq k}$
a sequence of reals such that
![]() $(\tau _{j}^{(k)} - E_j)_{j\geq k}$
is positive and nondecreasing,
$(\tau _{j}^{(k)} - E_j)_{j\geq k}$
is positive and nondecreasing,
![]() $x,z\in {\mathbb R}$
, define
$x,z\in {\mathbb R}$
, define
 $$ \begin{align} \nonumber Ev(k,a,E,x.z) &:= \left\{ \forall j\in [|k, N_+ |] ,\, l_j^{(N)}-a \leq \sqrt{\frac{1}{2}}W_{\tau_j^{(k)}-E_j}+x- \tau^{(k)}_{j} \leq u_j^{(N)}+a, \right.\\ &\quad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}-E_{N_+}}+x-\tau^{(k)}_{N_+}\in -\frac34 \log N +[z,z+\upsilon) \right\}, \end{align} $$
$$ \begin{align} \nonumber Ev(k,a,E,x.z) &:= \left\{ \forall j\in [|k, N_+ |] ,\, l_j^{(N)}-a \leq \sqrt{\frac{1}{2}}W_{\tau_j^{(k)}-E_j}+x- \tau^{(k)}_{j} \leq u_j^{(N)}+a, \right.\\ &\quad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}-E_{N_+}}+x-\tau^{(k)}_{N_+}\in -\frac34 \log N +[z,z+\upsilon) \right\}, \end{align} $$
 $$ \begin{align} GEv(k,a,E,x,z) &:= \left\{ \forall j\in [|k, N_+ |] ,\, l_j^{(N)}-a \leq \sqrt{\frac{1}{2}}W_{\tau_j^{(k)}-E_j} +x\leq u_j^{(N)}+a ,\right.\nonumber\\ &\quad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}-E_{N_+}}+x\in -\frac34 \log N +[z,z+\upsilon) \right\}. \end{align} $$
$$ \begin{align} GEv(k,a,E,x,z) &:= \left\{ \forall j\in [|k, N_+ |] ,\, l_j^{(N)}-a \leq \sqrt{\frac{1}{2}}W_{\tau_j^{(k)}-E_j} +x\leq u_j^{(N)}+a ,\right.\nonumber\\ &\quad \left. \sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}-E_{N_+}}+x\in -\frac34 \log N +[z,z+\upsilon) \right\}. \end{align} $$
Again, the event
![]() $GEv(k,a,E,x,z) $
is, up to an error due to the time shift E, ‘quasi equal’ to what we obtain when we apply the Girsanov’ transform with density
$GEv(k,a,E,x,z) $
is, up to an error due to the time shift E, ‘quasi equal’ to what we obtain when we apply the Girsanov’ transform with density
 $$ \begin{align*}\exp\left( \sqrt{2}W_{\tau_{N_+}^{(k)}-E_{N_+} } - (\tau_{N_+}^{(k)}- E_{N_+}) \right)\end{align*} $$
$$ \begin{align*}\exp\left( \sqrt{2}W_{\tau_{N_+}^{(k)}-E_{N_+} } - (\tau_{N_+}^{(k)}- E_{N_+}) \right)\end{align*} $$
to the event
![]() $ Ev(k,a,E,x,z)$
. This time, the inequality takes the form
$ Ev(k,a,E,x,z)$
. This time, the inequality takes the form
 $$ \begin{align} \mathbb{P}\left(Ev(k,a,E,x,z)\right) & \leq 2^{k-N_+} e^{-E_{N_+}+2(x-z+a+\upsilon)} N^{\frac{3}{2}} \mathbb{P}\left( GEv(k,a+\sup_{k \leq j \leq N} |E_j|,E,x,z) \right). \end{align} $$
$$ \begin{align} \mathbb{P}\left(Ev(k,a,E,x,z)\right) & \leq 2^{k-N_+} e^{-E_{N_+}+2(x-z+a+\upsilon)} N^{\frac{3}{2}} \mathbb{P}\left( GEv(k,a+\sup_{k \leq j \leq N} |E_j|,E,x,z) \right). \end{align} $$
Indeed, by the Girsanov transform and then using the barrier at time
![]() $N_+$
,
$N_+$
,

 $$ \begin{align*} &\quad \leq 2^{k-N_+} e^{E_{N_+}+2(x-z-E_{N_+}+a+\upsilon)} N^{\frac{3}{2}} \mathbb{P}\left( \forall j\in [|k, N_+ |] , l_j^{(N)}\!-\!a \leq \sqrt{\frac{1}{2}}W_{\tau_j^{(k)}-E_j}+x- E_j \leq u_j^{(N)}\!+\!a ,\right.\\ &\qquad \qquad\qquad\qquad \qquad \qquad \left. \left\{\sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}-E_{N_+}}+x\in -\frac34 \log N +[z,z+\upsilon) \right\} \right) \\ &\quad \leq 2^{k-N_+} e^{-E_{N_+}+2(x-z+a+\upsilon)} N^{\frac{3}{2}} \mathbb{P}\left( GEv(k,a+\sup_{k \leq j \leq N_+} |E_j|,E,x,z) \right). \end{align*} $$
$$ \begin{align*} &\quad \leq 2^{k-N_+} e^{E_{N_+}+2(x-z-E_{N_+}+a+\upsilon)} N^{\frac{3}{2}} \mathbb{P}\left( \forall j\in [|k, N_+ |] , l_j^{(N)}\!-\!a \leq \sqrt{\frac{1}{2}}W_{\tau_j^{(k)}-E_j}+x- E_j \leq u_j^{(N)}\!+\!a ,\right.\\ &\qquad \qquad\qquad\qquad \qquad \qquad \left. \left\{\sqrt{\frac{1}{2}}W_{\tau_{N_+}^{(k)}-E_{N_+}}+x\in -\frac34 \log N +[z,z+\upsilon) \right\} \right) \\ &\quad \leq 2^{k-N_+} e^{-E_{N_+}+2(x-z+a+\upsilon)} N^{\frac{3}{2}} \mathbb{P}\left( GEv(k,a+\sup_{k \leq j \leq N_+} |E_j|,E,x,z) \right). \end{align*} $$
Proof of Lemma B.4 in dyadic case.
When
![]() $\mathbf {{\mathtt k}_+ \leq r}$
: The increments of
$\mathbf {{\mathtt k}_+ \leq r}$
: The increments of
![]() $R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
and
$R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
and
![]() $R_{2^{j}}^{(2^r,\Delta )}(\theta ') $
after the time
$R_{2^{j}}^{(2^r,\Delta )}(\theta ') $
after the time
![]() ${\mathtt k}_+$
are independent and identically distributed; thus, we have
${\mathtt k}_+$
are independent and identically distributed; thus, we have
 $$ \begin{align*} \mathbb{P}_N(\theta,\theta) = \quad & \mathbb{P}\left(Ev(r,x,z)\right) \mathbb{P}\left(Ev(r,x',z')\right)\\ \stackrel{Eq. (B.20)}{\ll_v} & 2^{2r-2N_+} e^{2(x-z+x'-z')} \left( N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,x,z) \right) \right) \left( N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,x',z') \right) \right). \end{align*} $$
$$ \begin{align*} \mathbb{P}_N(\theta,\theta) = \quad & \mathbb{P}\left(Ev(r,x,z)\right) \mathbb{P}\left(Ev(r,x',z')\right)\\ \stackrel{Eq. (B.20)}{\ll_v} & 2^{2r-2N_+} e^{2(x-z+x'-z')} \left( N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,x,z) \right) \right) \left( N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,x',z') \right) \right). \end{align*} $$
Finally, by applying [Reference Chhaibi, Madaule and NajnudelCMN18, (A.15)] (with
![]() $E_{j-r}=\lambda _j^{(r)}/\log 2$
, which implies
$E_{j-r}=\lambda _j^{(r)}/\log 2$
, which implies
![]() $||E|| \leq 1$
for r large enough), we obtain (B.16).
$||E|| \leq 1$
for r large enough), we obtain (B.16).
When
![]() $\mathbf {{\mathtt k}_+ \geq r}$
: The increments of
$\mathbf {{\mathtt k}_+ \geq r}$
: The increments of
![]() $R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
and
$R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
and
![]() $R_{2^{j}}^{(2^r,\Delta )}(\theta ') $
after time
$R_{2^{j}}^{(2^r,\Delta )}(\theta ') $
after time
![]() ${\mathtt k}_+$
are independent and identically distributed. Moreover, all these increments are independent of those of
${\mathtt k}_+$
are independent and identically distributed. Moreover, all these increments are independent of those of
![]() $R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
for j between r and
$R_{2^{j}}^{(2^r,\Delta )}(\theta ) $
for j between r and
![]() ${\mathtt k}_+$
(we see this fact by first conditioning with respect to the
${\mathtt k}_+$
(we see this fact by first conditioning with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {G}_{2^{{\mathtt k}_+}}$
). We then have
$\mathcal {G}_{2^{{\mathtt k}_+}}$
). We then have
 $$ \begin{align*} &\mathbb{P}_N(\theta, \theta'x,z,x',z') \leq \mathbb{P}\left( Ev(r,x,z) \right) \sup_{ x'+l_{{\mathtt k}_+}^{(N)} \leq w\leq x'+u_{{\mathtt k}_+}^{(N)} }\mathbb{P}( Ev({\mathtt k}_+,w,z' ) )\\ \stackrel{Eq. (B.20)}{\ll} & 2^{r-N_+}e^{2(x-z)} \left( N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,x,z) \right) \right)\\ &\qquad\qquad\qquad 2^{{\mathtt k}_+-N_+} \sup_{ l_{{\mathtt k}_+}^{(N)} \leq w+x'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2(w+x'-z)} \mathbb{P}\left( GEv({\mathtt k}_+,w+x',z') \right) \right) \\ \ll \quad & |xzz'|2^{r-N_+} 2^{{\mathtt k}_+-N_+} e^{2(x-z-z')}\sup_{ l_{{\mathtt k}_+}^{(N)} \leq w'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2(w')} \mathbb{P}\left( GEv({\mathtt k}_+,w',z') \right) \right). \end{align*} $$
$$ \begin{align*} &\mathbb{P}_N(\theta, \theta'x,z,x',z') \leq \mathbb{P}\left( Ev(r,x,z) \right) \sup_{ x'+l_{{\mathtt k}_+}^{(N)} \leq w\leq x'+u_{{\mathtt k}_+}^{(N)} }\mathbb{P}( Ev({\mathtt k}_+,w,z' ) )\\ \stackrel{Eq. (B.20)}{\ll} & 2^{r-N_+}e^{2(x-z)} \left( N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,x,z) \right) \right)\\ &\qquad\qquad\qquad 2^{{\mathtt k}_+-N_+} \sup_{ l_{{\mathtt k}_+}^{(N)} \leq w+x'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2(w+x'-z)} \mathbb{P}\left( GEv({\mathtt k}_+,w+x',z') \right) \right) \\ \ll \quad & |xzz'|2^{r-N_+} 2^{{\mathtt k}_+-N_+} e^{2(x-z-z')}\sup_{ l_{{\mathtt k}_+}^{(N)} \leq w'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2(w')} \mathbb{P}\left( GEv({\mathtt k}_+,w',z') \right) \right). \end{align*} $$
If
![]() ${\mathtt k}_+ \leq N/4$
, according to [Reference Chhaibi, Madaule and NajnudelCMN18, (A.15)], for any
${\mathtt k}_+ \leq N/4$
, according to [Reference Chhaibi, Madaule and NajnudelCMN18, (A.15)], for any
![]() $w'\in {\mathbb R}$
, we have
$w'\in {\mathbb R}$
, we have
Recalling that
![]() $ w'\leq u_{{\mathtt k}_+}^{(N)}= -({\mathtt k}_+)^{\alpha _-} $
, we have
$ w'\leq u_{{\mathtt k}_+}^{(N)}= -({\mathtt k}_+)^{\alpha _-} $
, we have
 $$ \begin{align} \sup_{ l_{{\mathtt k}_+}^{(N)} \leq w'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2(w')} \mathbb{P}\left( GEv({\mathtt k}_+,w',z') \right) \right) \ll e^{- {\mathtt k}_+^{\alpha_-}}. \end{align} $$
$$ \begin{align} \sup_{ l_{{\mathtt k}_+}^{(N)} \leq w'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2(w')} \mathbb{P}\left( GEv({\mathtt k}_+,w',z') \right) \right) \ll e^{- {\mathtt k}_+^{\alpha_-}}. \end{align} $$
However, for
![]() ${\mathtt k}_+> N/4$
, we can crudely bound
${\mathtt k}_+> N/4$
, we can crudely bound
![]() $\mathbb{P} \left ( GEv({\mathtt k}_+,w',z; ) \right )$
by
$\mathbb{P} \left ( GEv({\mathtt k}_+,w',z; ) \right )$
by
![]() $1$
, and using the fact that
$1$
, and using the fact that
![]() $w' \leq - {\mathtt k}_+^{\alpha _-}$
if
$w' \leq - {\mathtt k}_+^{\alpha _-}$
if
![]() ${\mathtt k}_+<N/2$
and
${\mathtt k}_+<N/2$
and
![]() $w'\leq -(N-{\mathtt k}_+)^{\alpha _-}\leq -0.9 {\mathtt k}_+^{\alpha _-}$
if
$w'\leq -(N-{\mathtt k}_+)^{\alpha _-}\leq -0.9 {\mathtt k}_+^{\alpha _-}$
if
![]() ${\mathtt k}\leq N/2\leq {\mathtt k}_+$
, we obtain that
${\mathtt k}\leq N/2\leq {\mathtt k}_+$
, we obtain that
 $$ \begin{align} \sup_{ l_{{\mathtt k}_+}^{(N)} \leq w'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2w'} \mathbb{P}\left( GEv({\mathtt k}_+,w',z) \right) \right) \leq e^{2 w'} N^{\frac{3}{2}} \ll e^{- 1.8 {\mathtt k}_+^{\alpha_-}} N^{3/2} \ll e^{- {\mathtt k}_+^{\alpha_-}}, \end{align} $$
$$ \begin{align} \sup_{ l_{{\mathtt k}_+}^{(N)} \leq w'\leq u_{{\mathtt k}_+}^{(N)} } \left( N^{\frac{3}{2}} e^{2w'} \mathbb{P}\left( GEv({\mathtt k}_+,w',z) \right) \right) \leq e^{2 w'} N^{\frac{3}{2}} \ll e^{- 1.8 {\mathtt k}_+^{\alpha_-}} N^{3/2} \ll e^{- {\mathtt k}_+^{\alpha_-}}, \end{align} $$
since
![]() ${\mathtt k}_+\geq N/5$
for N large. (Recall that we take
${\mathtt k}_+\geq N/5$
for N large. (Recall that we take
![]() $N\to \infty $
before we take
$N\to \infty $
before we take
![]() $k_1\to \infty $
.)
$k_1\to \infty $
.)
In all cases, by combining Equations (B.24) and (B.25), we deduce
It concludes the proof of Lemma B.4 when ![]() is a negative power of
is a negative power of
![]() $2$
.
$2$
.
Proof of Lemma B.6 in the dyadic case.
Now we shall study
![]() $\mathbb{P} _N(\theta ,\theta ')$
, when the branching between the field in
$\mathbb{P} _N(\theta ,\theta ')$
, when the branching between the field in
![]() $\theta $
and the field in
$\theta $
and the field in
![]() $\theta '$
appears after the time
$\theta '$
appears after the time
![]() $N/2$
. This time we shall prove that when one restricts to the paths which are in the envelope, the increments of the path of the field at
$N/2$
. This time we shall prove that when one restricts to the paths which are in the envelope, the increments of the path of the field at
![]() $\theta $
and at
$\theta $
and at
![]() $\theta '$
are approximately independent after the time of decorrelation
$\theta '$
are approximately independent after the time of decorrelation
![]() $k_+$
. We recall that for this range,
$k_+$
. We recall that for this range,
![]() ${\mathtt k}_+ = {\mathtt k}+ 3\kappa ^{({\mathtt k})}$
, where
${\mathtt k}_+ = {\mathtt k}+ 3\kappa ^{({\mathtt k})}$
, where
![]() $\kappa ^{({\mathtt k})}:= \lfloor \frac {r }{100}\rfloor + 100 \lfloor \log (N-{\mathtt k})\rfloor ^2$
, if
$\kappa ^{({\mathtt k})}:= \lfloor \frac {r }{100}\rfloor + 100 \lfloor \log (N-{\mathtt k})\rfloor ^2$
, if
![]() ${\mathtt k} \leq N-1$
.
${\mathtt k} \leq N-1$
.
We need to exhibit the independence between the increments of the processes
![]() $(R_{2^j}^{(2^{{\mathtt k}_+},\Delta )}(\theta ))_{j\geq {\mathtt k}_+}$
and
$(R_{2^j}^{(2^{{\mathtt k}_+},\Delta )}(\theta ))_{j\geq {\mathtt k}_+}$
and
![]() $(R_{2^j}^{(2^{{\mathtt k}_+},\Delta )}(\theta '))_{j\geq {\mathtt k}_+}$
. The crucial observation we used in case of
$(R_{2^j}^{(2^{{\mathtt k}_+},\Delta )}(\theta '))_{j\geq {\mathtt k}_+}$
. The crucial observation we used in case of
![]() ${\mathtt k} \leq N/2$
does not work anymore for such a short decorrelation time. We first need to modify our field using similar arguments to those used for the proof of Proposition B.1.
${\mathtt k} \leq N/2$
does not work anymore for such a short decorrelation time. We first need to modify our field using similar arguments to those used for the proof of Proposition B.1.
In the following, we shall use the quantity
 $$ \begin{align*} J_{l,p}^{({\mathtt k})}(\theta) := \frac{ \sum_{j=0}^{2^{l-\kappa^{({\mathtt k})}}-1} {\mathcal N}^{\mathbb C}_{2^{l}+p 2^{l-\kappa^{({\mathtt k})}} + j} e^{i \theta j} }{\sqrt{{ 2^{l}+p 2^{l-\kappa^{({\mathtt k})}} }} } \operatorname{{\stackrel{{\mathcal L}}{=}}} {\mathcal N}^{{\mathbb C}}\left((0, 2^{\kappa^{({\mathtt k})}} +p)^{-1} \right). \end{align*} $$
$$ \begin{align*} J_{l,p}^{({\mathtt k})}(\theta) := \frac{ \sum_{j=0}^{2^{l-\kappa^{({\mathtt k})}}-1} {\mathcal N}^{\mathbb C}_{2^{l}+p 2^{l-\kappa^{({\mathtt k})}} + j} e^{i \theta j} }{\sqrt{{ 2^{l}+p 2^{l-\kappa^{({\mathtt k})}} }} } \operatorname{{\stackrel{{\mathcal L}}{=}}} {\mathcal N}^{{\mathbb C}}\left((0, 2^{\kappa^{({\mathtt k})}} +p)^{-1} \right). \end{align*} $$
Let
![]() ${\mathtt k} \in [N/2,N_+]$
and
${\mathtt k} \in [N/2,N_+]$
and ![]() . We have, for r large enough, since
. We have, for r large enough, since
![]() $N - {\mathtt k} \geq r/2$
is large,
$N - {\mathtt k} \geq r/2$
is large,
Recall that for
![]() $ \tilde {\theta }\in \{\theta ,\theta ' \}$
,
$ \tilde {\theta }\in \{\theta ,\theta ' \}$
,
![]() $r\leq k\leq N$
,
$r\leq k\leq N$
,
![]() $ R_{2^k}^{(2^{r},\Delta )}( \tilde {\theta }) = \Re (\sigma Z_{2^k}^{(2^{r},\Delta )}( \tilde {\theta })) $
. Since for
$ R_{2^k}^{(2^{r},\Delta )}( \tilde {\theta }) = \Re (\sigma Z_{2^k}^{(2^{r},\Delta )}( \tilde {\theta })) $
. Since for
![]() $l \geq {\mathtt k}_+$
,
$l \geq {\mathtt k}_+$
,
![]() $\kappa ^{({\mathtt k})} \leq \Delta ^{(l)}$
, we can write for all
$\kappa ^{({\mathtt k})} \leq \Delta ^{(l)}$
, we can write for all
![]() ${\mathtt k}_+ \leq k \leq N$
,
${\mathtt k}_+ \leq k \leq N$
,
![]() $ \tilde {\theta }\in \{ \theta ,\theta '\}$
,
$ \tilde {\theta }\in \{ \theta ,\theta '\}$
,

where

with
 $$ \begin{align} \left|\lozenge_j^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}} )}( \tilde{\theta})\right| \leq & \left| A_{ 2^{l}+p 2^{l-\kappa^{({\mathtt k})}} + \mathfrak{j} }^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}}) }( \tilde{\theta}) ) \right| + 2^{-\kappa^{({\mathtt k})}}. \end{align} $$
$$ \begin{align} \left|\lozenge_j^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}} )}( \tilde{\theta})\right| \leq & \left| A_{ 2^{l}+p 2^{l-\kappa^{({\mathtt k})}} + \mathfrak{j} }^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}}) }( \tilde{\theta}) ) \right| + 2^{-\kappa^{({\mathtt k})}}. \end{align} $$
Indeed,
 $$ \begin{align*} \lozenge_j^{ (2^{l}+p 2^{l-\kappa^{({\mathtt k})}} ) }( \tilde{\theta}) = & -1+ \sqrt{\frac{2^l+p2^{l-\kappa^{({\mathtt k})}}}{2^l+p2^{l-\kappa^{({\mathtt k})}} + \mathfrak{j} } }e^{i A_{ 2^{l}+p 2^{l-\kappa^{({\mathtt k})}} +\mathfrak{j} }^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}})}( \tilde{\theta}) } \\ = & - 1+ \left( 1 + \Theta \right) e^{i A_{2^{l}+p 2^{l-\kappa^{({\mathtt k})}} + \mathfrak{j}}^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}}) }( \tilde{\theta}) }, \end{align*} $$
$$ \begin{align*} \lozenge_j^{ (2^{l}+p 2^{l-\kappa^{({\mathtt k})}} ) }( \tilde{\theta}) = & -1+ \sqrt{\frac{2^l+p2^{l-\kappa^{({\mathtt k})}}}{2^l+p2^{l-\kappa^{({\mathtt k})}} + \mathfrak{j} } }e^{i A_{ 2^{l}+p 2^{l-\kappa^{({\mathtt k})}} +\mathfrak{j} }^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}})}( \tilde{\theta}) } \\ = & - 1+ \left( 1 + \Theta \right) e^{i A_{2^{l}+p 2^{l-\kappa^{({\mathtt k})}} + \mathfrak{j}}^{(2^{l}+p 2^{l-\kappa^{({\mathtt k})}}) }( \tilde{\theta}) }, \end{align*} $$
with
![]() $|\Theta | \leq 2^{-\kappa ^{({\mathtt k})}}$
which implies inequality (B.26). In the following, we shall denote
$|\Theta | \leq 2^{-\kappa ^{({\mathtt k})}}$
which implies inequality (B.26). In the following, we shall denote

Notice that, on the contrary of the proof of Proposition B.1, where
![]() $\Delta ^{(l)}$
varies with l, here we fix
$\Delta ^{(l)}$
varies with l, here we fix
![]() $\kappa ^{({\mathtt k})}$
as soon as we know that
$\kappa ^{({\mathtt k})}$
as soon as we know that ![]() . By using the same arguments used to prove (B.7) and (B.8), one can show similarly that for any
. By using the same arguments used to prove (B.7) and (B.8), one can show similarly that for any
![]() $l\geq {\mathtt k}_+$
,
$l\geq {\mathtt k}_+$
,
![]() $ \tilde {\theta }\in \{\theta , \theta '\}$
,
$ \tilde {\theta }\in \{\theta , \theta '\}$
,
 $$ \begin{align} & \mathbb{P}\left( | \blacklozenge^{({\mathtt k})}_l( \tilde{\theta}) |\geq 2^{-\frac{\kappa^{({\mathtt k})}}{8}}, \cap_{l \geq {\mathtt k}_+} \widetilde{G}_{l}( \tilde{\theta}) \Big| {\mathcal G}_{2^{{\mathtt k}_+}} \right) \ll e^{-2^{\frac{\kappa^{({\mathtt k})}}{8} }}, \end{align} $$
$$ \begin{align} & \mathbb{P}\left( | \blacklozenge^{({\mathtt k})}_l( \tilde{\theta}) |\geq 2^{-\frac{\kappa^{({\mathtt k})}}{8}}, \cap_{l \geq {\mathtt k}_+} \widetilde{G}_{l}( \tilde{\theta}) \Big| {\mathcal G}_{2^{{\mathtt k}_+}} \right) \ll e^{-2^{\frac{\kappa^{({\mathtt k})}}{8} }}, \end{align} $$
 $$ \begin{align} & \qquad \mathbb{P}\left(( \cap_{l\geq {\mathtt k}_+} \widetilde{G}_{l}( \tilde{\theta} ))^c \Big| {\mathcal G}_{2^{{\mathtt k}_+}} \right) \ll_{\beta} \exp\left( - \frac{\beta}{33} 2^{\frac{1}{2} \kappa^{({\mathtt k})}} \right) \end{align} $$
$$ \begin{align} & \qquad \mathbb{P}\left(( \cap_{l\geq {\mathtt k}_+} \widetilde{G}_{l}( \tilde{\theta} ))^c \Big| {\mathcal G}_{2^{{\mathtt k}_+}} \right) \ll_{\beta} \exp\left( - \frac{\beta}{33} 2^{\frac{1}{2} \kappa^{({\mathtt k})}} \right) \end{align} $$
with
 $$ \begin{align*} \widetilde{G}_{l}( \tilde{\theta} ) := & \ \bigcap_{p=0}^{2^{\kappa^{({\mathtt k})}}-1} \left\{ \sup_{0\leq j\leq 2^{l-{\kappa^{({\mathtt k})}}}-1} \left| A_{j+ 2^{l}+p 2^{l- \kappa^{({\mathtt k})}} }^{(2^{l}+p 2^{l- \kappa^{({\mathtt k})}})}( \tilde{\theta} ) \right| \leq 2^{-\frac{1}{4} \kappa^{({\mathtt k})} } \right\} . \end{align*} $$
$$ \begin{align*} \widetilde{G}_{l}( \tilde{\theta} ) := & \ \bigcap_{p=0}^{2^{\kappa^{({\mathtt k})}}-1} \left\{ \sup_{0\leq j\leq 2^{l-{\kappa^{({\mathtt k})}}}-1} \left| A_{j+ 2^{l}+p 2^{l- \kappa^{({\mathtt k})}} }^{(2^{l}+p 2^{l- \kappa^{({\mathtt k})}})}( \tilde{\theta} ) \right| \leq 2^{-\frac{1}{4} \kappa^{({\mathtt k})} } \right\} . \end{align*} $$
Moreover, it is plain to observe that for any r large enough, N large enough depending on r, and
![]() ${\mathtt k}\in [|N/2, N-r/2|]$
, and under the complement of the two events just above,
${\mathtt k}\in [|N/2, N-r/2|]$
, and under the complement of the two events just above,
 $$ \begin{align} \sum_{l={\mathtt k}_+}^{N-1} | \blacklozenge^{({\mathtt k})}_l( \tilde{\theta}) | \leq \sum_{l={\mathtt k}_+}^{N-1} 2^{- \frac{\kappa^{({\mathtt k})}}{8}} \leq (N-{\mathtt k}_+) 2^{- \frac{1}{8} \lfloor \frac{r}{100} \rfloor - \frac{25}{2}\lfloor\log (N-{\mathtt k})\rfloor^2 } \leq 1. \end{align} $$
$$ \begin{align} \sum_{l={\mathtt k}_+}^{N-1} | \blacklozenge^{({\mathtt k})}_l( \tilde{\theta}) | \leq \sum_{l={\mathtt k}_+}^{N-1} 2^{- \frac{\kappa^{({\mathtt k})}}{8}} \leq (N-{\mathtt k}_+) 2^{- \frac{1}{8} \lfloor \frac{r}{100} \rfloor - \frac{25}{2}\lfloor\log (N-{\mathtt k})\rfloor^2 } \leq 1. \end{align} $$
So for any
![]() $\tilde {\theta }\in \{\theta ,\theta '\}$
, we can replace
$\tilde {\theta }\in \{\theta ,\theta '\}$
, we can replace
![]() $(R_{2^k}^{(2^{{\mathtt k}_+},\Delta )}( \tilde {\theta }))_{{\mathtt k}_+ \leq k \leq N} $
by
$(R_{2^k}^{(2^{{\mathtt k}_+},\Delta )}( \tilde {\theta }))_{{\mathtt k}_+ \leq k \leq N} $
by
![]() $(R_{2^k}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}( \tilde {\theta }))_{ {\mathtt k}_+ \leq k \leq N} $
with an error at most
$(R_{2^k}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}( \tilde {\theta }))_{ {\mathtt k}_+ \leq k \leq N} $
with an error at most
![]() $1$
. Thus, we have
$1$
. Thus, we have

where
![]() $\tilde x=x'$
if
$\tilde x=x'$
if
![]() $\tilde \theta =\theta '$
and
$\tilde \theta =\theta '$
and
![]() $\tilde x=x$
otherwise.
$\tilde x=x$
otherwise.
We first deal with the sum in
![]() $\tilde {\theta }\in \{ \theta ,\theta '\}$
– that is, with
$\tilde {\theta }\in \{ \theta ,\theta '\}$
– that is, with
![]() $Q_N(\theta ,\theta ')$
. By using (B.27), then the Girsanov transform with density
$Q_N(\theta ,\theta ')$
. By using (B.27), then the Girsanov transform with density
![]() $e^{\sqrt {2 }W_{\tau ^{(r)}_{{\mathtt k}_+} }- \tau _{{\mathtt k}_+}^{(r)} }$
, and [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6] (when
$e^{\sqrt {2 }W_{\tau ^{(r)}_{{\mathtt k}_+} }- \tau _{{\mathtt k}_+}^{(r)} }$
, and [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6] (when
![]() ${\mathtt k}_+\geq \frac {2N}{3}$
), the sum is
${\mathtt k}_+\geq \frac {2N}{3}$
), the sum is
 $$ \begin{align*} \ll 2^{r-{\mathtt k}_+} N^{\frac{3}{2}} e^{ 2 (N-{\mathtt k}_+)^{\alpha_+}} \left( (N-{\mathtt k}_+)e^{-2^{\frac{\kappa^{({\mathtt k})}}{8}}} + \exp\left( - \frac{\beta}{33} 2^{\frac{1}{2} \kappa^{({\mathtt k})}} \right) \right),\;\text{when }\, {\mathtt k}_+ \leq \frac{2N}{3}, \\ \ll 2^{r-{\mathtt k}_+} \frac{N^{\frac{3}{2}}( N-{\mathtt k}_+)^{2\alpha_+} }{({\mathtt k}_+-r)^{\frac{3}{2}}} e^{ 2 (N-{\mathtt k}_+)^{\alpha_+}} \left( (N-{\mathtt k}_+)e^{-2^{\frac{\kappa^{({\mathtt k})}}{8}}} + \exp\left( - \frac{\beta}{33} 2^{\frac{1}{2} \kappa^{({\mathtt k})}} \right) \right),\; \text{when }\, {\mathtt k}_+ \geq \frac{2N}{3}, \end{align*} $$
$$ \begin{align*} \ll 2^{r-{\mathtt k}_+} N^{\frac{3}{2}} e^{ 2 (N-{\mathtt k}_+)^{\alpha_+}} \left( (N-{\mathtt k}_+)e^{-2^{\frac{\kappa^{({\mathtt k})}}{8}}} + \exp\left( - \frac{\beta}{33} 2^{\frac{1}{2} \kappa^{({\mathtt k})}} \right) \right),\;\text{when }\, {\mathtt k}_+ \leq \frac{2N}{3}, \\ \ll 2^{r-{\mathtt k}_+} \frac{N^{\frac{3}{2}}( N-{\mathtt k}_+)^{2\alpha_+} }{({\mathtt k}_+-r)^{\frac{3}{2}}} e^{ 2 (N-{\mathtt k}_+)^{\alpha_+}} \left( (N-{\mathtt k}_+)e^{-2^{\frac{\kappa^{({\mathtt k})}}{8}}} + \exp\left( - \frac{\beta}{33} 2^{\frac{1}{2} \kappa^{({\mathtt k})}} \right) \right),\; \text{when }\, {\mathtt k}_+ \geq \frac{2N}{3}, \end{align*} $$
which are both dominated by
![]() $|xz| e^{-(x-z-z')}2^{-2N_++ {\mathtt k}_+ +r} e^{- \frac {1}{2} (N-{\mathtt k}_+ )^{\alpha _-}} $
. It remains to bound the expression
$|xz| e^{-(x-z-z')}2^{-2N_++ {\mathtt k}_+ +r} e^{- \frac {1}{2} (N-{\mathtt k}_+ )^{\alpha _-}} $
. It remains to bound the expression
![]() $\mathbb{P}_N^{\Delta,\kappa}(\theta,\theta')$
. Let
$\mathbb{P}_N^{\Delta,\kappa}(\theta,\theta')$
. Let
![]() $\tau _j^{(r,{\mathtt k}_+)}:= \tau _j^{(r)}$
if
$\tau _j^{(r,{\mathtt k}_+)}:= \tau _j^{(r)}$
if
![]() $j\leq {\mathtt k}_+$
and
$j\leq {\mathtt k}_+$
and
![]() $\tau _j^{(r,{\mathtt k}_+)}:= \tau _{{\mathtt k}_+}^{(r)}+ \sum _{l={\mathtt k}_+}^{j-1} \sum _{p=0}^{2^{\kappa ^{({\mathtt k})}}-1} (2^{\kappa ^{({\mathtt k})}} +p)^{-1}$
if
$\tau _j^{(r,{\mathtt k}_+)}:= \tau _{{\mathtt k}_+}^{(r)}+ \sum _{l={\mathtt k}_+}^{j-1} \sum _{p=0}^{2^{\kappa ^{({\mathtt k})}}-1} (2^{\kappa ^{({\mathtt k})}} +p)^{-1}$
if
![]() $j\geq {\mathtt k}_+$
and
$j\geq {\mathtt k}_+$
and
![]() $E^{({\mathtt k}_+)}_j:= \tau _j^{(r)}-\tau _j^{(r,{\mathtt k}_+)}$
, for any
$E^{({\mathtt k}_+)}_j:= \tau _j^{(r)}-\tau _j^{(r,{\mathtt k}_+)}$
, for any
![]() $r\leq j\leq N_+$
. It is plain to check that
$r\leq j\leq N_+$
. It is plain to check that
![]() $\sum _{j=r}^{N_+}|E^{({\mathtt k}_+)}_{j+1} -E^{({\mathtt k}_+)}_{j} | \ll 2^{- \frac {r}{100}}$
and
$\sum _{j=r}^{N_+}|E^{({\mathtt k}_+)}_{j+1} -E^{({\mathtt k}_+)}_{j} | \ll 2^{- \frac {r}{100}}$
and

Now, it suffices to reproduce the proof of Lemma B.4. In this first part, we assume ![]() . In this case, we check the independence of
. In this case, we check the independence of
![]() $J_{l,p}^{({\mathtt k})}( \theta )$
and
$J_{l,p}^{({\mathtt k})}( \theta )$
and
![]() $J_{l,p}^{({\mathtt k})}( \theta ')$
for
$J_{l,p}^{({\mathtt k})}( \theta ')$
for
![]() $l \geq {\mathtt k}_+$
, since
$l \geq {\mathtt k}_+$
, since
![]() ${\mathtt k}_+ - \kappa ^{({\mathtt k})} \geq {\mathtt k}$
. We then show, by doing the suitable conditionings, that the increments of
${\mathtt k}_+ - \kappa ^{({\mathtt k})} \geq {\mathtt k}$
. We then show, by doing the suitable conditionings, that the increments of
![]() $(R_{2^k}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta ))_{{\mathtt k}_+ \leq k \leq N_+}$
,
$(R_{2^k}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta ))_{{\mathtt k}_+ \leq k \leq N_+}$
,
![]() $(R_{2^k}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta '))_{{\mathtt k}_+ \leq k \leq N_+}$
,
$(R_{2^k}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta '))_{{\mathtt k}_+ \leq k \leq N_+}$
,
![]() $(R_{2^k}^{(2^{r},\Delta )}(\theta '))_{r \leq k \leq {\mathtt k}_+}$
are independent. Thus, we have
$(R_{2^k}^{(2^{r},\Delta )}(\theta '))_{r \leq k \leq {\mathtt k}_+}$
are independent. Thus, we have
 $$ \begin{align*} \nonumber & \mathbb{P}_N^{(\Delta,\kappa)}(\theta,\theta')\leq \mathbb{P}\left( Ev(r,1,E^{({\mathtt k}_+)},x,z) \right) \max_{ l_{{\mathtt k}_+}^{(N)} -1 \leq w\leq u_{{\mathtt k}_+}^{(N)}+1 }\mathbb{P}( Ev({\mathtt k}_+,1,E^{({\mathtt k}_+)},w,z') ). \end{align*} $$
$$ \begin{align*} \nonumber & \mathbb{P}_N^{(\Delta,\kappa)}(\theta,\theta')\leq \mathbb{P}\left( Ev(r,1,E^{({\mathtt k}_+)},x,z) \right) \max_{ l_{{\mathtt k}_+}^{(N)} -1 \leq w\leq u_{{\mathtt k}_+}^{(N)}+1 }\mathbb{P}( Ev({\mathtt k}_+,1,E^{({\mathtt k}_+)},w,z') ). \end{align*} $$
By the same arguments as in the proof of Lemma B.4 in the dyadic case, we have
 $$ \begin{align*} \max_{ l_{{\mathtt k}_+}^{(N)}-1 \leq w\leq u_{{\mathtt k}_+}^{(N)} +1 }\mathbb{P}( Ev({\mathtt k}_+,1,E^{({\mathtt k}_+)},w,z') )\ll_{\upsilon} & |z'|2^{-(N_+-{\mathtt k}_+)} \max_{ l_{{\mathtt k}_+}^{(N)}-1 \leq w\leq u_{{\mathtt k}_+}^{(N)} +1 }|e^{2(w-z')}\\ &\leq |z'|2^{-(N_+-{\mathtt k}_+)} e^{-2z'-(N-{\mathtt k}_+)^\alpha_-}, \end{align*} $$
$$ \begin{align*} \max_{ l_{{\mathtt k}_+}^{(N)}-1 \leq w\leq u_{{\mathtt k}_+}^{(N)} +1 }\mathbb{P}( Ev({\mathtt k}_+,1,E^{({\mathtt k}_+)},w,z') )\ll_{\upsilon} & |z'|2^{-(N_+-{\mathtt k}_+)} \max_{ l_{{\mathtt k}_+}^{(N)}-1 \leq w\leq u_{{\mathtt k}_+}^{(N)} +1 }|e^{2(w-z')}\\ &\leq |z'|2^{-(N_+-{\mathtt k}_+)} e^{-2z'-(N-{\mathtt k}_+)^\alpha_-}, \end{align*} $$
where we used that in the stated range,
![]() $|w'|\geq (N-{\mathtt k}_+)^\alpha _-/2$
, and
$|w'|\geq (N-{\mathtt k}_+)^\alpha _-/2$
, and
Finally, one gets
This concludes the proof of Lemma B.6, when ![]() is a negative power of
is a negative power of
![]() $2$
.
$2$
.
B.3.2 General case
Proof of Lemma B.4 in general case.
Fix
![]() $\upsilon>0$
, r large enough, N large enough depending on r, and
$\upsilon>0$
, r large enough, N large enough depending on r, and
![]() ${\mathtt k}$
such that
${\mathtt k}$
such that
![]() $ {\mathtt k} \leq \frac {N}{2} $
. Unlike the previous dyadic case, for
$ {\mathtt k} \leq \frac {N}{2} $
. Unlike the previous dyadic case, for
![]() $ {\mathtt k}_+ \leq l \leq N-1$
and
$ {\mathtt k}_+ \leq l \leq N-1$
and
![]() $p\leq 2^{\Delta ^{(l)}}-1$
, the random variables
$p\leq 2^{\Delta ^{(l)}}-1$
, the random variables
![]() $ I_{l,p}(\theta )$
and
$ I_{l,p}(\theta )$
and
![]() $ I_{l,p}(\theta ')$
are not rigorously independent. However, observe that for any
$ I_{l,p}(\theta ')$
are not rigorously independent. However, observe that for any
![]() ${\mathtt k}_+ \leq l \leq N-1$
, the absolute value of their correlations decreases exponentially with l. Indeed, if
${\mathtt k}_+ \leq l \leq N-1$
, the absolute value of their correlations decreases exponentially with l. Indeed, if
![]() $C_{l,p}(\theta ,\theta ') := \mathbb {E} \left ( I_{l,p}(\theta )\overline {I_{l,p}(\theta ')} \right )$
, then
$C_{l,p}(\theta ,\theta ') := \mathbb {E} \left ( I_{l,p}(\theta )\overline {I_{l,p}(\theta ')} \right )$
, then
 $$ \begin{align*} \left| C_{l,p}(\theta,\theta')\right| &=\frac{1}{{2^l+p2^{l-\Delta^{(l)}}}}\left| \sum_{j=0}^{2^{l-\Delta^{(l)}}-1} e^{i(\theta-\theta') j} \right| \leq \frac{4}{2^l ||\theta-\theta'|| } \ll 2^{{\mathtt k}-l}. \end{align*} $$
$$ \begin{align*} \left| C_{l,p}(\theta,\theta')\right| &=\frac{1}{{2^l+p2^{l-\Delta^{(l)}}}}\left| \sum_{j=0}^{2^{l-\Delta^{(l)}}-1} e^{i(\theta-\theta') j} \right| \leq \frac{4}{2^l ||\theta-\theta'|| } \ll 2^{{\mathtt k}-l}. \end{align*} $$
Since
![]() $ \mathbb {E} \left ( I_{l,p}(\theta )I_{l,p}(\theta ') \right ) = 0$
, and
$ \mathbb {E} \left ( I_{l,p}(\theta )I_{l,p}(\theta ') \right ) = 0$
, and
![]() $(I_{l,p}(\theta ), I_{l,p} (\theta '))$
is a centered complex Gaussian vector, one checks, by computing covariances, that it is possible to write
$(I_{l,p}(\theta ), I_{l,p} (\theta '))$
is a centered complex Gaussian vector, one checks, by computing covariances, that it is possible to write
 $$ \begin{align*}I_{l,p} (\theta) = \frac{C_{l,p}(\theta,\theta')}{C_{l,p} (\theta', \theta')} I_{l,p} (\theta') + I^{ind}_{l,p} (\theta, \theta'),\end{align*} $$
$$ \begin{align*}I_{l,p} (\theta) = \frac{C_{l,p}(\theta,\theta')}{C_{l,p} (\theta', \theta')} I_{l,p} (\theta') + I^{ind}_{l,p} (\theta, \theta'),\end{align*} $$
where the two terms of the sums are independent, with an expectation of the square equal to zero. Note that
 $$ \begin{align*}C_{l,p} := C_{l,p}(\theta', \theta') = \frac{2^{l-\Delta^{(l)}}}{2^l + p2^{l-\Delta^{(l)}}} = (2^{\Delta^{(l)}} + p)^{-1}\end{align*} $$
$$ \begin{align*}C_{l,p} := C_{l,p}(\theta', \theta') = \frac{2^{l-\Delta^{(l)}}}{2^l + p2^{l-\Delta^{(l)}}} = (2^{\Delta^{(l)}} + p)^{-1}\end{align*} $$
does not depend on
![]() $\theta '$
. Moreover, we have by Pythagoras’ theorem,
$\theta '$
. Moreover, we have by Pythagoras’ theorem,
 $$ \begin{align*}\mathbb{E} [|I_{l,p}^{ind}(\theta, \theta')|^2] = \mathbb{E} [|I_{l,p}(\theta)|^2] - \left|\frac{C_{l,p}(\theta, \theta')}{C_{l,p}} \right|{}^2 \mathbb{E} [|I_{l,p}(\theta')|^2] = C_{l,p} - \frac{|C_{l,p}(\theta, \theta')|^2}{C_{l,p}}.\end{align*} $$
$$ \begin{align*}\mathbb{E} [|I_{l,p}^{ind}(\theta, \theta')|^2] = \mathbb{E} [|I_{l,p}(\theta)|^2] - \left|\frac{C_{l,p}(\theta, \theta')}{C_{l,p}} \right|{}^2 \mathbb{E} [|I_{l,p}(\theta')|^2] = C_{l,p} - \frac{|C_{l,p}(\theta, \theta')|^2}{C_{l,p}}.\end{align*} $$
Using this decomposition of
![]() $I_{l,p}(\theta )$
and the measurability of the different quantities with respect to the
$I_{l,p}(\theta )$
and the measurability of the different quantities with respect to the
![]() $\sigma $
-algebras of the form
$\sigma $
-algebras of the form
![]() $\mathcal {G}_j$
, we deduce that one can write
$\mathcal {G}_j$
, we deduce that one can write
Here,
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is a Gaussian process, independent of
$(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is a Gaussian process, independent of
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},\Delta )}(\theta '))_{l\geq {\mathtt k}_+}$
, and distributed as
$(R_{2^l}^{(2^{{\mathtt k}_+},\Delta )}(\theta '))_{l\geq {\mathtt k}_+}$
, and distributed as
![]() $ ( \sqrt {\frac {1}{2}}W_{ \tau ^{({\mathtt k}_+)}_l- \mathtt {C}_l} )_{l\geq {\mathtt k}_+}$
with
$ ( \sqrt {\frac {1}{2}}W_{ \tau ^{({\mathtt k}_+)}_l- \mathtt {C}_l} )_{l\geq {\mathtt k}_+}$
with
 $$ \begin{align*}\mathtt{C}_l:= \sum_{t={\mathtt k}_+}^{l-1} \sum_{p=0}^{2^{\Delta^{(t)}} -1 } \frac{ |C_{t,p}(\theta, \theta')|^2}{C_{t,p}} .\end{align*} $$
$$ \begin{align*}\mathtt{C}_l:= \sum_{t={\mathtt k}_+}^{l-1} \sum_{p=0}^{2^{\Delta^{(t)}} -1 } \frac{ |C_{t,p}(\theta, \theta')|^2}{C_{t,p}} .\end{align*} $$
Notice that
![]() $\mathtt {C}=\mathtt {C}^{({\mathtt k}_+)}$
implicitly depends of
$\mathtt {C}=\mathtt {C}^{({\mathtt k}_+)}$
implicitly depends of
![]() ${\mathtt k}_+$
.
${\mathtt k}_+$
.
![]() $(E_{2^l}^{(2^r)} )_{l\geq {\mathtt k}_+}$
, however, is defined by
$(E_{2^l}^{(2^r)} )_{l\geq {\mathtt k}_+}$
, however, is defined by

Furthermore, notice that:
Fact 1:
For any
![]() $l\geq {\mathtt k}_+$
,
$l\geq {\mathtt k}_+$
,
 $$ \begin{align*} |E_{2^{l+1}}^{(2^{l})}| \leq |E|_{2^{l+1}}^{(2^{l})}:= \sum_{p=0}^{2^{\Delta^{(l)}} -1 } |C_{l,p}(\theta, \theta')| (2^{\Delta^{(l)}}+p ) |I_{l,p}(\theta') | \end{align*} $$
$$ \begin{align*} |E_{2^{l+1}}^{(2^{l})}| \leq |E|_{2^{l+1}}^{(2^{l})}:= \sum_{p=0}^{2^{\Delta^{(l)}} -1 } |C_{l,p}(\theta, \theta')| (2^{\Delta^{(l)}}+p ) |I_{l,p}(\theta') | \end{align*} $$
is measurable with respect to the sigma field
![]() $\sigma \left ( {\mathcal N}_t^{\mathbb C},\, t\in [|2^{l},2^{l+1}-1|]\right )$
.
$\sigma \left ( {\mathcal N}_t^{\mathbb C},\, t\in [|2^{l},2^{l+1}-1|]\right )$
.
Fact 2:
The process
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+} $
is independent of the couple
$(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+} $
is independent of the couple
![]() $( R_{2^l}^{(2^{{\mathtt k}_+},\Delta )}(\theta ') , |E|_{2^l}^{(2^r)})_{l\geq {\mathtt k}_+}$
.
$( R_{2^l}^{(2^{{\mathtt k}_+},\Delta )}(\theta ') , |E|_{2^l}^{(2^r)})_{l\geq {\mathtt k}_+}$
.
Fact 3:
![]() $\sup _{l\geq {\mathtt k}_+}|\mathtt {C}_l| \ll 2^{-\Delta ^{({\mathtt k})}}$
if r is large enough. Indeed, in this case, since
$\sup _{l\geq {\mathtt k}_+}|\mathtt {C}_l| \ll 2^{-\Delta ^{({\mathtt k})}}$
if r is large enough. Indeed, in this case, since
![]() ${\mathtt k}_+ \geq 3 \Delta ^{({\mathtt k})} \geq 3e^{\sqrt {\log r}}$
is also large, we have
${\mathtt k}_+ \geq 3 \Delta ^{({\mathtt k})} \geq 3e^{\sqrt {\log r}}$
is also large, we have
 $$ \begin{align*} \sup_{l\geq {\mathtt k}_+}|\mathtt{C}_l| & \ll \sum_{l = {\mathtt k}_+}^{\infty} \sum_{p=0}^{2^{\Delta^{(l)}} - 1} (2^{{\mathtt k} - l})^2 (2^{\Delta^{(l)}} + p) \ll \sum_{l = {\mathtt k}_+}^{\infty} 2^{2{\mathtt k} - 2l + 2 \Delta^{(l)}} \ll \sum_{l = {\mathtt k}_+}^{\infty} 2^{2{\mathtt k} - 2l + 2e^{\sqrt{\log r}}+ 200 \log^2 l} \\ & \ll \sum_{{\mathtt k}_+ \leq l \leq 100 {\mathtt k}} 2^{2{\mathtt k} - 2 l + 2e^{\sqrt{\log r}} + 300 \log^2 {\mathtt k}} + \sum_{l \geq \max (100{\mathtt k}, {\mathtt k}_+)} 2^{2{\mathtt k} - 2 l + 0.8 {\mathtt k}_+ + 200 \log^2 l} \\ & \ll \sum_{{\mathtt k}_+ \leq l \leq 100 {\mathtt k}} 2^{2 {\mathtt k} - 2 l + 3 \Delta^{({\mathtt k})}} + \sum_{l\geq \max (100{\mathtt k}, {\mathtt k}_+)} 2^{2 {\mathtt k} + 0.8 {\mathtt k}_+ - 1.99 l} \\ & \ll 2^{2 {\mathtt k} - 2 {\mathtt k}_+ + 3 \Delta^{({\mathtt k})}} + 2^{2 {\mathtt k} + 0.8 {\mathtt k}_+ - 1.99[(0.05)(100 {\mathtt k}) + 0.95 ({\mathtt k}_+)]} \ll 2^{- 3 \Delta^{({\mathtt k})}} + 2^{- {\mathtt k}_+} \ll 2^{- 3 \Delta^{({\mathtt k})}}. \end{align*} $$
$$ \begin{align*} \sup_{l\geq {\mathtt k}_+}|\mathtt{C}_l| & \ll \sum_{l = {\mathtt k}_+}^{\infty} \sum_{p=0}^{2^{\Delta^{(l)}} - 1} (2^{{\mathtt k} - l})^2 (2^{\Delta^{(l)}} + p) \ll \sum_{l = {\mathtt k}_+}^{\infty} 2^{2{\mathtt k} - 2l + 2 \Delta^{(l)}} \ll \sum_{l = {\mathtt k}_+}^{\infty} 2^{2{\mathtt k} - 2l + 2e^{\sqrt{\log r}}+ 200 \log^2 l} \\ & \ll \sum_{{\mathtt k}_+ \leq l \leq 100 {\mathtt k}} 2^{2{\mathtt k} - 2 l + 2e^{\sqrt{\log r}} + 300 \log^2 {\mathtt k}} + \sum_{l \geq \max (100{\mathtt k}, {\mathtt k}_+)} 2^{2{\mathtt k} - 2 l + 0.8 {\mathtt k}_+ + 200 \log^2 l} \\ & \ll \sum_{{\mathtt k}_+ \leq l \leq 100 {\mathtt k}} 2^{2 {\mathtt k} - 2 l + 3 \Delta^{({\mathtt k})}} + \sum_{l\geq \max (100{\mathtt k}, {\mathtt k}_+)} 2^{2 {\mathtt k} + 0.8 {\mathtt k}_+ - 1.99 l} \\ & \ll 2^{2 {\mathtt k} - 2 {\mathtt k}_+ + 3 \Delta^{({\mathtt k})}} + 2^{2 {\mathtt k} + 0.8 {\mathtt k}_+ - 1.99[(0.05)(100 {\mathtt k}) + 0.95 ({\mathtt k}_+)]} \ll 2^{- 3 \Delta^{({\mathtt k})}} + 2^{- {\mathtt k}_+} \ll 2^{- 3 \Delta^{({\mathtt k})}}. \end{align*} $$
It means (see [Reference Chhaibi, Madaule and NajnudelCMN18, Lemma A.5]) that the process
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is very ‘similar’ to the process
$(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is very ‘similar’ to the process
![]() $ \sqrt {\frac {1}{2}} (W_{ \tau _{l}^{({\mathtt k}_+)}})_{l\geq {\mathtt k}_+ }$
. Moreover, if for
$ \sqrt {\frac {1}{2}} (W_{ \tau _{l}^{({\mathtt k}_+)}})_{l\geq {\mathtt k}_+ }$
. Moreover, if for
![]() ${\mathtt k}_+ \leq r \leq l$
,
${\mathtt k}_+ \leq r \leq l$
,
![]() $\mathtt {C}_l^{(r)} := \mathtt {C}_l - \mathtt {C}_r$
, then we have for r large enough,
$\mathtt {C}_l^{(r)} := \mathtt {C}_l - \mathtt {C}_r$
, then we have for r large enough,
Fact 4:
![]() $|E|$
is small. For any
$|E|$
is small. For any
![]() $m \geq 0$
,
$m \geq 0$
,
![]() $l\geq {\mathtt k}_+$
, we introduce the event
$l\geq {\mathtt k}_+$
, we introduce the event
For some universal constants
![]() $c, c'> 0$
, and
$c, c'> 0$
, and
![]() $m \geq 1/2$
, the probability of
$m \geq 1/2$
, the probability of
![]() $\mathtt {E}_m^{(l)} $
is smaller than
$\mathtt {E}_m^{(l)} $
is smaller than
 $$ \begin{align} \nonumber \mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \leq 2^{\Delta^{(l)}} \mathbb{P}\left( c 2^{{\mathtt k}-l} |I_{l,0}(\theta')|\geq m 2^{-\frac{9}{4}\Delta^{(l)}} \right) &\ll 2^{\Delta^{(l)}} e^{- c'm^2 2^{2(l-{\mathtt k} - \frac{7}{4}\Delta^{(l)}) } } \\ &\ll e^{- c'm^2 2^{2(l-{\mathtt k} - 2\Delta^{(l)}) } }. \end{align} $$
$$ \begin{align} \nonumber \mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \leq 2^{\Delta^{(l)}} \mathbb{P}\left( c 2^{{\mathtt k}-l} |I_{l,0}(\theta')|\geq m 2^{-\frac{9}{4}\Delta^{(l)}} \right) &\ll 2^{\Delta^{(l)}} e^{- c'm^2 2^{2(l-{\mathtt k} - \frac{7}{4}\Delta^{(l)}) } } \\ &\ll e^{- c'm^2 2^{2(l-{\mathtt k} - 2\Delta^{(l)}) } }. \end{align} $$
For r (and then
![]() ${\mathtt k}_+$
and l) large enough and
${\mathtt k}_+$
and l) large enough and
![]() $l \leq 100 {\mathtt k}$
,
$l \leq 100 {\mathtt k}$
,
![]() $2\Delta ^{(l)} \leq 3 \Delta ^{({\mathtt k})} +(\log (c')/\log 4)$
, and then,
$2\Delta ^{(l)} \leq 3 \Delta ^{({\mathtt k})} +(\log (c')/\log 4)$
, and then,
 $$ \begin{align*}\mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \ll e^{-m^2 2^{2(l-{\mathtt k}_+)} }.\end{align*} $$
$$ \begin{align*}\mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \ll e^{-m^2 2^{2(l-{\mathtt k}_+)} }.\end{align*} $$
If r is large enough and
![]() $l \geq \sup (100 {\mathtt k}, {\mathtt k}_+)$
(and therefore, also large), we use that
$l \geq \sup (100 {\mathtt k}, {\mathtt k}_+)$
(and therefore, also large), we use that
 $$ \begin{align*} 2(l-{\mathtt k}-2\Delta^{(l)})&=l-{\mathtt k}_++(l-2{\mathtt k}+{\mathtt k}_+-4\Delta^{(l)}) =l-{\mathtt k}_++(l-k+3\Delta^{({\mathtt k})}-4\Delta^{(l)})\\ &\geq l-{\mathtt k}+(l-{\mathtt k}-400(\log l)^2)\geq l-{\mathtt k}+(0.99 l-400 (\log l)^2)\\ &\geq l-{\mathtt k}-\log c', \end{align*} $$
$$ \begin{align*} 2(l-{\mathtt k}-2\Delta^{(l)})&=l-{\mathtt k}_++(l-2{\mathtt k}+{\mathtt k}_+-4\Delta^{(l)}) =l-{\mathtt k}_++(l-k+3\Delta^{({\mathtt k})}-4\Delta^{(l)})\\ &\geq l-{\mathtt k}+(l-{\mathtt k}-400(\log l)^2)\geq l-{\mathtt k}+(0.99 l-400 (\log l)^2)\\ &\geq l-{\mathtt k}-\log c', \end{align*} $$
and then, using (B.32),
 $$ \begin{align*}\mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \ll e^{-c' m^2 2^{2(l - {\mathtt k} - 2\Delta^{(l)})}} \leq e^{-m^2(l-{\mathtt k}_+)}. \end{align*} $$
$$ \begin{align*}\mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \ll e^{-c' m^2 2^{2(l - {\mathtt k} - 2\Delta^{(l)})}} \leq e^{-m^2(l-{\mathtt k}_+)}. \end{align*} $$
Hence, in any case, for r large and
![]() $l \geq {\mathtt k}_+$
,
$l \geq {\mathtt k}_+$
,
 $$ \begin{align*}\mathbb{P}\left(\mathtt{E}_m^{(l)}\right)=\mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \ll e^{-m^2 2^{l -{\mathtt k}_+}}.\end{align*} $$
$$ \begin{align*}\mathbb{P}\left(\mathtt{E}_m^{(l)}\right)=\mathbb{P}\left( |E|_{2^{l+1}}^{(2^l)} \geq 2^{-\frac{\Delta^{(l)}}{4}}m \right) \ll e^{-m^2 2^{l -{\mathtt k}_+}}.\end{align*} $$
When
![]() $\mathbf {{\mathtt k}_+\leq r}$
: Using the decomposition (B.30) and Fact 2, and noticing that
$\mathbf {{\mathtt k}_+\leq r}$
: Using the decomposition (B.30) and Fact 2, and noticing that
![]() $\sum _{l=r}^{+\infty } m 2^{-\frac {\Delta ^{(l)}}{4}} \leq m2^{-e^{\sqrt {\log r}}}$
, for r large enough, we can affirm that
$\sum _{l=r}^{+\infty } m 2^{-\frac {\Delta ^{(l)}}{4}} \leq m2^{-e^{\sqrt {\log r}}}$
, for r large enough, we can affirm that
 $$ \begin{align} \nonumber &\mathbb{P}_N(\theta,\theta')\leq \mathbb{P}\left( Ev(r,0,0,x,z) \right) \mathbb{P}\left( Ev(r, 2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right) \\ &\qquad +\sum_{m\geq 1} \mathbb{P}\left( Ev(r,0,0,x,z) ,\, \cup_{j\in [|r,N_+|]}\mathtt{E}_m^{(j)} \right) \mathbb{P}\left( Ev(r,(m+1)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right), \end{align} $$
$$ \begin{align} \nonumber &\mathbb{P}_N(\theta,\theta')\leq \mathbb{P}\left( Ev(r,0,0,x,z) \right) \mathbb{P}\left( Ev(r, 2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right) \\ &\qquad +\sum_{m\geq 1} \mathbb{P}\left( Ev(r,0,0,x,z) ,\, \cup_{j\in [|r,N_+|]}\mathtt{E}_m^{(j)} \right) \mathbb{P}\left( Ev(r,(m+1)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right), \end{align} $$
where the Brownian motion involved in the event
![]() $Ev(r,0,0,x,z)$
is suitably coupled with the complex Gaussian random walk whose increments are of the form
$Ev(r,0,0,x,z)$
is suitably coupled with the complex Gaussian random walk whose increments are of the form ![]() for
for
![]() $r \leq l \leq N-1$
and
$r \leq l \leq N-1$
and
![]() $0 \leq p \leq 2^{\Delta ^{(l)}} - 1$
.
$0 \leq p \leq 2^{\Delta ^{(l)}} - 1$
.
By using Equation (B.23) and then the fact that
![]() $\sup _{r \leq j \leq N}\mathtt {C}^{(r)}_j \leq 2^{1-e^{\sqrt {\log r}}}$
if r is large enough, we have for any
$\sup _{r \leq j \leq N}\mathtt {C}^{(r)}_j \leq 2^{1-e^{\sqrt {\log r}}}$
if r is large enough, we have for any
![]() $m \geq 0$
,
$m \geq 0$
,
 $$ \begin{align} \nonumber &\mathbb{P}\left( Ev(r,(m+1)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right) \\ \nonumber &\leq e^{-2(x'-z')}2^{r -N_+} e^{2\upsilon + 2(m+1)2^{-e^{\sqrt{\log r}}} - \mathtt{C}^{(r)}_N}N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,(m+1)2^{-e^{\sqrt{\log r}}} + \sup_{r \leq j \leq N}\mathtt{C}^{(r)}_j,\mathtt{C}^{(r)},x',z') \right) \\ &\leq e^{-2(x'-z')} 2^{r -N_+} e^{2\upsilon + 2(m+1) 2^{-e^{\sqrt{\log r}}} - \mathtt{C}^{(r)}_N}N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,2(m+2)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z') \right) . \end{align} $$
$$ \begin{align} \nonumber &\mathbb{P}\left( Ev(r,(m+1)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right) \\ \nonumber &\leq e^{-2(x'-z')}2^{r -N_+} e^{2\upsilon + 2(m+1)2^{-e^{\sqrt{\log r}}} - \mathtt{C}^{(r)}_N}N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,(m+1)2^{-e^{\sqrt{\log r}}} + \sup_{r \leq j \leq N}\mathtt{C}^{(r)}_j,\mathtt{C}^{(r)},x',z') \right) \\ &\leq e^{-2(x'-z')} 2^{r -N_+} e^{2\upsilon + 2(m+1) 2^{-e^{\sqrt{\log r}}} - \mathtt{C}^{(r)}_N}N^{\frac{3}{2}} \mathbb{P}\left( GEv(r,2(m+2)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z') \right) . \end{align} $$
Now, we invoke [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6] as, by the Fact 3, with the notation of the corollary,
![]() $||E||_1 \leq 1$
if r is large enough. Thus, we deduce, for N large enough depending on r, that
$||E||_1 \leq 1$
if r is large enough. Thus, we deduce, for N large enough depending on r, that
 $$ \begin{align} \mathbb{P}\left( Ev(r,(m+1)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right) \ll_{\upsilon} |x'z'|e^{2(x'-z')}2^{r -N} e^{ 2m 2^{-\frac{r}{400}} } (1 + (m+1) 2^{- e^{\sqrt{\log r}}})^3 . \end{align} $$
$$ \begin{align} \mathbb{P}\left( Ev(r,(m+1)2^{-e^{\sqrt{\log r}}}, \mathtt{C}^{(r)},x',z')\right) \ll_{\upsilon} |x'z'|e^{2(x'-z')}2^{r -N} e^{ 2m 2^{-\frac{r}{400}} } (1 + (m+1) 2^{- e^{\sqrt{\log r}}})^3 . \end{align} $$
Similarly, to compute
![]() $\mathbb{P} \left (Ev(r,0,0,x,z) ,\, \cup _{j\in [|r,N_+|]}\mathtt {E}_m^{(j)}\right )$
, we will apply the Girsanov transform with the density
$\mathbb{P} \left (Ev(r,0,0,x,z) ,\, \cup _{j\in [|r,N_+|]}\mathtt {E}_m^{(j)}\right )$
, we will apply the Girsanov transform with the density
![]() $e^{\sqrt {2 }W_{\tau _{N_+}^{(r)}}- \tau _{N_+}^{(r)} }$
. It requires to study what is the effect of this density on the event
$e^{\sqrt {2 }W_{\tau _{N_+}^{(r)}}- \tau _{N_+}^{(r)} }$
. It requires to study what is the effect of this density on the event
![]() $ \cup _{j\in [|r,N_+|]}\mathtt {E}_m^{(j)}$
. The increments of the complex random walk, which were
$ \cup _{j\in [|r,N_+|]}\mathtt {E}_m^{(j)}$
. The increments of the complex random walk, which were ![]() before the Girsanov transform, increase by
before the Girsanov transform, increase by
![]() $\sigma ^{-1} C_{j,p}$
afterward. Hence, between the two situations, before and after the Girsanov transform,
$\sigma ^{-1} C_{j,p}$
afterward. Hence, between the two situations, before and after the Girsanov transform,
![]() $|E|_{2^{j+1}}^{(2^{j})}$
, defined as the sum, for
$|E|_{2^{j+1}}^{(2^{j})}$
, defined as the sum, for
![]() $0 \leq p \leq 2^{\Delta ^{(j)}} - 1$
, of the absolute value of the increments of the random walk multiplied by
$0 \leq p \leq 2^{\Delta ^{(j)}} - 1$
, of the absolute value of the increments of the random walk multiplied by
![]() $|C_{j,p} (\theta , \theta ')|/C_{j,p}$
, vary, for r large enough, at most by
$|C_{j,p} (\theta , \theta ')|/C_{j,p}$
, vary, for r large enough, at most by
![]() $ 2^{2\Delta ^{(j)} +{\mathtt k} -j}$
, since
$ 2^{2\Delta ^{(j)} +{\mathtt k} -j}$
, since
 $$ \begin{align*}\sum_{p = 0}^{2^{\Delta^{(j)}}-1} |C_{j,p} (\theta, \theta')| \ll 2^{\Delta^{(j)}+ {\mathtt k} - j}.\end{align*} $$
$$ \begin{align*}\sum_{p = 0}^{2^{\Delta^{(j)}}-1} |C_{j,p} (\theta, \theta')| \ll 2^{\Delta^{(j)}+ {\mathtt k} - j}.\end{align*} $$
Now, for
![]() $j\geq r\geq {\mathtt k}_+$
and r large enough, we have
$j\geq r\geq {\mathtt k}_+$
and r large enough, we have
Indeed, for
![]() $j \leq 100 {\mathtt k}$
,
$j \leq 100 {\mathtt k}$
,
and for
![]() $j \geq \max ({\mathtt k}_+, 100 {\mathtt k})$
(necessarily large, since r is large),
$j \geq \max ({\mathtt k}_+, 100 {\mathtt k})$
(necessarily large, since r is large),
 $$ \begin{align*} 2^{2\Delta^{(j)} +{\mathtt k} -j} & \leq 2^{2\Delta^{(j)} -0.99j} \leq 2^{e^{\sqrt{\log r}}+ 200 \log^2 j -0.99j} \leq 2^{e^{\sqrt{\log j}}+ 200 \log^2 j -0.99j} \\ & \leq 2^{-0.96j} \leq 2^{-e^{\sqrt{\log r}} - 0.94j} \leq 2^{-\Delta^{(j)}}. \end{align*} $$
$$ \begin{align*} 2^{2\Delta^{(j)} +{\mathtt k} -j} & \leq 2^{2\Delta^{(j)} -0.99j} \leq 2^{e^{\sqrt{\log r}}+ 200 \log^2 j -0.99j} \leq 2^{e^{\sqrt{\log j}}+ 200 \log^2 j -0.99j} \\ & \leq 2^{-0.96j} \leq 2^{-e^{\sqrt{\log r}} - 0.94j} \leq 2^{-\Delta^{(j)}}. \end{align*} $$
Hence, if for
![]() $m \geq 1$
, before (respectively after) the Girsanov transform,
$m \geq 1$
, before (respectively after) the Girsanov transform,
![]() $ \cup _{j\in [|r,N_+|]}\mathtt {E}_m^{(j)} $
occurs, then
$ \cup _{j\in [|r,N_+|]}\mathtt {E}_m^{(j)} $
occurs, then
![]() $ \cup _{j\in [|r,N_+|]}\mathtt {E}_{\frac {1}{2} m}^{(j)} $
still occurs after (respectively before) the transform. Finally, we get, for any
$ \cup _{j\in [|r,N_+|]}\mathtt {E}_{\frac {1}{2} m}^{(j)} $
still occurs after (respectively before) the transform. Finally, we get, for any
![]() $m \geq 1$
,
$m \geq 1$
,

As
![]() $\mathtt {E}_{\frac {m}{2}}^{(l)}$
is measurable with respect to
$\mathtt {E}_{\frac {m}{2}}^{(l)}$
is measurable with respect to
![]() $\sigma ( {\mathcal N}_t^{\mathbb C},\, t\in [|2^{l},2^{l+1}-1|])$
, by applying [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6] and using the Fact 4, we get, for r large enough and N large enough depending on r,
$\sigma ( {\mathcal N}_t^{\mathbb C},\, t\in [|2^{l},2^{l+1}-1|])$
, by applying [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6] and using the Fact 4, we get, for r large enough and N large enough depending on r,
 $$ \begin{align*} \mathbb{P}\left( GEv(r,0,0,x,z)\cap \left\{ \cup_{j\in [|r,N_+|]}\mathtt{E}_{\frac{1}{2} m}^{(j)} \right\} \right) & \ll_{\upsilon} |xz| e^{2(x-z)}N^{-\frac{3}{2}} \sum_{j\geq r} \sqrt{\mathbb{P}(\mathtt{E}_{\frac{1}{2}m}^{(j)}) }\\ & \ll |xz| e^{2(x-z)} N^{-\frac{3}{2}} \sum_{j \geq r} e^{-(m^2/8) 2^{j - {\mathtt k}_+}}\\& \ll |xz| e^{2(x-z)} N^{-\frac{3}{2}} e^{-2^{r-{\mathtt k}_+}m^2/8}, \end{align*} $$
$$ \begin{align*} \mathbb{P}\left( GEv(r,0,0,x,z)\cap \left\{ \cup_{j\in [|r,N_+|]}\mathtt{E}_{\frac{1}{2} m}^{(j)} \right\} \right) & \ll_{\upsilon} |xz| e^{2(x-z)}N^{-\frac{3}{2}} \sum_{j\geq r} \sqrt{\mathbb{P}(\mathtt{E}_{\frac{1}{2}m}^{(j)}) }\\ & \ll |xz| e^{2(x-z)} N^{-\frac{3}{2}} \sum_{j \geq r} e^{-(m^2/8) 2^{j - {\mathtt k}_+}}\\& \ll |xz| e^{2(x-z)} N^{-\frac{3}{2}} e^{-2^{r-{\mathtt k}_+}m^2/8}, \end{align*} $$
since
![]() $r \geq {\mathtt k}_+$
.
$r \geq {\mathtt k}_+$
.
By combining this inequality with (B.35) and (B.33), we get
 $$ \begin{align} \nonumber & \mathbb{P}_N(\theta, \theta',x,z,x',z')\ll_{\upsilon} |xzx'z'|e^{2(x-z+x'-z')}2^{2 (r-N_+)} \\ & \nonumber \qquad+ \sum_{m\geq 1} |xzx'z'|e^{2(x-z+x'-z')}2^{r-N_+} 2^{2m 2^{-e^{\sqrt{\log r}} }} (1+ (m+1) 2^{-e^{\sqrt{\log r}}})^3 2^{r-N} e^{-(m^2/8) 2^{r-{\mathtt k}_+}} \\ & \leq |xzx'z'|e^{2(x-z+x'-z')}2^{2 (r-N_+)} \left[ 1+ \left(\sum_{m \geq 1} 2^{2m} (1+m)^3 e^{-m^2/8} \right) e^{-(1/8)(2^{r-{\mathtt k}_+} - 1)} \right]\nonumber\\ & \ll|xzx'z'|e^{2(x-z+x'-z')}2^{2 (r-N_+)} , \end{align} $$
$$ \begin{align} \nonumber & \mathbb{P}_N(\theta, \theta',x,z,x',z')\ll_{\upsilon} |xzx'z'|e^{2(x-z+x'-z')}2^{2 (r-N_+)} \\ & \nonumber \qquad+ \sum_{m\geq 1} |xzx'z'|e^{2(x-z+x'-z')}2^{r-N_+} 2^{2m 2^{-e^{\sqrt{\log r}} }} (1+ (m+1) 2^{-e^{\sqrt{\log r}}})^3 2^{r-N} e^{-(m^2/8) 2^{r-{\mathtt k}_+}} \\ & \leq |xzx'z'|e^{2(x-z+x'-z')}2^{2 (r-N_+)} \left[ 1+ \left(\sum_{m \geq 1} 2^{2m} (1+m)^3 e^{-m^2/8} \right) e^{-(1/8)(2^{r-{\mathtt k}_+} - 1)} \right]\nonumber\\ & \ll|xzx'z'|e^{2(x-z+x'-z')}2^{2 (r-N_+)} , \end{align} $$
which concludes the case
![]() ${\mathtt k}_+\leq r$
.
${\mathtt k}_+\leq r$
.
When
![]() $\mathbf {{\mathtt k}_+\geq r}$
: Using the decomposition (B.30) and Fact 2 and noticing that
$\mathbf {{\mathtt k}_+\geq r}$
: Using the decomposition (B.30) and Fact 2 and noticing that
![]() $\sum _{l={\mathtt k}_+}^{+\infty } m 2^{-\frac {\Delta ^{(l)}}{4}}\leq m2^{-e^{\sqrt {\log r}}/8}$
for r large enough, we can affirm that
$\sum _{l={\mathtt k}_+}^{+\infty } m 2^{-\frac {\Delta ^{(l)}}{4}}\leq m2^{-e^{\sqrt {\log r}}/8}$
for r large enough, we can affirm that
 $$ \begin{align} &\qquad\qquad\qquad \sup_{ l_{{\mathtt k}_+}^{(N)} \leq x'+w\leq u_{{\mathtt k}_+}^{(N)} } \mathbb{P}\left( Ev({\mathtt k}_+,(m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},x'+w,z')\right). \end{align} $$
$$ \begin{align} &\qquad\qquad\qquad \sup_{ l_{{\mathtt k}_+}^{(N)} \leq x'+w\leq u_{{\mathtt k}_+}^{(N)} } \mathbb{P}\left( Ev({\mathtt k}_+,(m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},x'+w,z')\right). \end{align} $$
By a similar computation as what we have done in the case
![]() ${\mathtt k}_+ \leq r$
, we get
${\mathtt k}_+ \leq r$
, we get
However, by using Equation (B.23), for any
![]() $w'\in [ l_{{\mathtt k}_+}^{(N)} , u_{{\mathtt k}_+}^{(N)} ]$
, we obtain
$w'\in [ l_{{\mathtt k}_+}^{(N)} , u_{{\mathtt k}_+}^{(N)} ]$
, we obtain
 $$ \begin{align} \nonumber &\mathbb{P}\left( Ev({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z')\right) \\ \nonumber &\ll_{\upsilon} e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} \mathbb{P}\left( GEv({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} + \sup_{{\mathtt k}_+ \leq j \leq N} |\mathtt{C}_j|,\mathtt{C},w',z') \right) \\ & \leq e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} \mathbb{P}\left( GEv({\mathtt k}_+, 2(m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z') \right), \end{align} $$
$$ \begin{align} \nonumber &\mathbb{P}\left( Ev({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z')\right) \\ \nonumber &\ll_{\upsilon} e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} \mathbb{P}\left( GEv({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} + \sup_{{\mathtt k}_+ \leq j \leq N} |\mathtt{C}_j|,\mathtt{C},w',z') \right) \\ & \leq e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} \mathbb{P}\left( GEv({\mathtt k}_+, 2(m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z') \right), \end{align} $$
where we used that
![]() $\sup _{j\geq {\mathtt k}_+} |\mathtt {C}_j|\leq 2^{-\Delta ^{({\mathtt k})}} \leq \frac {1}{2}(m+1) 2^{-e^{\sqrt {\log r}}/8}$
.
$\sup _{j\geq {\mathtt k}_+} |\mathtt {C}_j|\leq 2^{-\Delta ^{({\mathtt k})}} \leq \frac {1}{2}(m+1) 2^{-e^{\sqrt {\log r}}/8}$
.
For
![]() ${\mathtt k}_+ \leq N/4$
, we can use [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6] to deduce, for
${\mathtt k}_+ \leq N/4$
, we can use [Reference Chhaibi, Madaule and NajnudelCMN18, Corollary A.6] to deduce, for
![]() $w'\leq u_{{\mathtt k}^+}^{(N)}=- ({\mathtt k}_+)^{\alpha _-}$
,
$w'\leq u_{{\mathtt k}^+}^{(N)}=- ({\mathtt k}_+)^{\alpha _-}$
,
 $$ \begin{align} &\mathbb{P}\left( Ev({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z')\right) \nonumber\\& \ll e^{2(w'-z')} 2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-e^{\sqrt{\log r}}/8} } (1+ 2(m+1) 2^{-e^{\sqrt{\log r}}/8} )^3 |w'z'| \nonumber \\ & \ll_{\upsilon} |w'z'| e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{3(m +1)- ({\mathtt k}_+)^{\alpha_-}} . \end{align} $$
$$ \begin{align} &\mathbb{P}\left( Ev({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z')\right) \nonumber\\& \ll e^{2(w'-z')} 2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-e^{\sqrt{\log r}}/8} } (1+ 2(m+1) 2^{-e^{\sqrt{\log r}}/8} )^3 |w'z'| \nonumber \\ & \ll_{\upsilon} |w'z'| e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{3(m +1)- ({\mathtt k}_+)^{\alpha_-}} . \end{align} $$
For
![]() ${\mathtt k}_+ \geq N/4$
, we bound the probability of the
${\mathtt k}_+ \geq N/4$
, we bound the probability of the
![]() $GEv$
event by
$GEv$
event by
![]() $1$
and use the fact that
$1$
and use the fact that
![]() $w'\leq - 0.9({\mathtt k}_+ )^{\alpha _-}$
(the factor
$w'\leq - 0.9({\mathtt k}_+ )^{\alpha _-}$
(the factor
![]() $0.9$
coming from the case
$0.9$
coming from the case
![]() ${\mathtt k} \leq N/2 \leq {\mathtt k}_+$
). We then get
${\mathtt k} \leq N/2 \leq {\mathtt k}_+$
). We then get
 $$ \begin{align*} \mathbb{P}\left( Ev({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z')\right) & \ll_{\upsilon} |w'z'|e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-e^{\sqrt{\log r}}/8} }N^{\frac{3}{2}} \\ & \ll_{\upsilon} |z'|e^{-2z'}2^{{\mathtt k}_+ -N_+} e^{2m+2} e^{-({\mathtt k}_+ )^{\alpha_-}} (N^{3/2} e^{-0.8({\mathtt k}_+ )^{\alpha_-}}) \\ & \ll|z'|e^{-2z'} 2^{{\mathtt k}_+ -N_+} e^{2m+2} e^{-({\mathtt k}_+ )^{\alpha_-}}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left( Ev({\mathtt k}_+, (m+1) 2^{-e^{\sqrt{\log r}}/8} ,\mathtt{C},w',z')\right) & \ll_{\upsilon} |w'z'|e^{2(w'-z')}2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-e^{\sqrt{\log r}}/8} }N^{\frac{3}{2}} \\ & \ll_{\upsilon} |z'|e^{-2z'}2^{{\mathtt k}_+ -N_+} e^{2m+2} e^{-({\mathtt k}_+ )^{\alpha_-}} (N^{3/2} e^{-0.8({\mathtt k}_+ )^{\alpha_-}}) \\ & \ll|z'|e^{-2z'} 2^{{\mathtt k}_+ -N_+} e^{2m+2} e^{-({\mathtt k}_+ )^{\alpha_-}}. \end{align*} $$
This again implies (B.41). Finally, by combining this equation with (B.39) and (B.37), we get
 $$ \begin{align*} \mathbb{P}_{N}(\theta, \theta')& \ll_{\upsilon} |xzz'|e^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N_+} e^{- ({\mathtt k}_+)^{\alpha_-}} \sum_{m\geq 0} e^{3m+3-(m^2/8)}\\ & \ll |xzz'|e^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N_+} e^{- ({\mathtt k}_+)^{\alpha_-}}, \end{align*} $$
$$ \begin{align*} \mathbb{P}_{N}(\theta, \theta')& \ll_{\upsilon} |xzz'|e^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N_+} e^{- ({\mathtt k}_+)^{\alpha_-}} \sum_{m\geq 0} e^{3m+3-(m^2/8)}\\ & \ll |xzz'|e^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N_+} e^{- ({\mathtt k}_+)^{\alpha_-}}, \end{align*} $$
which concludes the proof of Lemma B.4.
Proof of Lemma B.5.
We can use (B.34) to get (for r large enough and N large enough depending on r)
 $$ \begin{align*} &\mathbb{P}(Ev(r,0,0,x,z)) \mathbb{P}(Ev(r, 2^{-e^{\sqrt{\log r}}/8} , \mathtt{C}^{(r)}, x',z')) \\ & \leq e^{2(x-z+x'-z')}e^{4 \upsilon + 2^{1-e^{\sqrt{\log r}}/8}} 2^{2(r-N_+)} N^{3} \mathbb{P}(GEv(r,0,0,x,z)) \mathbb{P}(GEv(r,2^{1-e^{\sqrt{\log r}}/8} ,\mathtt{C}^{(r)},x',z')), \end{align*} $$
$$ \begin{align*} &\mathbb{P}(Ev(r,0,0,x,z)) \mathbb{P}(Ev(r, 2^{-e^{\sqrt{\log r}}/8} , \mathtt{C}^{(r)}, x',z')) \\ & \leq e^{2(x-z+x'-z')}e^{4 \upsilon + 2^{1-e^{\sqrt{\log r}}/8}} 2^{2(r-N_+)} N^{3} \mathbb{P}(GEv(r,0,0,x,z)) \mathbb{P}(GEv(r,2^{1-e^{\sqrt{\log r}}/8} ,\mathtt{C}^{(r)},x',z')), \end{align*} $$
and then, by the majorization of the second term of (B.33) which is involved in (B.36),
 $$ \begin{align*} & \mathbb{P}_N(\theta, \theta',x,z,x',z')\\ &\leq e^{2(x-z+x'-z')} e^{4 \upsilon + 2^{1-e^{\sqrt{\log r}}/8}} 2^{2(r-N_+)} N^{3} \mathbb{P}(GEv(r,0,0,x,z)) \mathbb{P}(GEv(r,2^{1-e^{\sqrt{\log r}}/8} ,\mathtt{C}^{(r)},x',z'))\\ &+ \mathcal{O}_{\upsilon} \left( 2^{2(r-N_+)} e^{-\frac{2^{r-{\mathtt k}_+} - 1}{8}} \right). \end{align*} $$
$$ \begin{align*} & \mathbb{P}_N(\theta, \theta',x,z,x',z')\\ &\leq e^{2(x-z+x'-z')} e^{4 \upsilon + 2^{1-e^{\sqrt{\log r}}/8}} 2^{2(r-N_+)} N^{3} \mathbb{P}(GEv(r,0,0,x,z)) \mathbb{P}(GEv(r,2^{1-e^{\sqrt{\log r}}/8} ,\mathtt{C}^{(r)},x',z'))\\ &+ \mathcal{O}_{\upsilon} \left( 2^{2(r-N_+)} e^{-\frac{2^{r-{\mathtt k}_+} - 1}{8}} \right). \end{align*} $$
Hence, we have
 $$ \begin{align*} \mathbb{P}_N(\theta, \theta') & \leq e^{2(x-z+x'-z')} e^{4 \upsilon + 2^{1 -e^{\sqrt{\log r}}/8}} 2^{2(r-N_+)}\\ &\quad \times N^{3} \mathbb{P}(GEv(r,0,0,x,z)) \mathbb{P}(GEv(r,2^{1-e^{\sqrt{\log r}}/8} ,\mathtt{C}^{(r)},x',z')) \\ &\quad + \mathcal{O}_{\upsilon} \left( 2^{2(r-N_+)} e^{-\frac{2^{r - (r/2)- 3e^{\sqrt{\log r}}/8 - 100 \log^2 (r/2)} - 1}{8}} \right). \end{align*} $$
$$ \begin{align*} \mathbb{P}_N(\theta, \theta') & \leq e^{2(x-z+x'-z')} e^{4 \upsilon + 2^{1 -e^{\sqrt{\log r}}/8}} 2^{2(r-N_+)}\\ &\quad \times N^{3} \mathbb{P}(GEv(r,0,0,x,z)) \mathbb{P}(GEv(r,2^{1-e^{\sqrt{\log r}}/8} ,\mathtt{C}^{(r)},x',z')) \\ &\quad + \mathcal{O}_{\upsilon} \left( 2^{2(r-N_+)} e^{-\frac{2^{r - (r/2)- 3e^{\sqrt{\log r}}/8 - 100 \log^2 (r/2)} - 1}{8}} \right). \end{align*} $$
By applying [Reference Belius, Rosen and ZeitouniBRZ19, Lemmas 2.1,2.3] with the same argument as in Lemma C.1, using the fact that
![]() $||E||_1$
goes to zero when r goes to infinity, we get
$||E||_1$
goes to zero when r goes to infinity, we get
 $$ \begin{align*} \mathbb{P}_N(\theta, \theta') &\leq e^{2(x-z+x'-z')} e^{4 \upsilon} 2^{2(r -N_+)} N^{3} \mathbb{P}(Event_{r,N}(x,z)) \mathbb{P}(Event_{r,N}(x',z'))(1+ \eta_r)\\ &\quad + \mathcal{O}_{\upsilon} \left( 2^{2(r-N)} e^{-\frac{2^{r/3} - 1}{8}} \right), \end{align*} $$
$$ \begin{align*} \mathbb{P}_N(\theta, \theta') &\leq e^{2(x-z+x'-z')} e^{4 \upsilon} 2^{2(r -N_+)} N^{3} \mathbb{P}(Event_{r,N}(x,z)) \mathbb{P}(Event_{r,N}(x',z'))(1+ \eta_r)\\ &\quad + \mathcal{O}_{\upsilon} \left( 2^{2(r-N)} e^{-\frac{2^{r/3} - 1}{8}} \right), \end{align*} $$
where
![]() $\eta _r$
goes to zero when r goes to infinity. Using (B.12), we obtain Lemma B.4.
$\eta _r$
goes to zero when r goes to infinity. Using (B.12), we obtain Lemma B.4.
Proof of Lemma B.6 in the general case.
The general case needs to use exactly the same arguments as in the general case of the proof of Lemma B.4. This time, for
![]() $ {\mathtt k}_+ \leq l \leq N-1$
and
$ {\mathtt k}_+ \leq l \leq N-1$
and
![]() $p\leq 2^{\kappa ^{({\mathtt k})}}-1$
, the random variables
$p\leq 2^{\kappa ^{({\mathtt k})}}-1$
, the random variables
![]() $ J_{l,p}^{({\mathtt k})}(\theta )$
and
$ J_{l,p}^{({\mathtt k})}(\theta )$
and
![]() $ J_{l,p}^{({\mathtt k})}(\theta ')$
are not rigorously independent. However, we observe that for
$ J_{l,p}^{({\mathtt k})}(\theta ')$
are not rigorously independent. However, we observe that for
![]() ${\mathtt k}_+ \leq l \leq N_+$
, the absolute value of their correlations decreases exponentially with l. Indeed, if
${\mathtt k}_+ \leq l \leq N_+$
, the absolute value of their correlations decreases exponentially with l. Indeed, if
 $C_{l,p}^{({\mathtt k})}(\theta ,\theta ') := \mathbb {E} \left ( J_{l,p}^{({\mathtt k})}(\theta )\overline {J_{l,p}^{({\mathtt k})}(\theta ')} \right )$
, then
$C_{l,p}^{({\mathtt k})}(\theta ,\theta ') := \mathbb {E} \left ( J_{l,p}^{({\mathtt k})}(\theta )\overline {J_{l,p}^{({\mathtt k})}(\theta ')} \right )$
, then
 $$ \begin{align*} \left| C_{l,p}^{({\mathtt k})}(\theta,\theta')\right| &=\frac{1}{{2^l+p2^{l-\kappa^{({\mathtt k})}}}}\left| \sum_{j=0}^{2^{l-\kappa^{({\mathtt k})}}-1} e^{i(\theta-\theta') j} \right| \leq \frac{4}{2^l ||\theta-\theta'|| } \ll 2^{{\mathtt k}-l} . \end{align*} $$
$$ \begin{align*} \left| C_{l,p}^{({\mathtt k})}(\theta,\theta')\right| &=\frac{1}{{2^l+p2^{l-\kappa^{({\mathtt k})}}}}\left| \sum_{j=0}^{2^{l-\kappa^{({\mathtt k})}}-1} e^{i(\theta-\theta') j} \right| \leq \frac{4}{2^l ||\theta-\theta'|| } \ll 2^{{\mathtt k}-l} . \end{align*} $$
Since
![]() $ \mathbb {E} \left ( J_{l,p}^{({\mathtt k})}(\theta )J_{l,p}^{({\mathtt k})}(\theta ') \right ) = 0$
, and the vector
$ \mathbb {E} \left ( J_{l,p}^{({\mathtt k})}(\theta )J_{l,p}^{({\mathtt k})}(\theta ') \right ) = 0$
, and the vector
![]() $(J_{l,p}^{({\mathtt k})}(\theta ), J_{l,p}^{({\mathtt k})} (\theta '))$
is centered complex Gaussian, one checks, by computing covariances, that it is possible to write
$(J_{l,p}^{({\mathtt k})}(\theta ), J_{l,p}^{({\mathtt k})} (\theta '))$
is centered complex Gaussian, one checks, by computing covariances, that it is possible to write
 $$ \begin{align*}J_{l,p}^{({\mathtt k})} (\theta) = \frac{C_{l,p}^{({\mathtt k})}(\theta,\theta')}{C_{l,p}^{({\mathtt k})} (\theta', \theta')} J_{l,p}^{({\mathtt k})} (\theta') + J^{({\mathtt k}),ind}_{l,p} (\theta, \theta'),\end{align*} $$
$$ \begin{align*}J_{l,p}^{({\mathtt k})} (\theta) = \frac{C_{l,p}^{({\mathtt k})}(\theta,\theta')}{C_{l,p}^{({\mathtt k})} (\theta', \theta')} J_{l,p}^{({\mathtt k})} (\theta') + J^{({\mathtt k}),ind}_{l,p} (\theta, \theta'),\end{align*} $$
where the two terms of the sums are independent, with an expectation of the square equal to zero. Note that
 $$ \begin{align*}C^{({\mathtt k})}_{l,p} := C^{({\mathtt k})}_{l,p}(\theta', \theta') = \frac{2^{l-\kappa^{({\mathtt k})}}}{2^l + p2^{l-\kappa^{({\mathtt k})}}} = (2^{\kappa^{({\mathtt k})}} + p)^{-1}\end{align*} $$
$$ \begin{align*}C^{({\mathtt k})}_{l,p} := C^{({\mathtt k})}_{l,p}(\theta', \theta') = \frac{2^{l-\kappa^{({\mathtt k})}}}{2^l + p2^{l-\kappa^{({\mathtt k})}}} = (2^{\kappa^{({\mathtt k})}} + p)^{-1}\end{align*} $$
does not depend on
![]() $\theta '$
. Moreover, we have by Pythagoras’ theorem,
$\theta '$
. Moreover, we have by Pythagoras’ theorem,
 $$ \begin{align*}\mathbb{E} [|J_{l,p}^{({\mathtt k}),ind}(\theta, \theta')|^2] = \mathbb{E} [|J_{l,p}^{({\mathtt k})}(\theta)|^2] - \left|\frac{C_{l,p}^{({\mathtt k})}(\theta, \theta')}{C_{l,p}^{({\mathtt k})}} \right|{}^2 \mathbb{E} [|J_{l,p}^{({\mathtt k})}(\theta')|^2] = C_{l,p}^{({\mathtt k})} - \frac{|C_{l,p}^{({\mathtt k})}(\theta, \theta')|^2}{C_{l,p}^{({\mathtt k})}}.\end{align*} $$
$$ \begin{align*}\mathbb{E} [|J_{l,p}^{({\mathtt k}),ind}(\theta, \theta')|^2] = \mathbb{E} [|J_{l,p}^{({\mathtt k})}(\theta)|^2] - \left|\frac{C_{l,p}^{({\mathtt k})}(\theta, \theta')}{C_{l,p}^{({\mathtt k})}} \right|{}^2 \mathbb{E} [|J_{l,p}^{({\mathtt k})}(\theta')|^2] = C_{l,p}^{({\mathtt k})} - \frac{|C_{l,p}^{({\mathtt k})}(\theta, \theta')|^2}{C_{l,p}^{({\mathtt k})}}.\end{align*} $$
Using this decomposition of
![]() $J_{l,p}^{({\mathtt k})}(\theta )$
and the measurability of the different quantities with respect to the
$J_{l,p}^{({\mathtt k})}(\theta )$
and the measurability of the different quantities with respect to the
![]() $\sigma $
-algebras of the form
$\sigma $
-algebras of the form
![]() $\mathcal {G}_j$
, we deduce that one can write
$\mathcal {G}_j$
, we deduce that one can write
with
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is a Gaussian process, independent of
$(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is a Gaussian process, independent of
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta '))_{l\geq {\mathtt k}_+}$
, and distributed as
$(R_{2^l}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta '))_{l\geq {\mathtt k}_+}$
, and distributed as
![]() $ ( \sqrt {\frac {1}{2}}W_{ \tau ^{({\mathtt k}_+,{\mathtt k}_+)}_l- \mathtt {C}^{({\mathtt k})}_l} )_{l\geq {\mathtt k}_+}$
with
$ ( \sqrt {\frac {1}{2}}W_{ \tau ^{({\mathtt k}_+,{\mathtt k}_+)}_l- \mathtt {C}^{({\mathtt k})}_l} )_{l\geq {\mathtt k}_+}$
with
![]() $\tau ^{({\mathtt k}_+,{\mathtt k}_+)}_j= \sum _{l={\mathtt k}_+}^{j-1} \sum _{p=0}^{2^{\kappa ^{({\mathtt k})}}-1} (2^{\kappa ^{({\mathtt k})}} +p)^{-1}$
and
$\tau ^{({\mathtt k}_+,{\mathtt k}_+)}_j= \sum _{l={\mathtt k}_+}^{j-1} \sum _{p=0}^{2^{\kappa ^{({\mathtt k})}}-1} (2^{\kappa ^{({\mathtt k})}} +p)^{-1}$
and
 $$ \begin{align*}\mathtt{C}^{({\mathtt k})}_l:= \sum_{t={\mathtt k}_+}^{l-1} \sum_{p=0}^{2^{\kappa^{({\mathtt k})}} -1 } \frac{ |C_{t,p}^{({\mathtt k})}(\theta, \theta')|^2}{C_{t,p}^{({\mathtt k})}}\end{align*} $$
$$ \begin{align*}\mathtt{C}^{({\mathtt k})}_l:= \sum_{t={\mathtt k}_+}^{l-1} \sum_{p=0}^{2^{\kappa^{({\mathtt k})}} -1 } \frac{ |C_{t,p}^{({\mathtt k})}(\theta, \theta')|^2}{C_{t,p}^{({\mathtt k})}}\end{align*} $$
and
![]() $(E_{2^l}^{(2^{{\mathtt k}_+})} )_{l\geq {\mathtt k}_+}$
defined by
$(E_{2^l}^{(2^{{\mathtt k}_+})} )_{l\geq {\mathtt k}_+}$
defined by

Note that
![]() $\mathtt {C}^{({\mathtt k})}_l$
and
$\mathtt {C}^{({\mathtt k})}_l$
and
![]() $E_{2^{l+1}}^{(2^{l})}$
here represent quantities which are different from those denoted in the same way in the proof of Lemma B.4. Furthermore, notice that
$E_{2^{l+1}}^{(2^{l})}$
here represent quantities which are different from those denoted in the same way in the proof of Lemma B.4. Furthermore, notice that
Fact 1:
For any
![]() $l\geq {\mathtt k}_+$
,
$l\geq {\mathtt k}_+$
,
 $$ \begin{align*} |E_{2^{l+1}}^{(2^{l})}| \leq |E|_{2^{l+1}}^{(2^{l})}:= \sum_{p=0}^{2^{\kappa^{({\mathtt k})}} -1 } |C_{l,p}^{({\mathtt k})}(\theta, \theta')| (2^{\kappa^{({\mathtt k})}}+p ) |J_{l,p}^{({\mathtt k})}(\theta') | \end{align*} $$
$$ \begin{align*} |E_{2^{l+1}}^{(2^{l})}| \leq |E|_{2^{l+1}}^{(2^{l})}:= \sum_{p=0}^{2^{\kappa^{({\mathtt k})}} -1 } |C_{l,p}^{({\mathtt k})}(\theta, \theta')| (2^{\kappa^{({\mathtt k})}}+p ) |J_{l,p}^{({\mathtt k})}(\theta') | \end{align*} $$
is measurable with respect to the sigma field
![]() $\sigma \left ( {\mathcal N}_t^{\mathbb C},\, t\in [|2^{l},2^{l+1}-1|]\right )$
.
$\sigma \left ( {\mathcal N}_t^{\mathbb C},\, t\in [|2^{l},2^{l+1}-1|]\right )$
.
Fact 2:
The process
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+} $
is independent of the couple
$(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+} $
is independent of the couple
![]() $( R_{2^l}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta ') , |E|_{2^l}^{(2^{{\mathtt k}_+})})_{l\geq {\mathtt k}_+}$
.
$( R_{2^l}^{(2^{{\mathtt k}_+},\kappa ^{({\mathtt k})})}(\theta ') , |E|_{2^l}^{(2^{{\mathtt k}_+})})_{l\geq {\mathtt k}_+}$
.
Fact 3:
![]() $\sup _{l\geq {\mathtt k}_+}|\mathtt {C}_l^{({\mathtt k})}| \ll 2^{-\kappa ^{({\mathtt k})}}$
if r is large enough. Indeed, we have
$\sup _{l\geq {\mathtt k}_+}|\mathtt {C}_l^{({\mathtt k})}| \ll 2^{-\kappa ^{({\mathtt k})}}$
if r is large enough. Indeed, we have
 $$ \begin{align*} \sup_{l\geq {\mathtt k}_+}|\mathtt{C}_l^{({\mathtt k})}| & \ll \sum_{l = {\mathtt k}_+}^{\infty} \sum_{p=0}^{2^{\kappa^{({\mathtt k})}} - 1} (2^{{\mathtt k} - l})^2 (2^{\kappa^{({\mathtt k})}} + p) \ll \sum_{l = {\mathtt k}_+}^{\infty} 2^{2{\mathtt k} - 2l + 2 \kappa^{({\mathtt k})}} \ll \sum_{l = {\mathtt k} + 3\kappa^{({\mathtt k})}}^{\infty} 2^{2 ({\mathtt k} +3\kappa^{({\mathtt k})} - l) -4\kappa^{({\mathtt k})}} \ll 2^{- 2\kappa^{({\mathtt k})}}. \end{align*} $$
$$ \begin{align*} \sup_{l\geq {\mathtt k}_+}|\mathtt{C}_l^{({\mathtt k})}| & \ll \sum_{l = {\mathtt k}_+}^{\infty} \sum_{p=0}^{2^{\kappa^{({\mathtt k})}} - 1} (2^{{\mathtt k} - l})^2 (2^{\kappa^{({\mathtt k})}} + p) \ll \sum_{l = {\mathtt k}_+}^{\infty} 2^{2{\mathtt k} - 2l + 2 \kappa^{({\mathtt k})}} \ll \sum_{l = {\mathtt k} + 3\kappa^{({\mathtt k})}}^{\infty} 2^{2 ({\mathtt k} +3\kappa^{({\mathtt k})} - l) -4\kappa^{({\mathtt k})}} \ll 2^{- 2\kappa^{({\mathtt k})}}. \end{align*} $$
It means that the process
![]() $(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is very ‘similar’ to
$(R_{2^l}^{(2^{{\mathtt k}_+},ind)})_{l\geq {\mathtt k}_+}$
is very ‘similar’ to
![]() $ \sqrt {\frac {1}{2}} (W_{ \tau _{l}^{({\mathtt k}_+,{\mathtt k}_+)}})_{l\geq {\mathtt k}_+ }$
.
$ \sqrt {\frac {1}{2}} (W_{ \tau _{l}^{({\mathtt k}_+,{\mathtt k}_+)}})_{l\geq {\mathtt k}_+ }$
.
Fact 4:
![]() $|E|$
is small. For any
$|E|$
is small. For any
![]() $m \geq 0$
,
$m \geq 0$
,
![]() $l\geq {\mathtt k}_+$
, we introduce the event
$l\geq {\mathtt k}_+$
, we introduce the event
For some universal constants
![]() $c, c'> 0$
and
$c, c'> 0$
and
![]() $m \geq 1/2$
, the probability of
$m \geq 1/2$
, the probability of
![]() $\mathtt {E}_m^{(l)} $
is smaller than
$\mathtt {E}_m^{(l)} $
is smaller than
 $$ \begin{align*} \mathbb{P}\left( |E|_{2^{l+1}}^{2^l} \geq 2^{-\frac{\kappa^{({\mathtt k})}}{4}}m \right) \leq 2^{\kappa^{({\mathtt k})}} \mathbb{P}\left( c 2^{{\mathtt k}-l} |J_{l,0}^{({\mathtt k})}(\theta')|\geq m 2^{-\frac{9}{4}\kappa^{({\mathtt k})}} \right) & \ll 2^{\kappa^{({\mathtt k})}} e^{- c'm^2 2^{2(l-{\mathtt k} - \frac{7}{4}\kappa^{({\mathtt k})}) } }\\ & \ll e^{- c'm^2 2^{2(l-{\mathtt k} - 2\kappa^{({\mathtt k})}) } }. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left( |E|_{2^{l+1}}^{2^l} \geq 2^{-\frac{\kappa^{({\mathtt k})}}{4}}m \right) \leq 2^{\kappa^{({\mathtt k})}} \mathbb{P}\left( c 2^{{\mathtt k}-l} |J_{l,0}^{({\mathtt k})}(\theta')|\geq m 2^{-\frac{9}{4}\kappa^{({\mathtt k})}} \right) & \ll 2^{\kappa^{({\mathtt k})}} e^{- c'm^2 2^{2(l-{\mathtt k} - \frac{7}{4}\kappa^{({\mathtt k})}) } }\\ & \ll e^{- c'm^2 2^{2(l-{\mathtt k} - 2\kappa^{({\mathtt k})}) } }. \end{align*} $$
Then, for r large and
![]() $l \geq {\mathtt k}_+$
,
$l \geq {\mathtt k}_+$
,
 $$ \begin{align*}\mathbb{P}\left( |E|_{2^{l+1}}^{2^l} \geq 2^{-\frac{\kappa^{({\mathtt k})}}{4}}m \right) \ll e^{-m^2 2^{l -{\mathtt k}_+}} .\end{align*} $$
$$ \begin{align*}\mathbb{P}\left( |E|_{2^{l+1}}^{2^l} \geq 2^{-\frac{\kappa^{({\mathtt k})}}{4}}m \right) \ll e^{-m^2 2^{l -{\mathtt k}_+}} .\end{align*} $$
Using the decomposition (B.42) and Fact 2 and noticing that
![]() $\sum _{l={\mathtt k}_+}^{N} m 2^{-\frac {\kappa ^{({\mathtt k})}}{4}}\leq m2^{-\frac {r}{400}}$
for r large enough, we can affirm that
$\sum _{l={\mathtt k}_+}^{N} m 2^{-\frac {\kappa ^{({\mathtt k})}}{4}}\leq m2^{-\frac {r}{400}}$
for r large enough, we can affirm that
 $$ \begin{align} \mathbb{P}_N^{(\Delta,\kappa)}(\theta,\theta') &\leq \sum_{m\geq 0} \mathbb{P}\left( Ev(r,1,E^{({\mathtt k}_+)},x,z) ,\, \cup_{j\in [|{\mathtt k}_+,N-1|]}\mathtt{E}_m^{(j)} \right) \\ \nonumber & \quad \quad \sup_{ l_{{\mathtt k}_+}^{(N)}-1 \leq x'+w'\leq u_{{\mathtt k}_+}^{(N)}+1 } \mathbb{P}\left( Ev({\mathtt k}_+,1 +(m+1) 2^{-\frac{r}{400}},\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')\right). \end{align} $$
$$ \begin{align} \mathbb{P}_N^{(\Delta,\kappa)}(\theta,\theta') &\leq \sum_{m\geq 0} \mathbb{P}\left( Ev(r,1,E^{({\mathtt k}_+)},x,z) ,\, \cup_{j\in [|{\mathtt k}_+,N-1|]}\mathtt{E}_m^{(j)} \right) \\ \nonumber & \quad \quad \sup_{ l_{{\mathtt k}_+}^{(N)}-1 \leq x'+w'\leq u_{{\mathtt k}_+}^{(N)}+1 } \mathbb{P}\left( Ev({\mathtt k}_+,1 +(m+1) 2^{-\frac{r}{400}},\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')\right). \end{align} $$
Here, by abuse of notation, we refer to the same event
![]() $Ev(k, a, E, z)$
as in Equation (B.22), but for the new time clock
$Ev(k, a, E, z)$
as in Equation (B.22), but for the new time clock
![]() $\tau _.^{({\mathtt k}_+, {\mathtt k}_+)}$
. By the same arguments used to prove (B.36), we have
$\tau _.^{({\mathtt k}_+, {\mathtt k}_+)}$
. By the same arguments used to prove (B.36), we have
However, by using the inequality (B.23) deduced from the Girsanov transform (which still holds for the time clock
![]() $\tau ^{({\mathtt k}_+,{\mathtt k}_+)}_j = \sum _{l={\mathtt k}_+}^{j-1} \sum _{p=0}^{2^{\kappa ^{({\mathtt k})}}-1} (2^{\kappa ^{({\mathtt k})}} +p)^{-1}$
), we obtain for any
$\tau ^{({\mathtt k}_+,{\mathtt k}_+)}_j = \sum _{l={\mathtt k}_+}^{j-1} \sum _{p=0}^{2^{\kappa ^{({\mathtt k})}}-1} (2^{\kappa ^{({\mathtt k})}} +p)^{-1}$
), we obtain for any
![]() $x'+w'\in [ l_{{\mathtt k}_+}^{(N)}-1, u_{{\mathtt k}_+}^{(N)}+1 ]$
,
$x'+w'\in [ l_{{\mathtt k}_+}^{(N)}-1, u_{{\mathtt k}_+}^{(N)}+1 ]$
,
 $$ \begin{align} \nonumber &\mathbb{P}\left( Ev({\mathtt k}_+,1+ (m+1) 2^{-\frac{r}{400}},\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')\right) \\ & \ll_{\upsilon} 2^{{\mathtt k}_+ -N_+} e^{ 1+ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} e^{2(x'+w'-z') }\nonumber \\ &\qquad \times\mathbb{P}\left( GEv({\mathtt k}_+, 1+ 2(m+1) 2^{-\frac{r}{400}},\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')) \right), \end{align} $$
$$ \begin{align} \nonumber &\mathbb{P}\left( Ev({\mathtt k}_+,1+ (m+1) 2^{-\frac{r}{400}},\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')\right) \\ & \ll_{\upsilon} 2^{{\mathtt k}_+ -N_+} e^{ 1+ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} e^{2(x'+w'-z') }\nonumber \\ &\qquad \times\mathbb{P}\left( GEv({\mathtt k}_+, 1+ 2(m+1) 2^{-\frac{r}{400}},\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')) \right), \end{align} $$
where we used that
![]() $\sup _{j\geq {\mathtt k}_+} |\mathtt {C}^{({\mathtt k})}_j|\leq 2^{-\kappa ^{({\mathtt k})}} \leq (m+1) 2^{-\frac {r}{400}} $
. We bound the probability of the
$\sup _{j\geq {\mathtt k}_+} |\mathtt {C}^{({\mathtt k})}_j|\leq 2^{-\kappa ^{({\mathtt k})}} \leq (m+1) 2^{-\frac {r}{400}} $
. We bound the probability of the
![]() $GEv$
event by
$GEv$
event by
![]() $1$
and use the fact that
$1$
and use the fact that
![]() $x'+w' \leq 1+ u_{k_0}^{(N)}\leq 1 -(N_+-{\mathtt k}_+)^{\alpha _-}-\frac {3}{4}\log N$
. We then get
$x'+w' \leq 1+ u_{k_0}^{(N)}\leq 1 -(N_+-{\mathtt k}_+)^{\alpha _-}-\frac {3}{4}\log N$
. We then get
 $$ \begin{align*} &\mathbb{P}\left( Ev({\mathtt k}_+, 1+ (m+1) 2^{-\frac{r}{400}} ,\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')\right) \\ &\ll 2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} e^{2(x'+w'-z')} \\ & \ll_{\upsilon} 2^{-2z'}2^{{\mathtt k}_+ -N_+} e^{2m+2} N^{3/2} e^{- 2(N_+ - {\mathtt k}_+)^{\alpha_-} -\frac{3}{2}\log N} \\ & \ll 2^{-2z'}2^{{\mathtt k}_+ -N_+} e^{2m+2} e^{-(N_+ - {\mathtt k}_+)^{\alpha_-}}. \end{align*} $$
$$ \begin{align*} &\mathbb{P}\left( Ev({\mathtt k}_+, 1+ (m+1) 2^{-\frac{r}{400}} ,\mathtt{C}^{({\mathtt k})}+E^{({\mathtt k}_+)},x'+w',z')\right) \\ &\ll 2^{{\mathtt k}_+ -N_+} e^{ 2(m+1) 2^{-\frac{r}{400}}} N^{\frac{3}{2}} e^{2(x'+w'-z')} \\ & \ll_{\upsilon} 2^{-2z'}2^{{\mathtt k}_+ -N_+} e^{2m+2} N^{3/2} e^{- 2(N_+ - {\mathtt k}_+)^{\alpha_-} -\frac{3}{2}\log N} \\ & \ll 2^{-2z'}2^{{\mathtt k}_+ -N_+} e^{2m+2} e^{-(N_+ - {\mathtt k}_+)^{\alpha_-}}. \end{align*} $$
Finally, by combining this equation with (B.45) and (B.44), we get
 $$ \begin{align*} \mathbb{P}_{N}^{(\Delta,\kappa)}(\theta, \theta')& \ll_{\upsilon} |xz| 2^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N} e^{- (N_+-{\mathtt k}_+)^{\alpha_-}} \sum_{m\geq 0} e^{2m+2-(m^2/8)}\\ & \ll |xz|2^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N} e^{- (N_+-{\mathtt k}_+)^{\alpha_-}} , \end{align*} $$
$$ \begin{align*} \mathbb{P}_{N}^{(\Delta,\kappa)}(\theta, \theta')& \ll_{\upsilon} |xz| 2^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N} e^{- (N_+-{\mathtt k}_+)^{\alpha_-}} \sum_{m\geq 0} e^{2m+2-(m^2/8)}\\ & \ll |xz|2^{2(x-z-z')} 2^{r-N_+} 2^{{\mathtt k}_+ -N} e^{- (N_+-{\mathtt k}_+)^{\alpha_-}} , \end{align*} $$
which concludes the proof of Lemma B.6.
B.4 Short time barriers
We will also need the analogue of Lemmas B.4 and B.5 with
![]() $\mathfrak I_N$
replaced by
$\mathfrak I_N$
replaced by
![]() $\mathfrak I_{t,f}$
. Thus, let
$\mathfrak I_{t,f}$
. Thus, let
We have the following.
Lemma B.8 (Time of branching
 ${\mathtt k} \leq N/2$
).
${\mathtt k} \leq N/2$
).
For any
![]() $\upsilon \in (0,1)$
, r large enough,
$\upsilon \in (0,1)$
, r large enough,
![]() $C>1$
, t large enough depending on r,
$C>1$
, t large enough depending on r,
![]() $z,z'\in [-\sqrt {t}/C,C\sqrt {t}]$
,
$z,z'\in [-\sqrt {t}/C,C\sqrt {t}]$
,
![]() ${\mathtt k} \leq t$
and
${\mathtt k} \leq t$
and ![]() , we have
, we have
 $$ \begin{align} \mathbb{P}_{t,f}(\theta, \theta')&\ll \left\{ \begin{array}{ll} \frac{|zz' xx'|}{t^3} 2^{2r-2t +2(x-z+x'-z')} ,\qquad &\text{when } {\mathtt k}_+ \leq r,\\ \frac{|zz'x|}{t^{3/2}} e^{2(x-z-z')}2^{r-t} 2^{{\mathtt k}_+-t} e^{- {\mathtt k}_+^{\alpha_-}} ,\qquad &\text{when } {\mathtt k}_+ \geq r. \end{array} \right. \end{align} $$
$$ \begin{align} \mathbb{P}_{t,f}(\theta, \theta')&\ll \left\{ \begin{array}{ll} \frac{|zz' xx'|}{t^3} 2^{2r-2t +2(x-z+x'-z')} ,\qquad &\text{when } {\mathtt k}_+ \leq r,\\ \frac{|zz'x|}{t^{3/2}} e^{2(x-z-z')}2^{r-t} 2^{{\mathtt k}_+-t} e^{- {\mathtt k}_+^{\alpha_-}} ,\qquad &\text{when } {\mathtt k}_+ \geq r. \end{array} \right. \end{align} $$
Lemma B.9 (Time of branching
 ${\mathtt k} \leq r/2$
).
${\mathtt k} \leq r/2$
).
For any
![]() $\upsilon \in (0,1)$
,
$\upsilon \in (0,1)$
,
![]() $r\in {\mathbb N}$
large enough, r large enough,
$r\in {\mathbb N}$
large enough, r large enough,
![]() $C>1$
, t large enough depending on r,
$C>1$
, t large enough depending on r,
![]() $z,z'\in [-\sqrt {t}/C,C\sqrt {t}]$
,
$z,z'\in [-\sqrt {t}/C,C\sqrt {t}]$
,
![]() $ {\mathtt k} \leq \frac {r}{2}$
,
$ {\mathtt k} \leq \frac {r}{2}$
, ![]() and t large enough depending on r, we have
and t large enough depending on r, we have
where
C Classical estimates on Gaussian walks
The following estimates are classical and extend those in [Reference Chhaibi, Madaule and NajnudelCMN18] by keeping track of the dependence in starting and ending points. In the following, the process
![]() $\left ( W_s; s \in {\mathbb R}_+ \right )$
is a standard Brownian motion. We use the notation from B.2.
$\left ( W_s; s \in {\mathbb R}_+ \right )$
is a standard Brownian motion. We use the notation from B.2.
The following is classical. Since the proof is short, we bring it.
Lemma C.1. Notation as in Section B.2, with
![]() $x,z$
in the appropriate range. Then,
$x,z$
in the appropriate range. Then,

where
Proof. We show the lower bound; the upper bound is similar. Recall that

For
![]() $r,k_1$
large, we have that
$r,k_1$
large, we have that
![]() $|\tau ^{(r)}_j-(j-r)\log 2|\leq 1$
. Set, comparing with (B.10) and (B.11), for
$|\tau ^{(r)}_j-(j-r)\log 2|\leq 1$
. Set, comparing with (B.10) and (B.11), for
![]() $k\in [r,N_++1]$
,
$k\in [r,N_++1]$
,

and

The crucial fact is that for N large, we have that for all
![]() $k\in [r,N_+]$
,
$k\in [r,N_+]$
,
In particular, we have that

The conclusion of the lemma follows from a variant of [Reference Belius, Rosen and ZeitouniBRZ19, Lemma 2.1] and our assumptions on
![]() $x,z$
.
$x,z$
.
Acknowledgements
We thank Gaultier Lambert and Joseph Najnudel for their interest and useful comments, and anonymous referees for a detailed reading and very constructive comments and corrections.
Competing interest
The authors have no competing interest to declare.
Funding statement
The research of E. P. was partially supported by a NSERC discovery grant. The research of O. Z. was partially supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 692452) and by the Israel Science Foundation grant number 421/20.
Data availability statement
No data was produced in connection with this research.