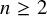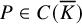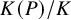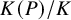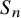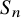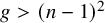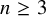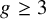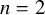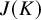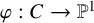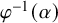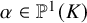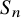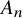1 Introduction
Low degree points on curves have long been a subject of intensive study, both from a theoretical point-of-view (e.g., [Reference Bourdon, Ejder, Liu, Odumodu and Viray2], [Reference Viray and Vogt31]) and algorithmically (e.g., [Reference Siksek28]). Perhaps the most celebrated result in this subject is Merel’s uniform boundedness theorem [Reference Merel23], which (thanks to a strengthening due to Oesterlé [Reference Derickx, Kamienny, Stein and Stoll10, Section 6]) asserts that the only degree n points on the modular curve
![]() $X_1(p)$
(with p prime) are cuspidal, for
$X_1(p)$
(with p prime) are cuspidal, for
![]() $n< 2 \log _{3}(\sqrt {p}-1)$
. A common theme in the subject is to seek a description of which curves can have infinitely many points of a certain degree. For example, a famous theorem of Harris and Silverman [Reference Harris and Silverman16] asserts that if a curve C over a number field K, of genus
$n< 2 \log _{3}(\sqrt {p}-1)$
. A common theme in the subject is to seek a description of which curves can have infinitely many points of a certain degree. For example, a famous theorem of Harris and Silverman [Reference Harris and Silverman16] asserts that if a curve C over a number field K, of genus
![]() $\ge 2$
, has infinitely many quadratic points, then it is either hyperelliptic or bielliptic. The strongest results to date on infinite families of low degree points on curves are due to Smith and Vogt [Reference Smith and Vogt29] and to Kadets and Vogt [Reference Kadets and Vogt20], whose works elucidate the geometric origin of such families provided the degree is small compared to the genus. By comparison, the question of which groups arise infinitely often as Galois groups of low degree points on a curve has received very little attention; the only results we are aware of concern degrees
$\ge 2$
, has infinitely many quadratic points, then it is either hyperelliptic or bielliptic. The strongest results to date on infinite families of low degree points on curves are due to Smith and Vogt [Reference Smith and Vogt29] and to Kadets and Vogt [Reference Kadets and Vogt20], whose works elucidate the geometric origin of such families provided the degree is small compared to the genus. By comparison, the question of which groups arise infinitely often as Galois groups of low degree points on a curve has received very little attention; the only results we are aware of concern degrees
![]() $3$
or
$3$
or
![]() $4$
(e.g., [Reference Bruin, Derickx and Stoll4], [Reference Bruin and Najman5], [Reference Derickx and Najman11], [Reference Jeon18], [Reference Jeon, Kim and Lee19]). This paper is concerned with giving insights into this question for primitive groups. Before we go further, we recall the notion of a primitive permutation group. Let G be a group acting on a finite set
$4$
(e.g., [Reference Bruin, Derickx and Stoll4], [Reference Bruin and Najman5], [Reference Derickx and Najman11], [Reference Jeon18], [Reference Jeon, Kim and Lee19]). This paper is concerned with giving insights into this question for primitive groups. Before we go further, we recall the notion of a primitive permutation group. Let G be a group acting on a finite set
![]() $\Omega $
. We say the action is primitive if it is transitive and the only partitions of
$\Omega $
. We say the action is primitive if it is transitive and the only partitions of
![]() $\Omega $
that are G-stable are
$\Omega $
that are G-stable are
![]() $\{\Omega \}$
and
$\{\Omega \}$
and
![]() $\{\{\omega \} : \omega \in \Omega \}$
. It is well-known that a
$\{\{\omega \} : \omega \in \Omega \}$
. It is well-known that a
![]() $2$
-transitive group acts primitively (Lemma 2.1 below), and thus,
$2$
-transitive group acts primitively (Lemma 2.1 below), and thus,
![]() $S_n$
and
$S_n$
and
![]() $A_n$
are primitive groups (with their natural action on
$A_n$
are primitive groups (with their natural action on
![]() $\{1,2,\dotsc ,n\}$
), for
$\{1,2,\dotsc ,n\}$
), for
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $n \ge 3$
, respectively.
$n \ge 3$
, respectively.
Let K be a perfect field and let
![]() $\overline {K}$
denote a fixed algebraic closure of K. Write
$\overline {K}$
denote a fixed algebraic closure of K. Write
![]() $G_K=\operatorname {\mathrm {Gal}}(\overline {K}/K)$
for the absolute Galois group of K. Let C be a curve defined over K (by which we mean a smooth projective and geometrically irreducible variety defined over K having dimension
$G_K=\operatorname {\mathrm {Gal}}(\overline {K}/K)$
for the absolute Galois group of K. Let C be a curve defined over K (by which we mean a smooth projective and geometrically irreducible variety defined over K having dimension
![]() $1$
). By a degree n point on
$1$
). By a degree n point on
![]() $C/K$
we mean an algebraic point
$C/K$
we mean an algebraic point
![]() $P \in C(\overline {K})$
such that
$P \in C(\overline {K})$
such that
![]() $[K(P):K]=n$
. Equivalently, the orbit of P under the action of
$[K(P):K]=n$
. Equivalently, the orbit of P under the action of
![]() $G_K$
has size n. If the orbit of P is
$G_K$
has size n. If the orbit of P is
![]() $\{P_1,\dotsc ,P_n\}$
, then we define the Galois group of P, which we denote by
$\{P_1,\dotsc ,P_n\}$
, then we define the Galois group of P, which we denote by
![]() $\operatorname {\mathrm {Gal}}(P/K)$
, to be the image of the natural permutation representation
$\operatorname {\mathrm {Gal}}(P/K)$
, to be the image of the natural permutation representation
![]() $G_K \rightarrow \operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\})$
. Thus, we may identify
$G_K \rightarrow \operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\})$
. Thus, we may identify
![]() $\operatorname {\mathrm {Gal}}(P/K)$
(up to conjugation) as a transitive subgroup of the n-th symmetric group
$\operatorname {\mathrm {Gal}}(P/K)$
(up to conjugation) as a transitive subgroup of the n-th symmetric group
![]() $S_n$
. The Galois group of P is also the Galois group of the Galois closure of
$S_n$
. The Galois group of P is also the Galois group of the Galois closure of
![]() $K(P)/K$
. Following [Reference Khawaja and Siksek21], we say that the point P is primitive if
$K(P)/K$
. Following [Reference Khawaja and Siksek21], we say that the point P is primitive if
![]() $\operatorname {\mathrm {Gal}}(P/K)$
acts primitively on
$\operatorname {\mathrm {Gal}}(P/K)$
acts primitively on
![]() $\{P_1,\dotsc ,P_n\}$
; this means that the only partitions of the orbit
$\{P_1,\dotsc ,P_n\}$
; this means that the only partitions of the orbit
![]() $\Omega =\{P_1,\dotsc ,P_n\}$
preserved by
$\Omega =\{P_1,\dotsc ,P_n\}$
preserved by
![]() $\operatorname {\mathrm {Gal}}(P/K)$
are
$\operatorname {\mathrm {Gal}}(P/K)$
are
![]() $\{\Omega \}$
and the singletons partition
$\{\Omega \}$
and the singletons partition
![]() $\{\{P_1\},\dotsc ,\{P_n\}\}$
. We call a divisor D on C rational if it is supported on
$\{\{P_1\},\dotsc ,\{P_n\}\}$
. We call a divisor D on C rational if it is supported on
![]() $C(\overline {K})$
and stable under the action of
$C(\overline {K})$
and stable under the action of
![]() $G_K$
. Henceforth, all divisors considered are assumed to be rational. An effective divisor D is said to be reducible if it admits a decomposition
$G_K$
. Henceforth, all divisors considered are assumed to be rational. An effective divisor D is said to be reducible if it admits a decomposition
![]() $D=D_1+D_2$
, where
$D=D_1+D_2$
, where
![]() $D_1>0$
,
$D_1>0$
,
![]() $D_2>0$
and both are rational; otherwise, we say that D is irreducible. Thus, an irreducible divisor consists of a single Galois orbit of algebraic points; an irreducible divisor of degree n is what many other authors (e.g., [Reference Bright and Siksek3], [Reference Kadets and Vogt20], [Reference Smith and Vogt29], [Reference Viray and Vogt31]) call a degree n closed point. We call an irreducible divisor primitive if it is the Galois orbit of a primitive point.
$D_2>0$
and both are rational; otherwise, we say that D is irreducible. Thus, an irreducible divisor consists of a single Galois orbit of algebraic points; an irreducible divisor of degree n is what many other authors (e.g., [Reference Bright and Siksek3], [Reference Kadets and Vogt20], [Reference Smith and Vogt29], [Reference Viray and Vogt31]) call a degree n closed point. We call an irreducible divisor primitive if it is the Galois orbit of a primitive point.
Theorem 1.1. Let K be a number field. Let
![]() $C/K$
be a curve of genus g, and write J for the Jacobian of C. Let
$C/K$
be a curve of genus g, and write J for the Jacobian of C. Let
![]() $n \ge 2$
and suppose
$n \ge 2$
and suppose
 $$ \begin{align} \begin{cases} g>(n-1)^2 & \text{if } n\ge 3 \\ g\ge 3 & \text{if } n=2. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} g>(n-1)^2 & \text{if } n\ge 3 \\ g\ge 3 & \text{if } n=2. \end{cases} \end{align} $$
Suppose that
![]() $A(K)$
is finite for every abelian subvariety
$A(K)$
is finite for every abelian subvariety
![]() $A/K$
of J of dimension
$A/K$
of J of dimension
![]() $ \le n/2$
. If C has infinitely many primitive points of degree n, then there is a degree n morphism
$ \le n/2$
. If C has infinitely many primitive points of degree n, then there is a degree n morphism
![]() $\varphi : C \rightarrow \mathbb {P}^1$
defined over K such that all but finitely many primitive degree n divisors are fibres
$\varphi : C \rightarrow \mathbb {P}^1$
defined over K such that all but finitely many primitive degree n divisors are fibres
![]() $\varphi ^{*}(\alpha )$
with
$\varphi ^{*}(\alpha )$
with
![]() $\alpha \in \mathbb {P}^1(K)$
.
$\alpha \in \mathbb {P}^1(K)$
.
We call Theorem 1.1 the “Single Source Theorem”, since, with finitely many exceptions, all primitive degree n points come from a single source which is the morphism
![]() $\varphi : C \rightarrow \mathbb {P}^1$
.
$\varphi : C \rightarrow \mathbb {P}^1$
.
Theorem 1.2. Let K be a number field. Let
![]() $C/K$
be a curve of genus g, and write J for the Jacobian of C. Let
$C/K$
be a curve of genus g, and write J for the Jacobian of C. Let
![]() $n \ge 2$
and suppose (1.1) holds. Suppose that
$n \ge 2$
and suppose (1.1) holds. Suppose that
![]() $A(K)$
is finite for every abelian subvariety
$A(K)$
is finite for every abelian subvariety
![]() $A/K$
of J of dimension
$A/K$
of J of dimension
![]() $ \le n/2$
. Suppose C has infinitely many degree n points with Galois group
$ \le n/2$
. Suppose C has infinitely many degree n points with Galois group
![]() $S_n$
or
$S_n$
or
![]() $A_n$
. Then C has only finitely many degree n points with any primitive Galois group
$A_n$
. Then C has only finitely many degree n points with any primitive Galois group
![]() $\ne A_n$
,
$\ne A_n$
,
![]() $S_n$
.
$S_n$
.
The above results show that primitive points are severely constrained if their degree is sufficiently small compared to the genus. If the degree is large compared to the genus, then the behaviour is very different. Indeed, Derickx [Reference Derickx9] has shown that if C is a smooth projective curve over a number field K of genus g with
![]() $C(K) \ne \emptyset $
, then C has infinitely many primitive degree n points for every
$C(K) \ne \emptyset $
, then C has infinitely many primitive degree n points for every
![]() $n>2g$
. For the intermediate range
$n>2g$
. For the intermediate range
![]() $g+1 \le n \le 2g$
, the existence of a single primitive degree n point guarantees the existence of infinitely many [Reference Khawaja and Siksek21, Theorem 12].
$g+1 \le n \le 2g$
, the existence of a single primitive degree n point guarantees the existence of infinitely many [Reference Khawaja and Siksek21, Theorem 12].
We point out that, in both Theorems 1.1 and 1.2, we may replace the assumption ‘
![]() $A(K)$
is finite for every abelian subvariety
$A(K)$
is finite for every abelian subvariety
![]() $A/K$
of J of dimension
$A/K$
of J of dimension
![]() $\le n/2$
’ with the stronger (but more simply-stated) assumption that ‘J is simple or
$\le n/2$
’ with the stronger (but more simply-stated) assumption that ‘J is simple or
![]() $J(K)$
is finite’. Later on, we give versions of both theorems where this assumption is replaced by a weaker but more technical hypothesis (Theorems 5.1 and 7.1).
$J(K)$
is finite’. Later on, we give versions of both theorems where this assumption is replaced by a weaker but more technical hypothesis (Theorems 5.1 and 7.1).
We mention two intermediate results that may be of independent interest.
Theorem 1.3. Let K be a perfect field. Let
![]() $n \ge 2$
. Let C be a curve of genus g defined over K. Suppose
$n \ge 2$
. Let C be a curve of genus g defined over K. Suppose
Let D be a primitive degree n divisor on C. Then
![]() $\ell (D) \le 2$
.
$\ell (D) \le 2$
.
Here,
![]() $L(D)$
denotes the Riemann–Roch space associated to D, and
$L(D)$
denotes the Riemann–Roch space associated to D, and
![]() $\ell (D)$
denotes its dimension. We believe that Theorem 1.3 is the first ever example of a relationship between the Galois group of a divisor and its Riemann–Roch dimension.
$\ell (D)$
denotes its dimension. We believe that Theorem 1.3 is the first ever example of a relationship between the Galois group of a divisor and its Riemann–Roch dimension.
Theorem 1.4. Let K be a perfect field. Let
![]() $C/K$
be a curve of genus g. Let
$C/K$
be a curve of genus g. Let
![]() $n \ge 2$
. Let
$n \ge 2$
. Let
![]() $D_1$
,
$D_1$
,
![]() $D_2$
be two primitive degree n divisors on C with
$D_2$
be two primitive degree n divisors on C with
![]() $\ell (D_1)=\ell (D_2)=2$
. Suppose
$\ell (D_1)=\ell (D_2)=2$
. Suppose
Then
![]() $D_1$
,
$D_1$
,
![]() $D_2$
are linearly equivalent.
$D_2$
are linearly equivalent.
The paper is structured as follows. In Section 2, we review some standard results on primitive group actions that are needed later in the paper. In Section 3, we prove Theorem 1.3: if
![]() $\ell (D) \ge 3$
and D is primitive, then we show that C is birational to a plane degree n curve which contradicts (1.2). In Section 4, we prove Theorem 1.4: if
$\ell (D) \ge 3$
and D is primitive, then we show that C is birational to a plane degree n curve which contradicts (1.2). In Section 4, we prove Theorem 1.4: if
![]() $D_1$
,
$D_1$
,
![]() $D_2$
are inequivalent and primitive, then we show that C is birational to an
$D_2$
are inequivalent and primitive, then we show that C is birational to an
![]() $(n,n)$
-curve on
$(n,n)$
-curve on
![]() $\mathbb {P}^1 \times \mathbb {P}^1$
contradicting (1.3). In Section 5, we show that Theorem 1.1 follows from Theorems 1.3, 1.4 and a famous theorem of Faltings on rational points lying on subvarieties of abelian varieties. The next two sections (Section 6 and Section 7) are devoted to deducing Theorem 1.2 from Theorem 1.1. Indeed, Theorem 1.1 allows us to focus on the fibres of a single degree n morphism
$\mathbb {P}^1 \times \mathbb {P}^1$
contradicting (1.3). In Section 5, we show that Theorem 1.1 follows from Theorems 1.3, 1.4 and a famous theorem of Faltings on rational points lying on subvarieties of abelian varieties. The next two sections (Section 6 and Section 7) are devoted to deducing Theorem 1.2 from Theorem 1.1. Indeed, Theorem 1.1 allows us to focus on the fibres of a single degree n morphism
![]() $\varphi : C \rightarrow \mathbb {P}^1$
defined over K. We show that this morphism has ‘generic Galois group’
$\varphi : C \rightarrow \mathbb {P}^1$
defined over K. We show that this morphism has ‘generic Galois group’
![]() $A_n$
or
$A_n$
or
![]() $S_n$
, and to prove Theorem 1.2, it will be enough to show that only finitely many fibres have primitive Galois groups
$S_n$
, and to prove Theorem 1.2, it will be enough to show that only finitely many fibres have primitive Galois groups
![]() $\ne A_n$
,
$\ne A_n$
,
![]() $S_n$
. The map
$S_n$
. The map
![]() $\varphi $
is not in general a Galois cover, and we will need to consider the ‘geometrically connected Galois closure’
$\varphi $
is not in general a Galois cover, and we will need to consider the ‘geometrically connected Galois closure’
![]() $\tilde {C} \rightarrow \mathbb {P}^1$
, which is defined over an extension L of K. We show, using the simplicity of
$\tilde {C} \rightarrow \mathbb {P}^1$
, which is defined over an extension L of K. We show, using the simplicity of
![]() $A_n$
, that either
$A_n$
, that either
![]() $L=K$
or
$L=K$
or
![]() $L/K$
is quadratic. The fibres
$L/K$
is quadratic. The fibres
![]() $\varphi ^*(\alpha )$
, for
$\varphi ^*(\alpha )$
, for
![]() $\alpha \in \mathbb {P}^1(L)$
, which have any given Galois group H, give rise to L-points on some subcover
$\alpha \in \mathbb {P}^1(L)$
, which have any given Galois group H, give rise to L-points on some subcover
![]() $D_H/L$
of
$D_H/L$
of
![]() $\tilde {C}$
. The proof of Theorem 1.2 boils down to noting that all these
$\tilde {C}$
. The proof of Theorem 1.2 boils down to noting that all these
![]() $D_H$
have genus
$D_H$
have genus
![]() $\ge 2$
, thanks to a theorem of Guralnick and Shareshian, and hence finitely many L-points by Faltings’ theorem.
$\ge 2$
, thanks to a theorem of Guralnick and Shareshian, and hence finitely many L-points by Faltings’ theorem.
2 Primitive group actions
In this section, we review some properties of primitive group actions. This is standard material (e.g. [Reference Dixon and Mortimer12]), and is included for the convenience of the reader. Let G be a group acting transitively on a finite set
![]() $\Omega $
. Let
$\Omega $
. Let
![]() $\mathcal {P}$
be a partition of
$\mathcal {P}$
be a partition of
![]() $\Omega $
. We say that
$\Omega $
. We say that
![]() $\mathcal {P}$
is G-stable if
$\mathcal {P}$
is G-stable if
![]() $\sigma (Y) \in \mathcal {P}$
for all
$\sigma (Y) \in \mathcal {P}$
for all
![]() $Y \in \mathcal {P}$
and all
$Y \in \mathcal {P}$
and all
![]() $\sigma \in G$
. We say that the action of G on
$\sigma \in G$
. We say that the action of G on
![]() $\Omega $
is primitive if the only G-stable partitions of
$\Omega $
is primitive if the only G-stable partitions of
![]() $\Omega $
are the trivial ones:
$\Omega $
are the trivial ones:
![]() $\{\Omega \}$
and
$\{\Omega \}$
and
![]() $\{ \{\omega \} : \omega \in \Omega \}$
. Here, is an equivalent formulation: the action of G on
$\{ \{\omega \} : \omega \in \Omega \}$
. Here, is an equivalent formulation: the action of G on
![]() $\Omega $
is imprimitive if and only if there is some
$\Omega $
is imprimitive if and only if there is some
![]() $Y \subset \Omega $
such that
$Y \subset \Omega $
such that
![]() $2 \le \# Y < \# \Omega $
, and for all
$2 \le \# Y < \# \Omega $
, and for all
![]() $\sigma \in G$
, either
$\sigma \in G$
, either
![]() $\sigma (Y)=Y$
or
$\sigma (Y)=Y$
or
![]() $\sigma (Y) \cap Y = \emptyset $
.
$\sigma (Y) \cap Y = \emptyset $
.
Lemma 2.1. Suppose the action of G on
![]() $\Omega $
is
$\Omega $
is
![]() $2$
-transitive. Then the action is primitive.
$2$
-transitive. Then the action is primitive.
Proof. Let Y be a subset of
![]() $\Omega $
with at least two elements and suppose that for all
$\Omega $
with at least two elements and suppose that for all
![]() $\sigma \in G$
, either
$\sigma \in G$
, either
![]() $\sigma (Y)=Y$
or
$\sigma (Y)=Y$
or
![]() $\sigma (Y) \cap Y=\emptyset $
. We want to show that
$\sigma (Y) \cap Y=\emptyset $
. We want to show that
![]() $Y=\Omega $
. Let
$Y=\Omega $
. Let
![]() $c \in \Omega $
; we want to show that
$c \in \Omega $
; we want to show that
![]() $c \in Y$
. Let a,
$c \in Y$
. Let a,
![]() $b \in Y$
be distinct. We may suppose
$b \in Y$
be distinct. We may suppose
![]() $c \ne a$
, b. As G is
$c \ne a$
, b. As G is
![]() $2$
-transitive on
$2$
-transitive on
![]() $\Omega $
, there is some
$\Omega $
, there is some
![]() $\sigma \in G$
such that
$\sigma \in G$
such that
![]() $\sigma (a)=a$
and
$\sigma (a)=a$
and
![]() $\sigma (b)=c$
. As
$\sigma (b)=c$
. As
![]() $a \in Y \cap \sigma (Y)$
, we have
$a \in Y \cap \sigma (Y)$
, we have
![]() $Y=\sigma (Y)$
and so
$Y=\sigma (Y)$
and so
![]() $c \in Y$
.
$c \in Y$
.
It follows from Lemma 2.1 that
![]() $S_n$
is primitive for all n, and
$S_n$
is primitive for all n, and
![]() $A_n$
is primitive for
$A_n$
is primitive for
![]() $n \ge 3$
.
$n \ge 3$
.
Lemma 2.2. Suppose
![]() $\lvert \Omega \rvert \ge 2$
. The action of G on
$\lvert \Omega \rvert \ge 2$
. The action of G on
![]() $\Omega $
is primitive if and only if
$\Omega $
is primitive if and only if
![]() $\operatorname {\mathrm {Stab}}(\omega )$
is maximal for any (and hence all)
$\operatorname {\mathrm {Stab}}(\omega )$
is maximal for any (and hence all)
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Proof. As the action is transitive, any two point stabilizers are conjugate, and thus, if one is maximal, then so are all of them. Let
![]() $\omega \in \Omega $
. As
$\omega \in \Omega $
. As
![]() $\lvert \Omega \rvert \ge 2$
, the stabilizer
$\lvert \Omega \rvert \ge 2$
, the stabilizer
![]() $\operatorname {\mathrm {Stab}}(\omega )$
is a proper subgroup of G. Suppose it is non-maximal, and let
$\operatorname {\mathrm {Stab}}(\omega )$
is a proper subgroup of G. Suppose it is non-maximal, and let
![]() $\operatorname {\mathrm {Stab}}(\omega ) \subsetneq H \subsetneq G$
be a subgroup. Let
$\operatorname {\mathrm {Stab}}(\omega ) \subsetneq H \subsetneq G$
be a subgroup. Let
![]() $Y=H\omega $
. Then
$Y=H\omega $
. Then
 $$ \begin{align} 2 \le \underbrace{[H:\operatorname{\mathrm{Stab}}(\omega)]}_{\#Y} < [G:\operatorname{\mathrm{Stab}}(\omega)] =\#\Omega. \end{align} $$
$$ \begin{align} 2 \le \underbrace{[H:\operatorname{\mathrm{Stab}}(\omega)]}_{\#Y} < [G:\operatorname{\mathrm{Stab}}(\omega)] =\#\Omega. \end{align} $$
Suppose
![]() $\sigma \in G$
and
$\sigma \in G$
and
![]() $Y \cap \sigma (Y) \ne \emptyset $
. Then, there are
$Y \cap \sigma (Y) \ne \emptyset $
. Then, there are
![]() $h_1$
,
$h_1$
,
![]() $h_2 \in H$
such that
$h_2 \in H$
such that
![]() $h_1 \omega =\sigma h_2 \omega $
, and so
$h_1 \omega =\sigma h_2 \omega $
, and so
![]() $h_1^{-1} \sigma h_2 \in \operatorname {\mathrm {Stab}}(\omega ) \subset H$
, so
$h_1^{-1} \sigma h_2 \in \operatorname {\mathrm {Stab}}(\omega ) \subset H$
, so
![]() $\sigma \in H$
, and hence,
$\sigma \in H$
, and hence,
![]() $\sigma (Y)=(\sigma H) \omega =H \omega =Y$
. Therefore, the action is imprimitive.
$\sigma (Y)=(\sigma H) \omega =H \omega =Y$
. Therefore, the action is imprimitive.
Conversely, suppose the action is imprimitive, so there is some
![]() $Y \subset \Omega $
satisfying
$Y \subset \Omega $
satisfying
![]() $2 \le \# Y <\#\Omega $
, and for all
$2 \le \# Y <\#\Omega $
, and for all
![]() $\sigma \in G$
, either
$\sigma \in G$
, either
![]() $\sigma (Y) \cap Y=\emptyset $
or
$\sigma (Y) \cap Y=\emptyset $
or
![]() $\sigma (Y)=Y$
. Let
$\sigma (Y)=Y$
. Let
![]() $\omega \in Y$
and let
$\omega \in Y$
and let
If
![]() $\sigma \in \operatorname {\mathrm {Stab}}(\omega )$
, then
$\sigma \in \operatorname {\mathrm {Stab}}(\omega )$
, then
![]() $\omega \in Y \cap \sigma (Y)$
so
$\omega \in Y \cap \sigma (Y)$
so
![]() $\sigma (Y)=Y$
and so
$\sigma (Y)=Y$
and so
![]() $\sigma \in H$
. Hence,
$\sigma \in H$
. Hence,
![]() $\operatorname {\mathrm {Stab}}(\omega ) \subseteq H$
. Moreover, as H acts transitively on the elements of Y, we have
$\operatorname {\mathrm {Stab}}(\omega ) \subseteq H$
. Moreover, as H acts transitively on the elements of Y, we have
![]() $[H:\operatorname {\mathrm {Stab}}(\omega )]=\#Y$
, so (2.1) holds, and therefore,
$[H:\operatorname {\mathrm {Stab}}(\omega )]=\#Y$
, so (2.1) holds, and therefore,
![]() $\operatorname {\mathrm {Stab}}(\omega )$
is non-maximal.
$\operatorname {\mathrm {Stab}}(\omega )$
is non-maximal.
Lemma 2.3. Suppose G acts primitively on
![]() $\Omega $
. Let N be a normal subgroup of G. Then N acts either transitively or trivially on
$\Omega $
. Let N be a normal subgroup of G. Then N acts either transitively or trivially on
![]() $\Omega $
.
$\Omega $
.
Proof. We may suppose
![]() $\# \Omega \ge 2$
. Let
$\# \Omega \ge 2$
. Let
![]() $\omega \in \Omega $
. By Lemma 2.2, the stabilizer
$\omega \in \Omega $
. By Lemma 2.2, the stabilizer
![]() $\operatorname {\mathrm {Stab}}(\omega )$
is maximal. Let
$\operatorname {\mathrm {Stab}}(\omega )$
is maximal. Let
As N is normal, H is a subgroup of G, and since
![]() $\operatorname {\mathrm {Stab}}(\omega )$
is maximal,
$\operatorname {\mathrm {Stab}}(\omega )$
is maximal,
![]() $H=\operatorname {\mathrm {Stab}}(\omega )$
or
$H=\operatorname {\mathrm {Stab}}(\omega )$
or
![]() $H=G$
. Suppose first that
$H=G$
. Suppose first that
![]() $H=G$
. Then
$H=G$
. Then
![]() $\Omega =G\omega =H\omega =N \omega $
, so N acts transitively. Suppose instead that
$\Omega =G\omega =H\omega =N \omega $
, so N acts transitively. Suppose instead that
![]() $H=\operatorname {\mathrm {Stab}}(\omega )$
. Then
$H=\operatorname {\mathrm {Stab}}(\omega )$
. Then
![]() $N \subseteq \operatorname {\mathrm {Stab}}(\omega )$
. As N is normal and all point stabilizers are conjugate, we see that N is contained in all point stabilizers and so acts trivially.
$N \subseteq \operatorname {\mathrm {Stab}}(\omega )$
. As N is normal and all point stabilizers are conjugate, we see that N is contained in all point stabilizers and so acts trivially.
3 Primitivity and Riemann–Roch dimension
In this section, we prove Theorem 1.3. We assume basic knowledge of divisors and linear series as in, for example, the standard text of Arbarello, Cornalba, Griffiths and Harris [Reference Arbarello, Cornalba, Griffiths and Harris1].
Lemma 3.1. Let K be a perfect field and let
![]() $C/K$
be a curve. Let D be an irreducible divisor and let
$C/K$
be a curve. Let D be an irreducible divisor and let
![]() $f \in L(D)$
be non-constant. Then
$f \in L(D)$
be non-constant. Then
![]() $\operatorname {\mathrm {div}}_\infty (f)=D$
, where
$\operatorname {\mathrm {div}}_\infty (f)=D$
, where
![]() $\operatorname {\mathrm {div}}_\infty (f)$
denotes the divisor of poles of f.
$\operatorname {\mathrm {div}}_\infty (f)$
denotes the divisor of poles of f.
Proof. As f is non-constant and belongs to
![]() $L(D)$
, we have
$L(D)$
, we have
![]() $0<\operatorname {\mathrm {div}}_\infty (f) \le D$
. However, D is irreducible; therefore,
$0<\operatorname {\mathrm {div}}_\infty (f) \le D$
. However, D is irreducible; therefore,
![]() $\operatorname {\mathrm {div}}_\infty (f)=D$
.
$\operatorname {\mathrm {div}}_\infty (f)=D$
.
Lemma 3.2. Let K be a perfect field and let
![]() $C/K$
be a curve. Let D be a primitive divisor. Let
$C/K$
be a curve. Let D be a primitive divisor. Let
![]() $f \in L(D)$
be non-constant. Suppose there is a (possibly singular) curve
$f \in L(D)$
be non-constant. Suppose there is a (possibly singular) curve
![]() $C^\prime /K$
, and rational maps
$C^\prime /K$
, and rational maps
![]() $\varphi : C \dashrightarrow C^\prime $
and
$\varphi : C \dashrightarrow C^\prime $
and
![]() $\psi : C^\prime \dashrightarrow \mathbb {P}^1$
defined over K such that
$\psi : C^\prime \dashrightarrow \mathbb {P}^1$
defined over K such that
![]() $f=\psi \circ \varphi $
. Then
$f=\psi \circ \varphi $
. Then
![]() $\deg (\varphi )=1$
or
$\deg (\varphi )=1$
or
![]() $\deg (\psi )=1$
.
$\deg (\psi )=1$
.
Proof. Since D is primitive, it is irreducible, and thus,
![]() $\operatorname {\mathrm {div}}_\infty (f)=D$
by Lemma 3.1.
$\operatorname {\mathrm {div}}_\infty (f)=D$
by Lemma 3.1.
Now let
![]() $\pi : C^{\prime \prime } \rightarrow C^\prime $
be the normalization of
$\pi : C^{\prime \prime } \rightarrow C^\prime $
be the normalization of
![]() $C^\prime $
. The map
$C^\prime $
. The map
![]() $\pi $
is birational, and we write
$\pi $
is birational, and we write
![]() $u=\pi ^{-1} \circ \varphi $
, and
$u=\pi ^{-1} \circ \varphi $
, and
![]() $v=\psi \circ \pi $
. As C and
$v=\psi \circ \pi $
. As C and
![]() $C^{\prime \prime }$
are proper,
$C^{\prime \prime }$
are proper,
![]() $u : C \rightarrow C^{\prime \prime }$
and
$u : C \rightarrow C^{\prime \prime }$
and
![]() $v: C^{\prime \prime } \rightarrow \mathbb {P}^1$
are morphisms defined over K. Consider the following commutative diagram:
$v: C^{\prime \prime } \rightarrow \mathbb {P}^1$
are morphisms defined over K. Consider the following commutative diagram:

We note that
![]() $f=\psi \circ \varphi =v \circ u$
. In particular,
$f=\psi \circ \varphi =v \circ u$
. In particular,
![]() $D=f^{*}(\infty )=u^{*} (v^*(\infty ))$
.
$D=f^{*}(\infty )=u^{*} (v^*(\infty ))$
.
Write
![]() $r=\deg (u)$
and
$r=\deg (u)$
and
![]() $s=\deg (v)$
. Write
$s=\deg (v)$
. Write
![]() $v^*(\infty )=Q_1+\cdots +Q_s$
. Note that
$v^*(\infty )=Q_1+\cdots +Q_s$
. Note that
is a partition of the points in D, into s subsets of size r, that is Galois-stable. As D is primitive, either
![]() $r=1$
or
$r=1$
or
![]() $s=1$
. However,
$s=1$
. However,
![]() $r=\deg (\varphi )$
and
$r=\deg (\varphi )$
and
![]() $s=\deg (\psi )$
, completing the proof.
$s=\deg (\psi )$
, completing the proof.
Proof of Theorem 1.3.
Suppose
![]() $\ell (D) \ge 3$
. Then there are f,
$\ell (D) \ge 3$
. Then there are f,
![]() $g \in K(C)$
such that
$g \in K(C)$
such that
![]() $1$
, f, g are linearly independent elements of
$1$
, f, g are linearly independent elements of
![]() $L(D)$
. Let V be the subspace of
$L(D)$
. Let V be the subspace of
![]() $L(D)$
spanned by
$L(D)$
spanned by
![]() $1$
, f, g, and consider the corresponding linear system:
$1$
, f, g, and consider the corresponding linear system:
We claim that (3.1) is base-point free. Indeed, let
![]() $D_0$
be the base locus of (3.1). Thus,
$D_0$
be the base locus of (3.1). Thus,
![]() $D_0$
is a K-rational divisor and
$D_0$
is a K-rational divisor and
![]() $D_0 \le D$
. Since D is irreducible, either
$D_0 \le D$
. Since D is irreducible, either
![]() $D_0=0$
or
$D_0=0$
or
![]() $D_0=D$
. If
$D_0=D$
. If
![]() $D_0=D$
, then all elements of the linear system (3.1) are equal to D, which makes all
$D_0=D$
, then all elements of the linear system (3.1) are equal to D, which makes all
![]() $h \in V$
constant, giving a contradiction. Thus,
$h \in V$
constant, giving a contradiction. Thus,
![]() $D_0=0$
, establishing our claim. We let
$D_0=0$
, establishing our claim. We let
and let
![]() $C^\prime $
be the image of C in
$C^\prime $
be the image of C in
![]() $\mathbb {P}^2$
under
$\mathbb {P}^2$
under
![]() $\varphi $
, which is a geometrically irreducible curve defined over K, but may be singular. We claim that
$\varphi $
, which is a geometrically irreducible curve defined over K, but may be singular. We claim that
![]() $[0:1:0] \notin C^\prime $
. Suppose
$[0:1:0] \notin C^\prime $
. Suppose
![]() $[0:1:0] \in C^\prime $
; thus, there is some point
$[0:1:0] \in C^\prime $
; thus, there is some point
![]() $P \in C$
such that
$P \in C$
such that
![]() $(f/g)(P)=(1/g)(P)=0$
. However, by Lemma 3.1, we have
$(f/g)(P)=(1/g)(P)=0$
. However, by Lemma 3.1, we have
![]() $\operatorname {\mathrm {div}}_\infty (f)=\operatorname {\mathrm {div}}_\infty (g)=D$
. Since
$\operatorname {\mathrm {div}}_\infty (f)=\operatorname {\mathrm {div}}_\infty (g)=D$
. Since
![]() $(1/g)(P)=0$
, we have
$(1/g)(P)=0$
, we have
![]() $\operatorname {\mathrm {ord}}_P(D)>0$
. But then
$\operatorname {\mathrm {ord}}_P(D)>0$
. But then
![]() $\operatorname {\mathrm {ord}}_P(f)=-\operatorname {\mathrm {ord}}_P(D)=\operatorname {\mathrm {ord}}_P(g)$
, contradicting
$\operatorname {\mathrm {ord}}_P(f)=-\operatorname {\mathrm {ord}}_P(D)=\operatorname {\mathrm {ord}}_P(g)$
, contradicting
![]() $(f/g)(P)=0$
and establishing our claim.
$(f/g)(P)=0$
and establishing our claim.
Write
We may interpret this as projection of the curve
![]() $C^\prime $
from the point
$C^\prime $
from the point
![]() $[0:1:0]$
to the line
$[0:1:0]$
to the line
![]() $\ell =\{[x:0:z] \; : \; [x:z] \in \mathbb {P}^1\}$
. For a suitably general point
$\ell =\{[x:0:z] \; : \; [x:z] \in \mathbb {P}^1\}$
. For a suitably general point
![]() $[a:b] \in \mathbb {P}^1$
, the pull-back
$[a:b] \in \mathbb {P}^1$
, the pull-back
![]() $\psi ^*[a:b]$
is the intersection of
$\psi ^*[a:b]$
is the intersection of
![]() $C^\prime $
with the line connecting
$C^\prime $
with the line connecting
![]() $[0:1:0]$
with
$[0:1:0]$
with
![]() $[a:0:b]$
. Thus,
$[a:0:b]$
. Thus,
![]() $\deg (\psi )$
is the degree of
$\deg (\psi )$
is the degree of
![]() $C^\prime $
as a plane curve.
$C^\prime $
as a plane curve.
We also denote by
![]() $\varphi $
the morphism
$\varphi $
the morphism
![]() $C \rightarrow C^\prime $
. Then
$C \rightarrow C^\prime $
. Then
![]() $\psi \circ \varphi =f$
. Applying Lemma 3.2 to
$\psi \circ \varphi =f$
. Applying Lemma 3.2 to
![]() $\psi \circ \varphi =f$
gives
$\psi \circ \varphi =f$
gives
![]() $\deg (\varphi )=1$
or
$\deg (\varphi )=1$
or
![]() $\deg (\psi )=1$
. However, if
$\deg (\psi )=1$
. However, if
![]() $\deg (\psi )=1$
, then
$\deg (\psi )=1$
, then
![]() $C^\prime $
is a line which contradicts the linear independence of
$C^\prime $
is a line which contradicts the linear independence of
![]() $1$
, f, g. Thus,
$1$
, f, g. Thus,
![]() $\deg (\varphi )=1$
, and so
$\deg (\varphi )=1$
, and so
![]() $\deg (\psi )=\deg (f)=\deg (D)=n$
since
$\deg (\psi )=\deg (f)=\deg (D)=n$
since
![]() $\operatorname {\mathrm {div}}_\infty (f)=D$
. In particular, the plane curve
$\operatorname {\mathrm {div}}_\infty (f)=D$
. In particular, the plane curve
![]() $C^\prime $
has degree n. As
$C^\prime $
has degree n. As
![]() $\deg (\varphi )=1$
, the map
$\deg (\varphi )=1$
, the map
![]() $\varphi : C \rightarrow C^\prime $
is birational. Hence, the geometric genus of
$\varphi : C \rightarrow C^\prime $
is birational. Hence, the geometric genus of
![]() $C^\prime $
is g. Since
$C^\prime $
is g. Since
![]() $C^\prime $
has degree n, its arithmetic genus is
$C^\prime $
has degree n, its arithmetic genus is
![]() $(n-1)(n-2)/2$
. As the geometric genus is bounded by the arithmetic genus, we have that
$(n-1)(n-2)/2$
. As the geometric genus is bounded by the arithmetic genus, we have that
![]() $g \le (n-1)(n-2)/2$
. This contradicts (1.2).
$g \le (n-1)(n-2)/2$
. This contradicts (1.2).
4 Proof of Theorem 1.4
As
![]() $\ell (D_i)=2$
, we may choose non-constant
$\ell (D_i)=2$
, we may choose non-constant
![]() $f_i \in L(D_i)$
. Then
$f_i \in L(D_i)$
. Then
![]() $\operatorname {\mathrm {div}}_\infty (f_i)=D_i$
by Lemma 3.1, and in particular,
$\operatorname {\mathrm {div}}_\infty (f_i)=D_i$
by Lemma 3.1, and in particular,
![]() $\deg (f_i)=n$
. Let
$\deg (f_i)=n$
. Let
and let
![]() $C^\prime =\varphi (C)$
. Then
$C^\prime =\varphi (C)$
. Then
![]() $C^\prime /K$
is an irreducible but possibly singular curve lying on
$C^\prime /K$
is an irreducible but possibly singular curve lying on
![]() $\mathbb {P}^1 \times \mathbb {P}^1$
; we also denote the map
$\mathbb {P}^1 \times \mathbb {P}^1$
; we also denote the map
![]() $C \rightarrow C^\prime $
by
$C \rightarrow C^\prime $
by
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $\pi _1$
,
$\pi _1$
,
![]() $\pi _2 : \mathbb {P}^1 \times \mathbb {P}^1 \rightarrow \mathbb {P}^1$
denote projection onto the first and second factor, respectively. Let
$\pi _2 : \mathbb {P}^1 \times \mathbb {P}^1 \rightarrow \mathbb {P}^1$
denote projection onto the first and second factor, respectively. Let
![]() $\mu _i= \pi _i \vert _{C^\prime } : C^\prime \rightarrow \mathbb {P}^1$
. Then
$\mu _i= \pi _i \vert _{C^\prime } : C^\prime \rightarrow \mathbb {P}^1$
. Then
![]() $f_i=\mu _i \circ \varphi $
. By Lemma 3.2, there are two possibilities:
$f_i=\mu _i \circ \varphi $
. By Lemma 3.2, there are two possibilities:
-
(I) either
 $\deg (\varphi )=1$
and
$\deg (\varphi )=1$
and
 $\deg (\mu _1)=\deg (\mu _2)=n$
;
$\deg (\mu _1)=\deg (\mu _2)=n$
; -
(II) or
 $\deg (\varphi )=n$
and
$\deg (\varphi )=n$
and
 $\deg (\mu _1)=\deg (\mu _2)=1$
.
$\deg (\mu _1)=\deg (\mu _2)=1$
.
Suppose that (I) holds. Then
![]() $\varphi $
is a birational map, and so C and
$\varphi $
is a birational map, and so C and
![]() $C^\prime $
have the same geometric genus g. Moreover,
$C^\prime $
have the same geometric genus g. Moreover,
![]() $C^\prime $
is a curve of bidegree
$C^\prime $
is a curve of bidegree
![]() $(n,n)$
on
$(n,n)$
on
![]() $\mathbb {P}^1 \times \mathbb {P}^1$
and therefore has arithmetic genus
$\mathbb {P}^1 \times \mathbb {P}^1$
and therefore has arithmetic genus
![]() $(n-1)^2$
(see [Reference Hartshorne17, Exercise III.5.6]). Thus,
$(n-1)^2$
(see [Reference Hartshorne17, Exercise III.5.6]). Thus,
![]() $g \le (n-1)^2$
giving a contradiction.
$g \le (n-1)^2$
giving a contradiction.
Therefore, (II) holds. Thus,
![]() $\mu _1$
,
$\mu _1$
,
![]() $\mu _2$
are birational, and we have a commutative diagram of morphisms
$\mu _2$
are birational, and we have a commutative diagram of morphisms

Write
![]() $\mu =\mu _2 \circ \mu _1^{-1}$
. Then
$\mu =\mu _2 \circ \mu _1^{-1}$
. Then
![]() $\mu : \mathbb {P}^1 \rightarrow \mathbb {P}^1$
is an automorphism satisfying
$\mu : \mathbb {P}^1 \rightarrow \mathbb {P}^1$
is an automorphism satisfying
![]() $f_2=\mu \circ f_1$
. Thus,
$f_2=\mu \circ f_1$
. Thus,
![]() $f_2^*=f_1^* \circ \mu ^*=f_1^* \circ \mu ^{-1}$
. Let
$f_2^*=f_1^* \circ \mu ^*=f_1^* \circ \mu ^{-1}$
. Let
![]() $\alpha =\mu ^{-1}(0)$
. Then
$\alpha =\mu ^{-1}(0)$
. Then
Hence,
![]() $D_2-D_1=\operatorname {\mathrm {div}}((f_1-\alpha )/f_2)$
establishing the theorem.
$D_2-D_1=\operatorname {\mathrm {div}}((f_1-\alpha )/f_2)$
establishing the theorem.
5 Proof of Theorem 1.1
Let C be a smooth projective and absolutely irreducible curve over a number field K, with genus
![]() $g \ge 2$
, and write J for its Jacobian. Let
$g \ge 2$
, and write J for its Jacobian. Let
![]() $n \ge 1$
. We denote the n-th symmetric power of C by
$n \ge 1$
. We denote the n-th symmetric power of C by
![]() $C^{(n)}$
; this is defined as the quotient
$C^{(n)}$
; this is defined as the quotient
![]() $C^{(n)}=C^n/S_n$
, where
$C^{(n)}=C^n/S_n$
, where
![]() $S_n$
is the n-th symmetric group acting naturally on the n-th Cartesian power
$S_n$
is the n-th symmetric group acting naturally on the n-th Cartesian power
![]() $C^n$
of C. Recall that
$C^n$
of C. Recall that
![]() $C^{(n)}(K)$
can be identified with the set of effective degree n divisors on C. Let
$C^{(n)}(K)$
can be identified with the set of effective degree n divisors on C. Let
![]() $D_0$
be a fixed rational divisor of degree n, and let
$D_0$
be a fixed rational divisor of degree n, and let
be the corresponding Abel–Jacobi map. Write
![]() $W_n(C)=W_n^0(C)$
for the image of
$W_n(C)=W_n^0(C)$
for the image of
![]() $C^{(n)}$
under
$C^{(n)}$
under
![]() $\iota $
; this is the degree n Brill–Noether locus [Reference Arbarello, Cornalba, Griffiths and Harris1, Section IV.3].
$\iota $
; this is the degree n Brill–Noether locus [Reference Arbarello, Cornalba, Griffiths and Harris1, Section IV.3].
We now state a stronger, but more technical, version of Theorem 1.1.
Theorem 5.1. Let
![]() $n \ge 2$
and suppose (1.1) holds. Suppose
$n \ge 2$
and suppose (1.1) holds. Suppose
![]() $W_n(C)$
does not contain the translate of an abelian subvariety
$W_n(C)$
does not contain the translate of an abelian subvariety
![]() $A/K$
of J of positive rank. If C has infinitely many primitive points of degree n, then there is a degree n morphism
$A/K$
of J of positive rank. If C has infinitely many primitive points of degree n, then there is a degree n morphism
![]() $\varphi : C \rightarrow \mathbb {P}^1$
defined over K such that all but finitely many primitive degree n divisors are fibres
$\varphi : C \rightarrow \mathbb {P}^1$
defined over K such that all but finitely many primitive degree n divisors are fibres
![]() $\varphi ^{*}(\alpha )$
with
$\varphi ^{*}(\alpha )$
with
![]() $\alpha \in \mathbb {P}^1(K)$
.
$\alpha \in \mathbb {P}^1(K)$
.
We point out that Derickx [Reference Derickx8] has developed a powerful computational method that is often capable of ruling out the existence of translates of abelian varieties within
![]() $W_n(C)$
, even when J has abelian subvarieties of small dimension.
$W_n(C)$
, even when J has abelian subvarieties of small dimension.
We shall need the following theorem of Debarre and Fahlaoui [Reference Debarre and Fahlaoui7, Corolllary 3.6].
Theorem 5.2 (Debarre and Fahlaoui).
Suppose
![]() $n \le g-1$
. Let A be an abelian subvariety of J with a translate contained in
$n \le g-1$
. Let A be an abelian subvariety of J with a translate contained in
![]() $W_n(C)$
. Then
$W_n(C)$
. Then
![]() $\dim (A) \le n/2$
.
$\dim (A) \le n/2$
.
Thanks to the theorem of Debarre and Fahlaoui, Theorem 5.1 immediately implies Theorem 1.1. It is therefore enough to prove Theorem 5.1.
We shall also need the following famous theorem of Faltings [Reference Faltings13] which establishes the Mordell–Lang conjecture for subvarieties of Abelian varieties.
Theorem 5.3 (Faltings).
Let B be an abelian variety defined over a number field K, and let
![]() $V \subset B$
be a subvariety defined over K. Then there is a finite number of abelian subvarieties
$V \subset B$
be a subvariety defined over K. Then there is a finite number of abelian subvarieties
![]() $B_1, \dotsc , B_r$
of B, defined over K, and a finite number of points
$B_1, \dotsc , B_r$
of B, defined over K, and a finite number of points
![]() $x_1,\dotsc ,x_r \in V(K)$
such that the translates
$x_1,\dotsc ,x_r \in V(K)$
such that the translates
![]() $x_i+B_i$
are contained in V, and, moreover, such that
$x_i+B_i$
are contained in V, and, moreover, such that
 $$\begin{align*}V(K)=\bigcup_{i=1}^r x_i+B_i(K). \end{align*}$$
$$\begin{align*}V(K)=\bigcup_{i=1}^r x_i+B_i(K). \end{align*}$$
For the proof of Theorem 5.1, we shall need the following proposition.
Proposition 5.4. Let
![]() $n \le g-1$
. Suppose that
$n \le g-1$
. Suppose that
![]() $W_n(C)$
does not contain the translate of an abelian subvariety
$W_n(C)$
does not contain the translate of an abelian subvariety
![]() $A/K$
of J of positive rank. Then there are a finite number of divisors
$A/K$
of J of positive rank. Then there are a finite number of divisors
![]() $D_1,D_2,\dotsc ,D_m \in C^{(n)}(\mathbb {Q})$
such that
$D_1,D_2,\dotsc ,D_m \in C^{(n)}(\mathbb {Q})$
such that
 $$\begin{align*}C^{(n)}(K)=\bigcup_{i=1}^m \lvert D_i \rvert. \end{align*}$$
$$\begin{align*}C^{(n)}(K)=\bigcup_{i=1}^m \lvert D_i \rvert. \end{align*}$$
Here,
![]() $\lvert D \rvert $
denotes the complete linear system corresponding to D:
$\lvert D \rvert $
denotes the complete linear system corresponding to D:
Proposition 5.4 is an elementary and straightforward consequence of the aforementioned theorem of Faltings; versions of the proposition have appeared elsewhere [Reference Bourdon, Ejder, Liu, Odumodu and Viray2, Theorem 4.2], [Reference Frey14, Proposition 2], [Reference Harris and Silverman16, Theorem 2], [Reference Khawaja and Siksek21, Proposition 18]. For the convenience of the reader, we give the proof.
Proof of Proposition 5.4.
Recall our assumption that
![]() $n \le g-1$
. The Brill–Noether locus
$n \le g-1$
. The Brill–Noether locus
![]() $W_n(C)$
has dimension n as it is birational to
$W_n(C)$
has dimension n as it is birational to
![]() $C^{(n)}$
(see, for example, [Reference Milne24, Theorem 5.1]) and is therefore a proper subvariety of J. We apply Faltings’ theorem to deduce that
$C^{(n)}$
(see, for example, [Reference Milne24, Theorem 5.1]) and is therefore a proper subvariety of J. We apply Faltings’ theorem to deduce that
 $$\begin{align*}W_n(C)(K)=\bigcup_{i=1}^r x_i+B_i(K), \end{align*}$$
$$\begin{align*}W_n(C)(K)=\bigcup_{i=1}^r x_i+B_i(K), \end{align*}$$
where
![]() $x_i \in W_n(K)$
, and
$x_i \in W_n(K)$
, and
![]() $B_i/K$
are abelian subvarities of J such that the translates
$B_i/K$
are abelian subvarities of J such that the translates
![]() $x_i+B_i$
are contained in
$x_i+B_i$
are contained in
![]() $W_n(C)$
. Thus,
$W_n(C)$
. Thus,
![]() $B_i(K)$
is finite by the assumption. Thus,
$B_i(K)$
is finite by the assumption. Thus,
![]() $W_n(C)(K)$
is finite.
$W_n(C)(K)$
is finite.
We note that
![]() $\iota (C^{(n)}(K))$
is a subset of
$\iota (C^{(n)}(K))$
is a subset of
![]() $W_n(K)$
and hence must be finite. Choose
$W_n(K)$
and hence must be finite. Choose
![]() $D_1,\dotsc ,D_m \in C^{(n)}(K)$
such that
$D_1,\dotsc ,D_m \in C^{(n)}(K)$
such that
![]() $\iota (C^{(n)}(K))=\{\iota (D_1),\dotsc ,\iota (D_m)\}$
. Now let
$\iota (C^{(n)}(K))=\{\iota (D_1),\dotsc ,\iota (D_m)\}$
. Now let
![]() $D \in C^{(n)}(K)$
. Then
$D \in C^{(n)}(K)$
. Then
![]() $[D-D_0]=\iota (D)=\iota (D_i)=[D_i-D]$
for some i, and therefore,
$[D-D_0]=\iota (D)=\iota (D_i)=[D_i-D]$
for some i, and therefore,
![]() $D\thicksim D_i$
, giving
$D\thicksim D_i$
, giving
![]() $D \in \lvert D_i\rvert $
.
$D \in \lvert D_i\rvert $
.
Proof of Theorem 5.1.
Write
![]() $C^{(n)}_{\operatorname {\mathrm {prim}}}(K)$
for the subset of
$C^{(n)}_{\operatorname {\mathrm {prim}}}(K)$
for the subset of
![]() $C^{(n)}(K)$
consisting of primitive divisors. We apply Proposition 5.4. Hence,
$C^{(n)}(K)$
consisting of primitive divisors. We apply Proposition 5.4. Hence,
 $$ \begin{align} C^{(n)}_{\operatorname{\mathrm{prim}}}(K) \; \subseteq \; \bigcup_{j=1}^m \, \lvert D_j \rvert \end{align} $$
$$ \begin{align} C^{(n)}_{\operatorname{\mathrm{prim}}}(K) \; \subseteq \; \bigcup_{j=1}^m \, \lvert D_j \rvert \end{align} $$
for some effective degree n divisors
![]() $D_1,\dotsc ,D_m$
. We may delete any
$D_1,\dotsc ,D_m$
. We may delete any
![]() $\lvert D_j \rvert $
from (5.2) that does not contain any primitive divisor. Recall that
$\lvert D_j \rvert $
from (5.2) that does not contain any primitive divisor. Recall that
![]() $D^\prime \in \lvert D\rvert $
if and only if
$D^\prime \in \lvert D\rvert $
if and only if
![]() $\lvert D^\prime \rvert =\lvert D \rvert $
. Hence, we may suppose that
$\lvert D^\prime \rvert =\lvert D \rvert $
. Hence, we may suppose that
![]() $D_1,\dotsc ,D_m$
are primitive. We now apply Theorem 1.3. This tells us that
$D_1,\dotsc ,D_m$
are primitive. We now apply Theorem 1.3. This tells us that
![]() $\ell (D_i)=1$
or
$\ell (D_i)=1$
or
![]() $2$
for
$2$
for
![]() $i=1,\dotsc ,m$
. Moreover, Theorem 1.4 tells us that
$i=1,\dotsc ,m$
. Moreover, Theorem 1.4 tells us that
![]() $\ell (D)=2$
for at most one divisor D among
$\ell (D)=2$
for at most one divisor D among
![]() $D_1,\dotsc ,D_m$
. If
$D_1,\dotsc ,D_m$
. If
![]() $\ell (D)=1$
, then
$\ell (D)=1$
, then
![]() $\lvert D \rvert =\{D\}$
. Since
$\lvert D \rvert =\{D\}$
. Since
![]() $C^{(n)}_{\operatorname {\mathrm {prim}}}(K)$
is infinite, we deduce, after permuting the
$C^{(n)}_{\operatorname {\mathrm {prim}}}(K)$
is infinite, we deduce, after permuting the
![]() $D_i$
, that
$D_i$
, that
where
![]() $\ell (D_m)=2$
. Let
$\ell (D_m)=2$
. Let
![]() $\varphi \in L(D_m)$
be a non-constant function, which we regard as a morphism
$\varphi \in L(D_m)$
be a non-constant function, which we regard as a morphism
![]() $\varphi : C \rightarrow \mathbb {P}^1$
satisfying
$\varphi : C \rightarrow \mathbb {P}^1$
satisfying
![]() $\varphi ^*(\infty )=D_m$
. If
$\varphi ^*(\infty )=D_m$
. If
![]() $D \in \lvert D_m \rvert $
, and
$D \in \lvert D_m \rvert $
, and
![]() $D \ne D_m$
, then
$D \ne D_m$
, then
![]() $D=D_m+\operatorname {\mathrm {div}}(\varphi -\alpha )$
for some
$D=D_m+\operatorname {\mathrm {div}}(\varphi -\alpha )$
for some
![]() $\alpha \in K$
, and so
$\alpha \in K$
, and so
![]() $D=\varphi ^*(\alpha )$
. This completes the proof.
$D=\varphi ^*(\alpha )$
. This completes the proof.
6 Galois Theory and specializations
Let K be a number field. Let
![]() $\varphi : C \rightarrow \mathbb {P}^1$
be a morphism of curves defined over K. Note that
$\varphi : C \rightarrow \mathbb {P}^1$
be a morphism of curves defined over K. Note that
![]() $K(C) \cap \overline {K}=K$
, as C is geometrically connected. We write
$K(C) \cap \overline {K}=K$
, as C is geometrically connected. We write
![]() $\operatorname {\mathrm {Ram}}(\varphi ) \subset C$
for the set of ramification points of C. The set of branch values for
$\operatorname {\mathrm {Ram}}(\varphi ) \subset C$
for the set of ramification points of C. The set of branch values for
![]() $\varphi $
is
$\varphi $
is
Let
![]() $\mathbb {K}$
be the Galois closure of the function field extension
$\mathbb {K}$
be the Galois closure of the function field extension
![]() $K(C)/K(\mathbb {P}^1)$
induced by
$K(C)/K(\mathbb {P}^1)$
induced by
![]() $\varphi $
. Write
$\varphi $
. Write
![]() $n=\deg (\varphi )$
. Then we may naturally identify
$n=\deg (\varphi )$
. Then we may naturally identify
![]() $G^\prime :=\operatorname {\mathrm {Gal}}(\mathbb {K}/K(\mathbb {P}^1))$
with a transitive subgroup of
$G^\prime :=\operatorname {\mathrm {Gal}}(\mathbb {K}/K(\mathbb {P}^1))$
with a transitive subgroup of
![]() $S_n$
. In what follows, when we speak of subgroups of
$S_n$
. In what follows, when we speak of subgroups of
![]() $G^\prime $
being transitive or primitive, it is with respect to the action on
$G^\prime $
being transitive or primitive, it is with respect to the action on
![]() $\{1,2,\dotsc ,n\}$
.
$\{1,2,\dotsc ,n\}$
.
Lemma 6.1. Let
![]() $\alpha \in \mathbb {P}^1(K)$
, and consider
$\alpha \in \mathbb {P}^1(K)$
, and consider
![]() $\alpha $
as a place of
$\alpha $
as a place of
![]() $\mathbb {P}^1$
. Let
$\mathbb {P}^1$
. Let
![]() $\mathcal {P}$
be a place of
$\mathcal {P}$
be a place of
![]() $\mathbb {K}$
above
$\mathbb {K}$
above
![]() $\alpha $
. Then
$\alpha $
. Then
![]() $K(\mathcal {P})/K$
is a Galois extension with Galois group isomorphic to the decomposition group
$K(\mathcal {P})/K$
is a Galois extension with Galois group isomorphic to the decomposition group
Proof. For this, see [Reference Stichtenoth30, Theorem III.8.2]. However, we will sketch some of the ideas in the proof of Lemma 6.2.
Let
![]() $L=\mathbb {K} \cap \overline {K}$
, which is a finite Galois extension of K. Let
$L=\mathbb {K} \cap \overline {K}$
, which is a finite Galois extension of K. Let
![]() $G=\operatorname {\mathrm {Gal}}(\mathbb {K}/L(\mathbb {P}^1))$
. Then we obtain an exact sequence of Galois groups
$G=\operatorname {\mathrm {Gal}}(\mathbb {K}/L(\mathbb {P}^1))$
. Then we obtain an exact sequence of Galois groups
 $$ \begin{align} 1 \rightarrow \underbrace{\operatorname{\mathrm{Gal}}(\mathbb{K}/L(\mathbb{P}^1))}_{G} \rightarrow \underbrace{\operatorname{\mathrm{Gal}}(\mathbb{K}/K(\mathbb{P}^1))}_{G^\prime} \rightarrow \underbrace{\operatorname{\mathrm{Gal}}(L(\mathbb{P}^1)/K(\mathbb{P}^1))}_{\cong \operatorname{\mathrm{Gal}}(L/K)} \rightarrow 1. \end{align} $$
$$ \begin{align} 1 \rightarrow \underbrace{\operatorname{\mathrm{Gal}}(\mathbb{K}/L(\mathbb{P}^1))}_{G} \rightarrow \underbrace{\operatorname{\mathrm{Gal}}(\mathbb{K}/K(\mathbb{P}^1))}_{G^\prime} \rightarrow \underbrace{\operatorname{\mathrm{Gal}}(L(\mathbb{P}^1)/K(\mathbb{P}^1))}_{\cong \operatorname{\mathrm{Gal}}(L/K)} \rightarrow 1. \end{align} $$
We note that
![]() $\mathbb {K}/L(\mathbb {P}^1)$
is regular in the sense that
$\mathbb {K}/L(\mathbb {P}^1)$
is regular in the sense that
![]() $\mathbb {K} \cap \overline {L}=L$
. Therefore,
$\mathbb {K} \cap \overline {L}=L$
. Therefore,
![]() $\mathbb {K}=L(\tilde {C})$
, where
$\mathbb {K}=L(\tilde {C})$
, where
![]() $\tilde {C}$
is a (geometrically connected) curve defined over L. The inclusions
$\tilde {C}$
is a (geometrically connected) curve defined over L. The inclusions
![]() $L(\mathbb {P}^1) \subseteq L(C) \subseteq L(\tilde {C})$
correspond to morphisms
$L(\mathbb {P}^1) \subseteq L(C) \subseteq L(\tilde {C})$
correspond to morphisms
and we write
![]() $\mu : \tilde {C} \rightarrow \mathbb {P}^1$
for the composition which is defined over L. We may naturally identify G with automorphisms of the cover
$\mu : \tilde {C} \rightarrow \mathbb {P}^1$
for the composition which is defined over L. We may naturally identify G with automorphisms of the cover
![]() $\mu $
.
$\mu $
.
Now let H be a subgroup of G. Write
![]() $\mathbb {K}^H$
for the subfield of
$\mathbb {K}^H$
for the subfield of
![]() $\mathbb {K}$
fixed by H. The function field extension
$\mathbb {K}$
fixed by H. The function field extension
![]() $\mathbb {K}^H/L(\mathbb {P}^1)$
corresponds to a morphism of curves
$\mathbb {K}^H/L(\mathbb {P}^1)$
corresponds to a morphism of curves
![]() $\pi _H : D_H \rightarrow \mathbb {P}^1$
defined over L, where
$\pi _H : D_H \rightarrow \mathbb {P}^1$
defined over L, where
![]() $L(D_H)=\mathbb {K}^H$
. Note that we have the following commutative diagram of morphisms:
$L(D_H)=\mathbb {K}^H$
. Note that we have the following commutative diagram of morphisms:

We note that
![]() $\operatorname {\mathrm {BV}}(\mu )=\operatorname {\mathrm {BV}}(\varphi )$
(see, for example, [Reference Stichtenoth30, Corollary III.8.4]). It follows that
$\operatorname {\mathrm {BV}}(\mu )=\operatorname {\mathrm {BV}}(\varphi )$
(see, for example, [Reference Stichtenoth30, Corollary III.8.4]). It follows that
![]() $\operatorname {\mathrm {BV}}(\pi _H) \subseteq \operatorname {\mathrm {BV}}(\varphi )$
.
$\operatorname {\mathrm {BV}}(\pi _H) \subseteq \operatorname {\mathrm {BV}}(\varphi )$
.
We shall use (6.2) to study fibres of the map
![]() $\varphi $
with certain Galois group. The curve
$\varphi $
with certain Galois group. The curve
![]() $D_H$
is important to us because of the following standard result.
$D_H$
is important to us because of the following standard result.
Lemma 6.2. Let
![]() $\mathcal {P} \in \tilde {C}$
be an algebraic point with
$\mathcal {P} \in \tilde {C}$
be an algebraic point with
![]() . Write
. Write
for the decomposition group of
![]() $\mathcal {P}$
. Let H be a subgroup of G, and suppose
$\mathcal {P}$
. Let H be a subgroup of G, and suppose
![]() $G_{\mathcal {P}} \subseteq H$
. Then
$G_{\mathcal {P}} \subseteq H$
. Then
![]() $\eta _H(\mathcal {P}) \in D_H(L)$
.
$\eta _H(\mathcal {P}) \in D_H(L)$
.
Proof. The lemma is implicit in most proofs of Hilbert’s Irreducibility Theorem (e.g., [Reference Serre27, Proposition 3.3.1]), but we give a proof as it helps make ideas precise. Note that
![]() $\mathcal {P}$
is unramified in
$\mathcal {P}$
is unramified in
![]() $\mu $
. Since
$\mu $
. Since
![]() $\mathbb {K}/L(\mathbb {P}^1)$
is a Galois extension, the extension
$\mathbb {K}/L(\mathbb {P}^1)$
is a Galois extension, the extension
![]() $L(\mathcal {P})/L$
is Galois, and its Galois group can be identified with
$L(\mathcal {P})/L$
is Galois, and its Galois group can be identified with
![]() $G_{\mathcal {P}}$
in a natural way; see, for example, [Reference Stichtenoth30, Theorem 3.8.2]. We shall in fact need some of the details of this identification, which we now sketch. Write
$G_{\mathcal {P}}$
in a natural way; see, for example, [Reference Stichtenoth30, Theorem 3.8.2]. We shall in fact need some of the details of this identification, which we now sketch. Write
for the valuation ring of
![]() $\mathcal {P}$
and its maximal ideal. Then
$\mathcal {P}$
and its maximal ideal. Then
![]() $L(\mathcal {P})$
may be identified with
$L(\mathcal {P})$
may be identified with
![]() $\mathcal {O}_{\mathcal {P}}/\mathfrak {m}_{\mathcal {P}}$
via the well-defined map
$\mathcal {O}_{\mathcal {P}}/\mathfrak {m}_{\mathcal {P}}$
via the well-defined map
Let
![]() $\sigma \in G_{\mathcal {P}}$
, and let
$\sigma \in G_{\mathcal {P}}$
, and let
![]() $f \in \mathbb {K}$
. Then
$f \in \mathbb {K}$
. Then
It follows that
![]() $\sigma (\mathcal {O}_{\mathcal {P}})=\mathcal {O}_{\mathcal {P}}$
and
$\sigma (\mathcal {O}_{\mathcal {P}})=\mathcal {O}_{\mathcal {P}}$
and
![]() $\sigma (\mathfrak {m}_{\mathcal {P}})=\mathfrak {m}_{\mathcal {P}}$
. Hence,
$\sigma (\mathfrak {m}_{\mathcal {P}})=\mathfrak {m}_{\mathcal {P}}$
. Hence,
![]() $\sigma \in G_{\mathcal {P}}$
induces a well-defined automorphism of
$\sigma \in G_{\mathcal {P}}$
induces a well-defined automorphism of
![]() $\mathcal {O}_{\mathcal {P}}/\mathfrak {m}_{\mathcal {P}}=L(\mathcal {P})$
given by
$\mathcal {O}_{\mathcal {P}}/\mathfrak {m}_{\mathcal {P}}=L(\mathcal {P})$
given by
![]() $\sigma (f+\mathfrak {m}_{\mathcal {P}})=\sigma (f)+\mathfrak {m}_{\mathcal {P}}$
. Since
$\sigma (f+\mathfrak {m}_{\mathcal {P}})=\sigma (f)+\mathfrak {m}_{\mathcal {P}}$
. Since
![]() $L \subseteq L(\mathbb {P}^1)$
which is fixed by G, the automorphism on
$L \subseteq L(\mathbb {P}^1)$
which is fixed by G, the automorphism on
![]() $L(\mathcal {P})$
induced by
$L(\mathcal {P})$
induced by
![]() $\sigma $
fixes L. We have now constructed a homomorphism
$\sigma $
fixes L. We have now constructed a homomorphism
![]() $G_{\mathcal {P}} \rightarrow \operatorname {\mathrm {Aut}}(L(\mathcal {P})/L)$
. It turns out [Reference Stichtenoth30, Theorem III.8.2], since
$G_{\mathcal {P}} \rightarrow \operatorname {\mathrm {Aut}}(L(\mathcal {P})/L)$
. It turns out [Reference Stichtenoth30, Theorem III.8.2], since
![]() $\mathbb {K}/L(\mathbb {P}^1)$
is Galois, that
$\mathbb {K}/L(\mathbb {P}^1)$
is Galois, that
![]() $L(\mathcal {P})/L$
is Galois, and that the homomorphism constructed is in fact an isomorphism
$L(\mathcal {P})/L$
is Galois, and that the homomorphism constructed is in fact an isomorphism
![]() $G_{\mathcal {P}} \xrightarrow {\sim } \operatorname {\mathrm {Gal}}(L(\mathcal {P})/L)$
.
$G_{\mathcal {P}} \xrightarrow {\sim } \operatorname {\mathrm {Gal}}(L(\mathcal {P})/L)$
.
Now write
![]() $R=\eta _H(\mathcal {P})$
. We would like to show that
$R=\eta _H(\mathcal {P})$
. We would like to show that
![]() $\eta _H(R) \in D_H(L)$
. It is enough to show that
$\eta _H(R) \in D_H(L)$
. It is enough to show that
![]() $g(R) \in L$
for all
$g(R) \in L$
for all
![]() $g \in \mathcal {O}_{R}$
. However,
$g \in \mathcal {O}_{R}$
. However,
![]() $g(R)=f(\mathcal {P})$
, where
$g(R)=f(\mathcal {P})$
, where
![]() $f=\eta _H^*(g) \in \mathcal {O}_{\mathcal {P}}$
. Thus, we need to show that
$f=\eta _H^*(g) \in \mathcal {O}_{\mathcal {P}}$
. Thus, we need to show that
![]() $f(\mathcal {P}) \in L$
. This is equivalent to showing that
$f(\mathcal {P}) \in L$
. This is equivalent to showing that
![]() $\sigma (f(\mathcal {P}))=f(\mathcal {P})$
for all
$\sigma (f(\mathcal {P}))=f(\mathcal {P})$
for all
![]() $\sigma \in \operatorname {\mathrm {Gal}}(L(\mathcal {P})/L)$
, which is equivalent to showing that
$\sigma \in \operatorname {\mathrm {Gal}}(L(\mathcal {P})/L)$
, which is equivalent to showing that
![]() $\sigma (f+\mathfrak {m}_{\mathcal {P}})=f+\mathfrak {m}_{\mathcal {P}}$
for all
$\sigma (f+\mathfrak {m}_{\mathcal {P}})=f+\mathfrak {m}_{\mathcal {P}}$
for all
![]() $\sigma \in G_{\mathcal {P}}$
. However, by the construction of the function field of
$\sigma \in G_{\mathcal {P}}$
. However, by the construction of the function field of
![]() $D_H$
, we see that
$D_H$
, we see that
![]() $\sigma (f)=f$
for all
$\sigma (f)=f$
for all
![]() $\sigma \in H \supseteq G_{\mathcal {P}}$
. This completes the proof.
$\sigma \in H \supseteq G_{\mathcal {P}}$
. This completes the proof.
Lemma 6.3. Let
![]() $P \in C/K$
be a primitive degree n point, with
$P \in C/K$
be a primitive degree n point, with
![]() $\varphi (P)=\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
, and suppose
$\varphi (P)=\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
, and suppose
![]() $P \notin C(L)$
. Let
$P \notin C(L)$
. Let
![]() $P_1=P,P_2,\dotsc ,P_n$
be the Galois orbit of P, and let
$P_1=P,P_2,\dotsc ,P_n$
be the Galois orbit of P, and let
be the permutation representation obtained from the Galois action of
![]() $\operatorname {\mathrm {Gal}}(\overline {K}/K)$
on the orbit. Let
$\operatorname {\mathrm {Gal}}(\overline {K}/K)$
on the orbit. Let
![]() $I=\rho (\operatorname {\mathrm {Gal}}(\overline {K}/K))$
and
$I=\rho (\operatorname {\mathrm {Gal}}(\overline {K}/K))$
and
![]() $J=\rho (\operatorname {\mathrm {Gal}}(\overline {K}/L))$
; these are the Galois groups of P over K and L, respectively. Then the following hold.
$J=\rho (\operatorname {\mathrm {Gal}}(\overline {K}/L))$
; these are the Galois groups of P over K and L, respectively. Then the following hold.
-
(i) J is a nontrivial normal subgroup of I and is a transitive subgroup of
 $\operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\}) \cong S_n$
.
$\operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\}) \cong S_n$
. -
(ii) Let
 $\mathcal {P} \in \tilde {C}$
be above P. Then
$\mathcal {P} \in \tilde {C}$
be above P. Then
 $G_{\mathcal {P}} \subseteq G$
is conjugate to J when both are regarded as subgroups of
$G_{\mathcal {P}} \subseteq G$
is conjugate to J when both are regarded as subgroups of
 $S_n$
.
$S_n$
. -
(iii) There is some transitive subgroup H of G, conjugate to J in
 $S_n$
, such that
$S_n$
, such that
 $R \in D_H(L)$
where
$R \in D_H(L)$
where
 $R=\eta _H(\mathcal {P})$
.
$R=\eta _H(\mathcal {P})$
.
Proof. By assumption,
![]() $\rho (\operatorname {\mathrm {Gal}}(\overline {K}/K))$
is a primitive subgroup of
$\rho (\operatorname {\mathrm {Gal}}(\overline {K}/K))$
is a primitive subgroup of
![]() $\operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\}) \cong S_n$
. Since
$\operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\}) \cong S_n$
. Since
![]() $L/K$
is Galois,
$L/K$
is Galois,
![]() $J=\rho (\operatorname {\mathrm {Gal}}(\overline {K}/L))$
is a normal subgroup of
$J=\rho (\operatorname {\mathrm {Gal}}(\overline {K}/L))$
is a normal subgroup of
![]() $\rho (\operatorname {\mathrm {Gal}}(\overline {K}/K))$
. By Lemma 2.3, the group
$\rho (\operatorname {\mathrm {Gal}}(\overline {K}/K))$
. By Lemma 2.3, the group
![]() $J \subset \operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\})$
is either trivial or transitive. However, since
$J \subset \operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\})$
is either trivial or transitive. However, since
![]() $P \notin C(L)$
, the group J is nontrivial and therefore transitive. This proves (i).
$P \notin C(L)$
, the group J is nontrivial and therefore transitive. This proves (i).
Recall that
![]() $\varphi (P)=\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
. Since P has precisely n conjugates, and
$\varphi (P)=\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
. Since P has precisely n conjugates, and
![]() $\deg (\varphi )=n$
, we see that the fibre
$\deg (\varphi )=n$
, we see that the fibre
![]() $\varphi ^*(\alpha )$
consists of
$\varphi ^*(\alpha )$
consists of
![]() $P_1,\dotsc ,P_n$
, each with multiplicity
$P_1,\dotsc ,P_n$
, each with multiplicity
![]() $1$
. By composing
$1$
. By composing
![]() $\varphi $
with a suitable automorphism of
$\varphi $
with a suitable automorphism of
![]() $\mathbb {P}^1$
, we may suppose that
$\mathbb {P}^1$
, we may suppose that
![]() $\alpha \in \mathbb {A}^1(K)=K$
. We shall find it convenient to think of
$\alpha \in \mathbb {A}^1(K)=K$
. We shall find it convenient to think of
![]() $\varphi $
as an element of
$\varphi $
as an element of
![]() $K(C)$
, and with this identification, we have
$K(C)$
, and with this identification, we have
![]() $K(\mathbb {P}^1)=K(\varphi ) \subseteq K(C)$
. The extension
$K(\mathbb {P}^1)=K(\varphi ) \subseteq K(C)$
. The extension
![]() $K(C)/K(\varphi )$
has degree n.
$K(C)/K(\varphi )$
has degree n.
Write
for the valuation ring of P and its maximal ideal. Then the residue field
![]() $\mathcal {O}_{D}/\mathfrak {m}_{D}$
can be identified with
$\mathcal {O}_{D}/\mathfrak {m}_{D}$
can be identified with
![]() $K(P)$
, where the identification is given by
$K(P)$
, where the identification is given by
![]() $g +\mathfrak {m}_{D} \mapsto g(P)$
. Now fix
$g +\mathfrak {m}_{D} \mapsto g(P)$
. Now fix
![]() $\theta \in K(P)$
such that
$\theta \in K(P)$
such that
![]() $K(P)=K(\theta )$
. Note that
$K(P)=K(\theta )$
. Note that
![]() $[K(\theta ) : K]=n$
since P has degree n. Then there is some
$[K(\theta ) : K]=n$
since P has degree n. Then there is some
![]() $g \in \mathcal {O}_{P}$
such that
$g \in \mathcal {O}_{P}$
such that
![]() $g(P)=\theta $
. As
$g(P)=\theta $
. As
![]() $g \in K(C)$
and
$g \in K(C)$
and
![]() $K(C)$
has degree n over
$K(C)$
has degree n over
![]() $K(\varphi )$
, there is a polynomial
$K(\varphi )$
, there is a polynomial
![]() $F(U,V) \in K[U,V]$
,
$F(U,V) \in K[U,V]$
,
 $$ \begin{align} F(U,V)=\sum_{i=1}^m a_i(V) U^i, \qquad a_i(V) \in K[V] \end{align} $$
$$ \begin{align} F(U,V)=\sum_{i=1}^m a_i(V) U^i, \qquad a_i(V) \in K[V] \end{align} $$
of degree
![]() $m \mid n$
, such that
$m \mid n$
, such that
![]() $\gcd (a_0(V),\dotsc ,a_m(V))=1$
, and
$\gcd (a_0(V),\dotsc ,a_m(V))=1$
, and
![]() $F(g,\varphi )=0$
. Now,
$F(g,\varphi )=0$
. Now,
![]() $F(\theta ,\alpha )=F(g(P),\varphi (P))=0$
, and so
$F(\theta ,\alpha )=F(g(P),\varphi (P))=0$
, and so
![]() $\theta $
is a root of the polynomial
$\theta $
is a root of the polynomial
![]() $F(U,\alpha ) \in K[U]$
; this polynomial is nonzero as
$F(U,\alpha ) \in K[U]$
; this polynomial is nonzero as
![]() $\gcd (a_0(V),\dotsc ,a_m(V))=1$
. As
$\gcd (a_0(V),\dotsc ,a_m(V))=1$
. As
![]() $\theta $
has degree n over K, it follows that
$\theta $
has degree n over K, it follows that
![]() $m=n$
, and that
$m=n$
, and that
![]() $F(U,V)$
is irreducible over
$F(U,V)$
is irreducible over
![]() $K(V)$
. In particular,
$K(V)$
. In particular,
![]() $F(U,V)=0$
is a (possibly singular) plane model for
$F(U,V)=0$
is a (possibly singular) plane model for
![]() $C/K$
, and the map
$C/K$
, and the map
![]() $\varphi $
is given by
$\varphi $
is given by
![]() $(u,v) \mapsto v$
. As C is absolutely irreducible,
$(u,v) \mapsto v$
. As C is absolutely irreducible,
![]() $F(U,V)$
is irreducible over
$F(U,V)$
is irreducible over
![]() $\overline {K}$
. Let
$\overline {K}$
. Let
![]() $g_1=g,g_2,\dotsc ,g_n$
be the roots of
$g_1=g,g_2,\dotsc ,g_n$
be the roots of
![]() $F(U,\varphi )=0$
in
$F(U,\varphi )=0$
in
![]() $\mathbb {K}$
; then
$\mathbb {K}$
; then
![]() $\mathbb {K}=K(\varphi )(g_1,\dotsc ,g_n)$
. In particular,
$\mathbb {K}=K(\varphi )(g_1,\dotsc ,g_n)$
. In particular,
![]() $G^\prime =\operatorname {\mathrm {Gal}}(\mathbb {K}/K(C))$
may be identified as a transitive subgroup of
$G^\prime =\operatorname {\mathrm {Gal}}(\mathbb {K}/K(C))$
may be identified as a transitive subgroup of
![]() $\operatorname {\mathrm {Sym}}(g_1,\dotsc ,g_n) \cong S_n$
.
$\operatorname {\mathrm {Sym}}(g_1,\dotsc ,g_n) \cong S_n$
.
Let
![]() $\theta _1=\theta ,\theta _2,\dotsc ,\theta _n$
be the roots of
$\theta _1=\theta ,\theta _2,\dotsc ,\theta _n$
be the roots of
![]() $F(U,\alpha )=0$
, which are distinct since
$F(U,\alpha )=0$
, which are distinct since
![]() $K(\theta )/K$
has degree n. We see that the affine plane model
$K(\theta )/K$
has degree n. We see that the affine plane model
![]() $F(U,V)=0$
for C has n distinct points
$F(U,V)=0$
for C has n distinct points
![]() $(\theta _1,\alpha ),\dotsc ,(\theta _n,\alpha )$
above
$(\theta _1,\alpha ),\dotsc ,(\theta _n,\alpha )$
above
![]() $\alpha \in \mathbb {P}^1$
. However, the smooth model C has precisely n points
$\alpha \in \mathbb {P}^1$
. However, the smooth model C has precisely n points
![]() $P_1,\dotsc ,P_n$
above
$P_1,\dotsc ,P_n$
above
![]() $\alpha \in \mathbb {P}^1$
. After relabeling, we may identify
$\alpha \in \mathbb {P}^1$
. After relabeling, we may identify
![]() $P_i=(\theta _i,\alpha )$
. Next, we consider the action of
$P_i=(\theta _i,\alpha )$
. Next, we consider the action of
![]() $\operatorname {\mathrm {Gal}}(\overline {K}/L)$
on
$\operatorname {\mathrm {Gal}}(\overline {K}/L)$
on
![]() $P_1,\dotsc ,P_n$
, and recall that
$P_1,\dotsc ,P_n$
, and recall that
![]() $\alpha \in K \subseteq L$
. It follows that J is conjugate to
$\alpha \in K \subseteq L$
. It follows that J is conjugate to
![]() $\operatorname {\mathrm {Gal}}(L(\theta _1,\dotsc ,\theta _n)/L)$
when we consider J as a subgroup of
$\operatorname {\mathrm {Gal}}(L(\theta _1,\dotsc ,\theta _n)/L)$
when we consider J as a subgroup of
![]() $\operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\}) \cong S_n$
and
$\operatorname {\mathrm {Sym}}(\{P_1,\dotsc ,P_n\}) \cong S_n$
and
![]() $\operatorname {\mathrm {Gal}}(L(\theta _1,\dotsc ,\theta _n)/L)$
as a subgroup of
$\operatorname {\mathrm {Gal}}(L(\theta _1,\dotsc ,\theta _n)/L)$
as a subgroup of
![]() $\operatorname {\mathrm {Sym}}(\{\theta _1,\dotsc ,\theta _n\}) \cong S_n$
.
$\operatorname {\mathrm {Sym}}(\{\theta _1,\dotsc ,\theta _n\}) \cong S_n$
.
Let
![]() $\mathcal {P}$
be a point of
$\mathcal {P}$
be a point of
![]() $\tilde {C}$
above P. Thus,
$\tilde {C}$
above P. Thus,
As in the proof of Lemma 6.2, the extension
![]() $L(\mathcal {P})/L$
is Galois. Since
$L(\mathcal {P})/L$
is Galois. Since
![]() $\theta =g_1(\mathcal {P}) \in L(\mathcal {P})$
, we see that
$\theta =g_1(\mathcal {P}) \in L(\mathcal {P})$
, we see that
![]() $\theta _1,\dotsc ,\theta _n \in L(\mathcal {P})$
. In particular, for each i, there is an automorphism
$\theta _1,\dotsc ,\theta _n \in L(\mathcal {P})$
. In particular, for each i, there is an automorphism
![]() $\sigma \in L(\mathcal {P})/L$
such that
$\sigma \in L(\mathcal {P})/L$
such that
![]() $\sigma (\theta )=\theta _i$
. Recalling the natural identification of
$\sigma (\theta )=\theta _i$
. Recalling the natural identification of
![]() $\operatorname {\mathrm {Gal}}(L(\mathcal {P})/L)$
with
$\operatorname {\mathrm {Gal}}(L(\mathcal {P})/L)$
with
![]() $G_{\mathcal {P}}$
, we see that there is an automorphism
$G_{\mathcal {P}}$
, we see that there is an automorphism
![]() $\sigma ^\prime \in G_{\mathcal {P}}$
such that
$\sigma ^\prime \in G_{\mathcal {P}}$
such that
![]() $\sigma ^\prime (g_1)(\mathcal {P})=\sigma (\theta )=\theta _i$
. However,
$\sigma ^\prime (g_1)(\mathcal {P})=\sigma (\theta )=\theta _i$
. However,
![]() $\sigma ^\prime (g_1)$
is a root of
$\sigma ^\prime (g_1)$
is a root of
![]() $F(U,\varphi )$
and is equal to one of the
$F(U,\varphi )$
and is equal to one of the
![]() $g_j$
. Thus,
$g_j$
. Thus,
![]() $g_i(\mathcal {P})=\theta _i$
, after suitably reordering
$g_i(\mathcal {P})=\theta _i$
, after suitably reordering
![]() $g_1,\dotsc ,g_n$
. Since
$g_1,\dotsc ,g_n$
. Since
![]() $g_1,\dotsc ,g_n$
generate
$g_1,\dotsc ,g_n$
generate
![]() $\mathbb {K}$
, we conclude that
$\mathbb {K}$
, we conclude that
![]() $L(\mathcal {P})=L(\theta _1,\dotsc ,\theta _n)$
and that
$L(\mathcal {P})=L(\theta _1,\dotsc ,\theta _n)$
and that
![]() $G_{\mathcal {P}}$
is conjugate to
$G_{\mathcal {P}}$
is conjugate to
![]() $\operatorname {\mathrm {Gal}}(L(\theta _1,\dotsc ,\theta _n)/L)$
, which is in turn conjugate to J. This proves (ii).
$\operatorname {\mathrm {Gal}}(L(\theta _1,\dotsc ,\theta _n)/L)$
, which is in turn conjugate to J. This proves (ii).
Finally, letting
![]() $H=G_{\mathcal {P}}$
, we deduce (iii) from Lemma 6.2.
$H=G_{\mathcal {P}}$
, we deduce (iii) from Lemma 6.2.
Of course, if
![]() $\operatorname {\mathrm {genus}}(D_H) \ge 2$
, then by Faltings’ theorem, there are only finitely many
$\operatorname {\mathrm {genus}}(D_H) \ge 2$
, then by Faltings’ theorem, there are only finitely many
![]() $R \in D_H(L)$
. The monodromy data for the morphism
$R \in D_H(L)$
. The monodromy data for the morphism
![]() $\varphi $
gives lower bounds for the genus of
$\varphi $
gives lower bounds for the genus of
![]() $D_H$
. We shall make use of lower bounds due to Guralnick and Shareshian [Reference Guralnick and Shareshian15]. Fix an embedding
$D_H$
. We shall make use of lower bounds due to Guralnick and Shareshian [Reference Guralnick and Shareshian15]. Fix an embedding
![]() $L \subset \overline {L} \subset \mathbb {C}$
. Then
$L \subset \overline {L} \subset \mathbb {C}$
. Then
![]() $\varphi $
induces an étale covering
$\varphi $
induces an étale covering
![]() $C(\mathbb {C}) - \varphi ^{-1}(\operatorname {\mathrm {BV}}(\varphi )) \rightarrow \mathbb {P}^1(C) - \operatorname {\mathrm {BV}}(\varphi )$
of Riemann surfaces. Since
$C(\mathbb {C}) - \varphi ^{-1}(\operatorname {\mathrm {BV}}(\varphi )) \rightarrow \mathbb {P}^1(C) - \operatorname {\mathrm {BV}}(\varphi )$
of Riemann surfaces. Since
![]() $\mathbb {K}/L(\mathbb {P}^1)$
is regular (i.e.
$\mathbb {K}/L(\mathbb {P}^1)$
is regular (i.e.
![]() $\mathbb {K} \cap \overline {L}=L$
), we can identify
$\mathbb {K} \cap \overline {L}=L$
), we can identify
![]() $G=\operatorname {\mathrm {Gal}}(\mathbb {K}/L(\mathbb {P}^1))$
with the image of the monodromy representation [Reference Miranda25, Chapter 4] of this covering. Moreover, monodromy attaches (e.g., [Reference Miranda25, Corollary 4.10]) elements
$G=\operatorname {\mathrm {Gal}}(\mathbb {K}/L(\mathbb {P}^1))$
with the image of the monodromy representation [Reference Miranda25, Chapter 4] of this covering. Moreover, monodromy attaches (e.g., [Reference Miranda25, Corollary 4.10]) elements
to the branch values
![]() $\operatorname {\mathrm {BV}}(\varphi )=\{\beta _1,\beta _2,\dotsc ,\beta _r\}$
, satisfying
$\operatorname {\mathrm {BV}}(\varphi )=\{\beta _1,\beta _2,\dotsc ,\beta _r\}$
, satisfying
In this context, G is known as the monodromy group.
Theorem 6.4 (Guralnick and Shareshian).
Let
![]() $n \ge 5$
. Let
$n \ge 5$
. Let
![]() $\varphi : C \rightarrow \mathbb {P}^1$
be a morphism with monodromy group
$\varphi : C \rightarrow \mathbb {P}^1$
be a morphism with monodromy group
![]() $G=A_n$
or
$G=A_n$
or
![]() $S_n$
. Suppose,
$S_n$
. Suppose,
![]() $\# \operatorname {\mathrm {BV}}(\varphi ) \ge 5$
. Let
$\# \operatorname {\mathrm {BV}}(\varphi ) \ge 5$
. Let
![]() $H \ne A_n$
be a maximal transitive subgroup of G. Then
$H \ne A_n$
be a maximal transitive subgroup of G. Then
![]() $D_H$
has genus
$D_H$
has genus
![]() $\ge 3$
.
$\ge 3$
.
Proof. For
![]() $n \ge 7$
, this is a special case of Theorem 1.1.2 of [Reference Guralnick and Shareshian15], and for
$n \ge 7$
, this is a special case of Theorem 1.1.2 of [Reference Guralnick and Shareshian15], and for
![]() $n=5$
,
$n=5$
,
![]() $6$
a special case of Corollary A.3.3 of the same paper.
$6$
a special case of Corollary A.3.3 of the same paper.
We note that Monderer and Neftin [Reference Monderer and Neftin26, Theorem 1.2] prove a stronger version of Theorem 6.4 that does not require the assumption of at least
![]() $5$
branch points, but at the expense of assuming that
$5$
branch points, but at the expense of assuming that
![]() $n>3.5\times 10^6$
.
$n>3.5\times 10^6$
.
Remark. In the present context, the Riemann–Hurwitz formula, maybe restated (e.g., [Reference Lombardo, Lorenzo García, Ritzenthaler and Sijsling22, Proposition 4.20]) as
 $$ \begin{align} \operatorname{\mathrm{genus}}(D_H)=1-[G:H]+\frac{1}{2} \sum_{i=1}^r \operatorname{\mathrm{ind}}(\sigma_i,G/H). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{genus}}(D_H)=1-[G:H]+\frac{1}{2} \sum_{i=1}^r \operatorname{\mathrm{ind}}(\sigma_i,G/H). \end{align} $$
We explain the notation. Given a group G acting on a finite set
![]() $\Omega $
, and an element
$\Omega $
, and an element
![]() $g \in G$
, we define the index of g to be
$g \in G$
, we define the index of g to be
![]() $\operatorname {\mathrm {ind}}(g,\Omega ) := \# \Omega \, - \, \# \operatorname {\mathrm {Orb}}(g,\Omega )$
, where
$\operatorname {\mathrm {ind}}(g,\Omega ) := \# \Omega \, - \, \# \operatorname {\mathrm {Orb}}(g,\Omega )$
, where
![]() $\operatorname {\mathrm {Orb}}(g,\Omega )$
is the set of orbits of g acting on
$\operatorname {\mathrm {Orb}}(g,\Omega )$
is the set of orbits of g acting on
![]() $\Omega $
. We define the minimal index of G acting on
$\Omega $
. We define the minimal index of G acting on
![]() $\Omega $
by
$\Omega $
by
Note that a large minimal index for the action of G on the coset space
![]() $G/H$
, together with a sufficiently large number of branch points r, forces the genus of
$G/H$
, together with a sufficiently large number of branch points r, forces the genus of
![]() $D_H$
to be large thanks to (6.7). A recent paper of Burness and Guralnick [Reference Burness and Guralnick6, Theorem 7] gives lower bounds for the minimal index for primitive actions, and in forthcoming work, we will use this to deduce a version of Theorem 6.4 for G other than
$D_H$
to be large thanks to (6.7). A recent paper of Burness and Guralnick [Reference Burness and Guralnick6, Theorem 7] gives lower bounds for the minimal index for primitive actions, and in forthcoming work, we will use this to deduce a version of Theorem 6.4 for G other than
![]() $A_n$
,
$A_n$
,
![]() $S_n$
.
$S_n$
.
7 Proof of Theorem 1.2
In this section, we prove Theorem 1.2, which we now restate in a stronger but more technical form.
Theorem 7.1. Let K be a number field. Let
![]() $C/K$
be a curve of genus g, and write J for the Jacobian of C. Let
$C/K$
be a curve of genus g, and write J for the Jacobian of C. Let
![]() $n \ge 2$
and suppose (1.1) holds. Suppose
$n \ge 2$
and suppose (1.1) holds. Suppose
![]() $W_n(C)$
does not contain the translate of an abelian subvariety
$W_n(C)$
does not contain the translate of an abelian subvariety
![]() $A/K$
of J of positive rank. Suppose C has infinitely many degree n points with Galois group
$A/K$
of J of positive rank. Suppose C has infinitely many degree n points with Galois group
![]() $S_n$
or
$S_n$
or
![]() $A_n$
. Then C has only finitely many degree n points with any primitive Galois group
$A_n$
. Then C has only finitely many degree n points with any primitive Galois group
![]() $\ne A_n$
,
$\ne A_n$
,
![]() $S_n$
.
$S_n$
.
We note that Theorem 1.2 follows from Theorem 7.1 thanks to the theorem of Debarre and Fahlaoui. It therefore remains to prove Theorem 7.1. We note that
![]() $S_n$
has no proper primitive subgroups
$S_n$
has no proper primitive subgroups
![]() $\ne A_n$
for
$\ne A_n$
for
![]() $n \le 4$
. Thus, we may suppose that
$n \le 4$
. Thus, we may suppose that
![]() $n \ge 5$
.
$n \ge 5$
.
Let K be a number field and let
![]() $C/K$
be a curve of genus g. Let
$C/K$
be a curve of genus g. Let
![]() $n \ge 5$
and suppose
$n \ge 5$
and suppose
![]() $g>(n-1)^2$
. Suppose
$g>(n-1)^2$
. Suppose
![]() $A(K)$
is finite for any abelian subvariety
$A(K)$
is finite for any abelian subvariety
![]() $A/K$
of J having a translate contained in
$A/K$
of J having a translate contained in
![]() $W_n(C)$
. Suppose C has infinitely many degree n points with Galois group
$W_n(C)$
. Suppose C has infinitely many degree n points with Galois group
![]() $A_n$
or
$A_n$
or
![]() $S_n$
. By Theorem 5.1, there is a degree n morphism
$S_n$
. By Theorem 5.1, there is a degree n morphism
![]() $\varphi : C \rightarrow \mathbb {P}^1$
such that all but finitely many primitive degree n divisors are fibres
$\varphi : C \rightarrow \mathbb {P}^1$
such that all but finitely many primitive degree n divisors are fibres
![]() $\varphi ^*(\alpha )$
with
$\varphi ^*(\alpha )$
with
![]() $\alpha \in \mathbb {P}^1(K)$
. Thus, to prove Theorem 1.2, we need to show that there are at most finitely many
$\alpha \in \mathbb {P}^1(K)$
. Thus, to prove Theorem 1.2, we need to show that there are at most finitely many
![]() $\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the Galois group of the fibre
$\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the Galois group of the fibre
![]() $\varphi ^*(\alpha )$
is primitive but not
$\varphi ^*(\alpha )$
is primitive but not
![]() $A_n$
,
$A_n$
,
![]() $S_n$
.
$S_n$
.
As in Section 6, we write
![]() $\mathbb {K}$
for the Galois closure of the function field extension
$\mathbb {K}$
for the Galois closure of the function field extension
![]() $K(C)/K(\mathbb {P}^1)$
induced by
$K(C)/K(\mathbb {P}^1)$
induced by
![]() $\varphi $
, and we let
$\varphi $
, and we let
![]() $G^\prime =\operatorname {\mathrm {Gal}}(\mathbb {K}/K(\mathbb {P}^1))$
. As
$G^\prime =\operatorname {\mathrm {Gal}}(\mathbb {K}/K(\mathbb {P}^1))$
. As
![]() $\varphi $
has degree n, we may identify
$\varphi $
has degree n, we may identify
![]() $G^\prime $
as a subgroup of
$G^\prime $
as a subgroup of
![]() $S_n$
.
$S_n$
.
Lemma 7.2.
![]() $G^\prime =A_n$
or
$G^\prime =A_n$
or
![]() $S_n$
.
$S_n$
.
Proof. There infinitely many fibres
![]() $\varphi ^*(\alpha )$
with
$\varphi ^*(\alpha )$
with
![]() $\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
that have Galois group
$\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
that have Galois group
![]() $A_n$
or
$A_n$
or
![]() $S_n$
. Choose such an
$S_n$
. Choose such an
![]() $\alpha $
, let
$\alpha $
, let
![]() $P \in \varphi ^*(\alpha )$
; thus, the Galois group of the Galois closure of the extension
$P \in \varphi ^*(\alpha )$
; thus, the Galois group of the Galois closure of the extension
![]() $K(P)/K$
has Galois group
$K(P)/K$
has Galois group
![]() $S_n$
or
$S_n$
or
![]() $A_n$
. Moreover,
$A_n$
. Moreover,
![]() $P \in C$
is a degree n point, and we regard it as a degree n place of
$P \in C$
is a degree n point, and we regard it as a degree n place of
![]() $K(C)$
. We let
$K(C)$
. We let
![]() $\mathcal {P}$
be a place of
$\mathcal {P}$
be a place of
![]() $\mathbb {K}$
above P. By Lemma 6.1, the extension
$\mathbb {K}$
above P. By Lemma 6.1, the extension
![]() $K(\mathcal {P})/K$
is Galois, and its Galois group is isomorphic to the decomposition group
$K(\mathcal {P})/K$
is Galois, and its Galois group is isomorphic to the decomposition group
![]() $G^\prime _{\mathcal {P}} \subseteq G^\prime $
. However,
$G^\prime _{\mathcal {P}} \subseteq G^\prime $
. However,
![]() $K(P) \subseteq K(\mathcal {P})$
and the Galois group of the Galois closure of
$K(P) \subseteq K(\mathcal {P})$
and the Galois group of the Galois closure of
![]() $K(P)/K$
is either
$K(P)/K$
is either
![]() $A_n$
or
$A_n$
or
![]() $S_n$
. It follows that
$S_n$
. It follows that
![]() $G^\prime =A_n$
or
$G^\prime =A_n$
or
![]() $S_n$
.
$S_n$
.
Lemma 7.3. Let
![]() $r=\# \operatorname {\mathrm {BV}}(\varphi )$
. Then
$r=\# \operatorname {\mathrm {BV}}(\varphi )$
. Then
![]() $r \ge 2n+1$
.
$r \ge 2n+1$
.
Proof. Write
![]() $\operatorname {\mathrm {BV}}(\varphi )=\{\beta _1,\dotsc ,\beta _r\}$
. We make use of the Riemann–Hurwitz formula applied to
$\operatorname {\mathrm {BV}}(\varphi )=\{\beta _1,\dotsc ,\beta _r\}$
. We make use of the Riemann–Hurwitz formula applied to
![]() $\varphi $
. Thus,
$\varphi $
. Thus,
 $$\begin{align*}2g-2 \; = \; -2n + \sum_{i=1}^r \sum_{P \in \varphi^*(\beta_i)} e(P)-1 \; \le \; -2n + r (n-1). \end{align*}$$
$$\begin{align*}2g-2 \; = \; -2n + \sum_{i=1}^r \sum_{P \in \varphi^*(\beta_i)} e(P)-1 \; \le \; -2n + r (n-1). \end{align*}$$
However,
![]() $g \ge (n-1)^2+1$
. Putting these together gives
$g \ge (n-1)^2+1$
. Putting these together gives
As in Section 6, let
![]() $L=\mathbb {K} \cap \overline {K}$
, and recall that
$L=\mathbb {K} \cap \overline {K}$
, and recall that
![]() $L/K$
is a finite Galois extension. Let
$L/K$
is a finite Galois extension. Let
![]() $G=\operatorname {\mathrm {Gal}}(\mathbb {K}/L(\mathbb {P}^1))$
.
$G=\operatorname {\mathrm {Gal}}(\mathbb {K}/L(\mathbb {P}^1))$
.
Lemma 7.4.
-
(a) Suppose
 $G^\prime = A_n$
. Then
$G^\prime = A_n$
. Then
 $L=K$
and
$L=K$
and
 $G=A_n$
.
$G=A_n$
. -
(b) Suppose
 $G^\prime = S_n$
. Then
$G^\prime = S_n$
. Then-
(i) either
 $L=K$
and
$L=K$
and
 $G = S_n$
,
$G = S_n$
, -
(ii) or
 $L/K$
is quadratic and
$L/K$
is quadratic and
 $G=A_n$
.
$G=A_n$
.
-
Proof. As
![]() $\varphi $
is ramified, the extension
$\varphi $
is ramified, the extension
![]() $\mathbb {K}/L(\mathbb {P}^1)$
is non-trivial. Therefore, by the exactness of (6.1), the group G is a nontrivial normal subgroup of
$\mathbb {K}/L(\mathbb {P}^1)$
is non-trivial. Therefore, by the exactness of (6.1), the group G is a nontrivial normal subgroup of
![]() $G^\prime $
. As
$G^\prime $
. As
![]() $n \ge 5$
, the only nontrivial normal subgroup of
$n \ge 5$
, the only nontrivial normal subgroup of
![]() $A_n$
is
$A_n$
is
![]() $A_n$
, and the only nontrivial normal subgroups of
$A_n$
, and the only nontrivial normal subgroups of
![]() $S_n$
are
$S_n$
are
![]() $S_n$
and
$S_n$
and
![]() $A_n$
. The lemma follows.
$A_n$
. The lemma follows.
We now complete the proof of Theorem 7.1. As observed at the beginning of the section, we need to show that there are at most finitely many
![]() $\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the Galois group of the fibre
$\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the Galois group of the fibre
![]() $\varphi ^*(\alpha )$
is primitive but not
$\varphi ^*(\alpha )$
is primitive but not
![]() $A_n$
,
$A_n$
,
![]() $S_n$
. It is therefore enough, for each primitive subgroup
$S_n$
. It is therefore enough, for each primitive subgroup
![]() $I \subset G^\prime $
, with
$I \subset G^\prime $
, with
![]() $I \ne A_n$
,
$I \ne A_n$
,
![]() $S_n$
, to show that there are finitely many
$S_n$
, to show that there are finitely many
![]() $\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the fibre
$\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the fibre
![]() $\varphi ^*(\alpha )$
has Galois group I. Fix a primitive subgroup
$\varphi ^*(\alpha )$
has Galois group I. Fix a primitive subgroup
![]() $I \subset G^\prime $
,
$I \subset G^\prime $
,
![]() $I \ne A_n$
,
$I \ne A_n$
,
![]() $S_n$
, and suppose there are infinitely many
$S_n$
, and suppose there are infinitely many
![]() $\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the fibre
$\alpha \in \mathbb {P}^1(K) - \operatorname {\mathrm {BV}}(\varphi )$
such that the fibre
![]() $\varphi ^*(\alpha )$
has Galois group I. Since
$\varphi ^*(\alpha )$
has Galois group I. Since
![]() $C(L)$
is finite by Faltings’ theorem, only finitely many of these fibres contain a point of
$C(L)$
is finite by Faltings’ theorem, only finitely many of these fibres contain a point of
![]() $C(L)$
. Thus, for infinitely many of the fibres, there is a primitive degree n point
$C(L)$
. Thus, for infinitely many of the fibres, there is a primitive degree n point
![]() $P \in C - C(L)$
whose Galois group is I. There are finitely many possibilities for the groups J, H in Lemma 6.3. As
$P \in C - C(L)$
whose Galois group is I. There are finitely many possibilities for the groups J, H in Lemma 6.3. As
![]() $I \ne A_n$
,
$I \ne A_n$
,
![]() $S_n$
, by the lemma,
$S_n$
, by the lemma,
![]() $H \ne A_n$
,
$H \ne A_n$
,
![]() $S_n$
is a transitive subgroup of G. If
$S_n$
is a transitive subgroup of G. If
![]() $H \subset A_n$
, then let
$H \subset A_n$
, then let
![]() $H^\prime $
be a maximal subgroup of
$H^\prime $
be a maximal subgroup of
![]() $A_n$
containing H. If
$A_n$
containing H. If
![]() $H \not \subset A_n$
, then in this case,
$H \not \subset A_n$
, then in this case,
![]() $G=S_n$
, and we let
$G=S_n$
, and we let
![]() $H^\prime $
be a maximal subgroup of
$H^\prime $
be a maximal subgroup of
![]() $S_n$
containing H, and note that
$S_n$
containing H, and note that
![]() $H^\prime \ne A_n$
. As
$H^\prime \ne A_n$
. As
![]() $H \subseteq H^\prime $
, we have
$H \subseteq H^\prime $
, we have
![]() $\mathbb {K}^{H^\prime } \subseteq \mathbb {K}^H$
, and so the map
$\mathbb {K}^{H^\prime } \subseteq \mathbb {K}^H$
, and so the map
![]() $\pi _H : D_H \rightarrow \mathbb {P}^1$
factors via the map
$\pi _H : D_H \rightarrow \mathbb {P}^1$
factors via the map
![]() $\pi _{H^\prime } : D_H^\prime \rightarrow \mathbb {P}^1$
. In particular, by Theorem 6.4 (applied with
$\pi _{H^\prime } : D_H^\prime \rightarrow \mathbb {P}^1$
. In particular, by Theorem 6.4 (applied with
![]() $H^\prime $
in place of H), the curve
$H^\prime $
in place of H), the curve
![]() $D_{H^\prime }$
has genus
$D_{H^\prime }$
has genus
![]() $\ge 2$
, and therefore, so does the curve
$\ge 2$
, and therefore, so does the curve
![]() $D_H$
. Therefore,
$D_H$
. Therefore,
![]() $D_H(L)$
is finite. This gives a contradiction and completes the proof.
$D_H(L)$
is finite. This gives a contradiction and completes the proof.
Acknowledgements
We are grateful to Gareth Tracey for useful discussions and for drawing our attention to the work of Burness and Guralnick [Reference Burness and Guralnick6] on minimal indices. We thank Martin Derickx for useful remarks on a previous version of this paper. We are indebted to the referees for many pertinent comments, corrections and improvements, which have substantially enhanced the paper, and for drawing our attention to the paper of Guralnick and Shareshian [Reference Guralnick and Shareshian15].
Competing interest
The authors have no competing interest to declare.
Funding statement
Khawaja is supported by an EPSRC studentship from the University of Sheffield (EP/T517835/1). Siksek is supported by the EPSRC grant Moduli of Elliptic Curves and Classical Diophantine Problems (EP/S031537/1).
Data availability statement
There is no data associated to this paper.