For flows in microchannels, a slip on the walls may be efficient in reducing viscous dissipation. A related issue, addressed in this article, is to decrease the effective viscosity of a dilute monodisperse suspension of spheres in Poiseuille flow by using two parallel slip walls. Extending the approach developed for no-slip walls in Feuillebois et al. (J. Fluid Mech., vol. 800, 2016, pp. 111–139), a formal expression is obtained for the suspension intrinsic viscosity 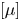 $[\mu ]$ solely in terms of a stresslet component and a quadrupole component exerted on a single freely suspended sphere. In the calculation of
$[\mu ]$ solely in terms of a stresslet component and a quadrupole component exerted on a single freely suspended sphere. In the calculation of 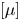 $[\mu ]$, the hydrodynamic interactions between a sphere and the slip walls are approximated using either the nearest wall model or the wall-superposition model. Both the stresslet and quadrupole are derived and accurately calculated using bipolar coordinates. Results are presented for
$[\mu ]$, the hydrodynamic interactions between a sphere and the slip walls are approximated using either the nearest wall model or the wall-superposition model. Both the stresslet and quadrupole are derived and accurately calculated using bipolar coordinates. Results are presented for 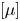 $[\mu ]$ in terms of
$[\mu ]$ in terms of 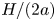 $H/(2a)$ and
$H/(2a)$ and 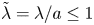 $\tilde{\lambda}=\lambda /a\leq 1$, where
$\tilde{\lambda}=\lambda /a\leq 1$, where 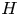 $H$ is the gap between walls,
$H$ is the gap between walls, 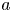 $a$ is the sphere radius and
$a$ is the sphere radius and 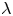 $\lambda$ is the wall slip length using the Navier slip boundary condition. As compared with the no-slip case, the intrinsic viscosity strongly depends on
$\lambda$ is the wall slip length using the Navier slip boundary condition. As compared with the no-slip case, the intrinsic viscosity strongly depends on 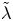 $\tilde{\lambda}$ for given
$\tilde{\lambda}$ for given 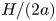 $H/(2a)$, especially for small
$H/(2a)$, especially for small 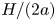 $H/(2a)$. For example, in the very confined case
$H/(2a)$. For example, in the very confined case 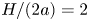 $H/(2a)=2$ (a lower bound found for practical validity of single-wall models) and for
$H/(2a)=2$ (a lower bound found for practical validity of single-wall models) and for 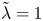 $\tilde{\lambda}=1$, the intrinsic viscosity is three times smaller than for a suspension bounded by no-slip walls and five times smaller than for an unbounded suspension (Einstein, Ann. Phys., vol. 19, 1906, pp. 289–306). We also provide a handy formula fitting our results for
$\tilde{\lambda}=1$, the intrinsic viscosity is three times smaller than for a suspension bounded by no-slip walls and five times smaller than for an unbounded suspension (Einstein, Ann. Phys., vol. 19, 1906, pp. 289–306). We also provide a handy formula fitting our results for 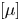 $[\mu ]$ in the entire range
$[\mu ]$ in the entire range 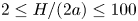 $2\leq H/(2a)\leq 100$ and
$2\leq H/(2a)\leq 100$ and 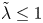 $\tilde{\lambda}\leq 1$.
$\tilde{\lambda}\leq 1$.