Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Parvar, S.
da Silva, C.B.
and
Pinho, F.T.
2020.
Local similarity solution for steady laminar planar jet flow of viscoelastic FENE-P fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 279,
Issue. ,
p.
104265.
Zecchetto, Marco
and
da Silva, Carlos B.
2021.
Universality of small-scale motions within the turbulent/non-turbulent interface layer.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Parvar, S.
da Silva, C. B.
and
Pinho, F. T.
2021.
Large eddy simulations of turbulent planar jets of viscoelastic fluids.
Physics of Fluids,
Vol. 33,
Issue. 4,
Yamani, Sami
Keshavarz, Bavand
Raj, Yashasvi
Zaki, Tamer A.
McKinley, Gareth H.
and
Bischofberger, Irmgard
2021.
Spectral Universality of Elastoinertial Turbulence.
Physical Review Letters,
Vol. 127,
Issue. 7,
Parvar, S.
da Silva, C. B.
and
Pinho, F. T.
2021.
Revisiting the flat plate laminar boundary layer flow of viscoelastic FENE-P fluids.
Physics of Fluids,
Vol. 33,
Issue. 2,
p.
023103.
Bansal, D.
Ghosh, D.
and
Sircar, S.
2021.
Spatiotemporal linear stability of viscoelastic free shear flows: Nonaffine response regime.
Physics of Fluids,
Vol. 33,
Issue. 5,
Guimarães, Mateus C.
Pinho, Fernando T.
and
da Silva, Carlos B.
2022.
Turbulent planar wakes of viscoelastic fluids analysed by direct numerical simulations.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Abreu, Hugo
Pinho, Fernando T.
and
da Silva, Carlos B.
2022.
Turbulent entrainment in viscoelastic fluids.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
Lin, Fenghui
Wan, Zhen-Hua
Zhu, Yabiao
Liu, Nansheng
Lu, Xi-Yun
and
Khomami, Bamin
2022.
High-fidelity robust and efficient finite difference algorithm for simulation of polymer-induced turbulence in cylindrical coordinates.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 307,
Issue. ,
p.
104875.
Parvar, S.
da Silva, C. B.
and
Pinho, F. T.
2022.
The steady laminar planar mixing layer flow of viscoelastic FENE-P fluids.
Journal of Engineering Mathematics,
Vol. 132,
Issue. 1,
Bansal, D.
Chauhan, T.
and
Sircar, S.
2022.
Spatiotemporal linear stability of viscoelastic Saffman–Taylor flows.
Physics of Fluids,
Vol. 34,
Issue. 10,
Soligo, Giovanni
and
Rosti, Marco Edoardo
2023.
Non-Newtonian turbulent jets at low-Reynolds number.
International Journal of Multiphase Flow,
Vol. 167,
Issue. ,
p.
104546.
2023.
Effects of polymer additives on the entrainment of turbulent water jet.
Physics of Fluids,
Vol. 35,
Issue. 4,
Guimarães, Mateus C.
Pinho, Fernando T.
and
da Silva, Carlos B.
2023.
Viscoelastic jet instabilities studied by direct numerical simulations.
Physical Review Fluids,
Vol. 8,
Issue. 10,
McDermott, M.
Riou, T. A. E.
Resende, P. R.
Wilson, M. C. T.
Afonso, A. M.
and
de Boer, G.
2023.
An open-source anisotropic k−ε−v2−f model for turbulent viscoelastic duct flows.
Physics of Fluids,
Vol. 35,
Issue. 9,
Yamani, Sami
Raj, Yashasvi
Zaki, Tamer A.
McKinley, Gareth H.
and
Bischofberger, Irmgard
2023.
Spatiotemporal signatures of elastoinertial turbulence in viscoelastic planar jets.
Physical Review Fluids,
Vol. 8,
Issue. 6,
Yamani, Sami
and
McKinley, Gareth H.
2023.
Master curves for FENE-P fluids in steady shear flow.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 313,
Issue. ,
p.
104944.
Soligo, Giovanni
and
Rosti, Marco Edoardo
2024.
Laminar planar jets of elastoviscoplastic fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 333,
Issue. ,
p.
105322.
Amor, Christian
Corrochano, Adrián
Rota, Giulio Foggi
Rosti, Marco Edoardo
and
Clainche, Soledad Le
2024.
Coherent structures in elastic turbulent planar jets.
Journal of Physics: Conference Series,
Vol. 2753,
Issue. 1,
p.
012020.
Anbarlooei, H.R.
Ramos, F.
Celis, G.E.O.
Mageski, C.
and
Cruz, D.O.A.
2024.
The rheological kolmogorov scales of viscoelastic Oldroyd-B fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 329,
Issue. ,
p.
105257.
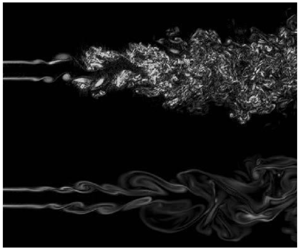
 $\unicode[STIX]{x1D6FF}(x)$, centreline velocity
$\unicode[STIX]{x1D6FF}(x)$, centreline velocity  $U_{c}(x)$ and maximum polymer stresses
$U_{c}(x)$ and maximum polymer stresses  $\unicode[STIX]{x1D70E}_{c}^{[p]}(x)$ are derived and validated by the new DNS data, yielding
$\unicode[STIX]{x1D70E}_{c}^{[p]}(x)$ are derived and validated by the new DNS data, yielding  $\unicode[STIX]{x1D6FF}(x)\sim x$,
$\unicode[STIX]{x1D6FF}(x)\sim x$,  $U_{c}(x)\sim x^{-1/2}$, and
$U_{c}(x)\sim x^{-1/2}$, and  $\unicode[STIX]{x1D70E}_{c}^{[p]}(x)\sim x^{-5/2}$, respectively, where
$\unicode[STIX]{x1D70E}_{c}^{[p]}(x)\sim x^{-5/2}$, respectively, where  $x$ is the coordinate in the streamwise direction. It is shown that, compared with a classical (Newtonian) turbulent jet, the effect of the polymers is to reduce the spreading rate, centreline velocity decay, Reynolds stresses and viscous dissipation rate. The self-preserving character of the flow is analysed and it is shown that profiles of mean velocity, Reynolds stresses and polymer stresses are self-similar provided the proper scales are used in the normalisation of these quantities. A fundamental difference from the Newtonian jet in this regard is the necessity for two, instead of only one, different velocity and length scales to properly characterise the evolution of the turbulent flow. These extra velocity and length scales are directly related to a time scale associated with the characteristic fading memory property of viscoelastic fluids.
$x$ is the coordinate in the streamwise direction. It is shown that, compared with a classical (Newtonian) turbulent jet, the effect of the polymers is to reduce the spreading rate, centreline velocity decay, Reynolds stresses and viscous dissipation rate. The self-preserving character of the flow is analysed and it is shown that profiles of mean velocity, Reynolds stresses and polymer stresses are self-similar provided the proper scales are used in the normalisation of these quantities. A fundamental difference from the Newtonian jet in this regard is the necessity for two, instead of only one, different velocity and length scales to properly characterise the evolution of the turbulent flow. These extra velocity and length scales are directly related to a time scale associated with the characteristic fading memory property of viscoelastic fluids.