Liquid drops deposited on a hot plate can experience a boiling crisis, when the vapour flux is strong enough to ensure the levitation of the drop and the relative insulation of the liquid from the solid. It is often denoted Leidenfrost effect, after the German Johann Gottlob Leidenfrost, who first reported it in 1756. While many studies have encompassed various applied issues associated with this phenomenon, aiming to control and prevent its appearance, Ma & Burton (J. Fluid Mech., vol. 846, 2018, pp. 263–291) focused on the spontaneous appearance of a standing wave at the free surface, together with temporal oscillations, making the drop adopt the shape of a star. Their far-reaching study presents exhaustive results using six different liquids with a range of different volumes and temperatures, in which they systematically extracted the drop dynamics together with the pressure fluctuations in the vapour cushion below.

We propose a dynamical vortex definition (the ‘$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ definition’) for flows dominated by density variation, such as compressible and multi-phase flows. Based on the search of the pressure minimum in a plane, $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ defines a vortex to be a connected region with two negative eigenvalues of the tensor $\unicode[STIX]{x1D64E}^{M}+\unicode[STIX]{x1D64E}^{\unicode[STIX]{x1D717}}$. Here, $\unicode[STIX]{x1D64E}^{M}$ is the symmetric part of the tensor product of the momentum gradient tensor $\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D66A})$ and the velocity gradient tensor $\unicode[STIX]{x1D735}\unicode[STIX]{x1D66A}$, with $\unicode[STIX]{x1D64E}^{\unicode[STIX]{x1D717}}$ denoting the symmetric part of momentum-dilatation gradient tensor $\unicode[STIX]{x1D735}(\unicode[STIX]{x1D717}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D66A})$, and $\unicode[STIX]{x1D717}\equiv \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D66A}$, the dilatation rate scalar. The $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ definition is examined and compared with the $\unicode[STIX]{x1D706}_{2}$ definition using the analytical isentropic Euler vortex and several other flows obtained by direct numerical simulation (DNS) – e.g. liquid jet breakup in a gas, a compressible wake, a compressible turbulent channel and a hypersonic turbulent boundary layer. For low Mach number ($M\lesssim 5$) compressible flows, the $\unicode[STIX]{x1D706}_{2}$ and $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ structures are nearly identical, so that the $\unicode[STIX]{x1D706}_{2}$ method is still valid for low $M$ compressible flows. But, the $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ definition is needed for studying vortex dynamics in highly compressible and strongly varying density flows.

In this paper, we examine triad resonances in a rotating shallow water system when there are two free interfaces. This allows for an examination in a relatively simple model of the interplay between baroclinic and barotropic dynamics in a context where there is also a geostrophic mode. In contrast to the much-studied one-layer rotating shallow water system, we find that as well as the usual slow geostrophic mode, there are now two fast waves, a barotropic mode and a baroclinic mode. This feature permits triad resonances to occur between three fast waves, with a mixture of barotropic and baroclinic modes, an aspect that cannot occur in the one-layer system. There are now also two branches of the slow geostrophic mode, with a repeated branch of the dispersion relation. The consequences are explored in a derivation of the full set of triad interaction equations, using a multiscale asymptotic expansion based on a small-amplitude parameter. The derived nonlinear interaction coefficients are confirmed using energy and enstrophy conservation. These triad interaction equations are explored, with an emphasis on the parameter regime with small Rossby and Froude numbers.

Vortex–wave interaction theory is used to describe new kinds of localised and distributed exact coherent structures. Starting with a localised vortex–wave interaction state driven by a single inviscid wave, regular arrays of interacting vortex–wave states are investigated. In the first instance the arrays described are operational in an infinite uniform shear flow; we refer to them as ‘uniform shear vortex–wave arrays’. The basic form of the interaction remains identical to the canonical one found by Hall & Smith (J. Fluid Mech., vol. 227, 1991, pp. 641–666) and subsequently used to describe exact coherent structures by Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). Thus in each cell of a vortex–wave array a roll stress jump is induced across the critical layer of an inviscid wave riding on the streak part of the flow. The theory is extended to arbitrary shear flows using a nonlinear Wentzel–Kramers–Brillouin–Jeffreys or ray theory approach with the wave–roll–streak field operating on a shorter length scale than the mean flow. The evolution equation governing the slow dynamics of the interaction turns out to be a modified form of the well-known mean equation for a turbulent flow, and its particular form can be interpreted as a ‘closure’ between the small and large scales of the flow. If the array structure is taken to be universal, in the sense that it applies to arbitrary shear flows, then the array takes on a form which supports a logarithmic mean velocity profile trapped between what can be identified with the ‘wake region’ and a ‘buffer layer’ well known in the context of wall-bounded turbulent flows. The many similarities between the distributed structures described and wall-bounded turbulence suggest that vortex–wave arrays might be involved in the self-sustaining process supporting the log layer. The modification of the mean profile within each cell of the array leads to ‘staircase’-like streamwise velocity profiles similar to those observed experimentally in turbulent flows. The wave field supporting the ‘staircase’ is concentrated in critical layers which can be associated with the shear layer structures that have been attributed by experimentalists to be the mechanism supporting the uniform-momentum zones of the staircase.

This paper is concerned with the application of porous treatments as a means of flow and aerodynamic noise reduction. An extensive experimental investigation is undertaken to study the effects of flow interaction with porous media, in particular in the context of the manipulation of flow over blunt trailing edges and attenuation of vortex shedding. Comprehensive boundary layer and wake measurements have been carried out for a long flat plate with solid and porous blunt trailing edges. Unsteady velocity and surface pressure measurements have also been performed to gain an in-depth understanding of the changes to the energy–frequency content and coherence of the boundary layer and wake structures as a result of the flow interaction with a porous treatment. Results have shown that permeable treatments can effectively delay the vortex shedding and stabilize the flow over the blunt edge via mechanisms involving flow penetration into the porous medium and discharge into the near-wake region. It has also been shown that the porous treatment can effectively destroy the spanwise coherence of the boundary layer structures and suppress the velocity and pressure coherence, particularly at the vortex shedding frequency. The flow–porous scrubbing and its effects on the near-wall and large coherent structures have also been studied. The emergence of a quasi-periodic recirculating flow field inside highly permeable surface treatments has also been investigated. Finally, the paper has identified several important mechanisms concerning the application of porous treatments for aerodynamic and aeroacoustic purposes, which can help more effective and tailored designs for specific applications.

We study wind turbulence over breaking waves based on direct numerical simulation (DNS) of two-fluid flows. In the DNS, the air and water are simulated as a coherent system, with the interface captured using the coupled level-set and volume-of-fluid method. Because the wave breaking is an unsteady process, we use ensemble averaging over 100 runs to define turbulence statistics. We focus on analysing the turbulence statistics of the airflow over breaking waves. The effects of wave age and wave steepness are investigated. It is found that before wave breaking, the turbulence statistics are largely influenced by the wave age. The vertical gradient of mean streamwise velocity is positive at small and intermediate wave ages, but it becomes negative near the wave surface at large wave age as the pressure force changes from drag to thrust. Furthermore, wave-coherent motions make increasingly important contributions to the momentum flux and kinetic energy of velocity fluctuations (KE-F) as the wave age increases. During the wave breaking process, spilling breakers do not influence the wind field significantly; in contrast, plunging breakers alter the structures of wind turbulence near the wave surface drastically. It is observed from the DNS results that during wave plunging, a high pressure region occurs ahead of the wave front, which further accelerates the wind in the downstream direction. Meanwhile, a large spanwise vortex is generated, which greatly disturbs the airflow around it, resulting in large magnitudes of Reynolds stress and turbulence kinetic energy (TKE) below the wave crest. Above the crest, the magnitude of KE-F is enhanced during wave plunging at small and large wave ages, but at intermediate wave age, the transient enhancement of KE-F is absent. The effect of wave breaking on the magnitude of KE-F is further investigated through the analysis of the KE-F production. It is discovered that at small wave age, the transient enhancement of KE-F is caused by the appearance of a local maximum in the profile of total momentum flux; but at large wave age, it results from the change in the sign of the KE-F production from negative to positive, due to the sign change in the wave-coherent momentum flux. At intermediate wave age, neither of these two processes is present, and the transient growth of KE-F does not take place.

A large-eddy simulation of laminar transonic buffet on an airfoil at a Mach number $M=0.735$, an angle of attack $\unicode[STIX]{x1D6FC}=4^{\circ }$, a Reynolds number $Re_{c}=3\times 10^{6}$ has been carried out. The boundary layer is laminar up to the shock foot and laminar/turbulent transition occurs in the separation bubble at the shock foot. Contrary to the turbulent case for which wall pressure spectra are characterised by well-marked peaks at low frequencies ($St=f\cdot c/U_{\infty }\simeq 0.06{-}0.07$, where $St$ is the Strouhal number, $f$ the shock oscillation frequency, $c$ the chord length and $U_{\infty }$ the free-stream velocity), in the laminar case, there are also well-marked peaks but at a much higher frequency ($St=1.2$). The shock oscillation amplitude is also lower: 6 % of chord and limited to the shock foot area in the laminar case instead of 20 % with a whole shock oscillation and intermittent boundary layer separation and reattachment in the turbulent case. The analysis of the phase-averaged fields allowed linking of the frequency of the laminar transonic buffet to a separation bubble breathing phenomenon associated with a vortex shedding mechanism. These vortices are convected at $U_{c}/U_{\infty }\simeq 0.4$ (where $U_{c}$ is the convection velocity). The main finding of the present paper is that the higher frequency of the shock oscillation in the laminar regime is due to a different mechanism than in the turbulent one: laminar transonic buffet is due to a separation bubble breathing phenomenon occurring at the shock foot.

Here, we examine the influence of small-scale turbulence on the evolution of fronts in the ocean and atmosphere. Specifically, we consider the evolution of an initially balanced density front subject to an imposed viscosity and diffusivity as a simple analogue for small-scale turbulence. At late times, the dominant balance is found to be the quasisteady turbulent thermal wind balance with time evolution due to an advection–diffusion balance in the buoyancy equation. We use the leading-order balance to determine analytical similarity solutions for the spreading of a front and find that the spreading rate is maximum for an intermediate value of the Ekman number, with the spreading resulting from shear dispersion associated with the cross-front flow and vertical diffusion of density. In response to shear dispersion, the front evolves towards a density profile that is nearly linear in the cross-front coordinate. At the edges of the frontal zone, the density field develops large curvature, and these regions are associated with narrow bands of intense vertical velocity.

Aeroacoustic measurements and analysis have been made for an unshrouded rotor partially immersed in a planar equilibrium turbulent boundary layer at low Mach number. This configuration provides an idealized model of inflow distortion effects seen when a rotor is mounted adjacent to the hull or fuselage of a vehicle. At low and moderate thrust conditions, the rotor produces broadband noise organized into haystacks produced by large eddies of the ingested turbulence being cut multiple times by successive rotor blades. At high thrust, however, the acoustic signature changes and becomes louder and more tonal. This change is accompanied by separation of the boundary layer from the wall in the vicinity of the rotor blade disk. The separation region is highly unsteady and populated by intense vortex structures. Acoustic analysis suggests that blade–vortex interactions with these structures are the source of the additional tonal noise at high thrust.

We report on the modification of drag by neutrally buoyant spherical finite-sized particles in highly turbulent Taylor–Couette (TC) flow. These particles are used to disentangle the effects of size, deformability and volume fraction on the drag, and are contrasted to the drag in bubbly TC flow. From global torque measurements, we find that rigid spheres hardly decrease or increase the torque needed to drive the system. The size of the particles under investigation has a marginal effect on the drag, with smaller diameter particles showing only slightly lower drag. Increase of the particle volume fraction shows a net drag increase. However, this increase is much smaller than can be explained by the increase in apparent viscosity due to the particles. The increase in drag for increasing particle volume fraction is corroborated by performing laser Doppler anemometry, where we find that the turbulent velocity fluctuations also increase with increasing volume fraction. In contrast to rigid spheres, for bubbles, the effective drag reduction also increases with increasing Reynolds number. Bubbles are also much more effective in reducing the overall drag.

The flow development in a groove-modified channel consisting of flat and grooved walls was investigated by direct numerical simulations based on the Navier–Stokes equations at a Reynolds number of $5\times 10^{3}$ based on the full channel height and the bulk velocity. Simulations were performed for highly disturbed initial flow conditions leading to the almost instantaneous appearance of turbulence in channels with flat walls. The surface morphology was designed in the form of profiled grooves aligned with the flow direction and embedded in the wall. Such grooves are presumed to allow development of only the statistically axisymmetric disturbances. In contrast to the rapid production of turbulence along a flat wall, it was found that such development was suppressed over a grooved wall for a remarkably long period of time. Owing to the difference in the flow structure, friction drag over the grooved wall was more than 60 % lower than that over the flat wall. Anisotropy-invariant mapping supports the conclusion, emerging from analytic considerations, that persistence of the laminar regime is due to statistical axisymmetry in the velocity fluctuations. Complementary investigations of turbulent drag reduction in grooved channels demonstrated that promotion of such a state across the entire wetted surface is required to stabilize flow and prevent transition and breakdown to turbulence. To support the results of numerical investigations, measurements in groove-modified channel flow were performed. Comparisons of the pressure differentials measured along flat and groove-modified channels reveal a skin-friction reduction as large as $\text{DR}\approx 50\,\%$ owing to the extended persistence of the laminar flow compared with flow development in a flat channel. These experiments demonstrate that early stabilization of the laminar boundary layer development with a grooved surface promotes drag reduction in a fully turbulent flow with a preserving magnitude as the Reynolds number increases.

We study through numerical simulation the optimal hydrodynamic interactions and basic vorticity control mechanisms for two fish-like bodies swimming in tandem. We show that for a fish swimming in the wake of an upstream fish, using independent pitch control of its caudal fin, in addition to optimized body motion, results in reduction of the energy needed for self-propulsion by more than 50 %, providing a quasi-propulsive efficiency of 90 %, up from 60 % without independent caudal fin control. Such high efficiency is found over a narrow parametric range and is possible only when the caudal fin is allowed to pitch independently from the motion of the main body. We identify the vorticity control mechanisms employed by the body and tail to achieve this remarkable performance through thrust augmentation and destructive interference with the upstream fish-generated vortices. A high sensitivity of the propulsive performance to small variations in caudal fin parameters is found, underlying the importance of accurate flow sensing and feedback control. We further demonstrate that using lateral line-like flow measurements to drive an unscented Kalman filter, the near-field vortices can be localized within 1 % of the body length, and be used with a phase-lock controller to drive the body and tail undulation of a self-propelled fish, moving within the wake of an upstream fish, to stably reach the optimal gait and fully achieve maximum energy extraction.

We use particle-resolved direct numerical simulation (PR-DNS) as a model-free physics-based numerical approach to validate particle acceleration modelling in gas-solid suspensions. To isolate the effect of the particle acceleration model, we focus on point-particle direct numerical simulation (PP-DNS) of a collision-free dilute suspension with solid-phase volume fraction $\unicode[STIX]{x1D719}=0.001$ in a decaying isotropic turbulent particle-laden flow. The particle diameter $d_{p}$ in the suspension is chosen to be the same as the initial Kolmogorov length scale $\unicode[STIX]{x1D702}_{0}$ ($d_{p}/\unicode[STIX]{x1D702}_{0}=1$) in order to overlap with the regime where PP-DNS is valid. We assess the point-particle acceleration model for two different particle Stokes numbers, $St_{\unicode[STIX]{x1D702}}=1$ and 100. For the high Stokes number case, the Stokes drag model for particle acceleration under-predicts the true particle acceleration. In addition, second moment quantities which play key roles in the physical evolution of the gas–solid suspension are not correctly captured. Considering finite Reynolds number corrections to the acceleration model improves the prediction of the particle acceleration probability density function and second moment statistics of the point-particle model compared with the particle-resolved simulation. We also find that accounting for the undisturbed fluid velocity in the acceleration model can be of greater importance than using the most appropriate acceleration model for a given physical problem.

Experiments have been conducted with a low mass-damping circular cylinder, elastically supported in a cross-flow, in the vicinity of a second stationary cylinder. The dynamic response, including amplitudes and frequencies of oscillation, together with the fluid excitation, were measured covering a large parametric space, consisting of variations in the gap distance between the cylinders as well as in the reduced velocity and Reynolds number. The flow dynamics in the near wake was also measured using planar particle image velocimetry. The results show how there is a strong wake interaction between the cylinders that greatly modifies the vortex-induced vibrations (VIV) of the elastically mounted cylinder when the centre-to-centre distance between the models is initially set to values smaller than $3.5D$, where $D$ is the external diameter. The wake interference leads to responding amplitudes that are reduced if compared to those of isolated cylinders undergoing VIV, while responding frequencies are increased. The transverse force coefficients observed in the lock-in region increase and the upper branch shifts to smaller reduced velocities. The phase between motion and excitation is also shifted and values measured in the lower branch of the response tend to be smaller than those typical of isolated cylinders. At the smallest separation distances investigated, the wakes of the cylinders are synchronised in an out-of-phase mode of shedding, characterised by a biased flow towards the oscillating cylinder.

We present new scaling expressions, including high-Reynolds-number ($Re$) predictions, for all Reynolds stress components in the entire flow domain of turbulent channel and pipe flows. In Part 1 (She et al., J. Fluid Mech., vol. 827, 2017, pp. 322–356), based on the dilation symmetry of the mean Navier–Stokes equation a four-layer formula of the Reynolds shear stress length $\ell _{12}$ – and hence also the entire mean velocity profile (MVP) – was obtained. Here, random dilations on the second-order balance equations for all the Reynolds stresses (shear stress $-\overline{u^{\prime }v^{\prime }}$, and normal stresses $\overline{u^{\prime }u^{\prime }}$, $\overline{v^{\prime }v^{\prime }}$, $\overline{w^{\prime }w^{\prime }}$) are analysed layer by layer, and similar four-layer formulae of the corresponding stress length functions $\ell _{11}$, $\ell _{22}$, $\ell _{33}$ (hence the three turbulence intensities) are obtained for turbulent channel and pipe flows. In particular, direct numerical simulation (DNS) data are shown to agree well with the four-layer formulae for $\ell _{12}$ and $\ell _{22}$ – which have the celebrated linear scalings in the logarithmic layer, i.e. $\ell _{12}\approx \unicode[STIX]{x1D705}y$ and $\ell _{22}\approx \unicode[STIX]{x1D705}_{22}y$. However, data show an invariant peak location for $\overline{w^{\prime }w^{\prime }}$, which theoretically leads to an anomalous scaling in $\ell _{33}$ in the log layer only, namely $\ell _{33}\propto y^{1-\unicode[STIX]{x1D6FE}}$ with $\unicode[STIX]{x1D6FE}\approx 0.07$. Furthermore, another mesolayer modification of $\ell _{11}$ yields the experimentally observed location and magnitude of the outer peak of $\overline{u^{\prime }u^{\prime }}$. The resulting $-\overline{u^{\prime }v^{\prime }}$, $\overline{u^{\prime }u^{\prime }}$, $\overline{v^{\prime }v^{\prime }}$ and $\overline{w^{\prime }w^{\prime }}$ are all in good agreement with DNS and experimental data in the entire flow domain. Our additional results include: (1) the maximum turbulent production is located at $y^{+}\approx 12$; (2) the location of peak value $-\overline{u^{\prime }v^{\prime }}_{p}$ has a scaling transition from $5.7Re_{\unicode[STIX]{x1D70F}}^{1/3}$ to $1.5Re_{\unicode[STIX]{x1D70F}}^{1/2}$ at $Re_{\unicode[STIX]{x1D70F}}\approx 3000$, with a $1+\overline{u^{\prime }v^{\prime }}_{p}^{+}$ scaling transition from $8.5Re_{\unicode[STIX]{x1D70F}}^{-2/3}$ to $3.0Re_{\unicode[STIX]{x1D70F}}^{-1/2}$ ($Re_{\unicode[STIX]{x1D70F}}$ the friction Reynolds number); (3) the peak value $\overline{w^{\prime }w^{\prime }}_{p}^{+}\approx 0.84Re_{\unicode[STIX]{x1D70F}}^{0.14}(1-48/Re_{\unicode[STIX]{x1D70F}})$; (4) the outer peak of $\overline{u^{\prime }u^{\prime }}$ emerges above $Re_{\unicode[STIX]{x1D70F}}\approx 10^{4}$ with its location scaling as $1.1Re_{\unicode[STIX]{x1D70F}}^{1/2}$ and its magnitude scaling as $2.8Re_{\unicode[STIX]{x1D70F}}^{0.09}$; (5) an alternative derivation of the log law of Townsend (1976, The Structure of Turbulent Shear Flow, Cambridge University Press), namely, $\overline{u^{\prime }u^{\prime }}^{+}\approx -1.25\ln y+1.63$ and $\overline{w^{\prime }w^{\prime }}^{+}\approx -0.41\ln y+1.00$ in the bulk.

We study the heat or mass transfer from a neutrally buoyant spherical drop embedded in an ambient Newtonian medium, undergoing a general shearing flow, in the strong convection limit. The latter limit corresponds to the drop Péclet number being large ($Pe\gg 1$). We consider two families of ambient linear flows: (i) planar linear flows with open streamlines (parametrized by $\unicode[STIX]{x1D6FC}$ with $0\leqslant \unicode[STIX]{x1D6FC}\leqslant 1$, the extremal members being simple shear flow ($\unicode[STIX]{x1D6FC}=0$) and planar extension ($\unicode[STIX]{x1D6FC}=1$)) and (ii) three-dimensional extensional flows (parameterized by $\unicode[STIX]{x1D716}$, with $0\leqslant \unicode[STIX]{x1D716}\leqslant 1$, the extremal members being planar ($\unicode[STIX]{x1D716}=0$) and axisymmetric extension ($\unicode[STIX]{x1D716}=1$)). For the first family, an analysis of the exterior flow field in the inertialess limit (the drop Reynolds number, $Re$, being vanishingly small) shows that there exist two distinct streamline topologies separated by a critical drop-to-medium viscosity ratio ($\unicode[STIX]{x1D706}$) given by $\unicode[STIX]{x1D706}_{c}=2\unicode[STIX]{x1D6FC}/(1-\unicode[STIX]{x1D6FC})$. For $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{c}$ all streamlines are open, while the near-field streamlines are closed for $\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{c}$. For the second family, the exterior streamlines remain open regardless of $\unicode[STIX]{x1D706}$. The two streamline topologies lead to qualitatively different mechanisms of transport for large $Pe$. The transport in the open streamline regime is enhanced in the usual manner via the formation of a boundary layer. In sharp contrast, the closed-streamline regime displays diffusion-limited transport, so there is only a finite enhancement even as $Pe\rightarrow \infty$. For $Re=0$, the drop surface streamlines in a planar linear flow may be regarded as generalized Jeffery orbits with a flow and viscosity dependent aspect ratio Jeffery orbits denote the aspect-ratio-dependent inertialess trajectories of a rigid axisymmetric particle in a simple shear flow; see Jeffery (Proc. R. Soc. Lond. A, vol. 102 (715), 1922, pp. 161–179). A Jeffery-orbit-based non-orthogonal coordinate system thus serves as a natural candidate to tackle the transport problem from a drop, in a planar linear flow, in the limit $Pe\gg 1$. Use of this system allows one to derive a closed-form expression for the dimensionless rate of transport (the Nusselt number $Nu$) from a drop in the open-streamline regime ($\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{c}$). Symmetry arguments point to a Jeffery-orbit-based coordinate system for any linear flow, and a variant of this coordinate system is therefore used to derive the Nusselt number for the family of three-dimensional extensional flows. For both classes of flows considered, the boundary-layer-enhanced transport implies that the Nusselt number takes the form $Nu={\mathcal{F}}(P,\unicode[STIX]{x1D706})Pe^{1/2}$, with the parameter $P$ being $\unicode[STIX]{x1D6FC}$ or $\unicode[STIX]{x1D716}$, and ${\mathcal{F}}(P,\unicode[STIX]{x1D706})$ given as a one and two-dimensional integral, respectively, which is readily evaluated numerically.

We analyse the singular effects of weak inertia on the heat (or equivalently mass) transport problem from drops in linear shearing flows. For small spherical drops embedded in hyperbolic planar linear flows, which constitute a one-parameter family (the parameter being $\unicode[STIX]{x1D6FC}$ with 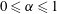$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 1$, and whose extremal members are simple shear (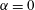$\unicode[STIX]{x1D6FC}=0$) and planar extension (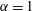$\unicode[STIX]{x1D6FC}=1$)), there are two distinct regimes for scalar (heat or mass) transport at large Péclet numbers (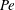$Pe$) depending on the exterior streamline topology (Krishnamurthy & Subramanian, J. Fluid Mech., vol. 850, 2018, pp. 439–483). When the drop-to-medium viscosity ratio (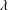$\unicode[STIX]{x1D706}$) is larger than a critical value, 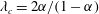$\unicode[STIX]{x1D706}_{c}=2\unicode[STIX]{x1D6FC}/(1-\unicode[STIX]{x1D6FC})$, the drop is surrounded by a region of closed streamlines in the inertialess limit (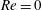$Re=0$, 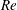$Re$ being the drop Reynolds number). Convection is incapable of transporting heat away on account of the near-field closed streamline topology, and the transport remains diffusion limited even for 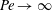$Pe\rightarrow \infty$. However, weak inertia breaks open the closed streamline region, giving way to finite-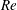$Re$ spiralling streamlines and convectively enhanced transport. For 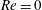$Re=0$ the closed streamlines on the drop surface, for 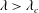$\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{c}$, are Jeffery orbits, a terminology originally used to describe the trajectories of an axisymmetric rigid particle in a simple shear flow. Based on this identification, a novel boundary layer analysis that employs a surface-flow-aligned non-orthogonal coordinate system, is used to solve the transport problem in the dual asymptotic limit 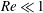$Re\ll 1$, 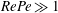$RePe\gg 1$, corresponding to the regime where inertial convection balances diffusion in an 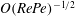$O(RePe)^{-1/2}$ boundary layer. Further, the separation of time scales in the aforementioned limit, between rapid convection due to the Stokesian velocity field and the slower convection by the 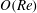$O(Re)$ inertial velocity field, allows one to average the convection–diffusion equation over the phase of the Stokesian surface streamlines (Jeffery orbits), allowing a simplification of the original three-dimensional non-axisymmetric transport problem to a form resembling a much simpler axisymmetric one. A self-similar ansatz then leads to the boundary layer temperature field, and the resulting Nusselt number is given by 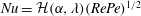$Nu={\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})(RePe)^{1/2}$ with 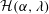${\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})$ given in terms of a one-dimensional integral; the prefactor 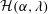${\mathcal{H}}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706})$ diverges for 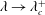$\unicode[STIX]{x1D706}\rightarrow \unicode[STIX]{x1D706}_{c}^{+}$ due to assumptions underlying the Jeffery-orbit-averaged analysis breaking down. Although the separation of time scales necessary for the validity of the analysis no longer exists in the transition regime (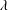$\unicode[STIX]{x1D706}$ in the neighbourhood of 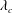$\unicode[STIX]{x1D706}_{c}$), scaling arguments nevertheless highlight the manner in which the Nusselt number function connects smoothly across the open and closed streamline regimes for any finite 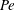$Pe$.

Buoyancy-driven exchange flows are common to a variety of natural and engineering systems, ranging from persistently active volcanoes to counterflows in oceanic straits. Laboratory experiments of exchange flows have been used as surrogates to elucidate the basic features of such flows. The resulting data have been analysed and interpreted mostly through core–annular flow solutions, the most common flow configuration at finite viscosity contrasts. These models have been successful in fitting experimental data, but less effective at explaining the variability observed in natural systems. In this paper, we demonstrate that some of the variability observed in laboratory experiments and natural systems is a consequence of the inherent bistability of core–annular flow. Using a core–annular solution to the classical problem of buoyancy-driven exchange flows in vertical tubes, we identify two mathematically valid solutions at steady state: a solution with fast flow in a thin core and a solution with relatively slow flow in a thick core. The theoretical existence of two solutions, however, does not necessarily imply that the system is bistable in the sense that flow switching may occur. Through direct numerical simulations, we confirm the hypothesis that core–annular flow in vertical tubes is inherently bistable. Our simulations suggest that the bistability of core–annular flow is linked to the boundary conditions of the domain, which implies that is not possible to predict the realized flow field from the material parameters of the fluids and the tube geometry alone. Our finding that buoyancy-driven exchange flows are inherently bistable systems is consistent with previous experimental data, but is in contrast to the underlying hypothesis of previous analytical models that the solution is unique and can be identified by maximizing the flux or extremizing the dissipation in the system. Our results have important implications for data interpretation by analytical models and may also have interesting ramifications for understanding volcanic degassing.

Direct numerical simulations were conducted to uncover physical aspects of a transverse sonic jet injected into a supersonic cross-flow at a Mach number of 2.7. Simulations were carried out for two different jet-to-cross-flow momentum flux ratios ($J$) of 2.3 and 5.5. It is identified that collision shock waves behind the jet induce a herringbone separation bubble in the near-wall jet wake and a reattachment valley is formed and embayed by the herringbone recirculation zone. The recirculating flow in the jet leeward separation bubble forms a primary trailing counter-rotating vortex pair (TCVP) close to the wall surface. Analysis on streamlines passing the separation region shows that the wing of the herringbone separation bubble serves as a micro-ramp vortex generator and streamlines acquire angular momentum downstream to form a secondary surface TCVP in the reattachment valley. Herringbone separation wings disappear in the far field due to the cross-interaction of lateral supersonic flow and the expansion flow in the reattachment valley, which also leads to the vanishing of the secondary TCVP. A three-dimensional schematic of surface trailing wakes is presented and explains the formation mechanisms of the surface TCVPs.

High-Reynolds-number experiments are conducted in the roughness sublayer of a turbulent boundary layer developing over a cubical canopy. Stereoscopic particle image velocimetry is performed in a wall-parallel plane to evidence a high degree of spatial modulation of the small-scale turbulence around the footprint of large-scale motions, despite the suppression of the inner layer by the high roughness elements. Both Fourier and wavelets analyses show that the near-wall cycle observed in smooth-wall-bounded flows is severely disrupted by the canopy, whose wake in the roughness sublayer generates a new range of scales, closer to that of the outer-layer large-scale motions. This restricts significantly scale separation, hence a diagnostic method is developed to divide carefully and rationally the fluctuating velocity fields into large- and small-scale components. Our analysis across all turbulent kinetic energy terms sheds light on the spatial imprint of the modulation mechanism, revealing a very different signature on each velocity component. The roughness sublayer shows a preferential arrangement of the modulated scales similar to what is observed in the outer layer of smooth-wall-bounded flows – small-scale turbulence is enhanced near the front of high momentum regions and damped at the front of low momentum regions. More importantly, accessing spanwise correlations reveals that modulation intensifies the most along the flanks of the large-scale motions.