Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T18:09:19.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Toward vortex identification based on local pressure-minimum criterion in compressible and variable density flows

Published online by Cambridge University Press:  02 July 2018

Jie Yao Open the ORCID record for Jie Yao [Opens in a new window]  and
Fazle Hussain Open the ORCID record for Fazle Hussain [Opens in a new window]
Jie Yao
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
Fazle Hussain*
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a dynamical vortex definition (the ‘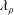$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ definition’) for flows dominated by density variation, such as compressible and multi-phase flows. Based on the search of the pressure minimum in a plane, 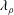$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ defines a vortex to be a connected region with two negative eigenvalues of the tensor 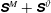$\unicode[STIX]{x1D64E}^{M}+\unicode[STIX]{x1D64E}^{\unicode[STIX]{x1D717}}$. Here, $\unicode[STIX]{x1D64E}^{M}$ is the symmetric part of the tensor product of the momentum gradient tensor 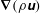$\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D66A})$ and the velocity gradient tensor 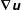$\unicode[STIX]{x1D735}\unicode[STIX]{x1D66A}$, with $\unicode[STIX]{x1D64E}^{\unicode[STIX]{x1D717}}$ denoting the symmetric part of momentum-dilatation gradient tensor 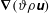$\unicode[STIX]{x1D735}(\unicode[STIX]{x1D717}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D66A})$, and 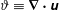$\unicode[STIX]{x1D717}\equiv \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D66A}$, the dilatation rate scalar. The 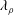$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ definition is examined and compared with the 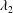$\unicode[STIX]{x1D706}_{2}$ definition using the analytical isentropic Euler vortex and several other flows obtained by direct numerical simulation (DNS) – e.g. liquid jet breakup in a gas, a compressible wake, a compressible turbulent channel and a hypersonic turbulent boundary layer. For low Mach number (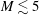$M\lesssim 5$) compressible flows, the 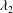$\unicode[STIX]{x1D706}_{2}$ and 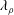$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ structures are nearly identical, so that the 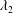$\unicode[STIX]{x1D706}_{2}$ method is still valid for low $M$ compressible flows. But, the 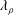$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$ definition is needed for studying vortex dynamics in highly compressible and strongly varying density flows.

JFM classification

Compressible Flows: Compressible Flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 5 - 17
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Chakraborty, N., Wang, L., Konstantinou, I. & Klein, M. 2017 Vorticity statistics based on velocity and density-weighted velocity in premixed reactive turbulence. J. Turbul. 18 (9), 1–29.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.Google Scholar
Cucitore, R., Quadrio, M. & Baron, A. 1999 On the effectiveness and limitations of local criteria for the identification of a vortex. Eur. J. Mech. (B/Fluids) 18 (2), 261–282.Google Scholar
Duan, L., Choudhari, M. M. & Zhang, C. 2016 Pressure fluctuations induced by a hypersonic turbulent boundary layer. J. Fluid Mech. 804, 578–607.Google Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 1 (1), 011.Google Scholar
Günther, T. & Theisel, H. 2017 The state of the art in vortex extraction. In Computer Graphics Forum. Wiley Online Library.Google Scholar
Haller, G. 2005 An objective definition of a vortex. J. Fluid Mech. 525, 1–26.Google Scholar
Hickey, J.-P., Hussain, F. & Wu, X. 2016 Compressibility effects on the structural evolution of transitional high-speed planar wakes. J. Fluid Mech. 796, 5–39.Google Scholar
Hunt, J. C., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Research Report CTR-S88 193.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Kim, K., Hickey, J.-P. & Scalo, C.2017 Pseudophase-change effects in turbulent channel flow under transcritical temperature conditions. arXiv:1712.05777.Google Scholar
Kolář, V. 2009 Compressibility effect in vortex identification. AIAA J. 47 (2), 473–475.Google Scholar
Kolář, V. & Šístek, J. 2015 Corotational and compressibility aspects leading to a modification of the vortex-identification q-criterion. AIAA J. 53 (8), 2406–2410.Google Scholar
Pierce, B., Moin, P. & Sayadi, T. 2013 Application of vortex identification schemes to direct numerical simulation data of a transitional boundary layer. Phys. Fluids 25 (1), 015102.Google Scholar
Pirozzoli, S., Bernardini, M. & Grasso, F. 2008 Characterization of coherent vortical structures in a supersonic turbulent boundary layer. J. Fluid Mech. 613, 205–231.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Shadloo, M. S., Hadjadj, A. & Hussain, F. 2015 Statistical behavior of supersonic turbulent boundary layers with heat transfer at m = 2. Intl J. Heat Fluid Flow 53, 113–134.Google Scholar
Shang, J. S., Surzhikov, S. T., Kimmel, R., Gaitonde, D., Menart, J. & Hayes, J. 2005 Mechanisms of plasma actuators for hypersonic flow control. Prog. Aerosp. Sci. 41 (8), 642–668.Google Scholar
Shu, C.-W. 1998 Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations, pp. 325–432. Springer.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2007 Vorticity and Vortex Dynamics. Springer Science & Business Media.Google Scholar
Zandian, A., Sirignano, W. A. & Hussain, F. 2018 Understanding liquid-jet atomization cascades via vortex dynamics. J. Fluid Mech. 843, 293–354.Google Scholar
Zhang, C., Duan, L. & Choudhari, M.2016 Acoustic radiation from a mach 14 turbulent boundary layer. In 54th AIAA Aerospace Sciences Meeting, pp. 2016–0048. AIAA.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar