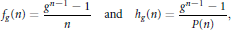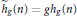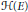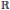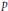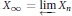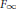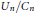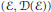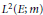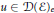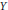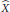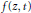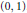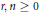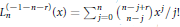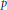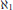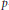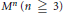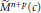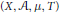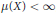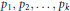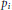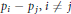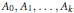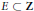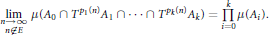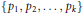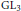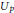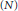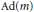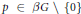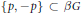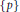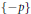Research Article
Uniform Distribution of Fractional Parts Related to Pseudoprimes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-502
-
- Article
-
- You have access
- Export citation
Subspaces of de Branges Spaces Generated by Majorants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-517
-
- Article
-
- You have access
- Export citation
Global Units Modulo Circular Units: Descent Without Iwasawa’s Main Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 518-533
-
- Article
-
- You have access
- Export citation
Girsanov Transformations for Non-Symmetric Diffusions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 534-547
-
- Article
-
- You have access
- Export citation
Fundamental Tone, Concentration of Density, and Conformal Degeneration on Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 548-565
-
- Article
-
- You have access
- Export citation
Convex Subordination Chains in Several Complex Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 566-582
-
- Article
-
- You have access
- Export citation
Algebraic Properties of a Family of Generalized Laguerre Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 583-603
-
- Article
-
- You have access
- Export citation
First Countable Continua and Proper Forcing
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 604-616
-
- Article
-
- You have access
- Export citation
Square Integrable Representations and the Standard Module Conjecture for General Spin Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 617-640
-
- Article
-
- You have access
- Export citation
Characterization of Parallel Isometric Immersions of Space Forms into Space Forms in the Class of Isotropic Immersions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 641-655
-
- Article
-
- You have access
- Export citation
Generalized Polynomials and Mild Mixing
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 656-673
-
- Article
-
- You have access
- Export citation
A Construction of Rigid Analytic Cohomology Classes for Congruence Subgroups of SL3(ℤ)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 674-690
-
- Article
-
- You have access
- Export citation
Prehomogeneity on Quasi-Split Classical Groups and Poles of Intertwining Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 691-707
-
- Article
-
- You have access
- Export citation
Regular Homeomorphisms of Finite Order on Countable Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 708-720
-
- Article
-
- You have access
- Export citation