Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T09:45:30.641Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE CROSSING NUMBER OF THE JOIN OF THE WHEEL ON FIVE VERTICES WITH THE DISCRETE GRAPH

Part of: Graph theory

Published online by Cambridge University Press:  21 November 2019

MICHAL STAŠ Open the ORCID record for MICHAL STAŠ [Opens in a new window]
MICHAL STAŠ*
Affiliation:
Department of Mathematics and Theoretical Informatics, Faculty of Electrical Engineering and Informatics, Technical University of Košice, Letná 9, 042 00 Košice, Slovak Republic email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give the crossing number of the join product 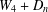$W_{4}+D_{n}$, where 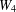$W_{4}$ is the wheel on five vertices and 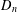$D_{n}$ consists of $n$ isolated vertices. The proof is based on calculating the minimum number of crossings between two different subgraphs from the set of subgraphs which do not cross the edges of the graph 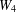$W_{4}$ and from the set of subgraphs which cross the edges of 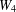$W_{4}$ exactly once.

Keywords

graphdrawingcrossing numberjoin productrotation

MSC classification

Primary: 05C10: Planar graphs; geometric and topological aspects of graph theory
Secondary: 05C38: Paths and cycles
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 353 - 361
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research was supported by the internal faculty research project no. FEI-2017-39.

References

Berežný, Š., Buša, J. Jr. and Staš, M., ‘Software solution of the algorithm of the cyclic-order graph’, Acta Electrotechnica Inform. 18(1) (2018), 3–10.Google Scholar
Berežný, Š. and Staš, M., ‘On the crossing number of the join of five vertex graph G with the discrete graph D n’, Acta Electrotechnica Inform. 17(3) (2017), 27–32.Google Scholar
Berežný, Š. and Staš, M., ‘Cyclic permutations and crossing numbers of join products of symmetric graph of order six’, Carpathian J. Math. 34(2) (2018), 1–14.Google Scholar
Chimani, M. and Wiedera, T., ‘An ILP-based proof system for the crossing number problem’, in: 24th European Symposium of Algorithms (ESA) 2016, Aarhus, Denmark, Leibniz International Proceedings in Informatics (Dagstuhl Publishing, Saarbrücken, 2019), Article ID 29, 29 pages.Google Scholar
Clancy, K., Haythorpe, M. and Newcombe, A., ‘A survey of graphs with known or bounded crossing numbers’, arXiv:1901.05155 (2019), Section 3.8.3.Google Scholar
Draženská, E., ‘On the crossing number of join of graph of order six with path’, in: Proceedings of the 22nd Czech–Japan Seminar on Data Analysis and Decision Making (Matfyz Press, Prague, 2019), 41–48.Google Scholar
He, P. and Huang, Y., ‘The crossing number of W 4 × S n’, J. Zhengzhou Univ. Nat. Sci. Ed. 39(4) (2007), 14–18.Google Scholar
Hernández-Vélez, C., Medina, C. and Salazar, G., ‘The optimal drawing of K 5, n’, Electron. J. Combin. 21(4) (2014), #P4.1, 29 pages.Google Scholar
Kleitman, D. J., ‘The crossing number of K 5, n’, J. Combin. Theory 9 (1970), 315–323.Google Scholar
Klešč, M., ‘The join of graphs and crossing numbers’, Electron. Notes Discrete Math. 28 (2007), 349–355.10.1016/j.endm.2007.01.049Google Scholar
Klešč, M., ‘The crossing number of join of the special graph on six vertices with path and cycle’, Discrete Math. 310 (2010), 1475–1481.Google Scholar
Klešč, M., Kravecová, D. and Petrillová, J., ‘The crossing numbers of join of special graphs’, in: Electrical Engineering and Informatics, 2 (Proceedings of the Faculty of Electrical Engineering and Informatics of the Technical University of Košice, Košice, 2011), 522–527.Google Scholar
Klešč, M., Petrillová, J. and Valo, M., ‘On the crossing numbers of Cartesian products of wheels and trees’, Discuss. Math. Graph Theory 71 (2017), 339–413.Google Scholar
Klešč, M. and Schrötter, Š., ‘The crossing numbers of join products of paths with graphs of order four’, Discuss. Math. Graph Theory 31 (2011), 312–331.10.7151/dmgt.1548Google Scholar
Klešč, M. and Schrötter, Š., ‘The crossing numbers of join of paths and cycles with two graphs of order five’, in: Mathematical Modeling and Computational Science, Lecture Notes in Computer Science, 7125 (Springer, Cham, 2012), 160–167.Google Scholar
Klešč, M. and Valo, M., ‘Minimum crossings in join of graphs with paths and cycles’, Acta Electrotechnica Inform. 12(3) (2012), 32–37.10.2478/v10198-012-0028-0Google Scholar
Staš, M., ‘On the crossing number of the join of the discrete graph with one graph of order five’, Math. Model. Geom. 5(2) (2017), 12–19.10.26456/mmg/2017-522Google Scholar
Staš, M., ‘Cyclic permutations: crossing numbers of the join products of graphs’, in: 17th Conference on Applied Mathematics, Aplimat 2018 (Slovak University of Technology, Bratislava, 2018), 979–987.Google Scholar
Staš, M., ‘Determining crossing numbers of graphs of order six using cyclic permutations’, Bull. Aust. Math. Soc. 98(3) (2018), 353–362.10.1017/S000497271800059XGoogle Scholar
Staš, M., ‘Determining crossing number of join of the discrete graph with two symmetric graphs of order five’, Symmetry 11(2) (2019), 1–9.10.3390/sym11020123Google Scholar
Staš, M., ‘Determining crossing number of one graph of order five using cyclic permutations’, in: 18th Conference on Applied Mathematics, Aplimat 2019 (Slovak University of Technology, Bratislava, 2019), 1126–1134.Google Scholar
Staš, M. and Petrillová, J., ‘On the join products of two special graphs on five vertices with the path and the cycle’, J. Math. Model. Geom. 6(2) (2018), 1–11.Google Scholar
Woodall, D. R., ‘Cyclic-order graphs and Zarankiewicz’s crossing number conjecture’, J. Graph Theory 17 (1993), 657–671.10.1002/jgt.3190170602Google Scholar