No CrossRef data available.
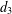 $d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
$d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS IIPublished online by Cambridge University Press: 26 September 2019
Let 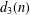 $d_{3}(n)$ be the divisor function of order three. Let
$d_{3}(n)$ be the divisor function of order three. Let 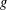 $g$ be a Hecke–Maass form for
$g$ be a Hecke–Maass form for  $\unicode[STIX]{x1D6E4}$ with
$\unicode[STIX]{x1D6E4}$ with 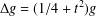 $\unicode[STIX]{x1D6E5}g=(1/4+t^{2})g$. Suppose that
$\unicode[STIX]{x1D6E5}g=(1/4+t^{2})g$. Suppose that 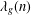 $\unicode[STIX]{x1D706}_{g}(n)$ is the
$\unicode[STIX]{x1D706}_{g}(n)$ is the  $n$th Hecke eigenvalue of
$n$th Hecke eigenvalue of 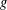 $g$. Using the Voronoi summation formula for
$g$. Using the Voronoi summation formula for 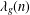 $\unicode[STIX]{x1D706}_{g}(n)$ and the Kuznetsov trace formula, we estimate a shifted convolution sum of
$\unicode[STIX]{x1D706}_{g}(n)$ and the Kuznetsov trace formula, we estimate a shifted convolution sum of 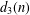 $d_{3}(n)$ and
$d_{3}(n)$ and 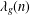 $\unicode[STIX]{x1D706}_{g}(n)$ and show that
$\unicode[STIX]{x1D706}_{g}(n)$ and show that 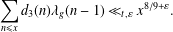 $$\begin{eqnarray}\mathop{\sum }_{n\leq x}d_{3}(n)\unicode[STIX]{x1D706}_{g}(n-1)\ll _{t,\unicode[STIX]{x1D700}}x^{8/9+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n\leq x}d_{3}(n)\unicode[STIX]{x1D706}_{g}(n-1)\ll _{t,\unicode[STIX]{x1D700}}x^{8/9+\unicode[STIX]{x1D700}}.\end{eqnarray}$$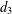 $d_{3}$ and the Fourier coefficients of Hecke–Maass forms’, Bull. Aust. Math. Soc.92 (2015), 195–204].
$d_{3}$ and the Fourier coefficients of Hecke–Maass forms’, Bull. Aust. Math. Soc.92 (2015), 195–204].
This project is supported by the National Natural Science Foundation of China (No. 11871193) and the Foundation of Henan University (No. CX3071A0780001).