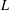Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T14:59:27.664Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FIRST COHOMOLOGY GROUP OF BANACH INVERSE SEMIGROUP ALGEBRAS WITH COEFFICIENTS IN $L$-EMBEDDED BANACH BIMODULES

Part of: Special classes of linear operators Abstract harmonic analysis

Published online by Cambridge University Press:  16 September 2019

HOGER GHAHRAMANI Open the ORCID record for HOGER GHAHRAMANI [Opens in a new window]
HOGER GHAHRAMANI*
Affiliation:
Department of Mathematics, University of Kurdistan, P. O. Box 416, Sanandaj, Iran email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 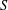$S$ be a discrete inverse semigroup, 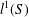$l^{1}(S)$ the Banach semigroup algebra on 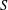$S$ and 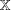$\mathbb{X}$ a Banach 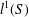$l^{1}(S)$-bimodule which is an 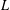$L$-embedded Banach space. We show that under some mild conditions 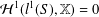${\mathcal{H}}^{1}(l^{1}(S),\mathbb{X})=0$. We also provide an application of the main result.

Keywords

Banach inverse semigroup algebrafirst cohomology groupderivation

MSC classification

Primary: 43A20: $L^1$-algebras on groups, semigroups, etc.
Secondary: 47B47: Commutators, derivations, elementary operators, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 488 - 495
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bader, U., Gelander, T. and Monod, N., ‘A fixed point theorem for L 1 spaces’, Invent. Math. 189 (2012), 143–148.Google Scholar
Blackmore, T. D., ‘Weak amenability of discrete semigroup algebras’, Semigroup Forum 55 (1997), 169–205.Google Scholar
Bowling, S. and Duncan, J., ‘First order cohomology of Banach semigroup algebras’, Semigroup Forum 56 (1998), 130–145.Google Scholar
Christensen, E., ‘Derivations of nest algebras’, Math. Ann. 229 (1977), 155–161.Google Scholar
Dales, H. G., Banach Algebras and Automatic Continuity, London Mathematical Society Monographs Series, 24 (Oxford University Press, Oxford, 2000).Google Scholar
Dales, H. G., Lau, A. T.-M. and Strauss, D., Banach Algebras on Semigroups and on Their Compactifications, Memoirs of the American Mathematical Society, 205 (American Mathematical Society, Providence, RI, 2010).Google Scholar
Donsig, A., Forrest, B. and Marcoux, M., ‘On derivations of seminest algebras’, Houston J. Math. 22 (1996), 375–398.Google Scholar
Duncan, J. and Namioka, I., ‘Amenability of inverse semigroups and their semigroup algebras’, Proc. Roy. Soc. Edinburgh Sect. A 80 (1978), 309–321.10.1017/S0308210500010313Google Scholar
Forrest, B. E. and Marcoux, L. W., ‘Derivations of triangular Bnach algebras’, Indiana Univ. Math. J. 45 (1996), 441–462.Google Scholar
Gilfeather, F. and Smith, R. R., ‘Cohomology for operator algebras: cones and suspensions’, Proc. Lond. Math. Soc. (3) 65 (1992), 175–198.10.1112/plms/s3-65.1.175Google Scholar
Gilfeather, F. and Smith, R. R., ‘Cohomology for operator algebras: joins’, Amer. J. Math. 116 (1994), 541–561.Google Scholar
Howie, J. M., An Introduction to Semigroup Theory (Academic Press, London, 1976).Google Scholar
Johnson, B. E., Cohomology in Banach Algebras, Memoirs of the American Mathematical Society, 127 (American Mathematical Society, Providence, RI, 1972).Google Scholar
Johnson, B. E., ‘The derivation problem for group algebras of connected locally compact groups’, J. Lond. Math. Soc. (2) 63 (2001), 441–452.Google Scholar
Kadison, R. V., ‘Derivations of operator algebras’, Ann. of Math. (2) 83 (1966), 280–293.Google Scholar
Li, P. T., Han, D. G. and Tang, W. S., ‘Derivations on the algebra of operators in Hilbert C ∗ -modules’, Acta Math. Sin. (Engl. Ser.) 28 (2012), 1615–1622.Google Scholar
Mewomo, O. T., ‘Notions of amenability on semigroup algebras’, J. Semigroup Theory Appl. 8 (2013), 1–18.Google Scholar
Munn, W. D., ‘A class of irreducible matrix representations of an arbitrary inverse semigroup’, Proc. Glasgow Math. Assoc. 5 (1961), 41–48.Google Scholar
Sakai, S., ‘Derivations of W ∗ -algebras’, Ann. of Math. (2) 83 (1966), 273–279.Google Scholar
Zhang, Y., ‘2m-weak amenability of group algebras’, J. Math. Anal. Appl. 396 (2012), 412–416.10.1016/j.jmaa.2012.06.037Google Scholar