§5. Some C(K) spaces that are not σ-fragmented. In [16] we remarked that the space (l∞, weak) is not σ-fragmented. Rosenthal [19] gives a number of conditions that ensure that a C(K) space contains an isomorphic copy of l∞. A Banach space is said to be injective if it is complemented in every Banach space containing it isomorphically. Rosenthal proves that every infinite dimensional injective Banach space contains a subspace isomorphic to l∞. It is known (see, for example, Day [2]) that C(K) is injective if K is extremally disconnected. Thus C(K) is not σ-fragmented when K is an infinite compact Hausdorff space that is extremally disconnected.

§1. Introduction and main results. A map f: A → R (A ⊂ R) is called piecewise contractive if there is a finite partition A = A1∪ … ∪ An such that the restriction f| Ai is a contraction for every i = 1, …, n. According to a theorem proved by von Neumann in [3], every interval can be mapped, using a piecewise contractive map, onto a longer interval. This easily implies that whenever A, B are bounded subsets of R with nonempty interior, then A can be mapped, using a piecewise contractive map, onto B (see [6], Theorem 7.12, p. 105). Our aim is to determine the range of the Lebesgue measure of B, supposing that the number of pieces in the partition of A is given. The Lebesgue outer measure will be denoted by λ. If I is an interval then we write |I| = λ(I).

We show that under certain circumstances quasi self-similar fractals of equal Hausdorff dimensions that are homeomorphic to Cantor sets are equivalent under Hölder bijections of exponents arbitrarily close to 1. By setting up algebraic invariants for strictly self-similar sets, we show that such sets are not, in general, equivalent under Lipschitz bijections.

“Regular systems” of numbers in ℝ and “ubiquitous systems” in ℝk, k ≥ 1, have been used previously to obtain lower bounds for the Hausdorff dimension of various sets in ℝ and ℝk respectively. Both these concepts make sense for systems of numbers in ℝ, but the definitions of the two types of object are rather different. In this paper it will be shown that, after certain modifications to the definitions, the two concepts are essentially equivalent.

We also consider the concept of a ℳs∞-dense sequence in ℝk, which was introduced by Falconer to construct classes of sets having “large intersection”. We will show that ubiquitous systems can be used to construct examples of ℳs∞-dense sequences. This provides a relatively easy means of constructing ℳs∞-dense sequences; a direct construction and proof that a sequence is ℳs∞-dense is usually rather difficult.

Given ξ in [0, 1] let ξ = [0, a1, a2…] denote a simple continued fraction expansion of ξ Given the expansion ξ = [0, a1, a2, …] let

Thus with the conventions p1 = q0 = 1 and q−1 = p0 = 0 we have

The second theorem of Minkowski establishes a relation between the successive minima and the volume of a 0-symmetric convex body. Here we show corresponding inequalities for arbitrary convex bodies, where the successive minima are replaced by certain successive diameters and successive widths.

We further give some applications of these results to successive radii, intrinsic volumes and the lattice point enumerator of a convex body.

Let A and B be two compact, convex sets in ℝn, each symmetric with respect to the origin 0. L is any (n - l)-dimensional subspace. In 1956 H. Busemann and C. M. Petty (see [6]) raised the question: Does vol (A ⌒ L) < vol (B ⌒ L) for every L imply vol (A) < vol(B)? The answer in case n = 2 is affirmative in a trivial way. Also in 1953 H. Busemann (see [4]) proved that if A is any ellipsoid the answer is affirmative. In fact, as he observed in [5], the answer is still affirmative if A is an ellipsoid with 0 as center of symmetry and B is any compact set containing 0.

In [7] the notion of minimal pairs of convex compact subsets of a Hausdorff topological vector space was introduced and it was conjectured, that minimal pairs in an equivalence class of the Hörmander-Rådström lattice are unique up to translation. We prove this statement for the two-dimensional case. To achieve this we prove a necessary and sufficient condition in terms of mixed volumes that a translate of a convex body in ℝn is contained in another convex body. This generalizes a theorem of Weil (cf. [10]).

An upper bound for the “sausage catastrophe” of dense sphere packings in 4-space is given.

A basic problem in the theory of finite packing is to determine, for a given positive integer k, the minimal volume of all convex bodies into which k translates of the unit ball Bd of the Euclidean d-dimensional space Ed can be packed ([5]). For d = 2 this problem was solved by Groemer ([6]).

Let K be a convex body in Euclidean space Rd, d≥2, with volume V(K) = 1, and n ≥ d +1 be a natural number. We select n independent random points y1, y2, …, yn from K (we assume they all have the uniform distribution in K). Their convex hull co {y1, y2, …, yn} is a random polytope in K with at most n vertices. Consider the expected value of the volume of this polytope

It is easy to see that if U: Rd → Rd is a volume preserving affine transformation, then for every convex body K with V(K) = 1, m(K, n) = m(U(K), n).

The temporal evolution of nonlinear, incompressible ensembles is examined first for the one-dimensional Burgers' equation and then for the incompressible, unsteady Navier-Stokes equations. It is shown that local closure of the averaged problem can be obtained for finite ensembles of Burgers' equation in the limit as the number of moments tends to infinity. This limit behaviour is verified via direct numerical computations for the onedimensional inviscid and viscous Burgers' equation. Closure is found to occur at reasonably low order. It is shown that this technique can be extended to obtain a local closure of the convective terms of the Navier-Stokes Reynoldsaveraged equations.

In this paper, the Opial's inequality, which has a wide range of applications in the study of differential and integral equations, is generalized to the case involving m functions of n variables, m, n ≥ 1.

The Shirshov-Cohn theorem asserts that in a Jordan algebra (with 1), any subalgebra generated by two elements (and 1) is special. Let J be a Jordan algebra with 1, a, b elements of J and let a1, a2, …, an be invertible elements of J such that

Where

are Jordan polynomials. In [2, p. 425] Jacobson conjectured that for any choice of the Pi the subalgebra of J generated by 1, a, b, a1…, an is special.

Let D be an atomic integral domain (i.e., a domain in which each nonzero nonunit of D can be written as a product of irreducible elements) and k any positive integer. D is known as a half factorial domain (HFD) if for any irreducible elements α1, …, αn, β1, …, βm of D the equality α1… αn = β1… βm implies that n = m. In [5] the present authors define D to be a k-half factorial domain (k-HFD) if the equality above along with the fact that n or m ≤ k implies that n = m. In this paper we consider the k-HFD property in Dedekind domains with small class group and prove the following Theorem: if D is a Dedekind domain with class group of order less than 16 then D is k-HFD for some integer k > 1, if, and only if, D is HFD.

Let f(x) be a monic polynomial of degree n with complex coefficients, which factors as f(x) = g(x)h(x), where g and h are monic. Let be the maximum of on the unit circle. We prove that , where β = M(P0) = 1 38135 …, where P0 is the polynomial P0(x, y) = 1 + x + y and δ = M(P1) = 1 79162…, where P1(x, y) = 1 + x + y - xy, and M denotes Mahler's measure. Both inequalities are asymptotically sharp as n → ∞.

Let K be an algebraic number field, [ K: 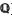] = KΣ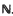. Most of what we shall discuss is trivial when K = 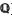, so that we assume that K ≥ 2 from now onwards. To describe our results, we consider the classical device [2] of Minkowski, whereby K is embedded (diagonally-) into the direct product MK of its completions at its (inequivalent) infinite places. Thus MK is 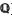-algebra isomorphic to 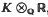, and is to be regarded as a topological 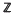-algebra, dimRMK = K, in which K is everywhere dense, while the ring Zx of integers of K embeds as a discrete 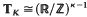-submodule of rank K. Following the ideas implicit in Hecke's fundamental papers [6] we may measure the “spatial distribution” of points of MK (modulo units of 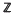κ) by means of a canonical projection onto a certain torus 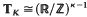. The principal application of our main results (Theorems I–III described below) is to the study of the spatial distribution of the 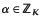which have a fixed norm n = NK/Q(α). In §2 we shall show that, with suitable interpretations, for “typical” n (for which NK/Q(α) = n is soluble), these α have “almost uniform” spatial distribution under the canonical projection onto TK. Analogous questions have been considered by several authors (see, e.g., [5, 9, 14]), but in all cases, they have considered weighted averages over such n of a type which make it impossible to make useful statements for “typical” n.

§1. Introduction. The literature on solving a system of linear equations in primes is quite limited, although the multi-dimensional Hardy-Littlewood method certainly provides an approach to this problem. The Goldbach- Vinogradov theorem and van der Corput's proof of the existence of infinitely many three term arithmetic progressions in primes are two particular results in the special case of only one equation. Recently Liu and Tsang [4] studied this case in full generality and obtained a result with excellent uniformity in the coefficients. Almost no other general result has appeared so far, due probably to the fact that such a theorem is clumsy to state.

The object of this paper is to obtain improvements in Vinogradov's mean value theorem widely applicable in additive number theory. Let Js,k(P) denote the number of solutions of the simultaneous diophantine equations

with 1 ≥ xi, yi ≥ P for 1 ≥ i ≥ s. In the mid-thirties Vinogradov developed a new method (now known as Vinogradov's mean value theorem) which enabled him to obtain fairly strong bounds for Js,k(P). On writing

in which e(α) denotes e2πiα, we observe that

where Tk denotes the k-dimensional unit cube, and α = (α1,…,αk).

Let k ≤ 2 be an integer, and set

Ek (X) = |{n ≤ X, n ≠ mk, n not a sum of a prime and a k-th power}|.

We prove that there exists δ = δ(k) > 0 such that Ek (X)Ek(X)≪kX1−δ.