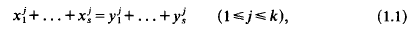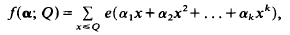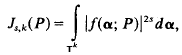Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1993.
The use in additive number theory of numbers without large prime factors.
Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences,
Vol. 345,
Issue. 1676,
p.
363.
Wooley, Trevor D.
1993.
Corrigendum: On Vinogradov's mean value theorem.
Mathematika,
Vol. 40,
Issue. 1,
p.
152.
Boklan, Kent D.
1994.
The asymptotic formula in Waring's problem.
Mathematika,
Vol. 41,
Issue. 2,
p.
329.
Wooley, Trevor D.
1994.
Quasi-diagonal behaviour in certain mean value theorems of additive number theory.
Journal of the American Mathematical Society,
Vol. 7,
Issue. 1,
p.
221.
Wooley, Trevor D.
1996.
Some remarks on Vinogradov's mean value theorem and Tarry's problem.
Monatshefte f�r Mathematik,
Vol. 122,
Issue. 3,
p.
265.
Vaughan, R. C.
1998.
Hardy's legacy to number theory.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 65,
Issue. 2,
p.
238.
Wooley, Trevor D.
1999.
On Weyl’s inequality, Hua’s lemma, and exponential sums over binary forms.
Duke Mathematical Journal,
Vol. 100,
Issue. 3,
Wooley, Trevor D.
2004.
A light-weight version of Waring's problem.
Journal of the Australian Mathematical Society,
Vol. 76,
Issue. 3,
p.
303.
Parsell, Scott
2009.
Asymptotic estimates for rational linear spaces on hypersurfaces.
Transactions of the American Mathematical Society,
Vol. 361,
Issue. 6,
p.
2929.
Elliott, P. D. T. A.
2010.
The value distribution of additive arithmetic functions on a line.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 642,
Kawada, Koichi
and
Wooley, Trevor D.
2010.
DAVENPORT'S METHOD AND SLIM EXCEPTIONAL SETS: THE ASYMPTOTIC FORMULAE IN WARING'S PROBLEM.
Mathematika,
Vol. 56,
Issue. 2,
p.
305.
Preobrazhenskii, S. N.
2011.
New estimate in Vinogradov’s mean-value theorem.
Mathematical Notes,
Vol. 89,
Issue. 1-2,
p.
277.
Преображенский, Сергей Николаевич
and
Preobrazhenskii, Sergei Nikolaevich
2011.
Новая оценка в теореме о среднем И. М. Виноградова.
Математические заметки,
Vol. 89,
Issue. 2,
p.
285.
Parsell, Scott T.
2012.
HUA‐TYPE ITERATION FOR MULTIDIMENSIONAL WEYL SUMS.
Mathematika,
Vol. 58,
Issue. 2,
p.
209.
Boklan, Kent D.
and
Wooley, Trevor D.
2012.
On Weyl sums for smaller exponents.
Functiones et Approximatio Commentarii Mathematici,
Vol. 46,
Issue. 1,
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
195.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Wooley, Trevor
2012.
Vinogradov's mean value theorem via efficient congruencing.
Annals of Mathematics,
Vol. 175,
Issue. 3,
p.
1575.
Spencer, Craig V.
and
Wooley, Trevor D.
2012.
Diophantine inequalities and quasi-algebraically closed fields.
Israel Journal of Mathematics,
Vol. 191,
Issue. 2,
p.
721.
Wooley, Trevor D.
2013.
Vinogradov’s mean value theorem via efficient congruencing, II.
Duke Mathematical Journal,
Vol. 162,
Issue. 4,