Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T19:13:15.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Two sharp inequalities for the norm of a factor of a polynomial

Part of: Geometric function theory

Published online by Cambridge University Press:  26 February 2010

David W. Boyd
David W. Boyd
Affiliation:
Department of Mathematics, The University of British Columbia, 121-1984 Mathematics Road, Vancouver, B.C., Canada V6T 1Y4.
Get access

Abstract

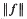Let f(x) be a monic polynomial of degree n with complex coefficients, which factors as f(x) = g(x)h(x), where g and h are monic. Let be the maximum of 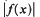on the unit circle. We prove that 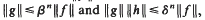, where β = M(P0) = 1 38135 …, where P0 is the polynomial P0(x, y) = 1 + x + y and δ = M(P1) = 1 79162…, where P1(x, y) = 1 + x + y - xy, and M denotes Mahler's measure. Both inequalities are asymptotically sharp as n → ∞.

MSC classification

Secondary: 30C10: Polynomials
Type
Research Article
Information
Mathematika , Volume 39 , Issue 2 , December 1992 , pp. 341 - 349
Copyright
Copyright © University College London 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[AS]Abramowitz, M. and Stegun, I. A.. “Handbook of Mathematical Functions” (Dover, N.Y., 1965).Google Scholar
[BE]Beauzamy, B. and Enflo, P.. Estimations de produits de polynômes. J Number Theory, 21 (1985), 390–412.CrossRefGoogle Scholar
[BBEM]Beauzamy, B.Bombieri, E.Enflo, P. and Montgomery, H. L.. Products of Polynomials in Many Variables. J. Number Theory, 36 (1990), 219–245.CrossRefGoogle Scholar
[B1]Boyd, D. W.. Speculations Concerning the Range of Mahler's Measure. Canad. Math. Bull., 24 (1981), 453–469.CrossRefGoogle Scholar
[B2]Boyd, D. W.. The Asymptotic Behaviour of the Binomial Circulant Determinant. J. Math. Anal. Appl., 86 (1982), 30–38.CrossRefGoogle Scholar
[EM]Evans, R. and Montgomery, P.. Some Unimodal Reciprocal Polynomials with Positive Coefficients, Advanced Problem 6631. Amer. Math. Monthly, 98 (1991), 870–872.CrossRefGoogle Scholar
[Fr]Frame, J. S.. Factors of the binomial circulant determinant. Fibronacci Quart., 18 (1980), 9–23.Google Scholar
[Ge]Gelfond, A. O.. Transcendental and Algebraic Numbers (Dover, N.Y., 1960). Translation by Boron, L. F. of the 1952 Russian edition.Google Scholar
[G1]Glesser, P.. Nouvelle Majoration de la norme des Facteurs d'un Polynôme. C. R. Math. Rep. Acad. Sci. Canada, 12 (1990), 224–228.Google Scholar
[Gr]Granville, A.. Bounding the Coefficients of a Divisor of a Given Polynomial. Monatsh. Math., 109 (1990), 271–277.CrossRefGoogle Scholar
[Le]Lewin, L.. Polylogarithms and Associated Functions (Elsevier North-Holland, Amsterdam, 1981).Google Scholar
[LSW]Lind, D.Schmidt, K. and Ward, T.. Mahler measure and entropy for commuting automorphisms of compact groups. Invent. Math., 101 (1990), 593–629.CrossRefGoogle Scholar
[M1]Mahler, K.. An application of Jensen's Formula to Polynomials. Mathematika, 7 (1960), 98–100.CrossRefGoogle Scholar
[M2]Mahler, K.. On Some Inequalities for Polynomials in Several Variables. J. Land. Math. Soc., 37 (1962), 341–344.CrossRefGoogle Scholar
[M3]Mahler, K.. A Remark on a Paper of Mine on Polynomials. Illinois J. Math., 8 (1964), 1–4.CrossRefGoogle Scholar
[Mig]Mignotte, M.. Some useful bounds. In: Buchberger, B. et al. (eds), Computer Algebra, Symbolic and Algebraic Computation (Springer, N.Y., 1982), 259–263.Google Scholar
[Mil]Milnor, J.. Hyperbolic Geometry: The First 150 Years. Bull. Amer. Math. Soc. (N.S.), 6 (1982), 9–24.CrossRefGoogle Scholar