Asymptotic formulae for the Titchmarsh—Weyl m-coefficient on rays in the complex λ-plane for the equation − y ″ + qy = λy whenthe potential is limit circle and non-oscillatory at x = 0 are obtained under assumptions slightly more general than xq(x) ∈ L1(0,c). The behaviour of q at the right end-point is arbitrary and may fall in either the limit-point or limit-circle case. A method of regularization of the equation is given that can be made to depend either on a solution of the equation for λ = 0 or more directly on an approximation to the solution in terms of q. This enables equivalent definitions of the m-coefficient to be given for the singular Sturm—Liouville problem associated with a singular limit-circle boundary condition, and its associatedregular Sturm—Liouville problem. As a consequence, it becomes possible to apply asymptotic results obtained by Atkinson for the regular problem in order to give asymptoticresults for the singular problem. Potentials of the form q(x) = C/xj, 1 ≤ j < 2, are included. In the case j = 1, an independent calculation of the limit-point m-coefficient over the range (0,∞), relying on Whittaker functions, verifies the main result.

This work connects the theory of commutators with analytic families of operators in abstract interpolation theory. Our main result asserts that if {Lξ}0≤Reξ≤1 is an analytic family of operators satisfying some conditions, then [Lθ,Ω] +(Lξ)′(θ): Āθ→ Bθ is bounded. From this, we can deduce the boundedness of the commutator .

The purpose of this paper is to establish a Lusin-type approximation of functions with bounded deformation by Lipschitz or C1 functions. The main ingredients inthe proof of our result are the maximal function of the measure Eu, the ‘Poincaré-type’ result by Kohn and the approximate symmetric differentiability of BD functions by Ambrosio and others.

If a Sturm—Liouville problem is given in an open interval of the real line, then regular boundary value problems can be considered on compact sub-intervals. For these regular problems, all with necessarily discrete spectra, the eigenvalues depend on both the end-points of the compact intervals, and upon the choice of the real separated boundary conditions at these end-points. These eigenvalues are not, in general, continuous functionsof the end-points and boundary conditions. The paper shows the surprising form of these discontinuities. The results have applications to the approximations of singular Sturm—Liouville problems by regular problems, and to the theoretical aspects of the Sleign2 Computer program.

This paper deals with the theory of point interactions for the one-dimensional Schrödinger equation. The familiar example of the δ-potential V(x) = gδ(x−x0), for which the transfer matrix across the singularity (point transfer matrix) is given by

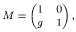
is extended to cover cases in which the transfer matrix M(z) is dependent on the (complex) spectral parameter z, and which can be obtained as limits of transfer matrices across finite intervals for sequences of approximating potentials Vn.

The case of point transfer matrices polynomially dependent on z is treated in detail, with a complete characterization of such matrices and a proof of their factorization as products of point transfer matrices linearly dependent on z.

The theory presented here has applications to the study of point interactions in quantum mechanics, and provides new classes of point interactions which can be obtained as limiting cases of regular potentials.

The Riemann initial value problem is studied for scalar conservation laws whose fluxes have a single inflection point. For a regularization consisting of balanced diffusive and dispersive terms, the travelling wave criterion is used to select admissible shocks. In some cases, the Riemann problem solution contains an undercompressive shock. The analysis is illustrated by exploring parameter space for the Buckley–Leverett flux. The boundary of the set of parameters for which there is a physical solution of the Riemann problem for all data is computed. Within the region of acceptable parameters, the solution hasseveral different forms, depending on the initial data; the different forms are illustrated by numerical computations. Qualitatively similar behaviour is observed in Lax–Wendroff approximations of solutions of the Buckley–Leverett equation with no dissipation or dispersion.

It is commonly believed that, as far as stabilities are concerned, ‘small delays are negligible in some modelling processes’. However, to have an affirmative answerfor this common belief is still an open problem for many nonlinear equations. In this paper, the classical Lotka–Volterra prey–predator equation with discrete delays

is considered, and, by using degenerate Lyapunov functionals method, an affirmative answer to this open problem on both local and global stabilities of the prey–predator delay equations is given. It is shown that degenerate Lyapunov functional method is a powerful tool for studying the stability of such nonlinear delay systems. A detailed and explicit procedure of constructing such functionals is provided. Furthermore, some explicit estimates on the allowable sizes of the delays are obtained.

Adjoint actions of compact simply connected Lie groups are studied by Kozima and the second author based on the series of studies on the classification of simple Lie groups and their cohomologies. At odd primes, the first author showed that there is a homotopy theoretic approach that will prove the results of Kozima and the second author for any 1-connected finite loop spaces. In this paper, we use the rationalization of the classifying space to compute the adjoint actions and the cohomology of classifying spaces assuming torsion free hypothesis, at the prime 2. And, by using Browder's work on the Kudo–Araki operations Q1 for homotopy commutative Hopf spaces, we show the converse for general 1-connected finite loop spaces, at the prime 2. This can be done because the inclusion j: G > BAG satisfies the homotopy commutativity for any non-homotopy commutative loop space G.

Using the ‘monotonicity trick’ introduced by Struwe, we derive a generic theorem. It says that for a wide class of functionals, having a mountain-pass (MP) geometry, almost every functional in this class has a bounded Palais-Smale sequence at the MP level. Then we show how the generic theorem can be used to obtain, for a given functional, a special Palais–Smale sequence possessing extra properties that help to ensure its convergence. Subsequently, these abstract results are applied to prove the existence of a positive solution for a problem of the form

We assume that the functional associated to (P) has an MP geometry. Our results cover the case where the nonlinearity f satisfies (i) f(x, s)s−1 → a ∈)0, ∞) as s →+∞; and (ii) f(x, s)s–1 is non decreasing as a function of s ≥ 0, a.e. x → ℝN.

We consider the Stokes problem with a small viscosity. When the viscosity goes to zero, the boundary-layer phenomenon can appear. In this case, the solution of the given perturbed Stokes equation cannot be properly approximated by the solution of its limiting equation ‘near’ the boundary Γ of the domain of study, say Ω To overcome this problem, we need to construct a corrector term in the neighbourhood of Γ Lions has studied this problem and has constructed a corrector for the case where Ω is a half space in ℝ2. The case where Ω is an open and bounded domain of ℝ2 or ℝ3, which remained unsolved, is the concern of this paper. The construction of the corrector to the perturbed Stokes equation depends heavily on the geometry of Ω In two dimensions, we construct the corrector in the form of a stream function, while in ℝ3 we construct it in the form of a potential vector. The corrector acts effectively in a neighbourhood of Γ that is the boundary layer. Using similar methods to those of Baranger and Tartar, we define the thickness of the boundary layer in a natural way. In addition, in this paper we study the behaviour of the corrected solution in some Hölder spaces.

The Hardy-Rellich inequality given here generalizes a Hardy inequality of Davies, from the case of the Dirichlet Laplacian of a region Ω ⊆ ℝN to that of the higher-order polyharmonic operators with Dirichlet boundary conditions. The inequality yields some immediate spectral information for the polyharmonic operators and also bounds on the trace of the associated semigroups and resolvents.

We introduce the spectral heat function H associated with the Dirichlet-Laplace–Beltrami operator ΔM on a compact smooth Riemannian manifold M with a non-empty smooth boundary. We obtain two-term asymptotics for H without assuming any billiard conditions on M. As a corollary, we obtain estimates for the integral of the k′th Dirichlet eigenfunction of ΔM over M for k→∞.

We shall prove multiplicity of non-trivial solutions for the following p-Laplacian problems

where f(x,u) is continuous, periodic in x and has superlinear growth in u.