Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T12:28:15.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Point transfer matrices for the Schrödinger equation: the algebraic theory

Published online by Cambridge University Press:  14 November 2011

N. A. Gordon  and
D. B. Pearson
N. A. Gordon
Affiliation:
Department of Mathematics, University of Hull, Cottingham Road, Hull HU6 7RX, UK
D. B. Pearson
Affiliation:
Department of Mathematics, University of Hull, Cottingham Road, Hull HU6 7RX, UK
Get access Rights & Permissions [Opens in a new window]

Extract

This paper deals with the theory of point interactions for the one-dimensional Schrödinger equation. The familiar example of the δ-potential V(x) = gδ(x−x0), for which the transfer matrix across the singularity (point transfer matrix) is given by

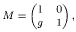
is extended to cover cases in which the transfer matrix M(z) is dependent on the (complex) spectral parameter z, and which can be obtained as limits of transfer matrices across finite intervals for sequences of approximating potentials Vn.

The case of point transfer matrices polynomially dependent on z is treated in detail, with a complete characterization of such matrices and a proof of their factorization as products of point transfer matrices linearly dependent on z.

The theory presented here has applications to the study of point interactions in quantum mechanics, and provides new classes of point interactions which can be obtained as limiting cases of regular potentials.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 4 , 1999 , pp. 717 - 732
Copyright
Copyright © Royal Society of Edinburgh 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Akhiezer, N. I. and Glazman, I. M.. Theory of linear operators in Hilbert space, vol. I (London: Pitman, 1981).Google Scholar
2Albeverio, S., Gesztesy, F., Hoegh-Krohn, R. and Holden, H.. Solvable models in quantum mechanics (London: Springer, 1988).CrossRefGoogle Scholar
3Albeverio, S., Gesztesy, F., Hoegh-Krohn, R. and Kirsch, W.. On point interactions in one dimension. J. Operator Theory 12 (1984), 101–126.Google Scholar
4Albeverio, S. and Hoegh-Krohn, R.. Point interactions as limits of short-range interactions. J. Operator Theory 6 (1981), 313–339.Google Scholar
5Albeverio, S., Kusuoka, S. and Streit, L.. Convergence of Dirichlet forms and associated Schrödinger operators. J. Funct. Analysis 68 (1986), 13–148.CrossRefGoogle Scholar
6Atkinson, F. V.. Discrete and continuous boundary problems (New York: Academic Press, 1964).Google Scholar
7Atkinson, D. A. and Crater, H. W.. An exact treatment of the Dirac δ-function potential in the Schrödinger equation. Am. J. Phys. 43 (1975), 301–304.CrossRefGoogle Scholar
8Dijksma, A.. Eigenfunction expansions for a class of J-self adjoint ordinary differential operators with boundary conditions containing the eigenvalue parameter. Proc.R. Soc. Edinb. A 86 (1980), 1–27.CrossRefGoogle Scholar
9Fulton, C. T.. Singular eigenvalue problems with eigenvalue parameter contained in the boundary conditions. Proc. R. Soc. Edinb. A 87 (1980), 1–34.CrossRefGoogle Scholar
10Fulton, C. T.. Two point boundary value problems with eigenvalue parameter contained in the boundary conditions. Proc. R. Soc. Edinb. A 77 (1977), 293–308.CrossRefGoogle Scholar
11Gesztesy, F. and Holden, F.. A new class of solvable models in quantum mechanics describing point interactions on the line. J. Phys. A 20 (1987), 5157–5177.Google Scholar
12Kato, T.. Perturbation theory for linear operators, 2nd edn (Berlin: Springer, 1976).Google Scholar
13Pavlov, B. S.. Model of zero-range potential with internal structure. Theor. Math. Phys. 69 (1986), 554–550.Google Scholar
14Pavlov, B. S. and Shushkov, A. A.. The theory of extensions and zero-radius potentials with internal structure. Math. USSR Sbornik 65 (1990), 147–185.CrossRefGoogle Scholar
15Pearson, D. B.. An example in potential scattering illustrating the breakdown of asymptotic completeness. Commun. Math. Phys. 40 (1975), 125–146.CrossRefGoogle Scholar
16Pearson, D. B. and Skelton, P. L. I.. The inverse method for transfer matrices. J. Lond. Math. Soc. 40 (1989), 476–489.CrossRefGoogle Scholar
17Pittner, L. and Valjavec, M.. Transition matrix of point interactions as scaling limit of integrable potentials on the real line. J. Math. Phys. 26 (1985), 1675–1679.CrossRefGoogle Scholar
18Reed, M. and Simon, B.. Methods of modern mathematical physics, vol. I: Functional analysis (New York: Academic Press, 1972).Google Scholar
19Simon, B.. Quantum mechanics for Hamiltonians defined as quadratic forms (Princeton University Press, 1971).Google Scholar
20Skelton, P. L. I.. Non-central potentials, and inverse methods, of the Schrödinger equation. PhD thesis (University of Hull, 1986).Google Scholar
21Wall, H. S.. Analytic theory of continued fractions (New York: Chelsea Publishing, 1973).Google Scholar
22Wolfram, S.. Mathematica (Redwood City: Addison-Wesley, 1988).Google Scholar
23Yosida, K.. Functional analysis (Berlin: Springer, 1965).Google Scholar