Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carro, Marı́a J.
2003.
A multiplier theorem using the Schechter's method of interpolation.
Journal of Approximation Theory,
Vol. 120,
Issue. 2,
p.
283.
Castillo, Jesús M. F.
and
Ferenczi, Valentin
2023.
Group Actions on Twisted Sums of Banach Spaces.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 4,
Castillo, Jesús M.F.
and
Pino, Raúl
2023.
The Rochberg garden.
Expositiones Mathematicae,
Vol. 41,
Issue. 2,
p.
333.


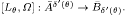 .
.