Published online by Cambridge University Press: 14 December 2022
We consider $L^{2}$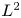 -constraint minimizers of the mass critical fractional Schrödinger energy functional with a ring-shaped potential $V(x)=(|x|-M)^{2}$
-constraint minimizers of the mass critical fractional Schrödinger energy functional with a ring-shaped potential $V(x)=(|x|-M)^{2}$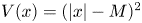 , where $M>0$
, where $M>0$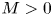 and $x\in \mathbb {R}^{2}$
and $x\in \mathbb {R}^{2}$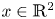 . By analysing some new estimates on the least energy of the mass critical fractional Schrödinger energy functional, we obtain the concentration behaviour of each minimizer of the mass critical fractional Schrödinger energy functional when $a\nearrow a^{\ast }=\|Q\|_{2}^{2s}$
. By analysing some new estimates on the least energy of the mass critical fractional Schrödinger energy functional, we obtain the concentration behaviour of each minimizer of the mass critical fractional Schrödinger energy functional when $a\nearrow a^{\ast }=\|Q\|_{2}^{2s}$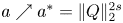 , where $Q$
, where $Q$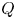 is the unique positive radial solution of $(-\Delta )^{s}u+su-|u|^{2s}u=0$
is the unique positive radial solution of $(-\Delta )^{s}u+su-|u|^{2s}u=0$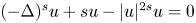 in $\mathbb {R}^{2}$
in $\mathbb {R}^{2}$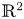 .
.