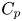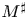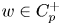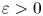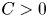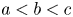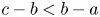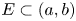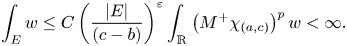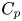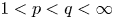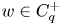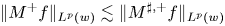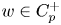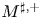1. Introduction and main result
One-sided theory of weights was begun by Sawyer in [Reference Sawyer35] where he provided the characterization of the two weighted inequalities for the one-sided maximal functions
In some sense it is a somehow curious fact that the results in [Reference Sawyer35] appeared more than a decade later than the characterization of the one weight inequalities for the maximal function due to Muckenhoupt [Reference Muckenhoupt29] if one bears in mind that actually the maximal operators studied by Hardy and Littlewood [Reference Hardy and Littlewood10] were $M^+$![]() and $M^{-}$
and $M^{-}$![]() .
.
Since Sawyer's work a number of papers such as [Reference Aimar, Forzani and Martín-Reyes1, Reference Forzani, Martín-Reyes and Ombrosi7, Reference Gurka, Martín-Reyes, Ortega, Pick, Sarrión and de la Torre9, Reference Lorente and Martín-Reyes20, Reference Lorente and Martín-Reyes21, Reference Martín-Reyes23–Reference Martín-Reyes, Pick and de la Torre26, Reference Martín-Reyes and de la Torre28, Reference Ombrosi31, Reference Ombrosi and de Rosa32] and even more that we will cite throughout this paper were devoted to develop the one-sided theory. However, at this point, we believe it is worth mentioning some papers which have expanded the field of one-sided estimates in the last years. Kinnunen and Saari [Reference Kinnunen and Saari13, Reference Kinnunen and Saari14] studied parabolic Muckenhoupt conditions in connection with PDEs and more recently Hytönen and Rosén devoted their work [Reference Hytönen and Rosén11] to causal sparse domination motivated by maximal regularity estimates for elliptic PDEs, obtaining results related to one-sided weighted estimates for singular integrals.
A well-known estimate in theory of weights that was settled by Coifman and Fefferman, says that if $w\in A_{\infty }$![]() then, for every $p\in (0,\infty )$
then, for every $p\in (0,\infty )$![]() we have that
we have that
where $T$![]() stands for any Calderón–Zygmund operator.
stands for any Calderón–Zygmund operator.
Although $w\in A_{\infty }$![]() is sufficient for (1.1) to hold, it turns out to not to be necessary. Muckenhoupt [Reference Muckenhoupt30] showed that if (1.1) holds for the Hilbert transform for $p>1$
is sufficient for (1.1) to hold, it turns out to not to be necessary. Muckenhoupt [Reference Muckenhoupt30] showed that if (1.1) holds for the Hilbert transform for $p>1$![]() then there exist $c,\varepsilon >0$
then there exist $c,\varepsilon >0$![]() such that for every cube $Q$
such that for every cube $Q$![]() and every measurable subset $E\subset Q$
and every measurable subset $E\subset Q$![]() ,
,
namely $w\in C_{p}$![]() . Later on, Sawyer [Reference Sawyer34] showed that if $1< p< q<\infty$
. Later on, Sawyer [Reference Sawyer34] showed that if $1< p< q<\infty$![]() and $w\in C_{q}$
and $w\in C_{q}$![]() , then (1.1) holds.
, then (1.1) holds.
Yabuta [Reference Yabuta37] provided a different approach to the question. He showed that if $1< p< q<\infty$![]() and $w\in C_{q}$
and $w\in C_{q}$![]()
and also that if such an inequality holds then $w\in C_{p}$![]() . An alternative proof of this estimate and a slight generalization of the $C_{p}$
. An alternative proof of this estimate and a slight generalization of the $C_{p}$![]() condition was studied by Lerner in [Reference Lerner15].
condition was studied by Lerner in [Reference Lerner15].
In the last years some advances have been made in the study of this kind of questions. Lerner [Reference Lerner16] fully characterized the weak type version of (1.1). Sawyer's result has been extended to the full range in [Reference Cejas, Li, Pérez and Rivera-Ríos6] and also quantitative estimates in terms of a suitable $C_{p}$![]() constant and further operators, such as rough singular integrals, have been explored in [Reference Canto4, Reference Canto, Li, Roncal and Tapiola5].
constant and further operators, such as rough singular integrals, have been explored in [Reference Canto4, Reference Canto, Li, Roncal and Tapiola5].
In the one-sided setting we are aware of just one work in this direction in which Riveros and de la Torre [Reference Riveros and de la Torre33] introduced the one-sided version of the $C_{p}$![]() condition, which reads as follows. We say that $w\in C_{p}^+$
condition, which reads as follows. We say that $w\in C_{p}^+$![]() if there exist $\varepsilon >0$
if there exist $\varepsilon >0$![]() and $C>0$
and $C>0$![]() such that for any $a< b< c$
such that for any $a< b< c$![]() with $c-b< b-a$
with $c-b< b-a$![]() and any measurable set $E\subset (a,b)$
and any measurable set $E\subset (a,b)$![]() , the following holds
, the following holds
The main result in that work was the following one-sided counterpart of [Reference Sawyer34].
Theorem 1.1 [Reference Riveros and de la Torre33, theorem 1]
Let $1< p< q<\infty$![]() . If $w\in C_{q}^+$
. If $w\in C_{q}^+$![]() and $(T^+)^{*}$
and $(T^+)^{*}$![]() is a maximal Calderón–Zygmund one-sided singular integral, then
is a maximal Calderón–Zygmund one-sided singular integral, then
Observe that in [Reference Riveros and de la Torre33], additionally the authors assume that the integral in the right-hand side of (1.3) is finite. Note that if the right-hand side of the condition $C_{q}^+$![]() is not finite, then the same happens to $\int _{\mathbb {R}}(M^+f)^{p}w$
is not finite, then the same happens to $\int _{\mathbb {R}}(M^+f)^{p}w$![]() and hence the inequality is trivial.
and hence the inequality is trivial.
Note that the $C_{p}^+$![]() class is defined in terms of the one-sided maximal operator $M^+$
class is defined in terms of the one-sided maximal operator $M^+$![]() . We will review the definitions of $M^+$
. We will review the definitions of $M^+$![]() and the remainder of the one-sided operators studied in this paper in § 2. We would like to observe as well that the assumption $c-b< b-a$
and the remainder of the one-sided operators studied in this paper in § 2. We would like to observe as well that the assumption $c-b< b-a$![]() can be dropped. Assume that $b-a\leq c-b$
can be dropped. Assume that $b-a\leq c-b$![]() . Let $\bar {a}< a$
. Let $\bar {a}< a$![]() such that $a-\bar {a}=c-a$
such that $a-\bar {a}=c-a$![]() . Note, that then, $b\in (\bar {a},c)$
. Note, that then, $b\in (\bar {a},c)$![]() , and $c-b< b-\bar {a}.$
, and $c-b< b-\bar {a}.$![]() On the other hand observe that $M^+\chi _{(\bar {a},c)}\simeq M^+\chi _{(a,c)}$
On the other hand observe that $M^+\chi _{(\bar {a},c)}\simeq M^+\chi _{(a,c)}$![]() and hence the $C_{p}^+$
and hence the $C_{p}^+$![]() condition would hold just with a larger constant $C$
condition would hold just with a larger constant $C$![]() but without the restriction $c-b< b-a$
but without the restriction $c-b< b-a$![]() .
.
The purpose of this paper is to provide a one-sided counterpart of Yabuta's characterization (1.2) and to derive a number of new results relying upon it. The precise statement of our theorem is the following.
Theorem 1.2 Let $1< p< q<\infty$![]() . If $f\in L^{p_{0}}(\mathbb {R})$
. If $f\in L^{p_{0}}(\mathbb {R})$![]() for some $1< p_{0}<\infty$
for some $1< p_{0}<\infty$![]() and $w\in C_{q}^+$
and $w\in C_{q}^+$![]() then
then
provided the left-hand side of the estimate is finite. Conversely if the preceding estimate holds, then $w\in C_{p}^+.$![]()
We would like to note that the corresponding counterpart for $T^{-}$![]() operators holds as well. However, here and throughout the remainder of this paper we will just deal with the case of $T^+$
operators holds as well. However, here and throughout the remainder of this paper we will just deal with the case of $T^+$![]() operators.
operators.
Exploiting the approach in [Reference Cejas, Li, Pérez and Rivera-Ríos6] we shall derive a number of consequences of this result. Among them we will recover the result for one-sided Calderón–Zygmund singular integrals due to de la Torre and Riveros that we stated above. We present those results in § 3.
The remainder of the paper is organized as follows. We devote § 2 to gather some results and definitions that will be useful throughout the remainder of the work. In § 3 we present the applications of theorem 1.2, namely counterparts of (1.4) for some other one-sided operators, and even for one-sided Calderón–Zygmund singular integrals themselves. Section 4 is devoted to the proof of theorem 1.2. Additionally we provide an appendix settling a suitable Cotlar inequality that we have not been able to find in the literature and that will be useful for us to recover and generalize [Reference Riveros and de la Torre33, theorem 1].
2. Preliminaries and definitions
We recall that the one-sided maximal function $M^+$![]() is defined, as we noted in the introduction, as
is defined, as we noted in the introduction, as
and the sharp maximal function $M^{\sharp,+}$![]() , that was introduced in [Reference Martín-Reyes and de la Torre27], as
, that was introduced in [Reference Martín-Reyes and de la Torre27], as
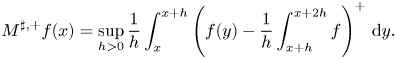
Another class of operators that we will be dealing with and that have already appeared in the previous section are one-sided singular integral operators that were introduced in [Reference Aimar, Forzani and Martín-Reyes1]. We say that a function $K\in L_{\text {loc}}^{1}(\mathbb {R}\setminus \{0\})$![]() is a Calderón–Zygmund kernel if the following properties hold.
is a Calderón–Zygmund kernel if the following properties hold.
(1) There exists a finite constant $B_{1}$
 such that
\[ \left|\int_{\varepsilon<|x|< N}K(x)\,{\rm d}x\right|\leq B_{1} \]for all $0<\varepsilon < N$
such that
\[ \left|\int_{\varepsilon<|x|< N}K(x)\,{\rm d}x\right|\leq B_{1} \]for all $0<\varepsilon < N$
 . Furthermore, $\lim _{\varepsilon \rightarrow 0^+}\int _{\varepsilon <|x|< N}K(x)\,{\rm d}x$
. Furthermore, $\lim _{\varepsilon \rightarrow 0^+}\int _{\varepsilon <|x|< N}K(x)\,{\rm d}x$ exists.
exists.(2) There exists a constant $B_{2}$
 such that
\[ |K(x)|\leq\frac{B_{2}}{|x|} \]for all $x\not =0$
such that
\[ |K(x)|\leq\frac{B_{2}}{|x|} \]for all $x\not =0$
 .
.(3) There exists a finite constant $B_{3}$
 such that
(2.1)\begin{equation} |K(x-y)-K(x)|\leq B_{3}\frac{|y|}{|x|^{2}}\end{equation}for all $x$
such that
(2.1)\begin{equation} |K(x-y)-K(x)|\leq B_{3}\frac{|y|}{|x|^{2}}\end{equation}for all $x$
 and $y$
and $y$ with $|x|>2|y|>0$
with $|x|>2|y|>0$ .
.
We say that $T^+$![]() is a one-sided Calderón–Zygmund singular integral if
is a one-sided Calderón–Zygmund singular integral if
where $K$![]() is a Calderón-Zygmund kernel with support in $\mathbb {R}^{-}$
is a Calderón-Zygmund kernel with support in $\mathbb {R}^{-}$![]() .
.
We would like to emphasize that this kind of operators are Calderón–Zygmund operators, and hence they have all the usual properties of operators in that class, but with the extra feature that $K$![]() is supported in $\mathbb {R}^{-}$
is supported in $\mathbb {R}^{-}$![]() . Examples of such operators are provided in [Reference Aimar, Forzani and Martín-Reyes1].
. Examples of such operators are provided in [Reference Aimar, Forzani and Martín-Reyes1].
Replacing (2.1) by some other smoothness conditions we obtain some more operators. For instance, we may assume that there exist numbers $c_{r},C_{r}>0$![]() such that for any $y\in \mathbb {R}$
such that for any $y\in \mathbb {R}$![]() and $R>c_{r}|y|$
and $R>c_{r}|y|$![]() ,
,
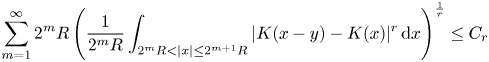
if $1\leq r<\infty$![]() and
and
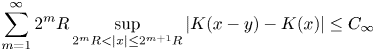
if $r=\infty$![]() . If $K$
. If $K$![]() satisfies an $L^{r}$
satisfies an $L^{r}$![]() -Hörmander condition we say that $K\in \mathcal {H}_{r}$
-Hörmander condition we say that $K\in \mathcal {H}_{r}$![]() . This yields that we may define an operator $T^+$
. This yields that we may define an operator $T^+$![]() exactly as we did in (2.2), but with $K$
exactly as we did in (2.2), but with $K$![]() satisfying (2.3) instead of (2.1). We may go even further. Let us recall first the notion of Orlicz average. Let $A:[0,\infty )\rightarrow [0,\infty )$
satisfying (2.3) instead of (2.1). We may go even further. Let us recall first the notion of Orlicz average. Let $A:[0,\infty )\rightarrow [0,\infty )$![]() a Young function, namely a convex function such that $A(0)=0$
a Young function, namely a convex function such that $A(0)=0$![]() , $A(1)=1$
, $A(1)=1$![]() and $\lim _{t\rightarrow \infty }A(t)=\infty$
and $\lim _{t\rightarrow \infty }A(t)=\infty$![]() . Given a measurable set $E$
. Given a measurable set $E$![]() we define the average of $f$
we define the average of $f$![]() over $E$
over $E$![]() with respect to $A$
with respect to $A$![]() as
as
Relying upon that definition we may define the maximal function $M_{A}^+$![]() as follows
as follows
It is also worth mentioning that we can define a function associated to $A$![]() , that we call $\overline {A}$
, that we call $\overline {A}$![]() , which turns out to be a Young function as well and satisfies the following inequalities
, which turns out to be a Young function as well and satisfies the following inequalities
Furthermore it can be shown that if $A_{1},A_{2},\ldots,A_{n}$![]() are Young functions such that
are Young functions such that
then
Coming back to the previous discussion, as we mentioned above, we may define a class of kernels generalizing the $L^{r}$![]() -Hörmander condition. Given a Young function $A$
-Hörmander condition. Given a Young function $A$![]() we say that it satisfies an $L^{A}$
we say that it satisfies an $L^{A}$![]() -Hörmander condition if there exist $c_{A},C_{A}\geq 1$
-Hörmander condition if there exist $c_{A},C_{A}\geq 1$![]() such that for any $x\in \mathbb {R}$
such that for any $x\in \mathbb {R}$![]() and $R>c_{A}|x|$
and $R>c_{A}|x|$![]()
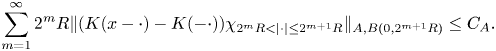
If $K$![]() satisfies this condition we say that $K\in \mathcal {H}_{A}$
satisfies this condition we say that $K\in \mathcal {H}_{A}$![]() . In order to be able to deal with commutators we introduce another condition. We say that $K\in \mathcal {H}_{A,k}$
. In order to be able to deal with commutators we introduce another condition. We say that $K\in \mathcal {H}_{A,k}$![]() if there exist $c_{A,k},C_{A,k}\geq 1$
if there exist $c_{A,k},C_{A,k}\geq 1$![]() such that for any $x\in \mathbb {R}$
such that for any $x\in \mathbb {R}$![]() and $R>c_{A,k}|x|$
and $R>c_{A,k}|x|$![]()
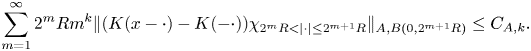
In both cases, whether $K\in \mathcal {H}_{A}$![]() or $K\in \mathcal {H}_{A,k}$
or $K\in \mathcal {H}_{A,k}$![]() , we may define a singular integral operator exactly as we did in (2.2). Those classes of kernels were introduced and studied in [Reference Lorente, Riveros and de la Torre17, Reference Lorente, Martell, Riveros and de la Torre19].
, we may define a singular integral operator exactly as we did in (2.2). Those classes of kernels were introduced and studied in [Reference Lorente, Riveros and de la Torre17, Reference Lorente, Martell, Riveros and de la Torre19].
We would like to end recalling that we may define a maximal version of any of the singular integral operators that we have just presented in this section as follows
3. Corollaries of the main theorem
As we announced in the previous section we will derive a number of applications of theorem 1.2. Our use of that theorem will rely upon the following lemma.
Lemma 3.1 Let $0< p<\infty$![]() . If $\delta \in (0,p)$
. If $\delta \in (0,p)$![]() then, if $w\in C_{\rho }^+$
then, if $w\in C_{\rho }^+$![]() with $\rho >\frac {p}{\delta }$
with $\rho >\frac {p}{\delta }$![]() , we have that
, we have that
where $M_{\delta }^+(f)=(M^+(|f|^{\delta }))^{\frac {1}{\delta }}$![]() and $M_{\delta }^{\sharp,+}(f)=(M^{\sharp,+}(|f|^{\delta }))^{\frac {1}{\delta }}$
and $M_{\delta }^{\sharp,+}(f)=(M^{\sharp,+}(|f|^{\delta }))^{\frac {1}{\delta }}$![]() .
.
Proof. Observe that, since $\delta \in (0,p)$![]() we have that $\frac {p}{\delta }>1$
we have that $\frac {p}{\delta }>1$![]() . Taking that into account and the fact that $w\in C_{\rho }^+$
. Taking that into account and the fact that $w\in C_{\rho }^+$![]() we have by theorem 1.2 that
we have by theorem 1.2 that
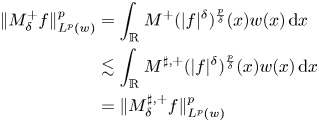
and we are done.
3.1 Singular integral operators, $L^{A}$ -Hörmander operators and their commutators
-Hörmander operators and their commutators
In this section we present our results for singular integral operators, $L^{A}$![]() -Hörmander operators and their commutators. We will provide some full arguments here, that we shall omit for the remainder of the corollaries since they will be analogous to the ones provided here.
-Hörmander operators and their commutators. We will provide some full arguments here, that we shall omit for the remainder of the corollaries since they will be analogous to the ones provided here.
We begin recalling that for one-sided Calderón–Zygmund singular integrals $T^+$![]() it was shown in [Reference Lorente and Riveros22, lemma 1] that for $0<\delta <1$
it was shown in [Reference Lorente and Riveros22, lemma 1] that for $0<\delta <1$![]() ,
,
Using that estimate we can derive the following result.
Theorem 3.2 Let $0< p<\infty$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$
and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$![]() Then
Then
Proof. Let $\delta \in (0,1)$![]() such that $1<\frac {p}{\delta }<\max \{p,1\}+\varepsilon$
such that $1<\frac {p}{\delta }<\max \{p,1\}+\varepsilon$![]() . For that choice of $\delta$
. For that choice of $\delta$![]() , taking into account (3.1) and lemma 3.1 with $\rho =\max \{p,1\}+\varepsilon$
, taking into account (3.1) and lemma 3.1 with $\rho =\max \{p,1\}+\varepsilon$![]() , we have that
, we have that
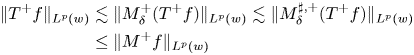
and we are done.
Recall that the commutator of a linear operator $T$![]() and a locally integrable function $b$
and a locally integrable function $b$![]() is defined as
is defined as
The iterated commutator $T_{b}^{k}$![]() consists precisely in iterating the commutator.
consists precisely in iterating the commutator.
where $T_{b}^{0}f(x)=Tf(x)$![]() . For the commutator and the iterated commutator of $b\in BMO$
. For the commutator and the iterated commutator of $b\in BMO$![]() and a Calderón–Zygmund one-sided singular integral $T^+$
and a Calderón–Zygmund one-sided singular integral $T^+$![]() again in [Reference Lorente and Riveros22, lemma 1], it was shown that for $0<\delta <\gamma <1$
again in [Reference Lorente and Riveros22, lemma 1], it was shown that for $0<\delta <\gamma <1$![]() , we have that
, we have that
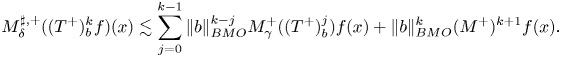
Relying upon that pointwise estimate we have the following theorem.
Theorem 3.3 Let $0< p<\infty$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$
and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$![]() Then
Then
Proof. Observe that it suffices to show that for $\delta _{1}\in (0,1)$![]() such that $1<\frac {p}{\delta _{1}}<\max \{p,1\}+\varepsilon$
such that $1<\frac {p}{\delta _{1}}<\max \{p,1\}+\varepsilon$![]() the following holds
the following holds
We proceed by induction. Assume first that $k=1$![]() . Let $0<\delta _{1}<\delta _{2}<1$
. Let $0<\delta _{1}<\delta _{2}<1$![]() such that $1<\frac {p}{\delta _{i}}<\max \{p,1\}+\varepsilon$
such that $1<\frac {p}{\delta _{i}}<\max \{p,1\}+\varepsilon$![]() . We have that, taking into account (3.2) and lemma 3.1,
. We have that, taking into account (3.2) and lemma 3.1,

where the estimate for $\|M_{\delta _{2}}(T^+f)\|_{L^{p}(w)}$![]() follows by the same argument provided in the proof of theorem 3.2.
follows by the same argument provided in the proof of theorem 3.2.
Assume now that (3.3) holds for $1,2,\ldots k-1$![]() . Let $0<\delta _{1}<\delta _{2}<1$
. Let $0<\delta _{1}<\delta _{2}<1$![]() such that $1<\frac {p}{\delta _{i}}<\max \{p,1\}+\varepsilon$
such that $1<\frac {p}{\delta _{i}}<\max \{p,1\}+\varepsilon$![]() . Then, again by (3.2) and lemma 3.1,
. Then, again by (3.2) and lemma 3.1,

and we are done.
With analogous arguments relying upon the corresponding pointwise sharp inequality we may settle the following result. We recall that if $\bar {A}$![]() is a Young function and $T^+$
is a Young function and $T^+$![]() is an operator associated to a kernel $K\in H_{\bar {A}}$
is an operator associated to a kernel $K\in H_{\bar {A}}$![]() with support in $(-\infty,0)$
with support in $(-\infty,0)$![]() , then as it was established in [Reference Lorente, Riveros and de la Torre17, p. 505]
, then as it was established in [Reference Lorente, Riveros and de la Torre17, p. 505]
and if, $A$![]() and $B$
and $B$![]() are Young functions, $\overline {C}^{-1}(t)={\rm e}^{t^{\frac {1}{k}}}$
are Young functions, $\overline {C}^{-1}(t)={\rm e}^{t^{\frac {1}{k}}}$![]() with $k$
with $k$![]() a positive integer such that $A^{-1}(t)B^{-1}(t)\overline {C}^{-1}(t)\leq t$
a positive integer such that $A^{-1}(t)B^{-1}(t)\overline {C}^{-1}(t)\leq t$![]() for $t\geq 1$
for $t\geq 1$![]() and $K\in H_{B}\cap H_{\bar {A},k}$
and $K\in H_{B}\cap H_{\bar {A},k}$![]() then, for $0<\delta <\gamma <1$
then, for $0<\delta <\gamma <1$![]() ,
,
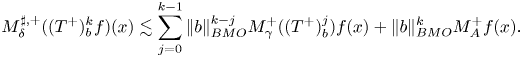
We remit the reader to [Reference Lorente, Martell, Riveros and de la Torre19, § 5.3].
Arguing as above, we have the following results.
Theorem 3.4 Let $A$![]() be a Young function and assume that $K\in \mathcal {H}_{\overline {A}}$
be a Young function and assume that $K\in \mathcal {H}_{\overline {A}}$![]() . Let $0< p<\infty$
. Let $0< p<\infty$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$
and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$![]() Then
Then
Theorem 3.5 Let $k$![]() be a positive integer and assume that $A$
be a positive integer and assume that $A$![]() and $B$
and $B$![]() are Young functions, and $A^{-1}(t)B^{-1}(t)\overline {C}^{-1}(t)\leq t$
are Young functions, and $A^{-1}(t)B^{-1}(t)\overline {C}^{-1}(t)\leq t$![]() for $t\geq 1$
for $t\geq 1$![]() where $\overline {C}^{-1}(t)={\rm e}^{t^{\frac {1}{k}}}$
where $\overline {C}^{-1}(t)={\rm e}^{t^{\frac {1}{k}}}$![]() . Assume also that $K\in \mathcal {H}_{B}\cap \mathcal {H}_{\bar {A},k}$
. Assume also that $K\in \mathcal {H}_{B}\cap \mathcal {H}_{\bar {A},k}$![]() and that $b\in BMO$
and that $b\in BMO$![]() . Then, if $0< p<\infty$
. Then, if $0< p<\infty$![]() , $\varepsilon >0$
, $\varepsilon >0$![]() and $w\in C_{\max \{p,1\}+\varepsilon }^+$
and $w\in C_{\max \{p,1\}+\varepsilon }^+$![]() , we have that
, we have that
We would like to end the section providing a result for maximal singular integral operators.
Theorem 3.6 Let $A$![]() be a Young function and assume that $K\in \mathcal {H}_{\overline {A}}$
be a Young function and assume that $K\in \mathcal {H}_{\overline {A}}$![]() . Let $0< p<\infty$
. Let $0< p<\infty$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$
and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$![]() Then
Then
Before settling this result, observe that if $K$![]() satisfies (2.1) in particular $K\in \mathcal {H}_{\infty }$
satisfies (2.1) in particular $K\in \mathcal {H}_{\infty }$![]() , and consequently, the preceding result recovers the main result in [Reference Riveros and de la Torre33].
, and consequently, the preceding result recovers the main result in [Reference Riveros and de la Torre33].
Proof of theorem 3.6 Observe that by the Cotlar type inequality in theorem A.1, we have that for any $\delta \in (0,1)$![]() .
.
and hence it suffices to deal with the first term. An analogous argument to the one provided to settle theorem 3.2, choosing a suitable $\delta$![]() , shows that
, shows that
and we are done.
3.2 The differential transform operator
Given $\{v_{j}\}\in \ell ^{\infty }$![]() we define
we define
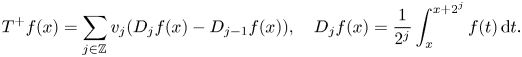
As the authors point out in [Reference Lorente, Martell, Riveros and de la Torre19] this operator, that was previously studied in [Reference Bernardis, Lorente, Martín-Reyes, Martínez, de la Torre and Torrea3, Reference Jones and Rosenblatt12], arises when studying the rate of convergence of the averages $D_{j}f$![]() . Note that $D_{j}f\rightarrow f$
. Note that $D_{j}f\rightarrow f$![]() a.e. when $j\rightarrow -\infty$
a.e. when $j\rightarrow -\infty$![]() and that $D_{j}f\rightarrow 0$
and that $D_{j}f\rightarrow 0$![]() when $j\rightarrow \infty$
when $j\rightarrow \infty$![]() for appropriate $f$
for appropriate $f$![]() .
.
Observe that $T^+$![]() is a one-sided singular integral since $T^+f=K*f$
is a one-sided singular integral since $T^+f=K*f$![]() for $K$
for $K$![]() supported on $(-\infty,0)$
supported on $(-\infty,0)$![]() and defined as
and defined as
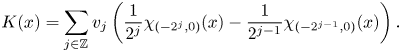
As it was stated in [Reference Lorente, Martell, Riveros and de la Torre19, remark 4.11], it is possible to show that $K\in \mathcal {H}_{A,k}$![]() with $A(t)=\exp \left (\frac {t^{\frac {1}{1+k}}}{(\log t)^{\frac {1+\varepsilon }{1+k}}}\right )$
with $A(t)=\exp \left (\frac {t^{\frac {1}{1+k}}}{(\log t)^{\frac {1+\varepsilon }{1+k}}}\right )$![]() , and hence by (3.4) we have that if $b\in BMO$
, and hence by (3.4) we have that if $b\in BMO$![]() and $k$
and $k$![]() is a non-negative integer, for $0<\delta <\gamma <1$
is a non-negative integer, for $0<\delta <\gamma <1$![]() ,
,

where the first term is interpreted as $0$![]() if $k=0$
if $k=0$![]() . Then, arguing as in the preceding section we have the following result.
. Then, arguing as in the preceding section we have the following result.
Theorem 3.7 Let $k$![]() be a non-negative integer. Then, if $0< p<\infty$
be a non-negative integer. Then, if $0< p<\infty$![]() , $\varepsilon >0$
, $\varepsilon >0$![]() and $w\in C_{\max \{p,1\}+\varepsilon }^+$
and $w\in C_{\max \{p,1\}+\varepsilon }^+$![]() , we have that
, we have that
3.3 The one-sided discrete square function and its commutator
We recall that the one-sided discrete square function is defined as follows. If $f$![]() is locally integrable in $\mathbb {R}$
is locally integrable in $\mathbb {R}$![]() and $s>0$
and $s>0$![]() we consider the averages
we consider the averages
Hence the one-sided discrete square function of $f$![]() is given by
is given by

This operator was studied in [Reference de la Torre and Torrea36] and [Reference Lorente, Riveros and de la Torre17]. In [Reference Lorente, Riveros and de la Torre18] the authors deal with the following operator

which dominates pointwise $S^+f$![]() , and show [Reference Lorente, Riveros and de la Torre18, Eq. (3.1) in p. 581] that if $0<\delta <1$
, and show [Reference Lorente, Riveros and de la Torre18, Eq. (3.1) in p. 581] that if $0<\delta <1$![]()
This fact allows them to settle the corresponding Coifman–Fefferman estimate. Here, arguing as we did to settle theorem 3.2, we have the following result.
Theorem 3.8 Let $0< p<\infty$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$
and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+.$![]() Then
Then
where $G$![]() stands either for $S^+$
stands either for $S^+$![]() or for $\mathcal {O}^+$
or for $\mathcal {O}^+$![]() .
.
Further assuming that $b\in BMO$![]() the authors also study the commutators associated to the operators above. In [Reference Lorente, Riveros and de la Torre18, lemma 4.6] it is shown that, for $0<\delta <\gamma <1$
the authors also study the commutators associated to the operators above. In [Reference Lorente, Riveros and de la Torre18, lemma 4.6] it is shown that, for $0<\delta <\gamma <1$![]() ,
,

As a consequence we can derive the following result.
Theorem 3.9 Let $0< p<\infty$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+$
and assume that $w\in C_{\max \{p,1\}+\varepsilon }^+$![]() and that $b\in BMO$
and that $b\in BMO$![]() . If $k$
. If $k$![]() is a positive integer, then
is a positive integer, then
where $G$![]() stands either for $S^+$
stands either for $S^+$![]() or for $\mathcal {O}^+$
or for $\mathcal {O}^+$![]() .
.
3.4 Riemann–Liouville and Weyl fractional integral operators and their commutators
We recall that given $0<\alpha <1$![]() and locally integrable functions $f$
and locally integrable functions $f$![]() and $b$
and $b$![]() , the Weyl fractional integral and its commutators are defined as
, the Weyl fractional integral and its commutators are defined as

respectively. Analogously we define the Riemann–Liouville fractional integral and its commutators as
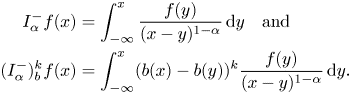
In [Reference Bernardis and Lorente2, lemma 4.1] it was shown that for every non-negative $k$![]() , if $b\in BMO$
, if $b\in BMO$![]() and $0<\delta <\gamma <1$
and $0<\delta <\gamma <1$![]() ,
,
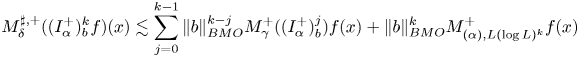
where
and the first term in the right-hand side is interpreted as $0$![]() if $k=0$
if $k=0$![]() . Relying upon that $M_{\delta }^{\sharp,+}$
. Relying upon that $M_{\delta }^{\sharp,+}$![]() estimate and arguing as in the proofs of theorems 3.2 and 3.3 it is possible to settle the following result.
estimate and arguing as in the proofs of theorems 3.2 and 3.3 it is possible to settle the following result.
Theorem 3.10 Let $k$![]() be a non-negative integer. Then, if $0< p<\infty$
be a non-negative integer. Then, if $0< p<\infty$![]() , $\varepsilon >0$
, $\varepsilon >0$![]() and $w\in C_{\max \{p,1\}+\varepsilon }^+$
and $w\in C_{\max \{p,1\}+\varepsilon }^+$![]() we have that
we have that
4. Proof of theorem 1.2
4.1 Sufficiency
By a standard approximation argument it is enough to settle the result assuming that $f\in L_{c}^{\infty }$![]() .
.
To settle the sufficiency part in theorem 1.2 we need to borrow two lemmas from [Reference Riveros and de la Torre33]. The first one is the following.
Lemma 4.1 [Reference Riveros and de la Torre33, lemma 1]
Assume that $w\in C_{q}^+$![]() with $1< q<\infty$
with $1< q<\infty$![]() . Then, for any $\delta >0$
. Then, for any $\delta >0$![]() there exists $c(\delta )$
there exists $c(\delta )$![]() such that for any disjoint family of intervals $J_{j}$
such that for any disjoint family of intervals $J_{j}$![]() contained in $I=(a,b)$
contained in $I=(a,b)$![]() we have that
we have that
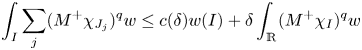
and
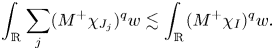
To state the next lemma we need to define a new operator, $M_{p,q}^+$![]() . Let $f$
. Let $f$![]() be an non-negative measurable function. Let us consider
be an non-negative measurable function. Let us consider
where $I_{i}^{k}$![]() are the connected components of $\Omega _{k}$
are the connected components of $\Omega _{k}$![]() . Then
. Then
Having this definition at our disposal we present the second lemma we borrow from [Reference Riveros and de la Torre33].
Lemma 4.2 [Reference Riveros and de la Torre33, lemma 2]
Let $1< p< q<\infty,$![]() $w\in C_{q}^+$
$w\in C_{q}^+$![]() and $f$
and $f$![]() non-negative, bounded and of compact support. Then
non-negative, bounded and of compact support. Then
Having those lemmas at our disposal we are in the position to settle theorem 1.2.
Proof of theorem 1.2 Let $\Omega _{k}=\{x\,:\,M^+f(x)>2\cdot 2^{k}\}=\bigcup _{j}J_{j}^{k}$![]() where $J_{j}^{k}$
where $J_{j}^{k}$![]() are the connected components of $\Omega _{k}$
are the connected components of $\Omega _{k}$![]() . Let us fix $(a,b)=J_{j}^{k}$
. Let us fix $(a,b)=J_{j}^{k}$![]() . We partition $(a,b)$
. We partition $(a,b)$![]() as follows. Let $x_{0}=a$
as follows. Let $x_{0}=a$![]() and choose $x_{i+1}$
and choose $x_{i+1}$![]() such that $x_{i+1}-x_{i}=b-x_{i+1}$
such that $x_{i+1}-x_{i}=b-x_{i+1}$![]() and let $I_{i}^{k}=(x_{i},x_{i+1})$
and let $I_{i}^{k}=(x_{i},x_{i+1})$![]() . By the good-$\lambda$
. By the good-$\lambda$![]() inequality established in [Reference Martín-Reyes and de la Torre27, theorem 4], we have that
inequality established in [Reference Martín-Reyes and de la Torre27, theorem 4], we have that
From the $C_{q}^+$![]() condition it follows that
condition it follows that
Summing on $i$![]() and taking into account lemma 4.1 we have that
and taking into account lemma 4.1 we have that

Now summing over all $j$![]() ,
,
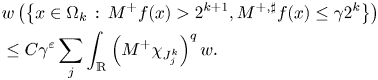
Having those estimates at our disposal we can argue as follows.
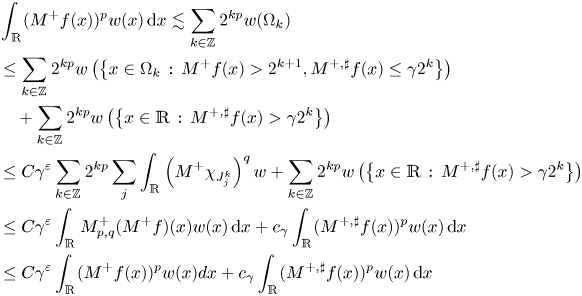
where in the last step we have used lemma 4.2.
Observe that if $\int _{\mathbb {R}}(M^+f(x)){}^{p}w(x)\,{\rm d}x<\infty$![]() , choosing $\gamma$
, choosing $\gamma$![]() small enough the desired estimate follows. We end the proof observing that for $f\in L_{c}^{\infty }$
small enough the desired estimate follows. We end the proof observing that for $f\in L_{c}^{\infty }$![]()
implies
Indeed, note that since $f\in L_{c}^{\infty }$![]() we may assume that $\operatorname {supp} f\subset [a,b]$
we may assume that $\operatorname {supp} f\subset [a,b]$![]() . For $x>b$
. For $x>b$![]() we have that $M^{+,\sharp }f(x)=M^+f(x)=0$
we have that $M^{+,\sharp }f(x)=M^+f(x)=0$![]() , and for $x\rightarrow -\infty$
, and for $x\rightarrow -\infty$![]() , $M^+f(x)\simeq M^{+,\sharp }f(x)\simeq \frac {1}{|x|}.$
, $M^+f(x)\simeq M^{+,\sharp }f(x)\simeq \frac {1}{|x|}.$![]()
4.2 Necessity
The proof of the necessity will rely upon the following lemma, which is a one-sided version of some of the results in [Reference Muckenhoupt30], namely theorem 4.1, lemma 5.1 and the proof of theorem 1.2 and of [Reference Sawyer34, lemma 1].
Lemma 4.3 If for every $a< b< c$![]() with $c-b< b-a$
with $c-b< b-a$![]() and $E\subset (a,b)$
and $E\subset (a,b)$![]()

then $w\in C_{p}^+$![]() .
.
Before settling the lemma we show how to derive from it the necessity in theorem 1.2.
Proof of the necessity in theorem 1.2 Assume that for a certain $1< p<\infty$![]() and a weight $w$
and a weight $w$![]() ,
,
Let $I=(a,c)$![]() an interval. Let $a< b< c$
an interval. Let $a< b< c$![]() . Assume that $E$
. Assume that $E$![]() is a measurable set contained in $(a,b)$
is a measurable set contained in $(a,b)$![]() . Let us define
. Let us define
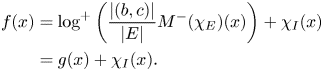
Analogously as in [Reference Sawyer34, theorem A] and [Reference Yabuta37] we have that
where $\|f\|_{BMO^+}=\|M^{\sharp,+}f\|_{L^{\infty }}$![]() . Note (4.4) readily follows from the definition of $f$
. Note (4.4) readily follows from the definition of $f$![]() . Assume by now that (4.2) and (4.3) hold as well. We shall show that this is the case at the end of this proof. We continue as follows.
. Assume by now that (4.2) and (4.3) hold as well. We shall show that this is the case at the end of this proof. We continue as follows.
Observe that $M^{-}(\chi _{E})\leq \frac {|E|}{\operatorname {dist}(x,E)}$![]() for $x\not \in E$
for $x\not \in E$![]() . In particular, if $x\geq c$
. In particular, if $x\geq c$![]() we have that
we have that
This yields $g(x)=0$![]() if $x\geq c$
if $x\geq c$![]() . On the other hand, if $x\leq a$
. On the other hand, if $x\leq a$![]() then also $M^{-}(\chi _{E})(x)=0$
then also $M^{-}(\chi _{E})(x)=0$![]() . And consequently $g(x)=0$
. And consequently $g(x)=0$![]() . Hence $\operatorname {supp} f\subset (a,c)$
. Hence $\operatorname {supp} f\subset (a,c)$![]() . Now we observe that if $x>c$
. Now we observe that if $x>c$![]() we have that $M^+f(x)=0$
we have that $M^+f(x)=0$![]() and $M^{\sharp,+}f(x)=0$
and $M^{\sharp,+}f(x)=0$![]() . If $x< c$
. If $x< c$![]() we have two cases. If $x\in (a-|I|,c)$
we have two cases. If $x\in (a-|I|,c)$![]() then, by (4.3)
then, by (4.3)
If $x< a-|I|$![]() then $M^+\chi _{(a,c)}(x)=\frac {c-a}{c-x}$
then $M^+\chi _{(a,c)}(x)=\frac {c-a}{c-x}$![]() and $c-x\geq 2|I|$
and $c-x\geq 2|I|$![]() , from which it follows that $a-x=c-x-|I|\geq \frac {c-x}{2}$
, from which it follows that $a-x=c-x-|I|\geq \frac {c-x}{2}$![]() . Hence, we have that by (4.2)
. Hence, we have that by (4.2)
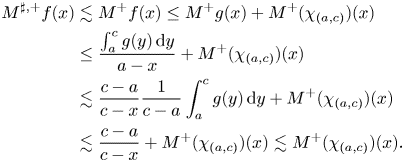
Gathering the estimates above we have that
Taking into account the preceding estimate and (4.4), we have that

and we are done.
As we mentioned above, we are left with settling (4.2) and (4.3).
To establish (4.2), note that
where $F=\left \{ \frac {|(b,c)|}{|E|}M^{-}(\chi _{E})\geq 1\right \} .$![]() If $|(a,c)\cap F|=0$
If $|(a,c)\cap F|=0$![]() then there is nothing to show. Hence we may assume that $|(a,c)\cap F|\not =0$
then there is nothing to show. Hence we may assume that $|(a,c)\cap F|\not =0$![]() . Taking that into account we argue as follows. Let $\delta \in (0,1)$
. Taking that into account we argue as follows. Let $\delta \in (0,1)$![]() . Then
. Then
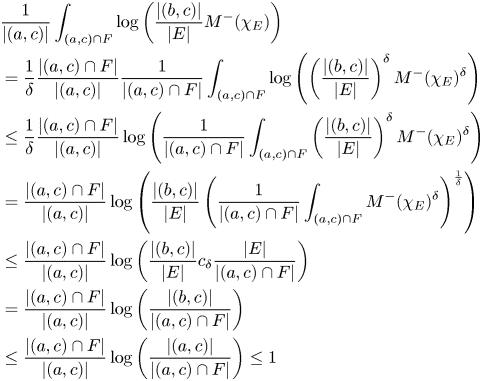
where in the third line we used Jensen's inequality, in the fifth Kolmogorov's inequality and in the last one that $\log (t)\leq t$![]() for every $t\geq 1$
for every $t\geq 1$![]() .
.
Now we focus on (4.3). First we observe that
so it suffices to provide a bound for $\|g\|_{BMO^+}$![]() . It is not hard to check that
. It is not hard to check that
Hence
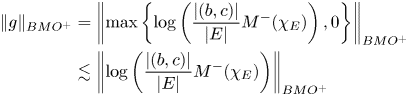
Now we observe that
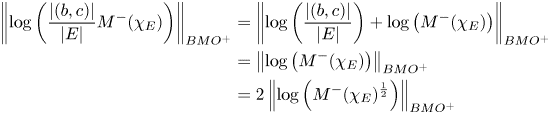
and since for every $\delta \in (0,1)$![]() we have that $M^{-}(\chi _{E})(\cdot )^{\delta }\in A_{1}^+$
we have that $M^{-}(\chi _{E})(\cdot )^{\delta }\in A_{1}^+$![]() with constant depending just on $\delta$
with constant depending just on $\delta$![]() , then using results in [Reference Martín-Reyes and de la Torre27, § 2],
, then using results in [Reference Martín-Reyes and de la Torre27, § 2],
Combining the estimates above yields (4.3). This ends the proof.
We devote the remainder of the section to settle lemma 4.3. First we will need the following lemma.
Lemma 4.4 Let $1< p<\infty$![]() . Assume that $w$
. Assume that $w$![]() is a weight such that
is a weight such that
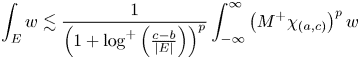
for every $a< b< c$![]() with $c-b< b-a$
with $c-b< b-a$![]() and where $E$
and where $E$![]() is any measurable set contained in $(a,b)$
is any measurable set contained in $(a,b)$![]() . Then, for every family $\{I_{k}\}_{k=1}^{n}$
. Then, for every family $\{I_{k}\}_{k=1}^{n}$![]() of disjoint subintervals of an interval $I$
of disjoint subintervals of an interval $I$![]() , if we denote
, if we denote
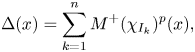
then
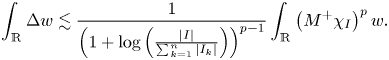
Proof. Let $I=(a,c)$![]() be an interval and $\{I_{k}\}$
be an interval and $\{I_{k}\}$![]() a family of disjoint subintervals of $I$
a family of disjoint subintervals of $I$![]() . First we note that
. First we note that
for each $x>c$![]() . Then we have that
. Then we have that

where $a'=a-|I|$![]() . First we deal with the second term. Observe that if $d_{k}$
. First we deal with the second term. Observe that if $d_{k}$![]() is the right endpoint of $I_{k}$
is the right endpoint of $I_{k}$![]() , then
, then
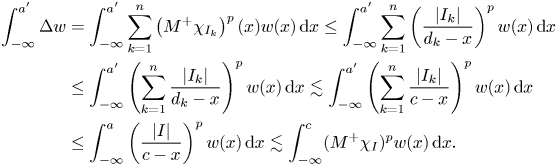
Now we deal with the first term. Let $j$![]() be the least integer such that
be the least integer such that
and $J$![]() the least integer such that for some $D\in (0,1)$
the least integer such that for some $D\in (0,1)$![]() to be chosen later,
to be chosen later,
Note that since $j\leq 0$![]() and $J>0$
and $J>0$![]() we have that $j< J$
we have that $j< J$![]() . Let
. Let

For $Q$![]() we have that
we have that
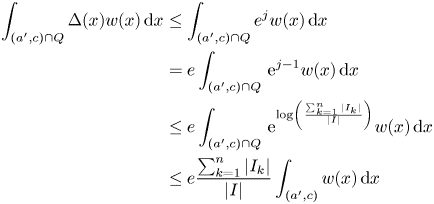
and the right-hand side is bounded by the right-hand side of (4.5). We continue with $S$![]() .
.
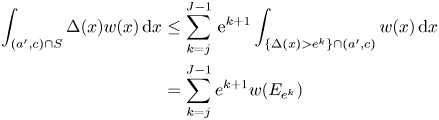
where
To continue with the argument, we borrow ideas from [Reference Riveros and de la Torre33, p. 406]. We begin noting that there exists $B>1$![]() and that we can choose the $D\in (0,1)$
and that we can choose the $D\in (0,1)$![]() above in such a way that
above in such a way that
At this point we use our hypothesis on the weight $w$![]() . For that purpose we split $(a',c)$
. For that purpose we split $(a',c)$![]() as follows. Let $x_{0}=a'$
as follows. Let $x_{0}=a'$![]() and let us define recursively $x_{i}-x_{i-1}=c-x_{i}$
and let us define recursively $x_{i}-x_{i-1}=c-x_{i}$![]() . Associated to the collection of intervals $(x_{i},x_{i+1})$
. Associated to the collection of intervals $(x_{i},x_{i+1})$![]() we consider the sets
we consider the sets
Observe that for each $i$![]() we may assume that the elements that we consider in the sum $\Delta (x)$
we may assume that the elements that we consider in the sum $\Delta (x)$![]() are contained in $(x_{i},c)$
are contained in $(x_{i},c)$![]() (the remaining terms are zero). Hence we have that
(the remaining terms are zero). Hence we have that
Now we use the hypothesis for $x_{i}$![]() , $x_{i+1}$
, $x_{i+1}$![]() , $x_{i+2}$
, $x_{i+2}$![]() and we have that
and we have that
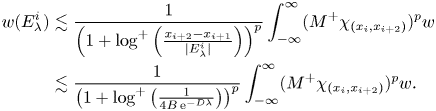
Summing in $i$![]() we have that it follows from the definition of the partition $x_{i}$
we have that it follows from the definition of the partition $x_{i}$![]() , which leads to a geometric series, that
, which leads to a geometric series, that
Hence,
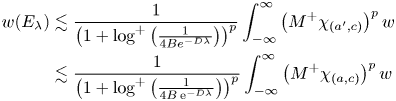
and we have that
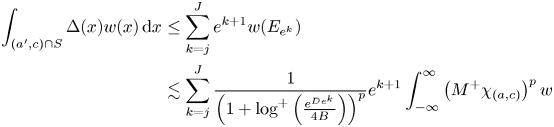
and it suffices to estimate the sum. We proceed as follows.

and again this term is bounded by the right-hand side of (4.5).
Finally, for $T$![]() we have that
we have that
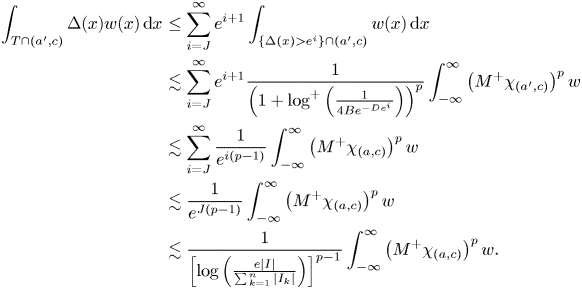
Armed with the preceding lemma we can finally settle lemma 4.3.
Proof of lemma 4.3 Let $I=(a,c)$![]() be an interval. Let $\delta >0$
be an interval. Let $\delta >0$![]() such that if $\sum |I_{k}|\leq 2\delta |I|$
such that if $\sum |I_{k}|\leq 2\delta |I|$![]() then
then
Now assume that $a< b< c$![]() where $c-b< b-a$
where $c-b< b-a$![]() and let $E\subset (a,b)$
and let $E\subset (a,b)$![]() be a measurable set. Let $n$
be a measurable set. Let $n$![]() be the least integer such that $\delta ^{n}|(a,b)|<|E|.$
be the least integer such that $\delta ^{n}|(a,b)|<|E|.$![]() Now we let $E_{j}= \{x\,:M^+(\chi _{E})(x)>\delta ^{j}\}$
Now we let $E_{j}= \{x\,:M^+(\chi _{E})(x)>\delta ^{j}\}$![]() for $1\leq j\leq n$
for $1\leq j\leq n$![]() . Let $J_{i}^{j}$
. Let $J_{i}^{j}$![]() be the component intervals of $E_{j}$
be the component intervals of $E_{j}$![]() and $\Delta _{j}(x)=\sum _{i}M^+(\chi _{J_{i}^{j}})(x){}^{p}$
and $\Delta _{j}(x)=\sum _{i}M^+(\chi _{J_{i}^{j}})(x){}^{p}$![]() . We claim that for $2\leq j\leq n$
. We claim that for $2\leq j\leq n$![]()
Assume by now that the claim holds. Note that since $ {\chi _{E}(x)\leq \Delta _{1}(x)}$![]() then
then
and iterating the preceding inequality,
and consequently
Note that by the definition of $n$![]() , and taking into account that $b-c< b-a$
, and taking into account that $b-c< b-a$![]() ,
,
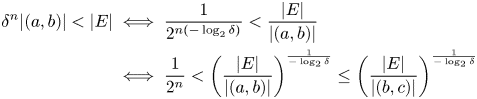
so if we can show that
then

and we would be done.
Let us settle (4.7). Observe that since
we have that $a\in J_{i}^{n}$![]() for some component $J_{i}^{n}$
for some component $J_{i}^{n}$![]() of $E_{n}$
of $E_{n}$![]() . Let us call $J_{i}^{n}=(a',b')$
. Let us call $J_{i}^{n}=(a',b')$![]() . Observe that since $a\in J_{i}^{n}$
. Observe that since $a\in J_{i}^{n}$![]() then $a'< a$
then $a'< a$![]() . Observe that $M^+\chi _{E}(a')=\delta ^{n}$
. Observe that $M^+\chi _{E}(a')=\delta ^{n}$![]() and since $(a',b')$
and since $(a',b')$![]() is a component, for some $\varepsilon >0$
is a component, for some $\varepsilon >0$![]() , we have that if $x\in [a'-\varepsilon,a')$
, we have that if $x\in [a'-\varepsilon,a')$![]() , then $M^+\chi _{E}(x)\leq \delta ^{n}.$
, then $M^+\chi _{E}(x)\leq \delta ^{n}.$![]() Note that since $E\subset (a,b)$
Note that since $E\subset (a,b)$![]() and $a>a'$
and $a>a'$![]() this yields that for every $x< a'-\varepsilon$
this yields that for every $x< a'-\varepsilon$![]()
This yields that all the connected components are contained in the interval $(a',b''),$![]() for some $b''\leq b$
for some $b''\leq b$![]() , since $M^+\chi _{E}(x)=0$
, since $M^+\chi _{E}(x)=0$![]() for every $x>b$
for every $x>b$![]() . Now, that by the weak type $(1,1)$
. Now, that by the weak type $(1,1)$![]() of $M^+$
of $M^+$![]() , combined with the definition of $n$
, combined with the definition of $n$![]() ,
,

Observe that since $(a',b')$![]() is some component $J_{i}^{n}$
is some component $J_{i}^{n}$![]() in $E_{n}$
in $E_{n}$![]() then
then
Consequently
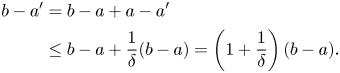
Since all the intervals $J_{i}^{n}$![]() are contained in $(a',b)$
are contained in $(a',b)$![]() , by (4.5) we have that
, by (4.5) we have that

We end the proof of (4.7) just noting that
since taking into account that $|(a'',b)|\leq \frac {1}{\delta }(\frac {1}{\delta }+1)|(a,b)|$![]() yields that $M^+(\chi _{(a'',b)})\simeq M^+(\chi _{(a,b)})$
yields that $M^+(\chi _{(a'',b)})\simeq M^+(\chi _{(a,b)})$![]() .
.
Since as we have just shown (4.7) holds, we are left with settling the claim. We argue as follows. Let $H$![]() be a component of $E_{j}$
be a component of $E_{j}$![]() . Note that, since $H$
. Note that, since $H$![]() is a component
is a component
Our next step is to show that
First, we observe that the components of $E_{j-1}$![]() are contained in the components of $E_{j}$
are contained in the components of $E_{j}$![]() . Hence
. Hence
where the $I_{k}^{j-1}$![]() are the components of $E_{j-1}$
are the components of $E_{j-1}$![]() contained in $H$
contained in $H$![]() . Then we have that if $x\in H\cap E_{j-1}$
. Then we have that if $x\in H\cap E_{j-1}$![]() then $x\in I_{k}^{j-1}=(\alpha,\beta )$
then $x\in I_{k}^{j-1}=(\alpha,\beta )$![]() for some $k$
for some $k$![]() . Since $x\in E_{j-1}$
. Since $x\in E_{j-1}$![]() , then $M^+(\chi _{E})(x)>\delta ^{j-1}$
, then $M^+(\chi _{E})(x)>\delta ^{j-1}$![]() and
and
Observe that $(x,\beta )\subset I_{k}^{j-1}\subset H$![]() , so
, so
Consequently
and this yields $\{M^+\chi _{H\cap E}>\delta ^{j-1}\}\supset H\cap E_{j-1}$![]() .
.
Now we prove the converse inclusion. Observe that if $M^+\chi _{H\cap E}(x)>\delta ^{j-1}$![]() then
then
and consequently $x\in E_{j-1}$![]() . Now we have to see that $x\in H$
. Now we have to see that $x\in H$![]() . Let us call $H=(d,e)$
. Let us call $H=(d,e)$![]() . Observe that $M^+\chi _{H\cap E}(x)=0$
. Observe that $M^+\chi _{H\cap E}(x)=0$![]() for every $x>e$
for every $x>e$![]() , and hence $x\not \in \{M^+\chi _{H\cap E}>\delta ^{j-1}\}$
, and hence $x\not \in \{M^+\chi _{H\cap E}>\delta ^{j-1}\}$![]() . On the other hand, observe that since $H$
. On the other hand, observe that since $H$![]() is a component of $E_{j}$
is a component of $E_{j}$![]() there exist some $\varepsilon <0$
there exist some $\varepsilon <0$![]() such that if $x\in [d-\varepsilon,d]$
such that if $x\in [d-\varepsilon,d]$![]() then $M^+\chi _{E}(x)\leq \delta ^{j}$
then $M^+\chi _{E}(x)\leq \delta ^{j}$![]() . Relying upon this fact, note that if $x< d$
. Relying upon this fact, note that if $x< d$![]() then we have that if $x\in [d-\varepsilon,d]$
then we have that if $x\in [d-\varepsilon,d]$![]() , then $M^+\chi _{H\cap E}(x)\leq M^+\chi _{E}(x)\leq \delta ^{j}$
, then $M^+\chi _{H\cap E}(x)\leq M^+\chi _{E}(x)\leq \delta ^{j}$![]() and consequently $x\not \in \{M^+\chi _{H\cap E}>\delta ^{j-1}\}$
and consequently $x\not \in \{M^+\chi _{H\cap E}>\delta ^{j-1}\}$![]() and if $x< d-\varepsilon$
and if $x< d-\varepsilon$![]() then, $M^+\chi _{H\cap E}(x)\leq M^+\chi _{H\cap E}(d-\varepsilon )\leq \delta ^{j}$
then, $M^+\chi _{H\cap E}(x)\leq M^+\chi _{H\cap E}(d-\varepsilon )\leq \delta ^{j}$![]() and also $x\not \in \{M^+\chi _{H\cap E}>\delta ^{j-1}\}$
and also $x\not \in \{M^+\chi _{H\cap E}>\delta ^{j-1}\}$![]() . Hence
. Hence
and we are done.
The weak type $(1,1)$![]() of $M^+$
of $M^+$![]() combined with (4.9) yields
combined with (4.9) yields
and combining this with (4.8) we have that
If we denote
where $\mathcal {H}$![]() is the set of component intervals in $H\cap E_{j-1}$
is the set of component intervals in $H\cap E_{j-1}$![]() , we have that
, we have that
By the definition of $\delta$![]() and (4.6) we have that
and (4.6) we have that
Adding those inequalities for all the components $H$![]() of $E_{j}$
of $E_{j}$![]() gives
gives
for $2\leq j\leq n$![]() as we wanted to show. This ends the proof of the theorem.
as we wanted to show. This ends the proof of the theorem.
Acknowledgments
The authors would like to thank the anonymous referee for suggestions that helped us making this paper easier to read. The first and the second authors were partially supported by Ministerio de Economía y Competitividad, Spain, grant PGC2018-096166-B-I00. The third author was supported as well by Agencia I+D+i grants PICT 2018-02501 and PICT 2019-00018. All the authors were partially supported by Junta de Andalucía UMA18-FEDERJA-002 and by grant FQM-354. Funding for open access charge: Universidad de Málaga.
Appendix A. Cotlar type inequalities
Since we have not been able to find the following Cotlar type inequality in the one-sided setting in the literature, we provide here a proof for reader's convenience.
Theorem A.1 Let $A$![]() be a Young function. Let $T^+$
be a Young function. Let $T^+$![]() be a one-sided singular integral operator with associated kernel $K\in \mathcal {H}_{\bar {A}}$
be a one-sided singular integral operator with associated kernel $K\in \mathcal {H}_{\bar {A}}$![]() . Then
. Then
Observe that if $T^+$![]() is a one-sided Calderón–Zygmund operator its associated kernel is in particular a $\mathcal {H}_{\infty }$
is a one-sided Calderón–Zygmund operator its associated kernel is in particular a $\mathcal {H}_{\infty }$![]() kernel and hence this result covers that case, with $M_{A}^+$
kernel and hence this result covers that case, with $M_{A}^+$![]() replaced by $M^+$
replaced by $M^+$![]() .
.
Proof of theorem A.1 Observe that it suffices to show that for every $\varepsilon >0$![]()
where
Observe that for $x>0$![]() we can write
we can write
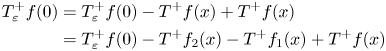
where $f_{1}(x)=f(x)\chi _{(0,\varepsilon )}(x)$![]() and $f_{2}(x)=f(x)\chi _{(\varepsilon,\infty )}(x)$
and $f_{2}(x)=f(x)\chi _{(\varepsilon,\infty )}(x)$![]() . Then we have that
. Then we have that
and $\delta$![]() -averaging over $x$
-averaging over $x$![]() , if we call $h=\frac {\varepsilon }{2c_{A}}$
, if we call $h=\frac {\varepsilon }{2c_{A}}$![]()

For $I$![]() , we observe that any Hörmander condition implies that $K\in \mathcal {H}_{1}$
, we observe that any Hörmander condition implies that $K\in \mathcal {H}_{1}$![]() and hence by [Reference Grafakos8], we have that $T^+$
and hence by [Reference Grafakos8], we have that $T^+$![]() is of weak type $(1,1)$
is of weak type $(1,1)$![]() . Then, by Kolmogorov inequality,
. Then, by Kolmogorov inequality,
For $II$![]()
and it remains to deal with $III.$![]() Observe that for $x\in \left (0,\frac {\varepsilon }{2c_{A}}\right )$
Observe that for $x\in \left (0,\frac {\varepsilon }{2c_{A}}\right )$![]()
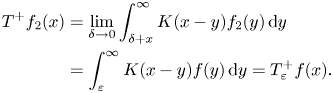
Bearing that in mind and since for every $x\in \left (0,\frac {\varepsilon }{2c_{A}}\right )$![]() we have that $x<\frac {\varepsilon }{2c_{A}}$
we have that $x<\frac {\varepsilon }{2c_{A}}$![]() or equivalently $xc_{A}<\frac {\varepsilon }{2}$
or equivalently $xc_{A}<\frac {\varepsilon }{2}$![]() , we have that
, we have that
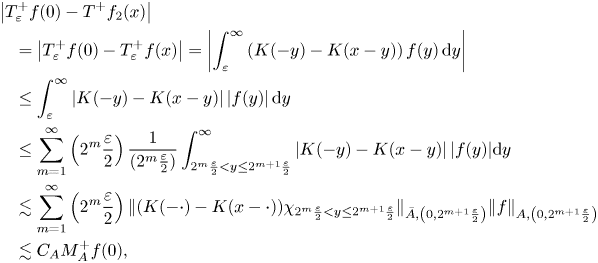
and consequently
This ends the proof.