H1. Equip ℝ3 with the group law

(1.1)

where (z, t) stands for (x, y, t). This is a nilpotent Lie group, usually referred to as the first Heisenberg group, H1. In general Hk denotes ℝ2k+1 equipped with a similar group law, namely

The existence of a first countable Lindelöf extension L of an uncountable discrete space D for which L-D is countable is considered. Assuming CH, such extensions exist; however it is also consistent that no such spaces exist, as follows from MA + ¬ CH

It is shown that if V=C(X) or V = L1(μ) then the subspace of compact (resp. weakly compact) operators from V into itself is not an M-ideal in the space of bounded operators. This is the contrary to what happens when V= Co(ℕ) or lp(ℕ). The main result is proved via the best approximation properties of M-ideals and some results concerning norm one projections in C(X) and L1(μ) are deduced from this fact.

Let Z be the additive group of integer numbers with discrete topology, the space of complex-valued integrable functions on Z with respect to normalized Haar measure, the space of bounded functions on Z.

In a paper by Wilansky and the writer [4] there were five questions left open, four of which have been answered by Beekman and the writer, [1], [3]. We shall consider the fifth one, namely, “If , must 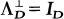for every matrix D with cD = cA?” Here A is a conservative summability matrix with column limits .

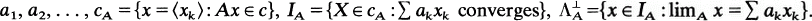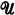Let be a small -category where is a fixed Grothendieck universe, i.e., the objects of 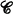form a set which is a subset of 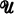and, for every pair of objects 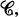X, Y of the set 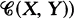is an element of . If S is a set of morphisms of , then, in general, the category of fractions [S- 1] would belong to a higher universe ([4], p. 256).

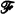A family of sets is said to have property 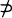B if there exists a set S such that S∩F≠ ϕ and SF for all F 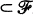. S is called a 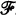B-set for . Let n≥2 and N≥2n-1. Let V = { 1, 2,≠, N} and let 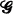= {G:G⊂ V, |G| = rc}. Erdös [3] defined m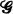N(n) to be the size of a smallest subfamily of which does not have property B and proved the following results:

Let C(X) be the ring of continuous real-valued functions on a (completely regular) topological space X. The structure of the prime ideals and the prime z-ideals of C(X) has been the subject of much investigation (see e-g- [1], [3], [5]). One of the surprising facts about C(X) is that the sum of two prime ideals is again prime.

If R is a ring such that x, y ∈ R and xy = 0 imply yx = 0 and G≠ 1, an ordered group, then we show that ∑ αgg is a unit in RG if and only if there exists ∑ βhh in RG such that ∑ αgβg-1 = 1 and αgβh is nilpotent whenever gh≠l. We also show that if R is a ring with no nilpotent elements ≠ 0 and no idempotents ≠ 0, 1 then RG has only trivial units. Some applications are also given.

This note continues the investigation of those rings R with unity which also satisfy the polynomial identity B(x, y) = (xy)n -xyn -xny +xy = 0, for some integer n > l. It is shown that when n is an even integer, or when n = 3, such rings are commutative. It is otherwise possible, as is shown by example, for such rings to fail to be commutative, although they are subdirect sums of local rings satisfying the polynomial identity. Each such ring has nilpotent commutator ideal.

A space Z is said to have the complete invariance property (CIP) provided that every nonempty closed subset of Z is the fixed point set of some continuous self-mapping of Z. In this paper it is shown that there exists a one-dimensional contractible planar continuum having CIP whose wedge with itself at a specified point is contractible, planar, and does not have CIP.

The classical rings of number theory, Dedekind domains, are characterized by the property that every ideal is a product of prime ideals. More generally, a commutative ring R with identity has the property that every ideal is a product of prime ideals if and only if R is a finite direct sum of Dedekind domains and special principal ideal rings. These rings, called general Z.P.I. rings, are also characterized by the property that every (prime) ideal is finitely generated and locally principal.

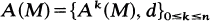Let X denote a non-vanishing infinitesimal isometry on a compact Riemannian manifold Mn. Let denote the deRham complex of M. We write i(X) for the operator of interior product, and L(X) the Lie derivative on the elements of A(M). We define E(M) = {u ∈ A(M)| i(X)u = 0, L(X)u= 0}.

It is shown that the boundary of the set of accumulation points of a metrizable space X is compact iff X has a compatible metric d such that d(A, B)>0 whenever A and B are disjoint closed subsets of X, each of which is disjoint from the set of accumulation points.

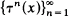Let τ be a transformation from a compact metric space X into itself. Conditions are presented which ensure that there exists an orbit which is dense in X. An example is given.

Let R be an associative ring and f(x1,…, xd) a polynomial in noncommuting variables. We say that f is periodic or nil in R if for all r1,…, rd ∈ R we have that f(r1,…, rd) is periodic, respectively nilpotent (recall that a ∈ R is periodic if for some integer ).

In this paper, it is proved that a reduced ring R has an orthogonal completion if and only if for every idempotent e e R, eR has an orthogonal completion. Every orthogonal subset X of R has a supremum in Q max(R), the maximal two sided ring of quotients of R, and the orthogonal completion of a reduced ring R, if it exists, is isomorphic to a unique subring of Q max(R). Hence the orthogonal completion of a reduced ring R, if it exists, is unique upto isomorphism. A reduced ring R has an orthogonal completion if and only if the collection of those elements of Q max(R) which are supremums of orthogonal subsets of R form a subring of Q max(R). 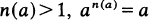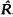Furthermore, every projectable ring R has an orthogonal completion , which is a Baer ring. It is also proved that 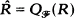for projectable rings 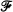R, where is the idempotent filter of those dense right ideals of R which contain a maximal orthogonal subset of idempotents of R.

Van der Waerden [1, 4, 5] proved that if the nonnegative integers are partitioned into a finite number of sets, then at least one set in the partition contains arbitrarily long finite arithmetic progressions. This is equivalent to the result that a strictly increasing sequence of integers with bounded gaps contains arbitrarily long finite arithmetic progressions. Szemerèdi [3] proved the much deeper result that a sequence of integers of positive density contains arbitrarily long finite arithmetic progressions. The purpose of this note is a quantitative comparison of van der Waerden's theorem and sequences with bounded gaps.

We give a simple proof of a theorem by Andrunakievič and Rjabuhin which states that a reduced ring is a subdirect product of entire rings. Our proof makes no use of m-systems and is in some sense similar to the proof of the corresponding theorem in the commutative case due to Krull.

A reduced ring is a ring without non-zero nilpotent elements. It is wellknown that if a reduced ring is commutative, then it is a subdirect product of integral domains [2]. This result has been generalized to arbitrary reduced rings [1]. The proof in the general case is somewhat complicated. We present a simple proposition which leads to a simple proof of the general case.

An example is given of a topological space that does not admit a strongly complete quasi-uniform structure.