Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T11:10:15.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitesimal Isometries on Compact Manifolds

Published online by Cambridge University Press:  20 November 2018

Chao-Chu Liang
Chao-Chu Liang*
Affiliation:
Department of Mathematics, University of Kansas, Lawrence, Kansas 66045.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X denote a non-vanishing infinitesimal isometry on a compact Riemannian manifold Mn. Let 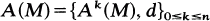denote the deRham complex of M. We write i(X) for the operator of interior product, and L(X) the Lie derivative on the elements of A(M). We define E(M) = {u ∈ A(M)| i(X)u = 0, L(X)u= 0}.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 4 , 01 December 1980 , pp. 461 - 464
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Borel, A., Seminar on transformation groups. Ann. of Math. Studies #46. Princeton Univ. Press 1960.Google Scholar
2. Bredon, G., Introduction to compact transformation groups. Academic Press, New York 1972.Google Scholar
3. Connor, P. E. and Floyd, E. E., Orbit spaces of circle groups of transformation. Ann. of Math. 67 (1958), 90-98.Google Scholar
4. Dold, A., Lectures on algebraic topology. Springer-Verlag, New York-Heidelberg-Berlin 1972.Google Scholar
5. Greub, W., Halperin, S., and Vanstone, R., Connections, curvature, and cohomology. Vol II, Academic Press, New York-London 1973.Google Scholar
6. Illman, S., Smooth equivariant triangulation of G-manifolds for G a finite group. Math. Ann. 233 (1978), 199-220.Google Scholar
7. Liang, C. C., Vector fields on V-manifolds, and locally free G x ^-actions on manifolds. Indiana Univ. Math. J. 27 (1978), 349-352.Google Scholar
8. Liang, C. C., Vector fields orthogonal to a non-vanishing infinitesimal isometry. Proc. Amer. Math. Soc. 75 (1979), 145-148.Google Scholar