Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Vries, Hans Ludwig
1984.
Historical notes on steiner systems.
Discrete Mathematics,
Vol. 52,
Issue. 2-3,
p.
293.
Abbott, H. L.
and
Hare, D. R.
1989.
Sparse color-critical hypergraphs.
Combinatorica,
Vol. 9,
Issue. 3,
p.
233.
Rozovskaya, A. P.
Titova, M. V.
and
Shabanov, D. A.
2010.
On balanced colorings of hypergraphs.
Journal of Mathematical Sciences,
Vol. 169,
Issue. 5,
p.
654.
Райгородский, Андрей Михайлович
Raigorodskii, Andrei Mikhailovich
Райгородский, Андрей Михайлович
Raigorodskii, Andrei Mikhailovich
Шабанов, Дмитрий Александрович
Shabanov, Dmitrii Aleksandrovich
Шабанов, Дмитрий Александрович
and
Shabanov, Dmitrii Aleksandrovich
2011.
Задача Эрдеша - Хайнала о раскрасках гиперграфов, ее обобщения и смежные проблемы.
Успехи математических наук,
Vol. 66,
Issue. 5,
p.
109.
Östergård, Patric R.J.
2014.
On the minimum size of 4-uniform hypergraphs without propertyB.
Discrete Applied Mathematics,
Vol. 163,
Issue. ,
p.
199.
Kazimierz Lewkowicz, Marek
2015.
Coloring Four-uniform Hypergraphs on Nine Vertices.
Canadian Mathematical Bulletin,
Vol. 58,
Issue. 2,
p.
317.


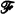 of sets is said to have property
of sets is said to have property 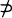 F for all F
F for all F 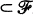 . S is called a
. S is called a 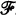 . Let n≥2 and N≥2n-1. Let V = { 1, 2,≠, N} and let
. Let n≥2 and N≥2n-1. Let V = { 1, 2,≠, N} and let 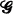 = {G:G⊂ V, |G| = rc}. Erdös [3] defined m
= {G:G⊂ V, |G| = rc}. Erdös [3] defined m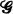 which does not have property
which does not have property 