Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T03:12:34.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthogonal Completions of Reduced Rings with Respect to Abian Order

Published online by Cambridge University Press:  20 November 2018

R. K. Rai
R. K. Rai*
Affiliation:
Department of Mathematics, Dalhousie University, Halifax, N.S.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, it is proved that a reduced ring R has an orthogonal completion if and only if for every idempotent e e R, eR has an orthogonal completion. Every orthogonal subset X of R has a supremum in Q max(R), the maximal two sided ring of quotients of R, and the orthogonal completion of a reduced ring R, if it exists, is isomorphic to a unique subring of Q max(R). Hence the orthogonal completion of a reduced ring R, if it exists, is unique upto isomorphism. A reduced ring R has an orthogonal completion if and only if the collection of those elements of Q max(R) which are supremums of orthogonal subsets of R form a subring of Q max(R). Furthermore, every projectable ring R has an orthogonal completion 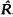, which is a Baer ring. It is also proved that 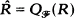for projectable rings R, where 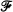is the idempotent filter of those dense right ideals of R which contain a maximal orthogonal subset of idempotents of R.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 4 , 01 December 1980 , pp. 477 - 489
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Abian, A., Rings without nilpotent elements, Mat. Cas. 25, 1975, No. 3, 289-291.Google Scholar
2. Direct product decomposition of commutative semi-simple rings, Proc. Amer. Math. Soc, 24 (1970), 502-507.Google Scholar
3. Direct sum decomposition of atomic and orthogonally complete rings, J. Austral. Math. Soc, 11 (1970), 357-361.Google Scholar
4. Order in a special class of rings and a structure theorem, Proc. Amer. Math. Soc, 52 (1975), 45-49.Google Scholar
5. Andrunakievic, V. A., and Rjabuhin, J. M., Rings without nilpotent elements and completely simple ideals, Dokl. Akad. Nauk SSSR, 180 (1968), 9-11.Google Scholar
6. Burgess, W. D., and Raphael, R., Abian's order relation and orthogonal completions for reduced rings, Pac J. Math., 54-1 (1974), 55-63.Google Scholar
7. Complete and orthogonally complete rings, Canad. J. Math., 27-4 (1975), 884-892.Google Scholar
8. Chacron, M., Direct product of division rings and a paper of Abian, Proc Amer. Math. Soc, 24 (1970), 502-507.Google Scholar
9. Cornish, W. H., and Stewart, P. N., Weakly regular algebras, Boolean orthogonalities and direct product of integral domains, Canad. J. Math., 28 (1976), 148-153.Google Scholar
10. Faith, C., Lectures on injective modules and quotient rings, Lecture notes in Math., Springer- Verlag, 149 (1967).Google Scholar
11. Keimel, K., The representation of lattice ordered groups and rings by sections in sheaves, Lecture notes in Math., Springer-Verlag, 248 (1970).Google Scholar
12. Koh, K., On the functional representation of a ring without a nilpotent element, Can. Math. Bui. 14 (1971), 349-352.Google Scholar
13. Lambek, , Lectures on Rings and Modules, Chelsea Publ. Co., New-York, N.Y., (1976).Google Scholar
14. Torsion theories, Additive semantics and rings of quotients, Lecture notes in Math., Springer-Verlag, 177 (1971).Google Scholar
15. Raphael, R., and Stephenson, W., Orthogonally complete rings, Can. Math. Bui., 20 (3) (1977), 347-351.Google Scholar
16. Schelter, W., Two sided ring of quotients, Archiv der Mathematic, 24 (1973), 274-277.Google Scholar
17. Steinberg, S. A., Rings of quotients of rings without nilpotent elements, Pac J. Math., 49-2 (1973), 493-506.Google Scholar
18. Stenstrom, B., Ring of quotients, Springer-Verlag, New-York, N.Y., (1975).Google Scholar
19. Utumi, Y., On rings of which any one sided quotient rings are two sided, Proc, Amer. Math. Soc, 14 (1963), 141-147.Google Scholar
20. Wong, E. T., and Johnson, R. E., Self injective rings, Can. Math. Bui., 2 (3) (1959), 167-173.Google Scholar