Let 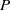 $P$ and
$P$ and 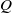 $Q$ be non-zero integers. The generalized Fibonacci sequence
$Q$ be non-zero integers. The generalized Fibonacci sequence 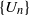 $\{ {U}_{n} \} $ and Lucas sequence
$\{ {U}_{n} \} $ and Lucas sequence 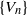 $\{ {V}_{n} \} $ are defined by
$\{ {V}_{n} \} $ are defined by 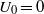 ${U}_{0} = 0$,
${U}_{0} = 0$, 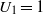 ${U}_{1} = 1$ and
${U}_{1} = 1$ and 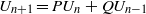 ${U}_{n+ 1} = P{U}_{n} + Q{U}_{n- 1} $ for
${U}_{n+ 1} = P{U}_{n} + Q{U}_{n- 1} $ for 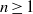 $n\geq 1$ and
$n\geq 1$ and 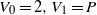 ${V}_{0} = 2, {V}_{1} = P$ and
${V}_{0} = 2, {V}_{1} = P$ and 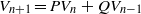 ${V}_{n+ 1} = P{V}_{n} + Q{V}_{n- 1} $ for
${V}_{n+ 1} = P{V}_{n} + Q{V}_{n- 1} $ for 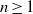 $n\geq 1$, respectively. In this paper, we assume that
$n\geq 1$, respectively. In this paper, we assume that 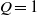 $Q= 1$. Firstly, we determine indices
$Q= 1$. Firstly, we determine indices  $n$ such that
$n$ such that 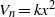 ${V}_{n} = k{x}^{2} $ when
${V}_{n} = k{x}^{2} $ when 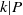 $k\vert P$ and
$k\vert P$ and 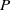 $P$ is odd. Then, when
$P$ is odd. Then, when 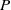 $P$ is odd, we show that there are no solutions of the equation
$P$ is odd, we show that there are no solutions of the equation 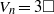 ${V}_{n} = 3\square $ for
${V}_{n} = 3\square $ for 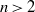 $n\gt 2$. Moreover, we show that the equation
$n\gt 2$. Moreover, we show that the equation 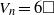 ${V}_{n} = 6\square $ has no solution when
${V}_{n} = 6\square $ has no solution when 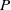 $P$ is odd. Lastly, we consider the equations
$P$ is odd. Lastly, we consider the equations 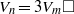 ${V}_{n} = 3{V}_{m} \square $ and
${V}_{n} = 3{V}_{m} \square $ and 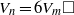 ${V}_{n} = 6{V}_{m} \square $. It has been shown that the equation
${V}_{n} = 6{V}_{m} \square $. It has been shown that the equation 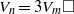 ${V}_{n} = 3{V}_{m} \square $ has a solution when
${V}_{n} = 3{V}_{m} \square $ has a solution when 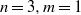 $n= 3, m= 1$, and
$n= 3, m= 1$, and 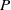 $P$ is odd. It has also been shown that the equation
$P$ is odd. It has also been shown that the equation 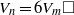 ${V}_{n} = 6{V}_{m} \square $ has a solution only when
${V}_{n} = 6{V}_{m} \square $ has a solution only when 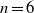 $n= 6$. We also solve the equations
$n= 6$. We also solve the equations 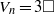 ${V}_{n} = 3\square $ and
${V}_{n} = 3\square $ and 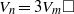 ${V}_{n} = 3{V}_{m} \square $ under some assumptions when
${V}_{n} = 3{V}_{m} \square $ under some assumptions when 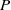 $P$ is even.
$P$ is even.
 $k$-TUPLES
$k$-TUPLES