Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T04:53:55.005Z Has data issue: false hasContentIssue false
  • English
  • Français

AN AFFINE FOURIER RESTRICTION THEOREM FOR CONICAL SURFACES

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  13 December 2013

Jonathan Hickman
Jonathan Hickman*
Affiliation:
The School of Mathematics, The University of Edinburgh, Room 5409, James Clerk Maxwell Building, King’s Buildings, Mayfield Road, Edinburgh, EH9 3JZ,U.K. email [email protected]
Get access

Abstract

A Fourier restriction estimate is obtained for a broad class of conic surfaces by adding a weight to the usual underlying measure. The new restriction estimate exhibits a certain affine-invariance and implies the sharp 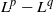${L}^{p} - {L}^{q} $ restriction theorem for compact subsets of a type 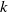$k$ conical surface, up to an endpoint. Furthermore, the chosen weight is shown to be, in some quantitative sense, optimal. Appended is a discussion of type 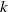$k$ conical restriction theorems which addresses some anomalies present in the existing literature.

MSC classification

Secondary: 42B10: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type
Type
Research Article
Information
Mathematika , Volume 60 , Issue 2 , July 2014 , pp. 374 - 390
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abi-Khuzam, F. and Shayya, B., Fourier restriction to convex surfaces of revolution in ${ \mathbb{R} }^{3} $. Publ. Mat. 50 (1) (2006), 71–85.CrossRefGoogle Scholar
Bak, J.-G. and Seeger, A., Extensions of the Stein–Tomas theorem. Math. Res. Lett. 18 (4) (2011), 767–781.Google Scholar
Barceló, B., On the restriction of the Fourier transform to a conical surface. Trans. Amer. Math. Soc. 292 (1) (1985), 321–333.Google Scholar
Barceló, B., The restriction of the Fourier transform to some curves and surfaces. Studia Math. 84 (1) (1986), 39–69.Google Scholar
Buschenhenke, S., A sharp ${L}_{p} - {L}_{q} $ Fourier restriction theorem for a conical surface of finite type, Preprint, 2012, arXiv:1208.5876v1 [math.CA].Google Scholar
Carbery, A., Christ, M. and Wright, J., Multidimensional van der Corput and sublevel set estimates. J. Amer. Math. Soc. 12 (4) (1999), 981–1015.Google Scholar
Carbery, A., Kenig, C. and Ziesler, S., Restriction for flat surfaces of revolution in ${\mathbf{R} }^{3} $. Proc. Amer. Math. Soc. 135 (6) (2007), 1905–1914; electronic.Google Scholar
Carbery, A. and Ziesler, S., Restriction and decay for flat hypersurfaces. Publ. Mat. 46 (2) (2002), 405–434.Google Scholar
Drury, S. W., Degenerate curves and harmonic analysis. Math. Proc. Cambridge Philos. Soc. 108 (1) (1990), 89–96.Google Scholar
Drury, S. W. and Guo, K., Some remarks on the restriction of the Fourier transform to surfaces. Math. Proc. Cambridge Philos. Soc. 113 (1) (1993), 153–159.Google Scholar
Federer, H., Geometric Measure Theory (Classics in Mathematics), Springer (1996).Google Scholar
Iosevich, A. and Lu, G., Sharpness results and Knapp’s homogeneity argument. Canad. Math. Bull. 43 (1) (2000), 63–68.Google Scholar
Nicola, F., A note on the restriction theorem and geometry of hypersurfaces. Math. Scand. 103 (1) (2008), 53–60.CrossRefGoogle Scholar
Nicola, F., Slicing surfaces and the Fourier restriction conjecture. Proc. Edinb. Math. Soc. (2) 52 (2) (2009), 515–527.Google Scholar
Oberlin, D. M., Fourier restriction for affine arclength measures in the plane. Proc. Amer. Math. Soc. 129 (11) (2001), 3303–3305; electronic.CrossRefGoogle Scholar
Oberlin, D. M., Some convolution inequalities and their applications. Trans. Amer. Math. Soc. 354 (6) (2002), 2541–2556; electronic.Google Scholar
Oberlin, D. M., A uniform Fourier restriction theorem for surfaces in ${ \mathbb{R} }^{3} $. Proc. Amer. Math. Soc. 132 (4) (2004), 1195–1199; electronic.CrossRefGoogle Scholar
Oberlin, D. M., A uniform Fourier restriction theorem for surfaces in ${ \mathbb{R} }^{d} $. Proc. Amer. Math. Soc. 140 (1) (2012), 263–265.Google Scholar
Shayya, B., An affine restriction estimate in ${ \mathbb{R} }^{3} $. Proc. Amer. Math. Soc. 135 (4) (2007), 1107–1113; electronic.Google Scholar
Shayya, B., Affine restriction for radial surfaces. Math. Z. 262 (1) (2009), 41–55.Google Scholar
Sjölin, P., Fourier multipliers and estimates of the Fourier transform of measures carried by smooth curves in ${R}^{2} $. Studia Math. 51 (1974), 169–182.Google Scholar
Sogge, C. D., A sharp restriction theorem for degenerate curves in ${\mathbf{R} }^{2} $. Amer. J. Math. 109 (2) (1987), 223–228.Google Scholar
Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals (Princeton Mathematical Series 43), Princeton University Press (1993).Google Scholar
Tao, T., Some recent progress on the restriction conjecture. In Fourier Analysis and Convexity (Applied and Numerical Harmonic Analysis), Birkhäuser (Boston, MA, 2004), 217–243.Google Scholar