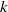Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T21:32:37.175Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST-PRIME $k$-TUPLES

Part of: Multiplicative number theory

Published online by Cambridge University Press:  06 September 2013

James Maynard
James Maynard*
Affiliation:
Mathematical Institute, 24–29 St Giles’, Oxford, OX1 3LB, U.K. email [email protected]
Get access

Abstract

Let 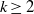$k\geq 2$ and 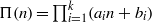$\Pi (n)= { \mathop{\prod }\nolimits}_{i= 1}^{k} ({a}_{i} n+ {b}_{i} )$ for some integers 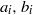${a}_{i} , {b}_{i} $ (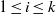$1\leq i\leq k$). Suppose that 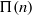$\Pi (n)$ has no fixed prime divisors. Weighted sieves have shown for infinitely many integers $n$ that the number of prime factors 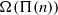$\Omega (\Pi (n))$ of 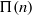$\Pi (n)$ is at most 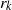${r}_{k} $, for some integer 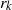${r}_{k} $ depending only on 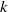$k$. We use a new kind of weighted sieve to improve the possible values of 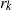${r}_{k} $ when 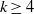$k\geq 4$.

MSC classification

Secondary: 11N05: Distribution of primes 11N35: Sieves 11N36: Applications of sieve methods
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 108 - 138
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chen, J. R., On the representation of a larger even integer as the sum of a prime and the product of at most two primes. Sci. Sinica 16 (1973), 157–176.Google Scholar
Diamond, H. and Halberstam, H., Some applications of sieves of dimension exceeding 1. In Sieve Methods, Exponential Sums, and their Applications in Number Theory (Cardiff, 1995) (London Mathematical Society Lecture Note Series 237) Cambridge University Press (Cambridge, 1997), 101–107.CrossRefGoogle Scholar
Goldston, D. A., Graham, S. W., Pintz, J. and Yıldırım, C. Y., Small gaps between products of two primes. Proc. Lond. Math. Soc. (3) 98 (3) (2009), 741–774.CrossRefGoogle Scholar
Goldston, D. A., Pintz, J. and Yıldırım, C. Y., Primes in tuples. II. Acta Math. 204 (1) (2010), 1–47.CrossRefGoogle Scholar
Heath-Brown, D. R., Almost-prime $k$-tuples. Mathematika 44 (2) (1997), 245–266.Google Scholar
Ho, K.-H. and Tsang, K.-M., On almost prime $k$-tuples. J. Number Theory 120 (1) (2006), 33–46.CrossRefGoogle Scholar
Maynard, J., 3-tuples have at most 7 prime factors infinitely often. Math. Proc. Cambridge Philos. Soc., to appear.Google Scholar
Motohashi, Y., An induction principle for the generalization of Bombieri’s prime number theorem. Proc. Japan Acad. 52 (6) (1976), 273–275.Google Scholar
Porter, J. W., Some numerical results in the Selberg sieve method. Acta Arith. 20 (1972), 417–421.CrossRefGoogle Scholar
Ramaré, O., On long $k$-tuples with few prime factors. Proc. Lond. Math. Soc. (3) 104 (1) (2012), 158–196.CrossRefGoogle Scholar
Selberg, A., Collected Papers. Vol. II, Springer (Berlin, 1991). With a foreword by K. Chandrasekharan.Google Scholar
Thorne, F., Bounded gaps between products of primes with applications to ideal class groups and elliptic curves. Int. Math. Res. Not. IMRN 5 (2008), 41; doi:10.1093/imrn/rnm156.Google Scholar