Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T01:04:36.611Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ERROR TERM IN THE COUNT OF ABUNDANT NUMBERS

Part of: Multiplicative number theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms Elementary number theory

Published online by Cambridge University Press:  02 January 2014

Mitsuo Kobayashi  and
Paul Pollack
Mitsuo Kobayashi
Affiliation:
Department of Mathematics and Statistics, Cal Poly Pomona, Pomona, CA 91768, U.S.A. email [email protected]
Paul Pollack
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602,U.S.A. email [email protected]
Get access

Abstract

A natural number $n$ is called abundant if the sum of the proper divisors of $n$ exceeds $n$. For example, 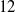$12$ is abundant, since 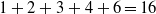$1+ 2+ 3+ 4+ 6= 16$. In 1929, Bessel-Hagen asked whether or not the set of abundant numbers possesses an asymptotic density. In other words, if 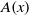$A(x)$ denotes the count of abundant numbers belonging to the interval 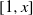$[1, x] $, does 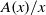$A(x)/ x$ tend to a limit? Four years later, Davenport answered Bessel-Hagen’s question in the affirmative. Calling this density 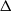$\Delta $, it is now known that 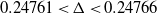$0. 24761\lt \Delta \lt 0. 24766$, so that just under one in four numbers are abundant. We show that 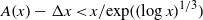$A(x)- \Delta x\lt x/ \mathrm{exp} (\mathop{(\log x)}\nolimits ^{1/ 3} )$ for all large $x$. We also study the behavior of the corresponding error term for the count of so-called $\alpha $-abundant numbers.

MSC classification

Secondary: 11A25: Arithmetic functions; related numbers; inversion formulas 11K65: Arithmetic functions 11N25: Distribution of integers with specified multiplicative constraints
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 43 - 65
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Behrend, F., Über numeri abundantes I, II. S.-Ber. Preuß. Akad. Wiss., math.-nat. Kl. (1932), 322–328; (1933), 119–127.Google Scholar
Behrend, F., Three reviews; of papers by Chowla, Davenport, and Erdős. Jahrbuch Fortschr. Math. 60 (1935), 146–149.Google Scholar
Bessel-Hagen, E., Zahlentheorie. In Repertorium der höheren Mathematik, 2nd edn., Vol. 1, B. G. Teubner (Leipzig, 1929), 1458–1574.Google Scholar
de Bruijn, N. G., On the number of positive integers $\leq x$ and free of prime factors $\gt y$. II. Indag. Math. 28 (1966), 239–247.Google Scholar
Chowla, S., On abundant numbers. J. Indian Math. Soc. 1 (1934), 41–44.Google Scholar
Davenport, H., Über numeri abundantes. S.-Ber. Preuß. Akad. Wiss., math.-nat. Kl. (1933), 830–837.Google Scholar
Deléglise, M., Bounds for the density of abundant integers. Experiment. Math. 7 (2) (1998), 137–143.Google Scholar
Elliott, P. D. T. A., Probabilistic Number Theory. I. Mean-value Theorems (Grundlehren der Mathematischen Wissenschaften 239), Springer (New York, 1979).Google Scholar
Erdős, P., On the density of the abundant numbers. J. Lond. Math. Soc. 9 (1934), 278–282.CrossRefGoogle Scholar
Erdős, P., On primitive abundant numbers. J. Lond. Math. Soc. 10 (1935), 49–58.CrossRefGoogle Scholar
Erdős, P., On the density of some sequences of numbers I. J. Lond. Math. Soc. 10 (1935), 120–125.CrossRefGoogle Scholar
Erdős, P., On the density of some sequences of numbers II. J. Lond. Math. Soc. 12 (1937), 7–11.Google Scholar
Erdős, P., On the density of some sequences of numbers III. J. Lond. Math. Soc. 13 (1938), 119–127.CrossRefGoogle Scholar
Erdős, P., Some remarks about additive and multiplicative functions. Bull. Amer. Math. Soc. 52 (1946), 527–537.Google Scholar
Erdős, P., Remarks on number theory. I. On primitive $\alpha $-abundant numbers. Acta Arith. 5 (1959), 25–33.Google Scholar
Erdős, P. and Wintner, A., Additive arithmetical functions and statistical independence. Amer. J. Math. 61 (1939), 713–721.Google Scholar
Fainleib, A. S., Distribution of values of Euler’s function. Mat. Zametki 1 (1967), 645–652 (Russian).Google Scholar
Fainleib, A. S., A generalization of Esseen’s inequality and its application in probabilistic number theory. Izv. Akad. Nauk SSSR Ser. Mat. 32 (1968), 859–879 (Russian).Google Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods (London Mathematical Society Monographs 4), Academic Press (London–New York, 1974).Google Scholar
Hall, R. R. and Tenenbaum, G., Divisors (Cambridge Tracts in Mathematics 90), Cambridge University Press (Cambridge, 1988).Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 6th edn., Oxford University Press (Oxford, 2008).Google Scholar
Kobayashi, M., On the density of abundant numbers. PhD Thesis, Dartmouth College, 2010.Google Scholar
Kobayashi, M., A new series for the density of the abundant numbers. Int. J. Number Theory (to appear).Google Scholar
Luca, F. and Pomerance, C., Irreducible radical extensions and Euler-function chains. In Combinatorial Number Theory, de Gruyter (Berlin, 2007), 351–361.Google Scholar
Pomerance, C., Two methods in elementary analytic number theory. In Number Theory and Applications (Banff, AB, 1988) (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 265), Kluwer Academic Publications (Dordrecht, 1989), 135–161.Google Scholar
Salié, H., Über die Dichte abundanter Zahlen. Math. Nachr. 14 (1955), 39–46.CrossRefGoogle Scholar
Schoenberg, I. J., Über die asymptotische Verteilung reeller Zahlen mod 1. Math. Z. 28 (1928), 171–200.Google Scholar
Schoenberg, I. J., On asymptotic distributions of arithmetical functions. Trans. Amer. Math. Soc. 39 (1936), 315–330.CrossRefGoogle Scholar
Schwarz, W. and Spilker, J., Arithmetical Functions (London Mathematical Society Lecture Note Series 184), Cambridge University Press (Cambridge, 1994).Google Scholar
Wall, C. R., Density bounds for the sum of divisors function. In The Theory of Arithmetic Functions (Lecture Notes in Mathematics 251), Springer (Berlin, 1972), 283–287.Google Scholar
Weingartner, A., The distribution functions of $\sigma (n)/ n$ and $n/ \varphi (n)$. Proc. Amer. Math. Soc. 135 (2007), 2677–2681.CrossRefGoogle Scholar
Weingartner, A., The distribution functions of $\sigma (n)/ n$ and $n/ \varphi (n)$, II. J. Number Theory 132 (2012), 2907–2921.CrossRefGoogle Scholar
Wirsing, E., Bemerkung zu der Arbeit über vollkommene Zahlen. Math. Ann. 137 (1959), 316–318.CrossRefGoogle Scholar