We compute the deficiency spaces of operators of the form $H_A{\hat {\otimes }} I + I{\hat {\otimes }} H_B$, for symmetric $H_A$ and self-adjoint $H_B$. This enables us to construct self-adjoint extensions (if they exist) by means of von Neumann's theory. The structure of the deficiency spaces for this case was asserted already in Ibort et al. [Boundary dynamics driven entanglement, J. Phys. A: Math. Theor.47(38) (2014) 385301], but only proven under the restriction of $H_B$ having discrete, non-degenerate spectrum.

An effective lower bound on the entropy of some explicit quadratic plane Cremona transformations is given. The motivation is that such transformations (Hénon maps, or Feistel ciphers) are used in symmetric key cryptography. Moreover, a hyperbolic plane Cremona transformation g is rigid, in the sense of [5], and under further explicit conditions some power of g is tight.

Classical results about peaking from complex interpolation theory are extended to polynomials on a closed disk, and on the complement of its interior. New results are obtained concerning interpolation by univalent polynomials on a Jordan domain whose boundary satisfies certain smoothness conditions.

A theory of infinite spanning sets and bases is developed for the first-order flex space of an infinite bar-joint framework, together with space group symmetric versions for a crystallographic bar-joint framework ${{\mathcal {C}}}$. The existence of a crystal flex basis for ${{\mathcal {C}}}$ is shown to be closely related to the spectral analysis of the rigid unit mode (RUM) spectrum of ${{\mathcal {C}}}$ and an associated geometric flex spectrum. Additionally, infinite spanning sets and bases are computed for a range of fundamental crystallographic bar-joint frameworks, including the honeycomb (graphene) framework, the octahedron (perovskite) framework and the 2D and 3D kagome frameworks.

We study the invariance of KMS states on graph $C^{\ast }$-algebras coming from strongly connected and circulant graphs under the classical and quantum symmetry of the graphs. We show that the unique KMS state for strongly connected graphs is invariant under the quantum automorphism group of the graph. For circulant graphs, it is shown that the action of classical and quantum automorphism groups preserves only one of the KMS states occurring at the critical inverse temperature. We also give an example of a graph $C^{\ast }$-algebra having more than one KMS state such that all of them are invariant under the action of classical automorphism group of the graph, but there is a unique KMS state which is invariant under the action of quantum automorphism group of the graph.

We introduce a general definition for coloured cyclic operads over a symmetric monoidal ground category, which has several appealing features. The forgetful functor from coloured cyclic operads to coloured operads has both adjoints, each of which is relatively simple. Explicit formulae for these adjoints allow us to lift the Cisinski–Moerdijk model structure on the category of coloured operads enriched in simplicial sets to the category of coloured cyclic operads enriched in simplicial sets.

The true complexity of a polynomial progression in finite fields corresponds to the smallest-degree Gowers norm that controls the counting operator of the progression over finite fields of large characteristic. We give a conjecture that relates true complexity to algebraic relations between the terms of the progression, and we prove it for a number of progressions, including $x, x+y, x+y^{2}, x+y+y^{2}$ and $x, x+y, x+2y, x+y^{2}$. As a corollary, we prove an asymptotic for the count of certain progressions of complexity 1 in subsets of finite fields. In the process, we obtain an equidistribution result for certain polynomial progressions, analogous to the counting lemma for systems of linear forms proved by Green and Tao.

The Toms–Winter conjecture is verified for those separable, unital, nuclear, infinite-dimensional real C*-algebras for which the complexification has a tracial state space with compact extreme boundary of finite covering dimension.

In this paper, we prove the equivalence between logarithmic Sobolev inequality and hypercontractivity of a class of quantum Markov semigroup and its associated Dirichlet form based on a probability gage space.

Let $G_1, \ldots , G_k$ be finite-dimensional vector spaces over a prime field $\mathbb {F}_p$. A multilinear variety of codimension at most $d$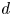 is a subset of $G_1 \times \cdots \times G_k$ defined as the zero set of $d$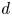 forms, each of which is multilinear on some subset of the coordinates. A map $\phi$ 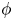defined on a multilinear variety $B$ 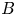is multilinear if for each coordinate $c$ 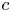and all choices of $x_i \in G_i$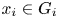, $i\not =c$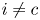, the restriction map $y \mapsto \phi (x_1, \ldots , x_{c-1}, y, x_{c+1}, \ldots , x_k)$ 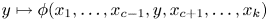is linear where defined. In this note, we show that a multilinear map defined on a multilinear variety of codimension at most $d$ coincides on a multilinear variety of codimension $O_{k}(d^{O_{k}(1)})$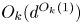 with a multilinear map defined on the whole of $G_1\times \cdots \times G_k$. Additionally, in the case of general finite fields, we deduce similar (but slightly weaker) results.

For the $p$-localized sphere $\mathbb {S}^{2m-1}_{(p)}$ with $p >3$ a prime, we prove that the homotopy nilpotency satisfies $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}<\infty$, with respect to any homotopy associative $H$-structure on $\mathbb {S}^{2m-1}_{(p)}$. We also prove that $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}= 1$ for all but a finite number of primes $p >3$. Then, for the loop space of the associated $\mathbb {S}^{2m-1}_{(p)}$-projective space $\mathbb {S}^{2m-1}_{(p)}P(n-1)$, with $m,n\ge 2$ and $m\mid p-1$, we derive that $\mbox {nil}\ \Omega (\mathbb {S}^{2m-1}_{(p)}P (n-1))\le 3$.

In this short article, we will be principally investigating two classes of modules over any given group ring – the class of Gorenstein projectives and the class of Benson's cofibrants. We begin by studying various properties of these two classes and studying some of these properties comparatively against each other. There is a conjecture made by Fotini Dembegioti and Olympia Talelli that these two classes should coincide over the integral group ring for any group. We make this conjecture over group rings over commutative rings of finite global dimension and prove it for some classes of groups while also proving other related results involving the two classes of modules mentioned.

The notions of chaos and frequent hypercyclicity enjoy an intimate relationship in linear dynamics. Indeed, after a series of partial results, it was shown by Bayart and Ruzsa in 2015 that for backward weighted shifts on $\ell _p(\mathbb {Z})$, the notions of chaos and frequent hypercyclicity coincide. It is with some effort that one shows that these two notions are distinct. Bayart and Grivaux in 2007 constructed a non-chaotic frequently hypercyclic weighted shift on $c_0$. It was only in 2017 that Menet settled negatively whether every chaotic operator is frequently hypercylic. In this article, we show that for a large class of composition operators on $L^{p}$-spaces, the notions of chaos and frequent hypercyclicity coincide. Moreover, in this particular class, an invertible operator is frequently hypercyclic if and only if its inverse is frequently hypercyclic. This is in contrast to a very recent result of Menet where an invertible operator frequently hypercyclic on $\ell _1$ whose inverse is not frequently hypercyclic is constructed.

We consider Akbarov's holomorphic version of the non-commutative Pontryagin duality for a complex Lie group. We prove, under the assumption that $G$ is a Stein group with finitely many components, that (1) the topological Hopf algebra of holomorphic functions on $G$ is holomorphically reflexive if and only if $G$ is linear; (2) the dual cocommutative topological Hopf algebra of exponential analytic functional on $G$ is holomorphically reflexive. We give a counterexample, which shows that the first criterion cannot be extended to the case of infinitely many components. Nevertheless, we conjecture that, in general, the question can be solved in terms of the Banach-algebra linearity of $G$.

We establish Bohr inequalities for operator-valued functions, which can be viewed as analogues of a couple of interesting results from scalar-valued settings. Some results of this paper are motivated by the classical flavour of Bohr inequality, while others are based on a generalized concept of the Bohr radius problem.

We present a sufficient condition for the $kG$-Scott module with vertex $P$ to remain indecomposable under the Brauer construction for any subgroup $Q$ of $P$ as $k[Q\,C_G(Q)]$-module, where $k$ is a field of characteristic $2$, and $P$ is a semidihedral $2$-subgroup of a finite group $G$. This generalizes results for the cases where $P$ is abelian or dihedral. The Brauer indecomposability is defined by R. Kessar, N. Kunugi and N. Mitsuhashi. The motivation of this paper is the fact that the Brauer indecomposability of a $p$-permutation bimodule (where $p$ is a prime) is one of the key steps in order to obtain a splendid stable equivalence of Morita type by making use of the gluing method due to Broué, Rickard, Linckelmann and Rouquier, that then can possibly be lifted to a splendid derived (splendid Morita) equivalence.

We say that a map $f$ from a Banach space $X$ to another Banach space $Y$ is a phase-isometry if the equality

\[ \{\|f(x)+f(y)\|, \|f(x)-f(y)\|\}=\{\|x+y\|, \|x-y\|\} \]

$x,\,y\in X$

$X$

$Y$

$f : X\rightarrow Y$

$\varepsilon : X \rightarrow \{-1,\,1\}$

$\varepsilon \cdot f$

The aim of this paper is to present some results about the space $L^{\varPhi }(\nu ),$ where $\nu$ is a vector measure on a compact (not necessarily abelian) group and $\varPhi$ is a Young function. We show that under natural conditions, the space $L^{\varPhi }(\nu )$ becomes an $L^{1}(G)$-module with respect to the usual convolution of functions. We also define one more convolution structure on $L^{\varPhi }(\nu ).$

We study the structure and compute the stable rank of $C^{*}$-algebras of finite higher-rank graphs. We completely determine the stable rank of the $C^{*}$-algebra when the $k$-graph either contains no cycle with an entrance or is cofinal. We also determine exactly which finite, locally convex $k$-graphs yield unital stably finite $C^{*}$-algebras. We give several examples to illustrate our results.

We show that if $X$ is an $m$-dimensional definable set in $\mathbb {R}_\text {an}^\text{pow}$, the structure of real subanalytic sets with real power maps added, then for any positive integer $r$ there exists a $C^{r}$-parameterization of $X$ consisting of $cr^{m^{3}}$ maps for some constant $c$. Moreover, these maps are real analytic and this bound is uniform for a definable family.