Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T00:55:42.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Chaos and frequent hypercyclicity for composition operators

Part of: General theory of linear operators Dynamical systems with hyperbolic behavior Special classes of linear operators

Published online by Cambridge University Press:  04 June 2021

Udayan B. Darji  and
Benito Pires
Udayan B. Darji
Affiliation:
Department of Mathematics, University of Louisville, Louisville, KY40292, USA ([email protected])
Benito Pires
Affiliation:
Departamento de Computaçao e Matemática, Faculdade de Filosofia, Ciências e Letras, Universidade de São Paulo, Ribeirão Preto, SP14040-901, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The notions of chaos and frequent hypercyclicity enjoy an intimate relationship in linear dynamics. Indeed, after a series of partial results, it was shown by Bayart and Ruzsa in 2015 that for backward weighted shifts on $\ell _p(\mathbb {Z})$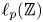, the notions of chaos and frequent hypercyclicity coincide. It is with some effort that one shows that these two notions are distinct. Bayart and Grivaux in 2007 constructed a non-chaotic frequently hypercyclic weighted shift on $c_0$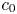. It was only in 2017 that Menet settled negatively whether every chaotic operator is frequently hypercylic. In this article, we show that for a large class of composition operators on $L^{p}$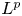-spaces, the notions of chaos and frequent hypercyclicity coincide. Moreover, in this particular class, an invertible operator is frequently hypercyclic if and only if its inverse is frequently hypercyclic. This is in contrast to a very recent result of Menet where an invertible operator frequently hypercyclic on $\ell _1$ 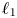whose inverse is not frequently hypercyclic is constructed.

Keywords

Frequently hypercyclicchaotic operatorcomposition operatorLp-space

MSC classification

Primary: 47A16: Cyclic vectors, hypercyclic and chaotic operators 47B33: Composition operators
Secondary: 37D45: Strange attractors, chaotic dynamics
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 513 - 531
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J., An introduction to infinite ergodic theory, Mathematical Surveys and Monographs, Volume 50 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Bayart, F., Darji, U. B. and Pires, B., Topological transitivity and mixing of composition operators, J. Math. Anal. Appl. 465(1) (2018), 125–139.10.1016/j.jmaa.2018.04.063CrossRefGoogle Scholar
Bayart, F. and Grivaux, S., Frequently hypercyclic operators, Trans. Amer. Math. Soc. 358(11) (2006), 5083–5117.CrossRefGoogle Scholar
Bayart, F. and Grivaux, S., Invariant Gaussian measures for operators on Banach spaces and linear dynamics, Proc. Lond. Math. Soc. (3) 94(1) (2007), 181–210.10.1112/plms/pdl013CrossRefGoogle Scholar
Bayart, F. and Ruzsa, I. Z., Difference sets and frequently hypercyclic weighted shifts, Ergodic Theory Dynam. Syst. 35(3) (2015), 691–709.10.1017/etds.2013.77CrossRefGoogle Scholar
Bernardes, N. C., Darji, U. B. Jr. and Pires, B., Li-Yorke chaos for composition operators on $L^{p}$-spaces, Monatsh. Math. 191(1) (2020), 13–35.CrossRefGoogle Scholar
Bongiorno, D., D'Aniello, E., Darji, U. B. and Di Piazza, L., Linear dynamics induced by odometers, 2019.Google Scholar
Bonilla, A. and Grosse-Erdmann, K.-G., Frequently hypercyclic operators and vectors, Ergodic Theory Dynam. Syst. 27(2) (2007), 383–404.CrossRefGoogle Scholar
Charpentier, S., Grosse-Erdmann, K. and Menet, Q., Chaos and frequent hypercyclicity for weighted shifts, 2019.10.1017/etds.2020.122CrossRefGoogle Scholar
D'Aniello, E., Darji, U. B. and Maiuriello, M., Generalized hyperbolicity and shadowing in $l^{p}$ spaces, 2020.10.1016/j.jde.2021.06.038CrossRefGoogle Scholar
Grivaux, S. and Matheron, É., Invariant measures for frequently hypercyclic operators, Adv. Math. 265 (2014), 371–427.Google Scholar
Grosse-Erdmann, K.-G., Hypercyclic and chaotic weighted shifts, Studia Math. 139(1) (2000), 47–68.10.4064/sm-139-1-47-68CrossRefGoogle Scholar
Grosse-Erdmann, K.-G. and Peris, A., Frequently dense orbits, C. R. Math. Acad. Sci. Paris 341(2) (2005), 123–128.10.1016/j.crma.2005.05.025CrossRefGoogle Scholar
Kadets, M. I. and Kadets, V. M., Series in Banach spaces, Operator Theory: Advances and Applications, Volume 94 (Birkhäuser Verlag, Basel, 1997), Conditional and unconditional convergence, Translated from the Russian by Andrei Iacob.Google Scholar
Krengel, U., Ergodic theorems, De Gruyter Studies in Mathematics, Volume 6 (Walter de Gruyter & Co., Berlin, 1985), With a supplement by Antoine Brunel.Google Scholar
Menet, Q., Linear chaos and frequent hypercyclicity, Trans. Amer. Math. Soc. 369(7) (2017), 4977–4994.CrossRefGoogle Scholar
Menet, Q., Inverse of frequently hypercyclic operators, 2019.Google Scholar
Palis, J. Jr and de Melo, W., Geometric theory of dynamical systems (Springer-Verlag, New York-Berlin, 1982). An introduction, Translated from the Portuguese by A. K. Manning.CrossRefGoogle Scholar
Singh, R. K. and Manhas, J. S., Composition operators on function spaces, North-Holland Mathematics Studies, Volume 179 (North-Holland Publishing Co., Amsterdam, 1993).Google Scholar