Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T01:06:33.806Z Has data issue: false hasContentIssue false
  • English
  • Français

On holomorphic reflexivity conditions for complex Lie groups

Part of: Hopf algebras, quantum groups and related topics Lie groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  30 September 2021

O. Yu. Aristov
O. Yu. Aristov*
Affiliation:
Obninsk, Russia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider Akbarov's holomorphic version of the non-commutative Pontryagin duality for a complex Lie group. We prove, under the assumption that $G$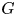 is a Stein group with finitely many components, that (1) the topological Hopf algebra of holomorphic functions on $G$ 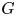is holomorphically reflexive if and only if $G$ 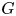is linear; (2) the dual cocommutative topological Hopf algebra of exponential analytic functional on $G$ 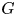is holomorphically reflexive. We give a counterexample, which shows that the first criterion cannot be extended to the case of infinitely many components. Nevertheless, we conjecture that, in general, the question can be solved in terms of the Banach-algebra linearity of $G$.

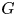Keywords

Arens-Michael envelopecomplex Lie groupdistorted subgroupholomorphic function of exponential typeholomorphic reflexivitylinearizertopological Hopf algebra

MSC classification

Primary: 22E10: General properties and structure of complex Lie groups
Secondary: 16T05: Hopf algebras and their applications 20F65: Geometric group theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 800 - 821
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbarov, S. S., Holomorphic functions of exponential type and duality for Stein groups with algebraic connected component of identity, (Russian) Fundam. Prikl. Mat. 14(1) (2008), 3–178. English transl. J. Math. Sci., 162:4 (2009), 459–586.Google Scholar
Akbarov, S. S., Continuous and smooth envelopes of topological algebras. Part 1, English Transl. J. Math. Sci. (N. Y.) 227(5) (2017), 531–668. (Russian), Functional analysis, Itogi Nauki i Tekhniki. Ser. Sovrem. Mat. Pril. Temat. Obz., 129, VINITI, Moscow, 2017, 3–133.CrossRefGoogle Scholar
Aristov, O. Yu., Holomorphically finitely generated Hopf algebras and quantum Lie groups, arXiv:2006.12175Google Scholar
Aristov, O. Yu., Holomorphic functions of exponential type on connected complex Lie groups, J. Lie Theory 29(4) (2019), 1045–1070. arXiv:1903.08080.Google Scholar
Aristov, O. Yu., Arens-Michael envelopes of nilpotent Lie algebras, functions of exponential type, and homological epimorphisms, Tr. Mosk. Mat. Obs. 81(1) (2020), 117–136. MCCME, M., Trans. Moscow Math. Soc. (2020), 97–114, arXiv:1810.13213.Google Scholar
Blackadar, B., Operator algebras. theory of $C^{*}$-algebras and von Neumann Algebras, Encyclopaedia of Mathematical Sciences, Vol. 122 (Springer, 2006).10.1007/3-540-28517-2CrossRefGoogle Scholar
Bogachev, V. I. and Smolyanov, O. G., Topological vector spaces and their applications (Moscow-Izhevsk, 2012). English transl.: (Springer 2017).Google Scholar
Bonneau, P., Flato, M., Gerstenhaber, M. and Pinczon, G., The hidden group structure of quantum groups: strong duality, rigidity and preferred deformations, Comm. Math. Phys. 161 (1994), 125–156.CrossRefGoogle Scholar
Dales, H. G., Banach algebras and automatic continuity. London mathematical society monographs. New Series, Vol. 24 (Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 2000).Google Scholar
Forster, O., Zur Theorie der Steinschen Algebren und Moduln, Math. Z. 97 (1967), 376–405.CrossRefGoogle Scholar
Hilgert, J. and Neeb, K.-H., Structure and geometry of Lie groups (Springer, New York, 2012).CrossRefGoogle Scholar
Litvinov, G. V, Group representations in locally convex spaces, and topological group algebras, Trudy Sem. Vektor. Tenzor. Anal. 16 (1972), 267–349. (Russian) English transl.: Selecta Math. Soviet. (Birkhäuser Publ.) 7(2) (1988), 101–182.Google Scholar
Litvinov, G. L., Dual topological algebras and topological Hopf algebras, Trudy Sem. Vektor. Tenzor. Anal. 18 (1978), 372–375. English transl.: Selecta Math. Soviet. (Birkhäuser Publ.) 10(4) (1991), 339–343.Google Scholar
Nica, B., Linear groups – Malcev's theorem and Selberg's lemma, arXiv:1306.2385.Google Scholar
Palmer, T. W., Banach algebras and the general theory of *-algebras: Vol. I, algebras and banach algebras (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar
Pirkovskii, A. Yu., Stably flat completions of universal enveloping algebras, Dissertat. Math. (Rozprawy Math.) 441 (2006), 1–60.Google Scholar
Pirkovskii, A. Yu., Arens-Michael envelopes, homological epimorphisms, and relatively quasi-free algebras, Tr. Mosk. Mat. Obs. 69 (2008), 34–125. (Russian) English transl.: Trans. Moscow Math. Soc. (2008), 27–104.Google Scholar
Pirkovskii, A. Yu., Holomorphically finitely generated algebras, J. Noncommut. Geom. 9 (2015), 215–264.CrossRefGoogle Scholar
Varopoulos, N. T., Distance distortion on Lie groups, in Random walks and discrete potential theory (M. Picardello and W. Woess, Eds.) (Cambridge University Press, Cambridge, 1999).Google Scholar
Vogt, D., The tensor algebra of power series spaces, Studia Math. 193 (2009), 189–202.CrossRefGoogle Scholar
Ya. Helemskii, A., Banach and polynormed algebras: general theory, representations, homology, (Nauka (Russian), Moscow, 1989). English transl. (Oxford University Press, 1993).Google Scholar