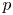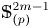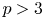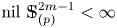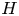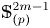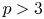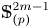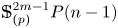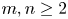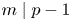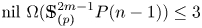Introduction
The homotopy nilpotency classes $\mbox {nil}\ X$![]() of associative $H$
of associative $H$![]() -spaces $X$
-spaces $X$![]() has been extensively studied, as well as their homotopy commutativity. In particular, Hopkins [Reference Hopkins10] made great progress by giving (co)homological criteria for homotopy associative finite $H$
has been extensively studied, as well as their homotopy commutativity. In particular, Hopkins [Reference Hopkins10] made great progress by giving (co)homological criteria for homotopy associative finite $H$![]() -spaces to be homotopy nilpotent. For example, he showed that if a homotopy associative finite $H$
-spaces to be homotopy nilpotent. For example, he showed that if a homotopy associative finite $H$![]() -space has no torsion in the integral homology, then it is homotopy nilpotent. Later, Rao [Reference Rao15, Reference Rao16] showed that the converse of the above criterion is true in the case of groups $Spin(m)$
-space has no torsion in the integral homology, then it is homotopy nilpotent. Later, Rao [Reference Rao15, Reference Rao16] showed that the converse of the above criterion is true in the case of groups $Spin(m)$![]() and $SO(m)$
and $SO(m)$![]() and a connected compact Lie group is homotopy nilpotent if and only if it has no torsion in homology. Eventually, Yagita [Reference Yagita21] proved that, when $G$
and a connected compact Lie group is homotopy nilpotent if and only if it has no torsion in homology. Eventually, Yagita [Reference Yagita21] proved that, when $G$![]() is a compact, simply-connected Lie group, its $p$
is a compact, simply-connected Lie group, its $p$![]() -localization $G_{(p)}$
-localization $G_{(p)}$![]() is homotopy nilpotent if and only if it has no torsion in the integral homology.
is homotopy nilpotent if and only if it has no torsion in the integral homology.
Although many results on the homotopy nilpotency have been obtained, the homotopy nilpotency classes have been determined in very few cases. It is well known that for the loop space $\Omega (\mathbb {S}^{m})$![]() of the $m$
of the $m$![]() -sphere $\mathbb {S}^{m}$
-sphere $\mathbb {S}^{m}$![]() , we have $\mbox {nil}\ \Omega (\mathbb {S}^{m})=1$
, we have $\mbox {nil}\ \Omega (\mathbb {S}^{m})=1$![]() if and only if $m=1,3,7$
if and only if $m=1,3,7$![]() and
and
Next, write $\mathbb {K}P^{m}$![]() for the projective $m$
for the projective $m$![]() -space for $\mathbb {K}=\mathbb {R},\,\mathbb {C}$
-space for $\mathbb {K}=\mathbb {R},\,\mathbb {C}$![]() , the field of reals or complex numbers and $\mathbb {H}$
, the field of reals or complex numbers and $\mathbb {H}$![]() , the skew $\mathbb {R}$
, the skew $\mathbb {R}$![]() -algebra of quaternions. Then, the homotopy nilpotency of $\Omega (\mathbb {K}P^{m})$
-algebra of quaternions. Then, the homotopy nilpotency of $\Omega (\mathbb {K}P^{m})$![]() has been first studied by Ganea [Reference Ganea7], Snaith [Reference Snaith17] and then their $p$
has been first studied by Ganea [Reference Ganea7], Snaith [Reference Snaith17] and then their $p$![]() -localization $\Omega ((\mathbb {K}P^{m})_{(p)})$
-localization $\Omega ((\mathbb {K}P^{m})_{(p)})$![]() by Meier [Reference Meier12]. The homotopy nilpotency of the loop spaces of Grassmann and Stiefel manifolds and their $p$
by Meier [Reference Meier12]. The homotopy nilpotency of the loop spaces of Grassmann and Stiefel manifolds and their $p$![]() -localization have been extensively studied in [Reference Golasiński8].
-localization have been extensively studied in [Reference Golasiński8].
Now, let $\mathbb {S}^{2m-1}_{(p)}$![]() be the $p$
be the $p$![]() -localization of the sphere $\mathbb {S}^{2m-1}$
-localization of the sphere $\mathbb {S}^{2m-1}$![]() at a prime $p$
at a prime $p$![]() . The paper grew out of our desire to develop techniques in calculating the homotopy nilpotency classes of $\mathbb {S}^{2m-1}_{(p)}$
. The paper grew out of our desire to develop techniques in calculating the homotopy nilpotency classes of $\mathbb {S}^{2m-1}_{(p)}$![]() with respect to any homotopy associative $H$
with respect to any homotopy associative $H$![]() -structure for $p>3$
-structure for $p>3$![]() . Its main result is the explicit determination of the homotopy nilpotence class of a wide range of homotopy associative multiplications on localized spheres $\mathbb {S}^{2m-1}_{(p)}$
. Its main result is the explicit determination of the homotopy nilpotence class of a wide range of homotopy associative multiplications on localized spheres $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
We begin with general results useful in the rest of the paper. In particular, we make use of [Reference Hopkins10, Theorem 2.1] to conclude the following corollary.
Corollary 1.4 Let $X$![]() be a finite simply-connected $CW$
be a finite simply-connected $CW$![]() -complex with torsion-free homology $H_\ast (X,\mathbb {Z})$
-complex with torsion-free homology $H_\ast (X,\mathbb {Z})$![]() . If the $p$
. If the $p$![]() -localization $X_{(p)}$
-localization $X_{(p)}$![]() for a prime $p$
for a prime $p$![]() admits a homotopy associative $H$
admits a homotopy associative $H$![]() -structure then $\mbox {nil}\ X_{(p)}<\infty$
-structure then $\mbox {nil}\ X_{(p)}<\infty$![]() .
.
Next, we consider the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$![]() with respect to any homotopy associative $H$
with respect to any homotopy associative $H$![]() -structures and the loop space $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$
-structures and the loop space $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$![]() of the associated $\mathbb {S}^{2m-1}_{(p)}$
of the associated $\mathbb {S}^{2m-1}_{(p)}$![]() -projective space $\mathbb {S}^{2m-1}_{(p)}P(n-1)$
-projective space $\mathbb {S}^{2m-1}_{(p)}P(n-1)$![]() for $p> 3$
for $p> 3$![]() . First, we make use of Corollary 1.4, to prove the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$
. First, we make use of Corollary 1.4, to prove the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
Theorem 1.5 If $m\ge 2$![]() and $p>3$
and $p>3$![]() is a prime then
is a prime then
with respect to any homotopy associative $H$![]() -structure on $\mathbb {S}^{2m-1}_{(p)}$
-structure on $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
Furthermore, we show that $\mathbb {S}^{2m-1}_{(p)}$![]() is homotopy associative and commutative for all but a finite number of primes $p$
is homotopy associative and commutative for all but a finite number of primes $p$![]() .
.
Then, we apply Zabrodsky's result [Reference Zabrodsky22, Lemma 2.6.6] to show the homotopy nilpotency of $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$![]() under some conditions.
under some conditions.
Theorem 3.12 Let $m\ge 2$![]() and $p> 3$
and $p> 3$![]() be a prime.
be a prime.
(1) If $n\ge 2$
 and $m\mid p-1$
and $m\mid p-1$ then
\[ \mbox{nil}\ \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))\le \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}+1\le 3; \]
then
\[ \mbox{nil}\ \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))\le \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}+1\le 3; \]
(2) if $j=s= 1$
 and $m \nmid p-1$
and $m \nmid p-1$ , or if we have $s\ge 1$
, or if we have $s\ge 1$ , $j\le p$
, $j\le p$ , $j$
, $j$ odd, and $m \mid p-1$
odd, and $m \mid p-1$ , then
\[ \mbox{nil}\ \Omega(\mathbb{S}^{2m-1}_{(p)}P(jp^{s}-1))=1. \]
, then
\[ \mbox{nil}\ \Omega(\mathbb{S}^{2m-1}_{(p)}P(jp^{s}-1))=1. \]
1. Prerequisites
All spaces and maps in this note are assumed to be connected, based and of the homotopy type of $CW$![]() -complexes. We also do not distinguish notationally between a continuous map and its homotopy class. We write $\Omega (X)$
-complexes. We also do not distinguish notationally between a continuous map and its homotopy class. We write $\Omega (X)$![]() (respectively $E(X)$
(respectively $E(X)$![]() ) for the loop (respectively suspension) space on a space $X$
) for the loop (respectively suspension) space on a space $X$![]() , $\simeq$
, $\simeq$![]() for the homotopy relation and $[Y,X]$
for the homotopy relation and $[Y,X]$![]() for the set of homotopy classes of maps $Y\to X$
for the set of homotopy classes of maps $Y\to X$![]() .
.
Given a space $X$![]() , we use the customary notation $X\vee X$
, we use the customary notation $X\vee X$![]() and $X\wedge X$
and $X\wedge X$![]() for the wedge and the smash product of $X$
for the wedge and the smash product of $X$![]() , respectively.
, respectively.
Recall that an $H$![]() -space is a pair $(X,\mu )$
-space is a pair $(X,\mu )$![]() , where $X$
, where $X$![]() is a space and $\mu : X \times X \to X$
is a space and $\mu : X \times X \to X$![]() is a map such that the diagram
is a map such that the diagram

commutes up to homotopy, where $\nabla : X\vee X\to X$![]() is the codiagonal map.
is the codiagonal map.
We call $\mu$![]() a multiplication or an $H$
a multiplication or an $H$![]() -structure on $X$
-structure on $X$![]() . Two examples of $H$
. Two examples of $H$![]() -spaces come in mind: topological groups and the spaces $\Omega (X)$
-spaces come in mind: topological groups and the spaces $\Omega (X)$![]() of loops on $X$
of loops on $X$![]() . In the sequel, we identify an $H$
. In the sequel, we identify an $H$![]() -space $(X,\mu )$
-space $(X,\mu )$![]() with the space $X$
with the space $X$![]() .
.
An $H$![]() -space $X$
-space $X$![]() is called a group-like space if $X$
is called a group-like space if $X$![]() satisfies all the axioms of groups up to homotopy. Recall that a homotopy associative an $H$
satisfies all the axioms of groups up to homotopy. Recall that a homotopy associative an $H$![]() -space always has a homotopy inverse. More precisely, according to [Reference Zabrodsky22, Corollary 1.3.2] (see also [Reference Arkowitz3, Proposition 8.4.4]), we have the following result.
-space always has a homotopy inverse. More precisely, according to [Reference Zabrodsky22, Corollary 1.3.2] (see also [Reference Arkowitz3, Proposition 8.4.4]), we have the following result.
Proposition 1.1 If $X$![]() is a homotopy associative $H$
is a homotopy associative $H$![]() -space then $X$
-space then $X$![]() is a group-like space.
is a group-like space.
If $X$![]() is a homotopy associative $H$
is a homotopy associative $H$![]() -space, then the functor $[ -, X]$
-space, then the functor $[ -, X]$![]() takes its values in the category of groups. One may then ask when this functor takes its values in various subcategories of groups.
takes its values in the category of groups. One may then ask when this functor takes its values in various subcategories of groups.
For example, $X$![]() is homotopy commutative if and only if $[Y, X]$
is homotopy commutative if and only if $[Y, X]$![]() is abelian for all $Y$
is abelian for all $Y$![]() .
.
For an integer $n\ge 1$![]() , let $X^{\times n}$
, let $X^{\times n}$![]() and $X^{\wedge n}$
and $X^{\wedge n}$![]() be the $n$
be the $n$![]() -fold Cartesian and smash power of $X$
-fold Cartesian and smash power of $X$![]() , respectively. Write $q_{X,n} : X^{\times n}\to X^{\wedge n}$
, respectively. Write $q_{X,n} : X^{\times n}\to X^{\wedge n}$![]() for the quotient map. Given a group-like space $X$
for the quotient map. Given a group-like space $X$![]() , we write $\gamma _{X,1}=\mbox {id}_X : X \to X$
, we write $\gamma _{X,1}=\mbox {id}_X : X \to X$![]() and $\gamma _{X,2} : X \times X \to X$
and $\gamma _{X,2} : X \times X \to X$![]() for the commutator map of $X$
for the commutator map of $X$![]() . Since the restriction ${\gamma _{X,2}}_{\mid X\vee X}\simeq \ast$
. Since the restriction ${\gamma _{X,2}}_{\mid X\vee X}\simeq \ast$![]() , we get a map $\bar {\gamma }_{X,2} : X \wedge X \to X$
, we get a map $\bar {\gamma }_{X,2} : X \wedge X \to X$![]() with $\bar {\gamma }_{X,2}q_{X,2}\simeq \gamma _{X,2}$
with $\bar {\gamma }_{X,2}q_{X,2}\simeq \gamma _{X,2}$![]() . Next, define inductively the maps
. Next, define inductively the maps
by $\gamma _{X,n+1}=\gamma _{X,2}\circ (\gamma _{X,1} \times \gamma _{X,n})$![]() and $\bar {\gamma }_{X,n+1}=\bar {\gamma }_{X,2}\circ (\gamma _{X,1} \wedge \bar {\gamma }_{X,n})$
and $\bar {\gamma }_{X,n+1}=\bar {\gamma }_{X,2}\circ (\gamma _{X,1} \wedge \bar {\gamma }_{X,n})$![]() for $n\ge 2$
for $n\ge 2$![]() , respectively. Then, the diagram
, respectively. Then, the diagram

commutes up to homotopy for $n\ge 2$![]() .
.
One might ask if there is an upper bound for the nilpotency class of $[Y, X]$![]() that is independent of $Y$
that is independent of $Y$![]() . The homotopy nilpotency class of $X$
. The homotopy nilpotency class of $X$![]() defined by Berstein–Ganea [Reference Berstein and Ganea5] is the least $n$
defined by Berstein–Ganea [Reference Berstein and Ganea5] is the least $n$![]() such that $\gamma _{X,n+1}\simeq \ast$
such that $\gamma _{X,n+1}\simeq \ast$![]() and $\gamma _{X,n}\not \simeq \ast$
and $\gamma _{X,n}\not \simeq \ast$![]() . Equivalently, the homotopy nilpotency class of $X$
. Equivalently, the homotopy nilpotency class of $X$![]() is the least $n$
is the least $n$![]() such that $\bar {\gamma }_{X,n+1}\simeq \ast$
such that $\bar {\gamma }_{X,n+1}\simeq \ast$![]() and $\bar {\gamma }_{X,n}\not \simeq \ast$
and $\bar {\gamma }_{X,n}\not \simeq \ast$![]() . In this case, we write $\mbox {nil}\ X =n$
. In this case, we write $\mbox {nil}\ X =n$![]() and call the homotopy associative $H$
and call the homotopy associative $H$![]() -space $X$
-space $X$![]() homotopy nilpotent. If no such integer exists, we put $\mbox {nil}\ X=\infty$
homotopy nilpotent. If no such integer exists, we put $\mbox {nil}\ X=\infty$![]() .
.
Note that $\mbox {nil}\ X=1$![]() if and only if $X$
if and only if $X$![]() is homotopy commutative. Given a space $X$
is homotopy commutative. Given a space $X$![]() , the number $\mbox {nil}\ \Omega (X)$
, the number $\mbox {nil}\ \Omega (X)$![]() (if any) is called the homotopy nilpotency class of $X$
(if any) is called the homotopy nilpotency class of $X$![]() .
.
Now, let $MU$![]() be the complex Thom spectrum, $BP^{\ast }(-)$
be the complex Thom spectrum, $BP^{\ast }(-)$![]() the Brown–Peterson cohomology with coefficients $BP^{\ast } = \mathbb {Z}_{(p)}[v_1,\ldots ]$
the Brown–Peterson cohomology with coefficients $BP^{\ast } = \mathbb {Z}_{(p)}[v_1,\ldots ]$![]() and $K(n)$
and $K(n)$![]() the $n$
the $n$![]() th Morava $K$
th Morava $K$![]() -theory at a prime $p$
-theory at a prime $p$![]() . Thus, $K(n)_\ast (pt) = \mathbb {Z}/p[v_n, v_n^{-1}]$
. Thus, $K(n)_\ast (pt) = \mathbb {Z}/p[v_n, v_n^{-1}]$![]() with $|v_n|=2p^{n}-2$
with $|v_n|=2p^{n}-2$![]() . Hopkins [Reference Hopkins10] described a cohomological criteria for the homotopy nilpotence of finite connected associative $H$
. Hopkins [Reference Hopkins10] described a cohomological criteria for the homotopy nilpotence of finite connected associative $H$![]() -spaces.
-spaces.
We recall Rao's formulation [Reference Rao15, Theorem 0.2] of Hopkins’ result [Reference Hopkins10, Theorem 2.1] needed in the sequel.
Theorem 1.2 Let $X$![]() be a finite homotopy associative $H$
be a finite homotopy associative $H$![]() -space. Then the following conditions are equivalent:
-space. Then the following conditions are equivalent:
(1) $X$
 is homotopy nilpotent;
is homotopy nilpotent;(2) $\widetilde {MU}^{\ast }(\bar {\gamma }_{X,n}) = 0$
 for sufficiently large $n$
for sufficiently large $n$ ;
;(3) for every prime $p$
 , $\widetilde {BP}^{\ast } (\bar {\gamma }_{X,n})= 0$
, $\widetilde {BP}^{\ast } (\bar {\gamma }_{X,n})= 0$ for sufficiently large $n$
for sufficiently large $n$ ;
;(4) for every prime $p$
 and positive integer m, $K(m)_\ast (\bar {\gamma }_{X,n})= 0$
and positive integer m, $K(m)_\ast (\bar {\gamma }_{X,n})= 0$ for sufficiently large $n$
for sufficiently large $n$ .
.
Then, in [Reference Hopkins10, Corollary 2.2], it was deduced the following homological criterion for the homotopy nilpotency.
Corollary 1.3 If $X$![]() is a finite associative $H$
is a finite associative $H$![]() -space and the integral homology $H_\ast (X,\mathbb {Z})$
-space and the integral homology $H_\ast (X,\mathbb {Z})$![]() is torsion free then $X$
is torsion free then $X$![]() is homotopy nilpotent.
is homotopy nilpotent.
Furthermore, we derive the following result the proof of which is essentially a small modification of Hopkins’ argument [Reference Hopkins10, Corollary 2.2].
Corollary 1.4 Let $X$![]() be a finite simply-connected $CW$
be a finite simply-connected $CW$![]() -complex with torsion free homology $H_\ast (X,\mathbb {Z})$
-complex with torsion free homology $H_\ast (X,\mathbb {Z})$![]() . If the $p$
. If the $p$![]() -localization $X_{(p)}$
-localization $X_{(p)}$![]() for a prime $p$
for a prime $p$![]() admits a homotopy associative $H$
admits a homotopy associative $H$![]() -structure then $\mbox {nil}\ X_{(p)}<\infty$
-structure then $\mbox {nil}\ X_{(p)}<\infty$![]() .
.
Proof. Note that $H\mathbb {Q}^{\ast }(\bar {\gamma }_n) = 0$![]() for the field of rationals $\mathbb {Q}$
for the field of rationals $\mathbb {Q}$![]() sufficiently large $n$
sufficiently large $n$![]() since $X_{(p)}^{\wedge n}$
since $X_{(p)}^{\wedge n}$![]() is at least $(n-1)$
is at least $(n-1)$![]() -connected. By assumption, the canonical map $MU^{\ast }(X_{(p)}^{\wedge n})\to MU^{\ast }(X_{(p)}^{\wedge n})\otimes \mathbb {Q}$
-connected. By assumption, the canonical map $MU^{\ast }(X_{(p)}^{\wedge n})\to MU^{\ast }(X_{(p)}^{\wedge n})\otimes \mathbb {Q}$![]() is injective, so by Theorem 1.2, it suffices to show that $MU^{\ast }(\bar {\gamma }_n)\otimes \mathbb {Q}=0$
is injective, so by Theorem 1.2, it suffices to show that $MU^{\ast }(\bar {\gamma }_n)\otimes \mathbb {Q}=0$![]() . But, for a finite $CW$
. But, for a finite $CW$![]() -complex $X$
-complex $X$![]() , there is a natural isomorphism
, there is a natural isomorphism

so the map $MU^{\ast }(\bar {\gamma }_n)\otimes \mathbb {Q}= 0$![]() as soon as $H\mathbb {Q}^{\ast }(\bar {\gamma }_n)=0$
as soon as $H\mathbb {Q}^{\ast }(\bar {\gamma }_n)=0$![]() . This completes the proof.
. This completes the proof.
Since the homology $H_\ast (\mathbb {S}^{2m-1},\mathbb {Z})$![]() are torsion free and $\mathbb {S}^{2m-1}$
are torsion free and $\mathbb {S}^{2m-1}$![]() is a finite $CW$
is a finite $CW$![]() -complex, Corollary 1.4 yields the result on the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$
-complex, Corollary 1.4 yields the result on the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
Theorem 1.5 If $m\ge 2$![]() and $p>3$
and $p>3$![]() is a prime then
is a prime then
with respect to any homotopy associative $H$![]() -structure on $\mathbb {S}^{2m-1}_{(p)}$
-structure on $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
In the sequel, we make use of the following. Let $f: X\to Y$![]() be an $H$
be an $H$![]() -map of homotopy associative $H$
-map of homotopy associative $H$![]() -spaces. Recall from [Reference Zabrodsky22, Chapter II] that:
-spaces. Recall from [Reference Zabrodsky22, Chapter II] that:
(1) it is said $\mbox {nil}\ f \le n$
 if $f\bar {\gamma }_{X,n}\simeq \ast$
if $f\bar {\gamma }_{X,n}\simeq \ast$ ;
;(2) $f$
 is called central if $\bar {\gamma }_{Y,2}(f \wedge \mbox {id}_Y)\simeq \ast$
is called central if $\bar {\gamma }_{Y,2}(f \wedge \mbox {id}_Y)\simeq \ast$ .
.
Notice that $\mbox {nil}\ f\le \min \{\mbox {nil}\ X,\mbox {nil}\ Y\}$![]() .
.
Then, in view of [Reference Zabrodsky22, Lemma 2.6.6], we have the following techniques for the study of the homotopy nilpotency.
Proposition 1.6 Let $F\stackrel {i}{\to } E\stackrel {q}{\to } B$![]() be an $H$
be an $H$![]() -fibration, i.e., $F\stackrel {i}{\to }E\stackrel {q}{\to }B$
-fibration, i.e., $F\stackrel {i}{\to }E\stackrel {q}{\to }B$![]() is a fibration, $F,E$
is a fibration, $F,E$![]() and $B$
and $B$![]() are $H$
are $H$![]() -spaces and the maps $i : F\to E$
-spaces and the maps $i : F\to E$![]() , and $q : E\to B$
, and $q : E\to B$![]() are $H$
are $H$![]() -maps.
-maps.
(1) If $\mbox {nil}\ q \le n$
 and $i : F\to E$
and $i : F\to E$ is central then $\mbox {nil}\ E \le n+1$
is central then $\mbox {nil}\ E \le n+1$ ;
;(2) if $\Omega (Y)\stackrel {i}{\to } E\stackrel {q}{\to } X$
 is the induced $H$
is the induced $H$ -fibration by an $H$
-fibration by an $H$ -map $f : X\to Y$
-map $f : X\to Y$ then the map $i : \Omega (Y)\to E$
then the map $i : \Omega (Y)\to E$ is central.
is central.
2. $A_m$ -spaces
-spaces
Recall that by Stasheff [Reference Stasheff18], an $A_m$![]() -structure on a space $X$
-structure on a space $X$![]() consists on $m$
consists on $m$![]() -tuples
-tuples

such that ${\frak q}_{n\ast } : \pi _k(\mathcal{E}_n(X),X)\to \pi _k(\mathcal {B}_n({X}))$![]() is an isomorphism for all $k\ge 1$
is an isomorphism for all $k\ge 1$![]() , together with a contracting homotopy $h: C\mathcal {E}_{n-1}(X)\to \mathcal {E}_n(X)$
, together with a contracting homotopy $h: C\mathcal {E}_{n-1}(X)\to \mathcal {E}_n(X)$![]() such that $h(C\mathcal {E}_{n-1}(X))\subseteq \mathcal {E}_n(X)$
such that $h(C\mathcal {E}_{n-1}(X))\subseteq \mathcal {E}_n(X)$![]() for $n=2,\ldots ,m$
for $n=2,\ldots ,m$![]() . For the purposes of homotopy theory, in the light of [Reference Stasheff18, Proposition 2], we can think of $X\to \mathcal {E}_n(X)\stackrel {\frak {q}_n}{\to }\mathcal {B}_n(X)$
. For the purposes of homotopy theory, in the light of [Reference Stasheff18, Proposition 2], we can think of $X\to \mathcal {E}_n(X)\stackrel {\frak {q}_n}{\to }\mathcal {B}_n(X)$![]() , as a fibration.
, as a fibration.
An $A_m$![]() -space for $m=0,1\ldots ,\infty$
-space for $m=0,1\ldots ,\infty$![]() is a space $X$
is a space $X$![]() with a multiplication $\mu : X\times X\to X$
with a multiplication $\mu : X\times X\to X$![]() that is associative up to higher homotopies involving up to $n$
that is associative up to higher homotopies involving up to $n$![]() variables. Further, an $A_\infty$
variables. Further, an $A_\infty$![]() -space has all coherent higher associativity homotopies and is equivalent to a loop space $\Omega (Y)$
-space has all coherent higher associativity homotopies and is equivalent to a loop space $\Omega (Y)$![]() for a space $Y$
for a space $Y$![]() called the classifying space of $X$
called the classifying space of $X$![]() .
.
By [Reference Stasheff18, Theorem 5], classes of spaces with $A_m$![]() -structures and $A_m$
-structures and $A_m$![]() -spaces coincide.
-spaces coincide.
Proposition 2.1 A space $X$![]() admits an $A_m$
admits an $A_m$![]() -structure if and only if $X$
-structure if and only if $X$![]() is an $A_m$
is an $A_m$![]() -space.
-space.
The $X$![]() -projective $n$
-projective $n$![]() -space $XP(n)$
-space $XP(n)$![]() for $n\le m$
for $n\le m$![]() , associated with an $A_m$
, associated with an $A_m$![]() -space X is the base space $\mathcal {B}_{n+1}(X)$
-space X is the base space $\mathcal {B}_{n+1}(X)$![]() of the derived $A_m$
of the derived $A_m$![]() -structure. The space $\mathcal {B}_1(X)$
-structure. The space $\mathcal {B}_1(X)$![]() is a point and $\mathcal {B}_2(X)$
is a point and $\mathcal {B}_2(X)$![]() can be recognized as the suspension $E(X)$
can be recognized as the suspension $E(X)$![]() . Notice that $\mathcal {B}_{m+1}(X)$
. Notice that $\mathcal {B}_{m+1}(X)$![]() can be defined even when $\frak {p}_{m+1}$
can be defined even when $\frak {p}_{m+1}$![]() cannot; it has the homotopy type of the mapping cone $C\mathcal {E}_m(X)\cup _{\frak {q}_m} \mathcal {B}_m(X)$
cannot; it has the homotopy type of the mapping cone $C\mathcal {E}_m(X)\cup _{\frak {q}_m} \mathcal {B}_m(X)$![]() . By means of [Reference Stasheff18, Theorem 11, Theorem 12], the spaces $\mathcal {E}_n(X)$
. By means of [Reference Stasheff18, Theorem 11, Theorem 12], the spaces $\mathcal {E}_n(X)$![]() and $\mathcal {B}_{n+1}(X)$
and $\mathcal {B}_{n+1}(X)$![]() have the homotopy types of the $n$
have the homotopy types of the $n$![]() th join $X^{\ast ^{n}}$
th join $X^{\ast ^{n}}$![]() and $C\mathcal {E}_n(X)\cup _{\frak {p}_n} \mathcal {B}_n(X)$
and $C\mathcal {E}_n(X)\cup _{\frak {p}_n} \mathcal {B}_n(X)$![]() for $n\le m$
for $n\le m$![]() , respectively provided $X$
, respectively provided $X$![]() is path-connected. Because of a homotopy equivalence $X^{\ast ^{n}}\simeq E^{n-1}(X^{\wedge n})$
is path-connected. Because of a homotopy equivalence $X^{\ast ^{n}}\simeq E^{n-1}(X^{\wedge n})$![]() for the $(n-1)$
for the $(n-1)$![]() th suspension $E^{n-1}$
th suspension $E^{n-1}$![]() , we deduce that the fibration $X\to \mathcal {E}_n(X)\stackrel {\frak {q}_n}{\to }\mathcal {B}_n(X)$
, we deduce that the fibration $X\to \mathcal {E}_n(X)\stackrel {\frak {q}_n}{\to }\mathcal {B}_n(X)$![]() is homotopy equivalent to
is homotopy equivalent to
3. Localized spheres $\mathbb {S}^{2m-1}_{(p)}$ and $\mathbb {S}^{2m-1}_{(p)}$
and $\mathbb {S}^{2m-1}_{(p)}$ -projective spaces $\mathbb {S}^{2m-1}_{(p)}P(n-1)$
-projective spaces $\mathbb {S}^{2m-1}_{(p)}P(n-1)$
Let $\mathbb {S}^{2m-1}_{(p)}$![]() be the $p$
be the $p$![]() -localization of the sphere $\mathbb {S}^{2m-1}$
-localization of the sphere $\mathbb {S}^{2m-1}$![]() at a prime $p$
at a prime $p$![]() . It is known by [Reference James11, Theorem 1.4] that $\mathbb {S}^{2m-1}_{(2)}$
. It is known by [Reference James11, Theorem 1.4] that $\mathbb {S}^{2m-1}_{(2)}$![]() does not admit a homotopy associative multiplication if $m\not =1,2$
does not admit a homotopy associative multiplication if $m\not =1,2$![]() . The sole obstruction to putting an $H$
. The sole obstruction to putting an $H$![]() -structure on $\mathbb {S}^{2m-1}$
-structure on $\mathbb {S}^{2m-1}$![]() is the Whitehead square $[\iota _{2m-1},\iota _{2m-1}]$
is the Whitehead square $[\iota _{2m-1},\iota _{2m-1}]$![]() of a generator $\iota _{2m-1}\in \pi _{2m-1}(\mathbb {S}^{2m-1})$
of a generator $\iota _{2m-1}\in \pi _{2m-1}(\mathbb {S}^{2m-1})$![]() . Since the order of $[\iota _{2m-1},\iota _{2m-1}]$
. Since the order of $[\iota _{2m-1},\iota _{2m-1}]$![]() is $\le 2$
is $\le 2$![]() , it follows that, if $p$
, it follows that, if $p$![]() is an odd prime, $\mathbb {S}^{2m-1}_{(p)}$
is an odd prime, $\mathbb {S}^{2m-1}_{(p)}$![]() admits an $H$
admits an $H$![]() -space structure. Which $p$
-space structure. Which $p$![]() -localized spheres $\mathbb {S}^{2m-1}_{(p)}$
-localized spheres $\mathbb {S}^{2m-1}_{(p)}$![]() with $p>2$
with $p>2$![]() have an $H$
have an $H$![]() -structures or loop structures is known by Adams [Reference Adams1]. More precisely, in view of [Reference Adams2] (see also [Reference Neisendorfer14, Proposition 11.2.2]), we have the following $H$
-structures or loop structures is known by Adams [Reference Adams1]. More precisely, in view of [Reference Adams2] (see also [Reference Neisendorfer14, Proposition 11.2.2]), we have the following $H$![]() -structure on $\mathbb {S}_{(p)}^{2m-1}$
-structure on $\mathbb {S}_{(p)}^{2m-1}$![]() .
.
Proposition 3.1 If $p$![]() is an odd prime and $n\ge 1$
is an odd prime and $n\ge 1$![]() then there is an $H$
then there is an $H$![]() -structure $\mu _A$
-structure $\mu _A$![]() on $\mathbb {S}_{(p)}^{2m-1}$
on $\mathbb {S}_{(p)}^{2m-1}$![]() $($
$($![]() unique up to homotopy if $p$
unique up to homotopy if $p$![]() is an odd prime and $n\ge 2$
is an odd prime and $n\ge 2$![]() or if $n \ge 1$
or if $n \ge 1$![]() and $p>3)$
and $p>3)$![]() such that the double suspension $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}\mathbb {S}_{(p)}^{2m+1}$
such that the double suspension $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}\mathbb {S}_{(p)}^{2m+1}$![]() is an $H$
is an $H$![]() -map.
-map.
Further:
(1) if $p>2$
 then $(\mathbb {S}^{2m-1}_{(p)},\mu _A)$
then $(\mathbb {S}^{2m-1}_{(p)},\mu _A)$ is a homotopy commutative $H$
is a homotopy commutative $H$ -space;
-space;(2) if $p>3$
 then $(\mathbb {S}^{2m-1}_{(p)},\mu _A)$
then $(\mathbb {S}^{2m-1}_{(p)},\mu _A)$ is a homotopy associative $H$
is a homotopy associative $H$ -space.
-space.
Loosely speaking, via the double suspension map $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$![]() , the multiplication on the double loop space $\Omega ^{2}\mathbb {S}_{(p)}^{2m+1}$
, the multiplication on the double loop space $\Omega ^{2}\mathbb {S}_{(p)}^{2m+1}$![]() restricts to the multiplication $\mu _A$
restricts to the multiplication $\mu _A$![]() on the bottom cell $\mathbb {S}_{(p)}^{2m-1}$
on the bottom cell $\mathbb {S}_{(p)}^{2m-1}$![]() . Next, by Mimura et al. [Reference Mimura, Nishida and Toda13, Proposition 6.8], Stasheff [Reference Stasheff18] and Sullivan [Reference Sullivan19], we have the result on $H$
. Next, by Mimura et al. [Reference Mimura, Nishida and Toda13, Proposition 6.8], Stasheff [Reference Stasheff18] and Sullivan [Reference Sullivan19], we have the result on $H$![]() -structures on $\mathbb {S}_{(p)}^{2m-1}$
-structures on $\mathbb {S}_{(p)}^{2m-1}$![]() .
.
Proposition 3.2 Let $m\ge 2$![]() and $p>3$
and $p>3$![]() be a prime. Then:
be a prime. Then:
(1) the $p$
 -localized sphere $\mathbb {S}_{(p)}^{2m-1}$
-localized sphere $\mathbb {S}_{(p)}^{2m-1}$ admits an $A_{p-1}$
admits an $A_{p-1}$ -structure;
-structure;(2) if $\mathbb {S}_{(p)}^{2m-1}$
 admits an $A_{p}$
admits an $A_{p}$ -structure then $m\mid p-1$
-structure then $m\mid p-1$ ;
;(3) $\mathbb {S}_{(p)}^{2m-1}$
 admits an $A_\infty$
admits an $A_\infty$ -structure if and only if $m\mid p-1$
-structure if and only if $m\mid p-1$ provided $p>3$
provided $p>3$ .
.
This implies that $\mathbb {S}^{2m-1}_{(p)}$![]() does not admit an $A_{p}$
does not admit an $A_{p}$![]() -structure provided $m\nmid p-1$
-structure provided $m\nmid p-1$![]() . We also point out that an $A_{p-1}$
. We also point out that an $A_{p-1}$![]() -structure on $\mathbb {S}^{2m-1}_{(p)}$
-structure on $\mathbb {S}^{2m-1}_{(p)}$![]() is induced from $\Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$
is induced from $\Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$![]() which is of course an $A_\infty$
which is of course an $A_\infty$![]() -space, via the double suspension map $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$
-space, via the double suspension map $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$![]() . Further, in view of Proposition 3.2, the sphere $\mathbb {S}_{(p)}^{2m-1}$
. Further, in view of Proposition 3.2, the sphere $\mathbb {S}_{(p)}^{2m-1}$![]() admits an $A_{p}$
admits an $A_{p}$![]() -structure if and only if it admits a classifying space.
-structure if and only if it admits a classifying space.
Now, we show the nilpotency of $\mathbb {S}^{2m-1}_{(p)}$![]() provided $m\mid p-1$
provided $m\mid p-1$![]() .
.
Proposition 3.3 If $m\mid p-1$![]() then $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}\le 2$
then $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}\le 2$![]() with respect to the $A_\infty$
with respect to the $A_\infty$![]() -structure on $\mathbb {S}^{2m-1}_{(p)}$
-structure on $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
Proof. Sullivan [Reference Sullivan19], to construct a classifying space for $\mathbb {S}_{(p)}^{2m-1}$![]() with $m\mid p-1$
with $m\mid p-1$![]() , considered the space $K(\mathbb {Z}_p, 2)$
, considered the space $K(\mathbb {Z}_p, 2)$![]() , where $\hat {\mathbb {Z}}_p$
, where $\hat {\mathbb {Z}}_p$![]() is the $p$
is the $p$![]() -adic integers and the cyclic subgroup $\Gamma <\mathbb {Z}_{p-1}<\hat {\mathbb {Z}}_p^{\ast }$
-adic integers and the cyclic subgroup $\Gamma <\mathbb {Z}_{p-1}<\hat {\mathbb {Z}}_p^{\ast }$![]() (the $p$
(the $p$![]() -adic units) of order $m$
-adic units) of order $m$![]() . Then $\Gamma$
. Then $\Gamma$![]() acts freely on a model of $K(\hat {\mathbb {Z}}_p,2)$
acts freely on a model of $K(\hat {\mathbb {Z}}_p,2)$![]() and $X = K(\hat {\mathbb {Z}}_p,2)/\Gamma$
and $X = K(\hat {\mathbb {Z}}_p,2)/\Gamma$![]() has cohomology $H^{\ast }(X,\mathbb {Z}/p\mathbb {Z}) = S(x,2m)$
has cohomology $H^{\ast }(X,\mathbb {Z}/p\mathbb {Z}) = S(x,2m)$![]() , the graded symmetric algebra generated by $x$
, the graded symmetric algebra generated by $x$![]() with degree $|x|=2m$
with degree $|x|=2m$![]() and $\pi _1(X) = \Gamma$
and $\pi _1(X) = \Gamma$![]() . After completing $X$
. After completing $X$![]() at $p$
at $p$![]() to $\hat {X}_p$
to $\hat {X}_p$![]() , we have a space with $\pi _1(\hat {X}_p) = 0$
, we have a space with $\pi _1(\hat {X}_p) = 0$![]() and $H^{\ast }(\hat {X}_p, \mathbb {Z}/p\mathbb {Z}) = S(x,2m)$
and $H^{\ast }(\hat {X}_p, \mathbb {Z}/p\mathbb {Z}) = S(x,2m)$![]() . The map $\mathbb {S}^{2m-1}\to \Omega (\hat {X}_p)$
. The map $\mathbb {S}^{2m-1}\to \Omega (\hat {X}_p)$![]() defines a homotopy equivalence $\mathbb {S}^{2m-1}_{(p)}\stackrel {\simeq }{\to } \Omega (\hat {X}_p)$
defines a homotopy equivalence $\mathbb {S}^{2m-1}_{(p)}\stackrel {\simeq }{\to } \Omega (\hat {X}_p)$![]() and $\hat {X}_p$
and $\hat {X}_p$![]() is a classifying space for $\mathbb {S}_{(p)}^{2m-1}$
is a classifying space for $\mathbb {S}_{(p)}^{2m-1}$![]() .
.
But, by [Reference Neisendorfer14, Chapter 2], the $p$![]() -completion preserves a fibration of simply-connected spaces. Hence, the $p$
-completion preserves a fibration of simply-connected spaces. Hence, the $p$![]() -completion of the fibration $\Gamma \to K(\hat {\mathbb {Z}}_p,2)\to X$
-completion of the fibration $\Gamma \to K(\hat {\mathbb {Z}}_p,2)\to X$![]() leads to the fibration $\hat {\Gamma }_p\to K(\hat {\mathbb {Z}}_p,2)\to \hat {X}_p$
leads to the fibration $\hat {\Gamma }_p\to K(\hat {\mathbb {Z}}_p,2)\to \hat {X}_p$![]() . Consequently, we get the $H$
. Consequently, we get the $H$![]() -fibration
-fibration
Since the space $X = K(\hat {\mathbb {Z}}_p,2)/\Gamma$![]() is simply-connected, we have $\widehat {(\Omega (X))}_p=\Omega (\hat {X}_p)$
is simply-connected, we have $\widehat {(\Omega (X))}_p=\Omega (\hat {X}_p)$![]() . Then, by means of the $p$
. Then, by means of the $p$![]() -completeness of $K(\hat {\mathbb {Z}}_p,1)$
-completeness of $K(\hat {\mathbb {Z}}_p,1)$![]() , the $p$
, the $p$![]() -completion of the fibration above yields the $H$
-completion of the fibration above yields the $H$![]() -fibration
-fibration
determined by the canonical $H$![]() -map $\hat {\Gamma }_p\to K(\hat {\mathbb {Z}}_p,2)$
-map $\hat {\Gamma }_p\to K(\hat {\mathbb {Z}}_p,2)$![]() .
.
Thus, by means of Proposition 1.6(2), we derive that the $H$![]() -map $\Omega ( K(\hat {\mathbb {Z}}_p,2))= K(\hat {\mathbb {Z}}_p,1)\to \Omega (X)$
-map $\Omega ( K(\hat {\mathbb {Z}}_p,2))= K(\hat {\mathbb {Z}}_p,1)\to \Omega (X)$![]() is central and so Proposition 1.6(1) yields
is central and so Proposition 1.6(1) yields
This completes the proof.
Then, Arkowitz, Ewing and Schiffman [Reference Arkowitz, Ewing and Schiffman4, Theorem 0.1] have proved the following result on $H$![]() -structures on $\mathbb {S}^{2m-1}_{(p)}$
-structures on $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
Theorem 3.4 Let $p$![]() be an odd prime and $n$
be an odd prime and $n$![]() a positive integer with $m\mid p-1$
a positive integer with $m\mid p-1$![]() .
.
(1) If $m< p-1$
 then $\mathbb {S}^{2m-1}_{(p)}$
then $\mathbb {S}^{2m-1}_{(p)}$ has a unique $H$
has a unique $H$ -structure which is both homotopy commutative and a loop multiplication.
-structure which is both homotopy commutative and a loop multiplication.(2) If $m=p-1$
 then $\mathbb {S}^{2m-1}_{(p)}$
then $\mathbb {S}^{2m-1}_{(p)}$ has precisely $p$
has precisely $p$ multiplications; one homotopy commutative and not a loop multiplication, and $(p-1)$
multiplications; one homotopy commutative and not a loop multiplication, and $(p-1)$ loop $H$
loop $H$ -structures which are $H$
-structures which are $H$ -equivalent but not homotopy commutative.
-equivalent but not homotopy commutative.
Thus, the above and Theorem 3.4(2) yield the conclusion.
Corollary 3.5 If $m\mid p-1$![]() and $p>3$
and $p>3$![]() then
then
with respect to all $(p-1)$![]() loop $H$
loop $H$![]() -structures on $\mathbb {S}^{2m-1}_{(p)}$
-structures on $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
We point out that Proposition 3.3 has been already shown by Meier [Reference Meier12] in the special case when $m = p-1$![]() using the result [Reference Toda20, Theorem 13.4].
using the result [Reference Toda20, Theorem 13.4].
Theorem 3.6 Let $p$![]() be an odd prime.
be an odd prime.

Given a pointed connected topological space $X$![]() and a prime $p$
and a prime $p$![]() , write $\pi _m(X;p)$
, write $\pi _m(X;p)$![]() for the $p$
for the $p$![]() -primary component of its $m$
-primary component of its $m$![]() th homotopy group $\pi _m(X)$
th homotopy group $\pi _m(X)$![]() for $m\ge 1$
for $m\ge 1$![]() . Recall that by [Reference Copeland6], the set of homotopy classes of possible $H$
. Recall that by [Reference Copeland6], the set of homotopy classes of possible $H$![]() -structures on $\mathbb {S}^{2m-1}_{(p)}$
-structures on $\mathbb {S}^{2m-1}_{(p)}$![]() is in one-to-one correspondence with $[\mathbb {S}^{2m-1}_{(p)}\wedge \mathbb {S}^{2m-1}_{(p)},\mathbb {S}^{2m-1}_{(p)}]=\pi _{4m-2}(\mathbb {S}^{2m-1},p)$
is in one-to-one correspondence with $[\mathbb {S}^{2m-1}_{(p)}\wedge \mathbb {S}^{2m-1}_{(p)},\mathbb {S}^{2m-1}_{(p)}]=\pi _{4m-2}(\mathbb {S}^{2m-1},p)$![]() . Consequently, if $p>3$
. Consequently, if $p>3$![]() then we may study the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$
then we may study the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
Nevertheless, in some particular cases, an estimation for $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}$![]() might be stated. First, notice that Theorem 3.6 implies that
might be stated. First, notice that Theorem 3.6 implies that
provided $k<2p(p-1)-2$![]() , $k\not =2i(p-1)-1$
, $k\not =2i(p-1)-1$![]() for $i = 1,\ldots , p-1$
for $i = 1,\ldots , p-1$![]() and $k\not =2i(p-1)-2$
and $k\not =2i(p-1)-2$![]() for $i = m,\ldots , p-1$
for $i = m,\ldots , p-1$![]() .
.
Certainly, the homotopy group $\pi _{4m-2}(\mathbb {S}^{2m-1})$![]() is finite and write $\sharp \pi _{4m-2}(\mathbb {S}^{2m-1})$
is finite and write $\sharp \pi _{4m-2}(\mathbb {S}^{2m-1})$![]() for its order. Then, for $p_m=\max \{p;\, p \,\mbox {is a prime with}\ p\mid \sharp \pi _{4m-2}(\mathbb {S}^{2m-1})\}$
for its order. Then, for $p_m=\max \{p;\, p \,\mbox {is a prime with}\ p\mid \sharp \pi _{4m-2}(\mathbb {S}^{2m-1})\}$![]() , we apply Theorem 3.6 to state the result on an $H$
, we apply Theorem 3.6 to state the result on an $H$![]() -structure on $\mathbb {S}^{2m-1}_{(p)}$
-structure on $\mathbb {S}^{2m-1}_{(p)}$![]() .
.
Proposition 3.8 Let $p>3$![]() and $m\ge 3$
and $m\ge 3$![]() .
.
If $m< p-1$![]() or $p>\max \{3,p_m\}$
or $p>\max \{3,p_m\}$![]() then $\mathbb {S}^{2m-1}_{(p)}$
then $\mathbb {S}^{2m-1}_{(p)}$![]() admits a unique homotopy associative and commutative $H$
admits a unique homotopy associative and commutative $H$![]() -structure and $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}=1$
-structure and $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}=1$![]() .
.
Proof. If $m< p-1$![]() then $2m-1<2p-3$
then $2m-1<2p-3$![]() and Equation (3.7) implies that
and Equation (3.7) implies that
If $p>\max \{3,p_m\}$![]() then $\pi _{2(2m-1)}(\mathbb {S}^{2m-1}_{(p)})=0$
then $\pi _{2(2m-1)}(\mathbb {S}^{2m-1}_{(p)})=0$![]() as well. Then, Proposition 3.1 provides an existence of a unique homotopy associative and commutative $H$
as well. Then, Proposition 3.1 provides an existence of a unique homotopy associative and commutative $H$![]() -structure on $\mathbb {S}^{2m-1}_{(p)}$
-structure on $\mathbb {S}^{2m-1}_{(p)}$![]() and the proof follows.
and the proof follows.
Now, we apply the results above to $\mathbb {S}^{2m-1}_{(p)}$![]() -projective spaces $\mathbb {S}^{2m-1}_{(p)}P(n-1)$
-projective spaces $\mathbb {S}^{2m-1}_{(p)}P(n-1)$![]() . Write $J_k(\mathbb {S}^{2n})$
. Write $J_k(\mathbb {S}^{2n})$![]() for the $k$
for the $k$![]() th stage of the James construction on the sphere $\mathbb {S}^{2m}$
th stage of the James construction on the sphere $\mathbb {S}^{2m}$![]() .
.
Since $\mathbb {S}^{2m-1}_{(p)}P(1)\simeq \mathbb {S}^{2m}_{(p)}$![]() and $\mathbb {S}^{2m-1}_{(p)}P(n-1)\simeq C\mathbb {S}^{2(n-1)m-1}_{(p)} \cup _{q_{n-1}}\mathbb {S}^{2m-1}_{(p)}P(n-2)$
and $\mathbb {S}^{2m-1}_{(p)}P(n-1)\simeq C\mathbb {S}^{2(n-1)m-1}_{(p)} \cup _{q_{n-1}}\mathbb {S}^{2m-1}_{(p)}P(n-2)$![]() for the fibration (2.2)
for the fibration (2.2)
with $X=\mathbb {S}^{2m-1}_{(p)}$![]() , we can define inductively a map
, we can define inductively a map
for $p>3$![]() provided $n-1< p$
provided $n-1< p$![]() with $m\nmid p-1$
with $m\nmid p-1$![]() or any $n\ge 1$
or any $n\ge 1$![]() with $m\mid p-1$
with $m\mid p-1$![]() .
.
Furthermore, one can state the result on some $\mathbb {S}^{2m-1}_{(p)}P(n-1)$![]() .
.
Proposition 3.9 The canonical map
is an integral homology isomorphism for $p>3$![]() provided $n-1< p$
provided $n-1< p$![]() with $m\nmid p-1$
with $m\nmid p-1$![]() or any $n\ge 1$
or any $n\ge 1$![]() with $m\mid p-1$
with $m\mid p-1$![]() .
.
Consequently, by means of the Whitehead Theorem, we get a homotopy equivalence $\mathbb {S}^{2m-1}_{(p)}P(n-1)\stackrel {\simeq }{\longrightarrow }J_{n-1}(\mathbb {S}^{2m}_{(p)})$![]() which yields an $H$
which yields an $H$![]() -homotopy equivalence
-homotopy equivalence
for $p>3$![]() provided $n-1< p$
provided $n-1< p$![]() with $m\nmid p-1$
with $m\nmid p-1$![]() or any $n\ge 1$
or any $n\ge 1$![]() with $m\mid p-1$
with $m\mid p-1$![]() . But, Gray showed [Reference Gray9, Theorem 1 and the footnote on p. 182] that $\Omega (J_{jp^{s}-1}(\mathbb {S}^{2m}))$
. But, Gray showed [Reference Gray9, Theorem 1 and the footnote on p. 182] that $\Omega (J_{jp^{s}-1}(\mathbb {S}^{2m}))$![]() with $p\ge 3$
with $p\ge 3$![]() is universal in the category of homotopy associative commutative $H$
is universal in the category of homotopy associative commutative $H$![]() -spaces, with its generating subspace being the $(2mp-2)$
-spaces, with its generating subspace being the $(2mp-2)$![]() -skeleton provided $p\ge 3$
-skeleton provided $p\ge 3$![]() with $s>0$
with $s>0$![]() and an odd $j\le p$
and an odd $j\le p$![]() . Hence, Proposition 3.9 yields the conclusion on the $H$
. Hence, Proposition 3.9 yields the conclusion on the $H$![]() -structure on $\Omega (\mathbb {S}^{2m-1}_{(p)}P(jp^{s}-1))$
-structure on $\Omega (\mathbb {S}^{2m-1}_{(p)}P(jp^{s}-1))$![]() .
.
Corollary 3.10 If $p>3$![]() and $m\ge 2$
and $m\ge 2$![]() then the associative $H$
then the associative $H$![]() -space $\Omega (\mathbb {S}^{2m-1}_{(p)}P(jp^{s}-1))$
-space $\Omega (\mathbb {S}^{2m-1}_{(p)}P(jp^{s}-1))$![]() is homotopy commutative provided $j=s=1$
is homotopy commutative provided $j=s=1$![]() and $m\nmid p-1$
and $m\nmid p-1$![]() or $s\ge 1$
or $s\ge 1$![]() , $j\le p$
, $j\le p$![]() is odd and $m\mid p-1$
is odd and $m\mid p-1$![]() .
.
For further studies of the homotopy nilpotency of $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$![]() , we need to show an existence of some $H$
, we need to show an existence of some $H$![]() -fibration.
-fibration.
Lemma 3.11 If $p> 3$![]() is a prime, $m\ge 2$
is a prime, $m\ge 2$![]() and $m\mid p-1$
and $m\mid p-1$![]() then for a fixed $A_\infty$
then for a fixed $A_\infty$![]() -structure on $\mathbb {S}^{2m-1}_{(p)}$
-structure on $\mathbb {S}^{2m-1}_{(p)}$![]() and $n\ge 2$
and $n\ge 2$![]() then there is an $H$
then there is an $H$![]() -fibration
-fibration
with the central map $\Omega (\mathbb {S}^{2mn-1}_{(p)})\longrightarrow \Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$![]() .
.
Proof. Recall that by Proposition 3.2(3) the space $\mathbb {S}^{2m-1}_{(p)}$![]() admits an $A_\infty$
admits an $A_\infty$![]() -structure provided $m\mid p-1$
-structure provided $m\mid p-1$![]() . Furthermore, for such the space $\mathbb {S}^{2m-1}_{(p)}$
. Furthermore, for such the space $\mathbb {S}^{2m-1}_{(p)}$![]() , Sullivan [Reference Sullivan19] constructed a classifying space denoted in the proof of Proposition 3.3 by $\hat {X}_p$
, Sullivan [Reference Sullivan19] constructed a classifying space denoted in the proof of Proposition 3.3 by $\hat {X}_p$![]() .
.
Next, write $i_n : \mathbb {S}^{2mn-1}_{(p)}\hookrightarrow \mathbb {S}^{2m-1}_{(p)}P(n-1)$![]() and $j_n : \mathbb {S}^{2m-1}_{(p)}P(n-1)\hookrightarrow \hat {X}_p$
and $j_n : \mathbb {S}^{2m-1}_{(p)}P(n-1)\hookrightarrow \hat {X}_p$![]() for the canonical inclusion maps and notice that $E^{n-1}(\mathbb {S}^{2m-1}_{(p)})^{\wedge n}=\mathbb {S}^{2mn-1}_{(p)}$
for the canonical inclusion maps and notice that $E^{n-1}(\mathbb {S}^{2m-1}_{(p)})^{\wedge n}=\mathbb {S}^{2mn-1}_{(p)}$![]() . Since $\Omega (\hat {X}_p)\simeq \mathbb {S}^{2m-1}_{(p)}$
. Since $\Omega (\hat {X}_p)\simeq \mathbb {S}^{2m-1}_{(p)}$![]() , we get the Puppe fibration sequence
, we get the Puppe fibration sequence
But, the $H$![]() -deviation [Reference Zabrodsky22, Definition 1.4.1.] of $\partial _n$
-deviation [Reference Zabrodsky22, Definition 1.4.1.] of $\partial _n$![]() is a map $\mathbb {S}^{2m-1}_{(p)}\wedge \mathbb {S}^{2m-1}_{(p)}\to \mathbb {S}^{2mn-1}_{(p)}$
is a map $\mathbb {S}^{2m-1}_{(p)}\wedge \mathbb {S}^{2m-1}_{(p)}\to \mathbb {S}^{2mn-1}_{(p)}$![]() which is null homotopic for dimension and connectivity reasons if $n\ge 2$
which is null homotopic for dimension and connectivity reasons if $n\ge 2$![]() . Then, by Zabrodsky [Reference Zabrodsky22, Proposition 1.5.1.], $\partial _n$
. Then, by Zabrodsky [Reference Zabrodsky22, Proposition 1.5.1.], $\partial _n$![]() is an $H$
is an $H$![]() -map. Hence, Proposition 1.6(2) implies that $\Omega (i_n) : \Omega (\mathbb {S}^{2mn-1}_{(p)})\to \Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$
-map. Hence, Proposition 1.6(2) implies that $\Omega (i_n) : \Omega (\mathbb {S}^{2mn-1}_{(p)})\to \Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$![]() is central in the $H$
is central in the $H$![]() -fibration
-fibration
and this completes the proof.
Thus, Propositions 1.6(1), 3.3, Corollary 3.10 and Lemma 3.11 yield the result on the homotopy nilpotency of $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$![]() under some conditions.
under some conditions.
Theorem 3.12 Let $m\ge 2$![]() and $p> 3$
and $p> 3$![]() be a prime.
be a prime.
(1) If $n\ge 2$
 and $m\mid p-1$
and $m\mid p-1$ then
\[ \mbox{nil}\ \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))\le \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}+1\le 3; \]
then
\[ \mbox{nil}\ \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))\le \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}+1\le 3; \]
(2) if $j=s= 1$
 and $m \nmid p-1$
and $m \nmid p-1$ , or if we have $s\ge 1$
, or if we have $s\ge 1$ , $j\le p$
, $j\le p$ , $j$
, $j$ odd, and $m \mid p-1$
odd, and $m \mid p-1$ , then
\[ \mbox{nil}\ \Omega(\mathbb{S}^{2m-1}_{(p)}P(jp^{s}-1))=1. \]
, then
\[ \mbox{nil}\ \Omega(\mathbb{S}^{2m-1}_{(p)}P(jp^{s}-1))=1. \]
To conclude, we point out that Theorem 3.12 applies to more cases than Meier's result [Reference Meier12, Theorem 5.4].
We close the paper with the following conjecture.
Conjecture 3.13 If $p> 3$![]() is a prime and $m,n\ge 2$
is a prime and $m,n\ge 2$![]() then
then
Acknowledgements
The author greatly appreciates the anonymous referee for a careful reading of the manuscript last version and his/her many insightful comments and suggestions. Even deeper debts are owed to him/her for suggesting Proposition 3.9, the proof of Lemma 3.11 and indicating paper [Reference Gray9].