We develop a model to predict the fragmentation limit of drops colliding off-centre. The prediction is excellent over a wide range of liquid properties and it can be used without adjusting any parameter. The so-called stretching separation is attributed to the extension of the merged drop above a critical aspect ratio of 3.25. The evolution of this aspect ratio is influenced by the liquid viscosity and can be interpreted via an energy balance. This approach is then adapted to drop–jet collisions, which we model as consecutive drop–drop collisions. The fragmentation criterion is similar to that observed for drop–drop collisions, while the evolution of the stretched jet aspect ratio is modified to account for the different flow fields and geometry.

Recently, an unusual scaling law has been observed in circular hydraulic jumps and has been attributed to a supposed missing term in the local energy balance of the flow (Bhagat et al., J. Fluid Mech., vol. 851, 2018, R5). In this paper, we show that – though the experimental observation is valuable and interesting – this interpretation is presumably not the right one. When transposed to the case of an axial sheet formed by two impinging liquid jets, the assumed principle leads in fact to a velocity distribution in contradiction with the present knowledge for this kind of flow. We show here how to correct this approach by maintaining consistency with surface tension thermodynamics: for Savart–Taylor sheets, when adequately corrected, we recover the well-known $1/r$ liquid thickness with a constant and uniform velocity dictated by Bernoulli's principle. In the case of circular hydraulic jumps, we propose here a simple approach based on Watson's description of the flow in the central region (Watson, J. Fluid Mech., vol. 20, 1964, pp. 481–499), combined with appropriate boundary conditions on the circular front formed. Depending on the specific condition, we find in turn the new scaling by Bhagat et al. (2018) and the more conventional scaling law found long ago by Bohr et al. (J. Fluid Mech., vol. 254, 1993, pp. 635–648). We clarify here a few situations in which one should hold rather than the other, hoping to reconcile the observations of Bhagat et al. with the present knowledge of circular hydraulic jump modelling. However, the question of a possible critical Froude number imposed at the jump exit and dictating logarithmic corrections to scaling remains an open and unsolved question.

Many recent studies have diagnosed opposite-signed diffusion eigenvalues to be a prevalent feature of the transfer tensor for diffusive tracer transport by oceanic mesoscale eddies. This diagnosed tensor, which we refer to as the diffusion tensor, therefore accounts for tracer filamentation effects. The preferential orientation of this filamentation is quantified by the principal axis of the diffusion tensor, namely the diffusion axis. Parameterisations of eddy diffusion commonly invoke a diffusion tensor, typically one with non-negative eigenvalues to avoid numerical issues. Motivated by the need to parameterise tracer filamentation, in this study we examine diffusion of a Gaussian tracer patch with imposed opposite-signed diffusion eigenvalues, and in particular we focus on the time scale for the onset of instability. For a fixed diffusion axis, numerical instability is an inevitable consequence of persistent up-gradient fluxes associated with the negative eigenvalue. For typical oceanic scales and diffusion magnitudes, this time scale is of the order of $100$ days, but is shorter for larger negative eigenvalues or for finer grid resolutions. We show that imposing a time-dependent diffusion axis can lead to simulations with no onset of instability after 100 000 days of tracer evolution. Although motivated by oceanographic fluid dynamics, our results have much broader applications since diffusive processes are present in a wide range of fluid flows.

We develop direct inversion methods for inferring the rheology of a fluid from observations of its shallow flow. First, the evolution equation for the free-surface flow of an inertia-less current with general constitutive law is derived. The relationship between the volume flux of fluid and the basal stress, $\tau _b$, is encapsulated by a single function $F(\tau _b)$, which depends only on the constitutive law. The inversion method consists of (i) determining the flux and basal stress from the free-surface evolution, (ii) comparing the flux with the basal stress to constrain $F$ and (iii) inferring the constitutive law from $F$. Examples are presented for both steady and transient free-surface flows demonstrating that a wide range of constitutive laws can be directly obtained. For flows in which the free-surface velocity is known, we derive a different method, which circumvents the need to calculate the flux.

The attenuation of two-dimensional boundary-layer instabilities by a finite-length, viscoelastic patch is investigated by means of global linear stability theory. First, the modal stability properties of the coupled problem are assessed, revealing unstable fluid-elastic travelling-wave flutter modes. Second, the Tollmien–Schlichting instabilities over a rigid wall are characterised via the analysis of the fluid resolvent operator in order to determine a baseline for the fluid-structural analysis. To investigate the effect of the elastic patch on the growth of these flow instabilities, we first consider the linear frequency response of the coupled fluid-elastic system to the dominant rigid-wall forcing modes. In the frequency range of Tollmien–Schlichting waves, the energetic flow amplification is clearly reduced. However, an amplification is observed for higher frequencies, associated with travelling-wave flutter. This increased complexity requires the analysis of the coupled fluid-structural resolvent operator; the optimal, coupled, resolvent modes confirm the attenuation of the Tollmien–Schlichting instabilities, while also being able to capture the amplification at the higher frequencies. Finally, a decomposition of the fluid-structural response is proposed to reveal the wave cancellation mechanism responsible for the attenuation of the Tollmien–Schlichting waves. The viscoelastic patch, excited by the incoming rigid-wall wave, provokes a fluid-elastic wave that is out-of-phase with the former, thus reducing its amplitude.

The Taylor–Couette flow of non-colloidal, neutrally buoyant spherical particle suspensions in the $\phi =0\,\%-28\,\%$ concentration range and (17–250) Reynolds number ($\mathcal {R})$ range is studied using synchronized flow visualization and torque measurements. Both methods are applied in ramp-up/down (acceleration/deceleration of the inner cylinder) experiments to detect the various flow structure states and bifurcation natures, their critical conditions and their lifetime in $\mathcal {R}$ range. Torque measurement allows us to discuss the evolution of the (pseudo) Nusselt number, $\mathcal {N}$, and friction coefficient with $\mathcal {R}$ or alternatively the Taylor number, Ta. Flow visualization brings additional information on the unsteady dynamics of flow states. For concentrations higher than $\phi =6\,\%$, two unsteady (spiral vortex flow, wavy vortex flow) and one steady (Taylor vortex flow) flow state are observed in both ramp-up/down experiments. Hysteretic behaviour is reported for some primary, secondary and tertiary bifurcations, which are thus found to be subcritical. A critical concentration is observed at $\phi =15\,\%$ for the range of $\mathcal {R}$ at which spiral vortex flow is encountered. Characteristic frequencies of unsteady flow state (spiral vortex flow, wavy vortex flow) for different suspension concentrations are evaluated. Finally, three hydrodynamic concentration subregimes are identified for the first time, with their distinct sets of concentration-dependent critical conditions, torque scaling exponents and friction coefficients.

Direct numerical simulations (DNS) are performed to investigate the spatial evolution of flat-plate zero-pressure-gradient turbulent boundary layers over long streamwise domains (${>}300\delta _i$, with $\delta _i$ the inflow boundary-layer thickness) at three different Mach numbers, $2.5$, $4.9$ and $10.9$, with the surface temperatures ranging from quasiadiabatic to highly cooled conditions. The settlement of turbulence statistics into a fully developed equilibrium state of the turbulent boundary layer has been carefully monitored, either based on the satisfaction of the von Kármán integral equation or by comparing runs with different inflow turbulence generation techniques. The generated DNS database is used to characterize the streamwise evolution of multiple important variables in the high-Mach-number, cold-wall regime, including the skin friction, the Reynolds analogy factor, the shape factor, the Reynolds stresses, and the fluctuating wall quantities. The data confirm the validity of many classic and newer compressibility transformations at moderately high Reynolds numbers (up to friction Reynolds number $Re_\tau \approx 1200$) and show that, with proper scaling, the sizes of the near-wall streaks and superstructures are insensitive to the Mach number and wall cooling conditions. The strong wall cooling in the hypersonic cold-wall case is found to cause a significant increase in the size of the near-wall turbulence eddies (relative to the boundary-layer thickness), which leads to a reduced-scale separation between the large and small turbulence scales, and in turn to a lack of an outer peak in the spanwise spectra of the streamwise velocity in the logarithmic region.

We investigate the formation and stability of a pair of identical soft capsules in channel flow under mild inertia. We employ a combination of the lattice Boltzmann, finite element and immersed boundary methods to simulate the elastic particles in flow. Validation tests show excellent agreement with numerical results obtained by other research groups. Our results reveal new trajectory types that have not been observed for pairs of rigid particles. While particle softness increases the likelihood of a stable pair forming, the pair stability is determined by the lateral position of the particles. A key finding is that stabilisation of the axial distance occurs after lateral migration of the particles. During the later phase of pair formation, particles undergo damped oscillations that are independent of initial conditions. These damped oscillations are driven by a strong hydrodynamic coupling of the particle dynamics, particle inertia and viscous dissipation. While the frequency and damping coefficient of the oscillations depend on particle softness, the pair formation time is largely determined by the initial particle positions: the time to form a stable pair grows exponentially with the initial axial distance. Our results demonstrate that particle softness has a strong impact on the behaviour of particle pairs. The findings could have significant ramifications for microfluidic applications where a constant and reliable axial distance between particles is required, such as flow cytometry.

Resonant gas oscillations in a closed straight tube contain shocks for frequencies near the linear resonant frequency. As the tube geometry changes from straight to a cone with slope $a,$ the shock strength decreases until, for large enough $a,$ the motion is continuous. The analytical result for small $a$ follows from a nonlinearization of the linear resonant response, while the result for large $a$ is a dominant single mode approximation. The connection between these two forms is analysed numerically. The shocked solutions change to multimode continuous solutions as $a$ increases to cross the curve $a_{s}\doteqdot 12.8M^{1/3}$, where $M\ll 1$ is the Mach number of the input. Then the amplitudes of the higher modes decrease as $a$ continues to increase until, having crossed $a_{m}\doteqdot 30M^{1/3}$, the single mode solution emerges.

Falling paper flutters and tumbles through air, whereas a paper airplane glides smoothly if its leading edge is appropriately weighted. We investigate this transformation from ‘plain paper’ to ‘paper plane’ through experiments, aerodynamic modelling and free flight simulations of thin plates with differing centre of mass (CoM) locations. Periodic modes such as fluttering, tumbling and bounding give way to steady gliding and then downward diving as the CoM is increasingly displaced towards one edge. To explain these observations, we formulate a quasi-steady aerodynamic model whose force and torque coefficients are informed by experimental measurements. The dependencies on angle of attack reflect the transition from attached to separated flow and a dynamic centre of pressure, effects that prove critical to reproducing the observed motions of paper planes in air and plates in water. Because the model successfully accounts for unsteady and steady flight modes, it may be usefully applied to further problems involving actuated motions, feedback control and interactions with ambient flows.

Computational fluid dynamics is increasingly used to investigate the inherently complicated phenomenon of wave breaking. To date, however, no single model has proved capable of accurately simulating the breaking process across the entirety of the surf zone for both spilling and plunging breakers. The present study newly considers the Reynolds stress–$\omega$ turbulence closure model for this purpose, where $\omega$ is the specific dissipation rate. Novel stability analysis proves that, unlike two-equation closures (at least in their standard forms), the stress–$\omega$ model is neutrally stable in the idealized potential flow region beneath surface waves. It thus naturally avoids unphysical exponential growth of turbulence prior to breaking, which has plagued numerous prior studies. The analysis is confirmed through simulation of a progressive surface wave train. The stress–$\omega$ model is then applied to simulate a turbulent wave boundary layer, demonstrating superior accuracy relative to a two-equation model, especially during flow deceleration. Finally, the stress–$\omega$ model is employed to simulate spilling and plunging breaking waves, with seemingly unprecedented accuracy. Specifically, the present work marks the first time that a single turbulence closure model collectively: (1) avoids turbulence over-production prior to breaking, (2) accurately predicts the breaking point, (3) provides reasonable evolution of turbulent normal stresses, while also (4) yielding accurate evolution of undertow velocity structure and magnitude across the surf zone, for both spilling and plunging cases. Differences in the predicted Reynolds shear stresses (hence flow resistance) are identified as key to the improved inner surf zone performance, relative to a state-of-the-art two-equation model.

We present a weakly nonlinear theory for the evolution of dispersive transient waves generated by moving seabed deformation. Using a perturbation expansion up to second order, we show that higher-order components affect mostly the leading wave and the region close to the deforming seabed. In particular, the leading wave in the nonlinear regime has higher crests and deeper troughs than the known linear solution, while the trough that propagates together with the moving seabed exhibits pulsating behaviour and has larger depth. We also validate the analytical model with experimental data and obtain good agreement between both approaches. Our results suggest a need to extend existing models that neglect the effects of wave dispersion and higher-order components, especially in view of practical applications in engineering and oceanography.

Direct numerical simulation is used to investigate effects of turbulent flow in the confined geometry of a face-centred cubic porous unit cell on the transport, clustering and deposition of fine particles at different Stokes numbers ($St = 0.01, 0.1, 0.5, 1, 2$) and at a pore Reynolds number of 500. Particles are advanced using one-way coupling and the collision of particles with pore walls is modelled as perfectly elastic with specular reflection. Tools for studying inertial particle dynamics and clustering developed for homogeneous flows are adapted to take into account the embedded, curved geometry of the pore walls. The pattern and dynamics of clustering are investigated using the volume change of Voronoi tesselation in time to analyse the divergence and convergence of the particles. Similar to the case of homogeneous, isotropic turbulence, the cluster formation is present at large volumes, while cluster destruction is prominent at small volumes and these effects are amplified with the Stokes number. However, unlike homogeneous, isotropic turbulence, the formation of a large number of very small volumes was observed at all Stokes numbers and attributed to the collision of particles with the pore wall. Multiscale wavelet analysis of the particle number density indicates that the peak of the energy density spectrum, representative of enhanced particle clustering, shifts towards larger scales with an increase in the Stokes number. Scale-dependent skewness and flatness quantify the intermittent void and cluster distribution, with cluster formation observed at small scales for all Stokes numbers, and void regions at large scales for large Stokes numbers.

Perturbation of the laminar boundary layer by free-stream travelling waves was shown to produce highly-localized skin friction modification via steady streaming. The forced boundary layer flow was calculated numerically and studied as a function of the phase speed, frequency and amplitude of the perturbations. Upstream-travelling waves always produced negative streaming, whereas downstream-travelling waves produced positive or negative streaming that varied with forcing strength and streamwise location. The sign of the resultant streaming was explained in terms of the inclination of the induced velocity modes, which evolved spatially in response to the streamwise variation and overlap of the Stokes and critical layers.

We investigate the temporal and spatio-temporal buoyancy instabilities in a horizontal liquid layer supported by a poorly conducting substrate and subjected to an oblique temperature gradient (OTG) with horizontal and vertical components, denoted as HTG and VTG, respectively. General linear stability analysis (GLSA) reveals a strong stabilizing effect of the HTG on the instabilities introduced by the VTG for Prandtl numbers $Pr>1$ via inducing an extra vertical temperature gradient opposing the VTG through energy convection. For $Pr<1$, a new mode of instability arises as a result of a velocity jump in the liquid layer caused by cellular circulation. A long-wave weakly nonlinear evolution equation governing the spatio-temporal dynamics of the temperature perturbations is derived. Spatio-temporal stability analysis reveals the existence of a convectively unstable long-wave regime due to the HTG. Weakly nonlinear stability analysis reveals the supercritical type of bifurcation changing from pitchfork in the presence of a pure VTG to Hopf in the presence of the OTG. Numerical investigation of the spatio-temporal dynamics of the temperature disturbances in the layer in the weakly nonlinear regime reveals the emergence of travelling wave regimes propagating against the direction of the HTG and whose phase speed depends on $Pr$. In the case of a small but non-zero Biot number, the wavelength of these travelling waves is larger than that of the fastest-growing mode obtained from GLSA.

This study investigates the dynamics of low-viscosity nanodroplets impacting surfaces with static contact angles from θ = 73° to 180° via molecular dynamics (MD) simulations. Two typical morphologies of impacting nanodroplets are observed at the maximum spreading state, a Hertz-ball-like in a low-Weber-number range and a thin-film-like in a high-Weber-number range. Only inertial and capillary forces dominate the impact for the former, whereas viscous force also becomes dominant for the latter. Regardless of morphologies at the maximum spreading state, the ratio of spreading time to contact time always remains constant on an ideal superhydrophobic surface with θ = 180°. With the help of different kinematic approximations of the spreading time and scaling laws of the contact time, scaling laws of the maximum spreading factor ${\beta _{max}}\sim W{e^{1/5}}$ in the low-Weber-number range (capillary regime) and ${\beta _{max}}\sim W{e^{2/3}}R{e^{ - 1/3}}$ (or ${\beta _{max}}\sim W{e^{1/2}}O{h^{1/3}}$) in the high-Weber-number range (cross-over regime) are obtained. Here, We, Re, and Oh are the Weber number, Reynolds number, and Ohnesorge number, respectively. Although the scaling laws are proposed only for the ideal superhydrophobic surface, they are tested valid for θ over 73° owing to the ignorable zero-velocity spreading effect. Furthermore, combining the two scaling laws leads to an impact number, $W{e^{3/10}}O{h^{1/3}} = 2.1$. This impact number can be used to determine whether viscous force is ignorable for impacting nanodroplets, thereby distinguishing the capillary regime from the cross-over regime.

This work presents evidence of the relation between the dynamics of intense events in the dissipative range of turbulence and the energy cascade. The generalised (Hölder) means are used to construct signals that track the temporal evolution of intense enstrophy and dissipation events in direct numerical simulations of isotropic turbulence. These signals are remarkably time-correlated with the average dissipation signal, and with its large-scale surrogate, despite describing only a small fraction of the flow domain, and they precede the dissipation signal with a temporal advancement that grows with their intensity and that scales in integral time units. Interpreted from a causal perspective, these results point to the energy cascade as the driver of the intense events in the dissipative range. Moreover, it is shown that the temporal advancements of the generalised means are consistent with a local energy cascade, whereby eddies cascade in a time proportional to their turnover time, causing intense eddies to reach the dissipative scales before weak eddies. These results shed light on the dynamics of intense and extreme events in small-scale turbulence, and provide empirical support to the phenomenological foundations of a broad class of intermittency models based on the turbulence cascade.

This investigation questions the importance of inverse interscale energy fluxes, the so-called energy backscatter, for the modelling of the energy cascade in large-eddy simulations (LES) of turbulent flows. The invariance of the filtered Navier–Stokes equations to divergence-preserving transformations of the subgrid-scale (SGS) stress tensor is exploited here to explore alternative representations of the local SGS energy fluxes. Numerical optimisation procedures are applied to the SGS stress tensor – obtained by filtering isotropic turbulence flow fields – to find alternative stresses that satisfy the filtered Navier–Stokes equations, but that produce negligible backscatter. These alternative SGS stresses show that backscatter represents not a flux of energy from the subgrid to the resolved scales, but conservative spatial fluxes, and that it need not be modelled to reproduce the local energetic exchange between the resolved and the subgrid scales in LES. From the perspective of statistical mechanics, it is argued that this is a consequence of the strong statistical irreversibility of inertial-range dynamics, which precludes inverse energy cascades even in a local sense. These findings show that the energy cascade is strongly unidirectional locally, and that it can be modelled as an irreversible sink of energy, justifying the extended use of purely dissipative SGS models in LES.

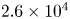We experimentally investigate the drag modification by neutrally buoyant finite-size particles with various aspect ratios in a Taylor–Couette (TC) turbulent flow. The current Reynolds number, $Re$, ranges from $6.5\times 10^3$ to $2.6\times 10^4$, and the particle volume fraction, 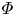$\varPhi$, is up to 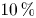$10\,\%$. Particles with three kinds of aspect ratio, 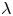$\lambda$, are used: 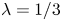$\lambda =1/3$ (oblate), 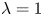$\lambda =1$ (spherical) and $\lambda =3$ (prolate). Unlike the case of bubbly TC flow (van Gils et al., J. Fluid Mech., vol. 722, 2013, pp. 317–347; Verschoof et al., Phys. Rev. Lett., vol. 117, issue 10, 2016, p. 104502), we find that the suspended finite-size particles increase the drag of the TC system regardless of their aspect ratios. The overall drag of the system increases with increasing 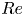$Re$, which is consistent with the literature. In addition, the normalized friction coefficient, 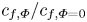$c_{f,\varPhi }/c_{f,\varPhi =0}$, decreases with increasing 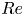$Re$, the reason could be that in the current low volume fractions the turbulent stress becomes dominant at higher 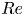$Re$. The particle distributions along the radial direction of the system are obtained by performing optical measurements at 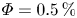$\varPhi =0.5\,\%$ and 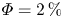$\varPhi = 2\,\%$. As 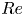$Re$ increases, the particles distribute more evenly in the entire system, which results from both the greater turbulence intensity and the more pronounced finite-size effects of the particles at higher 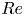$Re$. Moreover, it is found that the variation of the particle aspect ratios leads to different particle collective effects. The suspended spherical particles, which tend to cluster near the walls and form a particle layer, significantly affect the boundary layer and result in maximum drag modification. The minimal drag modification is found in the oblate case, where the particles preferentially cluster in the bulk region, and, thus, the particle layer is absent. Based on the optical measurement results, it can be concluded that, in the low volume fraction ranges (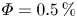$\varPhi =0.5\,\%$ and 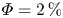$\varPhi = 2\,\%$ here), the larger drag modification is connected to the near-wall particle clustering. The present findings suggest that the particle shape plays a significant role in drag modification, and the collective behaviours of rigid particles provide clues to understand the bubbly drag reduction.

During a dynamic stall process, various flow structures leave their pressure footprints on a wing surface, through which it is possible to understand the development of different flow stages and predict the critical flow events. Based on a classical airfoil ramp-up pitching motion, proper orthogonal decomposition analysis of pressure on the suction surface is carried out in this study. Accordingly, the surface pressure evolution during dynamic stall is summarized into three basic physical schemas, based on which several real-time critical indicators for predicting the flow events related to the dynamic stall vortex (DSV) are constructed. These critical indicators include the spatial distribution coefficient of pressure (SDCP), the high-order central moment of pressure (HCMP), the location of peak pressure (LPP) and the modulated location of peak pressure (MLPP). These indicators can predict the formation of laminar separation bubbles, DSV initiation, DSV centre position and the detachment of DSV. Therefore, the real-time whole-life monitoring of DSV has been realized. Moreover, the effectiveness of these indicators has also been confirmed under different parameters, and testing using wind tunnel experimental data proves their noise robustness. Studies show that the SDCP and HCMP may also be effective even if only two transducers are used. Finally, a modification method of SDCP based on Z-score standardized pressure is proposed. It is found that the modified SDCP can effectively reduce sensitivity to kinematic parameters and the Reynolds number. The critical indicators in this study can be used as a reference for the standardized mathematical and physical description of DSV evolution, thus laying a foundation for constructing a universal theoretical framework of dynamic stall.