Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T10:18:43.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Circular hydraulic jumps: where does surface tension matter?

Published online by Cambridge University Press:  28 February 2022

Alexis Duchesne Open the ORCID record for Alexis Duchesne [Opens in a new window]  and
Laurent Limat
Alexis Duchesne*
Affiliation:
Univ. Lille, CNRS, Centrale Lille, Univ. Polytechnique Hauts-de-France, UMR 8520 - IEMN, F-59000Lille, France
Laurent Limat
Affiliation:
Université de Paris, CNRS, Laboratoire Matière et Systèmes Complexes (MSC), UMR 7057 - Bâtiment Condorcet, 10 rue Alice Domon et Léonie Duquet, 75013Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

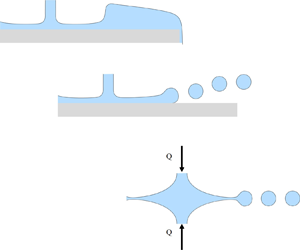
Recently, an unusual scaling law has been observed in circular hydraulic jumps and has been attributed to a supposed missing term in the local energy balance of the flow (Bhagat et al., J. Fluid Mech., vol. 851, 2018, R5). In this paper, we show that – though the experimental observation is valuable and interesting – this interpretation is presumably not the right one. When transposed to the case of an axial sheet formed by two impinging liquid jets, the assumed principle leads in fact to a velocity distribution in contradiction with the present knowledge for this kind of flow. We show here how to correct this approach by maintaining consistency with surface tension thermodynamics: for Savart–Taylor sheets, when adequately corrected, we recover the well-known $1/r$ liquid thickness with a constant and uniform velocity dictated by Bernoulli's principle. In the case of circular hydraulic jumps, we propose here a simple approach based on Watson's description of the flow in the central region (Watson, J. Fluid Mech., vol. 20, 1964, pp. 481–499), combined with appropriate boundary conditions on the circular front formed. Depending on the specific condition, we find in turn the new scaling by Bhagat et al. (2018) and the more conventional scaling law found long ago by Bohr et al. (J. Fluid Mech., vol. 254, 1993, pp. 635–648). We clarify here a few situations in which one should hold rather than the other, hoping to reconcile the observations of Bhagat et al. with the present knowledge of circular hydraulic jump modelling. However, the question of a possible critical Froude number imposed at the jump exit and dictating logarithmic corrections to scaling remains an open and unsolved question.

JFM classification

Interfacial Flows (free surface): Capillary flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 937 , 25 April 2022 , R2
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Argentina, M., Cerda, E., Duchesne, A. & Limat, L. 2017 Scaling the viscous circular hydraulic jump. APS Division of Fluid Dynamics (Fall) 2017 Meeting, Abstract ID A19.008.Google Scholar
Bélanger, J.B. 1841 Notes sur l'Hydraulique. Ecole Royale des Ponts et Chaussées, Paris, France, session 1842, 223.Google Scholar
Bhagat, R.K., Jha, N.K., Linden, P.F. & Wilson, D.I. 2018 On the origin of the circular hydraulic jump in a thin liquid film. J. Fluid Mech. 851, R5.CrossRefGoogle Scholar
Bhagat, R.K. & Linden, P.F. 2020 The circular capillary jump. J. Fluid Mech. 896, A25.CrossRefGoogle Scholar
Bohr, T., Dimon, P. & Putkaradze, V. 1993 Shallow-water approach to the circular hydraulic jump. J. Fluid Mech. 254, 635–648.CrossRefGoogle Scholar
Bohr, T. & Scheichl, B. 2021 Surface tension and energy conservation in a moving fluid. Phys. Rev. Fluids 6, L052001.CrossRefGoogle Scholar
Bouasse, H. 1923 Jets, Tubes et Canaux. Librairie Delagrave.Google Scholar
Bush, J.W.M. & Aristoff, J.M. 2003 The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229–238.CrossRefGoogle Scholar
Button, E.C., Davidson, J.F., Jameson, G.J. & Sader, J.E. 2010 Water bells formed on the underside of a horizontal plate. Part 2. Theory. J. Fluid Mech. 649, 45–68.CrossRefGoogle Scholar
Clanet, C. & Villermaux, E. 2002 Life of a smooth liquid sheet. J. Fluid Mech. 462, 307–340.CrossRefGoogle Scholar
Craik, A.D.D., Latham, R.C., Fawkes, M.J. & Gribbon, P.W.F. 1981 The circular hydraulic jump. J. Fluid Mech. 112, 347–362.CrossRefGoogle Scholar
Duchesne, A., Andersen, A. & Bohr, T. 2019 Surface tension and the origin of the circular hydraulic jump in a thin liquid film. Phys. Rev. Fluids 4 (8), 084001.CrossRefGoogle Scholar
Duchesne, A., Lebon, L. & Limat, L. 2013 Jet impact on an inclined plate: contact line versus hydraulic jump. In European Coating Symposium, ECS 2013, pp. 48–51. UMONS, Université de Mons.Google Scholar
Duchesne, A., Lebon, L. & Limat, L. 2014 Constant Froude number in a circular hydraulic jump and its implication on the jump radius selection. Europhys. Lett. 107 (5), 54002.CrossRefGoogle Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, vol. 336. Springer.CrossRefGoogle Scholar
Hagen, G. 1849 Ueber die scheiben, welche sich beim zusammenstossen von zwei wasserstrahlen bilden und über die auflösung einzelner wasserstrahlen in tropfen. Ann. Phys. 154 (12), 451–476.CrossRefGoogle Scholar
Huang, J.C.P. 1970 The break-up of axisymmetric liquid sheets. J. Fluid Mech. 43 (2), 305–319.CrossRefGoogle Scholar
Ipatova, A., Smirnov, K.V. & Mogilevskiy, E.I. 2021 Steady circular hydraulic jump on a rotating disk. J. Fluid Mech. 927, A24.CrossRefGoogle Scholar
Jameson, G.J., Jenkins, C.E., Button, E.C. & Sader, J.E 2010 Water bells formed on the underside of a horizontal plate. Part 1. Experimental investigation. J. Fluid Mech. 649, 19–43.CrossRefGoogle Scholar
Marmottant, P., Villermaux, E. & Clanet, C. 2000 Transient surface tension of an expanding liquid sheet. J. Colloid Interface Sci. 230 (1), 29–40.CrossRefGoogle ScholarPubMed
Maynes, D., Johnson, M. & Webb, B.W. 2011 Free-surface liquid jet impingement on rib patterned superhydrophobic surfaces. Phys. Fluids 23, 052104.CrossRefGoogle Scholar
Mohajer, B. & Li, R. 2015 Circular hydraulic jump on finite surfaces with capillary limit. Phys. Fluids 27 (11), 117102.CrossRefGoogle Scholar
Rayleigh, Lord 1914 On the theory of long waves and bores. Proc. R. Soc. Lond. A 90 (619), 324–328.Google Scholar
Salah, S.O.T., Duchesne, A., De Cock, N., Massinon, M., Sassi, K., Abrougui, K., Lebeau, F. & Dorbolo, S. 2018 Experimental investigation of a round jet impacting a disk engraved with radial grooves. Eur. J. Mech. B/Fluids 72, 302–310.CrossRefGoogle Scholar
Savart, F. 1833 Mémoire sur le choc d'une veine liquide lancée contre un plan circulaire. Ann. chim. 54, 56–87.Google Scholar
Sen, U., Chatterjee, S., Crockett, J., Ganguly, R., Yu, L. & Megaridis, C.M. 2019 Orthogonal liquid-jet impingement on wettability-patterned impermeable substrates. Phys. Rev. Fluids 4, 014002.CrossRefGoogle Scholar
Tani, I. 1949 Water jump in the boundary layer. J. Phys. Soc. Japan 4, 212–215.CrossRefGoogle Scholar
Villermaux, E., Pistre, V. & Lhuissier, H. 2013 The viscous savart sheet. J. Fluid Mech. 730, 607–625.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2019 The role of gravity in the prediction of the circular hydraulic jump radius for high-viscosity liquids. J. Fluid Mech. 862, 128–161.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2021 The effects of gravity and surface tension on the circular hydraulic jump for low-and high-viscosity liquids: a numerical investigation. Phys. Fluids 33 (1), 012105.CrossRefGoogle Scholar
Watson, E.J. 1964 The radial spread of a liquid over a horizontal plane. J. Fluid Mech. 20, 481–499.CrossRefGoogle Scholar
Wilson, D.I., Le, B.L., Dao, H.D.A., Lai, K.Y., Morison, K.R. & Davidson, J.F. 2012 Surface flow and drainage films created by horizontal impinging liquid jets. Chem. Engng Sci. 68 (1), 449–460.CrossRefGoogle Scholar