1. Introduction
Two experiments almost sixty years apart illustrate the effect of tube geometry on small amplitude resonant forced oscillations of a compressible gas in a closed tube. Lettau (Reference Lettau1939) found that, for a straight tube, even for small excitation amplitudes, shock waves are a feature of the motion. In contrast, Lawrenson et al. (Reference Lawrenson, Lipkens, Lucas, Perkins and Van Doren1998) showed that, by changing the shape of the tube, the resonant oscillations could reach much higher pressures while remaining shockless. This is the basis for resonant macrosonic synthesis (RMS). The significance of RMS is that continuous waveforms can be synthesized to allow a large amount of energy to be added to the wave and extremely high pressures achieved while avoiding acoustic saturation due to shocks. Lawrenson et al. (Reference Lawrenson, Lipkens, Lucas, Perkins and Van Doren1998) considered several tube shapes, including a cone resonator with (dimensionless) cross-sectional area ![]() $s(x)=(1+ax)^{2}$,
$s(x)=(1+ax)^{2}$, ![]() $0\leqslant x\leqslant 1$, for
$0\leqslant x\leqslant 1$, for ![]() $a=8,$ where
$a=8,$ where ![]() $a$ is the slope of the radius. Hence, for a straight tube
$a$ is the slope of the radius. Hence, for a straight tube ![]() $a=0$ shocks are a feature of the flow, while for a cone with
$a=0$ shocks are a feature of the flow, while for a cone with ![]() $a=8,$ there are no shocks. The purpose of this paper is to find the value of the slope parameter
$a=8,$ there are no shocks. The purpose of this paper is to find the value of the slope parameter ![]() $a$ at which the transition between continuous and shocked solutions occurs, and how the continuous solutions then evolve from a multimode to a single mode solution. To do so we first derive a new, more accurate, equation for small slopes, which is a generalization of the nonlinear geometric acoustics equation, by the nonlinearization of the linear resonance equation. The problem is completed by using a numerical technique to link the approximate small slope solutions to the solutions generated by the numerics for larger slopes.
$a$ at which the transition between continuous and shocked solutions occurs, and how the continuous solutions then evolve from a multimode to a single mode solution. To do so we first derive a new, more accurate, equation for small slopes, which is a generalization of the nonlinear geometric acoustics equation, by the nonlinearization of the linear resonance equation. The problem is completed by using a numerical technique to link the approximate small slope solutions to the solutions generated by the numerics for larger slopes.
1.1. Closed straight tube
The basic problem of resonant forced oscillations of a gas in a closed straight tube is classical. The experimental set-up is a piston with maximum displacement ![]() $\delta$ at one end of the tube oscillating at frequency
$\delta$ at one end of the tube oscillating at frequency ![]() $\hat {\omega }$; the other end of the tube is closed. The motion is determined by two dimensionless parameters: the amplitude parameter,
$\hat {\omega }$; the other end of the tube is closed. The motion is determined by two dimensionless parameters: the amplitude parameter, ![]() $\varepsilon =\delta /L$, where
$\varepsilon =\delta /L$, where ![]() $L$ is the tube length, and the frequency parameter,
$L$ is the tube length, and the frequency parameter, ![]() $\omega =\hat {\omega }L/c_{0},$ where
$\omega =\hat {\omega }L/c_{0},$ where ![]() $c_{0}$ is the ambient sound speed. The dimensionless Mach number of the piston motion is
$c_{0}$ is the ambient sound speed. The dimensionless Mach number of the piston motion is ![]() $M=2{\rm \pi} \varepsilon \omega$. Neglecting any damping, the solution to the linear problem is unbounded when the round trip travel time of a wave in the tube equals a multiple of the piston period , so
$M=2{\rm \pi} \varepsilon \omega$. Neglecting any damping, the solution to the linear problem is unbounded when the round trip travel time of a wave in the tube equals a multiple of the piston period , so ![]() $2L/c_{0}=n/\hat {\omega }$, for integer
$2L/c_{0}=n/\hat {\omega }$, for integer ![]() $n.$ This defines the resonant frequencies as
$n.$ This defines the resonant frequencies as ![]() $\omega _{n}=n/2$ and the fundamental resonance is when
$\omega _{n}=n/2$ and the fundamental resonance is when ![]() $\omega =1/2.$ We note that
$\omega =1/2.$ We note that ![]() $\omega _{n}=n\omega _{1}$ so that the eigenvalues are commensurate when
$\omega _{n}=n\omega _{1}$ so that the eigenvalues are commensurate when ![]() $a=0$.
$a=0$.
There are many examples of experimental results for gas oscillations in straight tubes, including Lettau (Reference Lettau1939) (![]() $\varepsilon =0.0028)$, Saenger & Hudson (Reference Saenger and Hudson1960) (
$\varepsilon =0.0028)$, Saenger & Hudson (Reference Saenger and Hudson1960) (![]() $\varepsilon =0.0019)$ and Sturtevant (Reference Sturtevant1974) (
$\varepsilon =0.0019)$ and Sturtevant (Reference Sturtevant1974) (![]() $\varepsilon =0.0147)$. All report that the gas motion for frequencies in a band around the fundamental frequency is finite, but contains shocks. The shocks have constant strength and travel at the constant adiabatic sound speed. This is confirmed in the analytical work of Betchov (Reference Betchov1958), Gorkov (Reference Gorkov1963), Chester (Reference Chester1964) and Seymour & Mortell (Reference Seymour and Mortell1973). For an input Mach number
$\varepsilon =0.0147)$. All report that the gas motion for frequencies in a band around the fundamental frequency is finite, but contains shocks. The shocks have constant strength and travel at the constant adiabatic sound speed. This is confirmed in the analytical work of Betchov (Reference Betchov1958), Gorkov (Reference Gorkov1963), Chester (Reference Chester1964) and Seymour & Mortell (Reference Seymour and Mortell1973). For an input Mach number ![]() $M\ll 1,$ the magnitude of the resulting nonlinear motion at a linear resonant frequency is significantly higher, at order
$M\ll 1,$ the magnitude of the resulting nonlinear motion at a linear resonant frequency is significantly higher, at order ![]() $O(M^{1/2})$, than the input at
$O(M^{1/2})$, than the input at ![]() $O(M).$ Note that we are using the notation
$O(M).$ Note that we are using the notation ![]() $Z=O(M)$ if
$Z=O(M)$ if ![]() $Z/M$ is finite as
$Z/M$ is finite as ![]() $M\rightarrow 0,$ and
$M\rightarrow 0,$ and ![]() $Z=o(M)$ if
$Z=o(M)$ if ![]() $Z/M\rightarrow 0$ as
$Z/M\rightarrow 0$ as ![]() $M\rightarrow 0.$
$M\rightarrow 0.$
1.2. Closed tube with varying cross-section
For resonant flows in tubes with varying cross-section there are several analytical and numerical investigations for both small and finite ![]() $a$, see Keller (Reference Keller1977), Chester (Reference Chester1991), Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993), Chun & Kim (Reference Chun and Kim2000), Ellermeier (Reference Ellermeier1994) and Amundsen, Mortell & Seymour (Reference Amundsen, Mortell and Seymour2015). Ellermeier (Reference Ellermeier1993) concluded that shocks must appear when the cross-section is sufficiently slowly varying and the system is close to resonance. He also noted in Ellermeier (Reference Ellermeier1994), possibly for the first time, that at cubic order in the amplitude, and when the cross-section is no longer slowly varying, the system has no shocks even at resonance. In this case the excited mode interacts with itself at third order and the result is a continuous output with an amplitude much greater than the shocked case. In the context of Fourier analysis and nonlinear interactions, Whitham (Reference Whitham1974) refers to the self-interaction term in (15.58) of § 15.6 as the Stokes term, see Stokes (Reference Stokes1847). Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993) discuss the response of resonators that deviate from being cylindrical and show that, in general, the detuning range in which shocks are possible decreases as the geometrical imperfection increases. They conclude that ‘shocks can only occur in the response when either the linearized spectrum contains an infinite number of commensurate frequencies or the amplitude of the geometric imperfection is
$a$, see Keller (Reference Keller1977), Chester (Reference Chester1991), Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993), Chun & Kim (Reference Chun and Kim2000), Ellermeier (Reference Ellermeier1994) and Amundsen, Mortell & Seymour (Reference Amundsen, Mortell and Seymour2015). Ellermeier (Reference Ellermeier1993) concluded that shocks must appear when the cross-section is sufficiently slowly varying and the system is close to resonance. He also noted in Ellermeier (Reference Ellermeier1994), possibly for the first time, that at cubic order in the amplitude, and when the cross-section is no longer slowly varying, the system has no shocks even at resonance. In this case the excited mode interacts with itself at third order and the result is a continuous output with an amplitude much greater than the shocked case. In the context of Fourier analysis and nonlinear interactions, Whitham (Reference Whitham1974) refers to the self-interaction term in (15.58) of § 15.6 as the Stokes term, see Stokes (Reference Stokes1847). Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993) discuss the response of resonators that deviate from being cylindrical and show that, in general, the detuning range in which shocks are possible decreases as the geometrical imperfection increases. They conclude that ‘shocks can only occur in the response when either the linearized spectrum contains an infinite number of commensurate frequencies or the amplitude of the geometric imperfection is ![]() $O(M^{1/2})$ or less, where the input is
$O(M^{1/2})$ or less, where the input is ![]() $O(M)$’. They also remark on the likelihood of a single mode response when the geometric variation is large enough, agreeing with Ellermeier (Reference Ellermeier1993). Thus, in general, there is a critical cutoff value of the geometric variation separating shocked from continuous solutions. Chester (Reference Chester1994) considers the effect of the cross-sectional variation of the container on the basic solution for a tube of constant cross-section given in Chester (Reference Chester1964). He also adverts to the feedback from third-order terms to the linear terms and the consequent continuous solution across the frequency range. Seymour, Mortell & Amundsen (Reference Seymour, Mortell and Amundsen2011) considered the case of resonant oscillations between concentric spheres, and found, as a by-product, the eigenvalue equation of a gas in the frustum of a cone. They also found (Seymour, Mortell & Amundsen Reference Seymour, Mortell and Amundsen2012) an estimate for the transition between shocked and continuous motion for the Mach number
$O(M)$’. They also remark on the likelihood of a single mode response when the geometric variation is large enough, agreeing with Ellermeier (Reference Ellermeier1993). Thus, in general, there is a critical cutoff value of the geometric variation separating shocked from continuous solutions. Chester (Reference Chester1994) considers the effect of the cross-sectional variation of the container on the basic solution for a tube of constant cross-section given in Chester (Reference Chester1964). He also adverts to the feedback from third-order terms to the linear terms and the consequent continuous solution across the frequency range. Seymour, Mortell & Amundsen (Reference Seymour, Mortell and Amundsen2011) considered the case of resonant oscillations between concentric spheres, and found, as a by-product, the eigenvalue equation of a gas in the frustum of a cone. They also found (Seymour, Mortell & Amundsen Reference Seymour, Mortell and Amundsen2012) an estimate for the transition between shocked and continuous motion for the Mach number ![]() $M=0.005$, where geometry dominates. The same authors (Seymour et al. Reference Seymour, Mortell and Amundsen2012) considered the case of nonlinear resonant oscillations of a gas contained between two concentric spheres or coaxial cylinders when shocks are present and the dominant first harmonic approximation is not valid. A nonlinear geometric acoustics approximation predicted shocked flows that are confirmed by numerical solutions for a range of
$M=0.005$, where geometry dominates. The same authors (Seymour et al. Reference Seymour, Mortell and Amundsen2012) considered the case of nonlinear resonant oscillations of a gas contained between two concentric spheres or coaxial cylinders when shocks are present and the dominant first harmonic approximation is not valid. A nonlinear geometric acoustics approximation predicted shocked flows that are confirmed by numerical solutions for a range of ![]() $a$ – the slope of a cone. In this paper we use a different technique, nonlinearization, to generalize the above approximation technique and present these solutions as a starting point for the numerical solutions with increasing
$a$ – the slope of a cone. In this paper we use a different technique, nonlinearization, to generalize the above approximation technique and present these solutions as a starting point for the numerical solutions with increasing ![]() $a$.
$a$.
In contrast to the theoretical work, where the validity depends on the cross-sectional variation being ![]() $o(1)$, Lawrenson et al. (Reference Lawrenson, Lipkens, Lucas, Perkins and Van Doren1998) investigated experimentally, inter alia, resonance in a conical container (frustum of a cone) when the slope
$o(1)$, Lawrenson et al. (Reference Lawrenson, Lipkens, Lucas, Perkins and Van Doren1998) investigated experimentally, inter alia, resonance in a conical container (frustum of a cone) when the slope ![]() $a=O(1)$, in fact
$a=O(1)$, in fact ![]() $a=8$, and found that the output was characterized by continuous large pressure amplitudes – macrosonic standing waves. For container shapes such as a cone, a horn-cone or a bulb, pressure amplitudes more than an order of magnitude larger than those in an acoustically saturated straight resonator appeared in a single-mode periodic solution. Mortell & Seymour (Reference Mortell and Seymour2004) then constructed analytically a continuous one-term, dominant first harmonic solution for the case when
$a=8$, and found that the output was characterized by continuous large pressure amplitudes – macrosonic standing waves. For container shapes such as a cone, a horn-cone or a bulb, pressure amplitudes more than an order of magnitude larger than those in an acoustically saturated straight resonator appeared in a single-mode periodic solution. Mortell & Seymour (Reference Mortell and Seymour2004) then constructed analytically a continuous one-term, dominant first harmonic solution for the case when ![]() $a=O(1)$ that gave good qualitative agreement with the experiments. In particular they showed that the output amplitude is
$a=O(1)$ that gave good qualitative agreement with the experiments. In particular they showed that the output amplitude is ![]() $O(M^{1/3})$ for an input of
$O(M^{1/3})$ for an input of ![]() $O(M)$. This solution is not valid when
$O(M)$. This solution is not valid when ![]() $a=o(1)$ and shocks form. There have been several numerical investigations of resonance in cylindrical and conical tubes (e.g. Ilinskii et al. Reference Ilinskii, Lipkens, Lucas, Van Doren and Zabolotskaya1998; Chun & Kim Reference Chun and Kim2000; Antao & Farouk Reference Antao and Farouk2013) but none investigate the transition from cylinder to cone.
$a=o(1)$ and shocks form. There have been several numerical investigations of resonance in cylindrical and conical tubes (e.g. Ilinskii et al. Reference Ilinskii, Lipkens, Lucas, Van Doren and Zabolotskaya1998; Chun & Kim Reference Chun and Kim2000; Antao & Farouk Reference Antao and Farouk2013) but none investigate the transition from cylinder to cone.
The general picture is that for sufficiently weak non-uniformities shock formation cannot be prevented if the undamped system is sufficiently close to resonance. An objective here is to find a good approximation to the resonant frustum problem for ![]() $a=o(1)$, and use this as a basis to numerically fill the gap between
$a=o(1)$, and use this as a basis to numerically fill the gap between ![]() $a=o(1)$ and
$a=o(1)$ and ![]() $a=O(1)$ solutions. We investigate numerically the transition from a shocked solution to a continuous solution as
$a=O(1)$ solutions. We investigate numerically the transition from a shocked solution to a continuous solution as ![]() $a$ increases. The conclusion is that shocked solutions change to multimode continuous solutions as
$a$ increases. The conclusion is that shocked solutions change to multimode continuous solutions as ![]() $a$ crosses
$a$ crosses ![]() $a_{s}\doteqdot 12.8M^{1/3}$. Then the amplitudes of the higher modes decrease until
$a_{s}\doteqdot 12.8M^{1/3}$. Then the amplitudes of the higher modes decrease until ![]() $a_{m}\doteqdot 30M^{1/3}$ when the single mode solution emerges. The important contrast is that when the slope of the cone is
$a_{m}\doteqdot 30M^{1/3}$ when the single mode solution emerges. The important contrast is that when the slope of the cone is ![]() $0\leqslant a\ll 1,$ the output is
$0\leqslant a\ll 1,$ the output is ![]() $O(M^{1/2})$ and contains shocks, whereas for a slope
$O(M^{1/2})$ and contains shocks, whereas for a slope ![]() $a\gg 1,$ the output is
$a\gg 1,$ the output is ![]() $O(M^{1/3})$ and is continuous. We examine the transition as
$O(M^{1/3})$ and is continuous. We examine the transition as ![]() $a$ increases.
$a$ increases.
2. Resonance in the frustum of a cone:  $s(x)=(1+ax)^{2}$
$s(x)=(1+ax)^{2}$
The fully nonlinear dimensionless governing equations for the motion of the gas in an Eulerian frame are statements of conservation of mass and momentum
 \begin{equation} \left.\begin{gathered} s(x)\frac{\partial e}{\partial t}+\frac{\partial }{\partial x}\left( s(x)(1+e)u\right) =0, \\ \frac{\partial u}{\partial t}+\frac{\partial }{\partial x}\left( \frac{u^{2}}{2}+\frac{(1+e)^{\gamma -1}}{\gamma -1}\right) = \nu \frac{\partial ^{2}u}{\partial x^{2}}, \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} s(x)\frac{\partial e}{\partial t}+\frac{\partial }{\partial x}\left( s(x)(1+e)u\right) =0, \\ \frac{\partial u}{\partial t}+\frac{\partial }{\partial x}\left( \frac{u^{2}}{2}+\frac{(1+e)^{\gamma -1}}{\gamma -1}\right) = \nu \frac{\partial ^{2}u}{\partial x^{2}}, \end{gathered}\right\}\end{equation}
where ![]() $u(x,t)$ is the particle velocity,
$u(x,t)$ is the particle velocity, ![]() $e(x,t)={\rho (x,t)}/{\rho _{0}}-1$ is the condensation,
$e(x,t)={\rho (x,t)}/{\rho _{0}}-1$ is the condensation, ![]() $\rho (x,t)$ is the density and
$\rho (x,t)$ is the density and ![]() $\nu$ is a dissipation constant. Here
$\nu$ is a dissipation constant. Here ![]() $s(x)$ is the varying cross-sectional area of the cone. The sound speed is normalized to
$s(x)$ is the varying cross-sectional area of the cone. The sound speed is normalized to ![]() $c_{0}=1$, and the equation of state for a polytropic gas is
$c_{0}=1$, and the equation of state for a polytropic gas is
where ![]() $\rho _{0},$
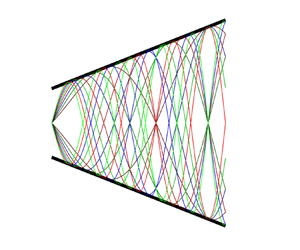
$\rho _{0},$ ![]() $p_{0}$ are the density and pressure in the reference state. Figure 1 provides a depiction of the physical configuration.
$p_{0}$ are the density and pressure in the reference state. Figure 1 provides a depiction of the physical configuration.

Figure 1. Polytropic gas in frustum of a closed cone and forced at one end.
The equivalent linear undamped equations are
For a tube closed at ![]() $x=0$ with an oscillating piston at
$x=0$ with an oscillating piston at ![]() $x=1,$the boundary conditions are
$x=1,$the boundary conditions are
where ![]() $M$ is the Mach number.
$M$ is the Mach number.
When the cross-section of the containing tube is given by
the general linear solution is
see Mortell & Seymour (Reference Mortell and Seymour2017a, p. 92) (where there is a typographical error), ![]() $\alpha =\omega (t-x)$ and
$\alpha =\omega (t-x)$ and ![]() $\beta =\omega (t+x-1)$ so that
$\beta =\omega (t+x-1)$ so that ![]() $\alpha =\omega t$ on
$\alpha =\omega t$ on ![]() $x=0$ and
$x=0$ and ![]() $\beta =\omega t$ on
$\beta =\omega t$ on ![]() $x=1$.
$x=1$. ![]() $\hat {F}(\alpha )$ and
$\hat {F}(\alpha )$ and ![]() $\hat {G}(\beta )$ are arbitrary functions to be determined from the boundary conditions.
$\hat {G}(\beta )$ are arbitrary functions to be determined from the boundary conditions.
2.1. Exact linear solution
The linear problem of resonant oscillations in a closed cone can be solved exactly. In § 5 we make use of this exceptional case to examine the range of frequencies in figure 9 for both small and large values of ![]() $a$ for which the linear solution is a good approximation to the full nonlinear solution computed numerically.
$a$ for which the linear solution is a good approximation to the full nonlinear solution computed numerically.
For ![]() $s(x)=(1+ax)^{2}$ the general solution to the linear equations for
$s(x)=(1+ax)^{2}$ the general solution to the linear equations for ![]() $u(x,t)$ is given by (2.6). The boundary conditions for the resonance problem are
$u(x,t)$ is given by (2.6). The boundary conditions for the resonance problem are ![]() $u=M\sin (2{\rm \pi} \omega t)$ at
$u=M\sin (2{\rm \pi} \omega t)$ at ![]() $x=1$ and a closed end
$x=1$ and a closed end ![]() $(u=0)$ at
$(u=0)$ at ![]() $x=0$, so that
$x=0$, so that
Then ![]() $\hat {F}$ and
$\hat {F}$ and ![]() $\hat {G}$ satisfy
$\hat {G}$ satisfy
with ![]() $l=a(1+a)^{-1}$ and
$l=a(1+a)^{-1}$ and ![]() $W=2{\rm \pi} \omega$.
$W=2{\rm \pi} \omega$.
After some algebra, the exact linear solution (see Mortell & Seymour Reference Mortell and Seymour2017a) can be written in the form
or
where
 \begin{align} K(x,W,a)&=\frac{(1+a)^{2}\sqrt{a^{2}+W^{2}\left( 1+ax\right) ^{2}}}{(1+ax)^{2} \sqrt{a^{2}+W^{2}\left( 1+a\right) ^{2}}},\quad\text{and}\quad\nonumber\\ \phi (x,W,a)&=\tan ^{{-}1} \left[ \frac{a^{2}xW}{a^{2}+W^{2}[1+ax]}\right]. \end{align}
\begin{align} K(x,W,a)&=\frac{(1+a)^{2}\sqrt{a^{2}+W^{2}\left( 1+ax\right) ^{2}}}{(1+ax)^{2} \sqrt{a^{2}+W^{2}\left( 1+a\right) ^{2}}},\quad\text{and}\quad\nonumber\\ \phi (x,W,a)&=\tan ^{{-}1} \left[ \frac{a^{2}xW}{a^{2}+W^{2}[1+ax]}\right]. \end{align}
Setting the denominator of (2.11) to zero, the resonant frequencies, ![]() $W={\varOmega }_{n},$ are given by
$W={\varOmega }_{n},$ are given by
For ![]() $a>0$, in general these are incommensurate, so that
$a>0$, in general these are incommensurate, so that ![]() ${\varOmega }_{n}\neq n{\varOmega }_{1}$. However, for small
${\varOmega }_{n}\neq n{\varOmega }_{1}$. However, for small ![]() $a$ (2.14) implies that the first two resonant frequencies are
$a$ (2.14) implies that the first two resonant frequencies are
where ![]() $\omega _{n}={\varOmega _{n}}/{2{\rm \pi} }$ is the normalized resonant frequency. Thus for small
$\omega _{n}={\varOmega _{n}}/{2{\rm \pi} }$ is the normalized resonant frequency. Thus for small ![]() $a$ the eigenvalues are commensurate to
$a$ the eigenvalues are commensurate to ![]() $O(a^{2})$. Then we anticipate a shocked solution.
$O(a^{2})$. Then we anticipate a shocked solution.
When ![]() $a\rightarrow 0$
$a\rightarrow 0$
So there is a singularity at ![]() $W={\rm \pi},$ or
$W={\rm \pi},$ or ![]() $\omega =1/2$ as
$\omega =1/2$ as ![]() $a\rightarrow 0$, confirming that
$a\rightarrow 0$, confirming that ![]() $\omega =1/2$ is a resonant frequency for a straight tube.
$\omega =1/2$ is a resonant frequency for a straight tube.
We note here that the equivalent linear problem for ![]() $s(x)=(1+ax)^{-2}$ also has an exact solution, given by
$s(x)=(1+ax)^{-2}$ also has an exact solution, given by
This is a rare example of a variable cross-section where all natural frequencies, ![]() $W=n{\rm \pi},$ are commensurate for all positive values of
$W=n{\rm \pi},$ are commensurate for all positive values of ![]() $a$. This allowed Keller (Reference Keller1977) to use the technique of Chester (Reference Chester1964) for a straight tube to find a solution to the nonlinear problem containing shocks, although it is unclear if it is relevant to any real physical problem. While attempting to solve the case of the frustum of a cone, Keller observed ‘there seems to be no elementary analytical method which would lead to a simple resonance equation’.
$a$. This allowed Keller (Reference Keller1977) to use the technique of Chester (Reference Chester1964) for a straight tube to find a solution to the nonlinear problem containing shocks, although it is unclear if it is relevant to any real physical problem. While attempting to solve the case of the frustum of a cone, Keller observed ‘there seems to be no elementary analytical method which would lead to a simple resonance equation’.
3. Augmented nonlinear geometric acoustics approximation
For small ![]() $a$ the linear solution is augmented using nonlinearization to include the corrected nonlinear characteristics. The ‘nonlinearization technique’ was first given by Landau (Reference Landau1945), and then independently by Whitham (Reference Whitham1952) in the context of the sonic boom problem. Whitham (Reference Whitham1952) made the fundamental hypothesis that ‘linear theory gives a valid approximation to the flow everywhere provided that in it the approximate characteristics are replaced by the exact ones or at least by a sufficiently good approximation to the exact ones’. These authors considered waves travelling outward from a given source. Mortell & Seymour (Reference Mortell and Seymour2017b) extended the technique to deal with reflected waves in a bounded medium, e.g. the resonant motion of a gas in a closed tube. The linear round trip travel time in the medium is replaced by the nonlinear travel time which is calculated from the ‘sufficiently good approximation’, viz., the superposition of the two non-interacting modulated simple waves. A full account of the Whitham theory is given in Whitham (Reference Whitham1974).
$a$ the linear solution is augmented using nonlinearization to include the corrected nonlinear characteristics. The ‘nonlinearization technique’ was first given by Landau (Reference Landau1945), and then independently by Whitham (Reference Whitham1952) in the context of the sonic boom problem. Whitham (Reference Whitham1952) made the fundamental hypothesis that ‘linear theory gives a valid approximation to the flow everywhere provided that in it the approximate characteristics are replaced by the exact ones or at least by a sufficiently good approximation to the exact ones’. These authors considered waves travelling outward from a given source. Mortell & Seymour (Reference Mortell and Seymour2017b) extended the technique to deal with reflected waves in a bounded medium, e.g. the resonant motion of a gas in a closed tube. The linear round trip travel time in the medium is replaced by the nonlinear travel time which is calculated from the ‘sufficiently good approximation’, viz., the superposition of the two non-interacting modulated simple waves. A full account of the Whitham theory is given in Whitham (Reference Whitham1974).
Here we nonlinearize the linear resonant equation (3.5) to obtain a generalization of nonlinear geometric acoustic theory. To do this we first use the boundary conditions (2.4a,b) to eliminate ![]() $\hat {F}$ in (2.9) and (2.10) exactly at resonance when
$\hat {F}$ in (2.9) and (2.10) exactly at resonance when ![]() $\omega =1/2$. However, because we are now exactly at resonance the functions are redefined for convenience as
$\omega =1/2$. However, because we are now exactly at resonance the functions are redefined for convenience as ![]() $G(t)=\hat {G}({t}/{2}),$
$G(t)=\hat {G}({t}/{2}),$ ![]() $F(t)=\hat {F}({t}/{2}),$
$F(t)=\hat {F}({t}/{2}),$ ![]() $g(t)=\frac {1}{2}\hat {G}^{\prime }({t}/{2}),$
$g(t)=\frac {1}{2}\hat {G}^{\prime }({t}/{2}),$ ![]() $f(t)=\frac {1}{2}\hat {F}^{\prime }({t}/{2}).$ This corresponds to defining
$f(t)=\frac {1}{2}\hat {F}^{\prime }({t}/{2}).$ This corresponds to defining ![]() $\alpha =t-x$ and
$\alpha =t-x$ and ![]() $\beta =t+x-1.$ With this notation the general linear solution is
$\beta =t+x-1.$ With this notation the general linear solution is
Then the boundary condition on ![]() $x=1$ implies
$x=1$ implies
where ![]() $\ell ={a}/({1+a})$. Similarly the boundary condition on
$\ell ={a}/({1+a})$. Similarly the boundary condition on ![]() $x=0$ implies
$x=0$ implies
The substitution of (3.4) into (3.3) gives the linear resonance equation
Then ![]() $F(t-1)$ is eliminated from (3.5) using
$F(t-1)$ is eliminated from (3.5) using ![]() $O(1)$ and
$O(1)$ and ![]() $O(a)$ terms from (3.4) as appropriate. The linear standing wave,
$O(a)$ terms from (3.4) as appropriate. The linear standing wave, ![]() $M=0$, has period 2.
$M=0$, has period 2.
The linear resonance equation (3.5) is now nonlinearized by replacing the linear travel time ![]() $2$ by the nonlinear travel time calculated by the superposition of the
$2$ by the nonlinear travel time calculated by the superposition of the ![]() $\alpha$-simple wave and the
$\alpha$-simple wave and the ![]() $\beta$-simple wave with
$\beta$-simple wave with ![]() $u$ and
$u$ and ![]() $e$ given by (3.1) and (3.2) to yield the nonlinear resonance equation (3.13).
$e$ given by (3.1) and (3.2) to yield the nonlinear resonance equation (3.13).
The first nonlinear correction to the linear characteristics found by a geometric acoustics expansion is for the ![]() $\alpha$-wave
$\alpha$-wave
see Mortell & Seymour (Reference Mortell and Seymour2017a), where ![]() $u$ and
$u$ and ![]() $e$ are given by (3.1) and (3.2) with
$e$ are given by (3.1) and (3.2) with ![]() $g(\beta )\equiv 0$, i.e. (3.6) is an
$g(\beta )\equiv 0$, i.e. (3.6) is an ![]() $\alpha$-simple wave. Then
$\alpha$-simple wave. Then
which integrates to the modulated simple wave result
where ![]() $\alpha =t$ on
$\alpha =t$ on ![]() $x=0$. We note that, for
$x=0$. We note that, for ![]() $a\geqslant 0.2$,
$a\geqslant 0.2$, ![]() $(({\gamma +1})/{2a})\ln {(1+ax)}\gg {ax}/({1+ax})$. Similarly for a
$(({\gamma +1})/{2a})\ln {(1+ax)}\gg {ax}/({1+ax})$. Similarly for a ![]() $\beta$-simple wave
$\beta$-simple wave
 \begin{align} \left. \frac{\partial t}{\partial x} \right|_{\beta } &={-}\left[1+u-\frac{\gamma -1}{2}e+\dots\right] \nonumber\\ &={-}1-\frac{1}{1+ax}\frac{\gamma +1}{2}g(\beta )+\frac{a}{(1+ax)^{2}}G(\beta ), \end{align}
\begin{align} \left. \frac{\partial t}{\partial x} \right|_{\beta } &={-}\left[1+u-\frac{\gamma -1}{2}e+\dots\right] \nonumber\\ &={-}1-\frac{1}{1+ax}\frac{\gamma +1}{2}g(\beta )+\frac{a}{(1+ax)^{2}}G(\beta ), \end{align}
with ![]() $f(\alpha )\equiv 0$. Then (3.9) integrates to
$f(\alpha )\equiv 0$. Then (3.9) integrates to
where ![]() $\beta =t$ on
$\beta =t$ on ![]() $x=1$ and
$x=1$ and ![]() $\ell ={a}/({1+a})$. Now a
$\ell ={a}/({1+a})$. Now a ![]() $\beta$-wave leaves
$\beta$-wave leaves ![]() $x=1$ at
$x=1$ at ![]() $t=t_{0}$, reaches
$t=t_{0}$, reaches ![]() $x=0$ at
$x=0$ at ![]() $t=t_{1}$ and is reflected as an
$t=t_{1}$ and is reflected as an ![]() $\alpha$-wave to arrive back at
$\alpha$-wave to arrive back at ![]() $x=0$ at
$x=0$ at ![]() $t=t_{2}$. Then (3.8) and (3.10), when added, give the nonlinear travel time
$t=t_{2}$. Then (3.8) and (3.10), when added, give the nonlinear travel time
and using the ![]() $O(1)$ and
$O(1)$ and ![]() $O(a)$ terms in (3.4) the result is
$O(a)$ terms in (3.4) the result is
on using the periodicity of ![]() $G(t)$. This is the nonlinear travel time that includes the first correction to the linear travel time
$G(t)$. This is the nonlinear travel time that includes the first correction to the linear travel time ![]() $2$. To nonlinearize the linear resonance equation (3.5) we replace the difference 2 (the linear travel time) by the right-hand side of (3.12) and expand in a Taylor series. The end result is
$2$. To nonlinearize the linear resonance equation (3.5) we replace the difference 2 (the linear travel time) by the right-hand side of (3.12) and expand in a Taylor series. The end result is
when terms at ![]() $O(\ell ^{2})$ are neglected. This is the nonlinear resonance equation.
$O(\ell ^{2})$ are neglected. This is the nonlinear resonance equation.
For ![]() $\ell =0$, (3.13) becomes
$\ell =0$, (3.13) becomes
which is the first term in a nonlinear geometric acoustics expansion (NLGA). The periodic solution to (3.14) is
 \begin{equation} g(t)={\pm} \left[ \frac{4a(1+a)M}{{\rm \pi} (\gamma +1)\ln {(1+a)}}\right] ^{{1}/{2}}\sin {\left( \frac{{\rm \pi} }{2}t\right) }. \end{equation}
\begin{equation} g(t)={\pm} \left[ \frac{4a(1+a)M}{{\rm \pi} (\gamma +1)\ln {(1+a)}}\right] ^{{1}/{2}}\sin {\left( \frac{{\rm \pi} }{2}t\right) }. \end{equation}
When ![]() $a=\ell =0$, (3.13) becomes
$a=\ell =0$, (3.13) becomes
with solutions, on letting ![]() $a\rightarrow 0$ in (3.15),
$a\rightarrow 0$ in (3.15),
 \begin{equation} g(t)={\pm} \left[ \frac{4M}{{\rm \pi} (\gamma +1)}\right] ^{{1}/{2}}\sin {\left( \frac{{\rm \pi} }{2}t\right) }, \end{equation}
\begin{equation} g(t)={\pm} \left[ \frac{4M}{{\rm \pi} (\gamma +1)}\right] ^{{1}/{2}}\sin {\left( \frac{{\rm \pi} }{2}t\right) }, \end{equation}which is the result in Chester (Reference Chester1964) for a straight tube. Equation (3.13) may be seen as the result of a corrected, or augmented, nonlinear geometric acoustics expansion.
Figure 2 provides a comparison of the NLGA approximations (3.15) with the solutions obtained by direct numerical simulation for increasing geometric effects ![]() $a$. The agreement is good for
$a$. The agreement is good for ![]() $0\leqslant a\leqslant 0.15$. However, at
$0\leqslant a\leqslant 0.15$. However, at ![]() $a=0.15$ we notice small discrepancies due to the impact of higher-order geometric terms. Figure 3 provides a comparison of solutions of the augmented equation (3.13) for the NLGA approximation with direct numerical solution for increasing
$a=0.15$ we notice small discrepancies due to the impact of higher-order geometric terms. Figure 3 provides a comparison of solutions of the augmented equation (3.13) for the NLGA approximation with direct numerical solution for increasing ![]() $a$. The approximation is reasonable for
$a$. The approximation is reasonable for ![]() $0\leqslant a\leqslant 0.2$, and, in particular captures the asymmetry of the numerical solution. To quantify further, table 1 provides the 2-norm errors in each case relative to the fully numerical solutions and table 2 shows the asymmetry induced by (3.13).
$0\leqslant a\leqslant 0.2$, and, in particular captures the asymmetry of the numerical solution. To quantify further, table 1 provides the 2-norm errors in each case relative to the fully numerical solutions and table 2 shows the asymmetry induced by (3.13).

Figure 2. Comparison of approximate solutions based on (3.15) (dashed lines) vs direct numerical simulation (solid) for ![]() $M=1.25\times 10^{-4}$ and (a)
$M=1.25\times 10^{-4}$ and (a) ![]() $a=0.05$, (b)
$a=0.05$, (b) ![]() $a=0.1$, (c)
$a=0.1$, (c) ![]() $a=0.15$, (d)
$a=0.15$, (d) ![]() $a=0.2$.
$a=0.2$.

Figure 3. Comparison of approximate solutions based on (3.13) (dashed lines) vs direct numerical simulation (solid) for ![]() $M=1.25\times 10^{-4}$ and (a)
$M=1.25\times 10^{-4}$ and (a) ![]() $a=0.05$, (b)
$a=0.05$, (b) ![]() $a=0.1$, (c)
$a=0.1$, (c) ![]() $a=0.15$, (d)
$a=0.15$, (d) ![]() $a=0.2$.
$a=0.2$.
Table 1. Relative 2-norm errors for approximations using (3.15), ![]() $\ell =0$ and (3.13),
$\ell =0$ and (3.13), ![]() $\ell >0$, for
$\ell >0$, for ![]() $M=1.25\times 10^{-4}$.
$M=1.25\times 10^{-4}$.

Table 2. Values of ![]() $u(0.5,t)$ on left-hand (
$u(0.5,t)$ on left-hand (![]() $u_l$) and right-hand (
$u_l$) and right-hand (![]() $u_r$) sides of upper continuous interval using approximation (3.13), with
$u_r$) sides of upper continuous interval using approximation (3.13), with ![]() $M=1.25\times 10^{-4}$.
$M=1.25\times 10^{-4}$.

For the case ![]() $s(x)=(1+ax)^{-2}$ Keller (Reference Keller1977) found an approximate solution for the nonlinear problem by using Chester's (Reference Chester1964) technique. Using the nonlinearization technique with
$s(x)=(1+ax)^{-2}$ Keller (Reference Keller1977) found an approximate solution for the nonlinear problem by using Chester's (Reference Chester1964) technique. Using the nonlinearization technique with ![]() $\ell =0$, for this case we find
$\ell =0$, for this case we find
 \begin{equation} g(t)={\pm} \left[ \frac{8M}{{\rm \pi} (1+a)(2+a)(\gamma +1)}\right] ^{{1}/{2}}\sin {\left( \frac{{\rm \pi} }{2}t\right) }. \end{equation}
\begin{equation} g(t)={\pm} \left[ \frac{8M}{{\rm \pi} (1+a)(2+a)(\gamma +1)}\right] ^{{1}/{2}}\sin {\left( \frac{{\rm \pi} }{2}t\right) }. \end{equation}
Chester's (Reference Chester1964) result for a straight tube follows by setting ![]() $a=0$, see (3.17).
$a=0$, see (3.17).
3.1. Damped oscillations
Damping is introduced by an impedance condition at ![]() $x=0$,
$x=0$,
where ![]() $i$ is the impedance of the interface and energy radiates out of the system through the end
$i$ is the impedance of the interface and energy radiates out of the system through the end ![]() $x=0$. We show that, even at resonance, a continuous solution is possible for sufficiently large damping.
$x=0$. We show that, even at resonance, a continuous solution is possible for sufficiently large damping.
On ![]() $x=0$, the condition (3.19) is
$x=0$, the condition (3.19) is
with ![]() $k=({1-i})/({1+i})$, where
$k=({1-i})/({1+i})$, where ![]() $F(t)$ and
$F(t)$ and ![]() $G(t)$ are defined through
$G(t)$ are defined through ![]() $u(x,t)$ and
$u(x,t)$ and ![]() $e(x,t)$ given by (3.1) and (3.2). On
$e(x,t)$ given by (3.1) and (3.2). On ![]() $x=1$, the forced condition is still (3.4). Then, following the same procedure as (3.4) to (3.5), the final result to
$x=1$, the forced condition is still (3.4). Then, following the same procedure as (3.4) to (3.5), the final result to ![]() $O(a^{2})$ is
$O(a^{2})$ is
 \begin{align} &(1+k)G^{\prime }-k(1-k)\hat{A}\left[ G^{\prime }G^{\prime \prime }+\ell (G^{\prime 2}\right] -(1-k)^{2}\hat{A}\frac{ia}{1+i}(G^{\prime 2})+\ell k(1-k)GG^{\prime \prime } \nonumber\\ &\quad -\ell (1-k)G+(1-k)\frac{ia}{1+i}G =M(1+a)\sin {({\rm \pi} t)}, \end{align}
\begin{align} &(1+k)G^{\prime }-k(1-k)\hat{A}\left[ G^{\prime }G^{\prime \prime }+\ell (G^{\prime 2}\right] -(1-k)^{2}\hat{A}\frac{ia}{1+i}(G^{\prime 2})+\ell k(1-k)GG^{\prime \prime } \nonumber\\ &\quad -\ell (1-k)G+(1-k)\frac{ia}{1+i}G =M(1+a)\sin {({\rm \pi} t)}, \end{align}
where ![]() $\hat {A}=(({\gamma +1})/{2a})\ln {(1+a)}$. We note that when
$\hat {A}=(({\gamma +1})/{2a})\ln {(1+a)}$. We note that when ![]() $k=-1$, i.e. no damping
$k=-1$, i.e. no damping ![]() $i\rightarrow \infty$, and given that
$i\rightarrow \infty$, and given that ![]() $\ell -a=O(a^{2})$ (3.21) reduces to (3.13) and (3.20) reduces to (3.4). If
$\ell -a=O(a^{2})$ (3.21) reduces to (3.13) and (3.20) reduces to (3.4). If ![]() $\ell =0$ then (3.21) gives the damped version of NLGA. When
$\ell =0$ then (3.21) gives the damped version of NLGA. When ![]() $k=-1$,
$k=-1$, ![]() $\ell =0$,
$\ell =0$, ![]() $0< a\ll 1$, the undamped NLGA equation (3.14) is recovered. Figure 4(a) shows the continuous solution that arises for
$0< a\ll 1$, the undamped NLGA equation (3.14) is recovered. Figure 4(a) shows the continuous solution that arises for ![]() $i=30$, which is essentially sinusoidal. This is further evidenced by the close agreement with the associated linear solution determined in the same way as in § 2.1 with the boundary condition modified accordingly. The damping at the boundary
$i=30$, which is essentially sinusoidal. This is further evidenced by the close agreement with the associated linear solution determined in the same way as in § 2.1 with the boundary condition modified accordingly. The damping at the boundary ![]() $x=0$ attenuates the signal periodically and prevents a shock from forming when
$x=0$ attenuates the signal periodically and prevents a shock from forming when ![]() $i=30.$ Thus damping can eliminate the shock even at resonance. An example of this is given in Seymour & Mortell (Reference Seymour and Mortell1973) and in the experiments of Sturtevant (Reference Sturtevant1974) by having a hole in the end of the tube. As
$i=30.$ Thus damping can eliminate the shock even at resonance. An example of this is given in Seymour & Mortell (Reference Seymour and Mortell1973) and in the experiments of Sturtevant (Reference Sturtevant1974) by having a hole in the end of the tube. As ![]() $i$ is increased to
$i$ is increased to ![]() $50$, or equivalently damping decreases beyond a critical value, the solution becomes shocked. Finally for
$50$, or equivalently damping decreases beyond a critical value, the solution becomes shocked. Finally for ![]() $i=100$ figure 4 shows the increased separation of the corresponding separatrices, in analogy to figure 2 of Seymour & Mortell (Reference Seymour and Mortell1973) for the case where no geometric variation is present.
$i=100$ figure 4 shows the increased separation of the corresponding separatrices, in analogy to figure 2 of Seymour & Mortell (Reference Seymour and Mortell1973) for the case where no geometric variation is present.
3.2. Resonant band
The range of frequencies around the resonant frequency for which the solution contains shocks is called the resonant band. Equation (3.13) is essentially the NLGA result with the correction at ![]() $O(\ell )$ included, but is only valid exactly at resonance when
$O(\ell )$ included, but is only valid exactly at resonance when ![]() $\omega =1/2$. To calculate the solution for frequencies in the resonant band we will confine ourselves to (3.15) – the NLGA when
$\omega =1/2$. To calculate the solution for frequencies in the resonant band we will confine ourselves to (3.15) – the NLGA when ![]() $\ell =0$ in (3.13).
$\ell =0$ in (3.13).
It is convenient to rescale the independent time variable with ![]() $\omega$ so that
$\omega$ so that ![]() $g(s)$ has unit period in
$g(s)$ has unit period in ![]() $s$. The corresponding nonlinear difference equation, equivalent to (3.5) with (3.12), is derived by following a wave leaving
$s$. The corresponding nonlinear difference equation, equivalent to (3.5) with (3.12), is derived by following a wave leaving ![]() $x=1$ at time
$x=1$ at time ![]() $r$, with amplitude
$r$, with amplitude ![]() $g(r)=\bar {G}(\omega r)$, through a full cycle and arriving back at
$g(r)=\bar {G}(\omega r)$, through a full cycle and arriving back at ![]() $x=1$ at time
$x=1$ at time ![]() $t$. Close to resonance the nonlinear difference equation then has the form
$t$. Close to resonance the nonlinear difference equation then has the form
where ![]() $y=\omega t,z=\omega r,$
$y=\omega t,z=\omega r,$ ![]() $N=-({\gamma +1})/{2},$
$N=-({\gamma +1})/{2},$ ![]() $M(a)=[s(1)]^{{1}/{2}}M=(1+a)M$ and
$M(a)=[s(1)]^{{1}/{2}}M=(1+a)M$ and ![]() $K(a)=A_{2}(0,a)-A_{1}(1,a)$ with
$K(a)=A_{2}(0,a)-A_{1}(1,a)$ with
 \begin{align} A_{1}(x,a)&=\int_{0}^{x}[s(r)]^{-{1}/{2}}\,{\rm d}r=\frac{1}{a}\ln {(1+ax)},\nonumber\\ A_{2}(x,a)&=\int_{1}^{x}[s(r)]^{-{1}/{2}}\,{\rm d}r=\frac{1}{a}\ln {\left( \frac{1+ax}{1+a}\right) }, \end{align}
\begin{align} A_{1}(x,a)&=\int_{0}^{x}[s(r)]^{-{1}/{2}}\,{\rm d}r=\frac{1}{a}\ln {(1+ax)},\nonumber\\ A_{2}(x,a)&=\int_{1}^{x}[s(r)]^{-{1}/{2}}\,{\rm d}r=\frac{1}{a}\ln {\left( \frac{1+ax}{1+a}\right) }, \end{align}
so that ![]() $K(a)=-({2}/{a})\ln {(1+a)}$.
$K(a)=-({2}/{a})\ln {(1+a)}$.
The off-resonant frequencies are given in terms of the detuning parameter ![]() $\varDelta$ by
$\varDelta$ by
Defining ![]() $\bar {M}(a)=\frac {1}{2}NK(a)M(a)$ and
$\bar {M}(a)=\frac {1}{2}NK(a)M(a)$ and ![]() $G(y)$ by
$G(y)$ by
(3.22a,b) become
on using unit periodicity of ![]() $G$. Assuming
$G$. Assuming ![]() $|G|\ll 1$ and
$|G|\ll 1$ and ![]() $|G^{\prime }|\ll 1$, (3.26a,b) reduces to
$|G^{\prime }|\ll 1$, (3.26a,b) reduces to
and the mean condition requires
Following the analysis in Seymour & Mortell (Reference Seymour and Mortell1973) we find the resonant band is given by ![]() $\varDelta ^{-}<\varDelta <\varDelta ^{+}$ where
$\varDelta ^{-}<\varDelta <\varDelta ^{+}$ where
 \begin{equation} \varDelta ^{{\pm} }={\pm} \left( \frac{2}{{\rm \pi} }\right) ^{{3}/{2}}[\bar{M}(a)]^{{1}/{2}}. \end{equation}
\begin{equation} \varDelta ^{{\pm} }={\pm} \left( \frac{2}{{\rm \pi} }\right) ^{{3}/{2}}[\bar{M}(a)]^{{1}/{2}}. \end{equation}
The solution ![]() $G(y)$ is given by
$G(y)$ is given by
 \begin{equation} G(y)=\left\{\begin{array}{@{}ll} Z^{+}(y), & 0\leqslant y< y_{s}, \\ Z^{-}(y), & y_{s}< y\leqslant 1, \end{array} \right. \end{equation}
\begin{equation} G(y)=\left\{\begin{array}{@{}ll} Z^{+}(y), & 0\leqslant y< y_{s}, \\ Z^{-}(y), & y_{s}< y\leqslant 1, \end{array} \right. \end{equation}where
 \begin{equation} Z^{{\pm} }(y)={\pm} \left[ \frac{2\bar{M}(a)}{{\rm \pi} }\right] ^{{1}/{2}}\sin {({\rm \pi} y)}. \end{equation}
\begin{equation} Z^{{\pm} }(y)={\pm} \left[ \frac{2\bar{M}(a)}{{\rm \pi} }\right] ^{{1}/{2}}\sin {({\rm \pi} y)}. \end{equation}
Now ![]() $y=y_{s}$ is the position of the shock and is determined by the mean condition (3.28) and uniqueness is guaranteed by the condition that the shock is compressive;
$y=y_{s}$ is the position of the shock and is determined by the mean condition (3.28) and uniqueness is guaranteed by the condition that the shock is compressive; ![]() $\bar {M}(a)=(({(\gamma +1)(1+a)})/{2a})\ln {(1+a)}M$. The range of frequencies in
$\bar {M}(a)=(({(\gamma +1)(1+a)})/{2a})\ln {(1+a)}M$. The range of frequencies in ![]() $(\varDelta ^{-},\varDelta ^{+})$ is called the resonant band, and the solution
$(\varDelta ^{-},\varDelta ^{+})$ is called the resonant band, and the solution ![]() $u(x,t)$ is discontinuous in this interval. The slope is discontinuous at
$u(x,t)$ is discontinuous in this interval. The slope is discontinuous at ![]() $\varDelta ^{-}$ and
$\varDelta ^{-}$ and ![]() $\varDelta ^{+}$.
$\varDelta ^{+}$.
The continuous solution ![]() $\bar {G}_{e}^{\pm }$ at the edges of the resonant band
$\bar {G}_{e}^{\pm }$ at the edges of the resonant band ![]() $\varDelta ^{\pm }$ is given by
$\varDelta ^{\pm }$ is given by
so that
 \begin{equation} \bar{G}_{e}^{+}=\left[ \frac{2M(a)}{{\rm \pi} \omega NK(a)}\right] ^{{1}/{2}}\left[ \sin {({\rm \pi} y)}-\frac{2}{{\rm \pi} }\right] . \end{equation}
\begin{equation} \bar{G}_{e}^{+}=\left[ \frac{2M(a)}{{\rm \pi} \omega NK(a)}\right] ^{{1}/{2}}\left[ \sin {({\rm \pi} y)}-\frac{2}{{\rm \pi} }\right] . \end{equation}
When ![]() $a=0$,
$a=0$,
 \begin{equation} \bar{G}_{e}^{+}(y)=\left[ \frac{4M}{{\rm \pi} (\gamma +1)}\right] ^{{1}/{2}} \left[ \sin {({\rm \pi} y)}-\frac{2}{{\rm \pi} }\right] , \end{equation}
\begin{equation} \bar{G}_{e}^{+}(y)=\left[ \frac{4M}{{\rm \pi} (\gamma +1)}\right] ^{{1}/{2}} \left[ \sin {({\rm \pi} y)}-\frac{2}{{\rm \pi} }\right] , \end{equation}
on approximating ![]() $\omega =\frac {1}{2}(1+\varDelta )\doteqdot \frac {1}{2}$, since
$\omega =\frac {1}{2}(1+\varDelta )\doteqdot \frac {1}{2}$, since ![]() $|\varDelta |\ll 1$. This is the signal at the positive end of the resonant band
$|\varDelta |\ll 1$. This is the signal at the positive end of the resonant band ![]() $\varDelta =\varDelta ^{+}$ for the case of a closed straight tube. Figure 5(b) provides a comparison with direct numerical simulation at
$\varDelta =\varDelta ^{+}$ for the case of a closed straight tube. Figure 5(b) provides a comparison with direct numerical simulation at ![]() $\varDelta =\varDelta ^{+}$ for
$\varDelta =\varDelta ^{+}$ for ![]() $a=0.1$ and
$a=0.1$ and ![]() $M=1.25\times 10^{-4}$. Relative to the case where
$M=1.25\times 10^{-4}$. Relative to the case where ![]() $a=0$ shown in figure 5(a), while some small discrepancies appear near the extrema, the agreement remains quite good. However, for
$a=0$ shown in figure 5(a), while some small discrepancies appear near the extrema, the agreement remains quite good. However, for ![]() $a=0.2$ in figure 5(c), the geometric effects are now sufficiently large that (3.33) no longer offers a good approximation.
$a=0.2$ in figure 5(c), the geometric effects are now sufficiently large that (3.33) no longer offers a good approximation.

Figure 5. Comparison of approximate solutions based on (3.33) (dashed lines) vs direct numerical simulation (solid) for ![]() $M=1.25\times 10^{-4}$, at the edge of the resonant band
$M=1.25\times 10^{-4}$, at the edge of the resonant band ![]() $\varDelta =\varDelta ^{+}$ and for (a)
$\varDelta =\varDelta ^{+}$ and for (a) ![]() $a=0$, (b)
$a=0$, (b) ![]() $a=0.1$, (c)
$a=0.1$, (c) ![]() $a=0.2$.
$a=0.2$.
For ![]() $a=0$,
$a=0$, ![]() $\varDelta =0$ i.e. on resonance
$\varDelta =0$ i.e. on resonance ![]() $\omega =\frac {1}{2}$
$\omega =\frac {1}{2}$
 \begin{equation} \bar{G}^{+}(y)=\left[ \frac{4M}{{\rm \pi} (\gamma +1)}\right] ^{{1}/{2}}\sin {({\rm \pi} y)}, \end{equation}
\begin{equation} \bar{G}^{+}(y)=\left[ \frac{4M}{{\rm \pi} (\gamma +1)}\right] ^{{1}/{2}}\sin {({\rm \pi} y)}, \end{equation}which is Chester's (Reference Chester1964) solution for a straight tube.
4. Nonlinear dominant first mode solution for  $a=O(1)$
$a=O(1)$
When the slope of the cone is large the experiments of Lawrenson et al. (Reference Lawrenson, Lipkens, Lucas, Perkins and Van Doren1998) show that the resonant motion is continuous with amplitudes that ‘far exceed previously predicted and demonstrated values’. The overpressure amplitudes achieved are far greater than previously predicted. The authors describe RMS as ‘the deliberate shaping of a resonant acoustic waveform by designing the shape of the resonator to give the desired result’. …‘By controlling both harmonic phase and amplitude it is possible to synthesize a continuum of extremely high overpressures of unshocked waveforms’. This is the essential contrast with the situation when the slope ![]() $a\ll 1.$
$a\ll 1.$
The analytic procedure given in Mortell & Seymour (Reference Mortell and Seymour2004) does not depend on the resonator shape being a small deviation from cylindrical. When the modes are incommensurate, shocks will not form and the resultant motion is continuous, periodic and dominated by the lowest eigenmode with the resultant motion ![]() $O(M^{1/3})$.
$O(M^{1/3})$.
In this case
where ![]() $A$ is an unknown amplitude,
$A$ is an unknown amplitude, ![]() $\phi (x)$ is the fundamental eigenfunction on
$\phi (x)$ is the fundamental eigenfunction on ![]() $[0,1]$ of
$[0,1]$ of
given by
and ![]() $\lambda =\lambda _{1}$ is the smallest positive eigenvalue satisfying (2.14); see Mortell & Seymour (Reference Mortell and Seymour2004).
$\lambda =\lambda _{1}$ is the smallest positive eigenvalue satisfying (2.14); see Mortell & Seymour (Reference Mortell and Seymour2004).
The application of the Fredholm alternative at the third order in ![]() $M$ yields a cubic amplitude–frequency equation for
$M$ yields a cubic amplitude–frequency equation for ![]() $A$ of the form
$A$ of the form
where ![]() $N_{1}$ and
$N_{1}$ and ![]() $N_{2}$ are constants that depend on integrals of
$N_{2}$ are constants that depend on integrals of ![]() $s(x)$ and
$s(x)$ and ![]() $\phi (x)$ and
$\phi (x)$ and ![]() $\varDelta$ is a measure of the detuning (3.24). The details of this long calculation are given in Mortell & Seymour (Reference Mortell and Seymour2004).
$\varDelta$ is a measure of the detuning (3.24). The details of this long calculation are given in Mortell & Seymour (Reference Mortell and Seymour2004).
5. Transition from  $a=o(1)$ to
$a=o(1)$ to  $a=O(1)$
$a=O(1)$
As the value of ![]() $a$ is increases beyond the range where the nonlinear resonance equation (3.13) is valid, the nature of the resonance undergoes a fundamental shift. As noted earlier, the qualitative nature of the response depends intrinsically on the commensurate structure of the underlying linear eigenvalue spectrum arising from (2.14). Moreover, we see from (3.13) that for sufficiently small geometric variation the amplitude of the response scales as
$a$ is increases beyond the range where the nonlinear resonance equation (3.13) is valid, the nature of the resonance undergoes a fundamental shift. As noted earlier, the qualitative nature of the response depends intrinsically on the commensurate structure of the underlying linear eigenvalue spectrum arising from (2.14). Moreover, we see from (3.13) that for sufficiently small geometric variation the amplitude of the response scales as ![]() $O(M^{1/2})$. In this regime the spectrum can be seen to be sufficiently commensurate that solutions based around the limiting case where
$O(M^{1/2})$. In this regime the spectrum can be seen to be sufficiently commensurate that solutions based around the limiting case where ![]() $a=0$ provide a good approximation. Beyond this, however, lies a transition regime through which the spectrum becomes no longer sufficiently commensurate, and beyond a certain threshold the response becomes composed of a single mode, with amplitude scaling as
$a=0$ provide a good approximation. Beyond this, however, lies a transition regime through which the spectrum becomes no longer sufficiently commensurate, and beyond a certain threshold the response becomes composed of a single mode, with amplitude scaling as ![]() $O(M^{1/3})$, in accordance with the dominant first harmonic approximation (Mortell & Seymour Reference Mortell and Seymour2004).
$O(M^{1/3})$, in accordance with the dominant first harmonic approximation (Mortell & Seymour Reference Mortell and Seymour2004).
The variation in the fundamental nature of the response and the underlying scaling with respect to the forcing amplitude ![]() $M$ presents a distinct challenge. In the limit that the geometric effects are weak, Ellermeier (Reference Ellermeier1993) provided an analysis of the discontinuous solutions which arise in the case of a closed tube with variable cross-section forced at or near resonance. He also provided a condition under which these solutions are no longer valid, alluding to the single mode limit. However, the nature of the transition between these regimes was not discussed. Likewise, Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993) considered the case of a frustum of a spherical annulus which through a parametric transformation is analogous to a cone, see Seymour et al. (Reference Seymour, Mortell and Amundsen2011). However, here too no direct connection was made between the two distinct response regimes. Subsequently Chester (Reference Chester1994) also investigated the case of weak geometric effects in the context of closed tubes with varying cross section. He discussed the potential for extending the underlying expansions so as to account for stronger geometric variation and to provide a condition for which shock wave solutions are completely eliminated but no such condition was provided. Seymour et al. (Reference Seymour, Mortell and Amundsen2012) provided an estimate for the parametric range of the transition in the case of a spherical annulus and for a specific forcing amplitude. More recently Amundsen, Mortell & Seymour (Reference Amundsen, Mortell and Seymour2017) considered the analogous transition in the context of an open axisymmetric tube. In this case, because of the weaker commensurate structure, the limiting regimes arise at the same asymptotic order in terms of the underlying forcing amplitude. As such a variably truncated multiple mode expansion was used to capture solutions across the transition regime. Therefore, in this section we will study in detail the way in which the resonant response transitions between these limiting cases,
$M$ presents a distinct challenge. In the limit that the geometric effects are weak, Ellermeier (Reference Ellermeier1993) provided an analysis of the discontinuous solutions which arise in the case of a closed tube with variable cross-section forced at or near resonance. He also provided a condition under which these solutions are no longer valid, alluding to the single mode limit. However, the nature of the transition between these regimes was not discussed. Likewise, Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993) considered the case of a frustum of a spherical annulus which through a parametric transformation is analogous to a cone, see Seymour et al. (Reference Seymour, Mortell and Amundsen2011). However, here too no direct connection was made between the two distinct response regimes. Subsequently Chester (Reference Chester1994) also investigated the case of weak geometric effects in the context of closed tubes with varying cross section. He discussed the potential for extending the underlying expansions so as to account for stronger geometric variation and to provide a condition for which shock wave solutions are completely eliminated but no such condition was provided. Seymour et al. (Reference Seymour, Mortell and Amundsen2012) provided an estimate for the parametric range of the transition in the case of a spherical annulus and for a specific forcing amplitude. More recently Amundsen, Mortell & Seymour (Reference Amundsen, Mortell and Seymour2017) considered the analogous transition in the context of an open axisymmetric tube. In this case, because of the weaker commensurate structure, the limiting regimes arise at the same asymptotic order in terms of the underlying forcing amplitude. As such a variably truncated multiple mode expansion was used to capture solutions across the transition regime. Therefore, in this section we will study in detail the way in which the resonant response transitions between these limiting cases, ![]() $a \ll 1$ and
$a \ll 1$ and ![]() $a=O(1)$, and determine precisely how the various qualitatively distinct outcomes depend upon the underlying forcing and geometric effects.
$a=O(1)$, and determine precisely how the various qualitatively distinct outcomes depend upon the underlying forcing and geometric effects.
To build a fuller understanding and draw a connection between the distinct solution regimes, we consider numerically computed solutions across the full parametric range associated with the transition. We simulate the fully nonlinear governing equations (2.1) for motion of a gas in an Eulerian frame. Boundary conditions, as in (2.4a,b), are taken to be ![]() $u(0,t)=0$,
$u(0,t)=0$, ![]() $u(1,t)=M\sin (Wt)$ and the geometric factor
$u(1,t)=M\sin (Wt)$ and the geometric factor ![]() $s(x)=(1+ax)^{2}$. We also note that, in the same way as Chester (Reference Chester1994), a small dissipative term is added to the momentum equation with parameter
$s(x)=(1+ax)^{2}$. We also note that, in the same way as Chester (Reference Chester1994), a small dissipative term is added to the momentum equation with parameter ![]() $\nu$. This is included to facilitate convergence to a steady periodic state while not appreciably impacting the form of the resonant response. From a physical standpoint this is equivalent to a uniformly imposed impedance throughout the domain and is in turn analogous to one imposed at the boundary with parameters chosen accordingly. The numerical computation is then carried out using an adaptive finite volume based approach (LeVeque Reference LeVeque2002) starting at the underlying unforced equilibrium state.
$\nu$. This is included to facilitate convergence to a steady periodic state while not appreciably impacting the form of the resonant response. From a physical standpoint this is equivalent to a uniformly imposed impedance throughout the domain and is in turn analogous to one imposed at the boundary with parameters chosen accordingly. The numerical computation is then carried out using an adaptive finite volume based approach (LeVeque Reference LeVeque2002) starting at the underlying unforced equilibrium state.
Figure 6 shows the sequence of periodic response profiles which arise as ![]() $a$ is varied for two distinct forcing amplitudes. In both cases for
$a$ is varied for two distinct forcing amplitudes. In both cases for ![]() $a=0$ we recover the well-known shocked solution associated with the closed tube (Chester Reference Chester1964). While, at the other extreme, (shown in blue) the discontinuity is no longer present and we recover the dominant first harmonic response. In between these extremes lies a progression of shocked solutions (in black) which transition to multi-modal continuous solutions (in red) before resulting in the single mode response. This then implies the existence of a critical geometric parameter value
$a=0$ we recover the well-known shocked solution associated with the closed tube (Chester Reference Chester1964). While, at the other extreme, (shown in blue) the discontinuity is no longer present and we recover the dominant first harmonic response. In between these extremes lies a progression of shocked solutions (in black) which transition to multi-modal continuous solutions (in red) before resulting in the single mode response. This then implies the existence of a critical geometric parameter value ![]() $a_{s}(M)$ with discontinuous, shocked, solutions to one side and continuous, multiple mode, solutions to the other. Likewise, within the continuous regime a second critical parameter value
$a_{s}(M)$ with discontinuous, shocked, solutions to one side and continuous, multiple mode, solutions to the other. Likewise, within the continuous regime a second critical parameter value ![]() $a_{m}(M)$ exists delineating the interface between multiple mode and single mode responses, as in figure 7.
$a_{m}(M)$ exists delineating the interface between multiple mode and single mode responses, as in figure 7.

Figure 6. Deformation of resonant profiles ![]() $u(0.5,t)$ for
$u(0.5,t)$ for ![]() $t\in [0,2]$ for increasing geometric parameter
$t\in [0,2]$ for increasing geometric parameter ![]() $a$, (a)
$a$, (a) ![]() $M=1.5625 \times 10^{-5}$, (
$M=1.5625 \times 10^{-5}$, (![]() $\nu =1 \times 10^{-5}$) and (b)
$\nu =1 \times 10^{-5}$) and (b) ![]() $M=1.25 \times 10^{-4}$ (
$M=1.25 \times 10^{-4}$ (![]() $\nu =2 \times 10^{-5}$).
$\nu =2 \times 10^{-5}$).

Figure 7. Variation of qualitatively distinct resonant profiles in terms of forcing amplitude (![]() $M$) and geometric variation (
$M$) and geometric variation (![]() $a$).
$a$).
To investigate this further, figure 7 shows how the various qualitative types of responses vary with geometric and forcing effects. Within the shocked region (![]() $0\leqslant a< a_{s}$) the shock amplitude, scaled by
$0\leqslant a< a_{s}$) the shock amplitude, scaled by ![]() $M^{1/2}$, was found to serve as a good proxy for the profiles themselves and is represented by the black contour lines. The dashed curve corresponds to the transition where the shock amplitude goes to zero and the profiles become continuous. In terms of the geometric parameter this transition scales as
$M^{1/2}$, was found to serve as a good proxy for the profiles themselves and is represented by the black contour lines. The dashed curve corresponds to the transition where the shock amplitude goes to zero and the profiles become continuous. In terms of the geometric parameter this transition scales as ![]() $O(M^{1/3})$. This goes beyond but includes the range identified by Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993). Specifically, the transition lies at
$O(M^{1/3})$. This goes beyond but includes the range identified by Ockendon et al. (Reference Ockendon, Ockendon, Peake and Chester1993). Specifically, the transition lies at ![]() $a_{s}=C_{s}M^{1/3}$ where
$a_{s}=C_{s}M^{1/3}$ where ![]() $C_{s}\doteqdot 12.8$. This curve, as indicated by the black dashed curve, corresponds to the points where the amplitude of the shock goes to zero. With the increased accuracy and resolution of these calculations, we also see that the transition lies close to, but slightly beyond, the range predicted in Seymour et al. (Reference Seymour, Mortell and Amundsen2012) in the context of concentric spheres. For the multimodal solutions (
$C_{s}\doteqdot 12.8$. This curve, as indicated by the black dashed curve, corresponds to the points where the amplitude of the shock goes to zero. With the increased accuracy and resolution of these calculations, we also see that the transition lies close to, but slightly beyond, the range predicted in Seymour et al. (Reference Seymour, Mortell and Amundsen2012) in the context of concentric spheres. For the multimodal solutions (![]() $a_{s}\leqslant a< a_{m}$) the red contours show how the relative amplitudes of the dominant mode and its first harmonic decrease until eventually becoming effectively single mode, i.e. where the amplitude of the first harmonic is less than one per cent that of the fundamental mode, see figure 8. As indicated by the blue dashed curve, this transition occurs at
$a_{s}\leqslant a< a_{m}$) the red contours show how the relative amplitudes of the dominant mode and its first harmonic decrease until eventually becoming effectively single mode, i.e. where the amplitude of the first harmonic is less than one per cent that of the fundamental mode, see figure 8. As indicated by the blue dashed curve, this transition occurs at ![]() $a_{m}=C_{m}M^{1/3}$ where
$a_{m}=C_{m}M^{1/3}$ where ![]() $C_{m}\doteqdot 30$. Finally, the dominant first harmonic response emerges for
$C_{m}\doteqdot 30$. Finally, the dominant first harmonic response emerges for ![]() $a\geqslant a_{m}$ with amplitude scaling as
$a\geqslant a_{m}$ with amplitude scaling as ![]() $O(M^{1/3})$.
$O(M^{1/3})$.

Figure 8. Scaling of response ![]() $O(M^{\kappa })$ and relative modal amplitudes as
$O(M^{\kappa })$ and relative modal amplitudes as ![]() $a$ varies for
$a$ varies for ![]() $M=1.25\times 10^{-4}$.
$M=1.25\times 10^{-4}$.
In terms of the intensity of the response, we note in figure 6 that as the amplitude of the forcing varies, and taking into account the associated scaling in ![]() $a$, a qualitatively similar progression emerges. One key difference, however, lies in the amplitude of the single mode response relative to the shocked response. This in turn relates to the different scaling regimes present at each extreme. Taking a general scaling
$a$, a qualitatively similar progression emerges. One key difference, however, lies in the amplitude of the single mode response relative to the shocked response. This in turn relates to the different scaling regimes present at each extreme. Taking a general scaling ![]() $O(M^{\kappa })$, for
$O(M^{\kappa })$, for ![]() $a=0$ we expect
$a=0$ we expect ![]() $\kappa =1/2$ which then transitions to
$\kappa =1/2$ which then transitions to ![]() $\kappa =1/3$ for
$\kappa =1/3$ for ![]() $a$ sufficiently large corresponding to the single mode response regime. To illustrate in more detail how this transition occurs figure 8(a) shows the way in which the scaling
$a$ sufficiently large corresponding to the single mode response regime. To illustrate in more detail how this transition occurs figure 8(a) shows the way in which the scaling ![]() $\kappa$ varies with
$\kappa$ varies with ![]() $a$ for
$a$ for ![]() $M=1.25\times 10^{-4}$. For
$M=1.25\times 10^{-4}$. For ![]() $0\leqslant a\leqslant a_{s}(M)$ (indicated in black) the response remains near
$0\leqslant a\leqslant a_{s}(M)$ (indicated in black) the response remains near ![]() $\kappa =1/2$ with, interestingly, a slight plateau for moderately large values of
$\kappa =1/2$ with, interestingly, a slight plateau for moderately large values of ![]() $a$. Then for
$a$. Then for ![]() $a_{s}(M)\leqslant a\leqslant a_{m}(M)$ (indicated in red), corresponding to the multiple mode regime, the scaling now smoothly decreases, with an asymptotic approach to
$a_{s}(M)\leqslant a\leqslant a_{m}(M)$ (indicated in red), corresponding to the multiple mode regime, the scaling now smoothly decreases, with an asymptotic approach to ![]() $\kappa =1/3$ as the solution transitions to the single mode regime (indicated in blue). While the latter transition remains somewhat arbitrary, the beginning of the smooth decrease in scaling provides another clear interpretation for the transition from shocked to multiple mode solutions at
$\kappa =1/3$ as the solution transitions to the single mode regime (indicated in blue). While the latter transition remains somewhat arbitrary, the beginning of the smooth decrease in scaling provides another clear interpretation for the transition from shocked to multiple mode solutions at ![]() $a_{s}(M)$. And to further illustrate, figure 8(b) shows the way in which the amplitudes of the higher harmonics (denoted by
$a_{s}(M)$. And to further illustrate, figure 8(b) shows the way in which the amplitudes of the higher harmonics (denoted by ![]() $A_{n}$ for the
$A_{n}$ for the ![]() $n$’th mode) in the solutions vary with the geometric parameter
$n$’th mode) in the solutions vary with the geometric parameter ![]() $a$ relative to the dominant first harmonic mode (denoted by
$a$ relative to the dominant first harmonic mode (denoted by ![]() $A_{1}$). Moreover, table 3 provides the associated numerical values of the modal amplitudes for
$A_{1}$). Moreover, table 3 provides the associated numerical values of the modal amplitudes for ![]() $a=0$ and
$a=0$ and ![]() $a=2$, further quantifying the attenuation of the higher modes. We see that within the shocked regime these modes play a significant role with relative amplitudes remaining largely constant. Then as the geometric effects increase, we observe a decay as the higher modal contributions begin to successively drop off within the multiple mode regime. Then, once past the threshold associated with
$a=2$, further quantifying the attenuation of the higher modes. We see that within the shocked regime these modes play a significant role with relative amplitudes remaining largely constant. Then as the geometric effects increase, we observe a decay as the higher modal contributions begin to successively drop off within the multiple mode regime. Then, once past the threshold associated with ![]() $a_{m}(M),$ we arrive at a response which is effectively single mode. Taken together this further demonstrates the interplay between the response and the underlying modal structure.
$a_{m}(M),$ we arrive at a response which is effectively single mode. Taken together this further demonstrates the interplay between the response and the underlying modal structure.
Table 3. Amplitudes for first harmonic ![]() $A_1$ and higher harmonics for
$A_1$ and higher harmonics for ![]() $a=0,2$ and when
$a=0,2$ and when ![]() $M=1.25\times 10^{-4}$, quantitatively showing how the higher modes attenuate in these distinct limiting cases.
$M=1.25\times 10^{-4}$, quantitatively showing how the higher modes attenuate in these distinct limiting cases.

5.1. Geometry and detuning
As discussed in § 3.2, the augmented nonlinear geometric acoustics (aNLGA) approximation (3.13) extends both the leading-order NLGA approximation (as shown in table 1) and the range of validity of the approximation to larger values of the geometric parameter. We now explore this comparison more fully over a fuller range of values of geometric parameter ![]() $a$ and detuning parameter
$a$ and detuning parameter ![]() $\varDelta$.
$\varDelta$.
Figure 9 shows that the aNLGA approximation (3.13) provides a good approximation for values of ![]() $a$ near zero and
$a$ near zero and ![]() $\varDelta$ within the resonant band. The regions of agreement are indicated by the locations of the text labels, with corresponding boundaries in the same colour. We see that in the case where no geometric variation is present,
$\varDelta$ within the resonant band. The regions of agreement are indicated by the locations of the text labels, with corresponding boundaries in the same colour. We see that in the case where no geometric variation is present, ![]() $a=0$, the validity extends across the resonant band (as indicated by the dashed lines, (3.29)). On resonance the aNLGA region extends up to approximately
$a=0$, the validity extends across the resonant band (as indicated by the dashed lines, (3.29)). On resonance the aNLGA region extends up to approximately ![]() $a=0.2$, in accordance with what was observed in table 1 and figure 3.
$a=0.2$, in accordance with what was observed in table 1 and figure 3.

Figure 9. Regions in ![]() $a$ vs
$a$ vs ![]() $\varDelta$ where aNLGA (3.13), dominant first harmonic and exact linear approximations provide agreement to within
$\varDelta$ where aNLGA (3.13), dominant first harmonic and exact linear approximations provide agreement to within ![]() $5\,\%$ for
$5\,\%$ for ![]() $M=1.25 \times 10^{-4}$.
$M=1.25 \times 10^{-4}$.
For comparison we also show how, for larger values of geometric variation and detuning, the dominant first harmonic approximation, see Mortell & Seymour (Reference Mortell and Seymour2004), and the exact linear solution from § 2.1 compare. As expected, the former provides good approximation away from resonance for ![]() $a$ sufficiently large and across the entire detuning spectrum, corresponding to the incommensurate nature of the linear spectrum. For moderately large values of the geometric parameter (up to approximately
$a$ sufficiently large and across the entire detuning spectrum, corresponding to the incommensurate nature of the linear spectrum. For moderately large values of the geometric parameter (up to approximately ![]() $a=0.5$) we see that the approximation begins to break down due to the now increasingly incommensurate structure. And due to the underlying rightward bend of the resonant response curve, i.e. that the resonant amplitude increases with detuning, this region correspondingly skews right. Finally, we note that in a narrow band near
$a=0.5$) we see that the approximation begins to break down due to the now increasingly incommensurate structure. And due to the underlying rightward bend of the resonant response curve, i.e. that the resonant amplitude increases with detuning, this region correspondingly skews right. Finally, we note that in a narrow band near ![]() $a=0$ and across all values of detuning, the dominant first harmonic approximation breaks down. This relates to the fact that the detuning itself is taken to scale with the amplitude of the response and therefore cannot mitigate the effects of the fully commensurate spectrum at
$a=0$ and across all values of detuning, the dominant first harmonic approximation breaks down. This relates to the fact that the detuning itself is taken to scale with the amplitude of the response and therefore cannot mitigate the effects of the fully commensurate spectrum at ![]() $a=0$.
$a=0$.
In addition, the exact linear solution provides good agreement off resonance. We note also that this is largely independent of the geometric variation as would be expected given that it is fully incorporated. However, one interesting feature is the slight bulge for moderately large ![]() $a$. This suggests that up to a certain point it follows the widening of the resonant band itself, but then the geometric and nonlinear effects combine, and we return to a comparison that is largely independent of
$a$. This suggests that up to a certain point it follows the widening of the resonant band itself, but then the geometric and nonlinear effects combine, and we return to a comparison that is largely independent of ![]() $a$.
$a$.
6. Conclusion
When the slope ![]() $a$ of the frustum of a cone is
$a$ of the frustum of a cone is ![]() $o(1)$ then, using the superposition of oppositely travelling modulated simple waves, it can be shown that the resonant output at
$o(1)$ then, using the superposition of oppositely travelling modulated simple waves, it can be shown that the resonant output at ![]() $O(M^{1/2})$ for an input of
$O(M^{1/2})$ for an input of ![]() $O(M)$ contains shocks, see Amundsen et al. (Reference Amundsen, Mortell and Seymour2015). In contrast, when the slope
$O(M)$ contains shocks, see Amundsen et al. (Reference Amundsen, Mortell and Seymour2015). In contrast, when the slope ![]() $a$ is
$a$ is ![]() $O(1)$ the resonant output is
$O(1)$ the resonant output is ![]() $O(M^{1/3})$ for an input of
$O(M^{1/3})$ for an input of ![]() $O(M)$ and the signal is continuous, see Lawrenson et al. (Reference Lawrenson, Lipkens, Lucas, Perkins and Van Doren1998) for the experimental result and Mortell & Seymour (Reference Mortell and Seymour2004) for the analytical result, which is obtained as a dominant first harmonic approximation. The problem investigated here is how the motion transitions as
$O(M)$ and the signal is continuous, see Lawrenson et al. (Reference Lawrenson, Lipkens, Lucas, Perkins and Van Doren1998) for the experimental result and Mortell & Seymour (Reference Mortell and Seymour2004) for the analytical result, which is obtained as a dominant first harmonic approximation. The problem investigated here is how the motion transitions as ![]() $a$ changes from
$a$ changes from ![]() $o(1)$ to
$o(1)$ to ![]() $O(1)$. In particular, we are interested in the transition from shocked solutions to single mode continuous solutions.
$O(1)$. In particular, we are interested in the transition from shocked solutions to single mode continuous solutions.
The nonlinear equation (3.13) for ![]() $a=o(1)$ is derived for the first time using a nonlinearization technique, see Mortell & Seymour (Reference Mortell and Seymour2017b). Then it is found numerically that the shocked solutions at
$a=o(1)$ is derived for the first time using a nonlinearization technique, see Mortell & Seymour (Reference Mortell and Seymour2017b). Then it is found numerically that the shocked solutions at ![]() $o(1)$ transition first to a multimode continuous solution as
$o(1)$ transition first to a multimode continuous solution as ![]() $a$ crosses the curve
$a$ crosses the curve ![]() $a_{s}=C_{s}M^{1/3}$, where
$a_{s}=C_{s}M^{1/3}$, where ![]() $M$ is the Mach number of the input and
$M$ is the Mach number of the input and ![]() $C_{s}\doteqdot 12.8$. As
$C_{s}\doteqdot 12.8$. As ![]() $a$ increases further the number of modes required for a good approximation decreases until the transition curve
$a$ increases further the number of modes required for a good approximation decreases until the transition curve ![]() $a_{m}=C_{m}M^{1/3}$, where
$a_{m}=C_{m}M^{1/3}$, where ![]() $C_{m}\doteqdot 30$, after which the dominant first harmonic response emerges due to the Stokes interaction at third order.
$C_{m}\doteqdot 30$, after which the dominant first harmonic response emerges due to the Stokes interaction at third order.
In cases off resonance and where the spectrum is sufficiently commensurate, the augmented NLGA approximation (3.13) provides improved agreement within the resonant band. For sufficiently large geometric variation, and where the underlying spectrum is sufficiently incommensurate, the response follows a dominant first harmonic approximation. However, there remains an intermediate range where, near resonance, neither of these approaches nor the exact linear solution apply.
Funding
D.E.A. gratefully acknowledges support from the Natural Sciences and Engineering Research Council (NSERC) Discovery Grant 2019-06169. The authors also gratefully acknowledge the referees for their constructive and helpful feedback during the review process.
Declaration of interests
The authors report no conflict of interest.