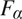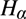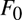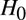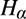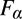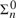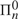Research Article
ABSOLUTE CONTRADICTION, DIALETHEISM, AND REVENGE
-
- Published online by Cambridge University Press:
- 25 February 2014, pp. 193-207
-
- Article
- Export citation
ON PATHOLOGICAL TRUTHS
-
- Published online by Cambridge University Press:
- 30 June 2014, pp. 601-617
-
- Article
- Export citation
SOME OBSERVATIONS ON TRUTH HIERARCHIES
-
- Published online by Cambridge University Press:
- 02 January 2014, pp. 1-30
-
- Article
- Export citation
WHAT IS THE CORRECT LOGIC OF NECESSITY, ACTUALITY AND APRIORITY?
-
- Published online by Cambridge University Press:
- 12 May 2014, pp. 385-414
-
- Article
- Export citation
THREE FORMS OF PHYSICAL MEASUREMENT AND THEIR COMPUTABILITY
-
- Published online by Cambridge University Press:
- 09 September 2014, pp. 618-646
-
- Article
- Export citation
PLACING PROBABILITIES OF CONDITIONALS IN CONTEXT
-
- Published online by Cambridge University Press:
- 28 May 2014, pp. 415-438
-
- Article
- Export citation
LOGICAL GROUNDS
-
- Published online by Cambridge University Press:
- 04 November 2013, pp. 31-59
-
- Article
- Export citation
THE EXPRESSIVITY OF FACTUAL CHANGE IN DYNAMIC EPISTEMIC LOGIC
-
- Published online by Cambridge University Press:
- 28 November 2013, pp. 208-221
-
- Article
- Export citation
BELIEF REVISION, PROBABILISM, AND LOGIC CHOICE
-
- Published online by Cambridge University Press:
- 09 September 2014, pp. 647-670
-
- Article
- Export citation
ON FLATTENING ELIMINATION RULES
-
- Published online by Cambridge University Press:
- 23 January 2014, pp. 60-72
-
- Article
- Export citation
QUANTIFIED MODAL LOGIC ON THE RATIONAL LINE
-
- Published online by Cambridge University Press:
- 12 May 2014, pp. 439-454
-
- Article
- Export citation
A SECOND PHILOSOPHY OF ARITHMETIC
-
- Published online by Cambridge University Press:
- 08 November 2013, pp. 222-249
-
- Article
- Export citation
SELF-REFERENCE IN ARITHMETIC I
-
- Published online by Cambridge University Press:
- 07 October 2014, pp. 671-691
-
- Article
- Export citation
UNIFORM INTERPOLATION IN SUBSTRUCTURAL LOGICS
-
- Published online by Cambridge University Press:
- 27 May 2014, pp. 455-483
-
- Article
- Export citation
AXIOMS FOR GROUNDED TRUTH
-
- Published online by Cambridge University Press:
- 30 October 2013, pp. 73-83
-
- Article
- Export citation
BILATERAL RELEVANT LOGIC
-
- Published online by Cambridge University Press:
- 16 April 2014, pp. 250-272
-
- Article
- Export citation
LOGICISM, INTERPRETABILITY, AND KNOWLEDGE OF ARITHMETIC
-
- Published online by Cambridge University Press:
- 14 February 2014, pp. 84-119
-
- Article
- Export citation
MODALITY AND AXIOMATIC THEORIES OF TRUTH I: FRIEDMAN-SHEARD
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 273-298
-
- Article
- Export citation
A MACHINE-ASSISTED PROOF OF GÖDEL’S INCOMPLETENESS THEOREMS FOR THE THEORY OF HEREDITARILY FINITE SETS
-
- Published online by Cambridge University Press:
- 03 April 2014, pp. 484-498
-
- Article
- Export citation
SELF-REFERENCE IN ARITHMETIC II
-
- Published online by Cambridge University Press:
- 07 October 2014, pp. 692-712
-
- Article
- Export citation