Published online by Cambridge University Press: 02 January 2014
We show how in the hierarchies 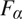 ${F_\alpha }$ of Fieldian truth sets, and Herzberger’s
${F_\alpha }$ of Fieldian truth sets, and Herzberger’s 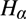 ${H_\alpha }$ revision sequence starting from any hypothesis for
${H_\alpha }$ revision sequence starting from any hypothesis for 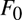 ${F_0}$ (or
${F_0}$ (or 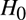 ${H_0}$) that essentially each
${H_0}$) that essentially each 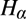 ${H_\alpha }$ (or
${H_\alpha }$ (or  ${F_\alpha }$) carries within it a history of the whole prior revision process.
${F_\alpha }$) carries within it a history of the whole prior revision process.
As applications (1) we provide a precise representation for, and a calculation of the length of, possible path independent determinateness hierarchies of Field’s (2003) construction with a binary conditional operator. (2) We demonstrate the existence of generalized liar sentences, that can be considered as diagonalizing past the determinateness hierarchies definable in Field’s recent models. The ‘defectiveness’ of such diagonal sentences necessarily cannot be classified by any of the determinateness predicates of the model. They are ‘ineffable liars’. We may consider them a response to the claim of Field (2003) that ‘the conditional can be used to show that the theory is not subject to “revenge problems”.’