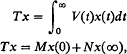Research Article
On compactification of mappings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 105-108
-
- Article
-
- You have access
- Export citation
The word problem for lattice ordered groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 217-219
-
- Article
-
- You have access
- Export citation
Summation and uncountable bi-orthogonal systems in locally convex spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-10
-
- Article
-
- You have access
- Export citation
Locally bounded spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 321-325
-
- Article
-
- You have access
- Export citation
On bounded sequences satisfying a linear inequality
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 11-16
-
- Article
-
- You have access
- Export citation
Inequalities concerning the inverses of positive definite matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 109-113
-
- Article
-
- You have access
- Export citation
Automorphisms of transformation semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 327-329
-
- Article
-
- You have access
- Export citation
Some results involving weak compactness in C(X), C(υX) and C(X)′
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 221-229
-
- Article
-
- You have access
- Export citation
Outer automorphisms of ordered permutation groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 331-344
-
- Article
-
- You have access
- Export citation
Some cyclic inequalities
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 115-118
-
- Article
-
- You have access
- Export citation
Spectra of irreducible matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 231-236
-
- Article
-
- You have access
- Export citation
A note on free inverse semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 17-23
-
- Article
-
- You have access
- Export citation
Near-rings of quotients of endomorphism near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 345-352
-
- Article
-
- You have access
- Export citation
A class of finite groups with zero deficiency
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 25-29
-
- Article
-
- You have access
- Export citation
The fundamental groupoid as a topological groupoid
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 237-244
-
- Article
-
- You have access
- Export citation
An application of a theorem of Singer
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 119-123
-
- Article
-
- You have access
- Export citation
On supports of semigroups of measures
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-33
-
- Article
-
- You have access
- Export citation
A boundary value problem on an infinite interval
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 245-252
-
- Article
-
- You have access
- Export citation
Some algebraic properties of F(X) and K(X)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 353-361
-
- Article
-
- You have access
- Export citation
Topological convexity spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 125-132
-
- Article
-
- You have access
- Export citation


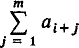 with the convention that
with the convention that 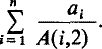 . Although it is by no means best possible, see (
. Although it is by no means best possible, see (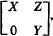
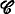 be a category with finite products and a final object and let
be a category with finite products and a final object and let 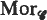 (
(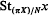 which is the fibre of the initial point map ∂′: (π
which is the fibre of the initial point map ∂′: (π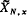 of
of  , of type
, of type  is absolutely continuous (where
is absolutely continuous (where  is the adjoint of μ) and the
is the adjoint of μ) and the  where supp μ is the support of μ ∈
where supp μ is the support of μ ∈