Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T01:34:29.218Z Has data issue: false hasContentIssue false
  • English
  • Français

A boundary value problem on an infinite interval

Published online by Cambridge University Press:  20 January 2009

Athanassios G. Kartsatos
Athanassios G. Kartsatos
Affiliation:
University of South Florida, Tampa, Florida 33620
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are interested here in proving the existence of solutions to the (generalised) boundary value problem

where A is a continuous n×n matrix on R+ = [0, ∞), F is a continuous n vector on R+ × S (S = a suitable subset of Rn), T is a bounded linear operator defined on (or on a subspace of) C[R+, Rn], the space of all bounded and continuous Rn-valued functions on R+, and r is a fixed vector in Rn. There is an abundance of papers dealing with the problem ((I), (II)) on finite intervals, either in its full generality (cf., for example, (1), (2), (3), (4), (6)), or for special cases of the operator T. The reader is especially referred to the work of Shreve (7), (8) for such problems on infinite intervals for scalar equations. A series representation of the solutions is given by Kravchenko and Yablonskii (5). Most of our methods are extensions of the corresponding ones on finite intervals with some variations concerning the application of fixed-point theorems. Examples of interesting operators T are

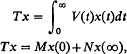
where V(t), M, N are n×n matrices with V(t) integrable.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 3 , March 1975 , pp. 245 - 252
Copyright
Copyright © Edinburgh Mathematical Society 1975

References

REFERENCES

(1) Avramescu, C., Sur l'éxistence des solutions pour un problème aux limites général, Ann. Mat. Pura ed Appl. 82 (1962), 69–81.CrossRefGoogle Scholar
(2) Corduneanu, C., Problèmes aux limites lineaires, Ann. Mat. Pura ed. Appl. 68 (1966), 65–73.CrossRefGoogle Scholar
(3) Esukov, L. N., On a functional problem for ordinary differential equations, Uspehi Mat. Nauk 13 (1958), 191–196.Google Scholar
(4) Kartsatos, A. G., Nonzero solutions to boundary value problems for nonlinear systems, Pacific J. Math., (to appear).Google Scholar
(5) Kravchenko, T. K. and Yablonskii, A. I., Solution of an infinite boundary value problem for a third order equation, Differentsial'nye Uravnenija 1 (1965), 327–329.Google Scholar
(6)Opial, Z., Linear problems for systems of nonlinear differential equations, J. Diff. Equations 3 (1967), 580–594.CrossRefGoogle Scholar
(7)Shreve, W. E., Boundary value problem for y″ = f(x,y,λ) on ⌈a,∞), SIAM J. Appl. Math. 17 (1969), 84–97.CrossRefGoogle Scholar
(8)Shreve, W. E., Terminal value problems for second order nonlinear differential equations, SIAM J. Appl. Math. 18 (1970), 783–791.CrossRefGoogle Scholar