Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T10:34:27.962Z Has data issue: false hasContentIssue false
  • English
  • Français

The fundamental groupoid as a topological groupoid

Published online by Cambridge University Press:  20 January 2009

R. Brown  and
G. Danesh-Naruie
R. Brown
Affiliation:
School of Mathematics and Computer Science, University College of North Wales, Bangor, Gwynedd. U.K.
G. Danesh-Naruie
Affiliation:
Daneshsaraye-Ali, Roozvelt Ave., Tehran, Iran
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a topological space. Then we may define the fundamental groupoid πX and also the quotient groupoid (πX)/N for N any wide, totally disconnected, normal subgroupoid N of πX (1). The purpose of this note is to show that if X is locally path-connected and semi-locally 1-connected, then the topology of X determines a “lifted topology” on (πX)/N so that it becomes a topological groupoid over X. 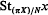With this topology the subspace which is the fibre of the initial point map ∂′: (πX)/N→X over x in X, is the usual covering space 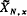of X determined by the normal subgroup N{x} of the fundamental group π(X, x).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 3 , March 1975 , pp. 237 - 244
Copyright
Copyright © Edinburgh Mathematical Society 1975

References

REFERENCES

(1) Brown, R., Elements of Modern Topology (McGraw-Hill, Maidenhead, 1968).Google Scholar
(2) Brown, R., Fibrations of groupoids, J. Algebra 15 (1970), 103–32.CrossRefGoogle Scholar
(3) Brown, R., Groupoids as coefficients, Proc. London Math. Soc. (3) 25 (1972), 413–426.CrossRefGoogle Scholar
(4) Danesh-Naruie, G., Topological groupoids, Ph.D. Thesis, Southampton University (1970).Google Scholar
(5) Ehresmann, CH., Catégories topologiques et catégories differentiables, Coll. Geom. Diff. Glob. Bruxelles (1959).Google Scholar
(6) Hardy, J. P. L., Topological groupoids, M.A. Dissertation, University of Wales (1972).Google Scholar
(7) Maclane, S., Categories for the Working Mathematician (Springer-Verlag, Berlin, 1971).Google Scholar
(8) Rhodes, F., On the fundamental group of a transformation group, Proc. London Math. Soc. (3) 16 (1966), 635–650.CrossRefGoogle Scholar
(9) Rhodes, F., On lifting transformation groups, Proc. Amer. Math. Soc. 19 (1968), 905–908.CrossRefGoogle Scholar
(10) Brown, R., Danesh-Naruk, G., Hardy, J. P. L., Topological groupoids II: covering morphisms and G-spaces, Math. Nachr. (to appear).Google Scholar