No CrossRef data available.
Article contents
Some cyclic inequalities
Published online by Cambridge University Press: 20 January 2009
Extract
In this note we prove some cyclic inequalities which are generalisations of known results. We shall assume throughout that ai+n = ai ≧ 0 for all i, that no denominator in the statement of a result vanishes and finally that p, m and q are positive integers. We shall also use A(i, m) to denote 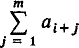 with the convention that A(i, 0) = 0. The most interesting of our results is probably Theorem 2 since, in the special case p = 1, m = 2, r = 0, it gives a lower bound of ⅓n for the Shapiro sum
with the convention that A(i, 0) = 0. The most interesting of our results is probably Theorem 2 since, in the special case p = 1, m = 2, r = 0, it gives a lower bound of ⅓n for the Shapiro sum 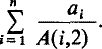 . Although it is by no means best possible, see (2), our method implicitly gives a really simple way of obtaining this lower bound which, incidentally, is an improvement on Rankin's original result (5).
. Although it is by no means best possible, see (2), our method implicitly gives a really simple way of obtaining this lower bound which, incidentally, is an improvement on Rankin's original result (5).
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 2 , September 1974 , pp. 115 - 118
- Copyright
- Copyright © Edinburgh Mathematical Society 1974


