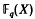It is shown that a ring R is a π-regular ring with no infinite trivial subring if and only if R is a subdirect sum of a strongly regular ring and a finite ring. Some other characterizations of such a ring are given. Similar result is proved for a periodic ring. As a corollary, it is shown that every δ-ring is a subdirect sum of a Unite ring and a commutative ring. This was conjectured by Putcha and Yaqub.

A study is made of the length L(h, k) of the continued fraction algorithm for h/k where h and k are co-prime polynomials in a finite field. In addition we investigate the sum of the degrees of the partial quotients in this expansion for h/k, h, k in . The above continued fraction is determined by means of the Euclidean algorithm for the polynomials h, k in .

Some properties of polynomials associated with strong distribution functions are given, including conditions for the polynomials to satisfy a three term recurrence relation. Strong distributions that are extensions to the four classical distributions are given as examples.

The class of prime Noetherian v-H orders is a class of Noetherian prime rings including the commutative integrally closed Noetherian domains, and the hereditary Noetherian prime rings, and designed to mimic the latter at the level of height one primes. We continue recent work on the structure of indecomposable injective modules over Noetherian rings by describing the structure of such a module E over a prime Noetherian v-H order R in the case where the assassinator P of E is a reflexive prime ideal. This description is then applied to a problem in torsion theory, so generalising work of Beck, Chamarie and Fossum.

By a divisibility semigroup we mean an algebra (S,., ∧) satisfying (Al) (S,.) is a semigroup; (A2) (S, ∧) is a semilattice; (A3) .

A divisibility semigroup is called representable if it admits a subdirect decomposition into totally ordered factors.

In this paper various types of representable divisibility semigroups are investigated and characterized, admitting a representation in general or even a special decomposition, like subdirect sums of archimedean factors, for instance.

Let X be an infinite set and S be a transformation semigroup on X invariant under conjugations by permutations of X. Such S is termed x-normal. In the paper, we describe elements of a x-normal semigroup S of one-to-one transformations.

In this paper we investigate totally geodesic surfaces in hyperbolic 3-manifolds. In particular we show that if M is a compact arithmetic hyperbolic 3-manifold containing an immersion of a totally geodesic surface then it contains infinitely many commensurability classes of such surfaces. In addition we show for these M that the Chern-Simons invariant is rational.

We also show, that unlike the figure-eight knot complement in S3, many knot complements in S3 do not contain an immersion of a closed totally geodesic surface.

We characterize regular bisimple rings in terms of some perspectivity conditions on their lattices of principal right ideals. We also show that, if S is the multiplicative subsemigroup generated by all the idempotents of a regular bisimple ring R, then

(i) if R does not have an identity, then S = R and has depth 2;

(ii) if R does have an identity but is not a division ring, then S = {a∈R:a is neither left nor right invertible} ∪ {1} and has depth 3.

An essentially bounded function on the unit circle gives a continuous linear functional on the Hardy space H1. In this paper we study when there exists at least one function which attains its norm. We apply the results to an interpolation problem, Hankel operators and a characterization of exposed points of the closed unit ball of H1.

It is known that for certain rings R (for example R = ℤ, the ring of rational integers) the group GL2(R) contains subnormal subgroups which have free, non-abelian quotients. When such a subgroup has finite index it follows that every countable group is embeddable in a quotient of GL2(R). (In this case GL2(R) is said to be SQ-universal.) In this note we prove that the existence of subnormal subgroups of GL2(R) with this property is a phenomenon peculiar to “n = 2”.

For a large class of rings (which includes all commutative rings) it is shown that, for all , no subnormal subgroup of En(R) has a free, non-abelian quotient, when n≧3. (En(R) is the subgroup of GLn(R) generated by the elementary matrices.) In addition it is proved that, if is an SRt-ring, for some t ≧ 2, then no subnormal subgroup of GLn(R) has a free, non-abelian quotient, when n ≧ max (t, 3). From the above these results are best possible since ℤ is an SR3 ring.

For a fixed integer q≧2, every positive integer k = Σr≧0ar(q, k)qr where each ar(q, k)∈{0,1,2,…, q−1}. The sum of digits function α(q, k) Σr≧0ar(q, k) behaves rather erratically but on averaging has a uniform behaviour. In particular if , where n>1, then it is well known that A(q, n)∼½((q − 1)/log q)n logn as n → ∞. For odd values of q, a lower bound is now obtained for the difference 2S(q, n) = A(q, n)−½(q − 1))[log n/log q, where [log n/log q] denotes the greatest integer ≦log n /log q. This complements an upper bound already found.

Conditions are given on two maximal monotone (multivalued) operators A and B which ensure that A + B is also maximal. One condition used is that ∥Bx∥≦k(∥x∥)Ax| +d|(A + B)x| + c(∥x∥) for every x∈D(A)⊆D(B), where 0≦k(r)<1, and c(r)≧0 are nondecreasing functions, and 0≦d≦1 is a constant. Here, for a set C, |C| denotes inf{∥y∥:y∈C}. This extends the well known result which has d = 0 (and is used in the proof here). The second part of the paper uses similar hypotheses to give conditions under which the range of the sum, R(A + B), has the same interior and same closure as the sum of the ranges, R(A) + R(B).

Let E be an injective module over the commutative Noetherian ring A, and let a be an ideal of A. The A-module (0:Eα) has a secondary representation, and the finite set AttA(0:Eα) of its attached prime ideals can be formed. One of the main results of this note is that the sequence of sets (AttA(0:Eαn))n∈N is ultimately constant. This result is analogous to a theorem of M. Brodmann that, if M is a finitely generated A-module, then the sequence of sets (AssA(M/αnM))n∈N is ultimately constant.

A module M is called a CC-module if every closed submodule of M is cyclic. It is shown that a cyclic module M is a direct sum of indecomposable submodules if all quotients of cyclic submodules of M are CC-modules. This theorem generalizes a recent result of B. L. Osofsky and P. F. Smith on cyclic completely CS-modules. Some further applications are given for cyclic modules which are decomposed into projectives and injectives.