Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:59:03.151Z Has data issue: false hasContentIssue false
  • English
  • Français

Representable divisibility semigroups

Published online by Cambridge University Press:  20 January 2009

Bruno Bosbach
Bruno Bosbach
Affiliation:
Fachbereich 17, MathematikGesamthochschule/Universität3500 Kassel, West Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a divisibility semigroup we mean an algebra (S,., ∧) satisfying (Al) (S,.) is a semigroup; (A2) (S, ∧) is a semilattice; (A3) .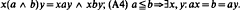

A divisibility semigroup is called representable if it admits a subdirect decomposition into totally ordered factors.

In this paper various types of representable divisibility semigroups are investigated and characterized, admitting a representation in general or even a special decomposition, like subdirect sums of archimedean factors, for instance.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 1 , February 1991 , pp. 45 - 64
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

REFERENCES

1.Bigard, A. and Eimel, K. K., Groupes et Anneaux Réticulés (Springer, Berlin-Göttingen-Heidelberg-New York, 1977).CrossRefGoogle Scholar
2.Bosbach, B., Schwache Teilbarkeitshalbgruppen, Semigroup Forum 12 (1976), 119–135.CrossRefGoogle Scholar
3.Bosbach, B., Archimedische Teilbarkeitshalbgruppen und Quader-Algebren, Semigroup Forum 20 (1980), 319–334.CrossRefGoogle Scholar
4.Bosbach, B., Lattice ordered binary systems, Acta. Sci. Math. 52 (1988), 257–289.Google Scholar
5.Bosbach, B., Teilbarkeitshalbgruppen mit vollständiger Erweiterung, J. Algebra 83 (1983), 237–255.CrossRefGoogle Scholar
6.Byrd, R. D., Lattice ordered groups (Thesis, Tulane University 1966).Google Scholar
7.Clifford, A. H., Naturally totally ordered commutative semigroups, Amer. J. Math. 76 (1954), 631–646.CrossRefGoogle Scholar
8.Conrad, P. F., Some structure theorems for lattice-ordered groups, Trans. Amer. Math. Soc. 99 (1961), 212–240.CrossRefGoogle Scholar
9.Conrad, P. F., Lattice ordered groups (Tulane University, Dpt. Math. 1970).Google Scholar
10.Fuchs, L., Teilweise geordnete algebraische Strukturen (Vandenhoeck und Ruprecht in Göttingen, 1966).Google Scholar
11.Fuchs, L., On partially ordered algebras I. Coll. Math. 13 (1966), 116–130.Google Scholar
12.Fuchs, L., A remark on lattice ordered semigroups, Semigroup Forum 7 (1974), 372–374.CrossRefGoogle Scholar
13.Hölder, O., Die Axiome der Quantität und die Lehre vom MaB. Sächs. Ges. Wiss., Math. Phys. Cl. 53 (1901), 1–64.Google Scholar
14.Jaffard, P., Contribution à l'étude des groupes ordonnés. J. Math. Pure Appl. 32 (1953), 203–280.Google Scholar
15.Lorenzen, P., Über halbgeordnete Gruppen, Math. Z. 52 (1949), 483–526.CrossRefGoogle Scholar
16.Repnitzkiì, V. B., On subdirectly irreducible lattice-ordered semigroups. Semigroup Forum 29 (1984), 277–318.CrossRefGoogle Scholar
17.Repnitzkiì, V. B., Varieties of lattice ordered semigroups (Diss. Cand., Acad. of Sc. of Moldavia, Kichinew 1984).Google Scholar
18.Šik, F., Über subdirekte Summen geordneter Gruppen. Czechoslovak Math. J. 10 (1960), 400–424.CrossRefGoogle Scholar