Research Article
On compactification of mappings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 105-108
-
- Article
-
- You have access
- Export citation
Inequalities concerning the inverses of positive definite matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 109-113
-
- Article
-
- You have access
- Export citation
Some cyclic inequalities
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 115-118
-
- Article
-
- You have access
- Export citation
An application of a theorem of Singer
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 119-123
-
- Article
-
- You have access
- Export citation
Topological convexity spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 125-132
-
- Article
-
- You have access
- Export citation
l-simple lattice-ordered groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 133-138
-
- Article
-
- You have access
- Export citation
On rings with quasi-injective cyclic modules
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 139-145
-
- Article
-
- You have access
- Export citation
Measurable selections in normed spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 147-150
-
- Article
-
- You have access
- Export citation
Basic sequences in F-spaces and their applications
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-167
-
- Article
-
- You have access
- Export citation
A completeness theorem for a nonlinear problem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 169-172
-
- Article
-
- You have access
- Export citation
Representations of normed algebras with minimal left ideals
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 173-190
-
- Article
-
- You have access
- Export citation
Functions and equations in classes of distributive lattices with pseudocomplementation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 191-203
-
- Article
-
- You have access
- Export citation
On the mean convergence of Markov operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 205-209
-
- Article
-
- You have access
- Export citation
Book Reviews
Irwin Kra, Automorphic Forms and Kleinian Groups (Benjamin, 1972),xiv+464 pp.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 211
-
- Article
-
- You have access
- Export citation
Allan M. Krall, Linear Methods of Applied Analysis (Addison-Wesley/Benjamin, Reading, Massachusetts, 1973), $16.00 (cloth), $9.50 (soft cover).
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 211-212
-
- Article
-
- You have access
- Export citation
Yau-Chuen Wong and Kung-Fu Ng, Partially Ordered Topological Vector Spaces (Clarendon Press, Oxford, 1973), ix+217 pp.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 212
-
- Article
-
- You have access
- Export citation
H. Cabannes and R. Temam (Eds) Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics1972, Volumes I and II (Springer-Verlag, Berlin).
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 213
-
- Article
-
- You have access
- Export citation
J. Milnor and D. Husemoller Symmetric Bilinear forms (Ergebnisse der Mathematik und ihrer Grenzgebiete Bd. 73, Springer-Verlag, 1973), ii+146 pp., $13.40.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 214
-
- Article
-
- You have access
- Export citation
J. D. Pryce Basic Methods of Linear Functional Analysis (Hutchinson, 1973), 320 pp., £4·00 cased, £2·25 paper.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 214-215
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 19 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation

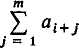 with the convention that
with the convention that 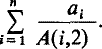 . Although it is by no means best possible, see (
. Although it is by no means best possible, see (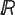 , of type
, of type 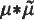 is absolutely continuous (where
is absolutely continuous (where 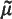 is the adjoint of μ) and the
is the adjoint of μ) and the 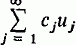 where
where 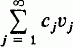 by means of a unique sequence {
by means of a unique sequence {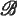 (
(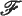 (
(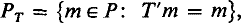 , where
, where